Play all audios:
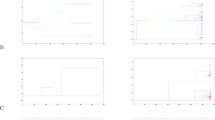
The genealogical properties of a small population with continuous overlapping generations that fluctuates randomly in size are studied using a model based on a stochastic birth–death
process. The distribution of the coalescence times is presented, as well as a method for computing the expected overall length of the genealogy as a function of the individual birth rate λ,
the individual death rate µ, and the present population size. The relationship between the birth and death rates and the shape of the resulting genealogy is studied. The total length of the
genealogy is shown to be maximized when λ = µ. The joint distribution of the coalescence times is shown to be invariant in λ and µ, conditional on the current population size, so that
exponential growth of a population cannot be distinguished from exponential decline based on the shape of the resulting genealogy. The model is used to predict the probability that all
genetic variation is lost from a recent founder population.
Anyone you share the following link with will be able to read this content:
