ABSTRACT We conducted controlled crosses in populations of the long-lived clonal shrub, _Vaccinium angustifolium_ (lowbush blueberry) to estimate inbreeding depression and mutation

parameters associated with somatic deleterious mutation. Inbreeding depression level was high, with many plants failing to set fruit after self-pollination. We also compared fruit set from

autogamous pollinations (pollen collected from within the same inflorescence) with fruit set from geitonogamous pollinations (pollen collected from the same plant but from inflorescences

separated by several meters of branch growth). The difference between geitonogamous versus autogamous fitness within single plants is referred to as ‘autogamy depression’ (AD). AD can be

within the crowns of the plants studied. We conclude that somatic mutation in this woody plant results in an overall genomic deleterious mutation rate that exceeds the rate measured to date

for annual plants. Some implications of this result for evolutionary biology and agriculture are discussed. SIMILAR CONTENT BEING VIEWED BY OTHERS ABSENCE OF LONG-TERM BALANCING SELECTION ON

VARIATION IN _EUMYB3_, AN _R2R3-MYB_ GENE RESPONSIBLE FOR THE ANTHER-COLOR POLYMORPHISM IN _ERYTHRONIUM UMBILICATUM_ Article Open access 04 March 2024 MATING SYSTEM AND POPULATION STRUCTURE

IN THE NATURAL DISTRIBUTION OF _TOONA CILIATA_ (MELIACEAE) IN SOUTH CHINA Article Open access 12 October 2020 OUTCROSSING RATES IN AN EXPERIMENTALLY ADMIXED POPULATION OF SELF-COMPATIBLE

AND SELF-INCOMPATIBLE _ARABIDOPSIS LYRATA_ Article Open access 16 December 2021 INTRODUCTION Plants violate the Weismann’s doctrine of the separation of germ line and soma (Weismann, 1893).

Although in theory, this means that mutations can be passed from the soma to gametes, it is unclear how often mutations occur in somatic tissue during plant development, and whether and by

how much intra-organismal selection filters out cells bearing such mutations before they are passed onto gametes (Otto and Orive, 1995). Somatic mutation and somatic selection are postulated

to have important roles in plant evolution through their influence on total mutational load and plant defense (Whitham and Slobodchikoff, 1981; Antolin and Strobeck, 1985; Klekowski, 1988;

Gill et al., 1995; Otto and Hastings, 1998). Despite frequent discussion of somatic mutation and selection in the plant evolutionary literature, published measurements of the magnitude of

these processes are virtually nonexistent. This lack of information stems in part from the difficulty inherent in studying mutation and selection within the soma. It is also attributable to

the fact that genomic mutation is an infrequent process, resulting in individual mutations whose effects are typically small and difficult to detect in reasonably sized experiments. Such

obstacles are familiar to those who have attempted to estimate mutation rates from phenotypic data in mutation accumulation experiments (Drake et al., 1998). In addition to the difficulties

noted above, questions remain about the number of somatic cell divisions that arise between formation of the zygote and establishment of the plant germ line, an issue that is difficult to

resolve without detailed knowledge of how plant meristems divide to produce additional stem cells and somatic tissue (Klekowski et al., 1985; Pineda-Krch and Lehtila, 2002). In some plant

species, it has been estimated that there are fewer than a hundred somatic cell divisions, separating zygote formation from gamete formation, whereas, in others, there may be many thousands

of such divisions. The actual number is difficult to determine with accuracy (Otto and Walbot, 1990; Cloutier et al., 2003; Scofield, 2006). In the case of long-lived plants, it has been

argued that because of the large numbers of somatic cell divisions separating zygote from gamete formation, significant numbers of somatic mutations in theory can accumulate within the cell

lineages that eventually differentiate into gametogenic tissue, and that this, in turn, should lead to a higher overall per-generation rate of mutation than observed in annual plants

(Klekowski, 1988). For instance, Klekowski and Godfrey (1989) estimated that rates of chlorophyll deficiency-causing mutation per generation are 25 times higher in mangrove trees than in the

annual plants barley and buckwheat. The focus of this paper is on the rate of deleterious somatic mutation. Deleterious mutations may influence patterns of evolution and are also of concern

in conservation biology (Kondrashov, 1988; Lynch and Gabriel, 1990; Schoen et al., 1998). For instance, deleterious somatic mutation may have a central role in mating system evolution. As a

group, trees and shrubs are known to exhibit a higher rate of outcrossing than annual plants (Barrett et al., 1996). Scofield and Schultz (2006) suggested that this correlation of mating

system and life history reflects evolved responses of the mating system to inbreeding depression levels. Specifically, they proposed that higher per-generation deleterious mutation rates

arising as a consequence of somatic mutation accumulation in long-lived plants should lead to higher equilibrium levels of inbreeding depression compared with those in annual plants, and

that this has favored the evolution of reproductive traits that enforce outcrossing (for example, self-incompatibility, dioecy). Data from the literature on the relationship between

inbreeding depression levels and selfing rates support this idea. The hypothesis is further supported by models of mating system modifier selection in annual and perennial plants, that have

shown that high rates of mitotic mutation promote the evolution of outcrossing in perennials (Morgan, 2001). Rates of somatic mutation have been estimated by direct assay of marker locus

genotypes in long-lived plants (for example, Cloutier _et al._, 2003; O’Connell and Ritland, 2004), but the fitness consequences of marker mutations are difficult to determine. In contrast,

a more direct approach involves assaying the phenotypic effects of somatic mutation by measuring fitness of progeny (or gametophytes) produced by different portions of the plant (Schultz and

Scofield, 2009). For instance, in a detailed study of the consequences of aging in the clonally spreading tree species _Populus tremuloides_, Ally et al. (2010) found that pollen grain

viability decreased with plant age, an effect that they attributed to somatic mutation accumulation, though this hypothesis was not directly tested. Schultz and Scofield (2009) formalized

methods for estimating the contribution of somatic mutation accumulation to the overall per-generation rate of deleterious mutation. One method, the so-called ‘autogamy depression (AD)

test’, compares the fitness of progeny derived by within-flower self-fertilization to that derived by between-flower self-fertilization (that is, progeny fitness following autogamy versus

geitonogamy). AD can be defined as 1−(_w_a/_w_g), where _w_a is the fitness of progeny derived via autogamy and _w__g_ is the fitness of progeny derived via geitonogamy (in parallel with the

definition of inbreeding depression), or alternatively, as _D_=_w_g−_w_a, the definition we use in the present study. AD is a direct outcome of the somatic mutational process, given that

certain conditions hold. First, in diploid organisms it is expected that three-quarters of progeny produced via autogamous pollination will inherit a _de novo_ somatic mutation one-half the

time as heterozygotes and one-quarter the time as homozygotes (Schultz and Scofield, 2009), whereas, progeny produced via geitonogamy will only bear such mutations in a heterozygous state.

Second, if the inherited somatic mutations are not expressed in the tissues of the crown that differentiate into meiocytes, then somatic selection will be ineffective at removing mutations

from the cell lineages that give rise to gametes. Third, if the somatic mutations are deleterious and recessive (or partially recessive), and expressed in the progeny, then AD should become

manifest. Although appropriate experimental designs to assess rates of somatic mutation in plants have now been described (Schultz and Scofield, 2009), there have been no studies published

to date that employ these methods to estimate somatic mutation parameters. In this study, we present measurements of inbreeding depression obtained from the clonal woody plant, _Vaccinium.

angustifolium_ (lowbush blueberry). The pollinations and fitness assays conducted were first used to assess overall levels of early-acting inbreeding depression. In a separate experiment, we

applied pollination treatments required to obtain measurements of AD. We derive a maximum-likelihood approach for estimating somatic mutation parameters from AD data, and use the data

obtained from experiments with _V. angustifolium_ to estimate somatic mutation parameters. MATERIALS AND METHODS TARGET SPECIES AND STUDY SITE _V. angustifolium_ is a clonal woody plant that

spreads through a system of underground rhizomes. Separate genotypes within the same population often differ in leaf morphology as well as leaf and flower color, and clones can often be

distinguished from one another in the field. The work reported here was conducted in commercial blueberry fields in the region around Neguac, New Brunswick, Canada. _V. angustifolium_ occurs

as an understory plant in the forests of the region, and commercial blueberry fields are established by clearing the forest and encouraging growth of the blueberry plants. The blueberry

clones in these fields were established from naturally occurring plants over 100 years ago, and many clones are large, covering more than 20 m2 in surface area. Hokanson and Hancock (1993)

studied inheritance in _V. angustifolium._ On the basis of several crosses, they were unable to distinguish with certainty between tetrasomic and disomic modes of inheritance. Accordingly,

we base our conclusions on the possibility that either mode of inheritance could apply to this species. ESTIMATION OF EARLY-ACTING INBREEDING DEPRESSION Pollinations were carried out in the

summer of 2011 to determine the level of early-acting inbreeding depression in lowbush blueberry plants. Twenty-four blueberry fields were selected. Twelve blueberry clones per field were

selected at 5 m intervals along 60 m transects. Inflorescences used for pollination were identified and labeled when flowers were in bud. Pollinations were conducted with inflorescences that

were bagged prior to anthesis and kept in bags until flowers senesced. In inflorescences selected for autogamous pollination, pollen was collected into sterile tubes and then applied to

stigmas with a fine paintbrush, cleaned with 70% ethanol between pollinations. Outcrossed pollinations were conducted using a similar procedure, but with pollen from clones located at least

5 m away. Flower counts and pollinations were conducted a minimum of three times per inflorescence during the flowering season. It has been previously shown that the closely related

blueberry species, _V. corymbosum_ (highbush blueberry), exhibits early-acting inbreeding depression, manifested as a high rate of fruit abortion following selfing. We therefore used percent

fruit set per inflorescence as the fitness measure for estimating inbreeding depression. Percent fruit set was calculated by counting the number of flowers pollinated per inflorescence and

comparing that value to the number of mature berries later in the season. Inbreeding depression (_∂_) was calculated using the formula _∂_=1−(_W_s_/W_o) (CharlesworthCharlesworth and

Charlesworth, 1987), where _W_s represents percent fruit set in self-pollinated inflorescences and _W_o represents percent fruit in outcross-pollinated inflorescences. CLONE IDENTIFICATION

FOR THE AD TEST In 2012, separate (putative) clones from one field were selected for the pollination treatments. These clones ranged in size from 9 to 30 m2 in surface area. For each clone,

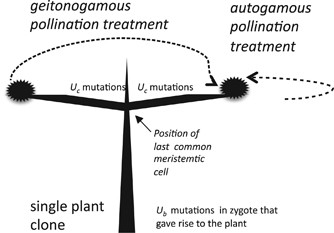
20 paired autogamous and geitonogamous pollinations (Figure 1) were conducted. The physical limits of each putative clone were initially determined from observations on homogeneity of growth

form (upright or spreading branches), leaf pigmentation (green or red-purple, anthocyanin-rich) and timing of leaf development (early in season or late), together with the presence of bare

ground or other species of plants between blueberry stems. Each putative clone was then genotyped at two highly polymorphic microsatellite loci by sampling leaf tissue from four widely

spaced edges of the clone. Leaf samples subtended the infloresences used in the controlled pollinations. Genomic DNA was extracted separately from each leaf sample using a QIAcube robot and

spin column kits (DNAeasy Plant Mini prep) with the appropriate preloaded standard plant DNA extraction protocol (Qiagen, Valencia, CA, USA). The two variable microsatellite loci used (CA

344F and CA 794F) are described in Boches et al. (2005) and primer sequences also are listed in that publication. PCR reactions were carried out in a final volume of 10 μl. The reaction

mixture consisted of 2 μl of DNA solution, 5 U μl−1 of Taq DNA polymerase, 1 μl of 10 × PCR buffer, 10 mM of dNTP mix, 2.5 mM MgCl2, 2 μM M13 Forward primer, 2 μM M13 5′-IRDye-labeled

forward primer (at 700 nm). The cycling program consisted of 300 s of initial denaturation at 94 °C and 25 cycles of 95 °C for 40 s, 61 °C for 40 s and 72 °C for 40 s. This was followed by

15 cycles of 94 °C for 40 s, 53 °C for 40 s and 72 °C for 40 s, with a final single cycle of 71 °C for 600 s. Microsatellite genotypes were determined using the LI-COR NEN Model 4300 DNA

analyzer and the SAGA software package (LI-COR Biosciences, Lincoln, NE, USA). Allelic richness at the microsatellite loci was high, and each of the 20 putative clones selected possessed a

multilocus genotype that was unique to the sample. The initial assignment of ramets, as belonging to a specific clone based on morphology and plant spacing alone, was verified in 19 out of

the 20 cases by genotypes obtained at the marker loci—that is, all four of the leaf samples collected from each of the 20 putative clones exhibited the same unique and diagnostic multilocus

marker genotypes. In the case of the one remaining clone, one out of the four leaf samples was shown to exhibit a multilocus genotype that differed from that of the other three leaf samples.

Although this could be due to a somatic microsatellite mutation, we opted to be conservative and not consider data from pollinations conducted with inflorescences in that portion of the

clone. POLLINATIONS FOR THE AD TEST Our implementation of the AD test involved pollinations made with inflorescences pairs, either close together on the same branch or widely separated, but

within the same clone. The inflorescences used for geitonogamous pollinations were typically separated by several meters of branch growth, and thus could acquire non-shared somatic mutations

(Figure 1). For the purpose of the AD test, all within-branch inflorescence pair pollinations were treated as ‘autogamous’, whereas all between-branch inflorescence pair pollinations were

treated as ‘geitonogamous’. Although this implementation of the AD test does not adhere to the strict botanical definition of autogamy and geitonogamy, it does, nevertheless, lead to

contrast between treatments in the expected incidence of homozygosity of somatic mutations, and was the only practical way in which to proceed. We refer below to such a pair of pollinations

as an ‘autogamous–geitonogamous’ crossing pair. As in the case of the inbreeding depression measurements, inflorescences were identified, labeled and bagged prior to and during the flowering

period. Upon flowering, inflorescences selected for the autogamous pollination treatment were pollinated with pollen collected from a within-branch inflorescence pair, placed in sterile

tubes and then applied to stigmas with a fine paintbrush. For geitonogamous pollinations, pollen was collected in sterile tubes from a distantly positioned inflorescence (an inflorescences

on an opposite side of the clone, as shown in Figure 1) and then applied to stigmas. FITNESS MEASURES FOR THE AD TEST As in the inbreeding depression study, percent fruit set per

inflorescence was used as the fitness measure, and so the data obtained pertain only to mutations that influence early survival. To obtain this information, flower counts and pollinations

were conducted every third or fourth day until senescence of all flowers occurred (early June). Bags were then removed. To minimize error in estimating percent fruit set due to fruit loss by

bird foraging, fruit set counts were obtained when the fruits were green, but fully developed in size (early August). A potential problem with the AD test when fruit set is the fitness

component is that fruits may fail to set for reasons not related to inbreeding depression. For example, problems with animal predation or the transfer of pollen could result in failed fruit

set. This could result in negative AD. We lost about half of our pollinated infloresences due to damage from animal predation, and discarded <10% of undamaged inflorescences due to

problems we encountered in transferring pollen between flowers. MAXIMUM-LIKELIHOOD ESTIMATION OF MUTATION PARAMETERS Somatic deleterious mutations influence both the mean and the variance of

fitness of progeny produced via autogamy and geitonogamy. Together the fitness difference (the measured AD) along with the (co-) variances in autogamous and geitonogamous fitnesses can

provide the information required to estimate mutation parameters, paralleling the classic Bateman–Mukai approach to estimating mutation parameters (Mukai, 1964; Schultz and Scofield, 2009).

Alternatively, a maximum-likelihood-based approach may be applied to estimate mutation parameters (Keightley, 1994), particularly when mutation rates are large and approximations based on

observed change in fitness and fitness variance breaks down—conditions that hold for the data collected in this study. We derived the likelihood function following the method of Keightley

(1994). For simplicity, we assume diploid inheritance. If inheritance in _V. angustifolium_ is actually tetrasomic rather than disomic, violation of this assumption would lead to an

underestimate of the somatic mutation rate, as the probability of autozygosity under tetrasomic inheritance is lower (Haldane, 1930). This is acceptable because our aim is to provide a

conservative estimate of the somatic mutation rate. Let _D_k denote the measured fitness difference between progeny produced in the _k_th autogamous–geitonogamous crossing pair. We assume

that there are _U_b deleterious ‘background’ mutations present in a heterozygous state in the zygoyte that gave rise to the plants where autogamously and geitonogamously produced progeny

were obtained. In addition, we assume that there are _U_c deleterious ‘crown’ mutations have occurred in the independent branches of this plant that bear the flowers used in the

geitonogamous crosses, and that arose since these branches last shared a common meristematic cell in the crown (Figure 1). The rate of crown mutation is assumed to be Poisson distributed

with mean _λ_=_U_c per branch. We note that it is also possible to formulate the model below using _λ_=_U_c per unit length of branch growth (rather than per branch), but we have opted not

to do so because we lacked precise information on the branch lengths. All mutations are assumed to have a constant additive effect on progeny fitness denoted by _s_, and to be expressed in

the progeny with dominance coefficient _h._ Moreover, we assume that these newly arising mutations do not experience somatic selection. Thus, our estimates apply to the class of mutations

with fitness effects that are not expressed during branch growth. Accordingly, we have: where and denote autogamous and geitonogamous fitnesses from the _k_th crossing pair, respectively,

and _j_ is a Poisson deviate with parameter _λ_=_U_c. We assume that environmental effects influencing autogamous and geitonogamous fitness (and their differences) are normally distributed

with variance _V_e. Thus, the likelihood associated with the autogamous fitness and AD measured from the _k_th autogamous–geitonogamous pair is: where _f_ is the Gaussian probability density

function, and _p_(_j_) is the Poisson probability that the branch in question has accumulated _j_ new (heterozygous) somatic mutations. Two other likelihoods were also used in estimating

the mutation parameters. These are: and Finally, we have the log likelihood of the intersection of each of the three quantities above: A four-step procedure was used to find mutation

parameters that maximized the likelihood of the data. First, a random grid search of the parameter space was performed, in which the Nelder–Mead downhill simplex method was applied to 15 000

random starting points satisfying 0<_h_<0.5, 0<_s_<1, 0<_U_c or _U_b<30, and 0<_V_e’s<0.5 (Nelder and Mead, 1965; Haag-Liautard). The resulting likelihood values

were used to find the maximum-likelihood estimates of the environmental variance parameters _V_e’s to construct the overall loess-interpolated likelihood surface and to construct the profile

likelihoods. Profile likelihoods are the projection of the multidimensional likelihood surface into the plane relating a particular mutational parameter to the log maximum likelihood of the

surface (Nocedal and Wright, 1999). Profile likelihoods were constructed for _U_c, _U_b, _U_c _s_, _h_, _hs_, and _s_. Second, the Nelder–Mead method was used to find the maximum-likelihood

estimates of _U_c, _U_b, _s_ and _h_ while holding the environmental variance components fixed at their maximum-likelihood values obtained from the grid search. The standard errors of these

estimates were obtained using the likelihood ratio method (Weir, 1996). Third, these results were checked and confirmed by two additional methods, the quasi-Newton or variable metric

algorithm developed by Broyden (1970, Fletcher (1970, Fletcher and Reeves (1964, Goldfarb (1970, Shanno and Kettler (1970) and Shanno (1970) (the Broyden-Fletcher-Goldfarb-Shanno algorithm

(BFGS)) and an intelligent grid search method (Heim, 2007; R Core Team, 2012), both of which gave results to within less than 1% of the values found by the Nelder–Mead method. Fourth, the

Nelder–Mead, BFGS and the intelligent grid search algorithms were each used separately to find the maximum-likelihood estimate of the product of _U_c and _s_, assuming fixed values of _h_

and _U_b that differed from their maximum-likelihood estimates to assess the sensitivity to the estimate of _U__c_ _s_ to variation in these parameter values. These methods again gave

results that differed from each other by less than one percent. All numerical optimization procedures were executed in R using the functions optim(), mle() and cleversearch() (Heim, 2007; R

Core Team, 2012). In theory, a more refined maximum-likelihood estimation procedure to estimate mutation parameters, one that entails a model with variable as opposed to constant mutation

effects, could be obtained by extending estimation along the lines described by Keightley (1994), in which mutational effects are assumed to be gamma distributed (with shape parameter-β,

scale parameter-α). But in view of the relatively modest-sized data set and the lower statistical power available for estimating additional parameters, we have opted not to do so here.

RESULTS INBREEDING AND AD The majority of the selfed plants showed low fruit set (mean=0.13±0.16) compared with the outcrossing treatment (mean=0.53±0.24). A Wilcoxon-signed rank test showed

that the difference was highly significant (_P_<0.0001). Consequently, inbreeding depression level is high in the populations studied with many values near 1 (Figure 2). Assuming diploid

inheritance and based on the approach by Morton et al. (1956), the estimate of the number of lethal equivalents per zygote (2_B_) is 2_B_=−4 ln(_W_s_/W_o)=2.41. Assuming tetrasomic

inheritance, in the absence of double reduction, autozygosity is approached at approximately one-third the rate compared with diploidy (Haldane, 1930). This leads to an estimate of numbers

of lethal equivalents per zygote (based on tetrasomy) of 2_B_=−12 ln(_W_s_/W_o)=7.22. AD was found to be approximately normally distributed with a mean value of 0.155 (95% confidence

intervals=0.106–0.204), and significantly different from 0 by a one-sample _t_-test (_t_=6.218, df=185, _P_<0.0025) (Figure 3). MUTATION PARAMETER ESTIMATES The maximum-likelihood profile

surface of _U_c against _s_ showed a prominent likelihood ridge corresponding to the product _U_c_s_∼2–3, suggesting strong support for 2–3 lethal equivalent mutations affecting fruit set

within the crown of our study plants (Figure 4a). This surface also showed very pronounced peaks for the individual mutation parameters, yielding strong maximum-likelihood estimates of

_U_c=3.1 (s.e.=0.1) crown mutations, homozygous effect _s_=0.86 (s.e.=0.01) and dominance _h_=0.43 (s.e.=0.02) within the fixed-effects mutational model (Figures 4a and c). The number of

background mutations affecting fruit set was estimated to be near zero, with maximum-likelihood estimate by the Nelder–Mead method yielding _U_b=0.005 (s.e.=0.02). The sensitivity of the

product _U_c_s_ to variation in _U_b and _h_ is moderate, with a minimum value of ∼2 for partially dominant canopy mutations, regardless of the number of background mutations up to 3 (Figure

4d). DISCUSSION INBREEDING DEPRESSION Inbreeding depression estimates in the populations of _V. angustifolium_ studied here are high, as reported by Bell et al. (2010) for populations of

this species located in the northeastern United States. Prior studies with this species suggest that this result is not due to a system of self-pollen rejection (self-incompatibility). For

instance, to distinguish self-incompatibility from early-acting inbreeding depression in _V. angustifolium_, Hokanson and Hancock (2000) emasculated flowers and then compared fruit set after

several pollination treatments, including: (1) application of self-pollen to stigmas on day 0, (2) application of cross-pollen to stigmas on day 0, (3) application of cross-pollen to

stigmas on day 3, (4) application of self-pollen to stigmas on day 0 followed by cross-pollen on day 1 and (5) application of self-pollen to stigmas on day 0 followed by cross-pollen on day

3. The latter two treatments produced statistically significantly greater seed per fruit than either the selfed treatment alone or the self followed by cross-pollen on day 3, suggesting that

low self-fertility is not due to self-incompatibility. AD AND SOMATIC MUTATION PARAMETER ESTIMATES The somatic mutation parameter estimation conducted here suggests that several mutations

arise during growth of the crown. These are mutations of large effect (_s_⩾0.8) and partially dominant (_h_⩾0.3). It is notable that this large value of _U__c_ results in a total genomic

deleterious mutation rate that exceeds that measured for most annual plants by up to an order of magnitude (Baer et al., 2007). The actual discrepancy could be greater than this, as we

examined only the effect of early-acting mutations, whereas studies of deleterious mutation in annuals have generally examined fitness effects that accrue over the entire lifespan of the

plant. The higher estimated rate of somatic mutation accords with suggestions that woody plants do indeed undergo higher overall mutation rate per generation than annuals (Klekowski, 1988),

and suggests that cell lineage selection may not be efficient at removing the class of mutations examined in this study. SOURCES OF BIAS IN THE ESTIMATION OF SOMATIC MUTATION PARAMETERS The

somatic mutation parameter estimates obtained here may potentially be biased downward. First, the estimates are based on autogamous–geitongamous cross pairs obtained from 20 different

plants. We have pooled the results from these 20 plants, thereby assuming uniform values of _U_b and _U_c for each plant; one-way analysis of variance treating clone as a random factor shows

that there is some variation in _D_ among clones (F19166=1.89, _P_<0.02). Second, with respect to the estimation of _U_c, the sizes of the plants sampled differ (there is about a twofold

range of plant surface area), so that even if the rate of somatic mutation per cell is constant, the number of mutations accumulating along the branches could vary, with larger plants

accumulating more mutations in the crown. Because our estimation of mutation parameters assumes that selection does not influence the estimation of the rate of somatic mutation (or

alternatively, that if somatic selection does act, it does so equally for each plant), selection combined with such size variability could introduce error. That is, if somatic selection

occurs and the opportunity for selection increases as the branch grows, mutations in flowers subtended by longer branches may experience more selection than those subtended by shorter ones.

This would tend to bias down the estimate of _U_c, though such an effect could be offset by the greater opportunity for somatic mutation to occur in longer branches. Third, the selective

effects and dominance coefficients associated with individual mutations likely vary for each mutation. Variation in the selective effects would lead to downward bias in the estimate of

mutation rate, with the degree of bias depending on the shape of the distribution of mutational effects (Simmons and Crow, 1977; Keightley, 1994). Fourth, the methods may underestimate the

true rate of somatic mutation, as we have assumed diploidy. As noted above, there is some evidence to suggest that _V. angustifolium_ exhibits tetrasomic inheritance, which if present, is

expected to give rise to a lower probability of homozygosity of mutations upon selfing, the actual amount depending on the degree of double reduction (Haldane, 1930). If inheritance is

tetrasomic, our estimates of mutation rates would be biased downward. Unfortunately, the exact degree of potential bias cannot be calculated, as there is no method for determining the

frequency of double reduction of the deleterious mutations. OTHER AUTOGAMY DEPRESSION STUDIES Although there exist no other detailed studies of AD, such as the one we have conducted here, a

survey of literature revealed a number of studies in which both autogamy and geitonogamy were conducted in the same plants. These studies show that _D_>0 is a common finding (Table 1).

Although these studies do not provide explicit information on within-plant distances (number of somatic cell divisions) separating flowers used in the geitonogamous crosses, it is reasonable

to expect that it would tend to be larger in woody plants, where there is greater latitude for using widely separated flowers. In this regard, it is noteworthy that _D_ for woody plants

tends to be larger than _D_ for herbs (_t_=1.74, df=20, _P_<0.10), as expected if somatic mutation is a general feature of plants, though it is important to note that this pattern could

also be an artifact of investigators unknowingly using different plants (that is, different ramets) when conducting geitonogamous crosses. CONCLUSIONS AND FUTURE WORK Our results provide

whole-genome estimates of the rate of somatic deleterious mutations. There have also been recent studies suggesting that somatic mutation accumulation can reduce fitness through its effect

on pollen viability (Ally et al., 2010). We have used phenotypic methods to estimate the deleterious mutation rate. An alternative approach would be to use DNA sequencing to assay the number

of mutations directly. We note that molecular and phenotypic estimates of mutation rate are both informative, but they provide fundamentally different kinds of information. Molecular

estimates inform us about processes that have occurred at the molecular level, whereas phenotypic studies tell us the fitness effect of mutations. Unfortunately, there is no reliable way to

convert estimates of point mutation and insertion–deletion events detected with sequencing into estimates of fitness effects. Our results are limited to one fitness component, an

early-acting one at that, where somatic selection may have limited power to remove mutations. It will be important to extend this type of estimation to other fitness components, such as

growth rate, flowering and so on. In these cases, there may be more opportunity for somatic selection to reduce the realized number of mutations passed onto gametes. Finally, we note that

our study was conducted in a commercially valuable clonal species rather than an annual species. There has been much discussion of the merits of relying more upon perennial plants for

agricultural production, as the use of such plants is expected to reduce soil erosion and reliance on high-input chemical fertilizers and herbicides, while promoting above- and below-ground

soil biodiversity and ecological processes (Glover et al., 2010). If, however, somatic mutation is a general feature of plant growth and occurs at a high rate, a switch to perennial or

clonal crop plants could have the effect of reducing seed and/or fruit yields (McKey et al., 2010). Indeed, in light of the results obtained here, it is reasonable to ask, for the blueberry

plantations investigated in this study, whether the practice of allowing unlimited vegetative expansion of clones may contribute to limiting yield, through its effect on augmenting somatic

mutation and consequent reduction in fruit set due to early-acting inbreeding depression. Smaller clone size could perhaps lead to lower inbreeding depression. Another possible strategy to

reduce the impact of inbreeding depression in clonal or tree crops is to increase pollen dispersal rates by deploying pollinator species that take longer flights on average between foraging

bouts so that more of the pollen transfer occurs between genets. DATA ARCHIVING Data deposited in the Dryad repository: doi:10.5061/dryad.t8q7t. REFERENCES * Ally D, Ritland K, Otto SP .

(2010). Aging in a long-lived clonal tree. _PLoS Biol_ 8: e1000454. Article  PubMed  PubMed Central  Google Scholar  * Antolin MF, Strobeck C . (1985). The population genetics of somatic

mutation in plants. _Am Nat_ 126: 52–62. Article  Google Scholar  * Baer CF, Miyamoto MM, Denver DR . (2007). Mutation rate variation in multicellular eukaryotes: causes and consequences.

_Nat Rev Genet_ 8: 619–631. Article  CAS  PubMed  Google Scholar  * Barrett SCH, Harder LD, Worley A . (1996). The comparative biology of pollination and mating in flowering plants. _Phil

Trans R Soc Ser B_ 351: 1271–1280. Article  Google Scholar  * Bell DJ, Rowland LJ, Stommel J . (2010). Yield variation among clones of lowbush blueberry as a function of genetic similarity

and self-compatibility. _J Amer Soc Hort Sci_ 135: 259–270. Article  Google Scholar  * Boches PS, Bassil NV . (2005). Microsatellite markers for Vaccinium from EST and genomic libraries.

_Mol Ecol Res_ 5: 657–660. CAS  Google Scholar  * Broyden CG . (1970). The convergence of a class of double-rank minimization algorithms 1. General considerations. _IMA J Appl Math_ 6:

76–90. Article  Google Scholar  * Charlesworth D, Charlesworth B . (1987). Inbreeding depression and its evolutionary consequences. _Ann Rev Ecol Syst_ 18: 237–268. Article  Google Scholar 

* Cloutier D, Rioux D, Beaulieu J, Schoen DJ . (2003). Somatic stability of microsatellite loci in Eastern white pine, Pinus strobus L. _Heredity_ 90: 247–252. Article  CAS  PubMed  Google

Scholar  * Drake JW, Charlesworth B, Charlesworth D, Crow JF . (1998). Rates of spontaneous mutation. _Genetics_ 148: 1667–1686. CAS  PubMed  PubMed Central  Google Scholar  * Fletcher R .

(1970). A new approach to variable metric algorithms. _Comp J_ 13: 317–322. Article  Google Scholar  * Fletcher R, Reeves C . (1964). Function minimization by conjugate gradients. _Comp J_

7: 149–154. Article  Google Scholar  * Gill DE, Chao L, Perkins SL, Wolf JB . (1995). Genetic mosaicism in plants and clonal animals. _Ann Rev Ecol Syst_ 26: 423–444. Article  Google Scholar

  * Glover JD, Culman SW, DuPont ST, Broussard W, Young L, Mangan ME _et al_. (2010). Harvested perennial grasslands provide ecological benchmarks for agricultural sustainability. _Agric

Ecosyst Environ_ 137: 3–12. Article  Google Scholar  * Goldfarb D . (1970). A family of variable-metric methods derived by variational means. _Math Comp_ 24: 23–26. Article  Google Scholar 

* Haag-Liautard C, Coffey N, Houle D, Lynch M, Charlesworth B, Keightley PD . (2008). Direct estimation of the mitochondrial DNA mutation rate in _Drosophila melanogaster_. _PLoS Biol_ 6:

1706–1714. Article  CAS  Google Scholar  * Haldane JBS . (1930). Theoretical genetics of autopolyploids. _J Genet_ 22: 359–372. Article  Google Scholar  * Heim S . (2007) svcm: 2d and 3sd

Space-Varying Coefficient Models in R. R package version 0.1.2 http://CRAN.R-project.org/package=svcm. * Hokanson K, Hancock J . (1993). The common lowbush blueberry, _Vaccinium

angustifolium_, may be an autotetraploid. _Can J Plant Sci_ 73: 889–891. Article  Google Scholar  * Hokanson K, Hancock J . (2000). Early-acting inbreeding depression in three species of

Vaccinium (Ericaceae). _Sex Plant Reprod_ 13: 145–150. Article  Google Scholar  * Keightley PD . (1994). The distribution of mutation effects on viability in _Drosophila melanogaster_.

_Genetics_ 138: 1315–1322. CAS  PubMed  PubMed Central  Google Scholar  * Klekowski EJ Jr . (1988) _Mutation, Developmental Selection, and Plant Evolution_. Columbia University Press: New

York. Google Scholar  * Klekowski EJ Jr, Godfrey PJ . (1989). Aging and mutation in plants. _Nature_ 340: 389–390. Article  Google Scholar  * Klekowski EJ Jr, Kazarinova-Fukshansky NK, Mohr

H . (1985). Shoot apical meristems and mutation: Selective loss of advantageous cell genotypes. _Am J Bot_ 71: 28–34. Article  Google Scholar  * Kondrashov AS . (1988). Deleterious mutation

and the evolution of sexual reproduction. _Nature_ 336: 435–440. Article  CAS  PubMed  Google Scholar  * Lynch M, Gabriel W . (1990). Mutation load and the survival of small populations.

_Evolution_ 44: 1725–1737. Article  PubMed  Google Scholar  * McKey D, Elias M, Pujol B, Duputie A . (2010). The evolutionary ecology of clonally propagated domesticated plants. _New Phytol_

186: 318–332. Article  PubMed  Google Scholar  * Morgan MT . (2001). Consequences of life history for inbreeding depression and mating system evolution in plants. _Proc Biol Sci._ 268:

1817–1824. Article  CAS  PubMed  PubMed Central  Google Scholar  * Morton NE, Crow JF, Muller HJ . (1956). An estimate of the mutational damage in man from data of consanguineous marriages.

_Proc Natl Acad Sci USA_ 42: 855–863. Article  CAS  PubMed  PubMed Central  Google Scholar  * Mukai T . (1964). The genetic structure of natural populations of _Drosophila melanogaster._ I.

Spontaneous mutation rate of polygenes controlling viability. _Genetics_ 72: 333–355. Google Scholar  * Nelder JA, Mead R . (1965). A simplex method for function minimization. _Comp J_ 7:

308–313. Article  Google Scholar  * Nocedal J, Wright SJ . (1999) _Numerical Optimization_ 2nd edn. Springer: New York, USA. Book  Google Scholar  * O’Connell LM, Ritland K . (2004). Somatic

mutations at microsatellite loci in western Redcedar (_Thuja plicata_: Cupressaceae). _J Hered_ 95: 172–176. Article  PubMed  Google Scholar  * Otto SP, Orive ME . (1995). Evolutionary

consequences of mutation and selection within an individual. _Genetics_ 141: 1173–1187. CAS  PubMed  PubMed Central  Google Scholar  * Otto SP, Hastings IM . (1998). Mutation and selection

within the individual. _Genetica_ 102-103: 507–524. Article  CAS  PubMed  Google Scholar  * Otto SP, Walbot V . (1990). DNA methylation in eukaryotes: kinetics of demethylation and de novo

methylation during the life cycle. _Genetics_ 124: 429–437. CAS  PubMed  PubMed Central  Google Scholar  * Pineda-Krch M, Lehtila K . (2002). Cell lineage dynamics in stratified shoot apical

meristems. _J Theor Biol_ 219: 495–505. Article  PubMed  Google Scholar  * R Core Team.. (2012) _R: A Language and Environment For Statistical Computing. R Foundation for Statistical

Computing_. ISBN: Vienna, Austria. ISBN. 3-900051-07-0 http://www.R-project.org/. * Schoen DJ, Bataillon TM, David JL . (1998). Deleterious mutation accumulation and the regeneration of

genetic resources. _Proc Natl Acad Sci USA_ 95: 394. Article  CAS  PubMed  PubMed Central  Google Scholar  * Schultz ST, Scofield DG . (2009). Mutation accumulation in real branches: fitness

assays for genomic deleterious mutation rate and effect in large-statured plants. _Am Nat_ 174: 163–175. Article  PubMed  Google Scholar  * Scofield DG, Schultz ST . (2006). Mitosis,

stature, and evolution of plant mating systems: low-Φ and high-Φ plants. _Proc Biol Sci_ 273: 275–282. Article  PubMed  Google Scholar  * Scofield DG . (2006). Medial pith cells per meter in

twigs as a proxy for mitotic growth rate (Φ/m) in the apical meristem. _Am J Bot_ 93: 1740–1747. Article  PubMed  Google Scholar  * Shanno DF . (1970). Conditioning of quasi-Newton methods

for function minimization. _Math Comp_ 24: 647–656. Article  Google Scholar  * Shanno DF, Kettler PC . (1970). Optimal conditioning of Quasi-Newton methods. _Math Comp_ 24: 657–664. Article

  Google Scholar  * Simmons MJ, Crow JF . (1977). Mutations affecting fitness in _Drosophila_ populations. _Ann Rev Genet_ 11: 49–78. Article  CAS  PubMed  Google Scholar  * Weir BS . (1996)

_Genetic Data Analysis II: Methods for Discrete Population Genetic Data_. Sinauer Associates: Sunderland, MA, USA. Google Scholar  * Weismann A . (1893) _The germ-plasm: a theory of

heredity_. Charles Scribner's and Sons: New York. Google Scholar  * Whitham TA, Slobodchikoff CN . (1981). Evolution by individuals, plant/herbivoreinteractions, and mosaics of

variability: the adaptive significance of somatic mutations in plants. _Oecologia_ 49: 287–292. Article  PubMed  Google Scholar  Download references ACKNOWLEDGEMENTS We thank Dr Douglas

Scofield for assistance during the planning stages of this work, Dr Doyle McKey for comments on the manuscript and Dr Sier-Ching Chantha for assistance with microsatellite genotyping. The

following persons provided help and logistics with the field and lab work: Dr Linley Jesson, Melissa Fulton, Kathryn Leyens, Duncan McGillivray, Irene McKechnie, Natasha Salter and Bonnie

Sim. We especially thank Mr Bernard Savoie for allowing us to work in his blueberry fields and also for arranging access to fields owned by growers in Neguac, New Brunswick. KB was supported

by an educational grant from the Mississauga First Nation Education Department. This work was supported by an NSERC Discovery Grant and an by an NSERC Strategic Network grant to the

Canadian Pollination Initiative (CANPOLIN). This is CANPOLIN paper number 86. AUTHOR INFORMATION Author notes * K Bobiwash and S T Schultz: These authors contributed equally to this work.

AUTHORS AND AFFILIATIONS * Department of Biology, McGill University, Montreal, Quebec, Canada K Bobiwash & D J Schoen * Department of Maritime Science, University of Zadar, M.

Pavlinovića bb, Zadar, Croatia S T Schultz Authors * K Bobiwash View author publications You can also search for this author inPubMed Google Scholar * S T Schultz View author publications

You can also search for this author inPubMed Google Scholar * D J Schoen View author publications You can also search for this author inPubMed Google Scholar CORRESPONDING AUTHOR

Correspondence to D J Schoen. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no conflict of interest. ADDITIONAL INFORMATION Supplementary Information accompanies this paper on

Heredity website SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION (DOC 105 KB) RIGHTS AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Bobiwash, K., Schultz,

S. & Schoen, D. Somatic deleterious mutation rate in a woody plant: estimation from phenotypic data. _Heredity_ 111, 338–344 (2013). https://doi.org/10.1038/hdy.2013.57 Download citation

* Received: 02 March 2013 * Revised: 13 May 2013 * Accepted: 15 May 2013 * Published: 19 June 2013 * Issue Date: October 2013 * DOI: https://doi.org/10.1038/hdy.2013.57 SHARE THIS ARTICLE

Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided

by the Springer Nature SharedIt content-sharing initiative KEYWORDS * somatic mutation * deleterious mutation * inbreeding depression * long-lived plants