ABSTRACT Entanglement is at the heart of the Einstein-Podolsky-Rosen paradox, where the non-locality is a necessary ingredient. Cooper pairs in superconductors can be split adiabatically,

thus forming entangled electrons. Here, we fabricate such an electron splitter by contacting an aluminium superconductor strip at the centre of a suspended InAs nanowire. The nanowire is

terminated at both ends with two normal metallic drains. Dividing each half of the nanowire by a gate-induced Coulomb blockaded quantum dot strongly impeds the flow of Cooper pairs due to

the large charging energy, while still permitting passage of single electrons. We provide conclusive evidence of extremely high efficiency Cooper pair splitting via observing positive

SPLITTING SHOWING STRONG NON-LOCAL CORRELATIONS Article Open access 04 November 2021 SPIN CROSS-CORRELATION EXPERIMENTS IN AN ELECTRON ENTANGLER Article 23 November 2022 STEADY-STATE

DYNAMICS AND NONLOCAL CORRELATIONS IN THERMOELECTRIC COOPER PAIR SPLITTERS Article Open access 08 March 2025 INTRODUCTION Two particles are entangled if a detection or a manipulation of the

quantum state instantaneously affects the other quantum state. Hence, being non-local, the entanglement of two separated particles must involve simultaneous, non-local, measurements. Such

two-particle state can be achieved, in principle, via particles interaction or by breaking apart a composite quantum object. For example, fully entangled photons are readily provided by

low-efficiency parametric down-conversion of higher energy photons1,2,3. Such a feat is not readily available for electrons. However, the closest electrical analogue to the high energy

photons are Cooper pairs in a superconductor, being a natural source of entangled electron pairs. Splitting them adiabatically may give birth to entangled electron pairs. Indeed, it had been

predicted and measured that Cooper pairs, emanating from a superconductor, can split into two normal metallic leads in the so-called cross Andreev reflection process4,5,6,7,8,9,10,11. Such

process can be conclusively verified by observing positive coincident arrival events, namely, positive cross-correlation of current fluctuations in two separated normal metallic leads that

collect the split pairs12,13,14,15,16,17,18. The main difficulty in identifying such process is the overwhelming flux of Cooper pairs that enters the normal leads via direct Andreev

reflection (the proximity effect). Such an experiment was attempted by Wei _et al_.10, where cross-correlation measurements were performed in an all metallic system (Al superconductor and Cu

normal metal) without quantum dots (QDs) at very low frequencies (2–6 Hz) at a temperature of 0.3–0.4 K. The large 1/_f_ noise, the relatively high temperature and a dominant Cooper pair

transport compromised the obtained data. Replacing each of the normal metallic leads with a QD in the Coulomb blockade regime (see ref. 12), performed by Hofstetter _et al._8, indeed

suppressed Cooper pairs transport, but lacked to prove coincidence splitting. Here, we provide results of coincidence measurements by observation of positive cross-correlation of current

fluctuations. These are reinforced by simultaneous non-local conductance measurements on both sides of the nanowire. Quenching superconductivity with a weak magnetic field suppressed the

positive correlations. We obtained a splitting efficiency, defined as the ratio between single-electron to two-electron transport, as high as ~100%. RESULTS EXPERIMENTAL SETUP Figure 1 shows

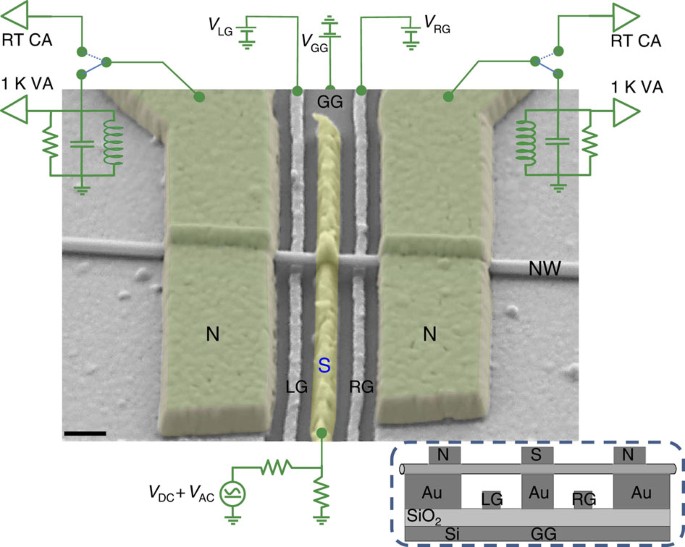
a SEM image of our device, as well as a schematic illustration of the measurement setup. A 50-nm diameter InAs nanowire, grown by a high purity Au-assisted MBE process19, was suspended on

Au pillars above a conducting Si substrate coated with 150 nm SiO2. A superconducting aluminium strip (S), ~100 nm wide, was intimately contacted at the centre of the nanowire, separating it

into two equal sections, each ~200 nm long, with two terminating gold ohmic contacts serving as drains (D). Aside from the conducting Si substrate, which served as a global gate (GG), two

narrow metallic gates, some 50 nm wide, were used to tune the local chemical potential on each side of the nanowire. Although the local gates (positively biased) accumulated electron

puddles, the GG (negatively biased) induced barriers on the sides of each puddle, thus forming two QDs on both sides of the superconducting contact. Although currents were amplified with a

room temperature current amplifier at ~575 Hz, current fluctuations (broad band auto-correlation or shot noise) and their cross-correlation, were first filtered by an inductor-capacitor (LC)

resonant circuit tuned to 725 kHz (bandwidth ~100 kHz); amplified by a home-made cold (1 K) preamplifier cascaded by a room temperature amplifier, and finally measured by a spectrum

analyser or an analogue cross-correlation setup. More details of the fabrication process and the measurement techniques are given in the Methods section. ONE SIDE TRANSPORT AND CHARGE

MEASUREMENT With all three gates unbiased, the InAs nanowire conductance is n-type with an approximate electron density of 5 × 106 cm−1. The differential conductance of one side of the wire,

say the left side, when the right side is pinched-off by its local gate (RG), is measured at 10 mK as a function of its gate voltage (_V_LG), whereas the GG is grounded. The conductance

varies around 2 _e_2/_h_ (Fig. 2a)—characteristic of Fabry-Perot type oscillations19. Note that conductance exceeding 2_e_2/_h_ for the first subband indicates the presence of Andreev

reflections with a barrier near the S–InAs interface (with maximum of 4 _e_2/_h_). Under similar conditions, the non-linear differential conductance as a function of bias _V_SD is shown in

Fig. 2b for two values of _V_LG (C and A in Fig. 2a). The gate voltage _V_LG mainly controls the barrier near the S–InAs interface, shifting the linear conductance from high at point C to

low at point A, with a strikingly different non-linear conductance in the two points. At point C, with a linear transmission probability _t_*=2.6/4=0.65, the conductance drops with bias—as

expected for a diminishing tunnelling probability of Cooper pairs as the bias approaches half the superconducting gap (Δ). Alternatively, at point A, with _t_*=0.4, the conductance increases

with bias and peaks at _V_SD=Δ. Here single electron tunnelling dominates. The superconducting gap 2Δ ~220 μeV is noted by the dotted line. A perpendicular magnetic field quenches the

non-linear differential conductance with a critical field _B_ ~0.12 T. For the above conditions, with the barrier at the S–InAs interface, the injected current is carrying shot noise, which

depends linearly on the injected current (_I_) and the tunnelling charge (_e_*)20,21,22,23. The low frequency spectral density of the excess noise (shot noise above the Johnson-Nyquist and

environment noise) in the single InAs channel takes the form: _S_i(0)=2_e_*_I_(1−_t_*)_F_(_T_), with _t_*=_t_ for electrons and _t_*=_t_2 for Cooper pairs, and _F_(_T_)=cothζ−1/ζ, with

ζ=_e_*_V_SD/_k_B_T_. Determination of the non-linear conductance (Fig. 2b) is crucial for accurate excess noise value as it affects the background noise (composed of thermal and current

noise of the preamplifier24); as explained further in the Supplementary Fig. S2. In Fig. 2e, we plot _S_i(0) as a function of _I_ for zero magnetic field _B_ and for _B_ ~0.2 T. The blue and

red solid lines are the 10-mK predictions for _t_*=0.4, _e_*=2_e_ and _t_=0.63, _e_*=_e_, respectively; demonstrating an excellent quantitative agreement with the data (black circles). The

distinct change of slope (from _e_*=2_e_ to _e_*=_e_) nicely corresponds to Δ that was deduced from the conductance (Fig. 2d). A perpendicular small magnetic field (~0.2 T) quenched the

superconductivity with the excess noise nicely agreeing with _e_*=_e_ across the full biasing range. QD AND COOPER PAIR SPLITTING We now turn to study the efficiency of Cooper pair

splitting. Introducing a Coulomb blockaded QD on each side of the nanowire is expected, under suitable conditions, to suppress Cooper pair transport due to the dot’s relatively large

charging energy _U_. Preventing single electron injection from the superconductor necessitates, _eV_SD, _k_B_T_<Δ, while quenching of Cooper pairs transport through the QD requires

_eV_SD<_U_. The characteristic energies of each QD is determined by measuring the non-linear differential conductance as a function of the DC bias (_V_SD) and the local gate voltage (via

the so-called diamond structure; see Supplementary Fig. S3). We estimated the average charging energy at _U_=8–10 meV and the single particle level broadening at Γ ~200–300 μeV. Under these

conditions, with _U_>Δ but Γ≈Δ>_k_B_T_, two-sequential-electron transport, proportional to (Γ/Δ)2, is barely suppressed12. The efficiency, defined as the ratio of splitted

current/Cooper pair current, η=_I_e/_I_CP, can be expressed as with , where ξ is the coherence length of a Cooper pair, _k_F, the Fermi wave vector and δ_r_=_r_1−_r_2, the distance between

the emerging split electrons; with all values related to the proximity region in the InAs12. As δ_r_ is likely to be smaller than the superconductor width, we believe that its suppression

factor is not important, leading to η(πΔ/Γ)2 ~1. NON-LOCAL CONDUCTANCE MEASUREMENTS We begin with non-local conductance measurements by forming two QDs on both sides of the nanowire.

Applying a large negative voltage to the GG (_V_GG=−15 V), while keeping the local gates (_V_LG and _V_RG) at small negative voltage, induces two barriers surrounding each of the two

electron puddles. Starting, with the left QDL, although the right side of the nanowire is blocked, the conductance peaks as a function of _V_LG are solely due to Cooper pairs transport. Such

transport takes place likely due to sequential tunnelling of single particles by higher order process within a time scale smaller than the coherence time of a Cooper pair; leading to a

finite conductance proportional to (Γ/Δ)2 (ref. 12). Now when the right side of the nanowire is also allowed to conduct, Cooper pairs splitting can take place, thus also enhancing current on

the left side. The largest one-electron transport on both sides is expected when the two QDs are at resonance (Fig. 3a), which is actually a two-particle conductance resonance12. Such

non-local conductance measurement is shown in Fig. 3b. We simultaneously measure the conductance of both sides of the nanowire by two individual current amplifiers. In Fig. 3b colour plot of

_G_L is plotted by scanning the _V_RG for different fixed values of _V_LG. The solid red line towards the left side of the colour plot as a function of _V_LG is the measured _G_L of one

Coulomb blockade peak due to Cooper pairs transport through QDL when the right side is blocked, _I_CP. The blue line on the top panel is the local conductance of QDR as a function of _V_RG

when the left side is blocked. Tunning to _V_LG=−0.558 V (the dashed white line in Fig. 3b) and scanning _V_RG leads to the non-local _G_L (projected red line). Conductance is enhanced

(Δ_G_, due to single electron transport, _I_e) by as much as 0.18 _e_2/_h_ (marked by a asterik in Fig. 3b), corresponding to the conductance peaks of QDR with _V_RG. The efficiency of

splitting, defined as η=_I_e/_I_CP=Δ_G_/_G_, is proportional to _t_R/_t_L for the left side. For tuning _V_LG=−0.558 V, the efficiency is ~70% (Δ_G_/_G_=0.18/0.26) and is more than 100% when

_V_LG is set to off resonance (see Supplementary Fig. S4a). Similarly, non-local enhancement of _G_R induced by _V_LG takes place (see Supplementary Fig. S4b). A full representation of the

non-local conductance, Cooper pair splitting currents, between the left QD (Coulomb blockade peak at _V_LG=−0.557 V) and the right QD (Coulomb blockade peak at _V_RG=−0.21 V) is shown in the

two colour plots in Fig. 3c; with Δ_G_L (_V_LG, _V_RG) (top representation) and Δ_G_R (_V_LG, _V_RG) (bottom representation). Note that the apparent Δ_G_L is bigger than Δ_G_R. The

two-particle conductance resonance can be seen in Fig. 3c, where each single particle transport is non-local, as it depends on the transmission of both QDs (_t_L_t_R). Here, we have shown

the resonance of split electrons with an energy close to the Fermi energy. In the presence of magnetic field (~0.2 T), the superconductivity quenches and the non-local conductance diminishes

(Fig. 3c). The residual non-local conductance, in the form of a weak saw-tooth-like dependence, is the familiar detection behaviour of electron occupation in QDs25. Owing to the proximity

between the two dots (~300 nm), the left dot senses the potential swing in the right dot when an electron is added to it, thus affecting its conductance. CROSS-CORRELATION MEASUREMENTS

Measuring positive cross-correlation of current fluctuations in the two drains, assuring coincident clicks, provides direct test for the existence of split Cooper pairs (as the Andreev

reflections on each side are uncorrelated). To measure the cross-correlation, the current fluctuations were first amplified by a home-made cooled preamp, with the amplified signals fed to an

analogue signal multiplier at 725 kHz. Starting with an unbiased device, the uncorrelated background noise in both drains was nulled (being only some 2–3% of the actual auto-correlated back

ground noise due to cross talk, see Supplementary Fig. S5). In Fig. 4a the cross-correlation, measured with the two dots around their respective resonances (_V_LG=−0.557 V and _V_RG=−0.21 

V), is displayed for _V_SD=20, 10 and 5 μV DC. The cross-correlation is positive and is highest when the two dots are at resonance; in full agreement with the nonlocal conductance

measurement (Fig. 3c). The dependence of the cross-correlation signal on _V_SD, for the two QDs at resonance, is shown in Fig. 4c. Applying a perpendicular magnetic field, _B_=0.2 T,

quenches the superconductivity and thus eliminates the (positive) correlation between the drains’ current fluctuations (Fig. 4b). DISCUSSION According to our model, the non-local conductance

is expected to be proportional to _t_L_t_R, and Δ_G_R=Δ_G_L. This was not observed. Although we do not understand the reason for this discrepancy, it might be related to a reduction in the

two-electron transport, be it Cooper pairs or sequential two-electron transport, accompanying the single electron transport. Near the resonance of the QD, charge fluctuations and thus wide

frequency range potential fluctuations are dominant and can partly dephase the neighbouring dot (see such saw-tooth behaviour in Fig. 3d), possibly affecting the higher order two-electron

transport. The spectral density of the cross-correlation signal at zero temperature is given by _S_CC=<Δ_I_LΔ_I_R> 2_eI_CAR(1−_t_), with _I_CAR the single electron current (due to

cross-Andreev reflections) on one side17. As _I_CAR/_I_AR ~0.14 (0.04/0.3 seen in Fig. 3c for the resonance peaks near _V_LG=−0.557 V and _V_RG=−0.21 V) and _I_AR=500 pA at _V_SD=30 μV,

_I_CAR=70 pA. Hence, we expect _S_CC ~1.7 × 10−29 A2 Hz−1. However, the experimentally obtained _S_CC ~7–10 × 10−29 A2 Hz−1 is more than four times higher than the estimated value. This

discrepancy may be attributed to an under-estimated value of Cooper pair splitting efficiency that is deduced from the non-local conductance measurement. In conclusion, we have shown Cooper

pair splitting efficiency with ratio approaching unity of split pairs vs unsplit pairs by measuring average and time-dependent cross-correlations of two electron transport. To prove the

entanglement, one still needs to show Bell's inequality by measuring the coherence and spin correlation using ferromagentic contacts. METHODS DEVICE FABRICATION The sample was

fabricated on a thermally oxidized Si. The nanowire was suspended on three gold pillars, ~50 nm high. Two lower gold pillars, ~25 nm high, provided local gating on both sides of the wire.

After wires spreading from the ethanol solution, the source and drain regions were etched by ammonium polysulphide ((NH4)2Sx=1.5 M) to remove the native oxide, and were immediately

transferred into the evaporation chamber. For normal-metallic contacts 5/100 nm Ti/Au were evaporated, whereas for the superconducting contact 5/100 nm Ti/Al was used. MEASUREMENT TECHNIQUE

The superconducting contact was biased by a voltage source, DC or AC (the voltage divider was placed on the cold finger, see Supplementary Fig. S1), with an AC excitation voltage of ~2 μV.

Conductance measurements were conducted at a rather low frequency (room temperature current preamplifier at 575 Hz; gain 107, input impedance ~200 ohm and current noise ), as well as at a

higher frequency (cooled to 1 K voltage preamplifier at 725 kHz, gain 2.5, voltage noise and current noise ). At the input of the ‘cold’ preamplifier, a LCR circuit determined the frequency

725 kHz and the bandwidth (100 kHz). The amplified signal is fed to a room temperature ‘NF amplifier’, followed by a spectrum analyser with a bandwidth of 30 kHz. To switch between the two

measurement systems a ‘Relay’, placed at the base temperature, was operated by a 100-ms, 1 V pulse. For cross-correlation measurements, we employed an analogue cross-correlation setup, where

the signals from the two NF amplifiers were multiplied and measured by a digital multimeter (at a bandwidth of 100 kHz). ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE: Das, A. _et al._

High-efficiency Cooper pair splitting demonstrated by two-particle conductance resonance and positive noise cross-correlation. _Nat. Commun._ 3:1165 doi: 10.1038/ncomms2169 (2012).

REFERENCES * Einstein A., Podolsky B., Rosen N. Can quantum-mechanical description of physical reality be considered complete? _Phys. Rev._ 47, 777–780 (1935). Article  ADS  CAS  Google

Scholar  * Aspect A., Grangier P., Roger G. Experimental realization of Einstein-Podolsky-Rosen-Bohm Gedanken experiment: a new violation of Bell's inequalities. _Phys. Rev. Lett._ 49,

91–94 (1982). Article  ADS  Google Scholar  * Ou Z. Y., Mandel L. Violation of Bell's inequality and classical probability in a two-photon correlation experiment. _Phys. Rev. Lett._ 61,

50–53 (1988). Article  ADS  MathSciNet  CAS  PubMed  Google Scholar  * Beckmann D., Weber H. B., Lohneysen H. V. Evidence for crossed Andreev reflection in superconductor-ferromagnet hybrid

structures. _Phys. Rev. Lett._ 93, 197003 (2004). Article  ADS  CAS  PubMed  Google Scholar  * Russo S., Kroug M., Klapwijk T. M., Morpurgo A. F. Experimental observation of bias-dependent

nonlocal Andreev reflection. _Phys. Rev. Lett._ 95, 027002 (2005). Article  ADS  CAS  PubMed  Google Scholar  * Zimansky P. C., Chandrasekhar V. Nonlocal correlations in normal-metal

superconducting systems. _Phys. Rev. Lett._ 97, 237003 (2006). Article  ADS  Google Scholar  * Kleine A., Baumgartner A., Trbovic J., Schonenberger C. Contact resistance dependence of

crossed Andreev reflection. _Europhys. Lett._ 87, 27011 (2009). Article  ADS  Google Scholar  * Hofstetter L., Csonka S., Nygard J., Schonenberger C. Cooper pair splitter realized in a

two-quantum-dot Y-junction. _Nature_ 461, 960–963 (2009). Article  ADS  CAS  PubMed  Google Scholar  * Herrmann L. G., Portier F., Roche P., Yeyati A. L., Kontos T., Strunk C. Carbon

nanotubes as cooper-pair beam splitters. _Phys. Rev. Lett._ 104, 026801 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Wei J., Chandrasekhar V. Positive noise cross-correlation in

hybrid superconducting and normal-metal three-terminal devices. _Nat. Phys_ 6, 494–498 (2010). Article  CAS  Google Scholar  * Hofstetter L. et al. Finite-bias cooper pair splitting. _Phys.

Rev. Lett._ 107, 136801 (2011). Article  ADS  CAS  PubMed  Google Scholar  * Recher P., Sukhorukov E. V., Loss D. Andreev tunneling, Coulomb blockade, and resonant transport of nonlocal

spin-entangled electrons. _Phys. Rev. B_ 63, 165314 (2001). Article  ADS  Google Scholar  * Torrès J., Martin T. Positive and negative Hanbury-Brown and Twiss correlations in normal

metal-superconducting devices. _Eur. Phys. J. B_ 12, 319–322 (1999). Article  ADS  Google Scholar  * Choi M. S., Bruder C., Loss D. Spin-dependent Josephson current through double quantum

dots and measurement of entangled electron states. _Phys. Rev. B_ 62, 13569 (2000). Article  ADS  CAS  Google Scholar  * Lesovik G. B., Martin T., Blatter G. Electronic Entanglement in the

Vicinity of a Superconductor. _Eur. Phys. J. B_ 24, 287–290 (2001). Article  ADS  CAS  Google Scholar  * Chevallier D., Rech J., Jonckheere T., Martin T. Current and noise correlations in a

double-dot Cooper-pair beam splitter. _Phys. Rev. B_ 83, 125421 (2011). Article  ADS  Google Scholar  * Bignon G., Houzet M., Pistolesi F., Hekking F. W. J. Current-current correlations in

hybrid superconducting and normal-metal multiterminal structures. _Europhys. Lett._ 67, 110–116 (2004). Article  ADS  CAS  Google Scholar  * Melin R., Benjamin C., Martin T. Positive cross

correlations of noise in superconducting hybrid structures: roles of interfaces and interactions. _Phys. Rev. B_ 77, 94512 (2008). Article  ADS  Google Scholar  * Kretinin A., Popovitz-Biro

R., Mahalu D., Shtrikman H. Multiple Fabry-Perot conductance oscillations in suspended stacking-Faults-free InAs nanowires. _Nano Lett._ 10, 3439–3445 (2010). Article  ADS  CAS  PubMed 

Google Scholar  * de-Picciotto R. et al. Direct observation of a fractional charge. _Nature_ 389, 162–164 (1997). Article  ADS  CAS  Google Scholar  * Jehl X., Sanquer M., Calemczuk R.,

Mailly D. Detection of doubled shot noise in short normal-metal superconductor junctions. _Nature_ 405, 50–53 (2000). Article  ADS  CAS  PubMed  Google Scholar  * Lefloch F., Hoffmann C.,

Sanquer M., Quirion D. Doubled full shot noise in quantum coherent superconductor-semiconductor junctions. _Phys. Rev. Lett._ 90, 067002 (2003). Article  ADS  CAS  PubMed  Google Scholar  *

Choi B.-R. et al. Shot-noise and conductance measurements of transparent superconductor two-dimensional electron gas junctions. _Phys. Rev. B_ 72, 024501 (2005). Article  ADS  Google Scholar

  * Bid A. et al. Observation of neutral modes in the fractional quantum Hall regime. _Nature_ 466, 585–590 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Field M. et al. Measurements

of Coulomb blockade with a noninvasive voltage probe. _Phys. Rev. Lett._ 70, 1311–1314 (1993). Article  ADS  CAS  PubMed  Google Scholar  Download references ACKNOWLEDGEMENTS We thank

Yunchul Chung for contributing to the cross-correlation measurement. We also thank Hyungkook Choi, Nissim Ofek, Ron Sabo, Itamar Gurman and Hiroyuki Inoue for their technical help. We are

grateful to Christian Schönenberger and Yuval Oreg for their helpful discussions. M.H. acknowledges partial support from the European Research Council under the European Community's

Seventh Framework Programme (FP7/2007-2013)/ERC Grant agreement no. 227716, the Israeli Science Foundation (ISF), the Minerva foundation, the German Israeli Foundation (GIF), the German

Israeli Project Cooperation (DIP) and the US-Israel Bi-National Science Foundation (BSF). H.S. acknowledges partial support from the Israeli Science Foundation Grant 530-08 and Israeli

Ministry of Science Grant 3-66799. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Condensed Matter Physics, Braun Center for Submicron Research, Weizmann Institute of Science,

Rehovot, 76100, Israel Anindya Das, Yuval Ronen, Moty Heiblum, Diana Mahalu, Andrey V Kretinin & Hadas Shtrikman Authors * Anindya Das View author publications You can also search for

this author inPubMed Google Scholar * Yuval Ronen View author publications You can also search for this author inPubMed Google Scholar * Moty Heiblum View author publications You can also

search for this author inPubMed Google Scholar * Diana Mahalu View author publications You can also search for this author inPubMed Google Scholar * Andrey V Kretinin View author

publications You can also search for this author inPubMed Google Scholar * Hadas Shtrikman View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS

A.D. and Y.R. contributed to the sample design, device fabrication, setup, data acquisition, analysis and paper writing. M.H. contributed to the design, data interpretation and paper

writing. D.M. contributed to electron beam lithography, lithography technique. A.V.K. contributed to fabrication techniques, initial measurements and comments on the manuscript. H.S.

contributed to MBE growth and structural study of InAs nanowires by Au-assisted VLS, discussions and manuscript editing. CORRESPONDING AUTHOR Correspondence to Moty Heiblum. ETHICS

DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION Supplementary Figures S1-S5 (PDF 649 kb) RIGHTS AND

PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Das, A., Ronen, Y., Heiblum, M. _et al._ High-efficiency Cooper pair splitting demonstrated by two-particle

conductance resonance and positive noise cross-correlation. _Nat Commun_ 3, 1165 (2012). https://doi.org/10.1038/ncomms2169 Download citation * Received: 08 May 2012 * Accepted: 25 September

2012 * Published: 06 November 2012 * DOI: https://doi.org/10.1038/ncomms2169 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable

link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative