ABSTRACT Magnetic reconnection, in which magnetic field lines break and reconnect to change their topology, occurs throughout the universe. The essential feature of reconnection is that it

energizes plasma particles by converting magnetic energy. Despite the long history of reconnection research, how this energy conversion occurs remains a major unresolved problem in plasma

physics. Here we report that the energy conversion in a laboratory reconnection layer occurs in a much larger region than previously considered. The mechanisms for energizing plasma

particles in the reconnection layer are identified, and a quantitative inventory of the converted energy is presented for the first time in a well-defined reconnection layer; 50% of the

FIRST-PRINCIPLES THEORY OF THE RATE OF MAGNETIC RECONNECTION IN MAGNETOSPHERIC AND SOLAR PLASMAS Article Open access 28 April 2022 NON-THERMAL ELECTRON ACCELERATION FROM MAGNETICALLY DRIVEN

RECONNECTION IN A LABORATORY PLASMA Article 16 January 2023 TURBULENT MAGNETIC RECONNECTION GENERATED BY INTENSE LASERS Article 16 January 2023 INTRODUCTION Magnetic reconnection, the

breaking and topological rearrangement of magnetic field lines in plasma, occurs everywhere in the universe, in solar flares, the Earth's magnetosphere, star formation and laboratory

fusion plasmas1,2,3,4. The most important feature of magnetic reconnection is that significant acceleration and heating of plasma particles occurs at the expense of magnetic energy. An

example of this efficient energy conversion is the observation of large amounts of high-energy electrons associated with the reconnection of magnetic field lines in solar flares5. In the

reconnection region of the Earth’s magnetosphere and the solar wind, convective outflows have been documented by _in situ_ satellite measurements. Despite these advances, the exact physical

mechanisms for bulk plasma heating, particle acceleration and energy flow channels remain unresolved. This paper addresses the key unresolved question: how is magnetic energy converted to

plasma kinetic energy during reconnection? Furthermore, the conversion of magnetic energy is quantitatively evaluated for the first time in a laboratory reconnection layer by assessing the

overall energy inventory in a well-defined boundary. In the classical Sweet–Parker model1, which is based on the collision-dominated resistive magneto-hydrodynamics (MHD), the energy

dissipation rate during reconnection is small (~(_B_2/2_μ_0)_V_A/_LS_(1/2)) due to the slow reconnection rate; _V_A is the Alfvén velocity and _S_ (>>1) is the Lundquist number2,3,4.

Observations in nearly collision-free space and laboratory plasmas show, however, that this prediction is not realized3,4. In the collisionless magnetic reconnection layer, electrons and

ions move quite differently from each other due to two-fluid dynamics3,4,6,7; furthermore, differential motion between the magnetized electrons and the unmagnetized ions generates strong

Hall currents in the reconnection layer. In the two-fluid formulation, the Ohm’s law of MHD should be replaced by a generalized Ohm’s law to describe the force balance of an electron flow,

namely, Here the conventional notations are used with _E_ being the electric field and _B_ reconnecting magnetic field, _V_e the electron flow velocity, _J_ the current density, _J_e is the

electron current density and _P_e the spatially dependent electron pressure tensor3. A large out-of-plane electric field caused by the Hall currents at the reconnection layer (_J_Hall × _B_)

causes an increase in the reconnection rate3,4,6,7 by inducing rapid movement of the reconnecting field lines. This explains why the reconnection rate in collisionless plasmas is much

faster than the classical Sweet–Parker rate. In spite of recent progress, a major question remains unresolved: how is energy transferred from the magnetic field to plasma particles? A simple

two-dimensional (2D) numerical simulation would expect that field line breaking and energy dissipation is localized in the small electron diffusion region whose width is on the order of the

electron skin depth (_d_e_=c/ω_pe, where _c_ is the speed of light and _ω_pe is the electron plasma frequency). However, significant acceleration and heating of both ions and electrons have

been observed and analyzed in a wide region of the actual reconnection layer8,9,10,11,12,13,14,15 of laboratory and space plasmas. Although quantitative studies of energy flow have been

recently reported based on multiple satellite data12,15, to our knowledge, a comprehensive analysis of energy inventory over a well-defined reconnection layer has not been made. A

quantitative analysis of the energy conversion rate together with the identification of heating mechanisms and location would provide key insights into the energy conversion processes. Here

we report that the energy conversion in a laboratory reconnection layer occurs in a much larger region than previously considered. We observe that electron heating occurs outside the

electron diffusion region and that ion acceleration and heating dominate in a wide region of the exhaust of the reconnection layer, which ranges beyond several ion skin depths. The

mechanisms for energizing plasma particles in the magnetic reconnection layer are identified, and a quantitative inventory of the converted energy is presented for the first time in a

well-defined reconnection layer. The study concludes that ~50% of the magnetic energy is converted to particle energy, two-thirds of which transferred to ions and one-third to electrons. Our

results are compared with numerical simulations and space measurements. RESULTS EXPERIMENTAL APPARATUS We use the MRX facility16 to experimentally study the conversion of magnetic energy to

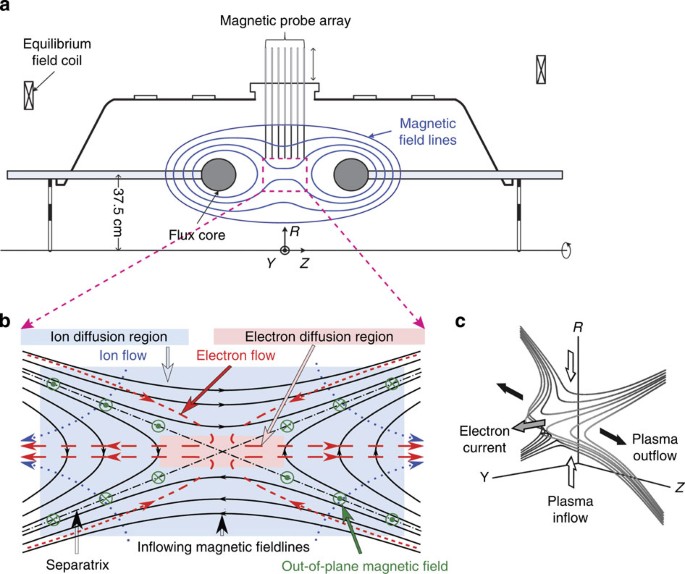
particle energy in a nearly collision-free reconnection layer. Figure 1a shows a schematic of the MRX apparatus, wherein two oppositely directed field lines merge and reconnect. Experiments

are carried out in a setup in which two toroidal plasmas with annular cross-section are formed around two flux cores as shown in Fig. 1a. As we induce magnetic reconnection by driving

oppositely directed field lines towards the X-point (_B_=0 at the centre of the layer) using pulsed flux core currents, ions and electrons also flow into the reconnection layer. The ions

become demagnetized at a distance of the ion skin depth (_d_i_=c/ω_pi, where _ω_pi is the ion plasma frequency) from the X-point where they enter the so-called ion diffusion region, and they

change their trajectories and are diverted into the reconnection exhaust as seen Fig. 1b. The electrons, on the other hand, remain magnetized through the ion diffusion region and continue

to flow towards the X-point. They become demagnetized only when they reach the much narrower electron diffusion region (~10_d_e~1 cm in MRX) as seen in Fig. 1b. Electron currents flow

dominantly in the out-of-plane direction (_Y_) near the centre (X-point) as shown in Fig.1c. For standard conditions, the electron density and temperature are, _n_e_~_(2–6) × 1013 cm−3_,

T_e=5–15 eV, for _B=_0.1–0.3 kG_, S_ _>_500; the electrons are well-magnetized (gyro-radius, _ρ_e~1 mm≪plasma size, _L_) while the ions are not. The mean free path for electron–ion

Coulomb collisions, _λ_mfp, is in the range of 6–20 cm that is larger than the layer thickness, and as a result, the reconnection dynamics are nearly collision-free and dominated by two

fluid and kinetic effects3,4. In this plasma, the energy exchange between electrons and ions is small since the characteristic energy transfer time is longer than the electron confinement

time. The ion skin depth is 6–8 cm and the electron skin depth is typically 1 mm. We use (_R, Y_ and _Z_) coordinates where _B__Z_ is the reconnecting field component and _Y_ is the

out-of-plane direction. Helium plasmas with a fill pressure of 4.5 mTorr are used for this study to facilitate ion temperature measurements. No external guide field is applied for this

study. The plasma beta in the inflow region is about 0.1. Our measurements are carried out in a steady state reconnection phase which last 20–30 μs, significantly longer than the Alfvén time

(~1 μs). We document comprehensively the dynamics of plasma particles and determine the mechanisms for energy conversion in the reconnection layer using extensive _in situ_ diagnostics. The

main diagnostic is a 2D magnetic probe array that measures the evolution of all three components of the magnetic field at >200 locations in the reconnection plane. The array consists of

seven probes with a separation of 3 cm along _Z_. Each probe has 35 miniature pickup coils with a maximum radial (_R_) resolution of 6 mm. The local ion temperature is measured by an

improved Ion Dynamics Spectroscopy Probe (IDSP)11,17. The line-of-sight for an inserted IDSP is typically 3 cm, which sets our spatial resolution. The ion flow vectors are measured by Mach

probes. Triple Langmuir probes are used to measure electron temperature and density16. The electric field in the reconnection plane is deduced from the in-plane plasma potential profile

measured by a floating potential probe and Langmuir probes11. The out-of-plane reconnection electric field is primarily inductive, which can be measured by following the movements of the

reconnecting flux lines11,13. ELECTRON DYNAMICS AND HEATING IN THE RECONNECTION LAYER The first goal of our work is to experimentally verify the two-fluid dynamics in the reconnection

region. Figure 2a depicts flow vectors of electrons in one half of the reconnection plane together with poloidal flux contours (representing magnetic field lines). The electron flow

velocities (_V_e) are derived from the electron current profile, which is obtained from the magnetic profile using _J_=∇ × _B_/_μ_0 and _V_e=_V_i− _J_/_en_e, where _V_i is the ion flow

velocity. The errors associated with the measurement of the current density are 5–10%. As conjectured by the two-fluid model, field lines moving towards the X-point (_B_=0 at the centre of

the layer) carry electrons into the layer. The electrons remain magnetized through the ion diffusion region and continue to flow towards the X-point at the _E_ × _B_ drift speed. In the

electron diffusion region, the magnetic field strength drops significantly, thereby driving up the in-plane electron drift speed (_E_/_B_) and injecting high-velocity electrons into the

reconnection exhaust. This feature is verified in Fig. 2a,b where the measured electron inflow velocity (_V_e_~V_i≪_V_A) is much slower than the measured outflow velocity of 5–10 _V_A. The

characteristic differential flow of ions and electrons described above generates net circulating currents that flow in the reconnection plane. These currents, in turn, create an out-of-plane

magnetic field with a quadrupole profile that is a signature of the Hall effect (Fig. 1b)18,19. The Hall currents also enhance the out-of-plane reconnection electric field, leading to the

observed fast motion of flux lines (_E__Y__=−_(1/2_πR_), where _Ψ_p is the poloidal flux representing a reconnecting magnetic field flux) in the reconnection plane (that is, the measured

fast rate of reconnection) as shown in equation (1)3,13. In the present work, we find a factor of 5–10 increase over the resistive term based on electron–ion Coulomb collisions. It is

verified in our experiment that the aforementioned out-of-plane Hall magnetic field has profound consequences for the 3D structure of the reconnecting field lines and of the electron flow in

the reconnection layer. In particular, magnetic field lines flowing into the layer are stretched in the out-of-plane direction by the quadrupole magnetic field components (see Fig. 2b).

When these stretched field lines break and reconnect at the X-point, electrons are rapidly ejected into the exhaust region with a large velocity in both the outflow (_Z_) and out-of-plane

(_Y_) directions. It should be noted that this flow velocity of the electrons near the X-point is nearly orthogonal to the magnetic field lines (Fig. 2b). A notable rise of electron

temperature (up to 50%) is measured over an area that is much wider than the electron diffusion region as seen Fig 2c. The energy deposition rate on electrons, _J_e·_E_, is concentrated near

the X-point as seen in Fig. 2d, but in a wider region (~10_d_e) than predicted by 2D numerical simulations20,21. The measured 2D electron temperature profile in Fig. 2c shows that the

electron heating spreads along the magnetic field lines likely due to strong parallel heat conduction. Consequently, the electron temperature in the exhaust region is higher than in the

inflow region. This observation agrees with the recent space observation of bulk electron heating in the reconnection exhaust region at the dayside magnetopause22. We note that Ohmic

dissipation based on classical resistivity accounts for <20% of the required heating power23. Magnetic and electrostatic fluctuations in the lower hybrid frequency range (1–15 MHz) are

observed23,24,25 near the X-point and throughout the downstream region, and are attributed to the observed strong electron heating, although a quantitative relationship is yet to be

determined. While the magnitude of the magnetic field decreases towards the X-point, the total electron kinetic and thermal energy with respect to the magnetic energy increases

substantially. The electron beta [~_n_e_T_e/(_B_02/2_μ_0)] is expected to significantly exceed unity inside the observed broad electron diffusion region, breaking the condition of a

magnetically confined state as is clearly seen in Fig. 2b. ION ACCELERATION AND HEATING IN THE RECONNECTION LAYER It is found that the flows of magnetized electrons, which cause the Hall

effects, also produce a strong electric field in the reconnection plane that is strongest across the separatrices, which separates the incoming field line region from the exhaust of

reconnected field lines as shown in Fig. 3a. It is experimentally verified in MRX that a saddle-shaped electric potential profile is formed in the reconnection plane to balance the Lorentz

force on the electron flows11. A strong in-plane electric field is generated near the separatrices with a wider and deeper potential well downstream. The MRX potential data is consistent

with measurements from the CLUSTER spacecraft8, which showed a narrow potential well near the X-point with a half width in the range of 60–100 km (3–5_d_e), and a deeper and wider well

towards the exhaust region. The in-plane electric field (or potential gradient) is largely perpendicular to the local magnetic field lines and is strongest near the separatrices20,26. The

electric potential is seen to be nearly constant along a poloidal flux contour (or magnetic field line) as seen in Fig. 3a in the half reconnection plane. In this figure, we note that a

large electric field across the separatrices extends to a significantly larger area of the reconnection layer (_L>>d_i), than the region in which field line breaking and reconnection

occur. A typical magnitude of the in-plane electric field, _E_sep is ~700 V m−1, which is much larger than the reconnection electric field in the out-of-plane direction, _E_rec~200 V m−1. We

observe electrostatic acceleration of ions near the separatrices due to the strong electric field mentioned above, whose spatial scale is ~2 cm, smaller than the ion gyro-radius of ~8 cm.

Figure 3a also shows 2D profile of ion flow vectors measured by Mach probes, along with colour contours of the plasma potential, _Φ_p. We observe clearly that the ion flows change their

direction at the separatrices and are accelerated in both the _Z_ and the _R_ directions. The energy deposition rate on ions, _J_i·_E_, is concentrated near the separatrices in the exhaust

region as seen in Fig. 3b. Figure 3d depicts the ion velocity distribution function versus _V__iZ_ as measured by the IDSP probes at the three locations specified in Fig. 3a. In this

measurement, the IDSP spectra are converted to the local velocity distributions of ions versus _V__iZ_ as described in the Methods section. Shifted Maxwellian distributions are observed at

typical positions (_R_, _Z_) as shown in Fig. 3d. Notable heating is observed as the ions flow out into the exhaust from the X-region, as demonstrated in Fig. 3d. The cause of this

anomalously rapid slowdown of ions, together with ion heating, is considered to be the remagnetization of the exiting ions. As the _R_ component of reconnected magnetic field becomes

stronger in the downstream region, the ion trajectories (black thick line in Fig. 3c) are significantly affected by the magnetic field of the exhaust and thus ions are remagnetized. A 2D

fully kinetic simulation has been carried out to verify these remagnetization mechanisms and understand how ions are heated downstream (Fig. 3c). In these simulations, realistic MRX global

boundary conditions are used in the particle-in-cell (PIC) code VPIC (vectorized particle-in-cell). VPIC is a first-principle, fully kinetic, electromagnetic PIC code that is optimized for

large-scale simulations27,28. The system size is about 15 × 30_d_i with 1,200 × 2,400 cells and 350 particles per cell. The mass ratio in the simulations is _m_i/_m_e=400, _ω_pe/_ω_ce=1, and

the initial electron thermal velocity is 0.125_c_ with _T_i=_T_e. Key physical parameters for the ions such as the ion skin depth and the mean free path are matched to experimentally

measured parameters. In the simulations, Coulomb collisions28 are included to study effects of collisions on the ion dynamics. We obtain good agreement between the observed ion temperature

profile and numerical simulation results only with realistic collision frequencies. This shows that ions are almost fully thermalized in the exhaust with a higher temperature than the

upstream value. As illustrated with the dashed line in Fig. 3c, the Coulomb collisions enhance the downstream ion thermalization process by scattering ions. In the completely collisionless

simulation, on the other hand, the ion distribution is different from Maxwellian. Ion velocity profiles at three different locations—upstream, at the separatrix and downstream—from our PIC

simulations with collisions (Fig. 3e) are in reasonably good agreement with experimentally measured profiles (Fig. 3d). ENERGY INVENTORY IN THE TWO-FLUID RECONNECTION LAYER When a

reconnection electric field is uniformly applied over a wide region in which opposite magnetic field lines meet, such as shown in Fig. 1, electrons with high mobility respond to this field

by creating a highly stressed region of magnetic and electric fields caused by Hall effects. This reconnection process partitions inflowing field lines from the reconnected ones by

separatrices, across which a notable potential drop (strong electric field) occurs, accumulating large free energy. While electrons are heated at the centre of the reconnection layer, ions

are accelerated across the separatrices by the strong electric field and heated through remagnetization by the magnetic field. This electric field structure extends to a very broad region,

much wider than the ion skin depth. Now, two important questions are raised: (1) How much energy is transported to particles; and (2) How is that energy partitioned? Using an energy

transport equation analogous to that adopted by Birn and Hesse29, we evaluate how much of the magnetic energy is converted to the kinetic energy of electrons and ions by assessing the energy

inventory of the reconnection layer. where _L_s is the loss term for each species including thermal conduction, radiation and ion energy loss to neutrals. The energy inventory is calculated

by monitoring the flow of magnetic energy, plasma enthalpy and bulk flow energy simultaneously, while measuring the incoming and outgoing electromagnetic Poynting flux (_S_), enthalpy flux

and bulk flow flux (kinetic energy flux) at a fixed boundary. The boundary of the volume of the plasma, Γb, is given by 31.5≤_R_≤43.5 cm and 0≤_Z_≤15 cm (Fig. 1), in which all key local

plasma parameters are measured within 10–15% error bars, assuming symmetry with respect to the major axis of the MRX plasma. Figure 4 presents a measured energy inventory, which flows from

the magnetic field to plasma particles. It is important to include the components of the Hall magnetic fields in both the incoming and exhaust regions to accurately track the Poynting

fluxes. As was done in the study by Birn and Hesse29, isotropic pressure is assumed in this calculation, which is justified in our plasma where anisotropy was only observed in a small region

near the X-point. The magnetic energy outflow rate is divided into two components, the conventional MHD part and the Hall-field part associated with the out-of-plane magnetic field and the

electrostatic in-plane field. Since the vacuum component of the magnetic field is slowly decreasing during the quasi-steady reconnection period, the first term of the LHS of equation (2) is

not negligible. The energy conversion rate to electrons and ions is independently calculated by integrating _J_s·_E_ over the volume Γb. As seen in the Fig. 4, about half of the incoming

magnetic energy is converted to particle energy, of which 1/3 goes to electrons (15% of magnetic energy) and 2/3 to ions (25–30% of magnetic energy). In our 2.5D simulation study using the

VPIC code, a similar result is obtained. The energy deposited on the electrons becomes thermal energy and is transferred to the exhaust by heat conduction, the energy deposited on the ions

is converted to thermal and flow energy with substantial conduction and convection losses. The conversion of magnetic energy in the experiment occurs across a broad region, much larger than

considered before. DISCUSSION Our quantitative measurements of the acceleration and heating of both electrons and ions demonstrate that more than half of the incoming magnetic energy is

converted to particle energy at a remarkably fast speed (~0.2_V_A) in the reconnection layer. This speed is significantly larger than the value calculated by MHD, 0.03_V_A for _S_=900. This

difference would become notably larger for space astrophysical plasmas with much larger _S_. A question arises as to whether the present results should be applied to magnetic reconnection

phenomena in space, astrophysical, or fusion plasmas. Recently, in a reconnection region of effectively similar size in the Earth’s magnetotail, the energy partition was carefully measured

during multiple passages of the Cluster satellites12. Although the moving X-line in these measurements made it difficult to identify the exact location of the magnetotail-reconnection

region, the half length of the tail reconnection layer (_L_) was estimated to be 2,000–4,000 km namely 3–6_d_i. The normalized scale length of this measurement is very similar to our cases,

_L_~3_d_i. Reconnection in the magnetotail is driven by external force, that is, the solar wind, and the boundary conditions are very similar to the MRX setup. The observed energy

partition12 is notably consistent with the present MRX data, namely, >50% of the magnetic energy flux is converted to the particle energy flux, which is dominated by the ion enthalpy

flux, with smaller contributions from both the electron enthalpy and heat flux. Also this comparison has implications for its scaling with Lundquist number. When we compare our results from

plasmas of _S_<1,000 with that of the magnetosphere where the Lundquist number is very large (>108), we find that the energy flow pattern is very similar, that is, the energization

characteristics do not strongly depend on the Lundquist number. This is consistent with the characteristics of the two-fluid plasma physics, where the classical resistivity based on

electron–ion collisions does not play a major role. Finally, in reversed field pinch fusion plasmas where magnetic reconnection plays a key role in self-organized plasma formation and

sustainment, it has been recently reported that a similar portion of magnetic energy (25–30%) is converted to ion thermal energy10. Is there a fundamental physics principle to explain these

observations from driven reconnection layers despite some differences in the boundary conditions? We believe the present results represent a key step towards resolving one of the most

important problems of plasma physics, how magnetic energy is transferred to plasma particles in the reconnection layer. METHODS ADDITIONAL DETAILS ON DIAGNOSTICS Triple Langmuir probes11 are

used to measure the electron temperature and density. The density measurements are calibrated by data from a CO2 interferometer. A radial profile of the floating potential is obtained from

a 17-tip floating potential probe with maximum resolution of 7 mm. Local ion temperature is measured by IDSPs (ref. 10), which obtain the spectrum of the He II 4686 Å line, which is

subsequently fitted to a sum of 13 Gaussian functions to take fine structure effects into account30; without considering fine structure, the ion temperature is overestimated by 15–25%. The

time and spatial resolution of the IDSPs are 5.6 μs and 3–4 cm, respectively. Mach probes are used to measure the ion flow velocity due to its better spatial and temporal resolutions. The

data from the Mach probe are calibrated by spectroscopic measurements from the IDSPs. DATA ACQUISITION AND ERROR ANALYSIS To select the final data set, more than 4,200 discharges were

scrutinized based on the reproducibility of the data from the 2D magnetic probe array and a reference Langmuir probe. The main criteria are the location of the X-point, the total plasma

current and the density and temperature measured by a reference Langmuir probe. The data values at each measurement point are determined by averaging over 7–15 discharges. The error bars for

each measurement are chosen between the standard deviation of each data set and the uncertainty in measurements, whichever is larger. Typical errors in magnetic field measurements are

<10%, while those in electrostatic measurements are 15%. The uncertainty in the ion temperature measurements mostly comes from the fitting process and is typically ~15%. CALCULATION OF

THE ENERGY INVENTORY The energy inventory is calculated by integrating each term in equation (2) over the volume Γb. The magnetic energy inflow rate is estimated by where

_S_in=(_E__Y__B__Z_/_μ_0)E_R_ is the incoming Poynting flux. Here E_R_ is the unit vector along the _R_ direction. The outgoing magnetic energy is obtained by integrating the divergence of

the outgoing Poynting flux. The outgoing Poynting flux is divided into the MHD component, _S_MHD=−(_E__Y__B__R_/_μ_0)E_Z_ and the Hall-field component,

_S_Hall=(_E__R__B__Y_/_μ_0)E_Z_−(_E__Z__B__Y_/_μ_0)E_R_. The integration of the first term of the right-hand side of equation (2) indicates the decrease of the magnetic energy per unit time

inside _v__B_. Total energy converted to each species per unit time is separately computed by To obtain change in a specific form of energy, we grouped associated terms in equation (2). The

flow energy change of species is given by The thermal energy change of species s is defined as We note that quantities in the inflow region are taken into account. We estimate the energy

loss rate of each species by considering the electron and ion heat flux, electron energy loss by impurity radiation and ion energy loss to neutrals by charge-exchange collisions. ADDITIONAL

INFORMATION HOW TO CITE THIS ARTICLE: Yamada, M. _et al_. Conversion of magnetic energy in the magnetic reconnection layer of a laboratory plasma. _Nat. Commun._ 5:4774 doi:

10.1038/ncomms5774 (2014). REFERENCES * Parker, E. N. Sweet's mechanism for merging magnetic fields in conducting fluids. _J. Geophys. Res._ 62, 509–520 (1957). Article  ADS  Google

Scholar  * Priest, E. & Forbes, T. _Magnetic reconnection—MHD theory and applications_ Cambridge University Press (2000). * Yamada, M., Kulsrud, R. & Ji, H. Magnetic reconnection.

_Rev. Mod. Phys._ 82, 603–664 (2010). Article  ADS  Google Scholar  * Zweibel, E. G. & Yamada, M. Magnetic reconnection in astrophysical and laboratory plasmas. _Annu. Rev. Astron.

Astrophys._ 47, 291–332 (2009). Article  ADS  CAS  Google Scholar  * Krucker, S. et al. Measurements of the coronal acceleration region of a solar flare. _Astrophys. J._ 714, 1108–1119

(2010). Article  ADS  Google Scholar  * Birn, J. et al. Geospace environmental modeling (GEM) magnetic reconnection challenge. _J. Geophys. Res._ 106, 3715–3719 (2001). Article  ADS  Google

Scholar  * Sonnerup, B. U. Ö. _Magnetic Field Reconnection_ eds Lanzerotti L. T., Kennel C. F., Parker E. N. Vol. 3North-Holland Publishing Co.45–108 (1979). * Wygant, J. R. et al. Cluster

observations of an intense normal component of the electric field at a thin reconnecting current sheet in the tail and its role in the shock-like acceleration of the ion fluid into the

separatrix region. _J. Geophys. Res._ 110, A09206 (2005). Article  ADS  Google Scholar  * Drake, J. F. et al. Ion heating resulting from pickup in magnetic reconnection exhausts. _J.

Geophys. Res._ 114, A05111 (2009). ADS  Google Scholar  * Fiksel, G. et al. Mass-dependent ion heating during magnetic reconnection in a laboratory plasma. _Phys. Rev. Lett._ 103, 145002

(2009). Article  ADS  CAS  PubMed  Google Scholar  * Yoo, J. et al. Observation of ion acceleration and heating during collisionless reconnection in a laboratory plasma. _Phys. Rev. Lett._

110, 215007 (2013). Article  ADS  PubMed  Google Scholar  * Eastwood, J. P. et al. Energy partition in magnetic reconnection in Earth’s magnetotail. _Phys. Rev. Lett._ 110, 225001 (2013).

Article  ADS  CAS  PubMed  Google Scholar  * Yamada, M. Progress in understanding magnetic reconnection in laboratory and space astrophysical plasmas. _Phys. Plasmas_ 14, 058102 (2007).

Article  ADS  Google Scholar  * Egedal, J. et al. Evidence and theory for trapped electrons in guide field magnetotail reconnection. _J. Geophys. Res._ 113, A12207 (2008). Article  ADS 

Google Scholar  * Angelopoulos, V. et al. Electromagnetic energy conversion at reconnection fronts. _Science_ 341, 1478 (2013). Article  ADS  CAS  PubMed  Google Scholar  * Yamada, M. et al.

Study of driven magnetic reconnection in a laboratory plasma. _Phys. Plasmas_ 4, 1936–1944 (1997). Article  ADS  CAS  Google Scholar  * Fiksel, G., Hartog, D. J. D. & Fontana, P. W. An

optical probe for local measurements of fast plasma ion dynamics. _Rev. Sci. Instrum._ 69, 2024–2026 (1998). Article  ADS  CAS  Google Scholar  * Ren, Y. et al. Experimental verification of

the Hall effect during magnetic reconnection in a laboratory plasma. _Phys. Rev. Lett._ 95, 055003 (2005). Article  ADS  PubMed  Google Scholar  * Yamada, M. et al. Experimental study of

two-fluid effects on magnetic reconnection in a laboratory plasma with variable collisionality. _Phys. Plasmas_ 13, 052119 (2006). Article  ADS  Google Scholar  * Pritchett, P. L. Onset of

magnetic reconnection in the presence of a normal magnetic field: realistic ion to electron mass ratio. _J. Geophys. Res._ 115, A10208 (2010). ADS  Google Scholar  * Ji, H. et al. New

insights into dissipation in the electron layer during magnetic reconnection. _Geophys. Res. Lett._ 35, L13106 (2008). Article  ADS  Google Scholar  * Phan, T. D. et al. Electron bulk

heating in magnetic reconnection at Earth’s magnetopause: dependence on the inflow Alfvén speed and magnetic shear. _Geophys. Res. Lett._ 40, 4475–4480 (2013). Article  ADS  Google Scholar 

* Yoo, J. et al. Bulk ion acceleration and particle heating during magnetic reconnection in a laboratory plasma. _Phys. Plasmas_ 21, 055706 (2014). Article  ADS  Google Scholar  * Ji, H. et

al. Electromagnetic fluctuations during fast reconnection in a laboratory plasma. _Phys. Rev. Lett._ 92, 115001 (2004). Article  ADS  PubMed  Google Scholar  * Ren, Y., Yamada, M., Ji, H.,

Gerhardt, S. P. & Kulsrud, R. Identification of the electron-diffusion region during magnetic reconnection in a laboratory plasma. _Phys. Rev. Lett._ 101, 085003 (2008). Article  ADS 

PubMed  Google Scholar  * Karimabadi, H., Daughton, W. & Scudder, J. Multi-scale structure of the electron diffusion regions. _Geophys. Res. Lett._ 34, L13104 (2007). Article  ADS 

Google Scholar  * Bowers, K. J. et al. Ultrahigh performance three-dimensional electromagnetic relativistic kinetic plasma simulation. _Phys. Plasmas_ 15, 055703 (2008). Article  ADS  Google

Scholar  * Roytershteyn, V. et al. Driven magnetic reconnection near the Dreicer limit. _Phys. Plasmas_ 17, 055706 (2010). Article  ADS  Google Scholar  * Birn, J. & Hesse, M. Energy

release and conversion by reconnection in the magnetotail. _Ann. Geophys._ 23, 3365–3373 (2005). Article  ADS  Google Scholar  * Wiese, W. L. & Fuhr, J. R. Accurate atomic transition

probabilities for hydrogen, helium, and lithium. _J. Phys. Chem. Ref. Data_ 38, 565–719 (2009). Article  ADS  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS We appreciate many

inputs from W. Daughton for our VPIC simulation and useful discussions with J. Eastwood on space observations. This work is supported by the Department of Energy as well as the NSF-funded

Center for Magnetic Self-Organization. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Center for Magnetic Self-organization, Princeton Plasma Physics Laboratory, Princeton University,

Princeton, 08544, New Jersey, USA Masaaki Yamada, Jongsoo Yoo, Jonathan Jara-Almonte, Hantao Ji, Russell M. Kulsrud & Clayton E. Myers Authors * Masaaki Yamada View author publications

You can also search for this author inPubMed Google Scholar * Jongsoo Yoo View author publications You can also search for this author inPubMed Google Scholar * Jonathan Jara-Almonte View

author publications You can also search for this author inPubMed Google Scholar * Hantao Ji View author publications You can also search for this author inPubMed Google Scholar * Russell M.

Kulsrud View author publications You can also search for this author inPubMed Google Scholar * Clayton E. Myers View author publications You can also search for this author inPubMed Google

Scholar CONTRIBUTIONS M.Y. carried out this research by collecting, analyzing and interpreting the data from MRX, and coordinated the experimental results with results from space

observation, numerical simulations and theory. J.Y. carried out experimental campaigns and key measurements reported here. He analyzed the data and generated the key figures used in this

manuscript. J.J.-A. assisted the experiments and carried out numerical simulations using the VPIC code. H.J., R.M.K., C.E.M. participated in this research by analyzing and interpreting the

data from MRX. CORRESPONDING AUTHOR Correspondence to Masaaki Yamada. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests. RIGHTS AND PERMISSIONS

Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Yamada, M., Yoo, J., Jara-Almonte, J. _et al._ Conversion of magnetic energy in the magnetic reconnection layer of a laboratory

plasma. _Nat Commun_ 5, 4774 (2014). https://doi.org/10.1038/ncomms5774 Download citation * Received: 05 May 2014 * Accepted: 23 July 2014 * Published: 10 September 2014 * DOI:

https://doi.org/10.1038/ncomms5774 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently

available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative