Play all audios:
ABSTRACT The adiabatic Born–Oppenheimer approximation (ABO) has been the standard ansatz to describe the interaction between electrons and nuclei since the early days of quantum
mechanics1,2. ABO assumes that the lighter electrons adjust adiabatically to the motion of the heavier nuclei, remaining at any time in their instantaneous ground state. ABO is well
justified when the energy gap between ground and excited electronic states is larger than the energy scale of the nuclear motion. In metals, the gap is zero and phenomena beyond ABO (such as
phonon-mediated superconductivity or phonon-induced renormalization of the electronic properties) occur3. The use of ABO to describe lattice motion in metals is, therefore, questionable4,5.
In spite of this, ABO has proved effective for the accurate determination of chemical reactions6, molecular dynamics7,8 and phonon frequencies9,10,11 in a wide range of metallic systems.
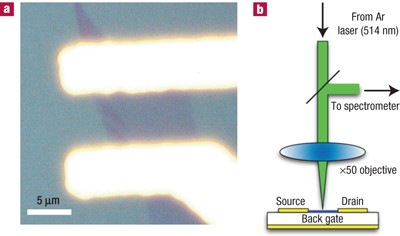
Here, we show that ABO fails in graphene. Graphene, recently discovered in the free state12,13, is a zero-bandgap semiconductor14 that becomes a metal if the Fermi energy is tuned applying a
gate voltage13,15, _V_g. This induces a stiffening of the Raman G peak that cannot be described within ABO. Access through your institution Buy or subscribe This is a preview of
subscription content, access via your institution ACCESS OPTIONS Access through your institution Subscribe to this journal Receive 12 print issues and online access $259.00 per year only
$21.58 per issue Learn more Buy this article * Purchase on SpringerLink * Instant access to full article PDF Buy now Prices may be subject to local taxes which are calculated during checkout
ADDITIONAL ACCESS OPTIONS: * Log in * Learn about institutional subscriptions * Read our FAQs * Contact customer support SIMILAR CONTENT BEING VIEWED BY OTHERS WEAK LOCALISATION DRIVEN BY
PSEUDOSPIN-SPIN ENTANGLEMENT Article Open access 18 November 2022 NON-TRIVIAL QUANTUM GEOMETRY AND THE STRENGTH OF ELECTRON–PHONON COUPLING Article 27 May 2024 ON THE FORBIDDEN GRAPHENE’S ZO
(OUT-OF-PLANE OPTIC) PHONONIC BAND-ANALOG VIBRATIONAL MODES IN FULLERENES Article Open access 05 July 2021 REFERENCES * Born, M. & Oppenheimer, J. R. Zur quantentheorie der molekeln.
_Ann. Phys._ 84, 457–484 (1927). Article CAS Google Scholar * Ziman, J. M. _Electrons and Phonons_ (Oxford Univ. Press, Oxford, 1960). Google Scholar * Grimvall, G. _The Electron-Phonon
Interaction in Metals_ (North-Holland, Amsterdam, 1981). Google Scholar * Ponosov, Y. S., Bolotin, G. A., Thomsen, C. & Cardona, M. Raman scattering in Os: Nonadiabatic renormalization
of the optical phonon self energies. _Phys. Status Solidi B_ 208, 257–269 (1988). Article Google Scholar * White, J. D., Chen, J., Matsiev, D., Auerbach, D. J. & Wodtke, A. M.
Conversion of large-amplitude vibration to electron excitation at a metal surface. _Nature_ 433, 503–505 (2005). Article CAS Google Scholar * Kroes, G. J., Gross, A., Baerends, E. J.,
Scheffler, M. & McCormack, D. A. Quantum theory of dissociative chemisorption on metal surfaces. _Acc. Chem. Res._ 35, 193–200 (2002). Article CAS Google Scholar * Alfe, D., Gillan,
M. J. & Price, G. D. The melting curve of iron at the pressures of the Earth’s core from _ab initio_ calculations. _Nature_ 401, 462–464 (1999). Article CAS Google Scholar * Walker,
B. G., Molteni, C. & Marzari, N. Ab initio molecular dynamics of metal surfaces. _J. Phys. Condens. Matter_ 16, S2575–S2596 (2004). Article CAS Google Scholar * Chester, G. V. The
theory of interaction of electrons with lattice vibrations in metals. _Adv. Phys._ 10, 357–400 (1961). Article CAS Google Scholar * Baroni, S., De Gironcoli, S., Dal Corso, A. &
Giannozzi, P. Phonons and related crystal properties from density functional perturbation theory. _Rev. Mod. Phys._ 73, 515–562 (2001). Article CAS Google Scholar * Savrasov, S. Y. &
Savrasov, D. Y. Electron-phonon interactions and related physical properties of metals from linear-response theory. _Phys. Rev. B_ 54, 16487–16501 (1996). Article CAS Google Scholar *
Novoselov, K. S. et al. Two dimensional atomic crystals. _Proc. Natl Acad. Sci. USA_ 102, 10451–10453 (2005). Article CAS Google Scholar * Novoselov, K. S. et al. Electric field effect in
atomically thin carbon films. _Science_ 306, 666–669 (2004). Article CAS Google Scholar * Wallace, P. R. The band theory of graphite. _Phys. Rev._ 71, 622–634 (1947). Article CAS
Google Scholar * Novoselov, K. S. et al. Two dimensional gas of massless Dirac fermions in graphene. _Nature_ 438, 197–200 (2005). Article CAS Google Scholar * Zhang, Y., Tan, Y. W.,
Stormer, H. L. & Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. _Nature_ 438, 201–204 (2005). Article CAS Google Scholar * Ferrari, A. C.
et al. Raman spectrum of graphene and graphene layers. _Phys. Rev. Lett._ 97, 187401 (2006). Article CAS Google Scholar * Yan, J., Zhang, Y., Kim, P. & Pinczuk, A. Electric field
effect tuning of electron-phonon coupling in graphene. Preprint at <http://www.arxiv.org/cond-mat/0612634> (2006). * Tuinstra, F. & Koenig, J. Raman spectrum of graphite.
_J. Chem. Phys._ 53, 1126–1130 (1970). Article CAS Google Scholar * Piscanec, S., Lazzeri, M., Mauri, F., Ferrari, A. C. & Robertson, J. Kohn anomalies and electron phonon
interactions in graphite. _Phys. Rev. Lett._ 93, 185503 (2004). Article CAS Google Scholar * Dubay, O. & Kresse, G. Accurate density functional calculations for the phonon dispersion
relations of graphite layer and carbon nanotubes. _Phys. Rev. B_ 67, 035401 (2003). Article Google Scholar * Lazzeri, M., Piscanec, S., Mauri, F., Ferrari, A. C. & Robertson, J. Phonon
linewidths and electron-phonon coupling in graphite and nanotubes. _Phys. Rev. B_ 73, 155426 (2006). Article Google Scholar * Zhang, Y. et al. Landau-level splitting in graphene in high
magnetic fields. _Phys. Rev. Lett._ 96, 136806 (2006). Article CAS Google Scholar * Moos, G., Gahl, C., Fasel, R., Wolf, M. & Hertel, T. Anisotropy of quasiparticle lifetimes and the
role of disorder in graphite from ultrafast time-resolved photoemission spectroscopy. _Phys. Rev. Lett._ 87, 267402 (2001). Article CAS Google Scholar * Kampfrath, T., Perfetti, L.,
Schapper, F., Frischkorn, C. & Wolf, M. Strongly coupled optical phonons in the ultrafast dynamics of electronic energy and current relaxation in graphite. _Phys. Rev. Lett._ 95, 187403
(2005). Article Google Scholar * Lazzeri, M. & Mauri, F. Non-adiabatic Kohn-anomaly in a doped graphene monolayer. _Phys. Rev. Lett._ 97, 266407 (2006). Article Google Scholar *
Ando, T. Anomaly of optical phonon in monolayer graphene. _J. Phys. Soc. Jpn._ 75, 124701 (2006). Article Google Scholar * Castro Neto, A. H. & Guinea, F. Electron-phonon coupling and
Raman spectroscopy in graphene. _Phys. Rev. B_ 75, 045404 (2007). Article Google Scholar * Ashcroft, N. W. & Mermin, N. D. _Solid State Physics_ (Saunders College, London, 1976).
Google Scholar * Piscanec, S., Lazzeri, M., Robertson, J., Ferrari, A. C. & Mauri, F. Optical phonons in carbon nanotubes: Kohn anomalies, peierls distortions and dynamic effects.
_Phys. Rev. B_ 75, 035427 (2007). Article Google Scholar Download references ACKNOWLEDGEMENTS The authors thank P. Kim and A. Pinczuk for useful discussions and for sending us a preprint
of ref. 18. A.C.F. acknowledges funding from the Royal Society and The Leverhulme Trust. The calculations were carried out at IDRIS (Orsay). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS *
Engineering Department, Cambridge University, Cambridge CB3 0FA, UK Simone Pisana, Cinzia Casiraghi & Andrea C. Ferrari * IMPMC, Universités Paris 6 et 7, CNRS, IPGP, 140 rue de Lourmel,
75015 Paris, France Michele Lazzeri & Francesco Mauri * Department of Physics and Astronomy, University of Manchester, Manchester M13 9PL, UK Kostya S. Novoselov & A. K. Geim
Authors * Simone Pisana View author publications You can also search for this author inPubMed Google Scholar * Michele Lazzeri View author publications You can also search for this author
inPubMed Google Scholar * Cinzia Casiraghi View author publications You can also search for this author inPubMed Google Scholar * Kostya S. Novoselov View author publications You can also
search for this author inPubMed Google Scholar * A. K. Geim View author publications You can also search for this author inPubMed Google Scholar * Andrea C. Ferrari View author publications
You can also search for this author inPubMed Google Scholar * Francesco Mauri View author publications You can also search for this author inPubMed Google Scholar CORRESPONDING AUTHORS
Correspondence to Andrea C. Ferrari or Francesco Mauri. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests. SUPPLEMENTARY INFORMATION SUPPLEMENTARY
INFORMATION Derivation of equations (PDF 128 kb) RIGHTS AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Pisana, S., Lazzeri, M., Casiraghi, C. _et al._
Breakdown of the adiabatic Born–Oppenheimer approximation in graphene. _Nature Mater_ 6, 198–201 (2007). https://doi.org/10.1038/nmat1846 Download citation * Received: 29 November 2006 *
Accepted: 18 January 2007 * Published: 11 February 2007 * Issue Date: March 2007 * DOI: https://doi.org/10.1038/nmat1846 SHARE THIS ARTICLE Anyone you share the following link with will be
able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing
initiative