ABSTRACT Isomerization and carbon chemistry in the gas phase are key processes in many scientific studies. Here we report on the isomerization process from linear \({{\rm C}}_{10}^ -\) to

its monocyclic isomer. \({{\rm C}}_{10}^ -\) ions were trapped in an electrostatic ion beam trap and then excited with a laser pulse of precise energy. The neutral products formed upon

photoexcitation were measured as a function of time after the laser pulse. It was found using a statistical model that, although the system is excited above its isomerization barrier energy,

the actual isomerization from linear to monocyclic conformation takes place on a very long time scale of up to hundreds of microseconds. This finding may indicate a general phenomenon that

COLLISIONAL EXCITATION OF HNC BY HE FOUND TO BE STRONGER THAN FOR STRUCTURAL ISOMER HCN IN EXPERIMENTS AT THE LOW TEMPERATURES OF INTERSTELLAR SPACE Article 05 May 2022 INTRODUCTION

Isomerization of polyatomic systems, such as molecules and clusters, is a common phenomenon in nature. The importance of this process can be gauged by its impact on many fundamental and

applied areas of research. From protein folding1,2,3 to photosynthesis4, 5, isomerization affects many basic biological processes. Various isomeric reactions are important in inorganic

chemistry6, 7 while cis-trans8, 9 as well as other types of isomerizations10 are vital in organic chemistry. Isomeric transitions have been utilized in such applied fields as

sub-diffraction-limited lithography11 and dye-sensitized solar cells12. Isomerization is also central in atmospheric chemistry13 and in interstellar medium (ISM)14. In the case of ISM, one

example of a key isomerization process is HCN ↔ NHC15, 16, in which the line ratio of HCN/NHC is used to trace gas temperatures in galaxies and to compare their luminosities. Unlike in

biological systems, where ambient factors like water and pH may dramatically affect the isomerization process17, 18, this process in ISM occurs in the gas phase and hence depends solely on

the internal molecular dynamics. Therefore, it is desirable to study such processes in gas phase in which less parameters are involved. One of the most important observables that reflects

the isomerization process is the isomerization rate. In the gas phase, it is usually assumed that isomerization rates are governed by molecular dynamics when there is enough internal energy

to reach different isomeric paths. Typical rates have the same time constant as rotation, i.e., atomic motion relative to the center of mass, which is on the order of picoseconds. This was

demonstrated in many experiments and calculations19, although some faster20 and slower processes21 have also been measured. Here, we present evidence of extremely slow isomerization rates

for the transition from a gas phase linear \({{\rm C}}_{10}^ -\) cluster to its monocyclic conformation after photoexcitation above the isomerization barrier. When a polyatomic system such

as \({{\rm C}}_{10}^ -\), which has a large number of degrees of freedom, is photoexcited, the excitation energy is quickly converted to vibrational energy due to nonadiabatic coupling

between the electronic and vibrational degrees of freedom, a process known as internal conversion22. The system may then de-excite via various processes such as recurrent fluorescence23,

infrared emissions, fragmentation, or vibrational autodetachment, where neutrals are produced by the delayed detachment of electrons24. Depending on the internal energy of the excited

system, neutrals are usually formed after a delay following photoexcitation. The neutralization rate is thus governed by the dynamics of the excited system and can reveal great insights into

various de-excitation processes. In this study, we measure the neutralization rate of photoexcited linear \({{\rm C}}_{10}^ -\) anions at various photoexcitation energies ranging from below

the isomerization barrier to above it. The contribution of isomerization to the neutralization rate is prominent and indicates very slow isomerization on the time scale of many

microseconds. To the best of our knowledge, such a slow isomerization is observed for the first time in a polyatomic system in gas phase. Carbonaceous molecules and clusters are the most

abundant polyatomic species in the ISM25 and are proposed to be one of the main contributors to the unidentified infrared emission bands and diffused absorption bands26. Negative ions of

such species, though predicted to be lower in abundance than their neutral counterparts, can play an important role in many astrophysical processes27. One of the most important creation

mechanisms of carbonaceous species, assuming bottom-up carbon growth occurs, is probably the transition from 1D (linear carbon chains) to 2D and 3D structures. Hence, our results may shed

light on the more general unexplained creation of large carbon-based systems like polycyclic aromatic hydrocarbons (PAH)28 and C6029, 30 in the ISM. Furthermore, our results on isomerization

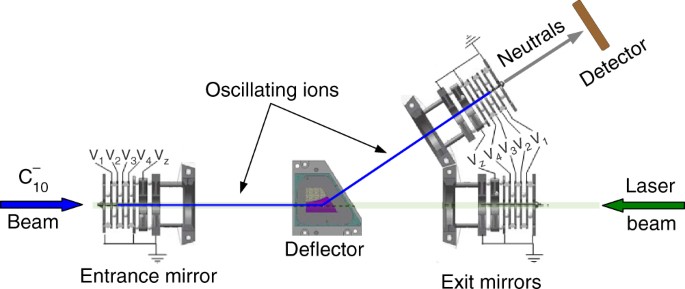
from linear to cyclic \({{\rm C}}_{10}^ -\) may also be instructive in nanographene production studies31. RESULTS EXPERIMENTAL SCHEME Vibrationally and rotationally excited \({{\rm

C}}_{10}^ -\) is produced by a cesium sputter source and trapped in a bent electrostatic ion beam trap (EIBT)32 (shown schematically in Fig. 1). In the EIBT, by applying appropriate voltages

to the entrance and exit mirrors, an ion beam can be kept oscillating in a field-free region between them, thus trapping the ions for a certain duration. In this study, the \({{\rm

C}}_{10}^ -\) beam was trapped for 250 ms. The trapped ion beam was merged with a single 5 ns-long pulse of photons from an energy-tunable laser after about 190 ms of trapping (see

Supplementary Note 1 and Supplementary Fig. 1 for discussion about photoexcitation at shorter trapping times than 190 ms). The neutral species flying out of the bent section exit mirror,

produced by electron detachment from \({{\rm C}}_{10}^ -\) either due to the laser impact or by residual gas collisions, are detected by a microchannel plate (MCP) detector with a phosphor

screen and recorded as a function of trapping time. A typical neutral counts versus trapping time curve is shown in Fig. 2. The peak at ~190 ms is due to photon-induced delayed detachment.

The peak is magnified and shown in the inset of the figure. Any neutrals that are produced promptly after the laser interaction are not recorded by the detector since they fly out of the

linear section of EIBT. Thus, the neutral counts shown in the inset of Fig. 2 are only those that are produced by vibrational autodetachment after a significant delay (>few microseconds)

from the time of laser impact. It can be clearly seen that the neutrals are produced even after a few hundred microseconds, and it is this neutralization rate that we studied to understand

the dynamics of the excited system. NEUTRALIZATION OF \({{\RM C}}_{10}^ -\) AT DIFFERENT PHOTON ENERGIES \({{\rm C}}_{10}^ -\) is the smallest carbon cluster anion for which the existence of

two isomeric forms (linear and monocyclic) has been experimentally reported33. The theoretical adiabatic electron affinity (AEA) and experimental electron affinity of linear \({{\rm

C}}_{10}^ -\) are 4.2234 and 4.46 eV35, respectively, while those of monocyclic \({{\rm C}}_{10}^ -\) are 1.6634 and 2.3 eV36, respectively. The isomerization barrier energy (_E_B) was

determined by generating the potential energy surfaces using density functional theory (DFT) (shown schematically in Fig. 3) and calculated to be 2.68 eV above the linear \({{\rm C}}_{10}^

-\) ground state. Since the trapped \({{\rm C}}_{10}^ -\) is rotationally excited, due to conservation of rotational angular momentum, the isomerization barrier, as well as all the energy

levels of cyclic \({{\rm C}}_{10}^ -\), will be shifted to higher energies relative to the linear conformation37. The degree of this shift depends on the rotational temperature of the

cluster at the time of the laser interaction. The experiments were performed using several laser photon energies. Figure 4 shows the neutral counts as a function of time after interaction of

\({{\rm C}}_{10}^ -\) with laser pulses of different energies. Neutrals are produced via photon-induced delayed electron emission upon vibrational autodetachment in anionic clusters and

large molecular anions under certain conditions on the photoexcitation energy. For electron emission to occur, the photon energy must be sufficiently high such that the total internal energy

of the system after photoexcitation is more than the adiabatic electron affinity. The time required for electron emission from such an anionic species depends on its internal dynamics and

decreases with the increase in its total internal energy. Thus, if the photoexcitation energy is much higher than the adiabatic electron affinity, electrons are mostly emitted promptly after

interaction with the photon. Electrons are emitted with a significant delay after photoexcitation only when the energies are close to the adiabatic electron affinity of a particular anionic

species. The neutral counts observed more than a few microseconds after the laser pulse cannot be from monocyclic \({{\rm C}}_{10}^ -\) as the photon energies are much higher than  the

adiabatic electron affinity (also the experimental electron affinity) of this species. In such a scenario, the total internal energy of the system after photoexcitation would be very high.

At these energies, electron detachment from monocyclic \({{\rm C}}_{10}^ -\) would be prompt and most of the neutrals produced would escape from the linear section of the trap. We measured

the neutrals produced immediately after the laser interaction by a detector placed after the linear section exit mirror (not shown in Fig. 1). The number of such neutrals was found to be

negligible at these photon energies, indicating the absence of a significant amount of monocyclic \({{\rm C}}_{10}^ -\) in the trapped ion beam (see Supplementary Note 2 and Supplementary

Fig. 2). Thus, the neutral counts we measure in our detector at the end of the bent section of the trap for hundreds of microseconds are from linear \({{\rm C}}_{10}^ -\). These neutrals

also cannot be due to vibrational autodetachment of linear \({{\rm C}}_{10}^ -\) as the energies are much lower than the adiabatic electron affinity of the system. Hence, the total internal

energy of linear \({{\rm C}}_{10}^ -\) after photoexcitation at these energies will not be sufficient for electron detachment. To understand the long neutralization process lasting several

microseconds, we calculated the neutralization rate using a statistical model that takes into account all the de-excitation processes occurring in photoexcited linear \({{\rm C}}_{10}^ -\).

The results from the model for each photon energy are depicted by the lines in Fig. 4. For all photon energies, there is excellent agreement within experimental error between the

neutralization rates computed by the model and those measured experimentally. The details of the model are discussed in the next section. ANALYSIS OF NEUTRALIZATION RATE Photoexcited linear

\({{\rm C}}_{10}^ -\) can relax by various complementary as well as competitive processes. The radiative relaxation mechanisms are infrared (IR) emissions upon transitions between the

vibrational levels of the system, and recurrent fluorescence (RF) due to transitions between the electronic excited states23, 38, 39. The non-radiative de-excitation in the excited cluster

can occur via vibrational autodetachment (VAD), which leads to electron detachment, or fragmentation. The lowest energy at which linear \({{\rm C}}_{10}^ -\) fragments is 5.68 eV34, which is

much higher than the excitation energies at which the experiments were performed. There might be the possibility of fragmentation upon two photon excitation, but it will not contribute to

the slow production of neutrals. In light of this, we have neglected fragmentation as a viable relaxation mechanism in our analysis. All these processes occur in competition with each other

with different rates that depend on the total energy of the excited system. These processes are common in any \({{\rm C}}_{n}^-\), where 3 < _n_ < 10. However, an additional process,

isomerization, can occur in competition with these processes when _n_ ≥ 1033. In our case, it is the isomerization from linear to monocyclic \({{\rm C}}_{10}^ -\). After isomerization, the

prominent relaxation mechanisms at these excitation energies for monocyclic \({{\rm C}}_{10}^ -\) are IR emissions and fast electron detachment by VAD, producing neutrals. Thus, the neutrals

that are produced in our experiment can be either due to VAD directly from linear \({{\rm C}}_{10}^ -\) or fast VAD from monocyclic \({{\rm C}}_{10}^ -\) after isomerization. With the

excitation energies used in our experiments, the latter process is more likely, and this is confirmed by our statistical model calculations. The neutralization rate is determined using

statistical rate theory40 considering the contributions from all relaxation mechanisms. The relaxation mechanisms are governed by their rate coefficients, which depend on the internal energy

of the system, _E_, after photoexcitation. The rate coefficients for the VAD, IR and RF emission processes are estimated by statistical phase space theory41,42,43. The rate coefficient for

VAD, based on a detailed balance approach considering the Langevin cross section for electron capture44, 45, is approximated by43 $$k_{{\rm VAD}_{\rm l,c}}(E) = f_{{\rm VAD}_{\rm

l,c}}{\int}_0^{E - {\rm AEA}_{\rm l,c}} {\kern 1pt} \frac{{2\mu G_{\rm l,c}e}}{{\pi \hbar ^3}} \sqrt {2\alpha _{\rm l,c}} \sqrt \varepsilon \frac{{\rho _{\rm l,c}\left( {E - {\rm AEA}_{\rm

l,c} - \varepsilon } \right)}}{{\rho _{\rm l,c}^ - (E)}}{\rm d}\varepsilon$$ (1) where the indices _l_ and _c_ denote the parameters for linear and monocyclic conformations, respectively,

_μ_ is the reduced electron mass, _G_ is the ratio of neutral-to-anion electronic degrees of freedom (_G_ _l_  = 3/2 and _G_ _c_  = 1/2), _ε_ and _e_ are the electronic energy and charge,

respectively, and _α_ is the polarizability of the neutrals (for linear C10, _α_ _l_  = 300.32 a.u46. and for monocyclic C10, _α_ _c_  = 108.65 a.u.47). _ρ_ and _ρ_− are the densities of the

vibrational states of C10 and \({{\rm C}}_{10}^ -\), respectively, in their electronic ground states calculated using the harmonic oscillator approach and the Beyer–Swinehart method48. The

fundamental vibrational frequencies used to calculate the densities of states were obtained from our DFT calculations. \(f_{{\rm VAD}_{\rm l,c}}\) is a correction factor we introduced to

account for any possible shortcomings in our model as determined by the experiment results. The rate coefficient for IR radiative relaxation is determined by43 $$k_{{\rm IR}_{\rm l,c}}(E) =

f_{{\rm IR}_{\rm l,c}}\mathop {\sum}\limits_{\begin{array}{c}s\end{array}} {\kern 1pt} A_s\left( {h\nu _s} \right)\mathop {\sum}\limits_{\begin{array}{c}n \ge 1\end{array}} {\kern 1pt}

\frac{{\rho _{\rm l,c}^ - \left( {E - nh\nu _s} \right)}}{{\rho _{\rm l,c}^ - (E)}}$$ (2) The harmonic frequencies _ν_ and their corresponding IR intensities used to calculate the Einstein

coefficient _A_ _s_ (_hν_ _s_ ) for IR transitions were obtained from our DFT calculations. The ratio of the densities of states \(\rho _{l,c}^ -\) gives the probability that \({{\rm

C}}_{10}^ -\) will be in a state that carries _n_ vibrational quanta _hν_. \(f_{{\rm IR}_{\rm l,c}}\) is the correction factor to compensate for any drawbacks in our model as determined by

the experimental data. The rate coefficient for RF radiative relaxation is computed by43 $$k_{{\rm RF_l}}(E) = f_{{\rm RF}}\mathop {\sum}\limits_{\begin{array}{c}j = 1 - 4\end{array}} {\kern

1pt} A_j\left( {E_j} \right)\frac{{\rho _{\rm l}^ - \left( {E - E_j} \right)}}{{\rho _{\rm l}^ - (E)}}$$ (3) where _A_ _j_ (_E_ _j_ ) denotes the Einstein coefficient for transition from

electronic state _j_ to the 2Π _u_ ground state of linear \({{\rm C}}_{10}^ -\) and are computed by considering the electronic states and oscillator strengths as per

CASPT2/cc-pVTZ//CCSD(T)/6-31G(d) results reported in ref. 49. The ratio of the density of states, \(\rho _{\rm l}^ -\), in Eq. (3), gives the probability that linear \({{\rm C}}_{10}^ -\)

will be excited to a particular electronic state. The correction factor introduced to overcome any shortcomings in the model as determined by the experimental data is denoted by _f_RF. We do

not considered RF to be a major relaxation mechanism in monocyclic \({{\rm C}}_{10}^ -\) due to the absence of any known excited electronic state close to its ground state. Finally, the

rate coefficient for isomerization from linear to monocyclic \({{\rm C}}_{10}^ -\) is obtained by Rice-Ramsperger-Kassel-Marcus (RRKM) theory and is given by14, 37 $$k_{\rm iso}(E) = f_{\rm

iso}\frac{{N_{\rm ts}\left( {E - E_{\rm B}} \right)c}}{{\rho _{\rm l}^ - (E)}}$$ (4) where _N_ts(_E_ − _E_B) is the sum of the vibrational states in the transition state that have energy

greater than or equal to the isomerization barrier energy _E_B and is estimated by the Beyer–Swinehart method48 using the vibrational frequencies of the transition state obtained from our

DFT calculations. _c_ is the speed of light and _f_iso is the correction factor as determined by experimental results. During isomerization, the rotational angular momentum of the systems is

conserved. Due to different symmetries and rotational constants of linear and monocyclic \({{\rm C}}_{10}^ -\)50, the shifts in their energy levels due to rotational energy are different.

Thus, _E_B is also shifted by an amount equal to the difference in the rotational energies of the two isomers. For our model, we assume an initial population before laser interaction that

follows a Boltzmann distribution at a rotational temperature of 1000 K. The calculations were performed for eight different rotational quantum numbers spanning this initial population

distribution. Varying the rotational temperature by ±500 K and increasing the number of rotational quantum numbers in our calculations did not significantly affect the results. The degree

that _E_B shifts in energy is different for each rotational quantum number, and the contribution to the isomerization rate for each quantum number is accounted for in the calculations. The

total neutralization rate \({\cal R}(t)\) due to one- and two-photon processes taking into account all of the relaxation mechanisms can be calculated using Eqs. (1), (2), (3), and (4). The

neutralization rate \({\cal R}_{\rm l}(t)\) by VAD directly from linear \({{\rm C}}_{10}^ -\) is given by39 $${\cal R}_{{\rm l}_{1,2}}(t) = N_{1,2}{\int}_{\rm AEA_l}^\infty {\kern 1pt}

f_0\left( {E = E_{\rm i} + E_{{\rm phot}_{1,2}}} \right)k_{\rm VAD_l}(E){\kern 1pt} e^{ - k_{\rm tot_l}(E)t}{\rm d}E$$ (5) where the indices 1, 2 denote one- and two-photon excitation

processes and _N_ is the corresponding normalization factor. \(f_0\left( {E = E_{\rm i} + E_{\rm phot_{1,2}}} \right)\) is the internal energy population distribution of the laser excited

linear \({{\rm C}}_{10}^ -\), where _f_o(_E_ = _E_i) denotes the initial internal energy population distribution before laser interaction. The vibrational temperature used to estimate the

initial internal energy population distribution was set to 670 K as this yielded the best agreement with the experimental data. \(k_{\rm tot_l}(E)\) = \(k_{\rm VAD_l}(E) + k_{\rm IR_l}(E) +

k_{\rm RF_l}(E) + k_{\rm iso}(E)\) gives the total de-excitation rate considering all relaxation mechanisms of the linear isomer. Neutrals are produced upon isomerization by a consecutive

two-step process. In the first step, linear \({{\rm C}}_{10}^ -\) isomerizes to monocyclic \({{\rm C}}_{10}^ -\), and neutrals are then formed by VAD from monocyclic \({{\rm C}}_{10}^ -\) in

the second step. The rate of production of neutrals in this case can thus be represented by51 $$\begin{array}{*{20}{l}} {{\cal R}_{\rm iso_{1,2}}(t)} \hfill & = \hfill &

{N_{1,2}{\int}_{E_{\rm B}}^\infty {\kern 1pt} f_0\left( {E = E_{\rm i} + E_{\rm phot_{1,2}}} \right)}\times \hfill \\ {} \hfill & {} \hfill & {\frac{{k_{\rm iso}(E)k_{\rm

VAD_c}(E)}}{{k_{\rm tot_c}(E) - k_{\rm tot_l}(E)}}\left( {e^{ - k_{\rm tot_l}(E)t} - e^{ - k_{\rm tot_c}(E)t}} \right){\rm d}E} \hfill \end{array}$$ (6) where \(k_{\rm tot_c}(E)\) = \(k_{\rm

VAD_c}(E) + k_{\rm IR_c}(E)\) gives the total rate for the relaxation mechanisms of monocyclic \({{\rm C}}_{10}^ -\). The neutralization rate for one-photon excitations is represented by

$${\cal R}_1(t) = {\cal R}_{\rm iso_1}(t) + {\cal R}_{\rm l_1}(t)$$ (7) while that due to two-photon excitations is denoted by $${\cal R}_2(t) = {\cal R}_{\rm iso_2}(t) + {\cal R}_{\rm

l_2}(t)$$ (8) The total neutralization rate is thus is given by $${\cal R}(t) = {\cal R}_1(t) + {\cal R}_2(t)$$ (9) The total neutralization rate calculated by our model represents the

neutralization rate that we measure in our experiment for various photon energies. DISCUSSION The total neutralization rate \({\cal R}(t)\) calculated by our model for each photon energy is

depicted in Fig. 4 by solid lines and shows very good agreement with the experimental data. The correction factors for all the rate coefficients were set to unity except for _f_RF which was

set to 0.8 so that the calculated neutralization rates best match our experimental results. The contribution to the neutralization rate from the one-photon excitations \({\cal R}_1(t)\) are

shown by dashed lines in Fig. 4 while those for the two-photon excitations \({\cal R}_2(t)\) are depicted by dotted lines. As expected for these photon energies, we observed that VAD

directly from linear \({{\rm C}}_{10}^ -\) does not contribute to the one-photon neutralization rate, i.e., \({\cal R}_1(t)\) = \({\cal R}_{\rm iso_1}(t)\), and it is this neutralization

pathway that occurs over an unusually long time of up to hundreds of microseconds. At a photon energy of 2.48 eV, the neutralization is dominated by two-photon processes with very little

contribution from one-photon excitation, because very little of the initial population distribution is excited above the isomerization barrier energy by absorbing a single photon. However,

in a two-photon process, there is more than sufficient energy to overcome the barrier for isomerization, and thus we see faster neutralization rates as the rate coefficients are much larger

at higher energies. As the photon energy increases, more of the initial population distribution is excited above the isomerization barrier by one-photon processes, resulting in an increased

contribution to the total neutralization rate, and this becomes dominant at energies higher than the isomerization barrier. It should be noted that isomerization starts at a photon energy of

2.58 eV, which is lower than the isomerization barrier energy because the linear \({{\rm C}}_{10}^ -\) in our experiments is not in the ro-vibrational ground state when photoexcited. This

initial internal energy of the system coupled with the photoexcitation energy is sufficient for part of the population to cross the isomerization barrier. The rate coefficients for each

relaxation mechanism are plotted in Fig. 5. The rate coefficients for isomerization and for relaxations from monocyclic \({{\rm C}}_{10}^ -\) in Fig. 5 include the effect of the rotational

energy shift corresponding to the smallest rotational quantum number considered for calculations. Due to the high rate coefficient for VAD from monocylic \({{\rm C}}_{10}^ -\), neutrals will

be produced by this process without any significant time delay. The slow rate for production of neutral species observed in our experimental results can only be explained by the small

isomerization rate coefficient. Thus, the neutrals produced up to hundreds of microseconds after photoexcitation are due to slow isomerization from linear \({{\rm C}}_{10}^ -\) to monocylic

\({{\rm C}}_{10}^ -\) followed by immediate electron detachment by VAD from monocylic \({{\rm C}}_{10}^ -\). To the best of our knowledge, this is the first observation of an ultraslow

isomerization in a cluster or molecule in the gas phase lasting hundreds of microseconds. Electron detachment mediated by isomerization is also observed in this study. Although in ISM the

relative abundance of carbon cluster anions such as \({{\rm C}}_{10}^ -\) is predicted to be lower than their corresponding neutral counterparts, they can facilitate the formation of many

neutral carbonaceous molecules, resulting in an enhancement of neutral abundances in environments such as dark molecular clouds52. This increase in neutral abundance is more prominent in

reactions involving \({{\rm C}}_{10}^ -\) than with smaller anionic species. To discern all of the possible chemical pathways that can lead to the formation of new species in ISM requires

understanding and characterization of all the competing processes and associated molecular parameters, like the ones discussed in this study. The ultraslow isomerization rates that we

observe, along with the rates for other relaxation mechanisms in gas phase \({{\rm C}}_{10}^ -\), can be key inputs in astrochemical models that try to explain or predict the formation of

various species in ISM. Our results, showing ultraslow isomerization in gas phase \({{\rm C}}_{10}^ -\), may be a general phenomenon in other large clusters or molecules and may help

understand the dynamics of large molecular systems in the excited state. METHODS EXPERIMENTAL DETAILS Carbon cluster anions were produced in a cesium sputter source by sputtering a graphite

target with Cs+ ions. Anions were then extracted and accelerated to 4.2 keV by applying the appropriate voltages to extractor and accelerator electrodes situated just after the source. The

anion beam was chopped into 55 μs-long bunches by an electrostatic chopper. \({{\rm C}}_{10}^ -\) ions were separated from this anion bunch by mass selection in a magnetic field of a 90°

bending magnet. The anion bunch was guided into the EIBT (Fig. 1) by various electrostatic deflectors, Einzel lenses and a quadrupole triplet. The pressure in the EIBT chamber was about 2 × 

10−10 Torr during the experiments. \({{\rm C}}_{10}^ -\) ions were trapped in the EIBT by applying the following voltages to its entrance and exit mirror electrodes: V1 = −6.75 kV, V2 = 

−4.875 kV, V3 = −3.25 kV, V4 = −1.625 kV, and V _z_  = −4.10 kV. To trap the ions in the bent section of the EIBT, ±670 V was applied to the electrodes of the spherical deflector. At the

beginning of each trapping cycle, the voltages on the entrance mirror were lowered to 0 V in order to inject the ion bunch into the trap. Once the ion bunch was inside the EIBT, the entrance

mirror voltages were quickly (~100 ns) raised before the ions returned after being reflected from the exit mirror. The \({{\rm C}}_{10}^ -\) ions were thus trapped in an oscillating

trajectory in the field free region between the two mirrors. The oscillation period of the \({{\rm C}}_{10}^ -\) ions in the EIBT was 16 μs. The gain of the MCP detector placed at the end of

the bent section exit mirror was set at about 2 kV, while that of the phosphor screen placed behind it was kept at about 4 kV to detect the neutrals from \({{\rm C}}_{10}^ -\). The detector

signal was amplified by a preamplifier and processed by a constant fraction discriminator before being digitized and recorded as a function of time by a National Instruments 6602

timer/counter multiscalar card installed in a computer using a 20 MHz clock (50 ns time resolution). LabVIEW53 programs were used to control the experimental parameters and to monitor and

store the data in a list-mode file on an event-by-event basis. DFT CALCULATIONS The isomerization barrier energy and vibrational frequencies of the transition state as well as of the linear

and monocyclic \({{\rm C}}_{10}^ -\) and C10 along with their corresponding IR intensities were calculated by density functional theory (DFT)54. The calculations were performed using

Gaussian09 Revision D.0155 and ORCA version 3.0.356. Gaussian09 was used for all calculations other than the double-hybrid energy calculations, for which ORCA was used. The calculations were

done by optimizing the geometries for linear and monocylic \({{\rm C}}_{10}^ -\) and C10 and the connecting transition states. Geometries were optimized with Adamo and Barone’s hybrid

version (i.e., PBE0)57 of the Perdew–Burke–Ernzerhof (PBE)58 generalized-gradient approximation (GGA) functional with an added empirical dispersion correction59, specifically the third

version of Grimme’s empirical dispersion correction60, 61 with Becke-Johnson dampening61,62,63. The def2-TZVPPD (triple-_ζ_ quality) basis set64, 65 was used for geometry optimization

calculations. Energies were calculated using a Kozuch and Martin’s dispersion-corrected (D3BJ), spin component scaled (i.e., an SCS66, 67-MP268-like correlation contribution), double hybrid

(DSD) functional, specifically DSD-PBEP8669. This functional incorporates the PBE exchange58 and the Perdew-86 (P86) correlation70 functionals. The def2-QZVPPD (quadruple-_ζ_ quality) basis

set65 was used for the double hybrid energy calculations. The efficiency of the calculation was improved by using the resolution of identity-chain of spheres (RIJCOSX) approximation71. This

class of DFT functionals has  shown to provide energies approaching that of the “Gold Standard” in computational chemistry. There are a number of reviews and benchmark studies of

double-hybrid functionals that clearly show that the use of this class of functionals is highly recommended72. Energies reported include zero-point vibrational energy (ZPVE) corrections

calculated at the PBE0/def2TZVPPD level of theory. Frequencies were scaled by 0.9824 as recommended by Kesharwani et al.73. The calculated vibrational frequencies of linear and monocyclic

\({{\rm C}}_{10}^ -\) and their corresponding IR intensities are given in Table 1 along with the vibrational frequencies of the transition state and linear and monocyclic C10. NEUTRALIZATION

RATE UPON ISOMERIZATION The neutralization rate and the rate coefficients were computed by a statistical model using MATLAB74. The functional form of the neutralization rate upon

isomerization, i.e., \({\cal R}_{\rm iso}(t)\), was obtained by considering the rate equations for the parallel and consecutive reactions for photoexcited linear \({{\rm C}}_{10}^ -\) as

shown in Fig. 6. Isomerization from excited linear \({{\rm C}}_{10}^ -\) occurs in competition with other relaxation mechanisms that take place in parallel. Neutral species are produced upon

isomerization by a consecutive reaction where linear \({{\rm C}}_{10}^ -\) isomerizes to excited monocyclic \({{\rm C}}_{10}^ -\), that then undergoes VAD to form monocyclic C10, which is

in competition with simultaneous IR relaxation. Though isomerization may be a reversible process, for the sake of simplicity and considering the high rate coefficient for VAD from monocylic

\({{\rm C}}_{10}^ -\) we neglect this possibility in our analysis. In a consecutive reaction of the form $${\cal A}\mathop{\longrightarrow}\limits^{{k_a}}{\cal B}\begin{array}{*{20}{c}}

{\mathop{\longrightarrow}\limits^{{k_{b1}}}{\cal C}} \\ {\mathop{\longrightarrow}\limits^{{k_{b2}}}{\cal D}} \end{array},$$ the rate equation for \({\cal B}\) is given by $$\frac{{{\rm

d}[{\cal B}]}}{{{\rm d}t}} = k_a[{\cal A}] - k_{b1}[{\cal B}] - k_{b2}[{\cal B}]$$ (10) where _k_ _a_ is the rate of creation of \({\cal B}\) while _k__b_1 and _k__b_2 are the rates of

depletion of \({\cal B}\). \([{\cal A}]\) and \([{\cal B}]\) are the concentrations of \({\cal A}\) and \({\cal B}\), respectively. In the formation of neutrals via isomerization, \({\cal

A}\) is the photoexcited linear \({{\rm C}}_{10}^ -\), the intermediate state \({\cal B}\) is the excited monocyclic \({{\rm C}}_{10}^ -\), \({\cal C}\) is the end product, i.e., monocyclic

C10 and \({\cal D}\) is the side product, monocyclic \({{\rm C}}_{10}^ -\). The intermediate state \({\cal B}\) is created by isomerization, thus $$k_a[{\cal A}] = k_{\rm iso}(E)f_0(E)e^{ -

k_{\rm tot_l}(E)t}$$ considering the fact that isomerization occurs in parallel with other relaxation processes from excited linear \({{\rm C}}_{10}^ -\). The intermediate excited monocyclic

\({{\rm C}}_{10}^ -\) is depleted by VAD and IR relaxation processes; thus $$k_{b1}[{\cal B}] + k_{b2}[{\cal B}] = k_{\rm VAD_c}(E)[{\cal B}] + k_{\rm IR_c}(E)[{\cal B}] = k_{\rm

tot_c}(E)[{\cal B}]$$ Therefore, Eq. (10) becomes $$\frac{{{\rm d}[{\cal B}]}}{{{\rm d}t}} = k_{\rm iso}(E)f_0(E)e^{ - k_{\rm tot_l}(E)t} - k_{\rm tot_c}(E)[{\cal B}]$$ (11) \([{\cal B}]\)

can be derived by solving  this differential equation, yielding $$[{\cal B}] = f_0(E)\frac{{k_{\rm iso}(E)}}{{k_{\rm tot_c}(E) - k_{\rm tot_l}(E)}} \left( {e^{ - k_{\rm tot_l}(E)t} - e^{ -

k_{\rm tot_c}(E)t}} \right)$$ (12) if \([{\cal B}]\) = 0 at time _t_ = 0. The rate equation for formation of \({\cal C}\), i.e., monocyclic C10 in our case, is given by

$$\begin{array}{*{20}{l}} {\frac{{{\rm d}[{\cal C}]}}{{{\rm d}t}} = k_{\rm VAD_c}(E)[{\cal B}] = f_0(E)\frac{{k_{\rm iso}(E)k_{\rm VAD_c}(E)}}{{k_{\rm tot_c}(E) - k_{\rm tot_l}(E)}}\left(

{e^{ - k_{\rm tot_l}(E)t} - e^{ - k_{\rm tot_c}(E)t}} \right)} \hfill \end{array}$$ (13) This differential form for the concentration of monocyclic C10, when integrated over all energies _E_

above the isomerization barrier _E_ _B_ , gives the instantaneous flux at a particular time _t_. Thus, $${\cal R}_{\rm iso_{1,2}}(t) = N_{1,2}{\int}_{E_{\rm B}}^\infty {\kern 1pt}

f_0(E)\frac{{k_{\rm iso}(E)k_{\rm VAD_c}(E)}}{{k_{\rm tot_c}(E) - k_{\rm tot_l}(E)}}\left( {e^{ - k_{\rm tot_l}(E)t} - e^{ - k_{\rm tot_c}(E)t}} \right){\rm d}E$$ (14) The instantaneous flux

of monocyclic C10 as a function of time is the neutralization rate upon isomerization from photoexcited linear \({{\rm C}}_{10}^ -\). DATA AVAILABILITY The data that support the plots

within this paper and other findings of this study are available from the corresponding authors upon reasonable request. REFERENCES * Ritchie, D. B. & Woodside, M. T. Probing the

structural dynamics of proteins and nucleic acids with optical tweezers. _Curr. Opin. Struct. Biol._ 34, 43–51 (2015). Article  CAS  PubMed  Google Scholar  * Best, R. B., Chen, Y.-G. &

Hummer, G. Slow protein conformational dynamics from multiple experimental structures: the helix/sheet transition of arc repressor. _Structure_ 13, 1755–1763 (2005). Article  CAS  PubMed 

Google Scholar  * Englander, S. W. & Mayne, L. The case for defined protein folding pathways. _Proc. Natl Acad. Sci. USA_ 114, 8253–8258 (2017). Article  CAS  PubMed  PubMed Central 

Google Scholar  * Giuliano, G., Giliberto, L. & Rosati, C. Carotenoid isomerase: a tale of light and isomers. _Trends Plant. Sci._ 7, 427–429 (2002). Article  CAS  PubMed  Google Scholar

  * Zubik, M. et al. Light-induced isomerization of the LHCII-bound xanthophyll neoxanthin: possible implications for photoprotection in plants. _Biochim. Biophys. Acta Bioenerg._ 1807,

1237–1243 (2011). Article  CAS  Google Scholar  * Levine, B. G. & Martnez, T. J. Isomerization through conical intersections. _Annu. Rev. Phys. Chem._ 58, 613–634 (2007). Article  ADS 

CAS  PubMed  Google Scholar  * Yao, L.-Y. & Yam, V. W.-W. Photoinduced isomerization-driven structural transformation between decanuclear and octadecanuclear gold (I) sulfido clusters.

_J. Am. Chem. Soc._ 137, 3506–3509 (2015). Article  CAS  PubMed  Google Scholar  * Dugave, C. & Demange, L. Cis-trans isomerization of organic molecules and biomolecules: implications

and applications. _Chem. Rev._ 103, 2475–2532 (2003). Article  CAS  PubMed  Google Scholar  * Irie, M., Fukaminato, T., Sasaki, T., Tamai, N. & Kawai, T. Organic chemistry: A digital

fluorescent molecular photoswitch. _Nature_ 420, 759–760 (2002). Article  ADS  CAS  PubMed  Google Scholar  * DeVine, J. A. et al. Encoding of vinylidene isomerization in its anion

photoelectron spectrum. _Science_ 358, 336–339 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Mueller, P. et al. A molecular switch for sub-diffraction laser lithography by photoenol

intermediate-state cis-trans isomerization. _ACS Nano_ 11, 6396–6403 (2017). Article  CAS  PubMed  Google Scholar  * El-Zohry, A., Orthaber, A. & Zietz, B. Isomerization and aggregation

of the solar cell dye D149. _J. Phys. Chem. C_ 116, 26144–26153 (2012). Article  CAS  Google Scholar  * de Oliveira-Filho, A. G. S., Aoto, Y. A. & Ornellas, F. R. New molecular species

of potential interest to atmospheric chemistry: isomers on the [H, S2, Br] potential energy surface. _J. Phys. Chem. A_ 113, 1397–1402 (2009). Article  PubMed  Google Scholar  * Petrie, S.

& Herbst, E. Some interstellar reactions involving electrons and neutral species: attachment and isomerization. _Astrophys. J._ 491, 210–215 (1997). Article  ADS  CAS  Google Scholar  *

Baraban, J. H. et al. Spectroscopic characterization of isomerization transition states. _Science_ 350, 1338–1342 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Mendes, M. B. et al.

Cold electron reactions producing the energetic isomer of hydrogen cyanide in interstellar clouds. _Astrophys. J. Lett._ 746, L8 (2012). Article  ADS  Google Scholar  * Chung, H. S.,

Piana-Agostinetti, S., Shaw, D. E. & Eaton, W. A. Structural origin of slow diffusion in protein folding. _Science_ 349, 1504–1510 (2015). Article  ADS  CAS  PubMed  Google Scholar  *

Qian, H., Wang, Y.-Y., Guo, D.-S. & Aprahamian, I. Controlling the isomerization rate of an Azo-BF2 switch using aggregation. _J. Am. Chem. Soc._ 139, 1037–1040 (2017). Article  CAS 

PubMed  Google Scholar  * Zhang, Y. & Pastor, R. W. A comparision of methods for computing transition rates from molecular dynamics simulation. _Mol. Simul._ 13, 25–38 (1994). Article 

Google Scholar  * Clark, J., Nelson, T., Tretiak, S., Cirmi, G. & Lanzani, G. Femtosecond torsional relaxation. _Nat. Phys._ 8, 225–231 (2012). Article  CAS  Google Scholar  * Dian, B.

C. et al. Conformational isomerization kinetics of pent-1-en-4-yne with 3,330 cm−1 of internal energy measured by dynamic rotational spectroscopy. _Proc. Natl Acad. Sci. USA_ 105,

12696–12700 (2008). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Bixon, M. & Jortner, J. Intramolecular radiationless transitions. _J. Chem. Phys._ 48, 715–726 (1968).

Article  ADS  CAS  Google Scholar  * Léger, A., Boissel, P. & d’Hendecourt, L. Predicted fluorescence mechanism in highly isolated molecules: the Poincaré fluorescence. _Phys. Rev.

Lett._ 60, 921–924 (1988). Article  ADS  PubMed  Google Scholar  * Adams, C., Schneider, H. & Weber, J. Vibrational autodetachment-intramolecular vibrational relaxation translated into

electronic motion. _J. Phys. Chem. A_ 114, 4017–4030 (2010). Article  CAS  PubMed  Google Scholar  * Henning, T. & Salama, F. Carbon in the universe. _Science_ 282, 2204–2210 (1998).

Article  ADS  CAS  PubMed  Google Scholar  * Bernstein, L. S. & Lynch, D. K. Small carbonaceous molecules, ethylene oxide (c-C2H4O) and cyclopropenylidene (c-C3H2): sources of the

unidentified infrared bands? _Astrophys. J._ 704, 226–239 (2009). Article  ADS  CAS  Google Scholar  * Millar, T. J., Walsh, C. & Field, T. A. Negative ions in space. _Chem. Rev._ 117,

1765–1795 (2017). Article  CAS  PubMed  Google Scholar  * Kaiser, R. I., Parker, D. S. & Mebel, A. M. Reaction dynamics in astrochemistry: Low-temperature pathways to polycyclic aromatic

hydrocarbons in the interstellar medium. _Annu. Rev. Phys. Chem._ 66, 43–67 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Berné, O. & Tielens, A. G. Formation of

buckminsterfullerene (C60) in interstellar space. _Proc. Natl Acad. Sci._ 109, 401–406 (2012). Article  ADS  PubMed  Google Scholar  * Dunk, P. W. et al. Metallofullerene and fullerene

formation from condensing carbon gas under conditions of stellar outflows and implication to stardust. _Proc. Natl Acad. Sci._ 110, 18081–18086 (2013). Article  ADS  CAS  PubMed  PubMed

Central  Google Scholar  * Kosimov, D., Dzhurakhalov, A. & Peeters, F. Carbon clusters: from ring structures to nanographene. _Phys. Rev. B_ 81, 195414 (2010). Article  ADS  Google

Scholar  * Aviv, O. et al. A bent electrostatic ion beam trap for simultaneous measurements of fragmentation and ionization of cluster ions. _Rev. Sci. Instrum._ 79, 083110 (2008). Article 

ADS  CAS  PubMed  Google Scholar  * Fromherz, R., Ganteför, G. & Shvartsburg, A. A. Isomer-resolved ion spectroscopy. _Phys. Rev. Lett._ 89, 083001 (2002). Article  ADS  PubMed  Google

Scholar  * Lépine, F., Allouche, A., Baguenard, B., Bordas, C. & Aubert-Frécon, M. Computed electron affinity of carbon clusters C _n_ up to n = 20 and fragmentation energy of anions.

_J. Phys. Chem. A_ 106, 7177–7183 (2002). Article  Google Scholar  * Kohno, M., Suzuki, S., Shiromaru, H., Moriwaki, T. & Achiba, Y. Ultraviolet photoelectron spectroscopy on the linear

conformer of negatively charged carbon clusters (10 ≤ _n_ ≤ 16). _Chem. Phys. Lett._ 282, 330–334 (1998). Article  ADS  CAS  Google Scholar  * Yang, S. et al. UPS of 2–30-atom carbon

clusters: Chains and rings. _Chem. Phys. Lett._ 144, 431–436 (1988). Article  ADS  CAS  Google Scholar  * Gutow, J. & Zare, R. Rotational effects on the overtone-induced isomerization

rate for CHD2NC → CHD2CN. _J. Phys. Chem._ 96, 2534–2543 (1992). Article  CAS  Google Scholar  * Ebara, Y. et al. Detection of recurrent fluorescence photons. _Phys. Rev. Lett._ 117, 133004

(2016). Article  ADS  PubMed  Google Scholar  * Chandrasekaran, V. et al. Determination of absolute recurrent fluorescence rate coefficients for . _J. Phys. Chem. Lett._ 5, 4078–4082 (2014).

Article  CAS  PubMed  Google Scholar  * Baer, T. & Hase, W. L. _Unimolecular Reaction Dynamics: Theory and Experiments_ (Oxford University Press, 1996). * Terzieva, R. & Herbst, E.

Radiative electron attachment to small linear carbon clusters and its significance for the chemistry of diffuse interstellar clouds. _Int. J. Mass. Spectrom._ 201, 135–142 (2000). Article 

CAS  Google Scholar  * Andersen, J. U., Bonderup, E. & Hansen, K. Thermionic emission from clusters. _J. Phys. B: At. Mol. Opt. Phys._ 35, R1–R30 (2002). ADS  CAS  Google Scholar  *

Chandrasekaran, V. et al. Formation and stabilization of by radiative electron attachment. _J. Chem. Phys._ 146, 094302 (2017). Article  ADS  Google Scholar  * Langevin, P. A fundamental

formula of kinetic theory. _Ann. Chim. Phys._ 5, 245–288 (1905). CAS  Google Scholar  * Kasperovich, V., Tikhonov, G. & Kresin, V. Low-energy electron capture by free C60 and the

importance of polarization interaction. _Chem. Phys. Lett._ 337, 55–60 (2001). Article  ADS  CAS  Google Scholar  * Abdurahman, A., Shukla, A. & Seifert, G. Ab initio many-body

calculations of static dipole polarizabilities of linear carbon chains and chainlike boron clusters. _Phys. Rev. B_ 66, 155423 (2002). Article  ADS  Google Scholar  * Namazian, M., Orangi,

N. & Noorbala, M. R. Thermodynamic stability and structural parameters of carbon nanoclusters. _J. Theor. Comput. Chem._ 13, 1450058 (2014). Article  CAS  Google Scholar  * Beyer, T.

& Swinehart, D. Algorithm 448: number of multiply-restricted partitions. _Commun. Acm._ 16, 379 (1973). Article  Google Scholar  * Guo, X.-G., Zhang, J.-L. & Zhao, Y. Ab initio

characterization of size dependence of electronic spectra for linear anionic carbon clusters (_n_ = 4–17). _J. Comput. Chem._ 33, 93–102 (2012). Article  PubMed  Google Scholar  * Giuffreda,

M., Deleuze, M. & François, J.-P. Structural, rotational, vibrational, and electronic properties of carbon cluster anions (_n_ = 3–13). _J. Phys. Chem. A._ 106, 8569–8582 (2002).

Article  CAS  Google Scholar  * House, J. E. _Principles of Chemical Kinetics_ (Academic Press, 2007). * Walsh, C., Harada, N., Herbst, E. & Millar, T. The effects of molecular anions on

the chemistry of dark clouds. _Astrophys. J._ 700, 752–761 (2009). Article  ADS  CAS  Google Scholar  * Elliott, C., Vijayakumar, V., Zink, W. & Hansen, R. National Instruments LabVIEW:

A programming environment for laboratory automation and measurement. _J. Assoc. Lab. Autom._ 12, 17–24 (2007). Article  Google Scholar  * Gross, E. K. & Dreizler, R. M. _Density

Functional Theory_ (Springer Science & Business Media, 2013). * Frisch, M. J. et al. _Gaussian 09, Revision D.01_. (Gaussian Inc., Wallingford, CT, 2013). Google Scholar  * Neese, F. The

ORCA program system. _Wiley Interdiscip. Rev.: Comput. Mol. Sci._ 2, 73–78 (2012). CAS  Google Scholar  * Adamo, C. & Barone, V. Toward reliable density functional methods without

adjustable parameters: The PBE0 model. _J. Chem. Phys._ 110, 6158–6170 (1999). Article  ADS  CAS  Google Scholar  * Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient

approximation made simple. _Phys. Rev. Lett._ 77, 3865 (1996). Article  ADS  CAS  PubMed  Google Scholar  * Grimme, S. Semiempirical GGA-type density functional constructed with a long-range

dispersion correction. _J. Comput. Chem._ 27, 1787–1799 (2006). Article  CAS  PubMed  Google Scholar  * Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab

initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. _J. Chem. Phys._ 132, 154104 (2010). Article  ADS  PubMed  Google Scholar  * Grimme, S.,

Ehrlich, S. & Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. _J. Comput. Chem._ 32, 1456–1465 (2011). Article  CAS  PubMed  Google Scholar

  * Johnson, E. R. & Becke, A. D. A post-Hartree-Fock model of intermolecular interactions. _J. Chem. Phys._ 123, 024101 (2005). Article  ADS  Google Scholar  * Johnson, E. R. &

Becke, A. D. A post-Hartree-Fock model of intermolecular interactions: Inclusion of higher-order corrections. _J. Chem. Phys._ 124, 174104 (2006). Article  ADS  PubMed  Google Scholar  *

Schäfer, A., Horn, H. & Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. _J. Chem. Phys._ 97, 2571–2577 (1992). Article  ADS  Google Scholar  * Weigend, F.

& Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. _Phys. Chem. Chem. Phys._ 7,

3297–3305 (2005). Article  CAS  PubMed  Google Scholar  * Szabados, Á. Theoretical interpretation of Grimme’s spin-component-scaled second order Møller-Plesset theory. _J. Chem. Phys._ 125,

214105 (2006). Article  ADS  PubMed  Google Scholar  * Grimme, S. Improved second-order møller-plesset perturbation theory by separate scaling of parallel-and antiparallel-spin pair

correlation energies. _J. Chem. Phys._ 118, 9095–9102 (2003). Article  ADS  CAS  Google Scholar  * Møller, C. & Plesset, M. S. Note on an approximation treatment for many-electron

systems. _Phys. Rev._ 46, 618–622 (1934). Article  ADS  MATH  Google Scholar  * Kozuch, S. & Martin, J. M. L. DSD-PBEP86: in search of the best double-hybrid DFT with spin-component

scaled MP2 and dispersion corrections. _Phys. Chem. Chem. Phys._ 13, 20104–20107 (2011). Article  CAS  PubMed  Google Scholar  * Perdew, J. P. Density-functional approximation for the

correlation energy of the inhomogeneous electron gas. _Phys. Rev. B_ 33, 8822–8824 (1986). Article  ADS  CAS  Google Scholar  * Neese, F., Wennmohs, F., Hansen, A. & Becker, U.

Efficient, approximate and parallel Hartree-Fock and hybrid DFT calculations. a ‘chain-of-spheres’ algorithm for the Hartree-Fock exchange. _Chem. Phys._ 356, 98–109 (2009). Article  ADS 

CAS  Google Scholar  * Sancho-Garcia, J.-C. & Adamo, C. Double-hybrid density functionals: merging wavefunction and density approaches to get the best of both worlds. _Phys. Chem. Chem.

Phys._ 15, 14581–14594 (2013). Article  CAS  PubMed  Google Scholar  * Kesharwani, M. K., Brauer, B. & Martin, J. M. L. Frequency and zero-point vibrational energy scale factors for

double-hybrid density functionals (and other selected methods): can anharmonic force fields be avoided? _J. Phys. Chem. A_ 119, 1701–1714 (2015). Article  CAS  PubMed  Google Scholar  *

MATLAB (R2013b). (The MathWorks Inc., Natick, MA, 2013). Download references ACKNOWLEDGEMENTS We would like to dedicate this paper to the memory of the late Professor Dr. Dirk Schwalm. This

work would not have been possible without his contributions and insightful comments. The research was supported by the Benoziyo Endowment Fund for the Advancement of Science. AUTHOR

INFORMATION Author notes * V. Chandrasekaran Present address: Department of Chemistry, School of Advanced Sciences, Vellore Institute of Technology, Vellore, 632014, India AUTHORS AND

AFFILIATIONS * Department of Particle Physics and Astrophysics, Weizmann Institute of Science, Rehovot, 7610001, Israel K. Saha, V. Chandrasekaran, O. Heber & D. Zajfman * Department of

Chemical Research Support, Weizmann Institute of Science, Rehovot, 7610001, Israel M. A. Iron * Department of Physics Core Facilities, Weizmann Institute of Science, Rehovot, 7610001, Israel

M. L. Rappaport Authors * K. Saha View author publications You can also search for this author inPubMed Google Scholar * V. Chandrasekaran View author publications You can also search for

this author inPubMed Google Scholar * O. Heber View author publications You can also search for this author inPubMed Google Scholar * M. A. Iron View author publications You can also search

for this author inPubMed Google Scholar * M. L. Rappaport View author publications You can also search for this author inPubMed Google Scholar * D. Zajfman View author publications You can

also search for this author inPubMed Google Scholar CONTRIBUTIONS Experiments and analysis of the experimental data were conducted by K.S. The experiment was designed by K.S. and V.C. The

experimental facilities were developed by O.H., M.L.R., and D.Z. Theoretical calculations were performed by K.S., V.C., and M.A.I. The manuscript was written by K.S. and O.H. All authors

discussed the results and commented on the paper. CORRESPONDING AUTHORS Correspondence to K. Saha or O. Heber. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing 

financial interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

ELECTRONIC SUPPLEMENTARY MATERIAL SUPPLEMENTARY INFORMATION PEER REVIEW FILE RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0

International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the

source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative

Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Saha, K., Chandrasekaran, V., Heber, O. _et al._ Ultraslow isomerization in

photoexcited gas-phase carbon cluster \({{\rm C}}_{10}^ -\). _Nat Commun_ 9, 912 (2018). https://doi.org/10.1038/s41467-018-03197-w Download citation * Received: 16 November 2017 * Accepted:

26 January 2018 * Published: 02 March 2018 * DOI: https://doi.org/10.1038/s41467-018-03197-w SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content:

Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative