ABSTRACT The coherent light source is one of the most important foundations in both optical physics studies and applied photonic devices. However, the whispering gallery microcavity, as a

prime platform for novel light sources, has the intrinsically chiral symmetry and severely rules out access to directional light output, all-optical flip-flops, efficient light extraction,

etc. Here, we demonstrate a reconfigurable symmetry-broken microlaser in an ultrahigh-Q whispering gallery microcavity with the symmetric structure, in which a chirality of lasing field is

empowered spontaneously by the optical nonlinear effect. Experimentally, the ratio of counter-propagating lasing intensities is found to exceed 160:1, and the chirality can be controlled

NANOCAVITIES Article Open access 08 July 2024 NON-HERMITIAN CHIRAL PHONONICS THROUGH OPTOMECHANICALLY INDUCED SQUEEZING Article 01 June 2022 A 2D CHIRAL MICROCAVITY BASED ON APPARENT

CIRCULAR DICHROISM Article Open access 09 April 2024 INTRODUCTION Coherent light sources lie at the heart of photonic integrated circuits and of fundamental physics1,2,3,4,5. Considerable

attention in this context has been dedicated to ultrahigh-_Q_ optical microcavities that have become indispensable in numerous high-performance coherent light sources with high

efficiency6,7,8. As a prominent platform, whispering-gallery-mode (WGM) microcavities, benefiting from ultrahigh-Q factors and small mode volumes, have witnessed significant development of

on-chip light sources ranging from orbital-angular-momentum lasers to soliton microcombs9,10,11,12,13,14. However, the intrinsic chiral symmetry of WGMs microcavity geometry and the

resulting equivalence between the two directions of light propagation in the cavity prevent many opportunities to further applications of microlasers, such as directional light

emission15,16, all-optical flip-flops17,18, and nonreciprocal light propagation19,20,21. Existing solutions to acquire the unidirectionality of the laser propagation in an ultrahigh-Q

microcavity are based on the explicit chiral-symmetry breaking of the micro-structures through gain-loss modulated system with \({\mathcal{PT}}\)-symmetry13,14, a shape deformation of the

cavity15,16, or an asymmetric scattering boundary22,23,24,25. The scalability and tunability of these preceding strategies are strongly limited, because the devices once fabricated impose a

prefixed chirality to the lasing mode and cannot meet the ever-increasing demands of dynamically controlling the directionality and chirality of the laser. For example, the controllable

optical bistability of the lasing direction can be used for an optical flip-flop17,18, and the balanced counter-propagating wave is also of importance for, such as, single nanoparticle

detection26,27 or dual frequency comb28. Thus, the controllable switch between the unidirectional and bidirectional emission is promising for the multiplex photonic devices. One proposed

solution is to work with a selectively pumped Brillouin laser, but satisfying the involved phase-matching condition poses a formidable challenge for any experimental implementation of this

concept20,21. Beyond the strategies by explicit symmetry breaking, the spontaneous symmetry breaking (SSB) of the counter-propagating optical field has been demonstrated recently in a

passive microcavity29,30, which holds potential to dynamically switch the direction of the propagating light. Nevertheless, it is still elusive for the SSB of a laser field in an active

microcavity due to the accompanying complex lasing dynamics. Moreover, the emission direction would also present randomness brought by the spontaneity of the lasing chirality, posing

obstacles for the controllable reconfigurability. In this work, we start from a symmetric WGM microcavity and experimentally realize a symmetry-broken Raman laser by extending the

fundamental concept of SSB into an active microcavity. The chiral symmetry of the lasing emission is broken spontaneously by the microcavity-enhanced optical Kerr nonlinearity. This SSB of

the Raman laser occurs above a threshold of a few tens of microwatts, and the ratio of counter-propagating emission intensities exceeds 160:1. Moreover, the chirality can be all-optically

and dynamically controlled by a bi-directional pump, and the threshold power of the SSB is adjustable using a nanotip scatterer. RESULTS THEORETICAL MODEL The microlaser operates based on

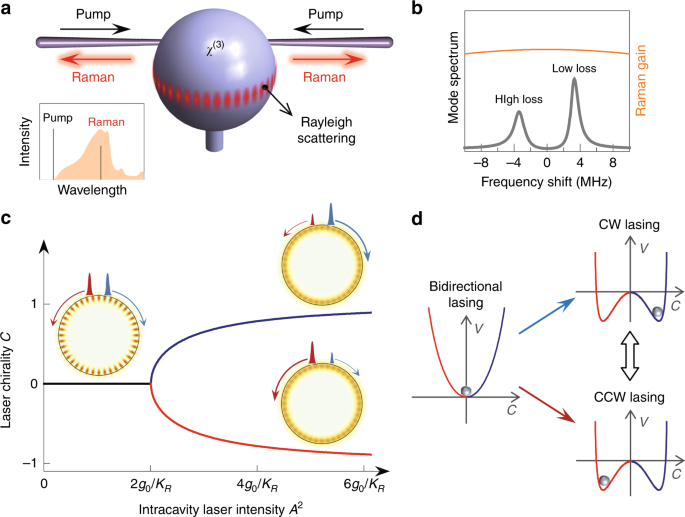
stimulated Raman scattering in a WGM microcavity (as shown in Fig. 1a)31,32,33. The corresponding Raman waves in clockwise (CW) and counterclockwise (CCW) directions are intrinsically

coupled and form two standing-wave supermodes by the inevitable Rayleigh scattering arising from the roughness of the surface34,35. Each of the two resulting supermodes emits in both

directions with equal CW and CCW intensity because of the chiral symmetry. However, only one supermode with the larger net gain will survive and consequently lase due to the mode clamping

(shown in Fig. 1b and “Methods”)33. In addition, the CW and CCW Raman waves are also nonlinearly scattered by the optical Kerr effect, in the form of self- and cross-phase

modulation29,30,31. Correspondingly, in the CW-CCW wave basis, the coupled-mode equation describing the evolution of Raman waves reads (see Supplementary Note 1),

$$\frac{{\rm{d}}{a}_{{\rm{R}},{\rm{m}}}}{{\rm{d}}t} \,= \,-\frac{\kappa }{2}{a}_{{\rm{R}},{\rm{m}}}+({G}_{{\rm{R}},{\rm{m}}}| {a}_{{\rm{P,m}}}{| }^{2}+{G}_{{\rm{R}},{\rm{m}}^{\prime} }|

{a}_{{\rm{P}},{\rm{m}}^{\prime} }{| }^{2}){a}_{{\rm{R}},{\rm{m}}}\\ +\, {\rm{i}}{g}_{0}{a}_{{\rm{R}},{\rm{m}}^{\prime} }+{\rm{i}}{K}_{{\rm{R}}}(| {a}_{{\rm{R}},{\rm{m}}}{| }^{2}+2|

{a}_{{\rm{R}},{\rm{m}}^{\prime} }{| }^{2}){a}_{{\rm{R}},{\rm{m}}},$$ (1) where _m_ and \(m^{\prime}\) (\(m^{\prime}\;\ne\;m\)) represent CW and CCW directions,

\({a}_{{\rm{R}},{\rm{m}}({\rm{m}}^{\prime} )}\) (\({a}_{{\rm{P}},{\rm{m}}({\rm{m}}^{\prime} )}\)) represents the Raman (pump) mode, _g_0 is the intrinsic coupling between the

counter-propagating Raman waves from the Rayleigh scattering; _κ_ is the decay rate of the passive Raman cavity mode, \({G}_{{\rm{R}},{\rm{m}}({\rm{m}}^{\prime} )}\) denotes the Raman gain

coefficient, and _K_R is the coefficient of Kerr nonlinearity (Supplementary Note 1). If not indicated otherwise, we will assume to work with an ideal medium, where

\({G}_{{\rm{R}},{\rm{m}}}={G}_{{\rm{R}},{\rm{m}}^{\prime} }\) due to the balanced forward and backward stimulated Raman scattering. As suggested by Eq. (1), the coupling between CW and CCW

Raman waves consists of both the linear Rayleigh scattering and the nonlinear scattering by the Kerr effect, resulting in an intensity-dependent effective coupling. When the nonlinearity is

turned off, the Raman laser circulates bidirectionally in the cavity as a conventional standing-wave field (Fig. 1c). As the nonlinear scattering strength increases with higher laser power,

the effective coupling can be reduced to zero with a particular phase condition, which corresponds to that the linear coupling is completely compensated by the nonlinear scattering36. Note

that this condition can only be reached for the supermode with the higher frequency29. Above this threshold, the chiral symmetry of the laser field spontaneously breaks and the original

standing-wave laser mode evolves into either one of two chiral states with a CW- or CCW-dominated laser propagation. This threshold Raman intensity of the chiral lasing is derived in

Methods, and shown by Fig. 1c. The resulting laser chirality \({\mathcal{C}}\) is conveniently quantified by the order parameter \({\mathcal{C}}\equiv

({P}_{{\rm{cw}}}-{P}_{{\rm{ccw}}})/({P}_{{\rm{cw}}}+{P}_{{\rm{ccw}}})\) as defined through the Raman power _P_cw(ccw) in the two counter-propagating directions. The physical nature of the

emergence of SSB can be visually revealed through the effective potential _V_ with a characteristic dependence on the chirality \({\mathcal{C}}\) (Fig. 1d), where the steady-state is found

at the minimum of the potential curve (see the detailed derivation in the “Methods” section). Below the SSB-threshold this potential only features a single minimum with a bidirectional

lasing mode and no chirality. Beyond the SSB-threshold this minimum splits into two such that the original standing-wave supermode becomes unstable. In this bistable regime either one of the

two chiral minima can be populated, in principle, but we will show in detail below how to selectively initialize a desired chiral mode through the external pump bias, resulting in a

dynamically switchable directionality of the laser. EXPERIMENTAL REALIZATION In the experiment, a silica microsphere resonator, with a diameter of around 30 μm and a Q factor of over 6 × 

107, is coupled with a tapered fiber, as illustrated in Fig. 1a and 2a. By continuously pumping in the 1470 nm band with power of 2 mW at room temperature, the Raman lasing in the 1570 nm

band is excited through stimulated Raman scattering (Fig. 2b). Here neither cascaded Raman scattering nor multimode lasing occurred. The Raman output waves are separated from the pump signal

by longpass filters, and the output Raman power is monitored in both directions on an oscilloscope. To demonstrate SSB with a fully symmetric system setting, the pump mode is excited on

both sides with identical power and polarization, as shown in Fig. 2a. The emergence of a symmetry-broken microlaser is depicted in Fig. 2c, d. The tunable laser scans through the pump mode

at a speed of  −2.2 THz/s in the blue-detuned region. As the scanning time grows, the frequency detuning between the input light and the pump mode decreases, resulting in an increasing

intracavity pump power. Right above the Raman lasing threshold, the CW and CCW output Raman powers first grow synchronously with increasing intracavity pump power. Such a bidirectional Raman

emission confirms that the chiral symmetry remains intact at this stage. At a sweeping time of 2.1 ms, a total Raman power of 114 μW is reached, where the chiral symmetry of the Raman laser

breaks spontaneously. In the chiral regime above these values, the CW (CCW) Raman power experiences a continuous growth, while the CCW (CW) Raman power is suppressed simultaneously, leading

to a CW (CCW) chiral laser in Fig. 2c (Fig. 2d). The dependence of chirality \({\mathcal{C}}\) on Raman power exhibits a balanced pitchfork bifurcation behavior, as plotted in Fig. 2e. Note

that here the direction of chirality is notably random, i.e., either CW or CCW, due to the spontaneous mechanism and the fully symmetric setting of the system. The chiral behaviors of the

spontaneously symmetry-broken lasers vary quantitatively from sample to sample because of the different _Q_ factors, mode volumes, intrinsic coupling strengths, etc. Among the different

modes for pump, a symmetry-broken Raman laser with a very low chirality-threshold power is obtained, accompanied by a larger chirality \({\mathcal{C}}\). The intensity ratio of the CW (CCW)

laser to CCW (CW) laser reaches beyond 160:1 with an absolute chirality of 0.988 and a threshold Raman power of 30 μW, as shown in Fig. 3a, b. Here the increasing chirality \({\mathcal{C}}\)

is bounded by the emergence of higher-order and multi-mode Raman lasing. The stability of the symmetry-broken Raman laser is further experimentally validated with a fixed-wavelength pump.

By employing the thermal self-lock technique37, the stable CW and CCW chiral Raman emissions are recorded for 4s in Fig. 3c, d, respectively, excluding that this behavior is just of

transient nature. The optical spectra of the emissions from the two directions also exhibit stable unidirectionality with high contrast, as shown in Fig. 3e, f. As aforementioned, the chiral

symmetry breaking emerges when the nonlinear scattering by the Kerr nonlinearity cancels out the intrinsic linear coupling, corresponding to the threshold of Raman intensity being

2_g_0_/K_R (see the “Methods” section). We now demonstrate that the proportionality between the threshold Raman intensity and the intrinsic coupling strength _g_0, as predicted above, is

directly accessible in the experiment (Fig. 4). In the corresponding measurements, a fiber nanotip (inset of Fig. 4c) is used as a Rayleigh scatterer to control the intrinsic coupling

strength, determined by the volume of the nanotip within the evanescent field of the cavity mode38. First, while the pump laser is muted, a probe laser is used to scan the transmission

spectrum of the Raman mode exhibiting a typical doublet, i.e., the two standing-wave supermodes arising from the intrinsic Rayleigh scattering. As the scatterer is moved closer to the

cavity, the splitting of the Raman mode changes, indicating an increased or decreased intrinsic coupling strength (Fig. 4a). For each of these configurations, we excite the pump mode to

study Raman lasing and the chirality of the laser associated with it (Fig. 4b). It is found that the symmetry-breaking threshold experiences an evident increase with larger intrinsic

coupling strength. Moreover, the dependence of the threshold power on the mode splitting exhibits a positive linear correlation (Fig. 4c) consistent with the theoretical prediction. In this

way we can thus dynamically switch between bi-directional and chiral emission of the laser by adjusting the intrinsic linear coupling that controls the threshold of breaking symmetry.

Furthermore, we show that a deterministic and reconfigurable direction of the chirality \({\mathcal{C}}\) can be obtained by adjusting the ratio of the CW to CCW pump intensity

_P_in,cw_/P_in,ccw. In the experiment, the pump powers from two sides are independently controlled by variable optical attenuators, and each experimental event of a realized laser chirality

is analyzed when the power is above the symmetry-breaking threshold. For each pump intensity ratio, more than 20 symmetry-broken-laser events are recorded during a period of time, which are

then averaged to showcase the preference in the direction of laser chirality. Figure 5a shows the dependence of the chirality direction on the imbalance in the two-sided pumping, averaged

over all the chiral laser events. Here the sign of \({\mathcal{C}}\in [-1,1]\) describes the direction of chirality in a specific Raman laser. When the pump intensities are balanced, the

random emergence of the CW and CCW chiral laser is equiprobable with an averaged sign of chirality being close to zero. Once the ratio in pump intensities becomes slightly unbalanced, the

directions of the chiral emissions exhibit a preference but are still not deterministic. When the CW-CCW (CCW-CW) ratio of pump intensities further increases to be over 1.4:1, the

unidirectional Raman emission becomes deterministic in CW- (CCW-) direction, whereby we achieve the desired and full control over the direction of the chiral laser emission. In the

deterministic chirality regime, the laser preferentially emits into the direction, along which the dominant pump light propagates. This phenomenon is mainly attributed to the slightly

asymmetric Raman gain _G_R,m and \({G}_{{\rm{R}},{\rm{m}}^{\prime} }\) brought by the directional pump within a non-ideal medium39. Besides, the occurrence of the deterministic chiral

direction is attributed to the pump-induced chiral performance, i.e., the intensity and phase differences between the two-sided inputs can control the emergence of chiral states as well as

the randomness. The asymmetric Raman gain can be described as \({G}_{{\rm{R}},{\rm{m}}}=(1+\delta ){G}_{{\rm{R}},{\rm{m}}^{\prime} }\) with the asymmetry factor _δ_. Through the theoretical

calculation (see Supplementary Note 2), it can be found that even though the Raman gain from two directions are only different slightly, the distinct chirality behavior appears, as shown in

Fig. 5b. For example, as for a positive asymmetry factor _δ_ of 10−4 (for which the forward Raman gain is slightly stronger than the backward gain), the chirality direction of the Raman

laser is completely random under the identical CW and CCW pump intensity. However, once the pump intensities are not balanced any more, the lasing direction becomes dependent on the dominant

direction of the pump, which is absent for the symmetric Raman gain. For a negative value of _δ_, the inverse phenomenon is obtained. To accurately model the actual situation in the

experiment we take into account that the phase of the input light fluctuates due to mechanical or thermal perturbations. Correspondingly, for every different pump ratio, we evaluate the

emergence of the laser chirality using equation (1) with 150 random phase differences between the two-sided inputs and plot the statistical diagram of the chiral events in Fig. 5c. The

dependence of the chirality sign on the input ratio is then averaged over these realizations, \(\langle {\rm{sgn}}({\mathcal{C}})\rangle\), resulting in the red curve of Fig. 5a that shows

good agreement with the experimental data. DISCUSSION In summary, we have demonstrated a reconfigurable symmetry-broken microlaser in a symmetric ultrahigh-Q WGM microcavity, which is free

from any delicate structure design. Such a chiral emitting Raman laser benefits from the Kerr nonlinearity and proves the long-standing prediction of SSB in an active microcavity induced by

third-order nonlinearity. Note that the directional laser can also be obtained by other mechanisms in semiconductors, depending on special properties of particular materials. For example, a

unidirectional Raman laser can emerge in a silicon ring resonator through the asymmetric nonlinear loss40 or the on-negligible longitudinal components of the optical field41. Besides, the

unidirectional lasing was also reported in III-V compound semiconductor ring lasers using self and cross-gain saturation effects from the carriers42,43. However, the limited Q factors of

these systems would strongly restrict further development and applications with ultralow power consumption. Our results extend nonlinear symmetric optics from the centimeter-scale to on-chip

micro-structures and, more importantly, from waveguides to microresonators. The mechanism behind our observations can be directly expanded to other optical microstructures and materials,

where the Raman gain could also be replaced by other nonlinear processes including those based on parametric amplification, quantum dots and rare-earth ions. METHODS LASING CONDITION AND

PUMP CLAMPING EFFECT When a cavity mode is lasing, the dissipation of the mode is completely compensated by the gain. Considering that the actual Raman mode is a standing-wave supermode

rather than an uncoupled propagating wave mode, we employ the coupled-mode equation with the supermode basis _a_1–_a_2 to investigate the lasing condition, and Eq. (1) is rewritten as,

$$\frac{{\rm{d}}{a}_{\mu }}{{\rm{d}}t}=-\frac{{\kappa }_{\mu }}{2}{a}_{\mu }+{G}_{{\rm{R}}}| {a}_{{\rm{P}}}{| }^{2}{a}_{\mu },$$ (2) where _κ__μ_ is the decay rate of the corresponding

standing-wave Raman mode. Note that here the Kerr nonlinearity term of the Raman mode in Eq. (1) is neglected, because the Raman light is extremely weak below the lasing threshold. As the

pump intensity ∣_a_P∣2 increases from zero, the total decay rates of both the low- and high-frequency standing-wave mode keep decreasing. When the increasing gain is strong enough to

compensate for the loss of one standing-wave mode with the lower decay rate \({\kappa }_{\min }\), the cavity mode reaches the lasing threshold. On the other hand, a stable lasing process

requires that the net gain (or loss) should remain zero, resulting in the pump intracavity power being clamped at the threshold \(| {a}_{{\rm{P}}}{| }^{2}={\kappa }_{\min

}/(2{G}_{{\rm{R}}})\). Therefore, only one mode can survive and lase due to the mode competition and pump clamping33. POTENTIAL WELL OF THE SYSTEM AND THE SYMMETRY-BREAKING THRESHOLD For the

stable lasing with balanced gain and loss, we can promote the amplitudes _a__μ_ to bosonic operators, e.g., \({a}^{* }\to \sqrt{\hslash {\omega }_{{\rm{R}}}}{a}^{\dagger }\), and construct

a Hamiltonian for the system, $$H = -\sum _{m={\rm{cw}},{\rm{ccw}}} [\hslash {g}_{0}{a}_{m^{\prime} }^{\dagger }{a}_{m}+\frac{1}{2}{\hslash }^{2}{K}_{{\rm{R}}}{\omega

}_{{\rm{R}}}({a}_{m}^{\dagger }{a}_{m}^{\dagger }{a}_{m}{a}_{m}+{a}_{m}^{\dagger }{a}_{m^{\prime} }^{\dagger }{a}_{m}{a}_{m^{\prime} }\\ \ \;\,+\,{a}_{m}^{\dagger }{a}_{m^{\prime} }^{\dagger

}{a}_{m^{\prime} }{a}_{m})].$$ (3) By employing the Bloch sphere parameters, \({a}_{{\rm{cw}}}=A{{\rm{e}}}^{{\rm{i}}\alpha }\cos (\theta /2)\) and

\({a}_{{\rm{ccw}}}=A{{\rm{e}}}^{{\rm{i}}\alpha }\sin (\theta /2){{\rm{e}}}^{{\rm{i}}\varphi }\) will be used from here on29, where _A_e_i__α_ is the total complex amplitude for the Raman

field, 0 ≤ _θ_ ≤ _π_ represents the composition of the propagating waves, and 0 ≤ _φ_ < 2_π_ is the relative phase. The chirality can be characterized by \({\mathcal{C}}=(|

{a}_{{\rm{cw}}}{| }^{2}-| {a}_{{\rm{ccw}}}{| }^{2})/(| {a}_{{\rm{cw}}}{| }^{2}+| {a}_{{\rm{ccw}}}{| }^{2})\equiv \cos \theta\). In this case, the behavior of symmetry breaking can also be

made clear via the classical Hamiltonian, $$H=-\frac{{g}_{0}}{{\omega }_{{\rm{R}}}}{A}^{2}\sin \theta \cos \varphi -\frac{{K}_{{\rm{R}}}}{4{\omega }_{{\rm{R}}}}{A}^{4}(2+{\sin }^{2}\theta

),$$ (4) from which the equation of motion of the chirality is derived,

$$\ddot{{\mathcal{C}}}=-{g}_{0}^{2}{\mathcal{C}}+\frac{{K}_{R}{A}^{2}}{2}{\mathfrak{C}}\sqrt{{g}_{0}^{2}(1-{{\mathcal{C}}}^{2})-{\dot{{\mathcal{C}}}}^{2}},$$ (5) where dots above variables

represent derivatives with respect to time. For steady states requiring \(\dot{{\mathcal{C}}}=0\), and we can rewrite the equation as

$$\frac{1}{{g}_{0}^{2}\sqrt{1-{{\mathcal{C}}}^{2}}}\ddot{{\mathcal{C}}}=-\frac{\partial V}{\partial {\mathcal{C}}},\ \

V=1-\sqrt{1-{{\mathcal{C}}}^{2}}-\frac{{K}_{{\rm{R}}}{A}^{2}}{4{g}_{0}}{{\mathcal{C}}}^{2}$$ (6) By analogy of classical mechanics \(m\ddot{x}=-\partial V/\partial x\), the steady state can

only be found at the minimum of this potential of chirality _V_. Particularly, the threshold point _A_2 = 2_g_0_/K_R is indicated by a zero second-order derivative, resulting the symmetry

breaking threshold of output Raman power being \({P}_{{\rm{R}},{\rm{th}}}=| \sqrt{{\kappa }_{{\rm{in}},{\rm{R}}}}A{| }^{2}=(2{\kappa }_{{\rm{in}},{\rm{R}}}{g}_{0})/{K}_{{\rm{R}}}\), where

_κ_in,R is the fiber-cavity coupling rate for the Raman mode. DATA AVAILABILITY The data that support the plots within this paper and other findings of this study are available from the

corresponding author upon reasonable request. Source data for Figs. 2–5 are available at https://doi.org/10.6084/m9.figshare.11439357. CODE AVAILABILITY The codes that support the plots

within this paper and other findings of this study are available from the corresponding author upon reasonable request. REFERENCES * Bittner, S. et al. Suppressing spatiotemporal lasing

instabilities with wave-chaotic microcavities. _Science_ 351, 1225–1231 (2018). Article  ADS  MathSciNet  MATH  CAS  Google Scholar  * Gaeta, A. L., Lipson, M. & Kippenberg, T. J.

Photonic-chip-based frequency combs. _Nat. Photon._ 13, 158–169 (2019). Article  ADS  CAS  Google Scholar  * Liang, D. & Bowers, J. E. Recent progress in lasers on silicon. _Nat.

Photon._ 4, 511–517 (2010). Article  ADS  CAS  Google Scholar  * Ma, R. M., Oulton, R. F., Sorger, V. J., Bartal, G. & Zhang, X. Room-temperature sub-diffraction-limited plasmon laser by

total internal reflection. _Nat. Mater._ 10, 110–113 (2011). Article  ADS  CAS  PubMed  Google Scholar  * Zambon, N. C. et al. Optically controlling the emission chirality of microlasers.

_Nat. Photon._ 13, 283–288 (2019). Article  ADS  CAS  Google Scholar  * Vahala, K. J. Optical microcavities. _Nature_ 424, 839–846 (2003). Article  ADS  CAS  PubMed  Google Scholar  * Feng,

S. et al. Silicon photonics: from a microresonator perspective. _Laser Photon. Rev._ 6, 145–177 (2012). Article  ADS  CAS  Google Scholar  * Ward, J. & Benson, O. WGM microresonators:

sensing, lasing and fundamental optics with microspheres. _Laser Photon. Rev._ 5, 553–570 (2011). Article  ADS  CAS  Google Scholar  * Kippenberg, T. J., Gaeta, A. L., Lipson, M. &

Gorodetsky, M. L. Dissipative Kerr solitons in optical microresonators. _Science_ 361, eaan8083 (2018). Article  PubMed  CAS  Google Scholar  * Peng, B. et al. Loss-induced suppression and

revival of lasing. _Science_ 346, 328–332 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Hodaei, H., Miri, M. A., Heinrich, M., Christodoulides, D. N. & Khajavikhan, M.

Parity-time-symmetric microring lasers. _Science_ 346, 975–978 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Feng, L., Wong, Z. J., Ma, R. M., Wang, Y. & Zhang, X. Single-mode

laser by parity-time symmetry breaking. _Science_ 346, 972–975 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Miao, P. et al. Orbital angular momentum microlaser. _Science_ 353,

464–467 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Feng, L., El-Ganainy, R. & Ge, L. Non-Hermitian photonics based on parity-time symmetry. _Nat. Photon._ 11, 752–762 (2017).

Article  ADS  CAS  Google Scholar  * Jiang, X.-F., Zou, C.-L., Wang, L., Gong, Q. & Xiao, Y.-F. Whispering-gallery microcavities with unidirectional laser emission. _Laser Photon. Rev._

10, 40–61 (2016). Article  ADS  CAS  Google Scholar  * Cao, H. & Wiersig, J. Dielectric microcavities: model systems for wave chaos and non-Hermitian physics. _Rev. Mod. Phys._ 87,

61–111 (2015). Article  ADS  MathSciNet  CAS  Google Scholar  * Hill, M. T. et al. A fast low-power optical memory based on coupled micro-ring lasers. _Nature_ 432, 206–209 (2004). Article 

ADS  CAS  PubMed  Google Scholar  * Liu, L. et al. An ultra-small, low-power, all-optical flip-flop memory on a silicon chip. _Nat. Photon._ 4, 182–187 (2010). Article  ADS  CAS  Google

Scholar  * Fan, L. et al. An all-silicon passive optical diode. _Science_ 335, 447–450 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Dong, C.-H. et al. Brillouin-scattering-induced

transparency and non-reciprocal light storage. _Nat. Commun._ 6, 6193 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Kim, J., Kuzyk, M. C., Han, K., Wang, H. & Bahl, G.

Non-reciprocal Brillouin scattering induced transparency. _Nat. Phys._ 11, 275–280 (2015). Article  CAS  Google Scholar  * Kim, M., Kwon, K., Shim, J., Jung, Y. & Yu, K. Partially

directional microdisk laser with two Rayleigh scatterers. _Opt. Lett._ 39, 2423–2426 (2014). Article  ADS  PubMed  Google Scholar  * Peng, B. et al. Chiral modes and directional lasing at

exceptional points. _Proc. Natl Acad. Sci. USA_ 113, 6845–6850 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Wiersig, J. Enhancing the sensitivity of frequency and

energy splitting detection by using exceptional points: application to microcavity sensors for singleparticle detection. _Phys. Rev. Lett._ 112, 203901 (2014). Article  ADS  CAS  Google

Scholar  * Chen, W., Özdemir, Ş. K., Zhao, G., Wiersig, J. & Yang, L. Exceptional points enhance sensing in an optical microcavity. _Nature_ 548, 192–196 (2017). Article  ADS  CAS 

PubMed  Google Scholar  * Li, B.-B. et al. Single nanoparticle detection using split-mode microcavity Raman lasers. _Proc. Natl Acad. Sci. USA_ 111, 14657–14662 (2014). Article  ADS  CAS 

PubMed  PubMed Central  Google Scholar  * Özdemir, Ş. K. et al. Highly sensitive detection of nanoparticles with a self-referenced and self-heterodyned whispering-gallery Raman microlaser.

_Proc. Natl Acad. Sci. USA_ 111, E3836–E3844 (2014). Article  PubMed  CAS  PubMed Central  Google Scholar  * Yang, Q.-F., Yi, X., Yang, K. Y. & Vahala, K. J. Counter-propagating solitons

in microresonators. _Nat. Photon._ 11, 560–564 (2017). Article  CAS  Google Scholar  * Cao, Q.-T. et al. Experimental demonstration of spontaneous chirality in a nonlinear microresonator.

_Phys. Rev. Lett._ 118, 033901 (2017). Article  ADS  PubMed  Google Scholar  * DelBino, L., Silver, J. M., Stebbings, S. L. & Del’Haye, P. Symmetry breaking of counter-propagating light

in a nonlinear resonator. _Sci. Rep._ 7, 43142 (2017). Article  ADS  CAS  Google Scholar  * Boyd,  R. W.  _Nonlinear Optics_ (Academic, 2003). * Spillane, S. M., Kippenberg, T. J. &

Vahala, K. J. Ultralow-threshold Raman laser using a spherical dielectric microcavity. _Nature_ 415, 621–623 (2002). Article  ADS  CAS  PubMed  Google Scholar  * Kippenberg, T. J., Spillane,

S. M., Min, B. & Vahala, K. J. Theoretical and experimental study of stimulated and cascaded Raman scattering in ultrahigh-Q optical microcavities. _IEEE J. Quantum Electron_ 10,

1219–1228 (2004). Article  CAS  Google Scholar  * Kippenberg, T. J., Spillane, S. M. & Vahala, K. J. Modal coupling in traveling-wave resonators. _Opt. Lett._ 27, 1669–1671 (2002).

Article  ADS  CAS  PubMed  Google Scholar  * Mazzei, A. et al. Controlled coupling of counterpropagating whispering-gallery modes by a single Rayleigh scatterer: a classical problem in a

quantum optical light. _Phys. Rev. Lett._ 99, 173603 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Burkhardt, S., Liertzer, M., Krimer, D. O. & Rotter, S. Steady-state _ab initio_

laser theory for fully or nearly degenerate cavity modes. _Phys. Rev. A_ 92, 013847 (2015). Article  ADS  CAS  Google Scholar  * Carmon, T., Yang, L. & Vahala, K. J. Dynamical thermal

behavior and thermal self-stability of microcavities. _Opt. Express_ 12, 4742–4750 (2004). Article  ADS  PubMed  Google Scholar  * Zhu, J., Özdemir, Ş. K., He, L. & Yang, L. Controlled

manipulation of mode splitting in an optical microcavity by two Rayleigh scatterers. _Opt. Express_ 18, 23535–23543 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Maier, M., Kaiser, W.

& Giordmaine, J. A. Backward stimulated Raman scattering. _Phys. Rev._ 177, 580 (1969). Article  ADS  CAS  Google Scholar  * Vermeulen, N. Lasing directionality and polarization

behavior in continuous-wave ring Raman lasers based on micro- and nano-scale silicon waveguides. _J. Lightwave Technol._ 29, 2180–2190 (2011). Article  ADS  Google Scholar  * Krause, M.,

Renner, H. & Brinkmeyer, E. Optical isolation in silicon waveguides based on nonreciprocal Raman amplification. _Electron. Lett._ 44, 691–693 (2008). Article  Google Scholar  * Sorel, M.

et al. Alternate oscillations in semiconductor ring lasers. _Opt. Lett._ 27, 1992–1994 (2002). Article  ADS  CAS  PubMed  Google Scholar  * Trita, A. et al. All-optical directional

switching in bistable semiconductor-ring lasers. _IEEE J. Quantum Electronics_ 49, 877–885 (2013). Article  ADS  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS The authors thank

Z.-W. Zhou, B.-B. Li, L. Ge, M. Amezcua, C.-H. Dong, J. Wiersig, J.-H. Chen and Q.-F. Yang for helpful discussions. This project is supported by the National Key R&D Program of China

(Grants No. 2018YFB2200401 and No. 2016YFA0301302), NSFC (Grants No. 11825402, No. 11654003, No. 61435001, and No. 11527901), Beijing Academy of Quantum Information Sciences (Y18G20), Key

R&D Program of Guangdong Province (2018B030329001) and High-performance Computing Platform of Peking University. AUTHOR INFORMATION Author notes * These authors contributed equally:

Qi-Tao Cao, Ruishan Liu, Heming Wang. AUTHORS AND AFFILIATIONS * State Key Laboratory for Mesoscopic Physics and Frontiers Science Center for Nano-optoelectronics, School of Physics, Peking

University, Beijing, 100871, China Qi-Tao Cao, Ruishan Liu, Heming Wang, Yu-Kun Lu, Qihuang Gong & Yun-Feng Xiao * Department of Electrical and Computer Engineering, National University

of Singapore, Singapore, 117583, Singapore Cheng-Wei Qiu * Institute for Theoretical Physics, Vienna University of Technology (TU Wien), Vienna, A-1040, Austria, EU Stefan Rotter *

Collaborative Innovation Center of Quantum Matter, Beijing, 100871, China Qihuang Gong & Yun-Feng Xiao * Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan,

030006, China Qihuang Gong & Yun-Feng Xiao * Peking University Yangtze Delta Institute of Optoelectronics, Nantong, 226010, Jiangsu, China Qihuang Gong & Yun-Feng Xiao Authors *

Qi-Tao Cao View author publications You can also search for this author inPubMed Google Scholar * Ruishan Liu View author publications You can also search for this author inPubMed Google

Scholar * Heming Wang View author publications You can also search for this author inPubMed Google Scholar * Yu-Kun Lu View author publications You can also search for this author inPubMed 

Google Scholar * Cheng-Wei Qiu View author publications You can also search for this author inPubMed Google Scholar * Stefan Rotter View author publications You can also search for this

author inPubMed Google Scholar * Qihuang Gong View author publications You can also search for this author inPubMed Google Scholar * Yun-Feng Xiao View author publications You can also

search for this author inPubMed Google Scholar CONTRIBUTIONS Q.-T.C. and R.L. fabricated the microcavity samples, built the experimental set-up and carried out measurements. H.W., Q.-T.C.,

and Y.-K.L. built the theoretical model. Q.-T.C., R.L., H.W., Y.-K.L., C.-W.Q., S.R., Q.G., and Y.-F.X. analysed the data, wrote the manuscript and contributed to the discussion. Y.-F.X.

conceived the idea and designed the experiment. Y.-F.X. and Q.G. supervised the project. CORRESPONDING AUTHOR Correspondence to Yun-Feng Xiao. ETHICS DECLARATIONS COMPETING INTERESTS The

authors declare no competing interests. ADDITIONAL INFORMATION PEER REVIEW INFORMATION _Nature Communications_ thanks the anonymous reviewer(s) for their contribution to the peer review of

this work. PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY

INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution

and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if

changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the

material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to

obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS

ARTICLE Cao, QT., Liu, R., Wang, H. _et al._ Reconfigurable symmetry-broken laser in a symmetric microcavity. _Nat Commun_ 11, 1136 (2020). https://doi.org/10.1038/s41467-020-14861-5

Download citation * Received: 23 July 2019 * Accepted: 05 February 2020 * Published: 28 February 2020 * DOI: https://doi.org/10.1038/s41467-020-14861-5 SHARE THIS ARTICLE Anyone you share

the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer

Nature SharedIt content-sharing initiative