ABSTRACT In a molecule formed by two atoms, energy difference between bonding and antibonding orbitals depends on distance between the two atoms. However, exploring molecular orbitals of two

natural atoms with tunable distance has remained an outstanding experimental challenge. Graphene quantum dots can be viewed as relativistic artificial atoms, thus offering a unique platform

to study molecular physics. Here, through scanning tunneling microscope, we create and directly visualize the formation process of relativistic artificial molecules based on two coupled

graphene quantum dots with tunable distance. Our study indicates that energy difference between the bonding and antibonding orbitals of the lowest quasibound state increases linearly with

whispering-gallery modes in the artificial atoms to figure-eight orbitals in the artificial molecules is directly imaged. The ability to resolve the coupling and orbitals of the

relativistic artificial molecule at the nanoscale level yields insights into the behavior of quantum-relativistic matter. SIMILAR CONTENT BEING VIEWED BY OTHERS GIANT ORBITAL MAGNETIC

MOMENTS AND PARAMAGNETIC SHIFT IN ARTIFICIAL RELATIVISTIC ATOMS AND MOLECULES Article 06 March 2023 ORBITAL HYBRIDIZATION IN GRAPHENE-BASED ARTIFICIAL ATOMS Article 26 February 2025 COULOMB

INTERACTIONS AND MIGRATING DIRAC CONES IMAGED BY LOCAL QUANTUM OSCILLATIONS IN TWISTED GRAPHENE Article Open access 14 February 2025 INTRODUCTION Quantum dots (QDs) can be viewed as

artificial atoms due to their abilities to confine electrons into atomic-like discrete energy levels1,2,3,4,5. With reducing the distance, orbitals of two coupled QDs can linearly combine to

form two new molecular-like states, i.e., the bonding and antibonding molecular orbitals, thus creating artificial molecules6. Artificial molecules not only provide significant advantages

in the study of atomic and molecular physics, but also play a vital role in the fabrication of quantum devices. Therefore, many efforts have been devoted to fabricate and study the

artificial molecules, including direct growing of traditional semiconductor artificial molecules7,8,9,10,11,12,13,14,15,16, gate-defined artificial molecules17,18,19,20,21,22,23, atomic

defects induced artificial molecules24,25,26, graphene heterojunction artificial molecules27,28,29, and so on. However, the systematic study of the evolution from the artificial atoms to the

artificial molecules has been only achieved for non-relativistic fermions24,25,26, while it remains lacking for relativistic fermions due to the difficulty in achieving continuous and

precise control of the coupling strength. Here, by applying scanning tunneling microscope (STM) tip pulses to a graphene/WSe2 heterostructure, we create two almost identical graphene/WSe2

heterostructure quantum dots (GQDs), and continuously tune the distance between the two GQDs with nanoscale precision. In this process, the two GQDs evolve from two artificial atoms to an

artificial molecule with clear bonding and antibonding states. Our experiment supported by theoretical calculations indicates that the energy spacing of the bonding and antibonding states

formed by the lowest quasibound state varies linearly with the inverse of the distance. This phenomenon is unique to relativistic artificial molecules and is different from that predicted in

semiconductor artificial molecules7,9,13,15,16,30,31,32,33. For quasibound states with higher orbital momenta, we observe figure-eight molecular orbits29 and repulsive circular orbits from

two coupled ring-like whispering-gallery modes (WGMs). The energy spacing between them is half of that in a single GQD, which arises from the fact that the length of the molecular-like orbit

is about twice than that of the atomic-like orbit. Spatial distributions of the molecular orbitals in the artificial molecule with custom-designed coupling are directly imaged using STM and

they are also reproduced well by our theoretical calculations. RESULTS In our experiment, high-quality graphene/WSe2 heterostructure was obtained by wet transfer technology of a graphene

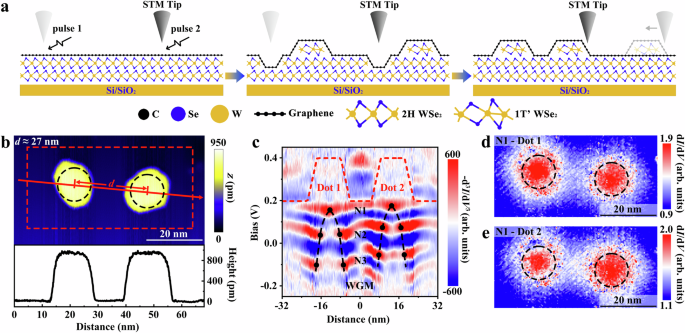
monolayer on mechanical-exfoliated thick 2H-phase WSe2 sheets28,34,35,36 (see Methods section for details of fabrication). Figure 1a shows a schematic of the strategy for fabricating and

manipulating the GQDs. As reported previously, a nanoscale pit and a 1 T’-phase monolayer WSe2 island can be created at the interface of the graphene/WSe2 heterostructure by using an STM tip

pulse36. The different doping levels of the 2H-phase and 1 T’-phase WSe2 to the supported graphene introduce a sharp electronic junction, which generates a nanoscale GQD in the continuous

graphene monolayer. By applying pulses of the same parameters to the STM tip, we created two almost identical GQDs (see Supplementary Fig. 1 for STM characterizations of the two GQDs). In

order to reduce the impact of the pits on the electrical properties of the GQDs, the two GQDs are moved to a flat area away from the pits. Then, the distance \(d\) between the two GQDs is

tuned continuously with nanoscale precision to change the coupling strength between them (see Methods and Supplementary Note 2 for the details of manipulation and Supplementary Fig. 2 for

more examples of manipulating other GQDs). Figure 1b shows a representative STM image of two GQDs with a distance _d_ ≈ 27 nm and the profile line across the GQDs indicates that they are

generated by two WSe2 monolayer islands. Figure 1c shows the \(-{{{{\rm{d}}}}}^{3}I/{{{\rm{d}}}}{V}^{3}\) scanning tunneling spectroscopy (STS) map measured across the centers of the two

GQDs indicated by the red line in Fig. 1b (see Supplementary Fig. 3 for the comparison of \({{{\rm{d}}}}I/{{{\rm{d}}}}V\) and \(-{{{{\rm{d}}}}}^{3}I/{{{\rm{d}}}}{V}^{3}\) STS maps and

Supplementary Note 4 for discussion about the use of \(-{{{{\rm{d}}}}}^{3}I/{{{\rm{d}}}}{V}^{3}\) STS maps). The confined potential introduced by the 1 T’-phase WSe2 islands generates a

series of quasibound states in the GQDs. The shape of the potential well here is not very broad or deep, and combined with the characteristics of massless Dirac fermions in graphene, which

causes most of the quasibound states outside the potential well (see Supplementary Note 5 for discussions on the origins of the quasibound states). Due to the similar size of the two GQDs,

the energies of the quasibound states in each GQD are almost the same, which is necessary for them to couple to form the bonding and antibonding orbitals according to molecular orbital

theory6. However, at this distance ~ 27 nm, the coupling between the two GQDs is very weak and the system can be regarded as two isolated GQDs approximately. To explicitly show this, we

carried out the energy-fixed \({{{\rm{d}}}}I/{{{\rm{d}}}}V\) mappings, which reflect the spatial distributions of the LDOS, at the N1 of the two GQDs, as shown in Fig. 1d, e. Due to the two

GQDs being almost identical, their levels are approximately degenerate and the spatial distribution of the N1 of the dot 1 is almost the same as that of the dot 2. The electronic states of

the N1 are mainly localized in the centers of each GQD, which is similar as that of an isolated GQD, further confirming that there is no significant coupling between the two GQDs. To fully

understand the observed quasibound states, the confined potential along one of the GQDs is measured according to the spatial dependence of the Dirac point \({E}_{{{{\rm{D}}}}}\) (see

Supplementary Fig 1d and 1h) and it can be approximately described by an electrostatic potential as follows:

$${V}_{{{{\rm{s}}}}}\left(r\right)=\left\{\begin{array}{c}{V}_{{{{\rm{in}}}}},\,\\ {V}_{{{{\rm{in}}}}}-k\left(r-{r}_{{{{\rm{in}}}}}\right)\\

{V}_{{{{\rm{out}}}}},\end{array}\right.\,\begin{array}{c}r\, < \,{r}_{{{{\rm{in}}}}}\\ {r}_{{{{\rm{in}}}}}\, < \,r\, < \,{r}_{{{{\rm{out}}}}}\\ r\, >

\,{r}_{{{{\rm{out}}}}}\end{array},$$ (1) where \(r\) is the distance from the center of GQD, \({r}_{{{{\rm{in}}}}}\) is the radius of the GQD, and \({V}_{{{{\rm{in}}}}}\) and

\({V}_{{{{\rm{out}}}}}\) are the constant electrostatic potentials inside and outside the GQD due to the screening effect (see Supplementary Note 6 for more details of

\({V}_{{{{\rm{s}}}}}\left(r\right)\)). Our theoretical calculation based on the confined potential well reproduces the main features of the quasibound states observed in our experiment and

confirms that the observed quasibound states are formed via the WGMs in an isolated GQD27,28,34,35,36,37,38,39,40,41,42,43,44 (see Supplementary Fig. 4). Therefore, the lowest quasibound

state exhibits a maximum in the center of the GQD and higher-energy quasibound states with higher angular momenta display ring-like structures along the edge of the GQD. To explore molecular

states formed by the two GQDs, we systematically decreased the distance between the two GQDs and studied their quasibound states. By moving one GQD to the other through STM tip

manipulation, twelve different distances ranging from 30 nm to 12 nm between the two GQDs are set in our experiment (see Supplementary Fig. 5 for STM images of the two GQDs with different

distances). Figure 2 shows representative results of the two GQDs with three different distances. For the distance _d_ > 21 nm, as shown in Fig. 1, the coupling between the two GQDs is

very weak and the quasibound states of the two GQDs are almost the same as that of the isolated GQD. By decreasing the distance to 21 nm > _d_ > 14 nm, the lowest quasibound states of

the two GQDs are slightly split, as shown in Fig. 2b, e. Such a result reminds us of the formation of the molecular states27,28,29. Then, the two states split from the lowest quasibound

states N1 of the two GQDs can be viewed as the bonding (N1 + ) and antibonding (N1-) states of the newly formed artificial molecule. The same conclusion can also be obtained from the

energy-fixed \({{{\rm{d}}}}I/{{{\rm{d}}}}V\) mappings. Figures 2c, f show the LDOS distributions of the two GQDs that are attractive at the bonding state and repulsive at the antibonding

state, which are consistent with the formation of the molecular states. By decreasing the distance from 18 nm to 15 nm, the potential fields of the two GQDs are strongly overlapped, as

indicated by the black dashed line in Fig. 2e. Then, the bonding and antibonding states become more pronounced and the energy splitting between them becomes larger, as shown in Fig. 2e, f.

By further decreasing the distance to _d_ < 14 nm, two GQDs are almost in contact. In this case, the potential fields of them are translated from two circular GQDs into a single

elliptical-like GQD, as shown in Fig. 2h, i (see Supplementary Figs. 6 and 7 for more \(-{{{{\rm{d}}}}}^{3}I/{{{\rm{d}}}}{V}^{3}\) STS maps and energy-fixed \({{{\rm{d}}}}I/{{{\rm{d}}}}V\)

mappings of other distances and see Supplementary Fig. 8 for the \({{{\rm{d}}}}I/{{{\rm{d}}}}V\) STS maps of all the measured distances). To further show the differences of the spatial

distributions of N1+ and N1- between different distances more directly, the intensities of STS signals as cross section of the molecules extracted from the energy-fixed

\({{{\rm{d}}}}I/{{{\rm{d}}}}V\) mappings at the N1+ and N1- for various distances are plotted in Supplementary Fig. 9. So far, we have realized the evolution from two atomic-like states into

molecular-like states in two GQDs through tip manipulation. To fully understand our experimental results, we calculated the evolution of the electronic properties of the two GQDs (see

Methods section for the model of theoretical simulations). To describe the coupling between two GQDs, we set a molecular potential field \({V}_{{{{\rm{m}}}}}\left({{{\bf{r}}}}\right)\),

which represents the superposition of the potential fields of two GQDs. Due to the fixed doping level of the 1 T’-phase WSe2 on graphene, the maximum value of

\({V}_{{{{\rm{m}}}}}\left({{{\bf{r}}}}\right)\) should not exceed the potential in the single GQD (\({V}_{{{{\rm{in}}}}}\)), therefore, we cut the value of

\({V}_{{{{\rm{m}}}}}\left({{{\bf{r}}}}\right)\) as \({V}_{{{{\rm{in}}}}}\) once it is larger than \({V}_{{{{\rm{in}}}}}\). That is, the molecular potential field

\({V}_{{{{\rm{m}}}}}\left({{{\bf{r}}}}\right)\) is set as:

$${V}_{{{{\rm{m}}}}}\left({{{\bf{r}}}}\right)=\left\{\begin{array}{cc}{V}_{{{{\rm{s}}}}}\left({r}_{1}\right)+{V}_{{{{\rm{s}}}}}\left({r}_{2}\right)-{V}_{{{{\rm{out}}}}}&{V}_{{{{\rm{s}}}}}\left({r}_{1}\right)+{V}_{{{{\rm{s}}}}}\left({r}_{2}\right)\le

{V}_{{{{\rm{in}}}}}\\ {V}_{{{{\rm{in}}}}}&{{V}_{{{{\rm{s}}}}}\left({r}_{1}\right)+{V}_{{{{\rm{s}}}}}\left({r}_{2}\right) \, > \, {V}_{{{{\rm{in}}}}}}\end{array}\,\right.,$$ (2) where

\({{{\bf{r}}}}=(x,y)\) is the position coordinate, and \({r}_{1}=|{{{\bf{r}}}}-\left(\frac{d}{2},0\right)|\) and \({r}_{2}=|{{{\bf{r}}}}-\left(-\frac{d}{2},0\right)|\) are the distances

from the centers of the dot 1 and dot 2, respectively. In the numerical simulation, the two GQDs are set at x axis with the inter-dot distance _d_. Figure 3a–f show the calculated LDOS

space-energy maps and the corresponding energy-fixed LDOS mappings of the bonding and antibonding states at the same distances as in Fig. 2, which are in good agreement with the experimental

results, thus further supporting our qualitative understanding (see Supplementary Figs. 10 and 11 for more LDOS space-energy maps and energy-fixed LDOS mappings with other distances,

respectively. See Supplementary Note 15 for the evolution of the quasibound states with distance smaller than 12 nm.). Both our experiments and theoretical simulations indicate that the

coupling between the two GQDs becomes stronger with decreasing the distance. To quantitatively show this, Fig. 3g summarizes the distance-dependent splitting (Δ_E_) of the lowest quasibound

states (N1+ and N1-) of the two GQDs obtained by both experiment and theoretical simulation (see Supplementary Note 16 for the method of extracting experimental results in Fig. 3g). The

obtained Δ_E_ in experiment and theory are quite similar and both results show that the relation between Δ_E_ and \(1/d\) is approximately linear (see Supplementary Note 17 for the

parameters of the linear fits in Fig. 3g). Theoretically, the bonding and antibonding states of the artificial molecules are formed by the overlapping of the electron wave functions of the

artificial atoms, and they can be also viewed as the quasibound states of the new molecular potential field with the effective confined size that is approximately proportion to the inter-dot

distance \(d\), as shown in the inset of Fig. 3g. Combining with the linear dispersion relation of massless Dirac fermions in graphene with Fermi velocity \({v}_{{{{\rm{F}}}}}\), the energy

spacing of the bonding and antibonding states Δ_E_ is approximatively proportional to \({\hslash v}_{{{{\rm{F}}}}}/d\). Therefore, this phenomenon underscores the uniqueness of the

relativistic artificial molecules compared with conventional molecules realized by coupled natural atoms or semiconductor QDs (see Supplementary Fig. 16 for the relation between Δ_E_ and

\(1/d\) of conventional molecules, see Supplementary Figs. 17 and 18 for the evolution of the molecular states and relation between Δ_E_ and \(1/d\) of the coupled 1 T’-phase WSe2 QDs). The

slight deviation of the slopes between experiment and simulation is probably due to the deviation in the experimental Fermi velocity from \({v}_{{{{\rm{F}}}}}=1.03\times {10}^{6}{m}/s\) used

in our simulation (see methods). The slight differences in the theoretical and experimental potential fields of the GQDs may also weakly affect the Δ_E_. However, the linear relation

between Δ_E_ and \(1/d\) of the coupled GQDs can be basically maintained even if the size or the shape of one GQD is changed slightly (see Supplementary Note 20 for the evolution of the

molecular states of two GQDs with different sizes and shapes). Besides the lowest quasibound states, the other quasibound states with higher angular momenta in the two GQDs can also couple

to form the molecular orbits29. Then, the two ring-like structures of the two GQDs are attractive in the bonding state and repulsive in the antibonding state, as schematically shown in Fig. 

4a. The formation of the molecular orbits by the quasibound states with higher angular momenta is clearly shown in the \(-{{{{\rm{d}}}}}^{3}I/{{{\rm{d}}}}{V}^{3}\,\)STS maps measured across

the centers of the two GQDs (Fig. 2b, e, h), which is more evident in the zoomed-in view, as shown in Fig. 4b as an example for the result of the two GQDs with _d_≈12 nm. The coupling of the

two GQDs strongly modifies the quasibound states with higher angular momenta, which exhibit a distinct behavior compared with that in an isolated GQD (see Supplementary Fig. 24 for the

energy-fixed \({{{\rm{d}}}}I/{{{\rm{d}}}}V\) mappings of the uncoupled quasibound states). In Fig. 4b, we can distinguish the bonding state N2+ and antibonding state N2- arising from two

ring-like atomic orbits N2 in Fig. 1c. In view of the strong coupling, they are also partially influenced by overlapping with quasibound states of other energies. The spatial distributions

of the molecular orbits formed by the quasibound states with higher angular momenta can be explicitly visualized in the energy-fixed \({{{\rm{d}}}}I/{{{\rm{d}}}}V\) mappings, as shown in

Fig. 4c, d. The bonding state exhibits a characteristic figure-eight orbital and the antibounding state exhibits two repulsive circular orbitals29. Such a result is also reproduced well in

our theoretical simulations with considering two coupled GQDs, as shown in Fig. 4e–g (see Supplementary Fig. 25 for more calculated energy-fixed LDOS mappings with other distances). A direct

and pronounced result of the formation of the molecular orbits by the quasibound states with higher angular momenta is that the energy spacing of the quasibound states (about 122 meV) is

changed to half of that in an isolated GQD (about 59 meV) (see Supplementary Table 1 for more details of the energy spacing). The half-energy spacing observed in the molecular-like states

compared with the atomic-like states is due to the length of the molecular-like orbit being twice that of the single atomic-like orbit. According to the semiclassical quantization rule, the

energy spacing between the quasibound states is proportional to \(\hslash {v}_{{{{\rm{F}}}}}/L\), where _L_ is the semiclassical orbit length. For a better understanding of orbital

hybridization of the artificial molecule, two larger size GQDs and two hetero-sized GQDs are fabricated to compare the differences of the coupled and uncoupled states, as shown in

Supplementary Note 24. In summary, we create and systematically study the relativistic artificial molecules based on two coupled GQDs with tunable distance. Our experiment reveals that the

energy spacing of the bonding and antibonding states formed by the lowest quasibound state increases linearly with the inverse of the distance because of the relativistic nature of the

artificial molecule. The formation of molecular states by quasibound states with higher orbital momenta leads to half-energy spacing of the confined states due to the twice length of the

molecular-like orbit compared to that of the atomic-like orbit. Our study, especially the direct visualization of the molecular orbits, lays a solid foundation for understanding the

relativistic molecular physics and provides an approach that is generally applicable for realizing patterns of coupled GQDs, such as Lieb lattice and kagome lattice, with tunable coupling

strength. METHODS SAMPLE FABRICATION The graphene/WSe2 heterostructure was fabricated by wet transfer technology of a graphene monolayer on mechanical-exfoliated thick 2H-phase WSe2 sheets.

Firstly, large area aligned graphene was grown on a 20 × 20 mm2 polycrystalline copper (Cu) foil (Alfa Aesar, 99.8% purity, 25 µm thick) through chemical vapor deposition (CVD) method. The

Cu foil was soaked in a solution of acetic acid and deionized water (volume ratio = 1:1) for 10 h. After that, the Cu foil was rinsed with alcohol and deionized water separately. The Cu foil

was put in the CVD furnace annealing under an Ar/H2 flow (both at 50 sccm) at 1035 °C for 12 h at low pressure. Then the large-area aligned monolayer graphene was grown under a flow of Ar,

H2 and CH4 (50 sccm, 50 sccm and 3 sccm separately) at 1035 °C for 30 min at low pressure. The system was cooled to room temperature slowly. Then, polymethyl methacrylate (PMMA) was

uniformly coated on Cu foil with graphene monolayer. The Cu/graphene/PMMA film was put into ammonium persulfate solution until that the Cu foil was etched away. And the graphene/PMMA film

was cleaned by deionized water for 6 times. The thick 2H-phase WSe2 sheets were separated from the bulk crystal by traditional mechanical exfoliation technology and transfered to the Si/SiO2

substrate using polydimethylsiloxane (PDMS). Then, the Cu/graphene/PMMA film was put on the Si/SiO2 substrate with thick 2H-phase WSe2 sheets. Lastly, after the film was dried, the PMMA was

removed using acetone and the sample is cleaned by alcohol. GQDS MANIPULATION Firstly, we set the size of the scanning frame to about 1 nm × 1 nm. Then, we move the scanning frame to the

edge of the GQD which is opposite to the target movement direction. Next, we set the scanning speed to 1 s/line and start scanning. Lastly, we change the proportion from 1 pm to 1 nm during

the scanning process for about 3 s and change back to 1 pm. STM/STS MEASUREMENTS The STM/STS measurements were performed in low-temperature (78 K) and ultrahigh-vacuum (~10−10 Torr) scanning

probe microscopes (USM-1500) from UNISOKU. The tips were obtained by electrochemical etching from a W (99.95%) alloy wire. The differential conductance (\({{{\rm{d}}}}I/{{{\rm{d}}}}V\))

measurements were taken by a standard lock-in technique with an ac bias modulation of 5 mV and 793 Hz signal added to the tunneling bias. THEORETICAL MODEL To numerically simulate the

experiment results, we use the tight-binding model on the hexagonal lattice to describe the graphene, with the Hamiltonian being: $${{{\rm{H}}}}=- {\sum}_{\left\langle

{{{\rm{ij}}}}\right\rangle }{t}_{{{{\rm{ij}}}}}{a}_{{{{\rm{i}}}}}^{{{\dagger}}

}{a}_{{{{\rm{j}}}}}+{\sum}_{{{{\rm{i}}}}}V\left({{{{\bf{r}}}}}_{{{{\rm{i}}}}}\right)\,{a}_{{{{\rm{i}}}}}^{{{\dagger}} }{a}_{{{{\rm{i}}}}}$$ (3) where

\({t}_{{{{\rm{ij}}}}}=3.2\,{{{\rm{eV}}}}\) is the hopping energy between two nearest-neighbor sites \({{{\rm{i}}}},{{{\rm{j}}}}\) and is directly related to the Fermi velocity

\({v}_{{{{\rm{F}}}}}\approx 1.03\times {10}^{6}{{{\rm{m}}}}/{{{\rm{s}}}}\) by \(\hslash {v}_{{{{\rm{F}}}}}=\frac{3}{2}{t}_{{{{\rm{ij}}}}}{a}_{{{{\rm{cc}}}}}\)

(\({a}_{{{{\rm{cc}}}}}=0.142\,{{{\rm{nm}}}}\) is the length of carbon-carbon bond). Here we only consider the nearest-neighbor bond \(\left\langle i,j\right\rangle\). \({a}_{{{{\rm{i}}}}}\)

and \({a}_{{{{\rm{i}}}}}^{{{\dagger}} }\) denote the annihilation and creation operators at site \(i\), \({{{{\bf{r}}}}}_{{{{\rm{i}}}}}=({x}_{{{{\rm{i}}}}},{y}_{{{{\rm{i}}}}})\) is the

position coordinate of the site _i_ relative to the origin, \({{{\rm{V}}}}\left({{{{\bf{r}}}}}_{{{{\rm{i}}}}}\right)\) denotes the potential field on the graphene. Specially, for the system

of the single GQD and coupled GQDs, we use \({V}_{{{{\rm{s}}}}}\left({{{\bf{r}}}}\right)\) and \({V}_{{{{\rm{m}}}}}\left({{{\bf{r}}}}\right)\) as shown in the main text, respectively. In the

detail of simulations, a large hexagonal graphene flake is built with all the armchair edges (to avoid zigzag edge states at the low energy). The side length of the hexagon is 200 nm and

the graphene flake system includes about 4 million carbon atoms, which is large enough to remove the finite size effect. We use the open source code package for numerical calculations:

_Pybinding_45. Using the fast implementation of kernel polynomial method46,47 in this package, we can quickly obtain the LDOS \(\widetilde{\rho }\left({{{{\bf{r}}}}}_{{{{\rm{i}}}}}\right)\)

for each site \(i\) with an appropriate energy broadening \(\varGamma\). Furthermore, to better compared with the experiment results, we also introduce the space broadening \({\lambda

}_{{{{\rm{s}}}}}\) (simulating the broadening of the STM tip) to reformulate the LDOS at position \({{{\bf{r}}}}\): \( \rho \left({{{\bf{r}}}}\right)={\sum}_{{{{\rm{i}}}}}\widetilde{\rho

}\left({{{\bf{r}}}_{{\bf{i}}}}\right){{{{\rm{e}}}}}^{-\frac{{\left|{{{\bf{r}}}}{{{-}}}{{{{\bf{r}}}}}_{{{{\rm{i}}}}}\right|}^{2}}{2{\lambda }_{{{{\rm{s}}}}}^{2}}}\). In the calculations, we

set \({\lambda }_{{{{\rm{s}}}}}=0.15\,{{{\rm{nm}}}}\) and \(\varGamma=0.01{{{\rm{eV}}}}\). DATA AVAILABILITY The data that support the findings of this work are available within the

manuscript, Supplementary Information files. Source data are provided with this paper. REFERENCES * Ashoori, R. C. Electrons in artificial atoms. _Nature_ 379, 413–419 (1996). Article  ADS 

CAS  Google Scholar  * Reimann, S. M. & Manninen, M. Electronic structure of quantum dots. _Rev. Mod. Phys._ 74, 1283–1342 (2002). Article  ADS  CAS  Google Scholar  * Yoffe, A. D.

Low-dimensional systems: quantum size effects and electronic properties of semiconductor microcrystallites (zero-dimensional systems) and some quasi-two-dimensional systems. _Adv. Phys._ 42,

173–262 (1993). Article  ADS  CAS  Google Scholar  * Kastner, M. A. Artificial atoms. _Phys. Today_ 46, 24–31 (1993). Article  ADS  CAS  Google Scholar  * Li, S.-Y. & He, L. Recent

progresses of quantum confinement in graphene quantum dots. _Front. Phys._ 17, 33201 (2021). Article  ADS  Google Scholar  * Roothaan, C. C. J. New developments in molecular orbital theory.

_Rev. Mod. Phys._ 23, 69–89 (1951). Article  ADS  CAS  Google Scholar  * Bayer, M. et al. Coupling and entangling of quantum states in quantum dot molecules. _Science_ 291, 451–453 (2001).

Article  ADS  CAS  PubMed  Google Scholar  * Grundmann, M. et al. Ultranarrow luminescence lines from single quantum dots. _Phys. Rev. Lett._ 74, 4043–4046 (1995). Article  ADS  CAS  PubMed

  Google Scholar  * Schedelbeck, G., Wegscheider, W., Bichler, M. & Abstreiter, G. Coupled quantum dots fabricated by cleaved edge overgrowth: from artificial atoms to molecules.

_Science_ 278, 1792–1795 (1997). Article  ADS  CAS  PubMed  Google Scholar  * Wang, L., Rastelli, A., Kiravittaya, S., Benyoucef, M. & Schmidt, O. G. Self-assembled quantum dot

molecules. _Adv. Mater._ 21, 2601–2618 (2009). Article  CAS  PubMed  Google Scholar  * Wegscheider, W., Schedelbeck, G., Abstreiter, G., Rother, M. & Bichler, M. Atomically precise

GaAs/AlGaAs quantum dots fabricated by twofold cleaved edge overgrowth. _Phys. Rev. Lett._ 79, 1917–1920 (1997). Article  ADS  CAS  Google Scholar  * Koley, S., Cui, J., Panfil, Y. E. &

Banin, U. Coupled colloidal quantum dot molecules. _Acc. Chem. Res._ 54, 1178–1188 (2021). Article  CAS  PubMed  PubMed Central  Google Scholar  * Wegscheider, W., Schedelbeck, G., Bichler,

M. & Abstreiter, G. Atomically precise quantum dots fabricated by two-fold cleaved edge overgrowth: from artificial atoms to molecules. _Phys. E_ 3, 103–111 (1998). Article  CAS  Google

Scholar  * Rodary, G. et al. Real space observation of electronic coupling between self-assembled quantum dots. _Nano Lett._ 19, 3699–3706 (2019). Article  ADS  CAS  PubMed  Google Scholar 

* Austing, D. G., Honda, T., Muraki, K., Tokura, Y. & Tarucha, S. Quantum dot molecules. _Phys. B: Condens. Matter_ 249–251, 206–209 (1998). Article  ADS  Google Scholar  * He, L.,

Bester, G. & Zunger, A. Electronic asymmetry in self-assembled quantum dot molecules made of identical InAs/GaAs quantum dots. _Phys. Rev. B_ 72, 081311 (2005). Article  ADS  Google

Scholar  * Oosterkamp, T. H. et al. Microwave spectroscopy of a quantum-dot molecule. _Nature_ 395, 873–876 (1998). Article  ADS  CAS  Google Scholar  * Craig, N. J. et al. Tunable nonlocal

spin control in a coupled-quantum dot system. _Science_ 304, 565–567 (2004). Article  ADS  CAS  PubMed  Google Scholar  * Jeong, H., Chang, A. M. & Melloch, M. R. The Kondo effect in an

artificial quantum dot molecule. _Science_ 293, 2221–2223 (2001). Article  ADS  CAS  PubMed  Google Scholar  * Holleitner, A. W., Blick, R. H., Hüttel, A. K., Eberl, K. & Kotthaus, J. P.

Probing and controlling the bonds of an artificial molecule. _Science_ 297, 70–72 (2002). Article  ADS  CAS  PubMed  Google Scholar  * Zheng, H., Zhang, J. & Berndt, R. A minimal double

quantum dot. _Sci. Rep._ 7, 10764 (2017). Article  ADS  PubMed  PubMed Central  Google Scholar  * Banszerus, L. et al. Gate-defined electron–hole double dots in bilayer graphene. _Nano

Lett._ 18, 4785–4790 (2018). Article  ADS  CAS  PubMed  Google Scholar  * Banszerus, L. et al. Single-electron double quantum dots in bilayer graphene. _Nano Lett._ 20, 2005–2011 (2020).

Article  ADS  CAS  PubMed  Google Scholar  * Fölsch, S., Martínez-Blanco, J., Yang, J., Kanisawa, K. & Erwin, S. C. Quantum dots with single-atom precision. _Nat. Nanotechnol._ 9,

505–508 (2014). Article  ADS  PubMed  Google Scholar  * Pan, Y., Yang, J., Erwin, S. C., Kanisawa, K. & Fölsch, S. Reconfigurable quantum-dot molecules created by atom manipulation.

_Phys. Rev. Lett._ 115, 076803 (2015). Article  ADS  PubMed  Google Scholar  * Sierda, E. et al. Quantum simulator to emulate lower-dimensional molecular structure. _Science_ 380, 1048–1052

(2023). Article  ADS  CAS  PubMed  Google Scholar  * Fu, Z.-Q. et al. Relativistic artificial molecules realized by two coupled graphene quantum dots. _Nano Lett._ 20, 6738–6743 (2020).

Article  ADS  CAS  PubMed  Google Scholar  * Zheng, Q. et al. Molecular collapse states in graphene/WSe2 heterostructure quantum dots. _Phys. Rev. Lett._ 130, 076202 (2023). Article  ADS 

CAS  PubMed  Google Scholar  * Ge, Z. et al. Giant orbital magnetic moments and paramagnetic shift in artificial relativistic atoms and molecules. _Nat. Nanotechnol._ 18, 250–256 (2023).

Article  ADS  CAS  PubMed  Google Scholar  * Partoens, B. & Peeters, F. M. Molecule-type phases and Hund’s rule in vertically coupled quantum dots. _Phys. Rev. Lett._ 84, 4433–4436

(2000). Article  ADS  CAS  PubMed  Google Scholar  * Wensauer, A., Steffens, O., Suhrke, M. & Rössler, U. Laterally coupled few-electron quantum dots. _Phys. Rev. B_ 62, 2605–2613

(2000). Article  ADS  CAS  Google Scholar  * Rontani, M., Rossi, F., Manghi, F. & Molinari, E. Multiple quantum phases in artificial double-dot molecules. _Solid State Commun._ 112,

151–155 (1999). Article  ADS  CAS  Google Scholar  * Baruffa, F., Stano, P. & Fabian, J. Theory of anisotropic exchange in laterally coupled quantum dots. _Phys. Rev. Lett._ 104, 126401

(2010). Article  ADS  PubMed  Google Scholar  * Zheng, Q., Zhuang, Y.-C., Sun, Q.-F. & He, L. Coexistence of electron whispering-gallery modes and atomic collapse states in graphene/WSe2

heterostructure quantum dots. _Nat. Commun._ 13, 1597 (2022). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Ren, H.-Y., Ren, Y.-N., Zheng, Q., He, J.-Q. & He, L.

Electron-electron interaction and correlation-induced two density waves with different Fermi velocities in graphene quantum dots. _Phys. Rev. B_ 108, L081408 (2023). Article  ADS  CAS 

Google Scholar  * Ren, Y.-N. et al. In situ creation and tailoring of interfacial quantum dots in graphene/transition metal dichalcogenide heterostructures. _Phys. Rev. B_ 110, 125416

(2024). * Young, A. F. & Kim, P. Quantum interference and Klein tunnelling in graphene heterojunctions. _Nat. Phys._ 5, 222–226 (2009). Article  CAS  Google Scholar  * Lee, J. et al.

Imaging electrostatically confined Dirac fermions in graphene quantum dots. _Nat. Phys._ 12, 1032–1036 (2016). Article  CAS  Google Scholar  * Zhao, Y. et al. Creating and probing electron

whispering-gallery modes in graphene. _Science_ 348, 672–675 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Gutiérrez, C., Brown, L., Kim, C.-J., Park, J. & Pasupathy, A. N. Klein

tunnelling and electron trapping in nanometre-scale graphene quantum dots. _Nat. Phys._ 12, 1069–1075 (2016). Article  Google Scholar  * Ghahari, F. et al. An on/off Berry phase switch in

circular graphene resonators. _Science_ 356, 845–849 (2017). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Jiang, Y. et al. Tuning a circular p–n junction in graphene from

quantum confinement to optical guiding. _Nat. Nanotechnol._ 12, 1045–1049 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Bai, K.-K. et al. Generating atomically sharp p-n junctions in

graphene and testing quantum electron optics on the nanoscale. _Phys. Rev. B_ 97, 045413 (2018). Article  ADS  CAS  Google Scholar  * Fu, Z.-Q., Bai, K.-K., Ren, Y.-N., Zhou, J.-J. & He,

L. Coulomb interaction in quasibound states of graphene quantum dots. _Phys. Rev. B_ 101, 235310 (2020). Article  ADS  CAS  Google Scholar  * Moldovan, D. & Peeters, F. pybinding

v0.9.5: a Python package for tight-binding calculations. _Zenodo_. https://doi.org/10.5281/zenodo.4010216 (2020). * Weiße, A., Wellein, G., Alvermann, A. & Fehske, H. The kernel

polynomial method. _Rev. Mod. Phys._ 78, 275–306 (2006). Article  ADS  MathSciNet  Google Scholar  * Covaci, L., Peeters, F. M. & Berciu, M. Efficient numerical approach to inhomogeneous

superconductivity: the Chebyshev-Bogoliubov–de Gennes method. _Phys. Rev. Lett._ 105, 167006 (2010). Article  ADS  CAS  PubMed  Google Scholar  Download references ACKNOWLEDGEMENTS L.H.

acknowledgs the National Key R and D Program of China (Grant Nos. 2021YFA1401900 and 2021YFA1400100), National Natural Science Foundation of China (Grant Nos. 12141401, 12425405), and “the

Fundamental Research Funds for the Central Universities” (Grant No. 310400209521). Q.F.S. acknowledges the National Natural Science Foundation of China (Grant Nos. 12374034, 11921005), the

Innovation Program for Quantum Science and Technology (2021ZD0302403), and the Strategic priority Research Program of Chinese Academy of Sciences (Grant No. XDB28000000). Y.C.Z. acknowledges

 the Postdoctoral Fellowship Program of CPS Funder Grant Number GZB20240031. The devices are fabricated from Shanghai Onway Technology Co., Ltd. The computational resources are supported by

High-performance Computing Platform of Peking University. AUTHOR INFORMATION Author notes * These authors contributed equally: Xiao-Feng Zhou, Yu-Chen Zhuang. AUTHORS AND AFFILIATIONS *

Center for Advanced Quantum Studies, School of Physics and Astronomy, Beijing Normal University, Beijing, 100875, China Xiao-Feng Zhou, Mo-Han Zhang, Hao Sheng & Lin He * Key Laboratory

of Multiscale Spin Physics, Ministry of Education, Beijing, 100875, China Xiao-Feng Zhou, Mo-Han Zhang, Hao Sheng & Lin He * International Center for Quantum Materials, School of

Physics, Peking University, Beijing, 100871, China Yu-Chen Zhuang & Qing-Feng Sun * Hefei National Laboratory, Hefei, 230088, China Qing-Feng Sun Authors * Xiao-Feng Zhou View author

publications You can also search for this author inPubMed Google Scholar * Yu-Chen Zhuang View author publications You can also search for this author inPubMed Google Scholar * Mo-Han Zhang

View author publications You can also search for this author inPubMed Google Scholar * Hao Sheng View author publications You can also search for this author inPubMed Google Scholar *

Qing-Feng Sun View author publications You can also search for this author inPubMed Google Scholar * Lin He View author publications You can also search for this author inPubMed Google

Scholar CONTRIBUTIONS X.F.Z. performed the sample synthesis, characterization and STM/STS measurements. X.F.Z., Y.C.Z., M.H.Z., H.S., and L.H. analyzed the data. Y.C.Z. carried out the

theoretical calculations. L.H. conceived and provided advice on the experiment and analysis. Q.F.S. conceived and provided advice on the theoretical calculations. X.F.Z. and L.H. wrote the

paper with the input from others. All authors participated in the data discussion. CORRESPONDING AUTHORS Correspondence to Qing-Feng Sun or Lin He. ETHICS DECLARATIONS COMPETING INTERESTS

The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature Communications_ thanks Guillemin Rodary and the other, anonymous, reviewer(s) for their contribution

to the peer review of this work. A peer review file is available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published

maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION PEER REVIEW FILE SOURCE DATA SOURCE DATA RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed

under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or

format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material.

You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the

article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use

is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit

http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Zhou, XF., Zhuang, YC., Zhang, MH. _et al._ Relativistic artificial molecule

of two coupled graphene quantum dots at tunable distances. _Nat Commun_ 15, 8786 (2024). https://doi.org/10.1038/s41467-024-52992-1 Download citation * Received: 17 January 2024 * Accepted:

23 September 2024 * Published: 10 October 2024 * DOI: https://doi.org/10.1038/s41467-024-52992-1 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this

content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative