ABSTRACT Structural imperfections can be a promising testbed to engineer the symmetries and topological states of solid-state platforms. Here, we present direct evidence of hierarchical

transitions of zero- (0D) and one-dimensional (1D) topological states in symmetry-enforced grain boundaries (GB) in 1T′–MoTe2. Using a scanning tunneling microscope tip press-and-pulse

procedure, we construct two distinct types of GBs, which are differentiated by the underlying symmorphic and nonsymmorphic symmetries. The GBs with the nonsymmorphic rotation symmetry harbor

first-order topological edge states protected by a nonsymmorphic band degeneracy. On the other hand, the edge state of the symmorphic GBs attains a band gap. More interestingly, the gapped

IN2SE3 Article Open access 24 January 2024 METALLIC NANOCRYSTALS WITH LOW ANGLE GRAIN BOUNDARY FOR CONTROLLABLE PLASTIC REVERSIBILITY Article Open access 18 June 2020 TWINNING-ASSISTED

DYNAMIC ADJUSTMENT OF GRAIN BOUNDARY MOBILITY Article Open access 18 November 2021 INTRODUCTION The topology of the electronic band is an essential factor in understanding the materials’

electrical and quantum properties. Bulk–boundary correspondence, as a guiding principle of the topological phase, dictates the intimate relationship between the topological invariant of bulk

and the metallic excitations at the boundary1,2,3. A prototypical example of materials with non-trivial topology is found in topological insulators (TIs), which have inverted band gaps by

large spin-orbit coupling and topological character protected by time-reversal symmetry4,5,6,7. Moreover, a larger class of topological materials is available when we add crystalline

symmetries, exemplified by topological crystalline insulators (TCIs)8,9 and higher-order topological insulators (HOTIs)10,11,12,13. HOTIs are especially interesting because they broaden the

concept of bulk-boundary correspondence not to be limited between _N_-dimensional bulk and (_N_-1)-dimensional boundary, but to be applicable between _N_-dimensional bulk and

(_N-n_)-dimensional boundaries with _n_  > 1. For example, second-order HOTI with 3D (2D) bulk should have topologically protected 1D hinge (0D boundary) states. Observing topological

boundary states is a key to identifying the non-trivial bulk topology. Crystallographic defects such as lattice dislocations and grain boundaries (GBs) are of particular interest since they

can trap the localized boundary states. The topological protection of the boundary state depends on the crystal symmetry and the dimensionality of both the parent topological state and the

defect14,15,16,17,18,19,20. In the case of 2D and 3D HOTI, realizing variant crystallographic defects provides a promising route to engineer topological boundary states by creating different

types of defects that either preserve or break the underlying crystalline symmetries21. With a local probe that can characterize and manipulate these crystallographic defects, we can

identify the non-trivial topology of the bulk as well as control the topological states by the symmetry of defects22,23,24. A scanning tunneling microscope (STM) is a unique atomic-scale

microscopy tool that has been extensively used for observing topological states1,2 as well as manipulating them with atom manipulation techniques25. The precise control of the bias pulse and

the sample-tip distance allows STM to manipulate individual atoms and defects with atomic precision. However, the application of such nanoscale manipulation to HOTI and demonstration of

hierarchical topological states with respect to the symmetries are challenging, because it requires finding the right bulk materials with non-trivial topology that at the same time can be

manipulated by STM to create atomic defects with suitable crystalline symmetries. In this work, we apply the tensile strain on 1T′-MoTe2 by poking the surface with an STM tip in a controlled

fashion to create and stabilize symmetry differentiable GBs. The boundary matching of the atomic structure admits the two possible types of GBs, each of which is characterized by the

distinct crystalline symmetries along the GBs: symmorphic C2– (SymC2) and non-symmorphic C2– (NonSymC2) rotational symmetries. The strain induces domain switching between three orientation

variants of the 1T′ phase and creates symmetry-dictated GBs1,26. To create GBs, we design a new STM manipulation method that induces ferroelastic switching between three orientational

variants of the 1T′ phase of MoTe2 in a controlled and reproducible way. The GBs created by STM manipulation exhibit different topological states depending on a type of crystalline symmetry,

i.e. the 1D topological edge states and the 0D topological boundary states for non-NonSymC2 and SymC2 rotational symmetries, respectively. Our results demonstrate that STM manipulation is a

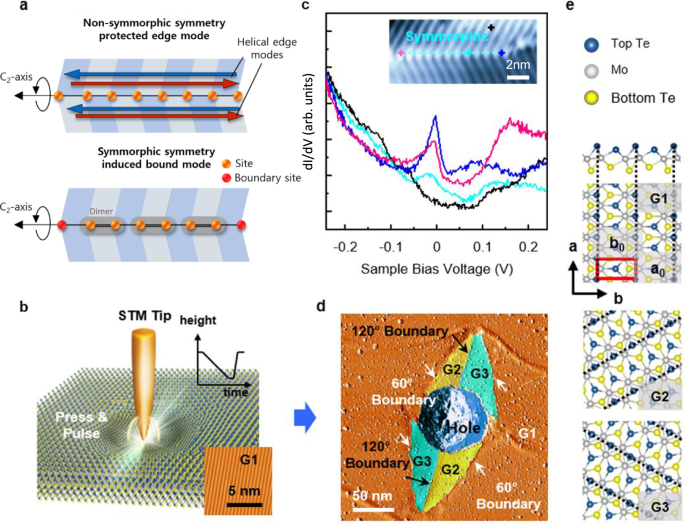
promising route to achieve the controllable manipulation of the HOTI states by ferroelastic switching. RESULTS CREATION OF SYMMETRY-ENFORCED GRAIN BOUNDARIES Due to the quantum spin Hall

phase of 1T’–MoTe2, the GBs of 1T’–MoTe2 harbor the pair of helical edge states originating from each side of the quantum spin Hall insulating bulk. In general, these pairs can be gapped

out, but NonSymC2 GBs stabilize the double helical edge mode, whose band degeneracy is protected by the nonsymmorphic symmetry (Fig. 1a top)16. On the other hand, the SymC2 GBs lose their

topological protection and acquire a finite band gap. Nevertheless, SymC2 symmetry gives rise to the higher-order topological classifications of the gapped edge. The resulting electronic

states of the SymC2 GB are analogous to the well-known Su-Schrieffer-Heeger chain27, which manifests as the 0D boundary states (Fig. 1a bottom)28. To create such GBs and to characterize 

their atomic and electronic structures, we employ STM and scanning tunneling spectroscopy (STS). A tensile strain can be applied by pressing the STM tip to the surface, and furthermore,

electrical and/or thermal energy can be transmitted by applying a tip voltage pulse at a desired position (Fig. 1b). Inset of Fig. 1c shows a representative topographic image of the SymC2 GB

between NonSymC2 GBs created by such STM manipulation. The differential conductance (d_I_/d_V_) spectra in Fig. 1c show a strong contrast between the ones taken at the center of GB (cyan),

ends of GB (magenta and blue), and bulk (black), which we will later show to originate from the topological boundary states of SymC2 GB. Figure 1d shows a representative large-scale 

derivative STM image of the strain-engineered GBs in 1T’–MoTe2. In the pristine surface of 1T’–MoTe2, the Te atoms form quasi-one-dimensional chains with a preferred direction due to the

dimerization of Mo atoms from the high symmetry phase (1T) (denoted by region G1 in Fig. 1b). By pressing the STM tip to the surface with applying a voltage pulse of –2.5 V, the pressed G1

region transforms to the diamond shape of different types of grains (G2 and G3) (Fig. 1d), corresponding to the two of the other six–fold rotation variants of the 1T’ phase with different

Te–chain direction (Fig. 1e). To characterize the optimal condition for obtaining the grain-switched diamond-shaped structure shown in Fig. 1d, we investigated several experimental

parameters: (1) applied voltage pulse (_V__p_); (2) depth of surface indentation (D, which is defined as the distance after the tunneling current reaches 100 nA. For delicate control of D,

we used z-spectroscopy before every switching process, and D was varied from a few angstroms to 30 nm); (3) time to lower the tip to the surface (T1, varied from 0.5 s to 10 s); (4) duration

at the lowest position for tip pulse (T2, varied from 0.2 to 0.5 s); and (5) time to lift the tip (T3, varied from 0.02 s to 10 s.). The various results from changing the parameters are

presented in the Supplementary Information. Subsequently, we determined the following optimal condition: _V__p_  = –2.5 ~ –3 V, D = –0.1 ~ –0.2 nm, T1 = 0.5 ~ 3 s, T2 = 200 ms and T3 = 20 ms

 (Supplementary Fig. S2). We note that applying only voltage pulse _V__p_ did not generate new grains, and applying tensile strain by pressing down the surface with certain D and T1 is

essential to form the diamond-shaped structure. Further details of their dependence are presented in Supplementary Note 2 and Figs. S2–S6. Many additional examples of the control of GBs are

provided in the Supplementary Information. HIERARCHICAL 0D AND 1D TOPOLOGICAL STATES The relative angles of Te-chain directions characterize the GBs between each region. Adjacent G2 and G3

grains bear a GB with the angle of 120° (G2–G3), and G2 and G3 regions form mostly GB with the angles of 60° with respect to the original G1 phase (G1–G2 and G1–G3) (See supplementary Fig. 

S7 for full geometric characterizations of the GBs and Supplementary Figs. S12–15 for geometric and electronic properties of 60° GBs). Further inspection of the STM image on the 120°

boundary reveals the coexistence of both the NonSymC2 and SymC2 GBs (Fig. 2a). Furthermore, the distinctive behaviors in the d_I_/d_V_ spectra are identified for different GBs. The d_I_/d_V_

 spectrum at the NonSymC2 GB, marked by the dotted orange line in Fig. 2a (also shown as the orange line in Fig. 2b), reveals a differential conductance peak near +28 mV, whereas no such

features are shown inside the grain far away from GBs (black line in Fig. 2b) as well as the SymC2 GB (cyan line in Fig. 2b). The atomic configurations of both types of 120° GBs are

characterized by a C2 rotation along the y-axis, offering greater energetic stability compared to the y-axis mirror reflection in 120° GBs18. These configurations can be further categorized

into NonSymC2 and SymC2 based on the presence or lack of half translation, illustrated in Supplementary Fig. S8a, c. Their electronic properties are depicted in Supplementary Fig. S8b, d.

The gapless metallic states originate from the non-trivial Z2 index of the quantum spin Hall insulator phase of MoTe2. In general, the double helical edge mode originating from the left, and

the right side of the domain can be trivially gapped out. Nonsymmorphic symmetry further protects the gapless crossings characterized by the bow-tie types band structure. Unlike the

nonsymmorhpic GB, the topological protection of the gapless state is removed at the symmorphic GB. The spatial d_I_/d_V_ maps of the 120° GB clearly show the 1D boundary state at the

NonSymC2 GBs (Fig. 3c). The boundary mode is well–localized at the NonSymC2 GB as seen in the d_I_/d_V_ map acquired at 34 mV in the upper right panel in Fig. 3c (further d_I_/d_V_ maps are

presented in Supplementary Fig. S9). The observed boundary mode in the NonSymC2 GB agrees with the theoretically predicted bowtie shape in-gap metallic states (Fig. 2e). The boundary states

originated from the pair of the helical edge states of each quantum spin Hall grain. In general, these boundary states are allowed to be gapped out by the interactions between the helical

edges, since each side of the GB has the same Z2 index. However, the additional NonSymC2 symmetry gives rise to the Young–Kane type nonsymmorphic band degeneracy29, which protects the band

crossings of the double-helical edge states. In contrast, the SymC2 GB shows no sign of the in-gap edge states, and it suggests the avoided level crossings between edge modes in the absence

of symmetry protection. However, interestingly, the measured d_I_/d_V_ spectrum at the end of SymC2 GB (violet line in Fig. 3b) reveals the additional peak near –4 mV (further clearly shown

in the d_I_/d_V_ spectra in Fig. 1c). The peaks are spatially localized at both ends of the GBs, as shown in the spatial d_I_/d_V_ map in the left panel in Fig. 3c, and it signifies the

presence of the 1D boundary states. The peaks are slightly broadened due to the finite size effect. A sharper peak is shown in the Fig. 3g, measured in longer GB in Fig. 3e. The

corresponding d_I_/d_V_ maps obtained at –4 and 34 mV are presented in Fig. 3f. Our theoretical calculation also verifies the gapped spectra of the edge mode (Fig. 2g). Further symmetry

analysis reveals the higher-order topological classifications of the edge mode. The approximate inversion symmetry along the grain boundary and chiral symmetry gives Z2 classification of the

gapped 1D edge (AIII class). (See supplementary Information for other AI topological classification). The corresponding symmetry classification is formally equivalent to that of the SSH

model, where the dimerizations of the hoppings give rise to the unpaired boundary states at each end30. In SymC2 GB, the dimerization of the Mo atoms (shown by the green stripes in

Supplementary Fig. S17) gives rise to the effective dimerization of the hoppings. Using the effective model, we also calculated local density of states (LDOS) near both SymC2 and NonSymC2

GBs (Supplementary Figs. S20, S21). To confirm that the 0D states are not artifacts of the states in the adjacent NonSymC2 GBs, we examined the possible hybridization between the 1D

topological boundary states in NonSymC2 GBs and the 0D boundary states in SymC2 GBs. Despite their positional proximity, the d_I/_d_V_ map on the side of the NonSymC2 GBs shows a diminishing

amplitude as it approaches the end of the chain. This behavior resembles a typical quantum confinement phenomenon31,32,33, with negligible hybridization with the 0D states. Consequently, we

conclude that there is vanishing tunneling of the 0D boundary state to the NonSymC2 GBs, confirming that the 0D boundary states are intrinsic to the SymC2 GBs and are not influenced by the

adjacent NonSymC2 GBs. We can read out information about the hybridization by analyzing the confined state by analyzing NonSymC2 GBs with a finite length (Fig. 4a). The d_I_/d_V_ maps reveal

the quantum well–like resonant bound states with the first (_n_ = 1) and the second harmonics (_n_ = 2) for the corresponding applied bias voltages 20 mV and 58 mV, respectively (Fig. 4b).

The change of the LDOS maxima depending on the measured position within the NonSymC2 GB shown in a series of d_I_/d_V_ spectra in Fig. 4c exhibits a typical quantum confinement

phenomenon3,4,5. These confinements are clearly observed in the d_I_/d_V_ line profiles in Fig. 4d. The wave function of the confined state with _n_ = 1 vanishes strongly at both ends of the

NonSymC2 GB, which indicates the physical separation from that of the SymC2. DISCUSSION CONTROLLABILITY OF GB CREATION AND THE UNDERLYING MECHANISMS Wenbin Li and Ju Li theoretically

predicted that only mechanical strain can derive the 1T’-to-1T’ phase transition26. In particular, they demonstrated that a few percent of biaxial supercell strain induce variant switching

from G1 to G2/G3. As we mention above, we also attempted to apply tensile strain without a voltage pulse. However, the surface of MoTe2 did not show grain switching. We hypothesized that

although grain switching occurred when pressing the surface, the switched grains, G2 and G3, reverted to G1, after the tip detached from the surface. Therefore, we surmised that applying a

bias voltage and resultant a hole play a key role to preventing the switched grains from reverting. The voltage pulse transmitted from the tip to the surface created an electric field, which

initially facilitated hole formation and then assisted in switching the grains. Our several experimental results support this scenario in several ways. First, the grain-switched

diamond-shaped structures are created with only at certain bias voltages, specifically _V__p_  = –2.5 to –3 V, which are appropriate for creating a hole and switching the grains. If the bias

of voltage is not sufficient to facilitate to switching the grain, the switching does not occur. Thus, with –2.0 V < _V__p_  < 0 V, only holes are created without any grain formation,

as we noted in previous Supplementary Note 1. Similarly, with –2.0 < _V__p_  < –2.5 V, G2 and/or G3 are occasionally formed, but not the diamond shape as shown in Fig. 1d. Second, the

scenario is further supported by the GB formation mechanism due to the in-plane electric field in Fig. 5. In this method, we first created a hole by pressing and applying a voltage pulse

with an STM tip, and then positioned the tip at the center of the hole to touch the edges of holes, as shown in Fig. 5a34. Lowering the tip slightly allowed full contact between the

circumference of the tip and the edge of the previously created hole. Note that this depth is defined from the distance between 1 and 2 in Fig. 5c. When a voltage pulse is applied, the

electric field is applied along the in-plane direction and inducing electrically strain-driven phase switching. As a result, the characteristic diamond structure is formed without any

mechanical stress. A more delicately controlled GB formation method shown in Fig. 5b further enabled probing the effect of in-plane electric field on the GB switching. We placed the tip very

close to the upper side of the edge, as indicated by the red cross in Fig. 5d. Then, we applied a voltage pulse to create GBs. As a result, we obtained only the upper half of the previously

observed diamond structure, because grain switching occurred only in the region next to the contact between the tip and the hole edge (Fig. 5e). The result substantiates that electric

field-induced phase switching requires a pre-existing hole structure with exposed step edges, which allows the pulse from the tip to transmit the strain in the in-plane direction. Third, the

diamond-shaped structure indicates that grain switching depends significantly on the in-plane structural anisotropy of 1T’–MoTe2. All grain switching preferably occurs along the Te rows (a

direction) and, consequently, produces the diamond-shaped structure. This suggests that the structural anisotropy of 1T’-MoTe2 on the anisotropy affects electrical conductivity and elastic

properties on the surface. In the previous reports, the electric conductivity of 1T'-MoTe2 exhibits anisotropic behavior, with conductivity along the a direction being approximately

twice as high as in the b direction at 10 K35. Consequently, transmitted bias voltage more quickly propagates along the _a_ direction than the _b_ direction. Density functional theory (DFT)

calculations were conducted to investigate the response of the lattice structure to an external electric field. Starting from the fully optimized MoTe2 structure, the lattice constant in one

direction was held fixed while the other was allowed to relax under an external field applied along the Te row (_a_ direction). The percent differences in the relaxed lattice constants,

relative to the optimized structure in the absence of the field, were calculated (Fig. 5i). The results reveal that the lattice constant in the _a_ direction increased, indicating a

stretching effect, while the _b_ direction contracted, demonstrating that the external electric field induces anisotropic deformation in the lattice. This spatially anisotropic grain

formation is further confirmed by additional experiments. We placed the STM tip for voltage pulsing at the edge of the existing hole as indicated by the red cross in Fig. 5g. In this case,

the tangent to the circular hole at the tip position lies parallel to the Te rows, and the electrically applied stress across the Te chains does not induce strain or grain switching.

Instead, it causes structural damage by removing atomic layers and creating an additional hole (Fig. 5h). The anisotropy of the elasticity in _a_ and _b_ directions of MoTe2 also affects on

the determination of the shape of grain switching36. We calculated the ratio of the extensions in the _a_ and _b_ directions when the surface is pressed along the _c_ direction36. Upon

applying a uniaxial strain \({\epsilon }_{z}\) in the c direction, the ratio of the extensions in the _b_ and _a_ direction is \(\frac{{\epsilon }_{a}}{{\epsilon }_{b}}\approx 1.316\)

(Details see Supplementary Note 3). This result indicates that the _a_ direction is further extend although we pressed the surface _z_ direction. These anisotropic properties are

intrinsically governed by the inherent characteristics of the material. To the control the transition between SymC2 and NonSymC2, we performed additional experiments. After obtaining GBs

through the same formation process, we pressed on the indicated position in Fig. 6a with an STM tip, without applying a pulse. We discovered that the upper part of the GB moved as shown in

Fig. 6b, and the d_I_/d_V_ spectra revealed that the NonSymC2 GB changed to the SymC2 GB (Fig. 6c, d). These results indicate that, although our GB formation process cannot initially

selectively create SymC2 and NonSymC2 GBs, the transition between the two can be controlled through tensile strain, as predicted by the theoretical results of Wenbin Li and Ju Li26. In

addition, we note that the newly created SymC2 in Fig. 6b is very short. As a results, the d_I_/d_V_ spectrum (cyan line) measured in the center of the GB shows the broadening effect of the

0D modes at its ends. In conclusion, we demonstrate hierarchical 0D and 1D topological states created in the NonSymC2 and SymC2 GBs created in a 1T’-MoTe2 by mechanically and electrically

induced tensile strain using the STM tip. While the 1D topological edge mode appears on the NonSymC2 GB, the SymC2 GB attains the topological band gap and realizes the higher-order

topological states at the GB ends. HOTIs have been theoretically well studied, however, their experimental observations have been rarely reported37,38. Thus, our experimental demonstration

not only provides direct evidence for the physical realization of higher–order topological states but also a new method for creating and controlling symmetry–dictated GBs. METHODS SCANNING

TUNNELING MICROSCOPY/SPECTROSCOPY MEASUREMENT We performed the experiments in two commercial low-temperature STM instruments (RHK and Unisoku operated  at 4.2 K and 2.8 K, respectively.) in

an ultrahigh vacuum (pressure < 1.0  10−10 Torr). 1T’-MoTe2 single crystal samples were purchased from HQ Graphene. The sample was cleaved in an ultrahigh vacuum chamber (~ 10−10 Torr) at

room temperature and then transferred to the low-temperature STM sample stage, where the temperature was kept at 4.2 K or 2.8 K. TIGHT-BINDING MODEL OF 1T’-MOTE2 To study the electronic

structure of the topological edge state, we construct the Slater-Koster type tight-binding model from the DFT based band structure. We have derived the tight-binding band structure of

1T’-MoTe2 based on the DFT model with three p-orbitals for Te-atoms and five d-orbitals for Mo-atoms. The tight-binding model in real space is generally written as, $$H={\sum}_{i,j}

{\sum}_{\alpha,{\alpha }^{{\prime} },\sigma,\sigma {\prime} }{t}_{{ij}}^{\alpha,{\alpha }^{{\prime} }}{c}_{i\alpha \sigma }^{{{\dagger}} }{c}_{i{\alpha }^{{\prime} }\sigma {\prime}

}+{H}_{{SOC}}.$$ Here, \(i,j\) represent the site index for each atom. \(\alpha,\alpha {\prime}\) represent the orbital degree of the freedom. For instance, in the case of Mo atoms,

\(\alpha,{\alpha }^{{\prime} }={d}_{{xy}},{d}_{{yz}},{d}_{{zx}},{d}_{{x}^{2}-{y}^{2}},{d}_{3{z}^{2}-{r}^{2}}\). In the case of Te atoms \(\alpha,\alpha {\prime}={p}_{x},{p}_{y},{p}_{z}\).

\({t}_{{ij}}^{\alpha,{\alpha }^{{\prime} }}\) is the transfer matrix, which is calculated from the Slater-Koster formula. \({H}_{{SOC}}\) is the onsite spin-orbit coupling term. BAND

STRUCTURE AND Z2 TOPOLOGICAL INVARIANT Z2 topological invariant, \(\nu\), can be calculated by the Fu-Kane formula as, $${\left(-1\right)}^{\nu }={\prod}_{i}{\delta }_{i},\, {\delta

}_{i}={\prod}_{m}{\xi }_{2m}({\Gamma }_{i})$$ where \({\xi }_{2m}({\Gamma }_{i})\) is the inversion eigenvalue of 2m-th occupied bands at the time-reversal invariant momenta \({\Gamma

}_{i}\). Due to the time-reversal and inversion symmetry, the band structure has the Kramers degeneracy at the momenta. The number of inversion-odd occupied band is summarized in Table 1,

which results in the non-trivial Z2 invariant. The non-trivial Z2 invariant is the robust quantity even in the presence of the inversion symmetry breaking perturbation as long as the

perturbation does no induce the additional band gap closing. The non-trivial topological invariant can be further examined by showing the edge states with the open boundary condition.

Supplementary Fig. 1 compares the energy spectra in the closed and open boundary conditions respectively. The emergence of the edge spectra confirms the non-trivial topological invariant.

DENSITY FUNCTIONAL THEORY CALCULATIONS DFT calculations were carried out using the Vienna ab initio simulation package (VASP) employing the generalized gradient approximation (GGA) with

Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional form and the projector-augmented wave methods39,40,41,42,43. For all calculations, wave functions were expanded in plane waves

with the cutoff energy of 350 eV, and the atomic positions were relaxed until the residual forces were less than 0.02 eV/Å or until the change of the total energy was less than 1.0 × 10−6

eV. All calculations were performed using a 1T’-MoTe2 monolayer, and a vacuum of at least 20 Å was applied to the cell to prevent interaction between the slabs. DATA AVAILABILITY The data

that support the findings of this study are available from the corresponding author upon request. REFERENCES * Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. _Rev. Mod.

Phys._ 82, 3045 (2010). Article  ADS  CAS  Google Scholar  * Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. _Rev. Mod. Phys._ 83, 1057 (2011). Article  ADS  CAS 

Google Scholar  * Isaev, L., Moon, Y. H. & Ortiz, G. Bulk-boundary correspondence in three-dimensional topological insulators. _Phys. Rev. B_ 84, 075444 (2011). Article  ADS  Google

Scholar  * Kane, C. L. & Mele, E. J. Quantum spin hall effect in graphene. _Phys. Rev. Lett._ 95, 226801 (2005). Article  ADS  PubMed  CAS  Google Scholar  * Kane, C. L. & Mele, E.

J. Z2 topological order and the quantum spin hall effect. _Phys. Rev. Lett._ 95, 146802 (2005). Article  ADS  PubMed  CAS  Google Scholar  * Bernevig, B. A. & Zhang, S.-C. Quantum spin

hall effect. _Phys. Rev. Lett._ 96, 106802 (2006). Article  ADS  PubMed  Google Scholar  * Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. _Phys. Rev.

Lett._ 98, 106803 (2007). Article  ADS  PubMed  Google Scholar  * Fu, L. Topological crystalline insulators. _Phys. Rev. Lett._ 106, 106802 (2011). Article  ADS  PubMed  Google Scholar  *

Ando, Y. & Fu, L. Topological crystalline insulators and topological superconductors: From concepts to materials. _Annu. Rev. Condens. Matter Phys._ 6, 361–381 (2015). Article  ADS  CAS

  Google Scholar  * Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Quantized electric multipole insulators. _Science_ 357, 61–66 (2017). Article  ADS  MathSciNet  PubMed  CAS  Google

Scholar  * Xie, B. et al. Higher-order band topology. _Nat. Rev. Phys._ 3, 520–532 (2021). Article  Google Scholar  * Schindler, F. et al. Higher-order topological insulators. _Sci. Adv._

4, eaat0346 (2018). Article  ADS  PubMed  PubMed Central  Google Scholar  * Trifunovic, L. & Brouwer, P. W. Higher-order bulk-boundary correspondence for topological crystalline phases.

_Phys. Rev. X_ 9, 011012 (2019). CAS  Google Scholar  * Ran, Y., Zhang, Y. & Vishwanath, A. One-dimensional topologically protected modes in topological insulators with lattice

dislocations. _Nat. Phys._ 5, 298–303 (2009). Article  CAS  Google Scholar  * Liu, C.-X., Zhang, R.-X. & VanLeeuwen, B. K. Topological nonsymmorphic crystalline insulators. _Phys. Rev.

B_ 90, 085304 (2014). Article  ADS  CAS  Google Scholar  * Hamasaki, H., Tokumoto, Y. & Edagawa, K. Dislocation conduction in Bi-Sb topological insulators. _Appl. Phys. Lett._ 110,

092105 (2017). Article  ADS  Google Scholar  * Nayak, A. K. et al. Resolving the topological classification of bismuth with topological defects. _Sci. Adv._ 5, eaax6996 (2019). Article  ADS

  PubMed  PubMed Central  CAS  Google Scholar  * Kim, H. W. et al. Symmetry dictated grain boundary state in a two-dimensional topological insulator. _Nano Lett._ 20, 5837–5843 (2020).

Article  ADS  PubMed  CAS  Google Scholar  * Juričić, V., Mesaros, A., Slager, R.-J. & Zaanen, J. Universal probes of two-dimensional topological insulators: Dislocation and π Flux.

_Phys. Rev. Lett._ 108, 106403 (2012). Article  ADS  PubMed  Google Scholar  * Slager, R.-J., Mesaros, A., Juričić, V. & Zaanen, J. Interplay between electronic topology and crystal

symmetry: Dislocation-line modes in topological band insulators. _Phys. Rev. B_ 90, 241403(R) (2014). Article  ADS  Google Scholar  * Roy, B. & Juričić, V. Dislocation as a bulk probe of

higher-order topological insulators. _Phys. Rev. Res._ 3, 033107 (2021). Article  CAS  Google Scholar  * Slager, R.-J., Juričić, V., Lahtinen, V. & Zaanen, J. Self-organized

pseudo-graphene on grain boundaries in topological band insulators. _Phys. Rev. B_ 93, 245406 (2016). Article  ADS  Google Scholar  * Amudsen, M. & Juričić, V. Grain-boundary topological

superconductor. _Commun. Phys._ 6, 232 (2023). Article  Google Scholar  * Salib, D. J., Juričić, V. & Ro, B. Emergent metallicity at the grain boundaries of higher-order topological

insulators. _Sci. Reps._ 13, 15308 (2023). Article  ADS  CAS  Google Scholar  * Ko, W., Ma, C., Nguyen, G. D., Kolmer, M. & Li, A.-P. Atomic-scale manipulation and in situ

characterization with scanning tunneling microscopy. _Adv. Funct. Mater._ 29, 190377 (2019). Article  Google Scholar  * Li, W. & Li, J. Ferroelasticity and domain physics in

two-dimensional transition metal dichalcogenide monolayers. _Nat. Commun._ 7, 10843 (2016). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Su, W. P., Schrieffer, J. R. &

Heeger, A. J. Solitons in polyacetylene. _Phys. Rev. Lett._ 42, 1698 (1979). Article  ADS  CAS  Google Scholar  * Li, L., Xu, Z. & Chen, S. Topological phases of generalized

Su-Schrieffer-Heeger models. _Phys. Rev. B_ 89, 085111 (2014). * Young, S. M. & Kane, C. L. Dirac semimetals in two dimensions. _Phys. Rev. Lett._ 115, 126803 (2015). Article  ADS 

PubMed  Google Scholar  * Chiu, C. K., Teo, J. C., Schnyder, A. P. & Ryu, S. Classification of topological quantum matter with symmetries. _Rev. Mod. Phys._ 88, 035005 (2016). Article 

ADS  Google Scholar  * Nilius, N., Wallis, T. M. & Ho, W. Development of one-dimensional band structure in artificial gold chains. _Science_ 297, 1853 (2002). Article  ADS  PubMed  CAS 

Google Scholar  * Do, E. H. & Yeom, H. W. Electron quantization in broken atomic wires. _Phys. Rev. Lett._ 115, 266803 (2015). Article  ADS  PubMed  Google Scholar  * Howard, S. et al.

Evidence for one-dimensional chiral edge states in a magnetic Weyl semimetal Co3Sn2S2. _Nat. Commun._ 12, 4269 (2021). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Gu, M. S.

et al. Electric field-assisted patterning of few-layer MoTe2 by scanning probe lithography. _J. Kor. Phys. Soc._ 82, 274 (2023). Article  ADS  CAS  Google Scholar  * Hughes, H. P. &

Friend, R. H. R. H. Electrical resistivity anomaly in β-MoTe2. _J. Phys. C: Solid State Phys._ 11, L103 (1978). Article  ADS  CAS  Google Scholar  * Rano, B. R., Syed, M. I. & Naqib, S.

H. Ab initio approach to the elastic, electronic, and optical properties of MoTe2 topological Weyl semimetal. _Alloy. Compd._ 39, 154522 (2020). Article  Google Scholar  * Schindler, F. et

al. Higher-order topology in bismuth. _Nat. Phys._ 14, 918–924 (2018). Article  PubMed  PubMed Central  CAS  Google Scholar  * Noguchi, R. et al. Evidence for a higher-order topological

insulator in a three-dimensional material built from van der Waals stacking of bismuth-halide chains. _Nat. Mater._ 20, 473–479 (2021). Article  ADS  PubMed  CAS  Google Scholar  * Kresse,

G. & Furthmüller, J. Efficiency of Ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. _Comp. Mater. Sci._ 6, 15–50 (1996). Article  CAS 

Google Scholar  * Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. _Phys. Rev. B_ 54, 11169–11186 (1996).

Article  ADS  CAS  Google Scholar  * Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. _Phys. Rev. Lett._ 77, 3865–3868 (1996). Article  ADS 

PubMed  CAS  Google Scholar  * Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. _Phys. Rev. Lett._ 78, 1396–1396 (1997). Article  ADS  CAS  Google

Scholar  * Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. _Phys. Rev. B_ 59, 1758–1775 (1999). Article  ADS  CAS  Google Scholar 

Download references ACKNOWLEDGEMENTS This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (Grants No. RS-2023-00218998).

M.J.P. was supported by the Institute for Basic Science in the Republic of Korea through the project IBS-R024-D1. AUTHOR INFORMATION Author notes * These authors contributed equally: Won-Jun

Jang, Heeyoon Noh. AUTHORS AND AFFILIATIONS * Samsung Advanced Institute of Technology, Suwon, 16678, Korea Won-Jun Jang, JiYeon Ku & Hyo Won Kim * Department of Physics, Yonsei

University, Seoul, 03722, Korea Heeyoon Noh * Materials Science and Technology Division, Oak Ridge National Laboratory, Oak Ridge, TN, 37831, USA Seoung-Hun Kang * The Department of Physics

and Astronomy, University of Tennessee at Knoxville, Knoxville, TN, 37996, USA Wonhee Ko * Center for Theoretical Physics of Complex Systems, Institute for Basic Science (IBS), Daejeon,

34126, Republic of Korea Moon Jip Park * Department of Physics, Hanyang University, Seoul, 04763, Korea Moon Jip Park Authors * Won-Jun Jang View author publications You can also search for

this author inPubMed Google Scholar * Heeyoon Noh View author publications You can also search for this author inPubMed Google Scholar * Seoung-Hun Kang View author publications You can also

search for this author inPubMed Google Scholar * Wonhee Ko View author publications You can also search for this author inPubMed Google Scholar * JiYeon Ku View author publications You can

also search for this author inPubMed Google Scholar * Moon Jip Park View author publications You can also search for this author inPubMed Google Scholar * Hyo Won Kim View author

publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS H.W.K. and M.J.P. proposed and designed the research. W.-J. J, H.N. and H.W.K. carried out the STM

experiments. H.W.K and W.-J. J analyzed the STM data. S.-H.K. and J.K. performed the DFT calculations. M.J.P developed the theoretical model. M.J.P, H.W.K, W.K, and S.-H. K wrote the

manuscript. All authors have read and approved the final version of the manuscript. CORRESPONDING AUTHORS Correspondence to Moon Jip Park or Hyo Won Kim. ETHICS DECLARATIONS COMPETING

INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature Communications_ thanks the anonymous, reviewer(s) for their contribution to the peer review

of this work. A peer review file is available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and

institutional affiliations. SUPPLEMENTARY INFORMATION PEER REVIEW FILE SUPPLEMENTARY INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons

Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give

appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission

under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons

licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit

http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Jang, WJ., Noh, H., Kang, SH. _et al._ Hierarchical zero- and one-dimensional

topological states in symmetry-controllable grain boundary. _Nat Commun_ 15, 9328 (2024). https://doi.org/10.1038/s41467-024-53315-0 Download citation * Received: 26 December 2023 *

Accepted: 07 October 2024 * Published: 29 October 2024 * DOI: https://doi.org/10.1038/s41467-024-53315-0 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this

content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative