ABSTRACT Node line band-touchings protected by mirror symmetry (named as _m_-NLs), the product of inversion and time reversal symmetry S = PT (named as _s_-NLs), or nonsymmorphic symmetry

are nontrivial topological objects of topological semimetals in the Brillouin Zone. In this work, we screened a family of MgSrSi-type crystals using first principles calculations, and

discovered that more than 70 members are node-line semimetals. A new type of multi-loop structure was found in AsRhTi that a _s_-NL touches robustly with a _m_-NL at some “nexus point”, and

in the meanwhile a second _m_-NL crosses with the _s_-NL to form a Hopf-link. Unlike the previously proposed Hopf-link formed by two _s_-NLs or two _m_-NLs, a Hopf-link formed by a _s_-NL

in real materials. SIMILAR CONTENT BEING VIEWED BY OTHERS HOSOHEDRAL NODAL-LINE SUPERCONDUCTIVITY IN HEXAGONAL ABC DIRAC SEMIMETALS Article Open access 05 January 2024 VACANCY-ENGINEERED

NODAL-LINE SEMIMETALS Article Open access 02 September 2022 THREE-TERMINAL WEYL COMPLEX WITH DOUBLE SURFACE ARCS IN A CUBIC LATTICE Article Open access 03 July 2020 INTRODUCTION The band

crossings of the conduction and valence bands in a topological semimetal are interesting topological objects of Brillouin Zone (BZ) which bring about unique electronic structures and

electrical properties, such as giant magnetoresistance, parity anomaly and “drum-head” states at material’s surfaces.1,2 Depending on the dimensionality of band crossings, topological

semimetals are classified into three categories, the Weyl semimetals (WSMs)3,4,5,6,7,8 or Dirac semimetals (DSMs),9,10,11 node-line semimetals

(NLSMs),12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41 and node-surface semimetals (NSSMs).42,43 Unlike the DSMs and WSMs whose band crossings take

place at discrete points in the BZ, the band crossings of NLSMs form closed loops. When circling around these loops, an electron picks up an nontrivial Berry phase _π_ in its wave function,

whose effect can be detected by transporting measurements. Though having been extensively proposed in graphene networks,13 anti-perovskites,14,15 SrIrO3,20 TlTaS2,17 BaTaS,42 HfC,29

CaP3/CaAs330,31, and Co2MnGa,35 etc, the direct evidence of existence of node-line (NL) states in real materials is rare.18,25,26,27 Finding new materials with clean and robust NL band

crossing around the fermi level is still a demanding task in the field of condensed matter physics. Three types of NLs have been discovered based on their protecting symmetry.2 The first

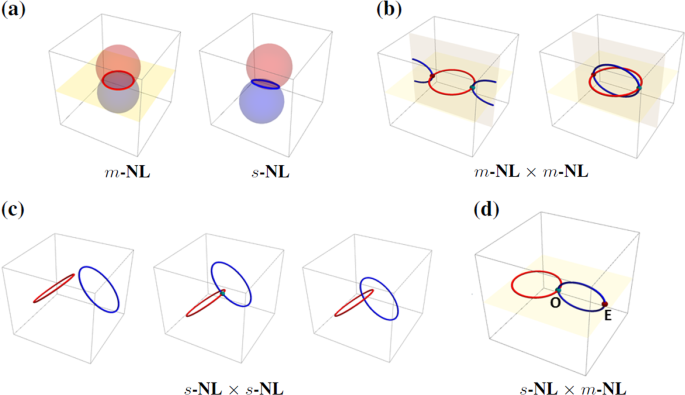
type of NLs is protected by mirror symmetry, which is named as _m_-NL in this work and shown schematically in Fig. 1a. Due to the mirror symmetry, the _m_-NL is pinned to the invariant plane

of the mirror symmetry. The second type of NLs is protected by the combination of time-reversal symmetry _T_ and inversion symmetry _P_, i.e., S=PT. This type of NLs, named as _s_-NL here,

can present at any region of the BZ as shown at the right of Fig. 1a. The last type of NLs is protected by nonsymmorphic symmetries and usually appears at the boundary of BZ.20,42 Recently,

there rises a new trend of investigating NLSMs with multiple NL loops.28,29,33,34,35,36,38 In those NLSMs, NL loops may intersect with each other and entangle into a variety of structures,

such as node-net,38 node-chain28, and Hopf-link,32,33,34,35,36 etc. For example, two _m_-NLs will be stuck together at some points dubbed as “nexus points” on the cross-line of two invariant

planes of mirror symmetries (see in Fig. 1b).44 In the case of two _s_-NLs, the _s_-NLs can be separated, touched or crossed with unrestricted locations in the BZ (see in Fig. 1c). The

crossed _s_-NLs are also called Hopf-link due to their topological invariant being the Hopf-link number.33 While the existence of multiple-loop NLs has been realized in photonic lattice,45

their existence in fermionic systems has not been identified thus far. In this work, using first principles calculations, we screened the family of MgSrSi-type crystals which consists of 660

members, and found more than 70 compounds are NLSMs showing a variety of NL structures. The NLs are protected by the mirror symmetry or the _S_ symmetry contained in the Pnma space group of

MgSrSi-type crystals. Importantly, in contrast to a previous report in which the member AsRhTi was predicted to be a NLSM with a single NL band crossing,22 we found in this material a new

type of multi-loop NL structure as shown in Fig. 1d, where a _s_-NL sticks to a _m_-NL at some “nexus point” (denoted by _O_) and penetrates the invariant plane of _m_-NL at some general

point (denoted by _E_ in Fig. (1d)). Interestingly, we also found a third _m_-NL crosses the _s_-NL and a Hopf link is formed. Unlike the case of two crossed _m_-NLs or two crossed _s_-NLs,

this novel multi-loop NL structure requires a minimal three-band model to describe its essential electronic structure. Even more exotic multi-loop NL structures were further uncovered in

AsFeNb and PNiNb. Some of the NLSMs show very clean band structures at the fermi level without other trivial bands. Our work therefore provides a promising platform for the material

realization of new topological semimetals with exotic NL structures. RESULTS AND DISCUSSION MULTI-LOOP NLS IN ASRHTI The group of MgSrSi-type crystal is consisted of 660 members as

documented in ICSD.46,47,48,49,50,51,52,53,54,55,56 It takes a _Pnma_ space group which contains a mirror plane _m__y_, two glide mirror planes \(\tilde m_x\) and \(\tilde m_z\) and the

space inversion _P_. On the _k__x_ = 0 and _k__z_ = 0 invariant planes, the glide planes \(\tilde m_x\) and \(\tilde m_z\) act in the same way as the normal mirror planes,20 while on the

boundary of BZ, they should be treated differently since their fractional translations may lead to additional band degeneracy. If the time reversal _T_ is also a symmetry, the compounds

become symmetrical under the composed operation S=PT. Both conditions of existence of the _s_-NL and _m_-NLs are therefore fulfilled in MgSrSi-type crystals. In Fig. (2a) we plotted the

crystal structure of a prototype compound, AsRhTi and the two key symmetries for NLs, a mirror plane _m__y_ and inversion symmetry _P_ are highlighted. It can be found that in the unit cell

of AsRhTi it contains two layers of atoms and the plane of the atom layers is overlapped with the mirror plane of _m__y_. The inversion center, on the other hand, is off the atom layers and

locates at the middle of two neighboring layers. The corresponding Brillouin Zone and high-symmetry paths are also shown below the crystal structure of AsRhTi. Let us show here that the

valence and conduction bands of AsRhTi do cross and produce a multi-loop NL structure. We plotted the GGA band structure of AsRhTi in Fig. 2b where one can readily find that the valence and

conduction bands cross at the intermediate points of Γ-X and Γ-Z, indicating a NL lying in the invariant plane _k__y_ = 0 of the mirror symmetry _m__y_. In order to demonstrate the NL

structure more clear, we further plotted in Fig. 2c the 2D band structure of AsRhTi on the _k__y_ = 0 plane with varying _k__x_ and _k__z_. Since the band structure is symmetrical under the

transformations _k__x_ → −_k__x_ and _k__z_ → −_k__z_, only the region of _k__x_ > 0 and _k__z_ > 0 is used for simplicity. From the profile of the energy difference of three bands

that has been projected on the bottom of Fig. 2c, one sees a central NL _α_ surrounding the Γ point. Outside the NL α is a _m_-NL _β_. Outmost is a third _m_-NL _γ_ that encloses the U

point. It is the _m__y_ provides the needed protection for the three _m_-NLs. Interestingly, besides these in-plane _m_-NLs, we also find an isolate band-touching point E outside the NL _γ_.

This band-touching point E is more obviously seen in the 2D energy band structure where it is highlighted by a dotted circle in Fig. 2c. The detail of the NLs near the point _E_ is revealed

by a 3D profile of energy differences of bands in Fig. 2d, where a denser discretion of BZ is adopted to obtain the energy bands with the tight-binding hamiltonian constructed by the MLWF

method. In this band-crossing profile, an extra NL _δ_ vertical to _k__y_ = 0 plane is discovered. Since NL _δ_ does not lie in any high symmetry path or plane, it must be an _s_-NL that is

protected by symmetry _S_. More detailly, the _s_-NL _δ_ is found to stick to the _m_-NL _β_ on a nexus point and the point E is the very point that NL _δ_ penetrates through the _k__y_ = 0

plane. Another interesting feature in Fig. 2d is that the _m_-NL _γ_ crosses the _s_-NL and the two form a Hopf-link. Previously Hopf-links made of two _m_-NLs or two _s_-NLs have been

already proposed and it is argued that for the first one needs a minimal four-band effective model to describe the electronic structure of the Hopf-link,35 while for the later one only needs

a minimal two-band model.33,34 Here we demonstrate that a Hopf-link can be made of a _s_-NL and a _m_-NL, and its corresponding electronic structure is correctly described by a minimal

three-band model given below. The reason that why we need a minimal three-band model to describe the multi-loop NL structure of Fig. 1d and of Fig. 2d is obvious: The _m_-NL is only produced

by a pair of bands with opposite mirror parities. A robust and isolate band crossing point E on the invariant plane _k__y_ = 0, however, is only possible when the crossing bands have equal

mirror parities. Otherwise there would be a _m_-NL passing through the isolate point.29 The general form of the three-band hamiltonian should be written as, $$H(k) = \left[

{\begin{array}{*{20}{c}} {H_{11}(k)} & {H_{12}(k)} & {H_{13}(k)} \\ {} & {H_{22}(k)} & {H_{23}(k)} \\ \dagger & {} & {H_{33}(k)} \end{array}} \right].$$ (1) Since the

system preserves the symmetry _S_, the imaginary part of the off-diagonal element _H__nm_ (_k_) (_n_, _m_ = 1, 2, 3, and _n_≠_m_) vanishes. On the other hand, The mirror symmetries, i.e.,

\(\tilde m_x\), \(m_y\), and \(\tilde m_z\), lay on the entries another constraint that the diagonal element _H__nn_(_k_) should be an even function of _k__x_, _k__y_, and _k__z_.15 For the

off-diagonal entry _H__nm_(_k_) with _n_≠_m_, it becomes an even (odd) function of _k__i_ (_i_ = _x_, _y_, _z_) if the orbital _n_ and _m_ have the equal (opposite) mirror parities with

respect to symmetry _m__i_.15 The above symmetry consideration helps us to reduce the hamiltonian of Eq. (1) to a simpler form up to a second order of _k_, $$H(k) = \left[

{\begin{array}{*{20}{c}} 0 & {\lambda _1k_y} & {\lambda _2k_y} \\ {} & {\varepsilon _1 + a_1k_x^2 + b_1k_y^2 + c_1k_z^2} & {\varepsilon _3 + a_3k_x^2 + b_3k_y^2 + c_3k_z^2}

\\ \dagger & {} & {\varepsilon _2 + a_2k_x^2 + b_2k_y^2 + c_2k_z^2} \end{array}} \right].$$ (2) Here we supposed that the second and third orbitals have the equal mirror parities

opposite to that of the first. A constant term \(H_{11}\hat I\) has been subtracted from the original Hamiltonian because of its irrelevance to the structure of NLs. The parameters of Eq.

(2) are chosen dimensionless for simplicity. By choosing suitable values of parameters _ε__i_, _a__i_, _b__i_, _c__i_, and _λ__j_ (_i_ = 1, 2, 3 and _j_ = 1, 2), the main features of

multi-loop NL structure of Fig. 2d are well reproduced as shown in Fig. 2e. The nontrivial electronic structure of a NLSM is revealed by its topological surface states (SSs). In a slab, the

projection of a NL in the bulk BZ onto the 2D BZ will divide it into regions of different topological orders characterized by _Z_2 topological charge _v_,57 $$\nu = \frac{1}{\pi }{\int}_{ -

\pi }^\pi dk_ \bot \mathop {\sum}\limits_{n \in occ.} \langle n,k|{\mathrm{i}}\partial _{{\mathrm{k}}_ \bot }|n,k\rangle mod\,2,$$ (3) where |_n_, _k_> denotes the Bloch eigenstate and

_k_⊥ is the component of momentum normal to the slab. In the regions of _v_ = 1, there exists in-gap topological surface states at each _k_ point, forming the so called 2D “drum-head”

states.57 In Fig. 3a, b we have shown the surface band structures of AsRhTi on the (010) and (001) surfaces, respectively. The corresponding 2D profiles of density of state (DOS) at fixed

energies of −30 and 0 meV are also plotted in Fig. 3c, d. In Fig. 3a and Fig. 3c, one finds SSs spread throughout the inner region enclosed by the projection of _m_-NL _β_ of Fig. 2d. Since

the _s_-NLs are normal to surface (010) (see in Fig. 2d), no SS is found at (010) surface for the _s_-NLs. In contrast, on the (001) surface the projection of _s_-NLs form two ellipses on

Γ-X and SSs link the two ellipses across the boundary of BZ (see in Fig. 3d). It is seen from Fig. 3d that the fermi surface also cuts some trivial bands, producing extra carrier pockets

above and below the _k__y_ = 0 plane as can be seen in Fig. 3d. In the above discussions, we have not included the spin-orbit coupling (SOC). The inclusion of SOC induces small gaps on the

NLs at the scale of several meV and thus its effect can be ignored at room temperature. For compounds containing heavier elements below, such as SiIrTa, the SOC gap is not small that the

NLSMs eventually are turned into topological insulators. We also checked the effect of electron interactions by adopting the hybrid density functional approximation (HSE06)58 and find the

HSE06 result reproduces GGA result very well (see in the Fig. 2b). One finds that HSE06 calculation reproduces GGA band structure and makes the fermi surface even clearer by pushing down the

valence band at Γ and U. DIVERSE NODE LINES STRUCTURES IN MGSRSI-TYPE CRYSTALS The MgSrSi-type crystals is a large family of binary and ternary crystals which contains more than 660

members. As expected that isostructure crystals may have similar electronic structure, we thus screened all 660 compounds to discover new NLSMs. More than 70 NLSMs are readily found and

listed in Table 1, where the NLSMs are divided into several groups based on their chemical compositions. A variety of NLs structures were discovered. The NL structures for each group is

similar. In Fig. 4 we plotted 5 representative NL structures and their corresponding fermi surfaces. From Fig. 4a, one sees PPtSc has a single NL loop lying in the _k__y_ = 0 plane and its

fermi surface takes a distorted torus-like shape (see in Fig. 4a). For SiNiZr, the NL extends across the boundary of BZ and one can see from Fig. 4b that some portions of the NL outside the

BZ is folded back. The single NL of SiCoV shown in Fig. 4c, contrarily, lies on the _k__z_ = 0 plane unlike those of PPtSc and SiNiZr in the _k__y_ = 0 plane, indicating its protecting

symmetry being \(\tilde m_z\). Both fermi surfaces of PPtSc and SiCoV take the simple torus-like shapes and show very clean fermi surfaces, a promising property for the experimental

detection of their nontrivial electronic structures. Interestingly, even more exotic NL geometries are found in AsFeNb and PNiNb. There exist multiple _m_-NLs in the _k__x_ = 0, _k__y_ = 0,

and _k__z_ = 0 planes, together with _s_-NLs sticking to the _m_-NLs (see in Fig. 4d, e). For AsFeNb, its NLs form a novel cage-like structure. However, its fermi surface is dirty which is

messed up by some trivial bands. For PNiNb, one finds an isolated _m_-NL lies in the invariant plane _k__y_ = 0, and off the plane NLs protected by \(\tilde m_x\) and \(\tilde m_z\) are

found touching near Y point. Around the planes of _k__x_ = ±_k__z_, there exist eight segments of _s_-NLs sticking to the _m_-NLs of _k__x_ = 0 plane. Luckily the fermi surface of PNiNb,

shown in Fig. 4j, is very clean and quite similar to the NLs structure of Fig. 4e. Therefore PNiNb can be a promising compound for exploring new NLSMs with exotic multi-loop NL structure.

From the summarized result in Table 1, we find that the electron counting is a useful indicator for the search of NLSMs. The number of electrons, being totally 32 electrons/unit cell

according to the counting scheme of Landrum et al.,54 are all the same for the AsRhTi_G_, PFeV_G_, PNiV_G_, SiCoV_G_, and SiNiTi_G_ groups, while the PPtSc_G_ has 40 electrons/unit cell. In

other words, all the NLSMs listed in Tab. 1 has an count of 8 electrons _per_ formula unit. According to a simple 8-N rules of Zintl, one may expect that a NiSiTi should be an insulator or

semiconductor.59 It is the strong bonding of transition metal atoms of SiNiTi leads to the semiemtal state rather than an insulating one.54 Here our high-throughput calculations and

screening of NLSMs in MgSrSi series teach us that semimetals with filled octet orbitals could be good candidate of topological SMs. It is worthy to note that many MgSrSi-type crystals,

though containing magnetic atoms, are actually non-magnetic. For example, the ternary MMʹX (M = transition metal, Mʹ = late transition metal, X = main group element) compounds exhibit

paramagnetic behaviors for M = Sc, Ti and V.54 Previously, TiCoP, ZrCoP, and VCoSi have already been characterized to be paramagnetic metallic conductors. The trends of nonmagnetic ground

state of MgSrSi-type crystal with open-shell magnetic atoms is attributed to the strong bonding of M-Mʹ by Goodenough that the M-Mʹ bonding energy of the MgSrSi-type ternary may dominate

over the intra-atomic Coulomb interaction which favors magnetic state in the free-atom limit.60 In conclusion, we screen the MgSrSi-type crystals and more than 70 compounds are found to host

node line band crossing in their band structures. Due to the coexistence of reflection symmetry and inversion symmetry in the space group, AsRhTi is found to take a novel multi-loop NL

structure, in which a _s_-NL protected by _PT_ symmetry touches robustly with a _m_-NL protected by mirror symmetry at some “nexus point”, and in the meanwhile a second _m_-NL crosses with

the _s_-NL to form a Hopf-link. A essential three-band _k p_ model is provided to give an effective description of the low energy electrons on the Fermi surface. Topological surface states

exhibiting the nontrivial NL structure is also demonstrated. Even more exotic multi-loop NL structures are uncovered in AsFeNb and PNiNb sub-groups. All the found NLSMs are consistent with

8-N valence rules of Zintl, indicating the valence rules should be an useful indicator for the searching of topological SMs. METHODS The first principles calculations were performed by the

Vienna ab initio simulation package (VASP)61 and the projected augmented-wave (PAW) potential is adopted.62,63 The exchange-correlation functional introduced by Perdew, Burke, and Ernzerhof

(PBE)64 within generalized gradient approximation (GGA) is applied in the calculations. The energy cutoff for the plane-wave basis is set as 520 eV and the forces are relaxed less than 0.01 

eV/Å. The positions of atoms are allowed to relax while the lattice constants of the unit cells are fixed to the experimental values documented in the Inorganic Crystal Structure Database

(ICSD). The band-crossings are calculated from tight-binding models which are constructed by using the Maximally Localized Wannier Functions (MLWF) method coded in WANNIER90.65 To give a

more accurate description of electron interaction, hybrid density functional approximation is further adopted.58 DATA AVAILABILITY The data that support the findings of this study are

available from the corresponding authors upon reasonable request. REFERENCES * Weng, H., Dai, X. & Fang, Z. Topological semimetals predicted from first-principles calculations. _J. Phys.

Condens. Matter_ 28, 303001 (2016). Article  Google Scholar  * Fang, C., Weng, H., Dai, X. & Fang, Z. Topological nodal line semimetals. _Chin. Phys. B_ 25, 9–18 (2016). Google Scholar

  * Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and fermi-arc surface states in the electronic structure of pyrochlore iridates. _Phys. Rev. B_ 83,

205101 (2011). Article  Google Scholar  * Burkov, A. A. & Balents, L. Weyl semimetal in a topological insulator multilayer. _Phys. Rev. Lett._ 107, 127205 (2011). Article  CAS  Google

Scholar  * Xu, G., Weng, H., Wang, Z., Dai, X. & Fang, Z. Chern semimetal and the quantized anomalous hall effect in _hgcr_ 2 _Se_ 4. _Phys. Rev. Lett._ 107, 186806 (2011). Article 

Google Scholar  * Weng, H., Fang, C., Fang, Z., Bernevig, B. A. & Dai, X. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. _Phys. Rev. X_ 5, 011029 (2015).

Google Scholar  * Lv, B. Q. et al. Experimental discovery of weyl semimetal taas. _Phys. Rev. X_ 5, 031013 (2015). Google Scholar  * Xu, S.-Y. et al. Topological matter: discovery of a weyl

fermion semimetal and topological fermi arcs. _Science_ 349, 613–617 (2015). Article  CAS  Google Scholar  * Murakami, S. Gap closing and universal phase diagrams in topological insulators.

_Phys. E_ 43, 748–754 (2011). Article  CAS  Google Scholar  * Wang, Z. et al. Dirac semimetal and topological phase transitions in _A_ 3bi (a = Na, k, rb). _Phys. Rev. B_ 85, 195320 (2012).

Article  Google Scholar  * Wang, Z., Weng, H., Wu, Q., Dai, X. & Fang, Z. Three-dimensional dirac semimetal and quantum transport in cd3as2. _Phys. Rev. B_ 88, 125427 (2013). Article 

Google Scholar  * Burkov, A. A., Hook, M. D. & Balents, L. Topological nodal semimetals. _Phys. Rev. B_ 84, 235126 (2011). Article  Google Scholar  * Weng, H. et al. Topological

node-line semimetal in three-dimensional graphene networks. _Phys. Rev. B_ 92, 045108 (2015). Article  Google Scholar  * Kim, Y., Wieder, B. J., Kane, C. L. & Rappe, A. M. Dirac line

nodes in inversion-symmetric crystals. _Phys. Rev. Lett._ 115, 036806 (2015). Article  Google Scholar  * Yu, R., Weng, H., Fang, Z., Dai, X. & Hu, X. Topological node-line semimetal and

dirac semimetal state in antiperovskite Cu3PdN. _Phys. Rev. Lett._ 115, 036807 (2015). Article  Google Scholar  * Xie, L. S. et al. A new form of Ca3P2 with a ring of dirac nodes. _APL Mat._

3, 083602 (2015). Article  Google Scholar  * Bian, G. et al. Drumhead surface states and topological nodal-line fermions in tltase2. _Phys. Rev. B_ 93, 121113 (2016). Article  Google

Scholar  * Bian, G. et al. Topological nodal-line fermions in spin-orbit metal pbtase2. _Nat. Commun._ 7, 10556 (2016). Article  CAS  Google Scholar  * Heikkila, T. T. & Volovik, G. E.

Flat bands as a route to high-temperature superconductivity in graphite. _arXiv_: 1504.05824 (2015). * Fang, C., Chen, Y., Kee, H.-Y. & Fu, L. Topological nodal line semimetals with and

without spin-orbital coupling. _Phys. Rev. B_ 92, 081201 (2015). Article  Google Scholar  * Phillips, M. & Aji, V. Tunable line node semimetals. _Phys. Rev. B_ 90, 115111 (2014). Article

  Google Scholar  * Weber, S. F., Chen, R., Yan, Q. & Neaton, J. B. Prediction of tirhas as a dirac nodal line semimetal via first-principles calculations. _Phys. Rev. B_ 96, 235145

(2017). Article  Google Scholar  * Huang, H., Liu, J., Vanderbilt, D. & Duan, W. Topological nodal-line semimetals in alkaline-earth stannides, germanides, and silicides. _Phys. Rev. B_

93, 201114 (2016). Article  Google Scholar  * Huang, H., Jin, K.-H. & Liu, F. Topological nodal-line semimetal in nonsymmorphic _Cmce_ -phase Ag2S. _Phys. Rev. B_ 96, 115106 (2017).

Article  Google Scholar  * Li, R. et al. Dirac node lines in pure alkali earth metals. _Phys. Rev. Lett._ 117, 096401 (2016). Article  Google Scholar  * Neupane, M. et al. Observation of

topological nodal fermion semimetal phase in zrsis. _Phys. Rev. B_ 93, 201104 (2016). Article  Google Scholar  * Hu, J. et al. Evidence of topological nodal-line fermions in zrsise and

zrsite. _Phys. Rev. Lett._ 117, 016602 (2016). Article  Google Scholar  * Bzdušek, T., Wu, Q., Rüegg, A., Sigrist, M. & Soluyanov, A. A. Nodal-chain metals. _Nature_ 538, 75 (2016).

Article  Google Scholar  * Yu, R., Wu, Q., Fang, Z. & Weng, H. From nodal chain semimetal to weyl semimetal in hfc. _Phys. Rev. Lett._ 119, 036401 (2017). Article  Google Scholar  * Xu,

Q., Yu, R., Fang, Z., Dai, X. & Weng, H. Topological nodal line semimetals in the cap3 family of materials. _Phys. Rev. B_ 95, 045136 (2017). Article  Google Scholar  * Quan, Y., Yin, Z.

P. & Pickett, W. E. Single nodal loop of accidental degeneracies in minimal symmetry: triclinic caas3. _Phys. Rev. Lett._ 118, 176402 (2017). Article  CAS  Google Scholar  * Yan, Z. et

al. Nodal-link semimetals. _Phys. Rev. B_ 96, 041103 (2017). Article  Google Scholar  * Bi, R., Yan, Z., Lu, L. & Wang, Z. Nodal-knot semimetals. _Phys. Rev. B_ 96, 201305 (2017).

Article  Google Scholar  * Chen, W., Lu, H.-Z. & Hou, J.-M. Topological semimetals with a double-helix nodal link. _Phys. Rev. B_ 96, 041102 (2017). Article  Google Scholar  * Chang, G.

et al. Topological hopf and chain link semimetal states and their application to co2MnGa. _Phys. Rev. Lett._ 119, 156401 (2017). Article  Google Scholar  * Zhou, Y., Xiong, F., Wan, X. &

An, J. Hopf-link topological nodal-loop semimetals. _Phys. Rev. B_ 97, 155140 (2018). Article  Google Scholar  * Huang, H., Jiang, W., Jin, K.-H. & Liu, F. Tunable topological semimetal

states with ultraflat nodal rings in strained yn. _Phys. Rev. B_ 98, 045131 (2018). Article  Google Scholar  * Wang, J.-T., Nie, S., Weng, H., Kawazoe, Y. & Chen, C. Topological

nodal-net semimetal in a graphene network structure. _Phys. Rev. Lett._ 120, 026402 (2018). Article  Google Scholar  * Wu, Q., Zhang, S., Song, H.-F., Troyer, M. & Soluyanov, A. A.

Wanniertools: an open-source software package for novel topological materials. _Comput. Phys. Commun._ 224, 405–416 (2018). Article  CAS  Google Scholar  * Wang, S.-S., Liu, Y., Yu, Z.-M.,

Sheng, X.-L. & Yang, S. A. Hourglass dirac chain metal in rhenium dioxide. _Nat. Commun._ 8, 1844 (2017). Article  Google Scholar  * Zhong, C. et al. Three-dimensional pentagon carbon

with a genesis of emergent fermions. _Nat. Commun._ 8, 15641 (2017). Article  CAS  Google Scholar  * Liang, Q.-F., Zhou, J., Yu, R., Wang, Z. & Weng, H. Node-surface and node-line

fermions from nonsymmorphic lattice symmetries. _Phys. Rev. B_ 93, 085427 (2016). Article  Google Scholar  * Zhang, X. et al. Nodal loop and nodal surface states in the ti3Al family of

materials. _Phys. Rev. B_ 97, 235150 (2018). Article  Google Scholar  * Heikkila, T. T. & Volovik, G. E. Nexus and dirac lines in topological materials. _New J. Phys._ 17, 093019 (2015).

Article  Google Scholar  * Yan, Q. et al. Experimental discovery of nodal chains. _Nat. Phys._ 14, 461–464 (2018). Article  CAS  Google Scholar  * Watts, G. _Rh Rhodium_ 107–114 (Springer,

1991). * Suzuki, N., Asahi, R., Kishida, Y., Masuoka, Y. & Sugiyama, J. Measurement and ab initio calculation of the structural parameters and physical properties of 3d transition

intermetallics timp (m=cr, mn, fe, co, or ni). _Mater. Res. Express_ 4, 046505 (2017). Article  Google Scholar  * Roy-Montreuil, M. et al. Nouveaux composes ternaires mm’p et mm’as

interactions metalliques et structures. _Mater. Res. Bull._ 7, 813–826 (1972). Article  CAS  Google Scholar  * Pies, W. & Weiss, A. _c1341, VII.1.2.1 Binary and ternary phosphides_,

45–60 (Springer, Berlin Heidelberg, 1979). * Johnson, V. Ternary transition metal germanides and arsenides. _Mater. Res. Bull._ 8, 1067–1072 (1973). Article  CAS  Google Scholar  * Imre, A.

& Mewis, A. Scptp und laptp–zwei phosphide mit, inverser tinisi-struktur/scptp and laptp–two phosphides with inverse tinisi-type structure. _Z. für Naturforsch. B_ 62, 1153–1156 (2007).

Article  CAS  Google Scholar  * Dinges, T., Eul, M. & Poettgen, R. Tarhge with tinisi-type structure. _Z. für Naturforsch. B_ 65, 95–98 (2010). Article  CAS  Google Scholar  * Mishra,

R., Poettgen, R. & Kotzyba, G. New metal-rich compounds nblrsi, nblrge, and talrsi-synthesis, structure, and magnetic properties. _Z. für Naturforsch. B_ 56, 463–468 (2001). Article  CAS

  Google Scholar  * Landrum, G. A., Hoffmann, R., Evers, J. & Boysen, H. The tinisi family of compounds: structure and bonding. _Inorg. Chem._ 37, 5754–5763 (1998). Article  CAS  Google

Scholar  * Zhao, J. & Parth, E. Ternary equiatomic hafnium-transition metal suicides. _J. Less Common Met._ 163, L7–L12 (1990). Article  CAS  Google Scholar  * Gil-Santos, A., Szakacs,

G., Moelans, N., Hort, N. & Van der Biest, O. Microstructure and mechanical characterization of cast mg-ca-si alloys. _J. Alloy Compd_ 694, 767–776 (2017). Article  CAS  Google Scholar 

* Rui, W. B., Zhao, Y. X. & Schnyder, A. P. Topological transport in Dirac nodal-line semimetals. _arXiv_: 1703.05958 (2017). * Heyd, J., Scuseria, G. E. & Ernzerhof, M. Erratum:

hybrid functionals based on a screened coulomb potential. _J. Chem. Phys._ 124, 219906 (2006). Article  Google Scholar  * Zintl, E. Intermetallische verbindungen. _Angew. Chem._ 52, 1–6

(1939). Article  CAS  Google Scholar  * Goodenough, J. Interpretation of structure and magnetism in transition-metal pnictides m2x and (m1- xm¡ä x) 2×. _J. Solid State Chem._ 7, 428–447

(1973). Article  CAS  Google Scholar  * Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. _Phys. Rev. B_ 54,

11169–11186 (1996). Article  CAS  Google Scholar  * Blöchl, P. E. Projector augmented-wave method. _Phys. Rev. B_ 50, 17953–17979 (1994). Article  Google Scholar  * Kresse, G. & Joubert,

D. From ultrasoft pseudopotentials to the projector augmented-wave method. _Phys. Rev. B_ 59, 1758–1775 (1999). Article  CAS  Google Scholar  * Perdew, J. P., Burke, K. & Ernzerhof, M.

Generalized gradient approximation made simple. _Phys. Rev. Lett._ 77, 3865–3868 (1996). Article  CAS  Google Scholar  * Mostofi, A. A. et al. wannier90: a tool for obtaining

maximally-localised wannier functions. _Comput. Phys. Commun._ 178, 685 (2008). Article  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS The work is supported by National Natural

Science Foundation of China (NSFC) (Grants No. 11574215, No. 11575116, No. 11274359, and No. 11422428). H. M. W is also supported by the National 973 program of China (Grants No.

2018YFA0305700 and No. 2013CB921700), and the “Strategic Priority Research Program (B)” of the Chinese Academy of Sciences (Grant No. XDB07020100). The calculations in this work were

performed on the supercomputers of Shanghai supercomputer Center and of the high performance computing center of Nanjing University. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department

of Physics, Shaoxing University, 312000, Shaoxing, China Jinling Lian, Lixian Yu & Qi-Feng Liang * National Laboratory of Solid State Microstructures and Department of Materials Science

and Engineering, Nanjing University, 210093, Nanjing, China Jian Zhou * School of Physics and Technology, Wuhan University, 430072, Wuhan, China Rui Yu * Beijing National Laboratory for

Condensed Matter Physics, and Institute of Physics, Chinese Academy of Sciences, 100190, Beijing, China Hongming Weng * Songshan Lake Materials Laboratory, Guangdong, 523808, China Hongming

Weng Authors * Jinling Lian View author publications You can also search for this author inPubMed Google Scholar * Lixian Yu View author publications You can also search for this author

inPubMed Google Scholar * Qi-Feng Liang View author publications You can also search for this author inPubMed Google Scholar * Jian Zhou View author publications You can also search for this

author inPubMed Google Scholar * Rui Yu View author publications You can also search for this author inPubMed Google Scholar * Hongming Weng View author publications You can also search for

this author inPubMed Google Scholar CONTRIBUTIONS Q.-F.L., R.Y., and H.M.W. conceived the study. J.L. and L.Y. wrote the necessary code, J.L., L.Y., and Q.-F.L. carried out the

calculations. Q.-F.L. analyzed the data. All four authors contributed to writing the manuscript. J.L. and L.Y. contributed equally to this work. CORRESPONDING AUTHORS Correspondence to

Qi-Feng Liang or Rui Yu. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE: Springer Nature remains neutral with

regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0

International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the

source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative

Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Lian, J., Yu, L., Liang, QF. _et al._ Multi-loop node line states in ternary

MgSrSi-type crystals. _npj Comput Mater_ 5, 10 (2019). https://doi.org/10.1038/s41524-018-0147-y Download citation * Received: 09 August 2018 * Accepted: 11 December 2018 * Published: 21

January 2019 * DOI: https://doi.org/10.1038/s41524-018-0147-y SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a

shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative