ABSTRACT Quantum computing with qudits is an emerging approach that exploits a larger, more connected computational space, providing advantages for many applications, including quantum

simulation and quantum error correction. Nonetheless, qudits are typically afflicted by more complex errors and suffer greater noise sensitivity which renders their scaling difficult. In

this work, we introduce techniques to tailor arbitrary qudit Markovian noise to stochastic Weyl–Heisenberg channels and mitigate noise that commutes with our Clifford and universal two-qudit

gate in generic qudit circuits. We experimentally demonstrate these methods on a superconducting transmon qutrit processor, and benchmark their effectiveness for multipartite qutrit

computational reach of today’s qudit processors. SIMILAR CONTENT BEING VIEWED BY OTHERS HIGH-FIDELITY THREE-QUBIT _I_TOFFOLI GATE FOR FIXED-FREQUENCY SUPERCONDUCTING QUBITS Article 02 May

2022 MEASUREMENT-INDUCED ENTANGLEMENT AND TELEPORTATION ON A NOISY QUANTUM PROCESSOR Article Open access 18 October 2023 EFFICIENT NOISE MITIGATION TECHNIQUE FOR QUANTUM COMPUTING Article

Open access 08 March 2023 INTRODUCTION In the noisy intermediate-scale quantum (NISQ) era1, the ability to effectively couple many quantum two-level systems (qubits) together has led to

experimental demonstrations of certain tasks that challenge the limits of current classical capabilities2,3,4,5. The computational power of these near-term devices can potentially be further

boosted by leveraging the innate multi-level structure to encode quantum information in the larger and more connected Hilbert space of _d_-level systems (qudits)6,7,8,9,10,11. Coherent

control of higher-level quantum systems has been demonstrated in superconducting circuits12,13,14,15,16,17,18, trapped ions19,20, and in photonic circuits21,22. The simplest and most

immediately experimentally viable member of the qudit family is the quantum three-level system or qutrit. Qutrits can yield specific advantages in quantum simulations, where they are a

natural platform for studying spin-1 physics23,24 and robust and resource efficient for simulating high-energy phenomena12,25. Additional applications include improvements in quantum

cryptography26,27, communication28, compactly synthesizing multi-qubit gates29,30,31,32,33,34, and improving qubit readout35,36,37. Eventually, qutrits are expected to provide significant

advantages for quantum error correction via improved error thresholds38,39,40,41, errors tailored to erasure42,43, enhanced fault tolerance44,45, and compact encodings of both logical

qutrits46 and logical qubits47,48. While fault tolerance remains the ultimate goal, alternative efforts in qubit devices to mitigate and extrapolate expectation values beyond the noise

present in the system have garnered interest lately due to the lack of an increase in hardware requirements and overall feasibility49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64. Notably,

recent works have demonstrated that error mitigation protocols can prove effective for large-scale qubit experiments, allowing an exciting pathway to high-fidelity results in the near term

for problems of interest51,52,53,57,59,61,62,63,64,65,66. Recent investigations have also explored the compatibility of noise tailoring, error mitigation, and quantum error correction67,68.

However, there is a dearth of similar studies for qudit devices, which are now approaching the maturity to scale to larger experimental sizes but are afflicted by more complicated noise

processes69. This opens the door to an interesting question: can the computational power of contemporary devices be augmented by enlarging their Hilbert space as qudits, while at the same

time retaining the ability to generate noiseless expectation values in this more complex noise environment? In this work, we attempt to answer this question and show that error mitigation

can be utilized to significantly extend the existing resources of a superconducting qutrit processor. More explicitly, we introduce two techniques for tailoring and mitigating noise in

qutrit circuits: randomized compiling (RC)68,70 and noiseless output extrapolation (NOX)66. We then explore the performance of these techniques in a variety of multi-qutrit experiments using

fixed frequency transmons. In particular, we study state tomography of a three-qutrit Greenberger–Horne–Zeilinger (GHZ) state, as well as random circuit sampling (RCS) with two and three

qutrits. We find that in all cases, despite the more complex noise environment, our results benefit greatly from these protocols, achieving up to a 3 times improvement in fidelity. Our work

is the first to experimentally demonstrate that error mitigation can be effectively implemented on qutrit platforms, and it paves the way to scaling near-term, large-scale qutrit

computations. RESULTS COMPUTING, TWIRLING, AND MITIGATING WITH QUTRITS COMPUTING With qutrits, information is encoded in the three energy levels that correspond to the computational basis

states \(\left\vert 0\right\rangle\), \(\left\vert 1\right\rangle\), and \(\left\vert 2\right\rangle\). As for qubits, gates are unitary operators relative to the computational basis. An

important set of qutrit gates is the Weyl operators, which are a generalization of the of the qubit Pauli group in a higher dimensional Hilbert space. The action of the Weyl gates is

specified by the operators _W__p_,_q_ = _ω_−_p__q_/2_Z__p__X__q_, where _X_ and _Z_ are defined by their action on the basis state \(\left\vert n\right\rangle\) as \(X\left\vert

n\right\rangle =\left\vert n\oplus 1\right\rangle\) and \(Z\left\vert n\right\rangle ={\omega }^{n}\left\vert n\right\rangle\) and _ω_ = _e_2_i__π_/3. Like the Pauli gates for qubit systems,

the Weyl operators form a unitary 1-design71 and are normalized by the qutrit Clifford group. That is, by definition72, given a gate _G_, we have that a product of local Weyl gates

\({\otimes }_{i}{W}_{{p}_{i},{q}_{i}}\) conjugated by _G_ remains a product of Weyl gates, e.g., $$G({\otimes }_{i}{W}_{{p}_{i},{q}_{i}}){G}^{-1}={\otimes }_{i}{W}_{{p}_{i}^{{\prime}

},{q}_{i}^{{\prime} }},$$ (1) if and only if _G_ is part of the qutrit Clifford group. Natural generalizations of two-qubit gates can also be constructed. For example, the two-qutrit analog

of the controlled-Z (CZ) gate is defined as, $${\rm{CZ}}=\mathop{\sum }\limits_{n=0}^{n=2}\left\vert n\right\rangle \left\langle n\right\vert \otimes {Z}^{n}.$$ (2) Both CZ and its inverse

CZ† are Clifford and universal (when combined with arbitrary SU(3) rotations) entangling gates that can be performed on our system14. Critically, the natural adoption of twirling and

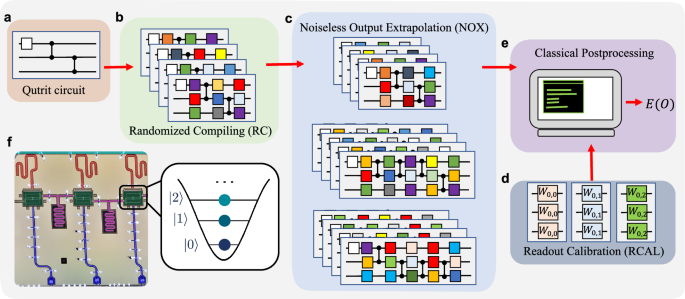
mitigation methods that have been developed for qubits is only possible through the ability to implement two-qutrit Clifford gates (see Fig. 1). TWIRLING Being a unitary 1-design, Weyl

operators can be used to _twirl_ noise68,71,73,74—that is, to transform arbitrary Markovian noise processes into stochastic channels of the form $${\mathcal{W}}(\rho )=\mathop{\sum

}\limits_{\bar{p},\bar{q}}^{{4}^{n}}{\rm{prob}}({W}_{\bar{p},\bar{q}}){W}_{\bar{p},\bar{q}}\,\rho \,{W}_{\bar{p},\bar{q}}^{\dagger },$$ (3) where _ρ_ is an _n_-qutrit state,

\({W}_{\bar{p},\bar{q}}={\otimes }_{i = 1}^{n}{W}_{\!{q}_{{k}_{i}},{p}_{{k}_{i}}}\) is a tensor product of one-qutrit Weyl operators, and \({\rm{prob}}({W}_{\bar{p},\bar{q}})\) is the

probability that a Weyl error \({W}_{\bar{p},\bar{q}}\) occurs. Twirling noise processes can significantly improve the performance of noisy devices68. Indeed, while coherent errors can

accumulate quadratically in the number of noisy gates, stochastic channels accumulate linearly and dramatically lower worst-case error rates75. In our experiments, we twirl the noise using

the RC protocol from ref. 70 generalized to qutrits. To illustrate this procedure, let us consider a “target” circuit of the type in Fig. 2a, i.e., a circuit that alternates between cycles

of single-qutrit gates (represented by Completely Positive Trace-Preserving, or CPTP, maps \({{\mathcal{U}}}_{j}\)) and cycles of multi-qutrit gates (represented by CPTP maps

\({{\mathcal{H}}}_{j}\)), implementing the operation $${\mathcal{C}}={{\mathcal{U}}}_{m+1}{{\mathcal{H}}}_{m}{{\mathcal{U}}}_{m}\cdots {{\mathcal{H}}}_{1}{{\mathcal{U}}}_{1}.$$ (4)

Expressing a noisy implementation of \({{\mathcal{U}}}_{j}\) (respectively \({{\mathcal{H}}}_{j}\)) as \({{\mathcal{D}}}_{j}{{\mathcal{U}}}_{j}\) (respectively

\({{\mathcal{F}}}_{j}{{\mathcal{H}}}_{j}\)), a noisy implementation of this circuit performs the operation

$$\widetilde{{\mathcal{C}}}={{\mathcal{D}}}_{m+1}{{\mathcal{U}}}_{m+1}{{\mathcal{E}}}_{m}{{\mathcal{H}}}_{m}{{\mathcal{U}}}_{m}\cdots

{{\mathcal{E}}}_{1}{{\mathcal{H}}}_{1}{{\mathcal{U}}}_{1},$$ (5) where \({{\mathcal{E}}}_{j}={{\mathcal{F}}}_{j}{{\mathcal{H}}}_{j}{{\mathcal{D}}}_{j}{{\mathcal{H}}}_{j}^{-1}\) is the

combined noise of \({{\mathcal{U}}}_{j}\) and \({{\mathcal{H}}}_{j}\). Analogous to the original protocol, to perform RC, we recompile randomly chosen Weyl gates and their inverses into the

cycles of one-qubit gates (Fig. 2b, c). Implementing the circuit _N_ > 1 times with different choices of random Weyl gates and averaging over the various implementations is equivalent to

implementing a circuit $${\widetilde{{\mathcal{C}}}}_{{\rm{RC}}}={{\mathcal{U}}}_{m+1}{{\mathcal{W}}}_{m}{{\mathcal{H}}}_{m}{{\mathcal{U}}}_{m}\cdots

{{\mathcal{W}}}_{1}{{\mathcal{H}}}_{1}{{\mathcal{U}}}_{1}$$ (6) afflicted by stochastic noise processes \({{\mathcal{W}}}_{j}\) of the type in Eq. (3), up to statistical fluctuations that

decrease exponentially with _N_. Specifically, denoting by \({\widetilde{{\mathcal{C}}}}_{1},\ldots ,{\widetilde{{\mathcal{C}}}}_{N}\) the _N_ circuits with random Weyl operators,

Hoeffding’s inequality76 ensures that for every state _ρ_, observable _O_, and positive number _ϵ_ < 1, we have $$\begin{array}{l}{\rm{prob}}\left(| E(O|

{\widetilde{{\mathcal{C}}}}_{{\rm{RC}}})-\frac{1}{N}\mathop{\sum }\limits_{k=1}^{N}E(O| {\widetilde{{\mathcal{C}}}}_{k})|\, <\, \epsilon \right)\\ \ge 1-\exp \left(-2{\epsilon

}^{2}N\right),\end{array}$$ (7) where \(E(O| {\mathcal{C}})={\rm{Tr}}\left[O{\mathcal{C}}\left(\rho \right)\right]\) is the expectation value of _O_ at the end of a circuit

\({\mathcal{C}}\). Importantly, the r.h.s. of the above inequality does not depend on the dimension of the Hilbert space. Hence, achieving the desired approximation level requires

implementing the same number of circuits for qutrits as for qubits (Fig. 2d). MITIGATING While implementing RC alone leads to significant performance gains, employing it in tandem with other

error-mitigation protocols leads to even larger gains. In our experiments, we utilize RC in combination with NOX, a protocol designed to mitigate stochastic errors that commute with cycles

of gates. In its simplest version, NOX requires implementing the target circuit \({\widetilde{{\mathcal{C}}}}_{{\rm{RC}}}\) alongside several copies of it. Each copy implements the same

computation as \({\widetilde{{\mathcal{C}}}}_{{\rm{RC}}}\), but the noise of one of its cycles is amplified in a controlled way. Specifically, the _j_th copy implements the operation

$$\begin{array}{l}{\widetilde{{\mathcal{C}}}}_{{\rm{RC}}}^{(j)}:= {{\mathcal{U}}}_{m+1}{{\mathcal{W}}}_{m}{{\mathcal{H}}}_{m}{{\mathcal{U}}}_{m}\cdots

{\left({{\mathcal{W}}}_{j}\right)}^{{\alpha }_{j}}{{\mathcal{H}}}_{j}{{\mathcal{U}}}_{j}\cdots {{\mathcal{W}}}_{1}{{\mathcal{H}}}_{1}{{\mathcal{U}}}_{1},\end{array}$$ (8) where _α__j_ > 1

is an integer specified by the user. By combining the outputs of the target circuit and those of the various copies, NOX returns the quantity $${E}_{{\rm{NOX}}}(O)=E(O|

{\widetilde{{\mathcal{C}}}}_{{\rm{RC}}})-\mathop{\sum }\limits_{j=1}^{m}\frac{E(O| {\widetilde{{\mathcal{C}}}}_{{\rm{RC}}})-E(O| {\widetilde{{\mathcal{C}}}}_{{\rm{RC}}}^{(j)})}{{\alpha

}_{j}-1}.$$ (9) _E_NOX(_O_) is an estimator of the correct result, \(E(O| {\mathcal{C}})\), and its bias is quadratically smaller than that of \(E(O| \widetilde{{\mathcal{C}}})\)66. In order

to perform noise amplification, in our experiments we utilize Unitary Folding (UF)54. That is, given a noisy cycle \({\mathcal{W}}{\mathcal{H}}\) and a number _α_ such that

\({{\mathcal{H}}}^{\alpha +1}={\mathcal{H}}\), we replace \({\mathcal{W}}{\mathcal{H}}\) with \({({\mathcal{W}}{\mathcal{H}})}^{\alpha +1}\). In the instance where the error channel

\({\mathcal{W}}\) commutes with the cycle \({\mathcal{H}}\), i.e., \({\mathcal{W}}{\mathcal{H}}={\mathcal{H}}{\mathcal{W}}\), UF leads to \({({\mathcal{W}}{\mathcal{H}})}^{\alpha

+1}={{\mathcal{W}}}^{\alpha +1}{\mathcal{H}}\), which provides the desired noise amplification. In the more general situation, UF leaves a remainder term:

$${({\mathcal{W}}{\mathcal{H}})}^{\alpha +1}={{\mathcal{W}}}^{\alpha +1}{\mathcal{H}}+{\mathcal{R}}{\mathcal{H}}.$$ (10) In Methods section “Error amplification via unitary folding (UF)”, we

briefly argue why the term \({\mathcal{R}}{\mathcal{H}}\) may have little impact on mitigated results in realistic scenarios. This argument is reflected in our results since we observe

significant improvements when resorting to UF amplification despite its possible imperfections. That being said, we acknowledge that more sophisticated techniques can be used to amplify

noise when \({\mathcal{W}}{\mathcal{H}}\not\approx {\mathcal{H}}{\mathcal{W}}\); some methods rely on learning the errors by using cycle-based noise reconstruction techniques66,77, and some

others rely on pulsed-based inverse evolution78. We leave the utilization of those methods for future work. In addition to RC and NOX, we employ readout calibration (RCAL) to mitigate

measurement noise79. RCAL requires implementing three simple circuits (the first with a _W_0,0 gate on every qutrit, the second with a _W_0,1 gate, and the third one with a _W_0,2 gate) to

estimate the probabilities of state-dependent readout errors—i.e., the probabilities that an output _s_ ∈ {0, 1, 2} is incorrectly reported as \({s}^{{\prime} }\ne s\). It then uses this

information to efficiently suppress readout errors by inverting confusion matrices. EXPERIMENT We test our ability to effectively twirl and extrapolate noiseless results in two sets of

multi-qutrit experiments. In the first experiment, we use state tomography to reconstruct a three-qutrit GHZ state. In the second experiment, we perform random circuit sampling (RCS) for two

and three qutrits at a variety of depths. In both experiments, we find significant improvements in our results via the combination of RC and NOX. Our experimental device consists of

fixed-frequency transmons, with fixed coupling mediated by coplanar waveguide resonators. Single-qutrit gates are performed via Rabi oscillations and virtual Z gates in two-level subspaces

of the qutrit, and two-qutrit gates are performed via a tunable cross-Kerr entangling interaction. More information on how we perform single and two-qutrit gates can be found in refs. 12,13

and ref. 14, respectively and additional device characterization is available in Supplementary Note 1. MULTIPARTITE QUTRIT ENTANGLEMENT Experimental demonstrations of multipartite

entanglement have been instrumental in demonstrating that local realism can be violated by quantum mechanics80. So far, studies of multipartite entanglement have mostly focused on coupled

qubits, and experimental demonstrations of multipartite qutrit entanglement have only been performed in a few cases12,81. In this work, we generate a maximally entangled state on a _D_ = 27

dimensional Hilbert space using only three transmon qutrits. Specifically, we realize the qutrit GHZ state \({\left\vert \Psi \right\rangle }_{{\rm{GHZ}}}=\frac{1}{\sqrt{3}}(\left\vert

000\right\rangle +\left\vert 111\right\rangle +\left\vert 222\right\rangle )\). To characterize this highly-entangled state, we perform tomography on the full three-qutrit Hilbert space82,

requiring a total of 729 circuits. We measure an informationally-complete set of projections to experimentally reconstruct the density matrix for \(\rho =\left\vert \Psi \right\rangle

\left\langle \Psi \right\vert _{{\rm{GHZ}}}\), finding a state fidelity of \({\mathcal{F}}=\,\text{Tr}\,(\sqrt{\sigma }\rho \sqrt{\sigma })=0.818\), where _σ_ is the ideal density matrix.

Even in the unmitigated case, our work represents, to the best of our knowledge, the highest fidelity exploration of multipartite qutrit entanglement to date. Next, we perform the same

experiment using RC and NOX, requiring a total of 43,740 (729 × 20 × 3) circuits, where we use 20 logically-equivalent compilations of the bare circuit and for each of the identity

insertions for the two different two-qutrit gate cycles. We find a mitigated state fidelity of \({\mathcal{F}}=0.951\), resulting in a greater than 3x reduction in infidelity compared to the

unmitigated case. The circuits and the experimentally reconstructed density matrices can be found in Fig. 3. Finally, we purify the reconstructed state measured with RC (no NOX)83 by

numerically finding the nearest density matrix that is idempotent (_ρ_2 = _ρ_)84, which improved the state fidelity from 0.912 to 0.998 (see Supplementary Note 4). These results demonstrate

the power of RC to tailor coherent errors to purely stochastic channels. A summary of the results of all the state tomography experiments and mitigation strategies can be found in Table 1.

QUTRIT RANDOM CIRCUIT SAMPLING RCS with qubits has recently garnered significant interest due to its role in demonstrating quantum advantage2,4, and it has been speculated that RCS may also

have pragmatic use cases85,86. In this work, we extend the task of RCS to qutrits and study the two and three-qutrit experiments at a number of depths. Notably, leveraging qutrits for RCS,

in principle, could allow one to probe the regime of quantum supremacy with significantly fewer qutrits (~35) than qubits (~55). In both the two and three-qutrit RCS experiments, Haar-random

single qutrit gates are interleaved with CZ† gates (hard cycles). We study 20 separate RCS instances for each circuit depth. In Fig. 4, the bare RCS results are compared to the mitigated

results measured using RC (20 randomizations) and NOX. To quantify circuit performance, we calculate the variation distance from the ideal trit string distributions, defined as $${\rm{VD}}:=

\frac{1}{2}\sum _{\bar{s}}| {p}_{{\rm{id}}}(\bar{s})-{p}_{\exp }(\bar{s})|$$ (11) where \(\bar{s}\in {(0,1,2)}^{\otimes n}\) and _p_id and \({p}_{\exp }\) are the ideal and experimentally

measured trit string distributions, respectively. The best results for the mitigated case were found with 3 insertions of the identity (see Supplementary Note 3). Notably, when employing

RC+NOX in both the two and three-qutrit RCS experiments, the variation distances at depth 6 were comparable to the unmitigated case at depth 2, and at all depths, we found at least a 30%

fractional improvement in our results with RC + NOX. DISCUSSION We introduced generalized versions of two powerful methods for tailoring and mitigating noise in contemporary qudit systems:

randomized compiling and noiseless output extrapolation. We tested the efficacy of these methods at generating noiseless expectation values on a system of three coupled transmon qutrits.

Specifically, we explored the experimentally reconstructed density matrix of a 3-qutrit GHZ state and the problem of multi-qutrit random circuit sampling. We found that despite the more

complex noise environment, added noise sensitivity, and more difficult control requirements, our protocols proved to be a powerful tool for significantly improving our results for all of the

aforementioned experiments. Specifically, we effectively tailored coherent errors to stochastic errors on both gate and spectator qutrits via the first demonstration of randomized compiling

for qudit dimension _d_ ≥ 3, and extrapolated beyond the noise in our system via the first demonstration of noiseless output extrapolation in _d_ ≥ 3. As higher-dimensional quantum devices

begin to mature and compete with qubit systems, the ability to perform longer-depth algorithms without significant errors will be critical to convincing the community of their feasibility

and scalability. To this end, our work opens the door to explore many of the advantages leveraged by qudit devices in both quantum algorithms and gate based quantum simulation in the near

term on contemporary devices. METHODS CALCULATING THE PROPORTION OF COHERENT ERRORS IN QUDIT PTMS In Fig. 2d, we show the numerical results of twirling away (using qudit RC) off-diagonal

elements (or coherent errors) in qudit PTMs. Here, we briefly comment on how one calculates the proportion of coherent errors present in a qudit PTM, following ref. 87. Consider a quantum

error channel with PTM denoted as \({\mathcal{E}}\). The process fidelity is defined as the normalized trace of the (_d_2 × _d_2) PTM: $$F({\mathcal{E}}):= {\rm{tr}}\,{\mathcal{E}}/{d}^{2}$$

(12) Let’s define the decoherent process fidelity of \({\mathcal{E}}\) as $${F}_{{\rm{decoh.}}}\,({\mathcal{E}}):= \sqrt{{\rm{tr}}\,{{\mathcal{E}}}^{\dagger

}{\mathcal{E}}/{d}^{2}}=\Vert{\mathcal{E}}{\Vert }_{F}/d.$$ (13) In ref. 87, it is shown that as long as the error channel is reasonably close to the identity, that is if

\(F({\mathcal{E}})\, >\, 1/2\) and \({F}_{{\rm{decoh.}}}\,({\mathcal{E}}) > 1/\sqrt{2}\), the error channel has a well-defined coherent-decoherent polar decomposition:

$${\mathcal{E}}={\mathcal{U}}{\mathcal{D}},$$ (14) where \({\mathcal{U}}\) is a coherent (i.e., unitary) error process and \({\mathcal{D}}\) is a purely decoherent process. The precise

definition of a decoherent channel is elaborated and justified in ref. 87. In realistic physical scenarios, the process fidelity can be expressed as a simple product:

$$F({\mathcal{E}})=F({\mathcal{U}})F({\mathcal{D}})+h.o.,$$ (15) where the higher order term (_h_. _o_.) is of second order in the infidelity, \(O\left({(1-F({\mathcal{E}}))}^{2}\right)\).

For reference, Eq. (15) does not hold in pathological cases where a significant part of the error process originates from specially crafted high-body interactions (e.g.,

Hamiltonian/Lindbladian terms that are made of tensor products of a large number of subsystems). A discussion of these pathological cases is included in ref. 87. Notice that by combining eq.

(13) and eq. (14), we get: $$\begin{array}{rcl}{F}_{{\rm{decoh.}}}\,({\mathcal{E}})&=&{F}_{{\rm{decoh.}}}\,({\mathcal{U}}{\mathcal{D}})\\ &=&\parallel

\!{\mathcal{U}}{\mathcal{D}}{\parallel }_{F}/d\\ &=&\parallel \!{\mathcal{D}}{\parallel }_{F}/d\\ &=&{F}_{{\rm{decoh.}}}\,({\mathcal{D}})\\

&=&F({\mathcal{D}})+O\left({(1-F({\mathcal{D}}))}^{2}\right)\end{array}$$ (16) where the last line comes from the fact that non-pathological decoherent errors obey (87)

$${\rm{tr}}\,{{\mathcal{D}}}^{\dagger }{\mathcal{D}}/{d}^{2}={\left({\rm{tr}}{\mathcal{D}}/{d}^{2}\right)}^{2}+O\left({(1-F({\mathcal{D}}))}^{2}\right).$$ (17) The above is essentially a

corollary from the fact that decoherent errors build up according to a multiplicative decay. By substituting eq. (16) in Eq. (15), we get, up to second order in the infidelity,

$$F({\mathcal{E}})=F({\mathcal{U}}){F}_{{\rm{decoh.}}}\,({\mathcal{E}}),$$ (18) or in terms of infidelity (up to second order in the infidelity)

$$\underbrace{1-F({{\mathcal{E}}})}_{{\rm{Tot.}}\,{\rm{infid.}}} = \underbrace{1-F({{\mathcal{U}}})}_{{\rm{Coh.}}\,{\rm{infid.}}} + \underbrace{1-

F_{{\rm{decoh.}}}\,{({\mathcal{E}})}}_{{\rm{Decoh.}}\,{\rm{infid.}}}.$$ (19) As such, the contribution of coherence to the process of infidelity is given by (up to the second order in the

infidelity): $$1-F({\mathcal{U}})={F}_{{\rm{decoh.}}}\,({\mathcal{E}})-F({\mathcal{E}}).$$ (20) The relative coherent contribution to the infidelity is therefore obtained via

$$\frac{{F}_{{\rm{decoh.}}}\,({\mathcal{E}})-F({\mathcal{E}})}{1-F({\mathcal{E}})}=\frac{{\rm{tr}}\,{\mathcal{E}}/{d}^{2}-d\parallel{\mathcal{E}}{\parallel

}_{F}/d}{1-{\rm{tr}}\,{\mathcal{E}}/{d}^{2}}.$$ (21) The above is the formula used in Fig. 2d to quantify the effect of twirling on the error channel. ERROR AMPLIFICATION VIA UNITARY FOLDING

(UF) Noise amplification through unitary folding (UF) is performed by repeating a desired noisy cycle \({\mathcal{W}}{\mathcal{H}}\)54. When the error channel \({\mathcal{W}}\) commutes

with the cycle \({\mathcal{H}}\), we get \({({\mathcal{W}}{\mathcal{H}})}^{\alpha +1}={{\mathcal{W}}}^{\alpha +1}{\mathcal{H}}\). In the more general situation where

\({\mathcal{W}}{\mathcal{H}}\,\ne\, {\mathcal{H}}{\mathcal{W}}\), we instead get a remainder term $${({\mathcal{W}}{\mathcal{H}})}^{\alpha +1}={{\mathcal{W}}}^{\alpha

+1}{\mathcal{H}}+{\mathcal{R}}{\mathcal{H}}.$$ (22) In this section, we briefly argue why one may expect the remainder \({\mathcal{R}}{\mathcal{H}}\) to be of little impact in some

instances. Given a cyclicity _c_ representing the smallest positive integer such that \({{\mathcal{H}}}^{c}=I\), we can express the error channel \({\mathcal{W}}\) as

$${\mathcal{W}}={e}^{\mathop{\sum }\nolimits_{k = 0}^{c-1}{L}_{k}},$$ (23) where the dissipator terms {_L_0, _L_1, ⋯ , _L__c_−1} obey: $${L}_{k}{\mathcal{H}}={\omega

}^{k}{\mathcal{H}}{L}_{k},$$ (24) where _ω_ = _e_2_i__π_/_c_. In our experiments, the cycle \({\mathcal{H}}\) is a tensor product of CZ† gates and has a cyclicity of _c_ = 3. This yields

\({\mathcal{W}}={e}^{{L}_{0}+{L}_{1}+{L}_{2}}\) with \({L}_{k}{\mathcal{H}}={\omega }^{k}{\mathcal{H}}{L}_{k}\) where _ω_ = _e_2_i__π_/3. In this case, UF yields:

$$\begin{array}{rcl}{({\mathcal{W}}{\mathcal{H}})}^{\alpha +1}&=&{\left({e}^{{L}_{0}+{L}_{1}+{L}_{2}}{\mathcal{H}}\right)}^{\alpha +1}\\ &=&\left(\mathop{\prod

}\limits_{k=0}^{k=\alpha }{e}^{{{\mathcal{H}}}^{k}({L}_{0}+{L}_{1}+{L}_{2}){{\mathcal{H}}}^{-k}}\right){\mathcal{H}}\\ &=&\left(\mathop{\prod }\limits_{k=0}^{k=\alpha

}{e}^{{L}_{0}+{\omega }^{k}{L}_{1}+{\omega }^{2k}{L}_{2}}\right){\mathcal{H}}\\ &\approx &{e}^{(\alpha +1){L}_{0}+{L}_{1}+{L}_{2}}{\mathcal{H}},\end{array}$$ (25) where in the last

line we truncated the second-order terms from the BCH expansion88 for simplicity. The purpose behind the derivation of Eq. (25) is to show that, up to a second-order approximation, only the

dissipator term _L_0 that commutes with the cycle \({\mathcal{H}}\) gets properly amplified by UF. One reason that makes UF an effective error amplification strategy despite this limitation

is that _L_0 is often a dominating source of error compared to the other dissipators. Indeed, following the derivation of78, given a noisy process \({\mathcal{W}}{\mathcal{H}}\) obtained

from integrating a Lindbladian, $${\mathcal{W}}{\mathcal{H}}=\mathop{\int}\nolimits_{\!\!0}^{T}-iH(t)+L(t)\,dt,$$ (26) where _H_(_t_) and _L_(_t_) correspond to the super-operator versions

of the ideal and noisy dynamics, respectively, we can approximate \({\mathcal{W}}\) as $${\mathcal{W}}\approx {\mathcal{H}}\exp

\left(\mathop{\int}\nolimits_{\!\!0}^{T}dt\,{{\mathcal{U}}}^{\dagger }(t)L(t){\mathcal{U}}(t)\right){{\mathcal{H}}}^{-1},$$ (27) where \({\mathcal{U}}(t)\) is the ideal evolution at time

_t_. This approximation corresponds to the truncation of the Magnus expansion to first order. The integral in Eq. (27) is close to a twirl operation, and has the effect of partially

suppressing the matrix components that do not commute with \({\mathcal{W}}\). To see this more clearly, let’s assume that _H_(_t_) and _L_(_t_) are time-independent and let’s perform

column-vectorization on the integral in Eq. (27): $${{\rm{vec}}}\left(\int_0^T dt \,{\mathcal{U}}^\dagger(t) L\,{\mathcal{U}}(t)\right) = \underbrace{\left(\int_0^T dt \,{\mathcal{U}}(t)^T

\otimes {\mathcal{U}}^\dagger(t)\right)}_{{\rm{Partial}}\,{\rm{twirl}}\,{\rm{operator.}}}\, {{\rm{vec}}}\left(L\right)$$ (28) where we used the identity vec(_A__B__C_) = _C__T_ ⊗

_A_vec(_B_). We denote the operator acting on vec(_L_) as a “partial twirl”; a full twirl would involve the self-inverting evolution from 0 to _τ_ where \({\mathcal{U}}(0)={\mathcal{U}}(\tau

)\). It is straightforward to show that the full twirl projects vec(_L_) unto the subspace of operators that commute with \({\mathcal{U}}(t)=\exp (iHt)\) for any time _t_. The partial twirl

operator instead dampens the components of _L_ that do not commute with the unitary evolution evolution. DATA AVAILABILITY All data are available from the corresponding author upon

reasonable request. CODE AVAILABILITY All front-end code and jupyter notebooks used for analysis are available upon request. The mitigation routines and circuit compilation were performed

using True-Q, a proprietary software package. REFERENCES * Preskill, J. Quantum computing in the NISQ era and beyond. _Quantum_ 2, 79 (2018). Article  Google Scholar  * Arute, F. et al.

Quantum supremacy using a programmable superconducting processor. _Nature_ 574, 505–510 (2019). Article  ADS  Google Scholar  * Zhong, H.-S. et al. Quantum computational advantage using

photons. _Science_ 370, 1460–1463 (2020). Article  ADS  Google Scholar  * Wu, Y. et al. Strong quantum computational advantage using a superconducting quantum processor. _Phys. Rev. Lett._

127, 180501 (2021). Article  ADS  Google Scholar  * Madsen, L. S. et al. Quantum computational advantage with a programmable photonic processor. _Nature_ 606, 75–81 (2022). Article  ADS 

Google Scholar  * Wang, Y., Hu, Z., Sanders, B. C. & Kais, S. Qudits and high-dimensional quantum computing. _Front. Phys_. 8 (2020). * Bocharov, A., Roetteler, M. & Svore, K. M.

Factoring with qutrits: Shor’s algorithm on ternary and metaplectic quantum architectures. _Phys. Rev. A_ 96, 012306 (2017). Article  ADS  Google Scholar  * Nikolaeva, A. S., Kiktenko, E. O.

& Fedorov, A. K. Efficient realization of quantum algorithms with qudits. _EPJ Quantum Technol._ 11, 43 (2024). Article  Google Scholar  * Bullock, S. S., O’Leary, D. P. & Brennen,

G. K. Asymptotically optimal quantum circuits for _d_-level systems. _Phys. Rev. Lett._ 94, 230502 (2005). Article  ADS  Google Scholar  * Lanyon, B. P. et al. Simplifying quantum logic

using higher-dimensional hilbert spaces. _Nat. Phys._ 5, 134–140 (2009). Article  Google Scholar  * Gedik, Z. et al. Computational speed-up with a single qudit. _Sci. Rep._ 5, 14671 (2015).

Article  ADS  Google Scholar  * Blok, M. S. et al. Quantum information scrambling on a superconducting qutrit processor. _Phys. Rev. X_ 11, 021010 (2021). Google Scholar  * Morvan, A. et al.

Qutrit randomized benchmarking. _Phys. Rev. Lett._ 126, 210504 (2021). Article  ADS  Google Scholar  * Goss, N. et al. High-fidelity qutrit entangling gates for superconducting circuits.

_Nat. Commun._ 13, 7481 (2022). Article  ADS  Google Scholar  * Luo, K. et al. Experimental realization of two qutrits gate with tunable coupling in superconducting circuits. _Phys. Rev.

Lett._ 130, 030603 (2023). Article  ADS  Google Scholar  * Roy, T., Li, Z., Kapit, E. & Schuster, D. I. Realization of two-qutrit quantum algorithms on a programmable superconducting

processor. _Phys. Rev. Applied_ 19, 064024 (2023). Article  ADS  Google Scholar  * Cao, S. et al. Emulating two qubits with a four-level transmon qudit for variational quantum algorithms.

_Quantum Sci. Technol._ 9, 035003 (2024). Article  ADS  Google Scholar  * Litteken, A. et al. Dancing the quantum waltz: Compiling three-qubit gates on four level architectures. In

_Proceedings of the 50th Annual International Symposium on Computer Architecture._ https://doi.org/10.1145/3579371.3589106 (ACM, 2023). * Ringbauer, M. et al. A universal qudit quantum

processor with trapped ions. _Nat. Phys._ 18, 1053–1057 (2022). Article  Google Scholar  * Hrmo, P. et al. Native qudit entanglement in a trapped ion quantum processor. _Nat. Commun._ 14,

2242 (2023). Article  ADS  Google Scholar  * Lanyon, B. P. et al. Manipulating biphotonic qutrits. _Phys. Rev. Lett._ 100, 060504 (2008). Article  ADS  Google Scholar  * Chi, Y. et al. A

programmable qudit-based quantum processor. _Nat. Commun._ 13, 1166 (2022). Article  ADS  Google Scholar  * Wang, Y., Snizhko, K., Romito, A., Gefen, Y. & Murch, K. Dissipative

preparation and stabilization of many-body quantum states in a superconducting qutrit array. _Phys. Rev. A._ 108, 013712 (2023). Article  ADS  Google Scholar  * Senko, C. et al. Realization

of a quantum integer-spin chain with controllable interactions. _Phys. Rev. X_ 5, 021026 (2015). Google Scholar  * Gustafson, E. Noise improvements in quantum simulations of sqed using

qutrits. Preprint at _arXiv_ https://arxiv.org/abs/2201.04546 (2022). * Bechmann-Pasquinucci, H. & Peres, A. Quantum cryptography with 3-state systems. _Phys. Rev. Lett._ 85, 3313–3316

(2000). Article  ADS  MathSciNet  Google Scholar  * Bruß, D. & Macchiavello, C. Optimal eavesdropping in cryptography with three-dimensional quantum states. _Phys. Rev. Lett._ 88, 127901

(2002). Article  ADS  Google Scholar  * Vaziri, A., Weihs, G. & Zeilinger, A. Experimental two-photon, three-dimensional entanglement for quantum communication. _Phys. Rev. Lett._ 89,

240401 (2002). Article  ADS  Google Scholar  * Gokhale, P. et al. Asymptotic improvements to quantum circuits via qutrits. In _Proceedings of the 46th International Symposium on Computer

Architecture_, ISCA ’19, 554–566. https://doi.org/10.1145/3307650.3322253 (Association for Computing Machinery, New York, NY, USA, 2019). * Fedorov, A., Steffen, L., Baur, M., da Silva, M.

P. & Wallraff, A. Implementation of a toffoli gate with superconducting circuits. _Nature_ 481, 170–172 (2012). Article  ADS  Google Scholar  * Chu, J. et al. Scalable algorithm

simplification using quantum and logic. _Nat. Phys._ 19, 126–131 (2023). Article  Google Scholar  * Nguyen, L. B. et al. Programmable heisenberg interactions between floquet qubits. _Nat.

Phys._ 20, 240–246 (2024). Article  Google Scholar  * Galda, A., Cubeddu, M., Kanazawa, N., Narang, P. & Earnest-Noble, N. Implementing a ternary decomposition of the toffoli gate on

fixed-frequencytransmon qutrits. Preprint at _arXiv_ https://doi.org/10.48550/arXiv.2109.00558 (2021). * Hill, A. D., Hodson, M. J., Didier, N. & Reagor, M. J. Realization of arbitrary

doubly-controlled quantum phase gates. Preprint at _arXiv_ https://doi.org/10.48550/arXiv.2108.01652 (2021). * Elder, S. S. et al. High-fidelity measurement of qubits encoded in multilevel

superconducting circuits. _Phys. Rev. X_ 10, 011001 (2020). MathSciNet  Google Scholar  * Jurcevic, P. et al. Demonstration of quantum volume 64 on a superconducting quantum computing

system. _Quantum Sci. Technol._ 6, 025020 (2021). Article  ADS  Google Scholar  * Chen, L. et al. Transmon qubit readout fidelity at the threshold for quantum error correction without a

quantum-limited amplifier. _npj Quantum Inf._ 9, 26 (2023). Article  ADS  Google Scholar  * Duclos-Cianci, G. & Poulin, D. Kitaev’s \({{\mathbb{z}}}_{d}\)-code threshold estimates. Phys.

Rev. A 87, 062338 (2013).. * Anwar, H., Brown, B. J., Campbell, E. T. & Browne, D. E. Fast decoders for qudit topological codes. _N. J. Phys._ 16, 063038 (2014). Article  MathSciNet 

Google Scholar  * Andrist, R. S., Wootton, J. R. & Katzgraber, H. G. Error thresholds for abelian quantum double models: Increasing the bit-flip stability of topological quantum memory.

_Phys. Rev. A_ 91, 042331 (2015). Article  ADS  Google Scholar  * Ma, Y., Hanks, M. & Kim, M. S. Non-Pauli errors can be efficiently sampled in qudit surface codes. _Phys. Rev. Lett._

131, 200602 (2023). Article  ADS  MathSciNet  Google Scholar  * Muralidharan, S., Zou, C.-L., Li, L., Wen, J. & Jiang, L. Overcoming erasure errors with multilevel systems. _N. J. Phys._

19, 013026 (2017). Article  Google Scholar  * Kubica, A., Haim, A., Vaknin, Y., Brandão, F. & Retzker, A. Erasure qubits: overcoming the _T_1 limit in superconducting circuits. _Phys.

Rev. X_ 13, 041022 (2023). Google Scholar  * Campbell, E. T., Anwar, H. & Browne, D. E. Magic-state distillation in all prime dimensions using quantum reed-muller codes. _Phys. Rev. X_

2, 041021 (2012). Google Scholar  * Campbell, E. T. Enhanced fault-tolerant quantum computing in _d_-level systems. _Phys. Rev. Lett._ 113, 230501 (2014). Article  ADS  Google Scholar  *

Majumdar, R., Basu, S., Ghosh, S. & Sur-Kolay, S. Quantum error-correcting code for ternary logic. _Phys. Rev. A_ 97, 052302 (2018). Article  ADS  Google Scholar  * Kapit, E.

Hardware-efficient and fully autonomous quantum error correction in superconducting circuits. _Phys. Rev. Lett._ 116, 150501 (2016). Article  ADS  Google Scholar  * Li, Z. et al. Autonomous

error correction of a single logical qubit using two transmons. _Nat Commun._ 15, 1681 (2024). Article  ADS  Google Scholar  * Li, Y. & Benjamin, S. C. Efficient variational quantum

simulator incorporating active error minimization. _Phys. Rev. X_ 7, 021050 (2017). Google Scholar  * Temme, K., Bravyi, S. & Gambetta, J. M. Error mitigation for short-depth quantum

circuits. _Phys. Rev. Lett._ 119, 180509 (2017). Article  ADS  MathSciNet  Google Scholar  * Endo, S., Benjamin, S. C. & Li, Y. Practical quantum error mitigation for near-future

applications. _Phys. Rev. X_ 8, 031027 (2018). Google Scholar  * Kandala, A. et al. Error mitigation extends the computational reach of a noisy quantum processor. _Nature_ 567, 491 (2019).

Article  ADS  Google Scholar  * Strikis, A., Qin, D., Chen, Y., Benjamin, S. & Li, Y. Learning-based quantum error mitigation. _PRX Quantum_ 2, 040330 (2021). Article  ADS  Google

Scholar  * Giurgica-Tiron, T., Hindy, Y., LaRose, R., Mari, A. & Zeng, W. Digital zero noise extrapolation for quantum error mitigation. _IEEE International Conference on Quantum

Computing and Engineering (QCE), Denver, CO, USA_ (2020). * LaRose, R., Mari, A., Karalekas, P., Shammah, N. & Zeng, W. Mitiq: a software package for error mitigation on noisy quantum

computers. _Quantum_ 6, 774 (2022). * Endo, S., Cai, Z., Benjamin, S. & Yuan, X. Hybrid quantum-classical algorithms and quantum error mitigation. _J. Phys. Soc. Jpn_. 90, 032001 (2021).

Article  ADS  Google Scholar  * Kim, Y. et al. Scalable error mitigation for noisy quantum circuits produces competitive expectation values. _Nat. Phys._ 19, 752–759 (2023). Article  Google

Scholar  * Koczor, B. Exponential error suppression for near-term quantum devices. _Phys. Rev. X_ 11, 031057 (2021). Google Scholar  * He, A., Nachman, B., de Jong, W. & Bauer, C.

Zero-noise extrapolation for quantum-gate error mitigation with identity insertions. _Phys. Rev. A_ 102, 012426 (2020). Article  ADS  MathSciNet  Google Scholar  * Huggins, W. et al. Virtual

distillation for quantum error mitigation. _Phys. Rev. X_ 11, 041036 (2021). Google Scholar  * Pascuzzi, V. et al. Computationally efficient zero noise extrapolation for quantum gate error

mitigation. _Phys. Rev. A_ 105, 042406 (2022). Article  ADS  MathSciNet  Google Scholar  * Song, C. et al. Quantum computation with universal error mitigation on a superconducting quantum

processor. _Sci. Adv._ https://www.science.org/doi/10.1126/sciadv.aaw5686 (2019). * Zhang, S. et al. Error-mitigated quantum gates exceeding physical fidelities in a trapped-ion system.

_Nat. Commun._ https://www.nature.com/articles/s41467-020-14376-z (2020). * Czarnik, P., Arrasmith, A., Coles, P. & Cincio, L. Error mitigation with clifford quantum-circuit data.

_Quantum_ 5, 592 (2021). Article  Google Scholar  * Van Den Berg, E., Minev, Z., Kandala, A. & Temme, K. Probabilistic error cancellation with sparse pauli-lindblad models on noisy

quantum processors. _Nat. Phys._ 19, 1116–1121 (2023). Article  Google Scholar  * Ferracin, S. et al. Efficiently improving the performance of noisy quantum computers. _Quantum_ 8, 1410

(2024). Article  Google Scholar  * Jain, A., Iyer, P., Bartlett, S. D. & Emerson, J. Improved quantum error correction with randomized compiling (2023). 2303.06846. * Hashim, A. et al.

Randomized compiling for scalable quantum computing on a noisy superconducting quantum processor. _Phys. Rev. X_ 11, 041039 (2021). Google Scholar  * Sung, Y. et al. Multi-level quantum

noise spectroscopy. _Nat. Commun._ 12, 967 (2021). Article  ADS  Google Scholar  * Wallman, J. J. & Emerson, J. Noise tailoring for scalable quantum computation via randomized compiling.

_Phys. Rev. A_ 94, 052325 (2016). Article  ADS  Google Scholar  * Graydon, M., Skanes-Norman, J. & Wallman, J. Designing stochastic channels. Preprint at _arXiv_

https://doi.org/10.48550/arXiv.2201.07156 (2022). * Appleby, D. M. Symmetric informationally complete-positive operator valued measures and the extended clifford group. _J. Math. Phys._

https://doi.org/10.1063/1.1896384 (2005). * Ferracin, S., Kapourniotis, T. & Datta, A. Accrediting outputs of noisy intermediate-scale quantum computing devices. _N. J. Phys._ 21, 113038

(2019). Article  MathSciNet  Google Scholar  * Ferracin, S., Merkel, S., McKay, D. & Datta, A. Experimental accreditation of outputs of noisy quantum computers. _Phys. Rev. A_ 104,

042603 (2021). Article  ADS  Google Scholar  * Hashim, A. et al. Benchmarking quantum logic operations relative to thresholds for fault tolerance. _npj Quantum Inf._ 9, 109 (2023). Article 

ADS  Google Scholar  * Hoeffding, W. Probability inequalities for sums of bounded random variables. _J. Am. Stat. Assoc._ 58, 13–30 (1963). Article  MathSciNet  Google Scholar  *

Carignan-Dugas, A. et al. The error reconstruction and compiled calibration of quantum computing cycles. Preprint at _arXiv_ https://doi.org/10.48550/arXiv.2303.17714 (2022). * Henao, I.,

Santos, J. P. & Uzdin, R. Adaptive quantum error mitigation using pulse-based inverse evolutions. _npj Quantum Inf._ https://doi.org/10.1038/s41534-023-00785-7 (2023). * Beale, S. et al.

_True-Q_. https://doi.org/10.5281/zenodo.3945250. * Hensen, B. et al. Loophole-free bell inequality violation using electron spins separated by 1.3 kilometres. _Nature_ 526, 682–686 (2015).

Article  ADS  Google Scholar  * Cervera-Lierta, A., Krenn, M., Aspuru-Guzik, A. & Galda, A. Experimental high-dimensional greenberger-horne-zeilinger entanglement with superconducting

transmon qutrits. _Phys. Rev. Appl._ 17, 024062 (2022). Article  ADS  Google Scholar  * Bianchetti, R. et al. Control and tomography of a three level superconducting artificial atom. _Phys.

Rev. Lett._ 105, 223601 (2010). Article  ADS  Google Scholar  * Ville, J.-L. et al. Leveraging randomized compiling for the quantum imaginary-time-evolution algorithm. _Phys. Rev. Res._ 4,

033140 (2022). Article  Google Scholar  * Truflandier, L. A., Dianzinga, R. M. & Bowler, D. R. Communication: generalized canonical purification for density matrix minimization. _J.

Chem. Phys_. https://doi.org/10.1063/1.4943213https://pubs.aip.org/aip/jcp/article-pdf/doi/10.1063/1.4943213/13330452/091102_1_online.pdf (2016). * Aaronson, S. & Hung, S.-H. Certified

randomness from quantum supremacy. _STOC 2023: Proceedings of the 55th Annual ACM Symposium on Theory of Computing,_ 933-944 (2023). * Gokhale, P. et al. Supercheq: quantum advantage for

distributed databases. Preprint at _arXiv_ https://doi.org/10.48550/arXiv.2212.03850 (2022). * Carignan-Dugas, A., Alexander, M. & Emerson, J. A polar decomposition for quantum channels

(with applications to bounding error propagation in quantum circuits). _Quantum_ 3, 173 (2019). Article  Google Scholar  * Hall, B. C. _Lie Groups, Lie Algebras, and Representations: An

Elementary Introduction_ (Springer). Download references ACKNOWLEDGEMENTS This material is based upon work supported by the National Science Foundation under Grant No. 2210391. Additional

support was provided by the Office of Advanced Scientific Computing Research, Testbeds for Science program, Office of Science of the U.S. Department of Energy under Contract No.

DE-AC02-05CH11231. A.H. acknowledges financial support from the Berkeley Initiative for Computational Transformation Fellows Program. N.G. acknowledges Long Nguyen, Karthik Siva, and Brian

Marinelli for useful discussions. S.F. acknowledges Joel Wallman and Anthony Chytros for useful discussions. AUTHOR INFORMATION Author notes * John Mark Kreikebaum Present address: Google

Quantum AI, Mountain View, CA, 94043, USA * These authors contributed equally: Noah Goss, Samuele Ferracin. AUTHORS AND AFFILIATIONS * Quantum Nanoelectronics Laboratory, Department of

Physics, University of California at Berkeley, Berkeley, CA, 94720, USA Noah Goss, Akel Hashim, David I. Santiago & Irfan Siddiqi * Applied Mathematics and Computational Research

Division, Lawrence Berkeley National Lab, Berkeley, CA, 94720, USA Noah Goss, John Mark Kreikebaum, Ravi K. Naik, David I. Santiago & Irfan Siddiqi * Keysight Technologies Canada,

Kanata, ON, K2K 2W5, Canada Samuele Ferracin & Arnaud Carignan-Dugas * Materials Sciences Division, Lawrence Berkeley National Lab, Berkeley, CA, 94720, USA John Mark Kreikebaum & 

Irfan Siddiqi Authors * Noah Goss View author publications You can also search for this author inPubMed Google Scholar * Samuele Ferracin View author publications You can also search for

this author inPubMed Google Scholar * Akel Hashim View author publications You can also search for this author inPubMed Google Scholar * Arnaud Carignan-Dugas View author publications You

can also search for this author inPubMed Google Scholar * John Mark Kreikebaum View author publications You can also search for this author inPubMed Google Scholar * Ravi K. Naik View author

publications You can also search for this author inPubMed Google Scholar * David I. Santiago View author publications You can also search for this author inPubMed Google Scholar * Irfan

Siddiqi View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS N.G. conceptualized and performed the experiment. S.F. developed the error

mitigation protocols. A.H. and A.C.D. aided with the design of the experiments and analysis. J.M.K. fabricated the superconducting chip. R.K.N., D.I.S., and I.S. supervised all experimental

work. N.G. and S.F. wrote the paper with input from all authors. CORRESPONDING AUTHOR Correspondence to Noah Goss. ETHICS DECLARATIONS COMPETING INTERESTS S.F. and A.C.D. have a financial

interest in Keysight Technologies and the use of True-Q software79. The remaining authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains

neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION CLEAN SI EXTENDING THE COMPUTATIONAL REACH OF A SUPERCONDUCTING

QUTRIT PROCESSOR: SUPPLEMENTAL INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use,

sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative

Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated

otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds

the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and

permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Goss, N., Ferracin, S., Hashim, A. _et al._ Extending the computational reach of a superconducting qutrit processor. _npj Quantum Inf_ 10,

101 (2024). https://doi.org/10.1038/s41534-024-00892-z Download citation * Received: 18 December 2023 * Accepted: 23 September 2024 * Published: 14 October 2024 * DOI:

https://doi.org/10.1038/s41534-024-00892-z SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative