ABSTRACT Motivated by recent experimental work on moiré systems in a strong magnetic field, we compute the compressibility as well as the spin correlations and Hofstadter spectrum of spinful

electrons on a honeycomb lattice with Hubbard interactions using the determinantal quantum Monte Carlo method. While the interactions in general preserve quantum and anomalous Hall states,

emergent features arise corresponding to an antiferromagnetic insulator at half-filling and other incompressible states following the Chern sequence ± (2_N_ + 1). These odd integer Chern

states exhibit strong ferromagnetic correlations and arise spontaneously without any external mechanism for breaking the spin-rotation symmetry. Analogs of these magnetic states should be

Article Open access 29 March 2021 OBSERVATION OF PLAQUETTE FLUCTUATIONS IN THE SPIN-1/2 HONEYCOMB LATTICE Article Open access 13 November 2020 EVIDENCE OF FRUSTRATED MAGNETIC INTERACTIONS IN

A WIGNER–MOTT INSULATOR Article 16 January 2023 INTRODUCTION The hallmark of nontrivial topology of filled bands is a quantized Hall conductance, an integer multiple of the quantum of

conductance. The integer is set by the Chern number1. Typically, deviations from integer Chern numbers indicate that electron-electron interactions are important, as in the fractional

quantum Hall effect. However, there are several examples of physical systems in which interactions dominate but the Chern number is still an integer. One such mechanism that involves spin

polarization and its generalizations is quantum Hall ferromagnetism2,3,4,5,6. Moiré systems in a magnetic field provide a second example in which symmetry-broken quantum Hall insulators

appear at high magnetic fields7,8,9,10,11. The extent to which these phenomena are generic beyond graphene-based systems and independent of lattice geometry is unknown. Motivated by these

phenomena, we report here a series of insulating states on the honeycomb and square lattice which are driven by interactions. The series we report has odd integer Chern numbers, ±1, 3, 5, ⋯ 

. An analysis of the spin correlations suggests that the spin rotation symmetry is spontaneously broken resulting in ferromagnetism. Our observations here add intrigue to the mixed role

played by topology and interactions in two-dimensional (2D) materials. Our simulations reveal that explicit single-particle symmetry breaking such as Zeeman splitting is not required and the

full ferromagnetic sequence arises spontaneously in a general bipartite lattice. The evolution of electronic states in a perpendicular magnetic field has a long history. Because a magnetic

field preserves the crystal momentum, the single-particle energy spectrum for non-interacting electrons is easily obtained12,13,14 by replacing the momentum P with P − _e_A/_c_ where A is

the magnetic vector potential, _e_ the electron charge and _c_ the speed of light. In 2D, the resultant Hofstadter14 spectrum adequately describes the evolution of the tight-binding

electronic states as a function of the magnetic flux. Hidden in the wings of the underlying butterfly spectrum are gapped states indexed by Chern numbers which fix1 the quantization of the

Hall conductance. Moiré systems as in the case of magic-angle twisted bilayer graphene (MATBG) offer a new route to engineering gaps in the electronic spectrum through the competition

between band filling and the interaction energy15,16,17,18. As the twist angle controls19 the ratio of the kinetic to the potential energy and leads to a complete quenching of the kinetic

energy at the magic angle, moiré systems in a magnetic field offer the ultimate playground for studying the physics from the interplay between strong correlation and magnetic field. With the

kinetic energy quenched, moiré systems encode the evolution of the Hofstadter spectrum in the presence of strong interactions. This is currently an unsolved non-trivial problem. This

problem is complicated by the fact that the simple replacement of the momentum by P − _e_A/_c_ fails in the presence of interactions because interactions in general mix crystal momenta as in

the case of the Hubbard interaction. Consequently, while theoretical efforts have addressed certain limits of the interacting Hofstadter

problem20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39, no analytical method exists to determine the complete spectrum in a magnetic field in the presence of interactions.

Nonetheless, this is an urgent problem in condensed matter physics given the plethora of experiments on MATBG and related systems that are focused on revealing the low-energy physics

resulting from the interplay between a magnetic field and strong correlation. Theoretically, one has three options: 1) phenomenology, 2) some type of mean-field theory, dynamical32,33 or

otherwise34,35,36,37 or 3) serious numerics which so far have been limited to exact diagonalization38,39 on few-particle systems. We pursue the last option in this paper as no benchmarks

have been established for even the simplest model of interacting electrons on any of the lattices relevant to either MATBG or the transition metal dichalcogenide systems. We focus on spinful

fermions primarily on a honeycomb lattice including only nearest neighbor hopping and Hubbard interactions under an external magnetic field, and perform a determinantal quantum Monte Carlo

(DQMC) simulation for all densities and magnetic fluxes. DQMC is an unbiased and numerically exact method to capture the full quantum fluctuations for correlated systems. In a prior work

with Hubbard interactions, features such as the local compressibility and other thermodynamic quantities were calculated using DQMC as a function of the magnetic flux for the square

lattice27 and no ferromagnetism was reported. We focus here on a honeycomb lattice as it is closer to the underlying geometry of most existing moiré systems. In general, we find that the

interactions preserve the integer quantum and anomalous Hall states of the non-interacting system. However, the interactions do generate an antiferromagnetic insulating state at

half-filling, as expected, and also emergent interaction-driven insulating states in both of the honeycomb and square lattices. The Chern sequence for these states is ±(2_N_ + 1). All such

states exhibit strong ferromagnetic correlations. This represents numerically exact evidence for such interaction-driven states in the full density region based on the Hubbard interaction.

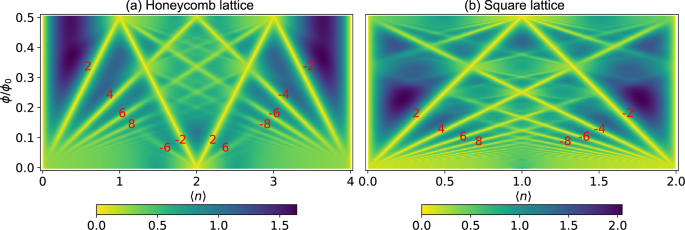
RESULTS NONINTERACTING QUANTUM HALL EFFECTS To begin with, we present the non-interacting charge compressibility _χ_ = ∂〈_n_〉/∂_μ_ in Fig. 1 as a function of magnetic flux and electron

density and compare with the results for the square lattice at _β_ = 20/_t_. In both the square and honeycomb lattices, particle-hole symmetry obtains as both are bipartite and the model

contains only nearest neighbor hopping. The straight lines in Fig. 1 correspond to solutions to the Diophantine equation1 $$\langle n\rangle =r\frac{\phi }{{\phi }_{0}}+s,$$ (1) in which

〈_n_〉 = 〈_N_e〉/_N__c_ (_N__c_ is the number of unit cells), _r_ is an integer given by the inverse slope of the straight lines and _s_ is the offset given by the intercept. _r_ defines the

Chern number. We have chosen to plot the filling from [0, 4] to take into account the spin and sublattice degeneracy in the honeycomb lattice but from [0, 2] for the square lattice in which

only a spin degeneracy exists. Hence, there is only a factor of 2 in translating the densities between the two systems. In both Fig. 1 panels a and b, the Diophantine lines1 starting from

the bottom left (right) corners have _r_ = ±2_N_ (the factor of 2 accounts for spin degeneracy) with _N_ = 1, 2 ⋯ corresponding to spin-unpolarized quantum Hall states, while in only Fig.

1a, the lines that start from half-filling (〈_n_〉 = 2) at zero-field and have _r_ = ± 4(_N_ + 1/2) (the factor of 4 accounts for spin and sub-lattice degeneracy) with _N_ = 0, 1, 2 ⋯ 

indicating the anomalous quantum Hall effect40,41,42. Thus, the honeycomb lattice is more closely aligned to the physics observed in MATBG than is the square lattice. TURNING ON INTERACTIONS

Next, we explore how interactions change this pattern in the honeycomb lattice. We use DQMC to calculate the compressibility, $$\chi =\beta {\chi }_{c}=\frac{\beta

}{N}\mathop{\sum}\limits_{{{{\bf{i}}}},{{{\bf{j}}}}}\left[\langle {n}_{{{{\bf{i}}}}}{n}_{{{{\bf{j}}}}}\rangle -\langle {n}_{{{{\bf{i}}}}}\rangle \langle {n}_{{{{\bf{j}}}}}\rangle \right],$$

(2) in the presence of Hubbard interactions, where _χ__c_ is the charge correlation function. Due to the Fermionic sign problem, we are only able to calculate the compressibility for the

full density and flux region for a system size _N_site = 6 × 6 × 2 with an interaction strength up to _U_/_t_ = 4 and temperature as low as _T_/_t_ = 0.125 (or _β_ = 8_t_−1). In the first

row of Fig. 2, as _U_ increases, the non-interacting lines in the compressibility are softened and a middle vertical line appears as a single-particle gap develops. At the largest _U_/_t_ = 

4, we can still observe the dominant and sub-dominant lines, indicating the resilience of the non-interacting quantum Hall effect against interactions. Note that the lines not merging at

_ϕ_/_ϕ_0 = 0, 0.5 in Fig. 2b, c is due to strong finite size effects (see Supplementary Figs. 1 and 2) and thus disregarded in Fig. 2e, f. Also of note is the emergence of a new feature at

〈_n_〉 = 2 for _U_/_t_ = 4. This corresponds to a dip in the density of states, a precursor to the Mott gap43,44. The second row of these figures corresponds to a simulation at the lower

temperature of _β_ = 20/_t_ for _U_ = 0 and _U_/_t_ = 2. Figure 2d shows a sharpening of the Diophantine features as the temperature is lowered by more than a factor of two to _β_ = 20/_t_.

At _U_/_t_ = 2, the vertical line at 〈_n_〉 = 2 possibly indicates a gap opening for finite field. At this temperature, even for such a modest value of _U_, the suppression of the density of

states is evident and the corresponding insulator is antiferromagnetic (see Supplementary Fig. 6). Also of note is the state indicated by the solid red line in Fig. 2c, e. This line evolves

as a function of the magnetic flux with a slope of unity. Such a state is absent from the non-interacting sequence as it has a Chern number of ±1. Notably this state is visible in the map of

the spin correlation (Fig. 2f), $${\chi }_{s}=\mathop{\sum}\limits_{{{{\bf{r}}}}}S({{{\bf{r}}}})=\frac{1}{N}\mathop{\sum}\limits_{{{{\bf{i}}}},{{{\bf{r}}}}}\langle

{S}_{{{{\bf{i}}}}}^{z}{S}_{{{{\bf{i}}}}+{{{\bf{r}}}}}^{z}\rangle .$$ (3) In fact, the light features in Fig. 2f reveal that these possibly incompressible states all have a markedly enhanced

spin correlation with distinct slopes as a function of magnetic flux and density which differ from those of the non-interacting system even at much lower temperatures (see Supplementary Fig.

4). It is the origin of these states that is the principal focus of this paper. We gain further insight into the possible emergence of incompressible states by taking slices through the

charge correlation, _χ__c_ = _χ_/_β_, at particular values of the magnetic flux. In Fig. 3a–c, we show the charge correlation explicitly at _ϕ_/_ϕ_0 = 11/36, chosen to avoid finite-size

effects (see Supplementary Figs. 1 and 2) for the honeycomb lattice and _ϕ_/_ϕ_0 = 2/9 for the square lattice. For the honeycomb lattice, Fig. 3a, b illustrates that as the temperature is

lowered from _β_ = 8/_t_ to _β_ = 20/_t_, the dual-dip feature for _U_ = 0 in the vicinity of 〈_n_〉 = 2 gives rise to a full quantum Hall state. With the interaction increasing to _U_ = 

4_t_, this dual-dip feature contains a depression precisely at 〈_n_〉 = 2. This is the incompressible Mott gap at 〈_n_〉 = 243,44. Panel Fig. 3c displays the analogous trend for the square

lattice. Away from half-filling, we find several emergent states which have a suppressed charge correlation indicating the possible onset of a gap. The states occur around fillings of 〈_n_〉 

= 11/36 and 11/12. The same is true of their particle-hole equivalents. It is precisely the first of such states that is highlighted in red in Fig. 2e. The analogous states are also present

for the square lattice in Fig. 3c. All such dips in _χ__c_ are enhanced as the interaction strength increases. Further, such behavior persists even as the system size increases (see

Supplementary Fig. 3). To uncover the possible cause of these states, we focus on the spin susceptibility _χ__s_. For _U_ = 0, _χ__c_ = 4_χ__s_. However, the second row of Fig. 3 shows that

whenever the charge correlation exhibits an interaction-driven dip, the spin correlation shows a peaked structure. Figure 3e shows that as the temperature is lowered, the peak of the spin

correlation increases at the fillings where the charge correlation develops a dip. Now we look at the full density- and magnetic-flux-dependent spin correlation _χ__s_ for _U_/_t_ = 2 and

_U_/_t_ = 4 in Fig. 4a and b respectively at their lowest temperatures. Straight lines with inverse slope corresponding to Chern number _C_ = ±1, 3, 5 are plotted and found to be aligned

with the ridges of the spin correlation. We choose one representative point (not the brightest) at each line and study its temperature evolution at different values of _U_, presented in Fig.

4c–e. In all cases, when _U_ = 0, the spin correlation deceases along with temperature. However, for a finite _U_, the spin correlation blows up as the temperature decreases (below a

critical temperature for Fig. 4d and e). The ultimate spin state is revealed from a spatial map of the real-space static spin susceptibility: $$S({{{\bf{r}}}},\omega

=0)=\frac{1}{N}\int\nolimits_{0}^{\beta }\mathop{\sum}\limits_{{{{\bf{i}}}}}\langle {S}_{{{{\bf{i}}}}+{{{\bf{r}}}}}^{z}(\tau ){S}_{{{{\bf{i}}}}}^{z}(0)\rangle d\tau ,$$ (4) presented in Fig.

4f–h, at _U_/_t_ = 2 and the lowest temperature (_β_ = 30/_t_ as circled in Fig. 4c–e respectively). This quantity is more sensitive in detecting fluctuating order at finite temperature

than the zero-time spin correlation45. The color map signifies positive spin correlation across the lattice relative to the site at the origin. Such same-sign correlations are indicative of

ferromagnetism. Figure 4f for a Chen number _C_ = 1 exhibits a strong ferromagnetic susceptibility. Figure 4g with a Chen number _C_ = 3 also displays a clear ferromagnetic pattern. Figure

4h corresponding to Chen number _C_ = 5 reveals an evident tendency towards ferromagnetism at lower _T_, though not fully ferromagnetic as in the other cases. In addition, we also expect the

_C_ = ±1 ferromagnetic states to exist in the middle of Fig. 4a, b (as depicted by the dashed line) with extrapolation to 〈_n_〉 = 2 at zero flux. But limited by the sign problem, we have

not yet been able to investigate low enough temperature to unearth a clear ferromagnetic pattern at these densities. The full picture is now apparent. The charge dips and enhanced spin

correlations, which have no counterpart in the non-interacting system in Fig. 2, correspond to ferromagnetic insulators with odd integer Chern numbers. Both the spin correlations and

magnitude of the charge gap are enhanced as the temperature is lowered. The same trend holds for the square lattice as is evident from Fig. 3c, f. This behavior matches expectations from

quantum Hall ferromagnetism, but here we show that local interactions are sufficient to induce odd Chern integer states on both the honeycomb and square lattices. We are led to the

conclusion that such insulating states are generically present in bipartite lattices with interactions with no need for fine-tuning or single-particle splitting. While there is some

indication of charge ordering (see Supplementary Fig. 5), it is not compelling at this level of study and hence we leave this for a future publication. We finally display the benchmark

calculation of the Hofstadter spectrum as defined by the local density of states, the quantity directly measured experimentally. Our focus in Fig. 5 is at half-filling and _U_/_t_ = 2, 4,

obtained from constructing an analytic continuation with Differential Evolution for Analytic Continuation (DEAC) on the DQMC local Green function. The comparison between DEAC and the

analytical result at _U_ = 0 (see Supplementary Fig. 7) gives us some idea about the resolution of DEAC and offers a guide as to how to interpret the interacting system results. Since there

is no sign problem at half-filling, we are able to conduct the calculation at a low temperature (_β_ = 30/_t_). Panels Fig. 5a, b show how the antiferromagnetic gap comes into full view by

_U_/_t_ = 4 and some hint of it appears already at the modest value of _U_/_t_ = 2 only with finite magnetic field. The gap at _U_/_t_ = 2 is most likely to be of the Slater type46,47

because the interaction strength is only around 1/3 of the bare bandwidth and the insulating state appears at much lower temperature than that required for the formation of antiferromagnetic

correlation. On the other hand, the gap at _U_/_t_ = 4 is closer to a Mott gap because it is established at a much high temperature (shown in Fig. 2c), consistent with previous studies on

the Hubbard model in honeycomb lattice43,44. While the corresponding experimental figure is at variable filling18, which is inaccessible because of the sign problem, the overall features

qualitatively reproduce the experimental results for moderate values of _U_/_t_ = 2. DISCUSSION We have studied here the evolution of the excitation spectrum of a Hubbard-interacting

electron gas in the presence of a strong perpendicular magnetic field on bipartite lattices. We have shown that while the interactions preserve the non-interacting integer quantum and

anomalous Hall states, new states do emerge from the interactions. In addition to the antiferromagnetic gap at half-filling, we have discovered a series of odd-integer Chern insulating

ferromagnetic states which exhibit enhanced positive spin correlations as the temperature is lowered. In light of ferromagnetism as the underlying cause of the insulating states, that the

Chern number is odd is easily understood. Our work suggests ferromagnetism is generic requiring just modest magnetic fields and strong interactions to generate the full sequence of

odd-integer states. Note while the sequence we observe departs from the middle or the edge of the band, an odd-integer sequence emanating from the 〈_n_〉 = 1 or 〈_n_〉 = 3 fillings on the

honeycomb lattice would require spin-orbit coupling in the Hamiltonian, thereby generalizing the utility of this work. METHODS We study the Hofstadter-Hubbard model on a honeycomb lattice,

$$\begin{array}{lll}H=\,-\,t\mathop{\sum}\limits_{\langle {{{\bf{i}}}}{{{\bf{j}}}}\rangle \sigma }\exp (i{\phi }_{{{{\bf{i}}}},{{{\bf{j}}}}}){c}_{{{{\bf{i}}}}\sigma }^{{\dagger}

}{c}_{{{{\bf{j}}}}\sigma }^{{\dagger} }-\mu \mathop{\sum}\limits_{{{{\bf{i}}}},\sigma }{n}_{{{{\bf{i}}}}\sigma }\\\qquad\,\,\,

+\,U\mathop{\sum}\limits_{{{{\bf{i}}}}}({n}_{{{{\bf{i}}}}\uparrow }-\frac{1}{2})({n}_{{{{\bf{i}}}}\downarrow }-\frac{1}{2}),\end{array}$$ (5) where _t_ represents the nearest neighbor

hopping; \({c}_{{{{\bf{i}}}}\sigma }^{{\dagger} }\) (_c_I_σ_) creates (annihilates) an electron with spin _σ_ at site I, _μ_ is the chemical potential, _U_ is the on-site interaction. Due to

the presence of a uniform magnetic field, we use the Peierls substitution12 to introduce the phase through the flux threading, $${\phi }_{{{{\bf{i}}}},{{{\bf{j}}}}}=\frac{2\pi }{{\phi

}_{0}}\int\nolimits_{{r}_{{{{\bf{i}}}}}}^{{r}_{{{{\bf{j}}}}}}{{{\bf{A}}}}\cdot d{{{\bf{l}}}},$$ (6) where _ϕ_0 = _h_/_e_ in the hopping term is a result of the quantized magnetic field and

the integration is over the straight line path from site I to J. We simulate this Hamiltonian Eq. (5) on a finite cluster _N_site = 2_L_2. The honeycomb lattice contains two sub-lattices,

which explains the factor of 2, with lattice constant _a_ = 1 and _L_ the number of site along either lattice basis respectively for each sub-lattice. We adjust the modified periodic

boundary conditions in Ref. 48 to the honeycomb lattice. To obtain a single-value wave function requires the flux quantization condition _ϕ_/_ϕ_0 = _n__f_/_N__c_ with _n__f_ an integer and

_N__c_ = _L_2 the number of unit cells. The symmetric gauge \({{{\bf{A}}}}=(x\hat{y}-y\hat{x})B/2\) is chosen for this calculation. We apply DQMC49,50,51 to this model Eq. (5) and calculate

the compressibility and Green function. The jackknife resampling is used to estimate the standard error of the mean as error bars in DQMC results. With the local Green function, we compute

the local density of states using the recently developed DEAC52. DATA AVAILABILITY The data for this study is available at https://zenodo.org/record/7608167#.Y-AxyezML6g. CODE AVAILABILITY

The DQMC code used for this project can be obtained at https://github.com/edwnh. REFERENCES * Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized hall conductance

in a two-dimensional periodic potential. _Phys. Rev. Lett._ 49, 405–408 (1982). Article  ADS  Google Scholar  * Sondhi, S. L., Karlhede, A., Kivelson, S. A. & Rezayi, E. H. Skyrmions and

the crossover from the integer to fractional quantum hall effect at small zeeman energies. _Phys. Rev. B_ 47, 16419–16426 (1993). Article  ADS  Google Scholar  * Manfra, M., Goldberg, B.,

Pfeiffer, L. & West, K. Skyrmions and the _ν_ = 1 quantum hall ferromagnet. _Acta Phys. Polonica A_ 92, 621 (1997). Article  ADS  Google Scholar  * Arovas, D. P., Karlhede, A. &

Lilliehöök, D. SU(_n_) quantum hall skyrmions. _Phys. Rev. B_ 59, 13147–13150 (1999). Article  ADS  Google Scholar  * Ezawa, Z. F. & Hasebe, K. Interlayer exchange interactions, SU(4)

soft waves, and skyrmions in bilayer quantum hall ferromagnets. _Phys. Rev. B_ 65, 075311 (2002). Article  ADS  Google Scholar  * Nomura, K. & MacDonald, A. H. Quantum hall

ferromagnetism in graphene. _Phys. Rev. Lett._ 96, 256602 (2006). Article  ADS  Google Scholar  * Spanton, E. M. et al. Observation of fractional chern insulators in a van der waals

heterostructure. _Science_ 360, 62–66 (2018). Article  ADS  Google Scholar  * Wang, L. et al. Evidence for a fractional fractal quantum hall effect in graphene superlattices. _Science_ 350,

1231–1234 (2015). Article  ADS  MathSciNet  MATH  Google Scholar  * Dean, C. R. et al. Hofstadter’s butterfly and the fractal quantum hall effect in moirésuperlattices. _Nature_ 497, 598–602

(2013). Article  ADS  Google Scholar  * Yu, G. L. et al. Hierarchy of hofstadter states and replica quantum hall ferromagnetism in graphene superlattices. _Nat. Phys._ 10, 525–529 (2014).

Article  Google Scholar  * Hunt, B. et al. Massive dirac fermions and hofstadter butterfly in a van der waals heterostructure. _Science_ 340, 1427–1430 (2013). Article  ADS  Google Scholar 

* Peierls, R. Zur theorie des diamagnetismus von leitungselektronen. _Z. Phys._ 80, 763–791 (1933). Article  ADS  MATH  Google Scholar  * Harper, P. G. Single band motion of conduction

electrons in a uniform magnetic field. _Proc. Phys. Soc. Sect. A_ 68, 874–878 (1955). Article  ADS  MATH  Google Scholar  * Hofstadter, D. R. Energy levels and wave functions of bloch

electrons in rational and irrational magnetic fields. _Phys. Rev. B_ 14, 2239–2249 (1976). Article  ADS  Google Scholar  * Saito, Y. et al. Hofstadter subband ferromagnetism and

symmetry-broken chern insulators in twisted bilayer graphene. _Nat. Phys._ 17, 478–481 (2021). Article  Google Scholar  * Park, J. M., Cao, Y., Watanabe, K., Taniguchi, T. &

Jarillo-Herrero, P. Flavour hund’s coupling, chern gaps and charge diffusivity in moirégraphene. _Nature_ 592, 43–48 (2021). Article  Google Scholar  * Choi, Y. et al. Correlation-driven

topological phases in magic-angle twisted bilayer graphene. _Nature_ 589, 536–541 (2021). Article  ADS  Google Scholar  * Yu, J. et al. Correlated hofstadter spectrum and flavour phase

diagram in magic-angle twisted bilayer graphene. _Nat. Phys._ 18, 825–831 (2022). Article  Google Scholar  * Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer

graphene. _Proc. Natl Acad. Sci._ 108, 12233–12237 (2011). Article  ADS  Google Scholar  * Gudmundsson, V. & Gerhardts, R. R. Effects of screening on the Hofstadter butterfly. _Phys.

Rev. B_ 52, 16744–16752 (1995). Article  ADS  Google Scholar  * Pfannkuche, D. & MacDonald, A. H. Quantum Hall effect of interacting electrons in a periodic potential. _Phys. Rev. B_ 56,

R7100–R7103 (1997). Article  ADS  Google Scholar  * Doh, H. & Salk, S.-H. S. Effects of electron correlations on the Hofstadter spectrum. _Phys. Rev. B_ 57, 1312–1315 (1998). Article 

ADS  Google Scholar  * Czajka, K., Gorczyca, A., Maśka, M. M. & Mierzejewski, M. Hofstadter butterfly for a finite correlated system. _Phys. Rev. B_ 74, 125116 (2006). Article  ADS 

Google Scholar  * Apalkov, V. M. & Chakraborty, T. Gap Structure of the Hofstadter System of Interacting Dirac Fermions in Graphene. _Phys. Rev. Lett._ 112, 176401 (2014). Article  ADS 

Google Scholar  * Mishra, A., Hassan, S. R. & Shankar, R. Effects of interaction in the Hofstadter regime of the honeycomb lattice. _Phys. Rev. B_ 93, 125134 (2016). Article  ADS  Google

Scholar  * Andrews, B. & Soluyanov, A. Fractional quantum Hall states for moir\’e superstructures in the Hofstadter regime. _Phys. Rev. B_ 101, 235312 (2020). Article  ADS  Google

Scholar  * Ding, J. K. et al. Thermodynamics of correlated electrons in a magnetic field. _Commun. Phys._ 5, 204 (2022). Article  Google Scholar  * Shaffer, D., Wang, J. & Santos, L. H.

Theory of hofstadter superconductors. _Phys. Rev. B_ 104, 184501 (2021). Article  ADS  Google Scholar  * Shaffer, D., Wang, J. & Santos, L. H. Unconventional self-similar hofstadter

superconductivity from repulsive interactions. _Nat. Commun._ 13, 7785 (2022). Article  ADS  Google Scholar  * Wang, X. & Vafek, O. Narrow bands in magnetic field and strong-coupling

hofstadter spectra. _Phys. Rev. B_ 106, L121111 (2022). Article  ADS  Google Scholar  * Herzog-Arbeitman, J., Chew, A., Efetov, D. K. & Bernevig, B. A. Reentrant correlated insulators in

twisted bilayer graphene at 25 t (2_π_ flux). _Phys. Rev. Lett._ 129, 076401 (2022). Article  ADS  Google Scholar  * Acheche, S., Arsenault, L.-F. & Tremblay, A.-M. S. Orbital effect of

the magnetic field in dynamical mean-field theory. _Phys. Rev. B_ 96, 235135 (2017). Article  ADS  Google Scholar  * Markov, A. A., Rohringer, G. & Rubtsov, A. N. Robustness of the

topological quantization of the hall conductivity for correlated lattice electrons at finite temperatures. _Phys. Rev. B_ 100, 115102 (2019). Article  ADS  Google Scholar  * Gudmundsson, V.

& Gerhardts, R. R. Effects of screening on the hofstadter butterfly. _Phys. Rev. B_ 52, 16744–16752 (1995). Article  ADS  Google Scholar  * Doh, H. & Salk, S.-H. S. Effects of

electron correlations on the hofstadter spectrum. _Phys. Rev. B_ 57, 1312–1315 (1998). Article  ADS  Google Scholar  * Tu, W.-L., Schindler, F., Neupert, T. & Poilblanc, D. Competing

orders in the hofstadter _t_ − − _j_ model. _Phys. Rev. B_ 97, 035154 (2018). Article  ADS  Google Scholar  * Zang, J., Wang, J., Cano, J. & Millis, A. J. Hartree-fock study of the moiré

hubbard model for twisted bilayer transition metal dichalcogenides. _Phys. Rev. B_ 104, 075150 (2021). Article  ADS  Google Scholar  * Barelli, A., Bellissard, J., Jacquod, P. &

Shepelyansky, D. L. Double butterfly spectrum for two interacting particles in the harper model. _Phys. Rev. Lett._ 77, 4752–4755 (1996). Article  ADS  Google Scholar  * Czajka, K.,

Gorczyca, A., Maśka, M. M. & Mierzejewski, M. Hofstadter butterfly for a finite correlated system. _Phys. Rev. B_ 74, 125116 (2006). Article  ADS  Google Scholar  * Semenoff, G. W.

Condensed-matter simulation of a three-dimensional anomaly. _Phys. Rev. Lett._ 53, 2449–2452 (1984). Article  ADS  Google Scholar  * Novoselov, K. S. et al. Two-dimensional gas of massless

dirac fermions in graphene. _Nature_ 438, 197–200 (2005). Article  ADS  Google Scholar  * Zhang, Y., Tan, Y.-W., Stormer, H. L. & Kim, P. Experimental observation of the quantum hall

effect and berry’s phase in graphene. _Nature_ 438, 201–204 (2005). Article  ADS  Google Scholar  * Assaad, F. F. & Herbut, I. F. Pinning the order: The nature of quantum criticality in

the hubbard model on honeycomb lattice. _Phys. Rev. X_ 3, 031010 (2013). Google Scholar  * Ostmeyer, J. et al. Semimetal–mott insulator quantum phase transition of the hubbard model on the

honeycomb lattice. _Phys. Rev. B_ 102, 245105 (2020). Article  ADS  Google Scholar  * Mai, P., Karakuzu, S., Balduzzi, G., Johnston, S. & Maier, T. A. Intertwined spin, charge, and pair

correlations in the two-dimensional hubbard model in the thermodynamic limit. _Proc. Natl Acad. Sci._ 119, e2112806119 (2022). Article  MathSciNet  Google Scholar  * Gull, E., Werner, P.,

Wang, X., Troyer, M. & Millis, A. J. Local order and the gapped phase of the hubbard model: A plaquette dynamical mean-field investigation. _Europhys. Lett._ 84, 37009 (2008). Article 

ADS  Google Scholar  * Schäfer, T. et al. Fate of the false mott-hubbard transition in two dimensions. _Phys. Rev. B_ 91, 125109 (2015). Article  ADS  Google Scholar  * Assaad, F. F.

Depleted kondo lattices: Quantum monte carlo and mean-field calculations. _Phys. Rev. B_ 65, 115104 (2002). Article  ADS  Google Scholar  * Blankenbecler, R., Scalapino, D. J. & Sugar,

R. L. Monte carlo calculations of coupled boson-fermion systems. i. _Phys. Rev. D._ 24, 2278–2286 (1981). Article  ADS  Google Scholar  * Hirsch, J. E. Two-dimensional hubbard model:

Numerical simulation study. _Phys. Rev. B_ 31, 4403–4419 (1985). Article  ADS  Google Scholar  * White, S. R. et al. Numerical study of the two-dimensional hubbard model. _Phys. Rev. B_ 40,

506–516 (1989). Article  ADS  Google Scholar  * Nichols, N. S., Sokol, P. & Del Maestro, A. Parameter-free differential evolution algorithm for the analytic continuation of imaginary

time correlation functions. _Phys. Rev. E_ 106, 025312 (2022). Article  ADS  Google Scholar  * Towns, J. et al. Xsede: Accelerating scientific discovery. _Comput. Sci. Eng._ 16, 62–74

(2014). Article  Google Scholar  Download references ACKNOWLEDGEMENTS B.E.F., P.M., P.W.P., and J.Y. acknowledge support for the computation and conception of this project from Quantum

Sensing and Quantum Materials (QSQM), an Energy Frontier Research Center funded by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), under award no.

DE-SC0021238. E.W.H. was supported by the Gordon and Betty Moore Foundation EPiQS Initiative through the grants GBMF 4305 and GBMF 8691. This work used an analysis of insulating states in

MATBG funded through DMR-2111379 for his work on MATBG. P.M. thanks Nathan Nichols for the help on DEAC simulation. The DQMC calculation of this work used the Advanced Cyberinfrastructure

Coordination Ecosystem: Services & Support (ACCESS) Expanse supercomputer through the research allocation TG-PHY220042, which is supported by National Science Foundation grant number

ACI-154856253. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Physics and Institute of Condensed Matter Theory, University of Illinois Urbana-Champaign, Urbana, IL, 61801, USA

Peizhi Mai, Edwin W. Huang & Philip W. Phillips * Department of Applied Physics, Stanford University, Stanford, CA, 94305, USA Jiachen Yu * Geballe Laboratory of Advanced Materials,

Stanford, CA, 94305, USA Jiachen Yu & Benjamin E. Feldman * Department of Physics, Stanford University, Stanford, CA, 94305, USA Benjamin E. Feldman * Stanford Institute for Materials

and Energy Sciences, SLAC National Accelerator Laboratory, Menlo Park, CA, 94025, USA Benjamin E. Feldman Authors * Peizhi Mai View author publications You can also search for this author

inPubMed Google Scholar * Edwin W. Huang View author publications You can also search for this author inPubMed Google Scholar * Jiachen Yu View author publications You can also search for

this author inPubMed Google Scholar * Benjamin E. Feldman View author publications You can also search for this author inPubMed Google Scholar * Philip W. Phillips View author publications

You can also search for this author inPubMed Google Scholar CONTRIBUTIONS E.W.H. and P.M. developed the DQMC code. P.M. carried out the calculations. All authors analyzed the results and

wrote the manuscript. B.E.F. and P.W.P. supervised the project. CORRESPONDING AUTHOR Correspondence to Philip W. Phillips. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no

competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

SUPPLEMENTARY INFORMATION SUPPLEMENT RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing,

adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons

license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a

credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted

use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT

THIS ARTICLE CITE THIS ARTICLE Mai, P., Huang, E.W., Yu, J. _et al._ Interaction-driven spontaneous ferromagnetic insulating states with odd Chern numbers. _npj Quantum Mater._ 8, 14 (2023).

https://doi.org/10.1038/s41535-023-00544-z Download citation * Received: 04 October 2022 * Accepted: 13 February 2023 * Published: 09 March 2023 * DOI:

https://doi.org/10.1038/s41535-023-00544-z SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative