ABSTRACT Interactions and emergent processes are essential for research on complex systems involving many components. Most studies focus solely on pairwise interactions and ignore

higher-order interactions among three or more components. To gain deeper insights into higher-order interactions and complex environments, we study antibiotic combinations applied to

pathogenic _Escherichia coli_ and obtain unprecedented amounts of detailed data (251 two-drug combinations, 1512 three-drug combinations, 5670 four-drug combinations, and 13608 five-drug

combinations). Directly opposite to previous assumptions and reports, we find higher-order interactions increase in frequency with the number of drugs in the bacteria’s environment.

better navigating problems associated with the combinatorial complexity of multi-component systems. SIMILAR CONTENT BEING VIEWED BY OTHERS SYSTEMATIC ANALYSIS OF DRUG COMBINATIONS AGAINST

GRAM-POSITIVE BACTERIA Article Open access 28 September 2023 EPISTASIS ARISES FROM SHIFTING THE RATE-LIMITING STEP DURING ENZYME EVOLUTION OF A Β-LACTAMASE Article Open access 23 February

2024 PHARMACODYNAMICS OF INTERSPECIES INTERACTIONS IN POLYMICROBIAL INFECTIONS Article Open access 21 January 2025 INTRODUCTION Interactions are the key to unlocking emergent and unintuitive

properties across many fields: reactions in biochemistry, food webs and flocking among birds in ecology, environmental stressors and effects on species diversity in conservation biology,

genetic interactions in evolution and bioinformatics, bound states and many-body interactions in physics, social interactions in economics and political science, and drug interactions in

pharmacology.1,2,3,4,5,6 Understanding whether components interact in a manner that enhances (synergy) or weakens (antagonism) the individual effects of the mixed components is important

because the type of interaction governs the dynamics of complex systems. For example, in conservation biology, understanding multiple-stressor effects informs the development of strategies

to prevent loss of biodiversity.6 In pharmacology, understanding drug interactions enables the effective design of treatment strategies to combat complex diseases such as cancer7 and HIV,8

which increasingly rely on multidrug treatments. Despite the structural and terminological differences between natural and social systems, multi-component interactions constitute a unifying

theme in studying and predicting patterns in large complex systems. The formation of complex structures and dynamics often results from emergent properties that cannot be explained based on

the effects of individual components or even interactions between pairwise parts or other lower-order interactions—fewer numbers of components than the whole combination. It is crucial to

distinguish between two types of higher-order interactions, namely net and emergent interactions. Net higher-order interactions are most commonly measured and defined relative to the null

expectation that would arise from a non-interacting combination of independent single components and their effects.9 Thus, for a four-drug combination, a net higher-order effect could arise

from pairwise interactions, three-way interactions, and/or four-way interactions. For this reason, we also define and measure emergent higher-order effects that require all components to be

present for an interaction to exist. For instance, when the addition of a small amount of a third drug alters the interaction between two drugs—as opposed to the third drug interacting with

either of the individual drugs already present—this is an emergent interaction. Moreover, some interactions only exist when many components are present, even though there is no interaction

between any of the isolated pairs or triples,9 such as a protein or molecule that requires all parts to be joined before it can properly function and any activity or response can be

measured. Therefore, an approach that explicitly distinguishes emergent interactions—interactions that are not due to the presence of lower-order interactions—from the existence of any (net)

interaction is indispensable to fully represent complex system dynamics.10,11 Despite the possibility of higher-order interactions, studies have often focused on pairwise

interactions,12,13,14,15 whereas presuming or concluding that higher-order effects—owing to three or more components—are either extremely rare or negligible.16,17,18 There are both

conceptual and practical reasons that have led to this view. On the conceptual side, it has been commonly argued that lower-order effects are likely to counteract each other in higher-order

combinations such that they essentially cancel out and result in zero or negligible net effect.19,20 Alternatively, it has been argued that higher-order interactions prevent large systems

from exhibiting stability, and thus concluded that these effects either do not exist or are insignificant.21 For these reasons, many studies either implicitly assume higher-order

interactions do not exist or argue against the importance of measuring and considering higher-order interactions.13,16,22,23 A practical reason why higher-order interactions have received

much less attention relative to two-way (pairwise) interactions is owing to combinatorial complexity, i.e., difficulty in collecting data for all subsets of combinations of components.15,16

Another practical challenge to examining and classifying higher-order interactions is that it entails calculating the contribution from all lower levels—subsets of fewer components—to the

emergent behavior of the whole combination. These calculations are surprisingly subtle and correspond to having well defined and understood emergent interaction metrics with straightforward

generalization to higher-orders and quantification of uncertainties. The lack of such methods in many fields has stood as a theoretical limitation for studying interacting systems.10,14

Recent progress has made it possible to overcome these latter two practical limitations and thus enables us to directly test the above conceptual presumption by measuring how frequent

higher-order interactions are and what types of interactions are present. In this regard, our recent studies of combinations of three stressors9,24 showed that many more interactions arise

with three-way interactions compared with two-way interactions. Moreover, these three-way interactions exhibit an important feature: higher degrees of emergent antagonism, compared with

pairwise interactions. This greater amount of emergent antagonism—reduced effect relative to the expected effect based on no-interaction—suggests a need to further explore interactions among

three, four, and five drugs. Correspondingly, an insightful study by Mayfield et al.13 found that incorporating higher-order interactions as opposed to a constrained approach of two-way

interactions leads to better expectations of variations in natural plant communities, and a very recent and intriguing review by Levine et al.14 has provided a theoretical approach that

shows how higher-order interactions can promote species richness. In addition, another compelling study demonstrated the existence of higher-order gene interactions and revealed how they can

explain complex alterations in gene expression.25 These studies have shown the presence of higher-order effects and the importance of exploring them. However, what is lacking is a

comprehensive framework and data set that can be used to reveal the patterns of higher-order interactions. In particular, a feasible empirical study design (which provides easy manipulation

of the environmental disturbances and the number of components in the system) and a comprehensive theoretical approach are necessary for gaining crucial insights into biological systems (or

more generally, complex systems) comprised of many components. Indeed, the theoretical framework in this setting should be conveniently generalizable to distinguish different types of

higher-order effects (i.e., net versus emergent) in the presence of any number of components. Here, net interactions refer to an overall interaction compared relative to non-interacting

single component effects, whereas emergent interactions correspond to higher-order effects that only exist when all the components are present. Using large numbers of drug combinations, we

ask: (1) Are there more (or fewer) interactions when more stressors are added? (2) Are there any trends in the frequency of interaction types that amplify or attenuate the complexity of a

system when the number of components is increased? (3) Do these trends in interaction types differ between net versus emergent interactions? In contrast to previous work, we show that

emergent higher-order interactions are much more pervasive than commonly assumed and that there are characteristic patterns of net versus emergent higher-order interactions as the number of

drugs increases. Addressing these issues will be extremely useful if we are to find a perspicuous path forward in searching for higher-order interactions and dealing with combinatorial

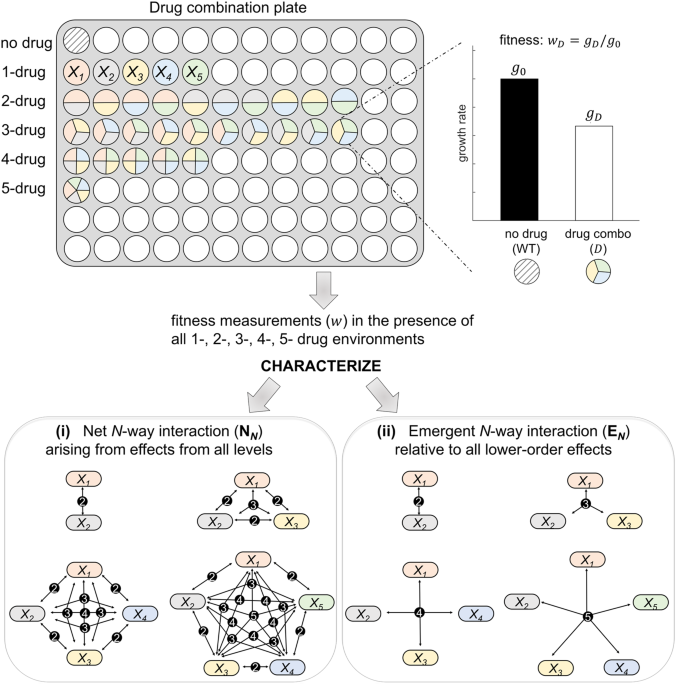
complexities. In this paper, we ground these questions in a highly controlled antibiotic study system that examines bacterial growth responses to an environment that consists of different

drug combinations. We obtain data for how eight single drugs with three concentrations each, 251 two-drug combinations, 1,512 three-drug combinations, 5,670 four-drug combinations, and

13,608 five-drug combinations affect pathogenic _E. coli_ growth rates (Fig. 1). This full-factorial design of drug combinations allows characterization of net and emergent interactions for

all five-way and lower-order interactions (two-, three-, four-way), and thus represents a staggering amount of data compared with previous studies, allowing us to shed new light on how

interactions change as more and more drugs (components) are added. THEORETICAL FRAMEWORK FOR THE CHARACTERIZATION OF HIGHER-ORDER INTERACTIONS To measure interactions, we must first

carefully define what an interaction is and what response measurements we use to assess the interactions. Based on standard definitions within the field, we can then extend and generalize

this interactions framework to higher orders for both net and emergent interactions. For drug studies the key response measurement is growth rate of a bacteria population in the presence of

a drug relative to growth of bacteria in a no-drug environment. This growth rate is interpreted as the relative fitness in the presence of a drug treatment _X_ and is typically denoted by

_w__X_ (Fig. 1), where no-growth (_w__X_ = 0) represents complete lethality and maximum-growth (_w__X_ = 1) represents the case that the drug treatment is not effective at all. Because we

are using relative fitness, the effect of each individual drug can be interpreted as a percent reduction in growth rate, so the null expectation for the combined effects of two

non-interacting drugs would be the product of two percentages, corresponding to a multiplicative definition of no interaction. Furthermore, the effect of drug treatment _X_ on the fitness

can also be represented in terms of the selection coefficient \(s_X:w_X = e^{ - s_X}\). The case when no drug is added would generate no effect on the bacterial fitness, i.e., _s__X_ = 0 and

the product of the effect of two single drugs, _X__1_ and _X__2_, would be \(w_{X_1}w_{X_2} = e^{ - (s_{X1} + s_{X2})}\), which means the null expectation of no interaction is additive in

terms of the selection coefficients. Consistent with the drug literature, we will use the term additivity to refer to no interaction throughout the rest of this paper. Interaction

classifications are then defined based on whether a drug combination yields more than (antagonistic) or less than (synergistic) the expected fitness measures when there are no

interactions.10,26 Here, we review net and emergent measures for the quantification of _N_-way interaction effects (see Fig. 1 and S1 Fig). Throughout the paper, we denote single drugs by

_X__i_, where _i_ > _0_ and use a list of _X__i_ to represent drug combinations (such as _X_1_X_2 for combining two drugs _X_1 and _X_2). Moreover, for notational tractability, _N_-way

interaction measures are defined for _X_1_X_2… _X__N_, which stands for any _N_-drug combination. NET _N_-WAY (N_N_) INTERACTIONS We follow the Bliss Independence model27 to characterize a

net _N_-way interaction (N_N_) for the total interaction in comparison with that expected from all the independent and individual effects of each drug. Based on Bliss Independence, drugs

_X_1 and _X_2 are not interacting when the addition of a second drug (_X_2) does not influence the percent decrease in the pathogen fitness due to another single drug (_X_1), i.e.,

\(w_{X_1X_2} = w_{X_1}w_{X_2}\). Accordingly, the interaction between _X_1 and _X_2 is measured by the deviation from the non-interacting (termed additive) case as $${\mathrm{N}}_2 =

w_{X_1X_2} - w_{X_1}w_{X_2}$$ (1) A correct rescaling method28 is needed to properly interpret the magnitude of these measures. After rescaling, a sufficiently large negative value of N2

suggests a synergistic interaction, as drugs together produce a superior inhibition effect relative to the case that drugs are not interacting, whereas a large positive value of N2 indicates

an antagonistic interaction. As a test of this model and baseline definition of no interaction, Beppler et al.9 performed experiments in which a single drug was treated as three different

drugs to see if there was any interaction. Confirming the expectation of our interaction model and validating its correctness, no interaction of a drug with itself was observed for the vast

majority of experiments (i.e., doubling and tripling the dosages of the same drug). Extending Eq. (1) to systems with more than two drugs enables measurements and calculations to determine

the presence of any kind of interaction relative to the single-drug effects. Thus, the generalized form of the net interaction measure for an _N_-drug combination is.10,29,30

$${\mathrm{N}}_N = w_{X_1X_2 \ldots X_N} - w_{X_1}w_{X_2} \ldots w_{X_N}$$ (2) Observe that the subscript _X_1_X_2… _X__N_ means the bacteria’s environment contains drug _X_1 plus drug _X_2

plus all drugs up to _X__N_. Therefore, if only _k_ of the _N_ drugs remain in the environment, the subscript becomes _X_1_X_2… _X__k_0…0, which is equivalent to _X_1_X_2… _X__k_ because

adding 0 or no drug is equivalent to just having the _k_-drug subset. Moreover, the relative fitness of the drugs at 0 concentration will be 1, so the net _N_-way interaction will reduce to

just a _k_-way interaction, as expected. EMERGENT _N_-WAY (E_N_) INTERACTIONS To assess interactions that require all _N_ drugs to be present, or equivalently, interactions beyond what is

expected from the effects of all lower-order combinations, we use and extend our emergent interaction framework presented in Beppler et al.9 When two drugs are combined, the definitions of

net and emergent interactions converge to become identical because single drugs constitute the one and only lower-order component of a two-drug environment, so there is nothing from which to

emerge except the single-order effects. Thus, the emergent two-way (E2) interaction is identical to the net two-way interaction, N2 (Eq. (1)). However, when there are more than two drugs in

the environment, interactions among different lower-order subsets (two-way versus three-way versus four-way or the combination of two-ways, etc.) of drugs can change the dynamics of _N_-way

interactions, and those effects need to be accounted for characterizing the emergent interactions.11 Here, the contribution to the effect that comes solely from a lower-order combination

corresponds to the total interaction when only that specific lower-order interaction is present. Based on this, we systematically determine all the lower-order interactions in an _N_-way

combination, calculate the total sum of all of these lower-order interactions, and subtract this sum from the net interaction to capture any emergent interaction (see details in the

Materials and Methods). When _N_ = 3, this corresponds to the total (net) three-drug interaction effect that is not due to the contributions from all the two-drug combinations. As described

in Materials and Methods, E3 yields an expression that includes fitness measurements in the presence of every possible drug combination in the three-drug environment. $${\mathrm{E}}_3 =

{\mathrm\it{w}}_{{\mathrm\it{X}}_1{\mathrm\it{X}}_2{\mathrm\it{X}}_3} - {\mathrm\it{w}}_{{\mathrm\it{X}}_1}{\mathrm\it{w}}_{{\mathrm\it{X}}_2{\mathrm\it{X}}_3} -

{\mathrm\it{w}}_{{\mathrm\it{X}}_2}{\mathrm\it{w}}_{{\mathrm\it{X}}_1{\mathrm\it{X}}_3} - {\mathrm\it{w}}_{{\mathrm\it{X}}_3}{\mathrm\it{w}}_{{\mathrm\it{X}}_1{\mathrm\it{X}}_2} +

2{\mathrm\it{w}}_{{\mathrm\it{X}}_1}w_{X_2}w_{X_3}$$ (3) The emergent four-way and five-way interaction formulas are derived in the Materials and Methods with explanation given for how to

correctly count the combinatorics of all drug subsets while avoiding any issues of double- or overcounting of contributions. Notably, recent papers22,31 have proposed new formulae to predict

three-way interactions based on equations with weighted mixtures of pairwise interactions. This valuable work is useful for trying to mechanistically understand how three-way interactions

might arise, with the recipe for the weights of the mixture perhaps corresponding to specific ways in which a third drug might affect the interaction of another pair. However, there is no

sense in which this explains away the existence of emergent higher-order drug interactions. Our goal in this paper is merely to measure the existence of emergent interactions and

characterize how prevalent they are and any patterns for their frequency. Therefore, the data produced and patterns identified in the present paper are complementary to these other recent

papers22,31 in trying to identify the patterns and mechanisms that underlie emergent interactions. RESULTS In this study, we explored the consequences of increased complexity in

multi-component systems by employing an experimental design of higher-order drug combinations and by using and extending our recently developed mathematical framework9,24 to characterize

higher-order interactions. We categorized net interactions based on the deviation of the whole combination effect from the expected effect of no-interaction among individual drugs. To

measure emergent interactions, we calculated the deviation of net interaction from the expected effect from all interactions that result from lower-order subsets/combinations of drugs (Fig.

1, S1 Fig, “Theoretical Framework for the Characterization of Higher-order Interactions” and “Materials and Methods”). As with pairwise studies for drugs, epistasis, and other biological

systems, interactions are defined as synergistic or antagonistic when the effect of two components is sufficiently (see Materials and Methods for precise values) stronger or weaker than

expected effects of no-interaction (net) or all lower-order interactions (emergent), respectively. As shown in Fig. 2a, (No-interaction bar) and S2 Fig, interactions become significantly

more frequent as the number of drugs in _E. coli_’s environment increases (sum of Synergy and Antagonism bars in Fig. 2a). This startling finding suggests not only that higher-order

interactions are not negligible and should not be ignored, but that they may be even more important than pairwise interactions in determining the structure and dynamics of systems because

they are substantially more prevalent than two-component interactions. Understanding this phenomenon is thus fundamental to understanding interactions in biological and complex systems in

general. Evaluating whether any patterns exist in the types of interactions as the number of drugs increases, we found that the net interactions among drugs tend toward more synergy, whereas

emergent interactions exhibit a shift toward more antagonism (Fig. 2). Further dissecting the nature of these interactions and comparing net with emergent interactions, we found that net

synergy seldom implies emergent synergy (Fig. 3a, Synergy column). This makes sense because any interactions will create a net effect, while emergence is only an interaction among all drugs

in the combination, so will almost certainly be a subset of net interactions. Consequently, a net three-way synergy is usually due to pairwise synergies between two drugs in which a third

drug may not be increasing efficacy but still increases toxicity to patients. In addition, we found that emergent antagonism is less likely to imply net antagonism as the number of drugs

increases (Fig. 3a, Antagonism column). Explicitly, this fraction is given by 26%, 18%, and 11% at the three-, four-, and five-drug level, respectively. As another method for summarizing the

data, we construct a breakdown score that is calculated as the sum over all lower-order interactions with a 1 added for each lower-order antagonism and a −1 added for each lower-order

synergy. With this breakdown score, we can then assess how the summarized category of lower-order interactions affects the net (overall) interaction. For example, when there are three drugs

in the bacterial environment (as denoted by _X_1_X_2_X_3in the Theoretical Framework above) and when all three pairwise parts (i.e., _X_1_X_2, _X_1_X_3, and _X_2_X_3) are synergistic, the

breakdown score equates to −3, whereas when all are antagonistic, the breakdown score is equal to 3. These two cases represent the minimum and maximum values attained with _N_ = 3,

respectively. Intriguingly, we showed that lower-order net synergistic effects tend to overcome lower-order net antagonistic effects (Fig. 3b). This demonstrates the fallacy of the prominent

presumption that higher-order interactions cancel out and are negligible. Establishing this result was only possible due to our full-factorial experiments and large-scale data set as well

as our development and comparison of emergent versus net interaction measures. Overall, our comparison analysis of net and emergent interactions indicates that emergent synergy mostly

suggests net synergy, whereas emergent antagonism does not imply net antagonism. DISCUSSION We have explored the consequences of increasing the number of components in the context of net and

emergent higher-order interactions through a systematic analysis of bacterial responses in the presence of drug combinations. For both net and emergent higher-order interactions we found

the number of interactions substantially increased as the number of drugs increased. Although this may not be surprising for net interactions, it is extremely surprising for emergent

interactions because these have been largely ignored in the literature. Yet our new analysis reveals emergent interactions are highly prevalent in our drug systems. Although we have only

shown this result for drug combinations, it contradicts the prevailing views and previous limited results in the field. We also observed an increasing trend toward synergy in net interaction

effects and toward antagonism in emergent interaction effects. These trends use tremendous amounts of data to extend and elaborate on recent patterns found in the comparison of two- with

three-drug combinations.24 These general trends suggest that increasing the number of drugs continually adds new layers of complexity and leads to the natural question of whether this

layering of complexity also applies to interactions among multiple components across a myriad of other systems. Indeed, if this finding continues to hold as the number of drugs increases and

also applies to other systems and fields, this bypass approach could revolutionize studies of both net and emergent higher-order interactions by making the intractability of the

combinatorics suddenly become tractable via systematic patterns that enable predictability. From a clinical standpoint, synergies offer higher treatment efficacies with low toxicity. Hence,

they are valued and used clinically, whereas antagonistic combinations have been traditionally avoided.11 Our study reveals that for most higher-order drug combinations, net synergy does not

imply emergent synergy. The abundance of such cases suggests the criteria for determining clinically advantageous (or disadvantageous) drug combinations should now consider both net and

emergent effects as it is also critical to identify whether addition of drugs yields a real (emergent) benefit that justifies the inclusion of each additional drug in the combination.

Studies on pairwise-drug combinations have shown that antagonistic interactions can lead to a selective advantage of the wild-type pathogen population and reduce the rate of adaptation to

drugs.32,33 Extending these ideas to more rugged fitness landscapes that correspond to higher-order interactions among drugs and determining the consequences for drug-resistance has not yet

been pursued. To our knowledge, this is one of the only and by far the largest set of empirical data obtained to examine the role of net and emergent higher-order interactions. Our

observations suggest that the fitness landscapes for multidrug combinations should be extremely rugged due to the pervasiveness of higher-order interactions. Although our study focuses on a

drug-bacteria system, the conceptualization of interaction types (net versus emergent, and synergy versus antagonism) and the systematic analysis of higher-order interactions can be

extrapolated into other fields. A relatively straightforward application of our framework includes multiple-stressor effects as drugs in our study are essentially stressors to the bacterial

population. Moreover, the interaction model used in multiple predator effect studies is equivalent to the net interaction measure,34 suggesting a strong correspondence of our mathematical

framework for characterizing emergent interactions.9 In microeconomics, relationships between individuals (creating demand) and market firms (supplying demand) affect the allocation of

resources.2 In the context of social groups, the idea of emergence can be well represented by one individual’s role in controlling a conflict between others in the group. Indeed, studies in

primates35 and in people36 have predicted that cohesion dynamics of groups differ significantly between dyads and triads—groups of two and three people, respectively—with triads being more

stable in conserving the association of a group. Here, we also note several caveats in our framework in its application to clinical practice as well as to other interaction-network settings.

From a clinical standpoint, drug combination experiments in this study are carried out in vitro, in highly controllable systems. Hence, in vivo studies of higher-order drug combinations are

needed for guiding studies with clinical applications. In addition, as opposed to the drug–bacteria system, natural systems are comprised of many interacting species and functional groups

that span trophic levels and that are impacted by diverse but sometimes correlated environmental drivers such as temperature, precipitation, stoichiometry, fires, etc. Consequently, new

theory needs to be developed that incorporates additional information to study higher-order interactions and their outcomes in natural systems that involve many more complexities. In

conclusion, we introduce an approach to studying higher-order interactions in biological systems. We provide an enormous amount of data that we analyze with a recently developed theoretical

framework to characterize net and emergent interactions among all possible combinations of two, three, four, and five drugs out of a set of eight antibiotics. Notably, we find many

interactions that only emerge when multiple drugs are present, and even more surprisingly, we find that the frequency of interactions increases as the number of components in the system

increases, contradicting the assumptions and limited findings of many previous studies. Beyond this, we find that emergent interactions tend toward antagonism, whereas net interactions tend

toward synergy. These findings suggest that higher-order interactions may be of fundamental importance in understanding and predicting the structure and dynamics of complex biological

systems with many interacting parts, such as drugs, genes, food webs, environmental stressors, and more. Intriguingly, the general questions explored here for drug interactions are highly

relevant for other fields, and we anticipate that the research program presented here will be useful for revealing higher-order emergent properties and patterns in ecological, medical,

evolutionary, and social systems. It is possible that the prevalence and patterns of higher-order interactions described here will be generic to many other biological and complex systems.

Alternatively, these findings may be specific to the type of system being studied. The answer can only be elucidated through future work in other systems. For our drug–bacteria system, we

have combined a large-scale experimental system with a new conceptual framework to establish the strong prevalence and importance of higher-order interactions and to identify patterns of

these interactions that should help to circumvent combinatorial complexity as well as to inform effective design of multidrug treatments. MATERIALS AND METHODS EXPERIMENTAL DETAILS BACTERIAL

STORAGE AND PREPARATION Pathogenic _E. Coli_ strain CFT073 (ATCC® 700928™) isolated from human clinical specimens was used for all experiments. Bacterial aliquots were made using a single

colony collected using streak purification. The aliquots were stored in 25% glycerol at − 80 °C. A culture was prepared each day using a thawed aliquot diluted 10−2 in Luria Broth (10 g/l

tryptone, 5 g/l yeast extract, and 10 g/l NaCl). The culture was grown at 37 °C for about 4 h. ANTIBIOTICS We used eight antibiotics in this study that were chosen specifically to cover a

broad range of antibiotic mechanisms of action.37 Additionally, drugs needed to be soluble in dimethyl sulfoxide (DMSO) and therefore were chosen based on solubility properties. These

antibiotics were Ampicillin (Sigma A9518), Cefoxitin Sodium Salt (Sigma C4786), Ciprofloxacin Hydrochloride (MP Biomedicals 199020), Doxycycline hyclate (Sigma D9891), Erythromycin (Sigma

Aldrich E6376), Fusidic Acid Sodium Salt (Sigma F0881), Streptomycin (Sigma Aldrich S6501), and Trimethoprim (Sigma T7883). A list of drugs, abbreviations, mechanisms of action, and

concentrations used in this assay is in Table 1. ANTIBIOTIC CONCENTRATION DETERMINATION AND PREPARATION A dose curve was generated to determine antibiotic drug concentrations for this assay.

Dose curves were generated using 20 drug concentrations with a dilution factor of two and a starting concentration of 0.1 mM. For Fusidic Acid, the highest concentration was 1 mM, as the

lower concentrations were found to be ineffective in generating lethality needed to determine the IC50 (50% inhibition concentration). Graphpad Prism 7 was used to graph the dose curve and

determine the IC50. In addition, Graphpad (http://www.graphpad.com/quickcalcs/Ecanything1/) was used to estimate the IC10, IC5, and IC1. Minimally effective concentrations were chosen in

order to maintain bacterial growth even in multidrug combinations. Each antibiotic was weighed and solubilized in 100% DMSO (Sigma), except for Streptomycin, which was solubilized in 50%

DMSO, to a final concentration of × 400 the determined IC10, IC5, and IC1 concentrations. Antibiotics were then pipetted into a source plate (Thermo Scientific) as either a single antibiotic

with additional DMSO or in combination with another antibiotic. The final concentration in the source plate was × 200 the target concentration. EXPERIMENTAL SETUP In total, we tested all

two-, three-, four-, and five-drug combinations from a set of eight antibiotics (Table 1), meaning that 28, 56, 70, and 56 distinct drug combinations were tested at given concentrations,

respectively. For each experiment, 25 µL of Luria Broth was added to each well of a 384-well plate (Greiner BioOne) using a Multidrop 384 (Thermo Scientific). An additional 25 µL of media

was added to the media-only control. Using a Biomek FX (Beckman Coulter) with a 250 nL pin tool (V&P Scientific), we pinned 250 nL from every well of each of the three premade source

plates (one plate with one antibiotic and DMSO and two plates with two antibiotics in combination) into the experimental plate. A 25 µL of a 10-4 dilution of the overday culture was then

added to each well (except for the negative control). Plates were incubated at 37°C and read using an OD590 measurement every 4 h for 16 h. Each two-, three-, four- and five-drug experiment

was tested at least three times (S1 Data). GROWTH MEASUREMENTS For each plate, the Z’-factor38 was calculated to determine the quality of the assay. If a Z’ value was below 0.5, the plate

was not used for final analysis. For a few plates, there was one well that was more than two standard deviations from the average of the negative control. For these plates, that well was

removed from the final Z’-factor calculation. The exponential rate of growth was determined for each experimental well and compared with the average exponential rate of growth for the no

drug control to give a growth percentage. Growth percentages were used to determine interaction types based on a framework developed in,9,24 as summarized below. MATHEMATICAL FRAMEWORK Here,

we derive the formula for emergent three-way interactions and also generalize the emergent interaction measure to higher orders and any _N_-way combination. As described briefly in

“Theoretical Framework for the Characterization of Higher-order Interactions”, we accomplish this by starting from the definition of Bliss Independence (i.e., N_N_) and by subtracting all

lower-order contribution effects from N_N_. For any _N_, we can denote these lower-order contributions by \(\left[ {{\mathrm{N}}_N} \right]_{D_1 \bot D_2 \bot \ldots \bot D_n}\), where ⊥

represents no-interaction, and _D__i_ represents one or more drugs that is a subset of interacting components (i.e., combinations of drugs). These subsets are composed of _n_ disjoint sets

of drugs with the union of all such sets equaling the total set of all drugs (i.e., _D_1U _D_2 U … U _D__n_ = _X_1_X_2… _X__N_) because all subsets must combine to produce the original

_N_-drug combination. For this reason, no drug is allowed to occur in more than one subset of drugs. In other words, for any lower-order contribution term, each drug can be part of only one

subset. For example, \(\left[ {{\mathrm{N}}_3} \right]_{X_1X_2 \bot X_3}\), where _D__1_ = _X_1_X_2 and _D__2_ = _X_3, represents the pairwise combination effect of _X_1_X_2 on the three-way

interaction, and it measures the expected three-way effect when the remaining drug _X_3 does not interact with the pair. This effect is calculated as $$\left[ {{\mathrm{N}}_3}

\right]_{X_1X_2 \bot X_3} = w_{X_1X_2}w_{X_3} - {\mathrm{w}}_{{\mathrm{X}}_1}w_{X_2}w_{X_3} = w_{X_3}\left[ {{\mathrm{N}}_2} \right]_{X_1X_2}$$ For measuring emergent interactions, all

different factorizations of drugs are subtracted in a combinatorial fashion. When _N_ = 3, all the pairwise combination effects are subtracted from the net three-way interaction

$${\mathrm{E}}_3 = {\mathrm{N}}_3 - \left[ {{\mathrm{N}}_3} \right]_{X_1X_2 \bot X_3} - \left[ {{\mathrm{N}}_3} \right]_{X_1X_3 \bot X_2} - \left[ {{\mathrm{N}}_3} \right]_{X_2X_3 \bot

X_1}$$ Analogously calculating the effects due to _X_1_X_3 and _X_2_X_3 (i.e., \(\left[ {{\mathrm{N}}_3} \right]_{{{X}}_1{{X}}_3 \bot {{X}}_2}\) and \(\left[ {{\mathrm{N}}_3}

\right]_{{{X}}_2{{X}}_3 \bot {{X}}_1}\)), the definition of _E_3 yields Eq. (3) in the “Theoretical Framework for the Characterization of Higher-order Interactions”. The most challenging

issue in deriving higher-order equations for more than three drugs is to carefully correct for the possible double counting of interactions when subtracting lower-order effects that may be

subsumed in multiple higher-order terms. For instance, the lower-order interaction terms of \(\left[ {{\mathrm{N}}_4} \right]_{X_1 \bot X_2X_3X_4}\) and \(\left[ {{\mathrm{N}}_4}

\right]_{X_2 \bot X_1X_3X_4}\)both subsume the effect of \(\left[ {{\mathrm{N}}_4} \right]_{X_3X_4 \bot X_1 \bot X_2}\) as all three are identical when _X_1, _X_2, and the combined drug pair

_X_3_X_4 are all non-interacting with respect to each other. Such cases should be dealt with systematically to make sure that each lower-order effect is subtracted off exactly once (see S1

Text). Moreover, when _N_ > 3, it is also necessary to exclude the effect that results from interactions of different subsets of drug combinations. For example, the two-way interactions

of _X_1_X_2 and _X_3_X_4 on the four-way combination of _X_1_X_2_X_3_X_4, as denoted by \(\left[ {{\mathrm{N}}_4} \right]_{X_1X_2 \bot X_3X_4}\) and calculated as \(w_{X_1X_2}w_{X_3X_4} -

{\mathrm{w}}_{{\mathrm{X}}_1}w_{X_2}w_{X_3}w_{X_4}\), must be accounted for when considering all lower-order effects. Following the same logic as in the calculation of pairwise interactions,

the lower-order contribution of drugs, i.e., \(\left[ {{\mathrm{N}}_N} \right]_{D_1 \bot D_2 \bot \ldots \bot D_n}\), is given by the expected _N_-way effect when only interactions within

the non-single-drug subsets (i.e., _D__i_ containing more than one drug) are present. Thus, lower-order effects from the mixture of lower-order combinations and single drugs complementing

the total combination will be calculated similarly by replacing the _N_-way drug response, \(w_{X_1X_2 \ldots X_N},\) with the product of drug combination responses that are assumed to be

only interacting pieces within the _N_-drug combination as $$\left[ {{\mathrm{N}}_N} \right]_{D_1 \bot D_2 \bot \ldots \bot D_n} = w_{D_1}w_{D_2} \ldots w_{D_n} - w_{D_1}w_{D_2} \ldots

w_{D_N}$$ For example, the _k_-drug effect of _X_1_X_2…_X__k_ on the _N_-way combination for any value of _N_ and _k_ with _k_ < _N_ is given by the expected _N_-way effect when only _k_

drugs interact, i.e. \(\left[ {{\mathrm{N}}_N} \right]_{X_1X_2 \ldots X_k \bot X_{k + 1} \bot \ldots \bot X_N} = w_{X_1X_2 \ldots X_k}w_{X_{k + 1}} \ldots w_{X_N} - w_{X_1}w_{X_2} \ldots

w_{X_N}\). Indeed, this is equivalent to the net interaction arising from the _k_-drug combination multiplied by the single-drug fitnesses of the remaining _N_−_k_ drugs: \(w_{X_{k + 1}}

\ldots w_{X_N}\left[ {{\mathrm{N}}_k} \right]_{X_1X_2 \ldots X_k}\). Subtracting all possible lower-order interaction contributions (via factorizations of _D_1⊥ _D_2⊥…⊥ _D__n_) from the net

_N_-way interaction defines newly emergent interactions among all _N_ drugs. Accordingly, we now define E4 and E5 purely in terms of fitness measurements based on the conceptual framework

just described and using the above formulas and notation for the lower-order component effects. Guaranteeing that overcounting is eliminated when distinguishing every possible lower-order

effect from the net interaction (see S1 Text), the emergent four-way interaction is given by $$\begin{array}{*{20}{l}} {{\mathrm{E}}_4} \hfill & = \hfill & {w_{X_1X_2X_3X_4} -

w_{X_1}w_{X_2X_3X_4} - w_{X_2}w_{X_1X_3X_4} - w_{X_3}w_{X_1X_2X_4} - w_{X_4}w_{X_1X_2X_3}} \hfill \cr {} \hfill & {} \hfill & { - w_{X_1X_2}w_{X_3X_4} - w_{X_1X_3}w_{X_2X_4} -

w_{X_1X_4}w_{X_2X_3} + 2w_{X_1}w_{X_2}w_{X_3X_4}} \hfill \cr {} \hfill & {} \hfill & { + 2w_{X_1}w_{X_3}w_{X_2X_4} + 2w_{X_1}w_{X_4}w_{X_2X_3} + 2w_{X_2}w_{X_3}w_{X_1X_4} +

2w_{X_2}w_{X_4}w_{X_1X_3}} \hfill \cr {} \hfill & {} \hfill & { + 2w_{X_3}w_{X_4}w_{X_1X_2} - 6w_{X_1}w_{X_2}w_{X_3}w_{X_4}} \hfill \end{array}$$ The emergent five-way measure in

terms of relative fitnesses is given as $$\it \begin{array}{l}{\mathrm{E}}_5 = w_{X_1X_2X_3X_4X_5} - w_{X_1}w_{X_2X_3X_4X_5} - w_{X_2}w_{X_1X_3X_4X_5} - w_{X_3}w_{X_1X_2X_4X_5} -

w_{X_4}w_{X_1X_2X_3X_5} - \cr w_{X5}w_{X_1X_2X_3X_4} - w_{X_1X_2}w_{X_3X_4X_5} - w_{X_1X_3}w_{X_2X_4X_5} - w_{X_1X_4}w_{X_2X_3X_5} - w_{X_1X_5}w_{X_2X_3X_4} - \cr w_{X_2X_3}w_{X_1X_4X_5} -

w_{X_2X_4}w_{X_1X_3X_5} - w_{X_2X_5}w_{X_1X_3X_4} - w_{X_3X_4}w_{X_1X_2X_5} - w_{X_3X_5}w_{X_1X_2X_4} - w_{X_4X_5} - \cr w_{X_4X_5}w_{X_1X_2X_3} + 2w_{X_1}w_{X_2}w_{X_3X_4X_5} +

2w_{X_1}w_{X_3}w_{X_2X_4X_5} + 2w_{X_1}w_{X_4}w_{X_2X_3X_5} + \cr 2w_{X_1}w_{X_5}w_{X_2X_3X_4} + 2w_{X_2}w_{X_3}w_{X_1X_4X_5} + 2w_{X_2}w_{X_4}w_{X_1X_3X_5} + 2w_{X_2}w_{X_5}w_{X_1X_3X_4} +

\cr 2w_{X_3}w_{X_4}w_{X_1X_2X_5} + 2w_{X_3}w_{X_5}w_{X_1X_2X_4} + 2w_{X_4}w_{X_5}w_{X_1X_2X_3} + 2w_{X_1X_2}w_{X_3X_4}w_{X_5} + \cr 2w_{X_1X_2}w_{X_3X_5}w_{X_4} +

2w_{X_1X_2}w_{X_4X_5}w_{X_3} + 2w_{X_1X_3}w_{X_2X_4}w_{X_5} + 2w_{X_1X_3}w_{X_2X_5}w_{X_4} + \cr 2w_{X_1X_3}w_{X_4X_5}w_{X_2} + 2w_{X_1X_4}w_{X_2X_3}w_{X_5} + 2w_{X_1X_4}w_{X_2X_5}w_{X_3} +

2w_{X_1X_4}w_{X_3X_5}w_{X_2} + \cr 2w_{X_1X_5}w_{X_2X_3}w_{X_4} + 2w_{X_1X_5}w_{X_2X_4}w_{X_3} + 2w_{X_1X_5}w_{X_3X_4}w_{X_2} + 2w_{X_2X_3}w_{X_4X_5}w_{X_1} + \cr

2w_{X_2X_4}w_{X_3X_5}w_{X_1} + 2w_{X_2X_5}w_{X_3X_4}w_{X_1} - 6w_{X_1X_2}w_{X_3}w_{X_4}w_{X_5} - 6w_{X_1X_3}w_{X_2}w_{X_4}w_{X_5} - \cr 6w_{X_1X_4}w_{X_2}w_{X_3}w_{X_5} -

6w_{X_1X_5}w_{X_2}w_{X_3}w_{X_4} - 6w_{X_2X_3}w_{X_1}w_{X_4}w_{X_5} - 6w_{X_2X_4}w_{X_1}w_{X_3}w_{X_5} - \cr 6w_{X_2X_5}w_{X_1}w_{X_3}w_{X_4} - 6w_{X_3X_4}w_{X_1}w_{X_2}w_{X_5} -

6w_{X_3X_5}w_{X_1}w_{X_2}w_{X_4} - 6w_{X_4X_5}w_{X_1}w_{X_2}w_{X_3} + \cr 24w_{X_1}w_{X_2}w_{X_3}w_{X_4}w_{X_5}\end{array}$$ Notably, analyzing deviations from appropriate baselines of these

interaction measures allows us to assign information and meaning to the magnitude of the interaction and thus form a correspondence with the type and strength of interaction. This is

accomplished via rescaling methods we developed for these interaction measures as defined in ref.24,28,29 (see S2 Text) and that we use to analyze the experimental data of drug combinations.

DETAILS OF DATA ANALYSIS AND CUTOFF VALUES FOR THE CATEGORIZATION OF INTERACTIONS Median growth measurements for each experiment across replicates were used to determine net and emergent

interaction types according to the rescaled interaction metric definitions. Owing to the full-factorial design of our experiments, bacterial growth in the presence of each _k_-drug

combination is measured within each drug combination experiment that contains that specific _k_-way drug combination (the pairwise combination _X_1_X__2_ is repeated within the experiments

of _X_1_X__2__X_3, _X_1_X__2__X_4, and so on). For such cases (i.e., for two-, three-, and four-drug combinations) the median interaction metric calculation across these experiments was used

to determine the interaction type of each drug combination. Given the interaction metric calculation, we categorize synergy, additivity, and antagonism regions according to cutoff values

established by previous work.24,28,39 The interaction among drugs is identified as synergistic when the interaction metric is < −0.5, antagonistic if it is larger than 0.5, and additive

if it ranges between −0.5 and 0.5. Note that the total range of the rescaled metric is from −1 to 1 when the combination of drugs reduces the growth relative to at least one of the

lower-order combination growth rates (i.e., fitness), hence leading to rare instances of values above 1. Finally, we excluded several specific cases in our analysis. First, for two-drug

combinations _X_1_X_2, the effect of the second drug on the bacterial growth is indistinguishable when both the maximum of single and pairwise growth measurements (i.e., \(\max \left(

{w_{X_1},w_{X_2}} \right)\) and \(w_{X_2}\)) are > 90% growth.40 Next, using the same reasoning, in the extreme case that _k_ drugs by themselves kill off the bacteria populations

(lethality: measurements below 4.7% as determined by Tekin et al.24) and the addition of another drug into the environment also leads to lethality, then it is meaningless to look for

emergent _k_ + 1 drug interactions. We identify these cases as inconclusive and excluded them in our data analysis of the frequency of interaction types. DATA AVAILABILITY The data sets for

this article have been uploaded as part of the Supplementary Information. CODE AVAILABILITY Data analysis is performed in MATLAB version R2015a. The scripts are available upon request.

REFERENCES * Bialek, W. et al. Statistical mechanics for natural flocks of birds. _Proc. Natl. Acad. Sci._ 109, 4786–4791 (2012). Article  CAS  Google Scholar  * Shi, S. Customer

relationship and sales. _J. Econ. Theory_ 166, 483–516 (2016). Article  Google Scholar  * Hamilton, L. C. Education, politics and opinions about climate change evidence for interaction

effects. _Clim. Change_ 104, 231–242 (2011). Article  Google Scholar  * Nishikawa, T. & Motter, A. E. Symmetric states requiring system asymmetry. _Phys. Rev. Lett._ 117, 114101 (2016).

Article  Google Scholar  * van Vliet, S. & Ackermann, M. Bacterial ventures into multicellularity: collectivism through individuality. _PLoS Biol._ 13, e1002162 (2015). Article  Google

Scholar  * Darling, E. S. & Côté, I. M. Quantifying the evidence for ecological synergies. _Ecol. Lett._ 11, 1278–1286 (2008). Article  Google Scholar  * Bozic, I. et al. Evolutionary

dynamics of cancer in response to targeted combination therapy. _eLife_ 2, e00747 (2013). * Shafer, R. & Vuitton, D. Highly active antiretroviral therapy (HAART) for the treatment of

infection with human immunodeficiency virus type 1. _Biomed. Pharmacother._ 53, 73–86 (1999). Article  CAS  Google Scholar  * Beppler, C. et al. Uncovering emergent interactions in three-way

combinations of stressors. _J. R. Soc. Interface_ 13, 20160800 (2016). Article  Google Scholar  * Foucquier, J. & Guedj, M. Analysis of drug combinations: current methodological

landscape. _Pharmacol. Res. Perspect._ 3, e00149 (2015). * Tekin, E., Savage, V. M. & Yeh, P. J. Measuring higher-order drug interactions: a review of recent approaches. _Curr. Opin.

Syst. Biol._ 4, 16–23 (2017). Article  Google Scholar  * Kareiva, P. Special feature: higher order interactions as a foil to reductionist ecology. _Ecology_ 75, 1527–1559 (1994). * Mayfield,

M. M. & Stouffer, D. B. Higher-order interactions capture unexplained complexity in diverse communities. _Nat. Ecol. Evol._ 1, 62 (2017). Article  Google Scholar  * Levine, J. M.,

Bascompte, J., Adler, P. B. & Allesina, S. Beyond pairwise mechanisms of species coexistence in complex communities. _Nature_ 546, 56–64 (2017). Article  CAS  Google Scholar  *

Weinreich, D. M., Lan, Y., Wylie, C. S. & Heckendorn, R. B. Should evolutionary geneticists worry about higher-order epistasis? _Curr. Opin. Genet. Dev._ 23, 700–707 (2013). Article  CAS

  Google Scholar  * Wood, K. B. Pairwise interactions and the battle against combinatorics in multidrug therapies. _Proc. Natl. Acad. Sci._ 113, 10231–10233 (2016). Article  CAS  Google

Scholar  * Wang, H. et al. Mechanism-independent optimization of combinatorial nanodiamond and unmodified drug delivery using a phenotypically driven platform technology. _ACS Nano_ 9,

3332–3344 (2015). Article  CAS  Google Scholar  * Van Belle, G. _Statistical rules of thumb_. 699 (John Wiley & Sons, New Jersey, 2011). * Wootton, J. T. The nature and consequences of

indirect effects in ecological communities. _Annu. Rev. Ecol. Syst._ 25, 443–466 (1994). Article  Google Scholar  * Phillips, P. C. Epistasis—the essential role of gene interactions in the

structure and evolution of genetic systems. _Nat. Rev. Genet._ 9, 855–867 (2008). Article  CAS  Google Scholar  * Wootton, K. L. & Stouffer, D. B. Species’ traits and food-web complexity

interactively affect a food web’s response to press disturbance. _Ecosphere_ 7, e01518 (2016). * Zimmer, A., Katzir, I., Dekel, E., Mayo, A. E. & Alon, U. Prediction of multidimensional

drug dose responses based on measurements of drug pairs. _Proc. Natl. Acad. Sci._ 113, 10442–10447 (2016). Article  CAS  Google Scholar  * Drain, D. C. _Handbook of experimental methods for

process improvement_. (Chapman & Hall/CRC Press, New York, 1997). * Tekin, E. et al. Enhanced identification of synergistic and antagonistic emergent interactions among three or more

drugs. _J. R. Soc. Interface_ 13, 20160332 (2016). Article  Google Scholar  * Taylor, M. B. & Ehrenreich, I. M. Transcriptional derepression uncovers cryptic higher-order genetic

interactions. _PLoS Genet._ 11, e1005606 (2015). Article  Google Scholar  * Chou, T.-C. Theoretical basis, experimental design, and computerized simulation of synergism and antagonism in

drug combination studies. _Pharmacol. Rev._ 58, 621–681 (2006). Article  CAS  Google Scholar  * Bliss, C. I. The toxicity of poisons applied jointly. _Ann. Appl. Biol._ 26, 585–615 (1939).

Article  CAS  Google Scholar  * Segre, D., DeLuna, A., Church, G. & Kishony, R. Modular epistasis in yeast metabolism. _Nat. Genet._ 37, 77–83 (2005). Article  CAS  Google Scholar  *

Sanjuán, R. & Elena, S. F. Epistasis correlates to genomic complexity. _Proc. Natl. Acad. Sci._ 103, 14402–14405 (2006). Article  Google Scholar  * Otto-Hanson, L., Grabau, Z., Rosen,

C., Salomon, C. & Kinkel, L. Pathogen variation and urea influence selection and success of Streptomyces mixtures in biological control. _Phytopathology_ 103, 34–42 (2013). Article  CAS

  Google Scholar  * Wood, K. B., Wood, K. C., Nishida, S. & Cluzel, P. Uncovering scaling laws to infer multidrug response of resistant microbes and cancer cells. _Cell Rep._ 6,

1073–1084 (2014). Article  CAS  Google Scholar  * Chait, R., Craney, A. & Kishony, R. Antibiotic interactions that select against resistance. _Nature_ 446, 668–671 (2007). Article  CAS 

Google Scholar  * Bollenbach, T., Quan, S., Chait, R. & Kishony, R. Non-optimal microbial response to antibiotics underlies suppressive drug interactions. _Cell_ 139, 707–718 (2009). *

Sih, A., Englund, G. & Wooster, D. Emergent impacts of multiple predators on prey. _Trends Ecol. Evol._ 13, 350–355 (1998). Article  CAS  Google Scholar  * Flack, J. C., Girvan, M., de

Waal, F. B. & Krakauer, D. C. Policing stabilizes construction of social niches in primates. _Nature_ 439, 426–429 (2006). Article  CAS  Google Scholar  * Yoon, J., Thye, S. R. &

Lawler, E. J. Exchange and cohesion in dyads and triads: a test of Simmel’s hypothesis. _Soc. Sci. Res._ 42, 1457–1466 (2013). Article  Google Scholar  * Scott, G. M. & Kyi, M. S.

_Handbook of essential Antibiotics_. (Harwood Academic, Amsterdam, 2001). * Zhang, J.-H., Chung, T. D. & Oldenburg, K. R. A simple statistical parameter for use in evaluation and

validation of high throughput screening assays. _J. Biomol. Screen._ 4, 67–73 (1999). Article  CAS  Google Scholar  * Yeh, P., Tschumi, A. & Kishony, R. Functional classification of

drugs by properties of their pairwise interactions. _Nat. Genet._ 38, 489–494 (2006). Article  CAS  Google Scholar  * Beppler, C. et al. When more is less: emergent suppressive interactions

in three-drug combinations. _BMC Microbiol._ 17, 107 (2017 Article  Google Scholar  Download references ACKNOWLEDGEMENTS This work was supported by a James F. McDonnell Complex Systems

Scholar Award, an NSF DBI Career award 1254159, a UCLA Faculty Career Development Award, a Hellman Foundation Award, and an NIH/National Center for Advancing Translational Science (NCATS)

UCLA CTSI Grant Number UL1TR001881. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Ecology and Evolutionary Biology, University of California, Los Angeles, CA, 90095, USA Elif

Tekin, Cynthia White, Tina Manzhu Kang, Nina Singh, Van M. Savage & Pamela J. Yeh * Department of Biomathematics, University of California, David Geffen School of Medicine, Los Angeles,

CA, 90095, USA Elif Tekin, Mauricio Cruz-Loya & Van M. Savage * California NanoSystems Institute, University of California, Los Angeles, 570 Westwood Plaza, Los Angeles, CA, 90095, USA

Robert Damoiseaux * Santa Fe Institute, Santa Fe, NM, 87501, USA Van M. Savage & Pamela J. Yeh Authors * Elif Tekin View author publications You can also search for this author inPubMed 

Google Scholar * Cynthia White View author publications You can also search for this author inPubMed Google Scholar * Tina Manzhu Kang View author publications You can also search for this

author inPubMed Google Scholar * Nina Singh View author publications You can also search for this author inPubMed Google Scholar * Mauricio Cruz-Loya View author publications You can also

search for this author inPubMed Google Scholar * Robert Damoiseaux View author publications You can also search for this author inPubMed Google Scholar * Van M. Savage View author

publications You can also search for this author inPubMed Google Scholar * Pamela J. Yeh View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS

E.T., V.M.S, and P.J.Y. conceived of the project and designed the study. C.W. and T.M.K. conducted the experiments, E.T., V.M.S, and M.C.L. devised new theoretical analysis tools. R.D.

contributed experimental reagents and materials. All authors wrote and revised the manuscript. CORRESPONDING AUTHOR Correspondence to Pamela J. Yeh. ETHICS DECLARATIONS COMPETING INTERESTS

The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and

institutional affiliations. ELECTRONIC SUPPLEMENTARY MATERIAL SUPPLEMENTARY INFORMATION DATASET RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons

Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original

author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the

article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use

is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Tekin, E., White, C., Kang, T.M. _et al._ Prevalence and patterns of higher-order

drug interactions in _Escherichia coli_. _npj Syst Biol Appl_ 4, 31 (2018). https://doi.org/10.1038/s41540-018-0069-9 Download citation * Received: 25 December 2017 * Revised: 02 July 2018 *

Accepted: 03 July 2018 * Published: 03 September 2018 * DOI: https://doi.org/10.1038/s41540-018-0069-9 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this

content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative