ABSTRACT Present-day liquid-state lasers are based on organic dyes. Here we demonstrate an alternative class of liquid lasers that use solutions of colloidal quantum dots (QDs). Previous

efforts to realize such devices have been hampered by the fast non-radiative Auger recombination of multicarrier states required for optical gain. Here we overcome this challenge by using

type-(I + II) QDs, which feature a trion-like optical gain state with strongly suppressed Auger recombination. When combined with a Littrow optical cavity, static (non-circulated) solutions

of these QDs exhibit stable lasing tunable from 634 nm to 575 nm. These results indicate the feasibility of technologically viable dye-like QD lasers that exhibit broad spectral tunability

wavelengths that can be selected by controlling the composition, size and structure of the QDs. SIMILAR CONTENT BEING VIEWED BY OTHERS PROSPECTS AND CHALLENGES OF COLLOIDAL QUANTUM DOT LASER

DIODES Article 27 August 2021 COLLOIDAL QUANTUM DOT LASERS Article 15 February 2021 BLUE LASERS USING LOW-TOXICITY COLLOIDAL QUANTUM DOTS Article 01 November 2024 MAIN Chemically prepared

semiconductor nanocrystals, or colloidal quantum dots (QDs), have been actively investigated as optical gain media for solution-processable lasers1,2,3. A majority of the reported studies

have focused on solid-state systems such as close-packed QD films4,5,6,7,8,9. However, there is also a considerable interest in QD-enabled liquid-state lasers, analogous to existing dye

lasers. Although dye lasers are less common than solid-state devices, they remain useful in research and diagnostics10,11,12,13. They are also uniquely suited for application in emerging

areas such as optofluidics14,15. Factors limiting the performance of dye lasers include interference from non-emissive triplet states and material degradation under high pump intensities.

These problems have been typically circumvented using free-floating jet streams. However, this complicates the device, increases its footprint and makes integration with other devices

difficult. QDs are grown in liquid media and can be easily manipulated in solutions like large molecules16. This makes them well suited for the implementation of liquid lasers, which could

potentially solve the problem of the limited stability of traditional dyes. However, initial attempts to realize lasing with solutions of ordinary QDs were not successful1. Although there

are a few reports in the literature regarding amplified spontaneous emission17 (ASE) and microcavity lasing18,19,20 achieved with QD solutions, the initial demonstration of ASE4 as well as

the majority of the reported lasing studies have utilized solid-state QD films. A primary complication in colloidal QD lasing is the fast non-radiative Auger recombination of multicarrier

optical gain states, which competes with stimulated emission and hinders laser action4,21. Since the stimulated emission rate decreases with decreasing QD concentration, fast Auger decay

becomes a particularly serious problem in the case of dilute gain media such as QD solutions. In fact, as established elsewhere4, there is a critical QD concentration (_n_QD,cr) below which

laser action is not possible. It was further found that _n_QD,cr scales inversely with the optical gain relaxation time (_τ_g), which is directly related to the lifetime of a multicarrier

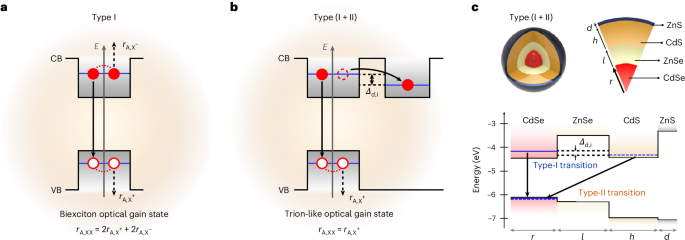
optical gain state. Typically, optical gain in QDs is generated by two electron–hole (e–h) pair states or biexcitons. In standard (non-engineered) QDs, biexciton decay is dominated by

non-radiative Auger recombination, during which the e–h recombination energy is transferred to a third carrier21. Typical timescales of this process are extremely short (tens to hundreds of

picoseconds depending on the QD size21,22), resulting in very short gain lifetimes and correspondingly high _n_QD,cr values (since _n_QD,cr scales as 1/_τ_g), which are difficult to achieve

with liquid QD samples due to solubility limits. Here we resolve the problem of fast Auger decay using type-(I + II) QDs, which exhibit optical gain due to hybrid (direct/indirect)

biexcitons with slow, charged-exciton-like relaxation dynamics. This reduces the critical concentration _n_QD,cr and allows us to realize stable, spectrally tunable liquid-state lasing using

‘static’ (non-circulated) solutions of the type-(I + II) QDs placed in a standard Littrow-type cavity. OPTICAL GAIN DUE TO HYBRID BIEXCITONS As mentioned earlier, most commonly, optical

gain in a QD medium is due to neutral biexcitons (Fig. 1a) whose Auger lifetime (_τ_A,XX) determines the optical gain lifetime. On the basis of the ‘universal’ volume scaling1,22, _τ_A,XX

ranges from ~4 ps to ~100 ps for typical colloidal QD diameters of ~2–6 nm, resulting in very short optical gain relaxation constants. The gain lifetime can be increased by using charged

excitons as optical gain species23. For example, due to the reduction in the number of recombination paths, the Auger lifetime of singly charged excitons (trions) can be four times (or more)

longer than that of biexcitons24. Originally proposed in ref. 25, the charged-exciton gain mechanism has been used to practically demonstrate ‘zero-threshold’ optical gain23,26 and

‘sub-single-exciton’ lasing27. The reported studies used QD films that were charged (doped) electrochemically25,26, photochemically23,27 or chemically28. Here we aim to realize the

charged-exciton gain mechanism in QD solutions using specially designed particles in which biexcitons exhibit characteristics similar to those of charged excitons. The proposed QD design is

shown in Fig. 1b. Along with the primary confinement volume (the ‘direct’ compartment), it contains an additional spatially separated (‘indirect’) electron compartment whose interaction with

the primary volume is controlled by an interfacial potential barrier. The electron energy in the indirect compartment should be slightly lower than that in the primary QD volume, so that a

single e–h pair is easily spatially separated, forming an indirect exciton. In the case of a biexciton, the energetic driving force should still be sufficient to facilitate the transfer of

one electron to the indirect compartment. However, it should not be too large such that the Coulombic effects (attraction to the two holes in the direct compartment and repulsion from an

electron in the indirect compartment) prevent the transfer of the second electron. As a result, the biexciton will be stabilized in a hybrid state consisting of a direct and indirect

exciton. An advantage of the hybrid biexciton for lasing applications is the increased Auger lifetime. For a standard biexciton, Auger decay can be described by a superposition of four

recombination pathways, two associated with the positive trion and two with the negative trion (the rates per pathway are _r_A,X+ and _r_A,X–, respectively)24,29. Therefore, the Auger decay

rate of the biexciton can be expressed as _r_A,XX = 2_r_A,X+ + 2_r_A,X– (Fig. 1a and Extended Data Fig. 1a). For the hybrid biexciton, the Auger dynamics are expected to be dominated by the

carriers located in the direct compartment. Such carriers form a state similar to the positive trion, which decays via a single Auger pathway. Therefore, the decay rate is reduced to _r_A,XX

 = _r_A,X+ (Fig. 1b and Extended Data Fig. 1b). On the basis of these considerations, we hypothesize that by implementing a hybrid biexciton gain scheme, we can increase the gain lifetime

and therefore realize lasing with QD solutions. TYPE-(I + II) QDS To implement the hybrid biexciton scheme, we chose the core/multishell design (Fig. 1c, top). The proposed heterostructure

comprises a CdSe core (direct compartment), a ZnSe shell (barrier layer), a CdS shell (indirect compartment) and a final ZnS layer added to enhance the QD stability. In the barrier layer, we

grade the semiconductor composition using a Cd1–_x_Zn_x_Se alloy for which _x_ increases from 0 to 1 in the radial direction. This helps to inhibit the Auger recombination for both neutral

and charged multicarrier species7 due to the suppression of intraband transition involving the energy-accepting carrier30. For simplicity, we refer to the barrier layer as the ZnSe shell or

ZnSe barrier in this work. The use of a wide-gap ZnSe shell allows us to create a confinement potential for both electron and hole (Fig. 1c, bottom), as required by the scheme shown in Fig.

1b. CdS used in the indirect compartment layer also has a bandgap that is wider than that of CdSe. At the same time, its conduction band edge is close to that of CdSe. Therefore, by changing

the width of the CdS shell, we can fine-tune the energy of the electron in the indirect compartment compared with the energy in the core and consequently realize the desired regime in which

charge transfer is favoured only for one electron of the biexciton state but not for two. When expressed quantitatively, these conditions can be expressed as _Δ_d,i = _E_d – _E_i > 

_k_B_T_, _Δ_dd,id = _E_dd – _E_id > _k_B_T_ and _Δ_id,ii = _E_id – _E_ii < _k_B_T_ (Fig. 2a), hereafter referred to as hybrid biexciton conditions 1–3, respectively. Here _E_d and _E_i

are the energies of direct (Xd) and indirect (Xi) excitons, respectively. _E_dd, _E_ii and _E_id are the energies of all-direct (XdXd), all-indirect (XiXi) and hybrid direct/indirect (XiXd)

biexcitons, respectively. _T_ and _k_B are the temperature and the Boltzmann constant, respectively. To determine the range of QD parameters for which these three conditions can be

satisfied, we applied the effective-mass approximation to calculate the energies of single excitons and biexcitons using the conduction- and valence-band confinement potentials shown in Fig.

1c and taking into account the carrier–carrier Coulomb interactions (Supplementary Note 1)31. The latter is an essential part of the simulation since the ‘giant’ exciton–exciton repulsion

characteristic of an all-indirect biexciton31,32 is required to raise the energy of the XiXi state above the energy of two non-interacting Xi excitons and thus simultaneously satisfy

conditions 1 and 3, leading to stable hybrid biexcitons. Extended Data Fig. 2 shows the region of energetic stability of the hybrid biexciton in the coordinates _l_ (ZnSe barrier width) and

_h_ (CdS shell thickness), calculated for a fixed CdSe core radius (_r_ = 2.6 nm) and a fixed ZnS layer thickness (_d_ = 0.3 nm) at _T_ = 300 K (room temperature). In the same diagram, we

also show the region for which the lowest and first excited e–h (exciton) states are of well-defined indirect and direct characters, respectively, as indicated by the calculated values of

the e–h overlap integral (_θ_eh < 0.1 and _θ_eh > 0.9, respectively). According to this simulation, the realization of hybrid direct/indirect biexcitons requires _l_ of at least ~1.3 

nm and _h_ of at least ~1.8 nm. Typically, QDs are classified as type I if their band-edge transition is associated with a spatially direct exciton and as type II if the band-edge exciton is

spatially indirect. Since the targeted heterostructures are expected to simultaneously support both direct and indirect excitons, we call them type-(I + II) QDs. To realize type-(I + II)

QDs with the desired hybrid biexciton characteristics, we synthesized CdSe/ZnSe/CdS/ZnS samples with _r_ = 2.6 nm, _l_ = 1.7 nm, _h_ = 2.2 nm and _d_ = 0.3 nm (Extended Data Fig. 2a (red

circle); the Methods provides the synthesis details). The transmission electron microscopy images of the synthesized structures are shown in Fig. 2b (final CdSe/ZnSe/CdS/ZnS QDs) and

Extended Data Fig. 3 (final and intermediate structures). The synthesized QDs exhibit excellent monodispersity (size standard deviation, <8%) and show the expected Cd, Zn, S and Se

compositional profiles measured by energy-dispersive X-ray spectroscopy (Extended Data Fig. 3). In Fig. 2c, we show a series of absorption and photoluminescence (PL) spectra of the

structures that occur at different growth stages of the type-(I + II) QDs. The PL spectrum evolves from a spectrally symmetric single-band emission due to e–h radiative recombination in the

CdSe cores (Fig. 2c, black solid line) to a double-hump structure in the case of CdSe/ZnSe/CdS/ZnS QDs (Fig. 2c, red solid line). The emergence of the lower-energy PL feature indicates the

formation of a lower-energy indirect exciton (Xi) consisting of an electron in the CdS shell and a hole in the CdSe core. On the basis of the dual-band deconvolution of the PL spectrum

(Supplementary Fig. 1), the energies of the direct and indirect excitons are 2.02 eV and 1.95 eV, respectively, which satisfy the required condition _E_d – _E_i = 70 meV > _k_B_T_. The

measured values are also in reasonable agreement with those obtained from our simulations (_E_i = 1.99 eV and _E_d = 2.04 eV; Supplementary Note 1 and Supplementary Fig. 2). The dual-exciton

character of the emission of the final hetero-QDs is also evident in the PL excitation measurements (Supplementary Fig. 3) and single-dot PL spectra (Supplementary Fig. 4a). In addition to

its manifestation in the PL and PL excitation spectra, the two-state emission mechanism is evident in the PL dynamics. In particular, PL exhibits double-exponential relaxation in both

ensemble (Fig. 2d) and single-dot (Supplementary Fig. 4b) measurements, which reveal distinct fast (_τ_f,X = 29 ns) and slow (_τ_s,X = 697 ns) components. As expected, the fast signal is

more pronounced in the spectral range of the higher-energy peak associated with the Xd state, whereas the slowly relaxing component is enhanced in the range of the Xi exciton (Fig. 2e). The

measured biexponential PL dynamics and the relative intensities of the Xd and Xi PL features can be quantitatively described using a model of two coupled electron states (related to the

direct and indirect compartments of the QD) emitting via optical transitions involving a common hole state in the direct compartment (Fig. 2d (inset) and Supplementary Note 2). On the basis

of the simulation of the measured PL dynamics (Fig. 2d), the radiative Xd and Xi lifetimes are _τ_d = 44 ns and _τ_i = 735 ns, and the Xd → Xi and Xi → Xd population transfer time constants

are _τ_d-i = 85 ns and _τ_i-d = 8.8 μs. The fact that _τ_d-i is longer than _τ_d is important to explain the discernible PL signal from the Xd state, which is energetically higher than the

Xi state. The above analysis confirms that the prepared QDs indeed simultaneously support direct and indirect excitons, as expected based on their dimensions, which correspond to the type-(I

 + II) region shown in Extended Data Fig. 2 (red circle). Importantly, when we synthesized QD samples whose dimensions were outside the type-(I + II) region, their measured characteristics

were consistent with those of traditional type-I and quasi-type-II QDs31,33 (Extended Data Fig. 2, blue square and black triangle, respectively), which is again in agreement with our

calculations. BIEXCITONS IN TYPE-(I + II) QDS On the basis of the modelling of biexciton states (Supplementary Note 1), the XiXi and XiXd biexcitons in the synthesized type-(I + II) QDs have

comparable energies (4.020 eV and 4.024 eV, respectively), which are considerably lower than the energy of the XdXd biexciton (_E_dd = 4.07 eV). Importantly, all three energies satisfy the

conditions _Δ_dd,id > _k_B_T_ and _Δ_id,ii < _k_B_T_, for which the biexciton emission should be dominated by the hybrid direct/indirect state. Since the XiXd biexciton is anticipated

to emit mainly via the direct transition, its radiative decay should produce an Xi exciton. The same final state is generated by the radiative recombination of the XiXi biexciton. Therefore,

the expected biexciton emission energies are _hv_ii = _E_ii – _E_i = 2.03 eV and _hv_id = _E_id – _E_i = 2.04 eV. Both values are close to the energy of the Xd state (2.04 eV), which is why

the double-hump PL spectrum should be gradually replaced with a narrower single-band spectrum (near the Xd PL feature) as the photoexcited system evolves from the exciton to the biexciton

state with increasing excitation intensity. This expected trend is well expressed in the measured single-dot PL spectra. At low, sub-single-exciton pump levels, the PL line shape indicates

the presence of two distinct transitions due to direct and indirect excitons (Fig. 3a). As the pump level increases, the relative contribution of the lower-energy Xi feature gradually

decreases and the spectra become dominated by a single band located slightly below the Xd energy. At the same time, we detect the expected narrowing of the emission profile from 107 meV to

57 meV. Similar trends are systematically observed for other measured QDs (Extended Data Fig. 4). Due to highly stable (virtually, ‘non-blinking’) single-dot emission (Extended Data Fig. 5),

these trends are consistently reproduced in repeated measurements of the same QD. Although the two biexcitonic components are not easily distinguished in the PL spectra, they appear as

distinct components in the PL time transients. In particular, the single-dot biexciton dynamics (Fig. 3b) exhibit a two-component decay with time constants of 13.5 ns (_τ_f,XX) and 83 ns

(_τ_s,XX), which we attribute to the XiXd and XiXi states, respectively. The fast biexciton PL component is contributed by the recombination of the XiXd state (radiative and Auger) and its

population exchange with the XiXi state. From this, the XiXd recombination time is 13.5 ns or longer, indicating a strong suppression of Auger recombination. In fact, this time constant is

an order of magnitude longer than the biexciton lifetimes previously reported for plain and engineered CdSe-based QDs including continuously graded CdSe/Cd1–_x_Zn_x_Se QDs (cg-QDs)

specifically designed to impede Auger decay7,34 (Fig. 3c). The strong suppression of Auger decay in type-(I + II) QDs is also indicated by the high biexciton emission efficiency (_q_XX). In

particular, _q_XX, determined either from the PL dynamics (Supplementary Note 3) or from single-dot two-photon correlation measurements (Methods), is consistently between ~60% and ~76%.

(Fig. 3d, Supplementary Fig. 5 and Supplementary Table 1). OPTICAL GAIN IN TYPE-(I + II) QDS Due to the hindered Auger decay, type-(I + II) QDs exhibit excellent optical gain properties.

Femtosecond transient absorption (TA) measurements (Methods) show that the optical gain bandwidth reaches ~300 meV at 〈_N_〉 = 34.3 (Fig. 4a; 〈_N_〉 is the average number of e–h pairs

generated per QD per pump pulse), which is similar to the optical gain bandwidth of organic laser dyes35 (Supplementary Table 2). At the same pump level, the gain lifetime is ~3.0 ns (Fig.

4b). This is larger than _τ_g previously observed for quantum-confined CdSe-based nanocrystals, including cg-QD samples (Supplementary Table 1)1,17 and comparable to the _τ_g values of very

large CdS nanocrystals for which Auger decay is absent due to the bulk-like character of the electronic states8. The type-(I + II) QDs also exhibit a large peak material gain reaching 1,110 

cm−1, as indicated by the TA measurements (Fig. 4a and Supplementary Table 1). LIQUID-STATE LASING WITH TYPE-(I + II) QDS The increased optical gain lifetime in type-(I + II) QDs results in

a decrease in the critical concentration required for lasing. In particular, using _τ_g = 3.0 ns, we estimate _n_QD,cr to be ~6 × 1015 cm−3 or ~10 μmol l−1 (Supplementary Note 4)1,36. Such

concentrations are readily available using standard toluene solutions of type-(I + II) QDs. To realize wavelength-tunable liquid-state QD lasing, we use a Littrow-type resonator37 that

includes a highly reflective planar mirror and a reflection grating whose angle controls the cavity resonance (Fig. 5a and Methods). A QD solution with a concentration of 14 μmol l−1

(slightly higher than the estimated _n_QD,cr) loaded into a standard 1-mm-thick quartz cuvette serves as the gain medium. The QDs are excited using 2.33 eV, 5 ns second-harmonic pulses from

a neodymium-doped yttrium aluminium garnet (Nd:YAG) laser. In Fig. 5b, we show the measurements of the output-beam intensity as a function of the per-pulse pump fluence (_J_p) for the

situation in which the cavity is tuned to 1.984 eV. When _J_p reaches 44 mJ cm−2, an intense beam emerges from the cavity. It is highly directional and is detected as a bright spot with a

radius of 1.8 mm at a distance of 2.5 m from the cavity (Fig. 5c). The measurements of beam profile yield a divergence half-angle of _θ_ = 0.66 mrad (or only 0.038°) and a beam waist radius

of _w_0 = 0.28 mm (Fig. 5d). As shown in Fig. 5b (inset), the emitted light is characterized by a narrow linewidth of 2 meV (full-width at half-maximum _Γ_). This value is in agreement with

the measured coherence time (_τ_c) of 0.7 ps (Extended Data Fig. 6), which corresponds to _Γ_ = 1.9 meV (calculated using _Γ_ = _h_/(π_τ_c); _h_ is Planck’s constant). The linewidth can be

further narrowed to 0.38 meV or 1.2 Å (Fig. 5e, inset) by including a beam expander into the cavity, which improves its spectral selectivity by increasing the size of the illuminated region

of the grating. Polarization measurements (Extended Data Fig. 7) show that the emitted light is almost perfectly linearly polarized (~95% degree of polarization) in the direction

perpendicular to the grooves of the Littrow grating. This is a result of the strong dependence of the grating reflectivity on the polarization of the incident light (~80% and ~15% for _p_-

and _s_-polarized light, respectively). The narrow linewidth of the emitted light, low beam divergence and nearly perfect linear polarization clearly indicate the implementation of the

lasing regime. We can exclude that the observed effect is due to ASE as the ASE signal is observed as a broader, low-amplitude spectrally distinct band, the threshold of which exceeds the

lasing threshold (Extended Data Fig. 8). To test for the reproducibility of the laser action, we synthesized and studied three additional batches of type-(I + II) QDs with parameters

nominally identical to those of the QDs shown in Fig. 5b–d. All the additional samples exhibited lasing in the liquid state. Tests of gradually diluted samples showed that stable lasing can

be realized at QD concentrations as low as ~8 μmol l−1, which is close to the calculated _n_QD,cr value (~10 μmol l−1). By changing the grating blaze angle, we can tune the lasing line from

1.96 eV to 2.10 eV (633 nm to 590 nm, respectively; Fig. 5e, coloured lines). The tunability range achieved with a single QD sample simultaneously covers the lasing windows of two popular

laser dyes, rhodamine B and rhodamine 101 (Fig. 5e, black dotted and solid lines, respectively). We can further extend the range of the covered spectral energies by exploiting the bandgap

tunability of QDs by controlling the particle size. In particular, by using type-(I + II) QDs with a smaller CdSe core (_r_ = 2.3 nm) and a correspondingly larger bandgap (2.08 eV; Extended

Data Fig. 9 shows the details of the sample structure and spectroscopic characteristics), we could realize lasing at higher spectral energies (from 2.01 eV to 2.16 eV; Fig. 5e, bottom

panel), which reach the lasing range of rhodamine 6G. Thus, in addition to the broadband spectral tunability realizable with a single QD sample, the QD approach allows for the easy shifting

of the entire lasing window to a desired wavelength range through the easy manipulation of QD size and/or composition. Another useful characteristic of QDs is their high operational

stability, achieved without sample agitation (for example, by stirring or flowing). This is an important advantage compared with laser dyes, which require high-speed circulation for stable

operation. For example, although rhodamine 6G exhibits a lower lasing threshold when used instead of QDs in our Littrow cavity configuration (Supplementary Table 2), its output intensity

degrades rapidly (in less than an hour) even when the device is operated just slightly above the lasing threshold (Extended Data Fig. 10). In contrast, ‘static’ solutions of type-(I + II)

QDs show no signs of degradation over 5 h of continuous operation (Extended Data Fig. 10). At the same time, they exhibit a broader optical gain profile and a wider range of lasing

tunability when compared side by side with rhodamine 6G (Supplementary Table 2). In summary, our results demonstrate the considerable potential of type-(I + II) QDs as a direct alternative

to traditional laser dyes. Importantly, QD lasers do not require the circulation of the gain medium for stable operation. This should simplify the laser design compared with existing

dye-based systems and reduce the device footprint. The elimination of circulation also removes safety concerns due to, for example, accidental splashing, expanding the scope of applications

to areas currently inaccessible to dye lasers due to safety regulations. The additional advantages of QD solutions as liquid optical gain media stem from the unrivalled flexibility of their

chemical properties and optical characteristics. All these features should prompt renewed interest in liquid lasers in the context of both traditional applications (for example, compact

wavelength converters) and emerging technologies including optofluidics, lab-on-a-chip diagnostics and high-contrast sensing and imaging. METHODS CHEMICALS Cadmium oxide (99.5%, trace metals

basis), zinc acetate (99.99%, trace metals basis), oleic acid (OA, 90%, technical grade), 1-octadecene (ODE, 90%, technical grade), 1-octanethiol (≥98.5%), selenium (Se, ≥99.99%, trace

metals basis) and sulfur (S, ≥99.0%) were purchased from Sigma-Aldrich. Tri-_n_-octylphosphine (TOP, 97%) was purchased from Strem Chemicals. All chemicals were used as received. PRECURSOR

PREPARATION All the chemical procedures were conducted in an inert atmosphere using the Schlenk line technique. Before the QD synthesis, stock solutions of 0.5 M zinc oleate, 0.5 M cadmium

oleate (Cd(OA)2), 2 M TOPSe and 2 M TOPS were prepared. For the Zn(OA)2 stock solution, a mixture of 100 mmol zinc acetate and a stoichiometric amount of OA were loaded into a flask and

degassed under a vacuum at 140 °C for 2 h to achieve a clear solution. The flask was then purged with nitrogen, and the precursor concentrations were adjusted to 0.5 M using ODE. These

precursor solutions were stored under an inert atmosphere at 100 °C for future use. To prepare the 0.5 M Cd(OA)2 precursor solution, a combination of 20 mmol cadmium oxide, 20 ml OA and 20 

ml ODE was degassed in a vacuum at 110 °C. The mixture was slowly heated to 300 °C to obtain a transparent solution. The reaction flask was subsequently cooled to 110 °C and vacuum-degassed

again to eliminate any residual water. Stock solutions of 2 M TOPSe and TOPS were prepared by dissolving 100 mmol of Se and S in 50 ml of TOP at an elevated temperature. These stock

solutions were then stored in a glove box for future use. SYNTHESIS OF TYPE-(I + II) QDS Below, we describe a procedure used to prepare type-(I + II) QDs with the following structure: CdSe

(_r_ = 2.6 nm)/ZnSe (_l_ = 1.7 nm)/CdS (_h_ = 2.2 nm)/ZnS (_d_ = 0.3 nm). We started the synthesis by loading 0.1 mmol Cd(OA)2 and 6 ml ODE into a reaction flask. The mixture was degassed

under a vacuum at 110 °C and subsequently filled with nitrogen. After the mixture was heated to 310 °C, 0.2 mmol TOPSe was rapidly injected into the flask, immediately followed by a gradual

dropwise addition of 1 ml TOP. This process led to the formation of CdSe cores with _r_ = 1.5 nm. A further increase in the CdSe core radius to 2.6 nm was achieved by the additional

injection of Cd(OA)2 (0.25 mmol) and TOPSe (0.25 mmol) precursors. To grow a compositionally graded Cd1–_x_Zn_x_Se barrier layer on top of the CdSe cores, a solution containing 0.4 mmol

Zn(OA)2, 0.19 mmol Cd(OA)2 and 0.38 mmol TOPSe was injected at an elevated temperature (310 °C) and allowed to react with the cores for 30 min. An additional dropwise injection of 1.31 mmol

Zn(OA)2 and 1.52 mmol TOPSe was carried out over 30 min, followed by an additional 30 min reaction period to complete the Cd1–_x_Zn_x_Se barrier layer. To grow a CdS layer, 4 mmol

1-octanethiol was slowly added along with the stepwise injection of Cd(OA)2. For growing an exterior ZnS shell, a mixture containing 2 mmol 1-octanethiol and 4 mmol Zn(OA)2 was injected into

the reaction flask. The temperature was then raised to 320 °C and the reaction was allowed to proceed for 1 h. Then, an additional 2 mmol amount of Zn(OA)2 was added, and the reaction

continued for 30 min. After the completion of the reaction, the mixture was cooled to room temperature and the synthesized QDs were purified using precipitation/redispersion with

acetone/toluene. Subsequently, the purified QDs were diluted with toluene for further use. OPTICAL CHARACTERIZATION Optical absorption and steady-state PL spectra of the synthesized QDs were

measured using a Lambda 950 ultraviolet–visible spectrometer (PerkinElmer) and a FluoroMax+ spectrofluorometer (Horiba), respectively. TIME-RESOLVED PL MEASUREMENTS Time-resolved PL spectra

were measured using a streak camera (Hamamatsu C10910). A continuously stirred QD sample in a 1-mm-thick quartz cuvette was excited by 343 nm (3.6 eV), 190 fs pulses of a tripled output of

a regeneratively amplified ytterbium-doped potassium gadolinium tungstate femtosecond laser (PHAROS and HIRO, LIGHT CONVERSION). The pulse repetition rate was 40 kHz. The PL was spectrally

dispersed using a Czerny–Turner spectrograph (Acton 2300i) and sent into the streak camera unit to produce a two-dimensional PL intensity map with time as the vertical axis and spectral

energy as the horizontal axis. Low-jitter, long-delay data were acquired by triggering the streak unit in a dump mode, where the laser 40 kHz pulse picker signal was used to start the

triggering sequence and the first available pulse in the 76 MHz oscillator train was used to generate a stable trigger signal. Using the Hamamatsu slow single-sweep unit, two-dimensional

(spectral energy–time) maps were acquired using different time ranges and incident-pump fluences. In the case of the shortest time range used in the experiments (5 ns), the resolution of the

streak camera was 12 ps, as inferred from the width of an instrument response function obtained using a femtosecond laser pulse as the input signal. TA MEASUREMENTS Purified QDs were loaded

into a 1-mm-thick quartz cuvette and stirred continuously. The TA measurements were performed using a pump–probe setup based on a regeneratively amplified ytterbium-doped potassium

gadolinium tungstate femtosecond laser (PHAROS, LIGHT CONVERSION) generating 190 fs pulses at 1,030 nm with a 500 Hz repetition rate. Half of the laser fundamental output was used to seed a

harmonic generator (HIRO, LIGHT CONVERSION), producing second-harmonic pulses (515 nm or 2.4 eV) used as the pump. The pump beam was modulated using an optical chopper synchronized such that

every other pulse was picked from the pulse sequence. The pump pulses were focused into a 120–150-µm-diameter spot onto the sample. The other half of the fundamental laser output at 1,030 

nm was fed into an optical delay line with an optical path varied from 0 ns to 4 ns. The delayed pulses were tightly focused onto a 5-mm-thick sapphire plate (EKSMA Optics) to generate a

broadband white-light continuum. The generated white light was focused onto the sample into a 90-µm-diameter spot in the middle of the pump spot. The actual pump and probe-beam sizes were

measured at the overlap using a beam profiler. The transmitted white light was detected using an Avantes AvaSpec-Fast ULS1350F-USB2 spectrometer. Pump-induced absorption changes (Δ_α_ = _α_ 

– _α_0) were measured for each pump–probe delay; here _α_ and _α_0 are the absorption coefficients of the excited and unexcited samples, respectively. The correction for the probe chirp

(spectro-temporal broadening) was performed following the procedure described elsewhere42. Excited-state absorption spectra were obtained from _α_ = _α_0 + Δ_α_. The realization of optical

gain was indicated by the emergence of spectral regions in which _α_ was negative. Experimentally, this corresponded to the situation when sample excitation led to absorption bleaching (Δ_α_

 < 0) and the magnitude of the bleach signal was greater than that of linear absorption: |Δ_α_| > _α_0. SINGLE-DOT MEASUREMENTS For single-dot studies, QD samples were prepared as

dilute sub-single-monolayer films (QD areal density, ~0.01 per μm2) deposited onto coverslips via drop casting. The samples were excited using 485 nm light generated by a PicoQuant

LDH-D-C-485 laser diode. The laser operated at either 250 kHz or 500 kHz repetition rate (100 ps pulse duration) or in the continuous-wave (cw) mode. The excitation beam was focused onto the

sample using an Olympus objective lens (×50, 0.70 numerical aperture). The PL signal was collected through the same objective lens. To measure single-dot PL spectra, QD emission was coupled

into an imaging spectrometer (Acton Research, SpectraPro 500i) equipped with a charge-coupled device camera (Princeton Instruments, PYLON). To measure the PL dynamics, QD emission was

spectrally filtered and detected by a pair of avalanche photodiodes (Micro Photon Devices, PDM Series) coupled to a start–stop time correlator (PicoQuant, HydraHarp 400). The temporal

resolution of these measurements was 300 ps. To isolate biexciton decay from single-exciton dynamics, we applied two-photon correlation measurements conducted using the Hanbury Brown–Twiss

(HBT) setup43. In this experiment, the emission from an individual QD is split between two channels equipped with single-photon detectors. Correlations between photon arrival events as a

function of the time difference between the two channels (_τ_) yield information about second-order intensity correlation function _g_(2)(_τ_). In the case of pulsed measurements, a non-zero

_g_(2) signal at _τ_ = 0 implies that one pump pulse produced two photons, that is, the emitting state was a biexciton. Hence, the statistics of the delay of the first detected photon

versus the pump pulse can be used to reconstruct biexciton dynamics. The HBT setup was also used to evaluate the biexciton emission quantum yields _q_XX. The HBT determination of _q_XX uses

the fact that the ratio of the _g_(2) amplitudes for the central (_τ_ = 0) and side (_τ_ = _T_) peaks is determined by the ratio of the biexciton and single-exciton PL quantum yields44,45

(_T_ is the interpulse separation in a pump–pulse sequence). All the measurements were performed at room temperature under ambient conditions. The analysis of the experimental data was

performed using custom-built software developed in Python (v3.9). LIQUID-STATE QD LASER A solution sample of QDs in toluene with a concentration of about 14 µmol l–1 was loaded into a

1-cm-wide, 1-mm-thick quartz cuvette. The cuvette was placed inside a cavity composed of a high-reflectivity mirror and a reflection grating having 2,400 grooves mm–1 (Thorlabs). The wide

side of the cuvette was aligned with the cavity axis. The grating angle was selected to send the first-order (_m_ = 1) diffraction beam back into the cavity (Littrow configuration). The

zeroth-order (_m_ = 0) diffraction was used to outcouple light from the cavity. The cavity resonance was tuned by rotating the grating assembly, which allowed us to tune the output

wavelength. Two intracavity lenses were used to collimate the beam and to ensure uniform illumination on the grating. The QD sample was excited from a wider side of the cuvette using 532 nm,

5 ns second-harmonic pulses of a Nd:YAG laser (Amplitude Laser, Minilite II). The pump beam was shaped as a 1-cm-long, 200-µm-wide horizontal stripe using two cylindrical lenses. The

spectral analysis of the output beam of liquid-state QD lasers was performed using an imaging spectrometer (Acton Research, SpectraPro 500i) paired with a charge-coupled device camera

(Princeton Instruments, PYLON). The spectral resolution of this system was 120 μeV. MEASUREMENTS OF TEMPORAL COHERENCE We used a Michelson interferometer to measure the temporal coherence of

the QD laser output. In these measurements, the beam was split between two channels using a non-polarizing 50/50 beamsplitter. Each channel was equipped with a flat mirror reflecting light

back towards the beamsplitter. One of the mirrors was mounted onto a single-axis linear delay stage (Aerotech ANT130L), which allowed us to control the time delay between the two paths.

After passing the beamsplitter, the two interfering beams were directed along the same path where they were collected using an Olympus PLN ×10 objective used to couple light into a

single-photon avalanche photodiode (Micro Photon Devices, PDM series). To record the intensity of the interference pattern, we used a time-tagged, time-resolved mode provided by a

time-correlated single-photon-counting module (PicoQuant HydraHarp 400). The subsequent analysis of the time-tagged, time-resolved data was performed using a Python code. MEASUREMENTS OF

DIVERGENCE Beam divergence was assessed by measuring the beam radius (_R_beam) with a beam profiler (BladeCam-HR, DataRay). The light intensity profile was recorded as a function of distance

from the cavity (_z_), and the beam halfwidth at the 1/_e_2 intensity level was used as a measure of beam radius. The collected data were fitted to a hyperbolic function _R_beam = _w_0(1 + 

_z_tan(_θ_))0.5, where _θ_ is the divergence half-angle and _w_0 is the beam-waist radius. REPORTING SUMMARY Further information on research design is available in the Nature Portfolio

Reporting Summary linked to this article. DATA AVAILABILITY Source data are provided with this paper. The remaining data are available from the corresponding author upon reasonable request.

REFERENCES * Park, Y.-S., Roh, J., Diroll, B. T., Schaller, R. D. & Klimov, V. I. Colloidal quantum dot lasers. _Nat. Rev. Mater._ 6, 382–401 (2021). Article  CAS  Google Scholar  *

Geiregat, P., Van Thourhout, D. & Hens, Z. A bright future for colloidal quantum dot lasers. _NPG Asia Mater._ 11, 41 (2019). Article  CAS  Google Scholar  * Ahn, N., Livache, C.,

Pinchetti, V. & Klimov, V. I. Colloidal semiconductor nanocrystal lasers and laser diodes. _Chem. Rev._ 123, 8251–8296 (2023). Article  CAS  PubMed  PubMed Central  Google Scholar  *

Klimov, V. I. et al. Optical gain and stimulated emission in nanocrystal quantum dots. _Science_ 290, 314–317 (2000). Article  CAS  PubMed  Google Scholar  * García-Santamaría, F. et al.

Suppressed Auger recombination in ‘giant’ nanocrystals boosts optical gain performance. _Nano Lett._ 9, 3482–3488 (2009). Article  PubMed  PubMed Central  Google Scholar  * Yakunin, S. et

al. Low-threshold amplified spontaneous emission and lasing from colloidal nanocrystals of caesium lead halide perovskites. _Nat. Commun._ 6, 8056 (2015). Article  CAS  PubMed  Google

Scholar  * Lim, J., Park, Y.-S. & Klimov, V. I. Optical gain in colloidal quantum dots achieved by direct-current charge injection. _Nat. Mater._ 17, 42–49 (2018). Article  CAS  PubMed 

Google Scholar  * Tanghe, I. et al. Optical gain and lasing from bulk cadmium sulfide nanocrystals through bandgap renormalization. _Nat. Nanotechnol._ 18, 1423–1429 (2023). Article  CAS 

PubMed  Google Scholar  * Dang, C. et al. Red, green and blue lasing enabled by single-exciton gain in colloidal quantum dot films. _Nat. Nanotechnol._ 7, 335–339 (2012). Article  CAS 

PubMed  Google Scholar  * Nikaido, M., Mizuse, K. & Ohshima, Y. Torsional wave-packet dynamics in 2-fluorobiphenyl investigated by state-selective ionization-detected impulsive

stimulated Rraman spectroscopy. _J. Phys. Chem. A_ 127, 4964–4978 (2023). Article  CAS  PubMed  Google Scholar  * Suryanarayana, M. Isotope separation of 176Lu a precursor to 177Lu medical

isotope using broadband lasers. _Sci. Rep._ 11, 6118 (2021). Article  CAS  PubMed  PubMed Central  Google Scholar  * Tang, R. et al. Candidate for laser cooling of a negative ion:

high-resolution photoelectron imaging of Th−. _Phys. Rev. Lett._ 123, 203002 (2019). Article  CAS  PubMed  Google Scholar  * Henderson, B. W. _Photodynamic Therapy: Basic Principles and

Clinical Applications_. Vol. 1 (CRC Press, 1992). * Li, Z. & Psaltis, D. Optofluidic dye lasers. _Microfluid. Nanofluid._ 4, 145–158 (2008). Article  CAS  Google Scholar  * Schmidt, H.

& Hawkins, A. R. The photonic integration of non-solid media using optofluidics. _Nat. Photon._ 5, 598–604 (2011). Article  CAS  Google Scholar  * Murray, C. B., Norris, D. J. &

Bawendi, M. G. Synthesis and characterization of nearly monodisperse CdE (E = S, Se, Te) semiconductor nanocrystallites. _J. Am. Chem. Soc._ 115, 8706–8715 (1993). Article  CAS  Google

Scholar  * Li, X. et al. Two-color amplified spontaneous emission from Auger-suppressed quantum dots in liquids. _Adv. Mater._ 36, 2308979 (2023). Article  Google Scholar  * Kazes, M.,

Lewis, D. Y., Evenstein, Y., Mokari, T. & Banin, U. Lasing from semiconductor quantum rods in a cylindrical microcavity. _Adv. Mater._ 14, 317–321 (2002). Article  CAS  Google Scholar  *

Wang, Y. et al. Blue liquid lasers from solution of CdZnS/ZnS ternary alloy quantum dots with quasi‐continuous pumping. _Adv. Mater._ 27, 169–175 (2015). Article  CAS  PubMed  Google

Scholar  * Maskoun, J. et al. Optical microfluidic waveguides and solution lasers of colloidal semiconductor quantum wells. _Adv. Mater._ 33, 2007131 (2021). Article  CAS  Google Scholar  *

Klimov, V. I., Mikhailovsky, A. A., McBranch, D. W., Leatherdale, C. A. & Bawendi, M. G. Quantization of multiparticle Auger rates in semiconductor quantum dots. _Science_ 287, 1011–1013

(2000). Article  CAS  PubMed  Google Scholar  * Robel, I., Gresback, R., Kortshagen, U., Schaller, R. D. & Klimov, V. I. Universal size-dependent trend in Auger recombination in

direct-gap and indirect-gap semiconductor nanocrystals. _Phys. Rev. Lett._ 102, 177404 (2009). Article  PubMed  Google Scholar  * Wu, K., Park, Y.-S., Lim, J. & Klimov, V. I. Towards

zero-threshold optical gain using charged semiconductor quantum dots. _Nat. Nanotechnol._ 12, 1140–1147 (2017). Article  CAS  PubMed  Google Scholar  * Wu, K., Lim, J. & Klimov, V. I.

Superposition principle in Auger recombination of charged and neutral multicarrier states in semiconductor quantum dots. _ACS Nano_ 11, 8437–8447 (2017). Article  CAS  PubMed  Google Scholar

  * Wang, C., Wehrenberg, B. L., Woo, C. Y. & Guyot-Sionnest, P. Light emission and amplification in charged CdSe quantum dots. _J. Phys. Chem. B_ 108, 9027–9031 (2004). Article  CAS 

Google Scholar  * Geuchies, J. J. et al. Quantitative electrochemical control over optical gain in quantum-dot solids. _ACS Nano_ 15, 377–386 (2021). Article  CAS  PubMed  Google Scholar  *

Kozlov, O. V. et al. Sub–single-exciton lasing using charged quantum dots coupled to a distributed feedback cavity. _Science_ 365, 672–675 (2019). Article  CAS  PubMed  Google Scholar  *

Whitworth, G. L., Dalmases, M., Taghipour, N. & Konstantatos, G. Solution-processed PbS quantum dot infrared laser with room-temperature tunable emission in the optical

telecommunications window. _Nat. Photon._ 15, 738–742 (2021). Article  CAS  Google Scholar  * Park, Y.-S., Bae, W. K., Pietryga, J. M. & Klimov, V. I. Auger recombination of biexcitons

and negative and positive trions in individual quantum dots. _ACS Nano_ 8, 7288–7296 (2014). Article  CAS  PubMed  Google Scholar  * Cragg, G. E. & Efros, A. L. Suppression of Auger

processes in confined structures. _Nano Lett._ 10, 313–317 (2010). Article  CAS  PubMed  Google Scholar  * Piryatinski, A., Ivanov, S. A., Tretiak, S. & Klimov, V. I. Effect of quantum

and dielectric confinement on the exciton−exciton interaction energy in type II core/shell semiconductor nanocrystals. _Nano Lett._ 7, 108–115 (2007). Article  CAS  PubMed  Google Scholar  *

Klimov, V. I. et al. Single-exciton optical gain in semiconductor nanocrystals. _Nature_ 447, 441–446 (2007). Article  CAS  PubMed  Google Scholar  * Brovelli, S. et al. Nano-engineered

electron–hole exchange interaction controls exciton dynamics in core–shell semiconductor nanocrystals. _Nat. Commun._ 2, 280 (2011). Article  CAS  PubMed  Google Scholar  * Ahn, N. et al.

Electrically driven amplified spontaneous emission from colloidal quantum dots. _Nature_ 617, 79–85 (2023). Article  CAS  PubMed  PubMed Central  Google Scholar  * Schäfer, F. P. _Dye

Lasers_ Vol. 1 (Springer Science & Business Media, 2013). * Park, Y.-S., Bae, W. K., Baker, T., Lim, J. & Klimov, V. I. Effect of Auger recombination on lasing in heterostructured

quantum dots with engineered core/shell interfaces. _Nano Lett._ 15, 7319–7328 (2015). Article  CAS  PubMed  Google Scholar  * Littman, M. G. & Metcalf, H. J. Spectrally narrow pulsed

dye laser without beam expander. _Appl. Opt._ 17, 2224–2227 (1978). Article  CAS  PubMed  Google Scholar  * Pandey, A. & Guyot-Sionnest, P. Multicarrier recombination in colloidal

quantum dots. _J. Chem. Phys._ 127, 111104 (2007). Article  PubMed  Google Scholar  * Fisher, B., Caruge, J.-M., Chan, Y.-T., Halpert, J. & Bawendi, M. G. Multiexciton fluorescence from

semiconductor nanocrystals. _Chem. Phys._ 318, 71–81 (2005). Article  CAS  Google Scholar  * Achermann, M., Hollingsworth, J. A. & Klimov, V. I. Multiexcitons confined within a

subexcitonic volume: spectroscopic and dynamical signatures of neutral and charged biexcitons in ultrasmall semiconductor nanocrystals. _Phys. Rev. B_ 68, 245302 (2003). Article  Google

Scholar  * Park, Y.-S., Lim, J., Makarov, N. S. & Klimov, V. I. Effect of interfacial alloying versus ‘volume scaling’ on Auger recombination in compositionally graded semiconductor

quantum dots. _Nano Lett._ 17, 5607–5613 (2017). Article  CAS  PubMed  Google Scholar  * Livache, C. et al. High-efficiency photoemission from magnetically doped quantum dots driven by

multi-step spin-exchange Auger ionization. _Nat. Photon._ 16, 433–440 (2022). Article  CAS  Google Scholar  * Brown, R. H. & Twiss, R. Q. Correlation between photons in two coherent

beams of light. _Nature_ 177, 27–29 (1956). Article  Google Scholar  * Nair, G., Zhao, J. & Bawendi, M. G. Biexciton quantum yield of single semiconductor nanocrystals from photon

statistics. _Nano Lett._ 11, 1136–1140 (2011). Article  CAS  PubMed  PubMed Central  Google Scholar  * Park, Y. S. et al. Near-unity quantum yields of biexciton emission from CdSe/CdS

nanocrystals measured using single-particle spectroscopy. _Phys. Rev. Lett._ 106, 187401 (2011). Article  PubMed  Google Scholar  * Park, Y.-S., Bae, W. K., Padilha, L. A., Pietryga, J. M.

& Klimov, V. I. Effect of the core/shell interface on Auger recombination evaluated by single-quantum-dot spectroscopy. _Nano Lett._ 14, 396–402 (2014). Article  CAS  PubMed  Google

Scholar  Download references ACKNOWLEDGEMENTS This project was supported by the Laboratory Directed Research and Development (LDRD) program at the Los Alamos National Laboratory under

project no. 20230352ER. V.P. and N.A. acknowledge support from a LANL Director’s Postdoctoral Fellowship. We thank P. R. Bowlan and P. J. Skrodzki for providing access to the Nd:YAG laser

used as a pump source in the QD liquid-state lasing experiments. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Nanotechnology and Advanced Spectroscopy Team, C-PCS, Chemistry Division, Los

Alamos National Laboratory, Los Alamos, NM, USA Donghyo Hahm, Valerio Pinchetti, Clément Livache, Namyoung Ahn, Jungchul Noh, Jun Du, Kaifeng Wu & Victor I. Klimov * State Key Laboratory

of Molecular Reaction Dynamics, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dalian, China Xueyang Li, Jun Du & Kaifeng Wu Authors * Donghyo Hahm View author

publications You can also search for this author inPubMed Google Scholar * Valerio Pinchetti View author publications You can also search for this author inPubMed Google Scholar * Clément

Livache View author publications You can also search for this author inPubMed Google Scholar * Namyoung Ahn View author publications You can also search for this author inPubMed Google

Scholar * Jungchul Noh View author publications You can also search for this author inPubMed Google Scholar * Xueyang Li View author publications You can also search for this author inPubMed

 Google Scholar * Jun Du View author publications You can also search for this author inPubMed Google Scholar * Kaifeng Wu View author publications You can also search for this author

inPubMed Google Scholar * Victor I. Klimov View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS V.I.K. initiated the study and, together with

D.H., conceived the idea of ‘hybrid biexciton’ optical gain. V.I.K. also analysed the data and coordinated the project execution. D.H. and J.N. synthesized the type-(I + II) QDs and

performed their structural analysis. C.L. and V.P. carried out the TA and time-resolved PL measurements. D.H. performed the single-dot spectroscopic measurements of the type-(I + II) QDs and

also conducted the quantum-mechanical calculations of their electronic structures. X.L., J.D. and K.W. performed the initial optical gain and ASE studies of liquid QD suspensions using the

cg-QD samples. V.P., D.H., C.L. and N.A. developed the laser cavity design and performed the liquid-state lasing experiments with type-(I + II) QDs. D.H. and V.I.K. wrote the manuscript with

inputs from all co-authors. CORRESPONDING AUTHOR Correspondence to Victor I. Klimov. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER

REVIEW INFORMATION _Nature Materials_ thanks Uri Banin and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. ADDITIONAL INFORMATION PUBLISHER’S NOTE

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. EXTENDED DATA EXTENDED DATA FIG. 1 APPLICATION OF THE SUPERPOSITION

PRINCIPLE TO AUGER DECAY OF AN ORDINARY (XX) BIEXCITON AND A HYBRID (XIXD) BIEXCITON. A, According to the superposition principle, the Auger decay rate of any multicarrier state can be

presented as the sum of the rates of independent negative and positive trion Auger pathways (rA,X- and rA,X+, respectively)24,29,46. In the case of an ordinary biexciton, there are 2

negative trion pathways and 2 positive trion pathways. Therefore, the overall Auger rate is rA,XX = 2rA,X- + 2rA,X+. B, In the case of a hybrid XiXd biexciton, the pathways involving the

indirect transition can be neglected, leaving only one positive-trion pathway active. This yields rA,XiXd = \({\rm{r}}_{{\rm{A,X}}^+}\) . EXTENDED DATA FIG. 2 MODELING OF ELECTRONIC STATES

AND MEASUREMENTS OF CDSE/ZNSE/CDS/ZNS QDS. A, Calculated band-edge transition energy of the CdSe (_r_ = 2.6 nm)/ZnSe (_l_)/CdS (_h_)/ZnS (_d_ = 0.3 nm) QDs as a function of _l_ and _h_. The

region within the green boundary corresponds to the regime of well-defined indirect and direct exciton states, as indicated by the electron-hole (e-h) overlap integrals (_θ_eh) of <0.1

and >0.9 for the lowest and the first excited e-h states, respectively. The region within the blue boundary corresponds to the regime where we simultaneously satisfy the conditions _Δ_d,i

= _E_d – _E_i > _k_B_T_ and _Δ_id,ii = _E_id – _E_ii < _k_B_T_ (_k_B is the Boltzmann constant and _T_ is the temperature; it is assumed that _T_ is 300 K). According to our

simulations (Supplementary Note 1), this automatically implies that we also satisfy the condition _Δ_dd,id = _E_dd – _E_id > _k_B_T_. Thus, the region highlighted by the diagonal grey

lines corresponds to the QD dimensions for which all requirements necessary for the realization of hybrid direct/indirect biexcitons are satisfied. B-D, Single-dot and ensemble measurements

of three CdSe/ZnSe/CdS/ZnS QD samples, the dimensions of which correspond to three different points in the diagram shown in panel A: (B) red open circle (_l_ = 1.7 nm, _h_ = 2.2 nm; same

sample as in Figs. 2 to 4); (C) blue open square (_l_ = 1.7 nm, _h_ = 0.7 nm); (D) black open triangle (_l_ = 0.9 nm, _h_ = 2.4 nm). The top row shows single-dot second-order intensity

correlation (_g_(2)) measurements. The middle row presents the spectrally integrated ensemble PL dynamics measured using low-intensity (sub-single-exciton) pulsed excitation with a photon

energy of 2.54 eV. The bottom presents the ensemble PL spectra of the QDs obtained using low-intensity _cw_ excitation with a photon energy of 2.76 eV. The observed characteristics of the

samples shown in panels C and D are consistent with those of type-I and quasi-type-II QDs31,33, respectively. EXTENDED DATA FIG. 3 STRUCTURAL CHARACTERISTICS OF FINAL TYPE-(I+II) QDS AND

INTERMEDIATE STRUCTURES. A-D, Transmission electron microscope (TEM) images illustrating the progression of the synthesis of the type-(I+II) CdSe (_r_ = 2.6 nm)/ZnSe (_l_ = 1.7 nm)/CdS (_h_

= 2.2 nm)/ZnS (_d_ = 0.3 nm) QDs: (A) CdSe cores, (B) CdSe/ZnSe QDs, (C) CdSe/ZnSe/CdS QDs, and (D) final CdSe/ZnSe/CdS/ZnS QDs. E, Scanning transmission electron microscope (STEM) image of

type-(I+II) QDs. Scale bar is 10 nm. F, Energy-dispersive X-ray spectroscopy (EDS) elemental maps for Se (magenta), S (blue), Cd (green), and Zn (red). G, Elemental radial profiles extracted

from EDS maps for the region shown in panel E by the dashed box. EXTENDED DATA FIG. 4 PL SPECTRA OF INDIVIDUAL TYPE-(I+II) QDS AT DIFFERENT PUMP INTENSITIES. Representative measurements of

single-dot PL spectra for 5 individual type-(I+II) QDs conducted using _cw_ excitation with a photon energy of 2.54 eV and an intensity of 5.6, 61 and 570 W cm−2. The PL spectrum with the

lowest pump intensity is presented as a sum of two Gaussian bands describing the emission spectra of direct and indirect excitons (narrower and wider bands, respectively). EXTENDED DATA FIG.

5 SINGLE-DOT PL INTENSITY TRAJECTORIES OF TYPE-(I+II) QDS. A-C, Single-dot PL trajectories (left panels) and corresponding histograms (right panels) measured for an individual type-(I+II)

QD using _cw_ excitation with a photon energy of 2.54 eV and different pump intensities: (A) 570 W cm−2, (B) 61 W cm−2, and (C) 5.6 W cm−2. EXTENDED DATA FIG. 6 MEASUREMENTS OF TEMPORAL

COHERENCE OF A LASER BEAM USING MICHELSON INTERFEROMETRY. The fringe visibility as a function of the time delay between the two interferometer arms (blue points) is fitted to the

biexponential decay (red line). The time constant of the longer-lived component is ~700 fs. The inset shows a representative interferogram. EXTENDED DATA FIG. 7 POLARIZATION MEASUREMENTS OF

A LASER BEAM. The emission intensity collected through a linear polarizer as a function of the polarizer angle (green circles) shown using polar coordinates. The dotted line represents the

ideal sin2(_α_) dependence expected for a perfectly linearly polarized beam. These measurements indicate a high degree of linear polarization of 0.95. EXTENDED DATA FIG. 8 LASING VERSUS ASE.

a, Representative spectrum of a liquid laser based on type-(I+II) CdSe QDs with _r_ = 2.6 nm, _l_ = 1.7 nm, _h_ = 2.2 nm, and _d_ = 0.3 nm. The narrow line at 1.952 eV is due to lasing, and

the broader band at 1.97 eV is due to ASE. The amplitude of the ASE band is more than two orders of magnitude smaller than the amplitude of the lasing line (the vertical axis is

logarithmic). The QD gain medium is excited using second harmonic pulses of a Nd:YAG laser (photon energy 2.33 eV, pulse duration 5 ns, repetition rate 10 Hz). B, The ASE signal intensity as

a function of pump level indicates an ASE threshold of 89 mJ cm−2. This is approximately twice the lasing threshold. EXTENDED DATA FIG. 9 PL AND OPTICAL GAIN CHARACTERISTICS OF

WIDER-BANDGAP TYPE-(I+II) QDS. A, PL spectrum of type-(I+II) CdSe QDs with _r_ = 2.3 nm, _l_ = 2.2 nm, _h_ = 1.6 nm, and _d_ = 0.3 nm. The experimental data are shown as open grey circles,

and the double Gaussian fit is shown as a black line. The two individual Gaussian bands used in the fit are shown as blue and orange lines. The PL spectrum was measured using _cw_ excitation

with a photon energy of 2.76 eV. B, PL dynamics of the same sample collected for two different pump levels: 〈_N_〉 = 0.08 (black) and 0.38 (red) (the traces are normalized to match the

signal intensity at 500 ns). The biexciton dynamics obtained by subtracting these two traces are shown as blue circles. A biexponential fit (blue line) yields a hybrid (direct/indirect)

biexciton lifetime of 10.1 ns. The sample was excited using 190 fs, 3.1 eV pulses. C, The TA spectrum of wider bandgap type-(I+II) QDs presented as the excited state absorption coefficient

(_α_) for a pump-probe delay of 10 ps and an excitation level 〈_N_〉 = 54 (190 fs, 2.4 eV pump pulses). The optical gain regime corresponds to _α_ < 0. D, The TA dynamics yields an optical

gain lifetime of 3.1 ns. EXTENDED DATA FIG. 10 COMPARISON OF OPERATIONAL STABILITY OF LASERS BASED ON TYPE-(I+II) QDS AND RHODAMINE 6G DYE. Comparison of laser output intensity as a

function of time for a solution of type-(I+II) QDs (_r_ = 2.6 nm, _l_ = 1.7 nm, _h_ = 2.2 nm, and _d_ = 0.3 nm) (blue circles) and rhodamine 6G dye (pale red and red squares). In both cases,

the gain medium was excited by 532 nm, 5 ns, 10 Hz second harmonic pulses of a Nd:YAG laser. The QDs were dispersed in toluene, and rhodamine 6G was dissolved in a mixture of methanol and

ethylene glycol (5:95 %, v/v). During the measurements, both solutions were in ‘static form’, that is, they were not stirred, flowed or otherwise agitated. During the stability test, the

type-(I+II) QDs were excited using a per-pulse fluence of approximately 50 mJ cm−2. The rhodamine 6G dye was excited using a per-pulse fluence of 15 mJ cm−2 (pale red) and 50 mJ cm−2 (red);

the former intensity corresponded to excitation near the lasing threshold (14 mJ cm−2). The dye laser output intensity decreased continuously during the test. The initial rapid decay could

be fitted to an exponential relaxation with a time constant of 30 min. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION Supplementary Notes 1–4, Figs. 1–5 and Tables 1 and 2. REPORTING

SUMMARY SOURCE DATA SOURCE DATA FIG. 2 Raw data for Fig. 2c–e. SOURCE DATA FIG. 3 Raw data for Fig. 3a–c. SOURCE DATA FIG. 4 Raw data for Fig. 4a,b. SOURCE DATA FIG. 5 Raw data for Fig.

5b–e. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial

use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons

licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or

other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in

the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the

copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Hahm, D., Pinchetti,

V., Livache, C. _et al._ Colloidal quantum dots enable tunable liquid-state lasers. _Nat. Mater._ 24, 48–55 (2025). https://doi.org/10.1038/s41563-024-02048-y Download citation * Received:

15 January 2024 * Accepted: 11 October 2024 * Published: 22 November 2024 * Issue Date: January 2025 * DOI: https://doi.org/10.1038/s41563-024-02048-y SHARE THIS ARTICLE Anyone you share the

following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer

Nature SharedIt content-sharing initiative