Play all audios:
ABSTRACT Fractionalization is a phenomenon in which strong interactions in a quantum system drive the emergence of excitations with quantum numbers that are absent in the building blocks.
Outstanding examples are excitations with charge _e_/3 in the fractional quantum Hall effect1,2, solitons in one-dimensional conducting polymers3,4 and Majorana states in topological
superconductors5. Fractionalization is also predicted to manifest itself in low-dimensional quantum magnets, such as one-dimensional antiferromagnetic _S_ = 1 chains. The fundamental
features of this system are gapped excitations in the bulk6 and, remarkably, _S_ = 1/2 edge states at the chain termini7,8,9, leading to a four-fold degenerate ground state that reflects the
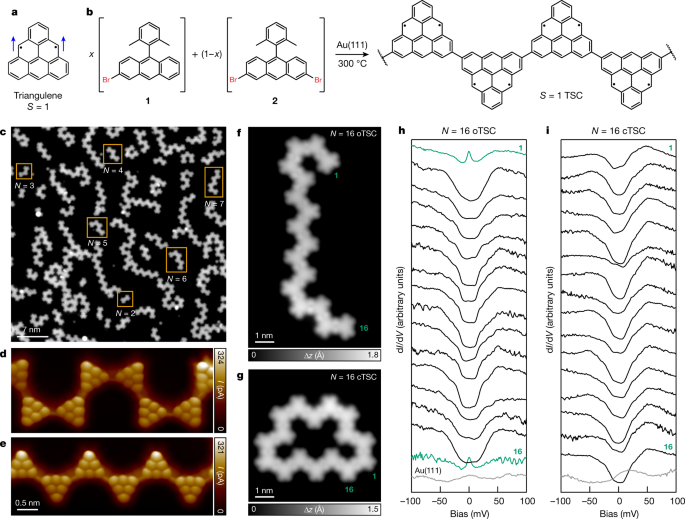
underlying symmetry-protected topological order10,11. Here, we use on-surface synthesis12 to fabricate one-dimensional spin chains that contain the _S_ = 1 polycyclic aromatic hydrocarbon
triangulene as the building block. Using scanning tunnelling microscopy and spectroscopy at 4.5 K, we probe length-dependent magnetic excitations at the atomic scale in both open-ended and
cyclic spin chains, and directly observe gapped spin excitations and fractional edge states therein. Exact diagonalization calculations provide conclusive evidence that the spin chains are
described by the _S_ = 1 bilinear-biquadratic Hamiltonian in the Haldane symmetry-protected topological phase. Our results open a bottom-up approach to study strongly correlated phases in
purely organic materials, with the potential for the realization of measurement-based quantum computation13. Access through your institution Buy or subscribe This is a preview of
subscription content, access via your institution ACCESS OPTIONS Access through your institution Access Nature and 54 other Nature Portfolio journals Get Nature+, our best-value
online-access subscription $29.99 / 30 days cancel any time Learn more Subscribe to this journal Receive 51 print issues and online access $199.00 per year only $3.90 per issue Learn more
Buy this article * Purchase on SpringerLink * Instant access to full article PDF Buy now Prices may be subject to local taxes which are calculated during checkout ADDITIONAL ACCESS OPTIONS:
* Log in * Learn about institutional subscriptions * Read our FAQs * Contact customer support SIMILAR CONTENT BEING VIEWED BY OTHERS TUNABLE TOPOLOGICAL PHASES IN NANOGRAPHENE-BASED SPIN-1/2
ALTERNATING-EXCHANGE HEISENBERG CHAINS Article 28 October 2024 SPIN EXCITATIONS IN NANOGRAPHENE-BASED ANTIFERROMAGNETIC SPIN-1/2 HEISENBERG CHAINS Article Open access 14 March 2025 HIGHLY
ENTANGLED POLYRADICAL NANOGRAPHENE WITH COEXISTING STRONG CORRELATION AND TOPOLOGICAL FRUSTRATION Article 19 February 2024 DATA AVAILABILITY The data that support the findings of this study
are available at the Materials Cloud platform (https://doi.org/10.24435/materialscloud:e8-aq). CODE AVAILABILITY The custom-designed Python codes that were used for solving the
bilinear-biquadratic spin Hamiltonian by exact diagonalization are available on the GitHub repository (https://github.com/GCatarina/ED_BLBQ). All other codes are available from J.F.R.
([email protected]) upon reasonable request. CHANGE HISTORY * _ 03 NOVEMBER 2021 A Correction to this paper has been published: https://doi.org/10.1038/s41586-021-04150-6 _
REFERENCES * Tsui, D. C., Stormer, H. L. & Gossard, A. C. Two-dimensional magnetotransport in the extreme quantum limit. _Phys. Rev. Lett._ 48, 1559–1562 (1982). Article ADS CAS
Google Scholar * Laughlin, R. B. Anomalous quantum hall effect: an incompressible quantum fluid with fractionally charged excitations. _Phys. Rev. Lett._ 50, 1395–1398 (1983). Article ADS
Google Scholar * Jackiw, R. & Rebbi, C. Solitons with fermion number 1/2. _Phys. Rev. D_ 13, 3398–3409 (1976). Article ADS MathSciNet CAS Google Scholar * Su, W. P., Schrieffer,
J. R. & Heeger, A. J. Solitons in Polyacetylene. _Phys. Rev. Lett._ 42, 1698–1701 (1979). Article ADS CAS Google Scholar * Kitaev, A. Unpaired Majorana fermions in quantum wires.
_Phys.-Uspekhi_ 44, 131–136 (2001). Article ADS Google Scholar * Haldane, F. D. M. Nonlinear field theory of large-spin Heisenberg antiferromagnets: semiclassically quantized solitons of
the one-dimensional easy-axis Néel state. _Phys. Rev. Lett._ 50, 1153–1156 (1983). Article MathSciNet Google Scholar * Affleck, I., Kennedy, T., Lieb, E. H. & Tasaki, H. Rigorous
results on valence-bond ground states in antiferromagnets. _Phys. Rev. Lett._ 59, 799–802 (1987). Article ADS CAS PubMed Google Scholar * Kennedy, T. Exact diagonalisations of open
spin-1 chains. _J. Phys. Condens. Matter_ 2, 5737–5745 (1990). Article ADS Google Scholar * White, S. R. & Huse, D. A. Numerical renormalization-group study of low-lying eigenstates
of the antiferromagnetic _S_=1 Heisenberg chain. _Phys. Rev. B_ 48, 3844–3852 (1993). Article ADS CAS Google Scholar * Gu, Z.-C. & Wen, X.-G. Tensor-entanglement-filtering
renormalization approach and symmetry-protected topological order. _Phys. Rev. B_ 80, 155131 (2009). Article ADS Google Scholar * Pollmann, F., Berg, E., Turner, A. M. & Oshikawa, M.
Symmetry protection of topological phases in one-dimensional quantum spin systems. _Phys. Rev. B_ 85, 075125 (2012). Article ADS Google Scholar * Clair, S. & de Oteyza, D. G.
Controlling a chemical coupling reaction on a surface: tools and strategies for on-surface synthesis. _Chem. Rev._ 119, 4717–4776 (2019). Article CAS PubMed PubMed Central Google Scholar
* Wei, T.-C., Affleck, I. & Raussendorf, R. Two-dimensional Affleck-Kennedy-Lieb-Tasaki state on the honeycomb lattice is a universal resource for quantum computation. _Phys. Rev. A_
86, 032328 (2012). Article ADS Google Scholar * Bethe, H. Zur Theorie der Metalle. _Z. Physik_ 71, 205–226 (1931). Article ADS CAS MATH Google Scholar * Renard, J.-P., Regnault,
L.-P. & Verdaguer, M. in _Magnetism: Molecules to Materials I: Models and Experiments_ (eds. Miller, J. S. & Drillon, M.) 49–93 (John Wiley & Sons, 2001). * Soe, W.-H., Manzano,
C., De Sarkar, A., Chandrasekhar, N. & Joachim, C. Direct observation of molecular orbitals of pentacene physisorbed on Au(111) by scanning tunneling microscope. _Phys. Rev. Lett._ 102,
176102 (2009). Article ADS PubMed Google Scholar * Hirjibehedin, C. F., Lutz, C. P. & Heinrich, A. J. Spin coupling in engineered atomic structures. _Science_ 312, 1021–1024 (2006).
Article ADS CAS PubMed Google Scholar * Choi, D.-J. et al. Colloquium: atomic spin chains on surfaces. _Rev. Mod. Phys._ 91, 041001 (2019). Article ADS CAS Google Scholar *
Toskovic, R. et al. Atomic spin-chain realization of a model for quantum criticality. _Nat. Phys._ 12, 656–660 (2016). Article CAS Google Scholar * Yang, K. et al. Probing resonating
valence bond states in artificial quantum magnets. _Nat. Commun._ 12, 993 (2021). Article ADS CAS PubMed PubMed Central Google Scholar * Delgado, F., Batista, C. D. &
Fernández-Rossier, J. Local probe of fractional edge states of _S_ = 1 Heisenberg spin chains. _Phys. Rev. Lett._ 111, 167201 (2013). Article ADS CAS PubMed Google Scholar * Lieb, E. H.
Two theorems on the Hubbard model. _Phys. Rev. Lett._ 62, 1201–1204 (1989). Article ADS MathSciNet CAS PubMed Google Scholar * Fernández-Rossier, J. & Palacios, J. J. Magnetism in
graphene nanoislands. _Phys. Rev. Lett._ 99, 177204 (2007). Article ADS PubMed Google Scholar * Clar, E. & Stewart, D. G. Aromatic hydrocarbons. LXV. Triangulene derivatives1. _J.
Am. Chem. Soc._ 75, 2667–2672 (1953). Article CAS Google Scholar * Goto, K. et al. A stable neutral hydrocarbon radical: synthesis, crystal structure, and physical properties of
2,5,8-tri-_tert_-butyl-phenalenyl. _J. Am. Chem. Soc._ 121, 1619–1620 (1999). Article CAS Google Scholar * Inoue, J. et al. The first detection of a Clar’s hydrocarbon,
2,6,10-tri-_tert_-butyltriangulene: a ground-state triplet of non-Kekulé polynuclear benzenoid hydrocarbon. _J. Am. Chem. Soc._ 123, 12702–12703 (2001). Article CAS PubMed Google Scholar
* Pavliček, N. et al. Synthesis and characterization of triangulene. _Nat. Nanotechnol._ 12, 308–311 (2017). Article ADS PubMed Google Scholar * Mishra, S. et al. Synthesis and
characterization of π-extended triangulene. _J. Am. Chem. Soc._ 141, 10621–10625 (2019). Article CAS PubMed Google Scholar * Su, J. et al. Atomically precise bottom-up synthesis of
π-extended [5]triangulene. _Sci. Adv._ 5, eaav7717 (2019). Article ADS CAS PubMed PubMed Central Google Scholar * Mishra, S. et al. Synthesis and characterization of [7]triangulene.
_Nanoscale_ 13, 1624–1628 (2021). Article CAS PubMed Google Scholar * Mishra, S. et al. Collective all-carbon magnetism in triangulene dimers. _Angew. Chem. Int. Ed._ 59, 12041–12047
(2020). Article CAS Google Scholar * Lado, J. L. & Fernández-Rossier, J. Magnetic edge anisotropy in graphenelike honeycomb crystals. _Phys. Rev. Lett._ 113, 027203 (2014). Article
ADS CAS PubMed Google Scholar * Ternes, M., Heinrich, A. J. & Schneider, W.-D. Spectroscopic manifestations of the Kondo effect on single adatoms. _J. Phys. Condens. Matter_ 21,
053001 (2008). Article ADS PubMed Google Scholar * Li, J. et al. Single spin localization and manipulation in graphene open-shell nanostructures. _Nat. Commun._ 10, 200 (2019). Article
ADS PubMed PubMed Central Google Scholar * Mishra, S. et al. Topological frustration induces unconventional magnetism in a nanographene. _Nat. Nanotechnol._ 15, 22–28 (2020). Article
ADS CAS PubMed Google Scholar * Ortiz, R. & Fernández-Rossier, J. Probing local moments in nanographenes with electron tunneling spectroscopy. _Progr. Surf. Sci._ 95, 100595 (2020).
Article CAS Google Scholar * Oberg, J. C. et al. Control of single-spin magnetic anisotropy by exchange coupling. _Nat. Nanotechnol._ 9, 64–68 (2014). Article ADS CAS PubMed Google
Scholar * Jacob, D., Ortiz, R. & Fernández-Rossier, J. Renormalization of spin excitations and Kondo effect in open-shell nanographenes. _Phys. Rev. B_ 104, 075404 (2021). Article ADS
CAS Google Scholar * Li, J. et al. Uncovering the triplet ground state of triangular graphene nanoflakes engineered with atomic precision on a metal surface. _Phys. Rev. Lett._ 124,
177201 (2020). Article ADS CAS PubMed Google Scholar * Savary, L. & Balents, L. Quantum spin liquids: a review. _Rep. Prog. Phys._ 80, 016502 (2016). Article ADS PubMed Google
Scholar * Georgescu, I. M., Ashhab, S. & Nori, F. Quantum simulation. _Rev. Mod. Phys._ 86, 153–185 (2014). Article ADS Google Scholar * Hieulle, J. et al. On-surface synthesis and
collective spin excitations of a triangulene-based nanostar. _Angew. Chem. Int. Ed._ https://doi.org/10.1002/anie.202108301 (2021). * Giannozzi, P. et al. Quantum ESPRESSO toward the
exascale. _J. Chem. Phys._ 152, 154105 (2020). Article ADS CAS PubMed Google Scholar * Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple.
_Phys. Rev. Lett._ 77, 3865–3868 (1996). Article ADS CAS PubMed Google Scholar * Lejaeghere, K. et al. Reproducibility in density functional theory calculations of solids. _Science_
351, aad3000 (2016). Article PubMed Google Scholar * Hutter, J., Iannuzzi, M., Schiffmann, F. & VandeVondele, J. CP2K: atomistic simulations of condensed matter systems. _Wiley
Interdiscip. Rev. Comput. Mol. Sci._ 4, 15–25 (2014). Article CAS Google Scholar * Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization
of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. _J. Chem. Phys._ 132, 154104 (2010). Article ADS PubMed Google Scholar * Goedecker, S., Teter, M. &
Hutter, J. Separable dual-space Gaussian pseudopotentials. _Phys. Rev. B_ 54, 1703–1710 (1996). Article ADS CAS Google Scholar * VandeVondele, J. & Hutter, J. Gaussian basis sets for
accurate calculations on molecular systems in gas and condensed phases. _J. Chem. Phys._ 127, 114105 (2007). Article ADS PubMed Google Scholar * Wilhelm, J., Del Ben, M. & Hutter,
J. GW in the Gaussian and plane waves scheme with application to linear acenes. _J. Chem. Theory Comput._ 12, 3623–3635 (2016). Article CAS PubMed Google Scholar * Neaton, J. B.,
Hybertsen, M. S. & Louie, S. G. Renormalization of molecular electronic levels at metal-molecule interfaces. _Phys. Rev. Lett._ 97, 216405 (2006). Article ADS CAS PubMed Google
Scholar * Kharche, N. & Meunier, V. Width and crystal orientation dependent band gap renormalization in substrate-supported graphene nanoribbons. _J. Phys. Chem. Lett._ 7, 1526–1533
(2016). Article CAS PubMed Google Scholar * Yakutovich, A. V. et al. AiiDAlab – an ecosystem for developing, executing, and sharing scientific workflows. _Comput. Mater. Sci._ 188,
110165 (2021). Article CAS Google Scholar * Ortiz, R. et al. Exchange rules for diradical π-conjugated hydrocarbons. _Nano Lett._ 19, 5991–5997 (2019). Article ADS CAS PubMed Google
Scholar * Tran, V.-T., Saint-Martin, J., Dollfus, P. & Volz, S. Third nearest neighbor parameterized tight binding model for graphene nano-ribbons. _AIP Adv._ 7, 075212 (2017). Article
ADS Google Scholar * Fishman, M., White, S. R. & Stoudenmire, E. M. The ITensor software library for tensor network calculations. Preprint at https://arxiv.org/abs/2007.14822 (2020).
* Weinberg, P. & Bukov, M. QuSpin: a Python package for dynamics and exact diagonalisation of quantum many body systems part I: spin chains. _SciPost Phys._ 2, 003 (2017). Article ADS
Google Scholar * Weinberg, P. & Bukov, M. QuSpin: a Python package for dynamics and exact diagonalisation of quantum many body systems. Part II: bosons, fermions and higher spins.
_SciPost Phys._ 7, 020 (2019). Article ADS CAS Google Scholar * Fernández-Rossier, J. Theory of single-spin inelastic tunneling spectroscopy. _Phys. Rev. Lett._ 102, 256802 (2009).
Article ADS PubMed Google Scholar * Spinelli, A., Bryant, B., Delgado, F., Fernández-Rossier, J. & Otte, A. F. Imaging of spin waves in atomically designed nanomagnets. _Nat. Mater._
13, 782–785 (2014). Article ADS CAS PubMed Google Scholar * Coleman, P. New approach to the mixed-valence problem. _Phys. Rev. B_ 29, 3035–3044 (1984). Article ADS CAS Google
Scholar * Jacob, D. & Kurth, S. Many-body spectral functions from steady state density functional theory. _Nano Lett._ 18, 2086–2090 (2018). Article ADS CAS PubMed Google Scholar *
Jacob, D. Simulation of inelastic spin flip excitations and Kondo effect in STM spectroscopy of magnetic molecules on metal substrates. _J. Phys. Condens. Matter_ 30, 354003 (2018). Article
PubMed Google Scholar * Jacob, D. & Fernández-Rossier, J. Competition between quantum spin tunneling and Kondo effect. _Eur. Phys. J. B_ 89, 210 (2016). Article ADS MathSciNet
Google Scholar Download references ACKNOWLEDGEMENTS We thank O. Gröning and J. C. Sancho-García for fruitful discussions. This work was supported by the Swiss National Science Foundation
(grant numbers 200020-182015 and IZLCZ2-170184), the NCCR MARVEL funded by the Swiss National Science Foundation (grant number 51NF40-182892), the European Union’s Horizon 2020 research and
innovation program (grant number 881603, Graphene Flagship Core 3), the Office of Naval Research (N00014-18-1-2708), ERC Consolidator grant (T2DCP, grant number 819698), the German Research
Foundation within the Cluster of Excellence Center for Advancing Electronics Dresden (cfaed) and EnhanceNano (grant number 391979941), the Basque Government (grant number IT1249-19), the
Generalitat Valenciana (Prometeo2017/139), the Spanish Government (grant number PID2019-109539GB-C41), and the Portuguese FCT (grant number SFRH/BD/138806/2018). Computational support from
the Swiss Supercomputing Center (CSCS) under project ID s904 is gratefully acknowledged. AUTHOR INFORMATION Author notes * Shantanu Mishra Present address: IBM Research—Zurich, Rüschlikon,
Switzerland * These authors contributed equally: Shantanu Mishra and Gonçalo Catarina AUTHORS AND AFFILIATIONS * Empa—Swiss Federal Laboratories for Materials Science and Technology,
Dübendorf, Switzerland Shantanu Mishra, Kristjan Eimre, Carlo A. Pignedoli, Pascal Ruffieux & Roman Fasel * International Iberian Nanotechnology Laboratory, Braga, Portugal Gonçalo
Catarina & Joaquín Fernández-Rossier * University of Alicante, Sant Vicent del Raspeig, Spain Gonçalo Catarina & Ricardo Ortiz * Technical University of Dresden, Dresden, Germany
Fupeng Wu, Ji Ma & Xinliang Feng * University of the Basque Country, San Sebastián, Spain David Jacob * IKERBASQUE, Basque Foundation for Science, Bilbao, Spain David Jacob * Max Planck
Institute of Microstructure Physics, Halle, Germany Xinliang Feng * University of Bern, Bern, Switzerland Roman Fasel Authors * Shantanu Mishra View author publications You can also search
for this author inPubMed Google Scholar * Gonçalo Catarina View author publications You can also search for this author inPubMed Google Scholar * Fupeng Wu View author publications You can
also search for this author inPubMed Google Scholar * Ricardo Ortiz View author publications You can also search for this author inPubMed Google Scholar * David Jacob View author
publications You can also search for this author inPubMed Google Scholar * Kristjan Eimre View author publications You can also search for this author inPubMed Google Scholar * Ji Ma View
author publications You can also search for this author inPubMed Google Scholar * Carlo A. Pignedoli View author publications You can also search for this author inPubMed Google Scholar *
Xinliang Feng View author publications You can also search for this author inPubMed Google Scholar * Pascal Ruffieux View author publications You can also search for this author inPubMed
Google Scholar * Joaquín Fernández-Rossier View author publications You can also search for this author inPubMed Google Scholar * Roman Fasel View author publications You can also search for
this author inPubMed Google Scholar CONTRIBUTIONS X.F., P.R. and R.F. conceived the project. F.W. and J.M. synthesized and characterized the precursor molecules. S.M. performed the
on-surface synthesis, and STM and STS measurements. G.C., R.O. and J.F.R. performed the tight-binding, CAS, ED and DMRG calculations. D.J. performed the MOAM-NCA calculations. K.E. and
C.A.P. performed the DFT and _GW_ calculations. All authors contributed toward writing the manuscript. CORRESPONDING AUTHORS Correspondence to Xinliang Feng, Pascal Ruffieux or Joaquín
Fernández-Rossier. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PEER REVIEW INFORMATION _Nature_ thanks Berthold Jäck, Yi Zhou
and the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available. PUBLISHER’S NOTE Springer Nature remains neutral with regard to
jurisdictional claims in published maps and institutional affiliations. EXTENDED DATA FIGURES AND TABLES EXTENDED DATA FIG. 1 SCANNING TUNNELLING SPECTROSCOPY MEASUREMENTS OF THE FRONTIER
BANDS OF TRIANGULENE SPIN CHAINS. A, B, d_I_/d_V_ spectroscopy on TSCs with _cis_ (A) and _trans_ (B) intertriangulene bonding configurations (open feedback parameters: _V_ = −1.5 V, _I_ =
250 pA; _V_rms = 16 mV). Acquisition positions are marked with filled circles in C, D. Irrespective of the bonding configuration, TSCs exhibit an electronic band gap of 1.6 eV. C, D,
High-resolution STM images (top panels), and constant-current d_I_/d_V_ maps of the valence (middle panels) and conduction (bottom panels) bands of _cis_ (C) and _trans_ (D) TSCs. Scanning
parameters: _V_ = −0.4 V, _I_ = 250 pA (top and middle panels, C, D) and _V_ = 1.1 V, _I_ = 280 pA (bottom panels, C, D); _V_rms = 30 mV. All measurements were performed with a CO
functionalized tip. EXTENDED DATA FIG. 2 GAS-PHASE DENSITY FUNCTIONAL THEORY CALCULATIONS ON TRIANGULENE SPIN CHAINS. A, E, DFT band structure and density of states (DOS) plots of TSCs with
_cis_ (A) and _trans_ (E) intertriangulene bonding configurations in their antiferromagnetic ground state. Energies _E_ are given with respect to the vacuum level. A Gaussian broadening of
100 meV has been applied to the DOS plots. Note that spin up and spin down bands are energetically degenerate. B, F, Corresponding band structure plots around the frontier bands. _k_ denotes
the reciprocal lattice vector. The unit cells for the band structure calculations contain four and two triangulene units for _cis_ and _trans_ TSCs, respectively, with the lattice
periodicities _a_ = 30.0 Å (_cis_ TSC) and 17.4 Å (_trans_ TSC). The dashed lines indicate the middle of the band gap. The calculations reveal nearly dispersionless frontier bands due to a
weak intertriangulene electronic hybridization. In addition, TSCs exhibit a band gap of 0.68 eV irrespective of the intertriangulene bonding configuration. C, G, Ground state spin density
distributions for _cis_ (C) and _trans_ (G) TSCs. Spin up and spin down densities are denoted in blue and red, respectively. D, H, Local DOS maps of the valence (VB) and conduction (CB)
bands of _cis_ (D) and _trans_ (H) TSCs. Spin density distributions and local DOS maps were calculated at a height of 3 Å above the TSCs. EXTENDED DATA FIG. 3 DERIVATION OF THE
BILINEAR-BIQUADRATIC MODEL. A, B, Schematic energy level diagram of _N_ = 2 (A) and 3 (B) oTSCs for the Heisenberg, Hubbard and BLBQ models. Analytical expressions for the spin models are
provided in the Supplementary Information (Supplementary Note 2). The Hubbard model is defined such that each triangulene unit is represented by a four-site lattice (C) and the many-body
energy levels are computed with DMRG, taking _t_ = −1.11 eV, _t_′ = −0.20 eV and _U_ = 1.45|_t_|. The parameters of the BLBQ model (\(J\) = 18 meV and \(\beta \) = 0.09) are obtained by
matching its excitation energies to those of the Hubbard model for the _N_ = 2 TSC. C, Description of the four-site toy model with the intra- and intertriangulene hopping, _t_ and _t_′,
respectively, indicated. The coloured filled circles denote the two sublattices. D, E, Comparison of the excitation energies for an _N_ = 3 oTSC computed with CAS(6,6) for the complete
Hubbard model with _t_1 = −2.70 eV, _t_2 = 0 eV and _t_3 = −0.35 eV (D), and with DMRG for the four-site Hubbard model (E), as the atomic Hubbard _U_ is varied. Dashed lines indicate the
experimental spin excitation energies of 14 meV for _N_ = 2 TSC (A) and, 11 and 35 meV for _N_ = 3 oTSC (B, D, E). Note that the Heisenberg model fails to capture both the experimental spin
excitation energies for the _N_ = 3 oTSC (B), and the Hubbard model results for the _N_ = 2 (A) and _N_ = 3 (B) oTSCs. EXTENDED DATA FIG. 4 EXPERIMENTAL AND THEORETICAL SPECTROSCOPIC
SIGNATURES OF SPIN EXCITATIONS IN AN _N_ = 4 OPEN-ENDED TRIANGULENE SPIN CHAIN. Comparison between experimental and theoretical (using the four-site Hubbard and BLBQ models) d2_I_/d_V_2
spectra of an _N_ = 4 oTSC shows a good agreement in both the energies and the modulation of the spin spectral weight across the different units in the TSC. Numerals along the abscissa
denote the unit number of the TSC. BLBQ model calculations are performed with two different _T_eff values for the tunnelling quasiparticle, which determine the linewidth of the d2_I_/d_V_2
profile. Model parameters are the same as in Extended Data Fig. 3. EXTENDED DATA FIG. 5 AVERAGE MAGNETIZATION FOR THE FIRST THREE _S__Z_ = +1 STATES OF AN _N_ = 16 OPEN-ENDED TRIANGULENE
SPIN CHAIN, OBTAINED WITH THE BILINEAR-BIQUADRATIC MODEL. Calculations were performed with \(J\) = 18 meV and \(\beta \) = 0.09. Orange filled circles denote the magnetization profile of the
state with the lowest excitation energy _E_ = 0.4 meV, much smaller than the theoretical Haldane gap (9 meV), and \(|S,{S}_{z}\rangle =|1,+1\rangle \). The average magnetization is clearly
the largest at the terminal units, and is strongly depleted at the central units, as expected for an edge state. Blue and green filled circles denote spin excitations with energies larger
than the theoretical Haldane gap. Blue filled circles correspond to a state with _E_ = 12.1 meV and \(|S,{S}_{z}\rangle =|1,+1\rangle \), where the magnetization profile forms a nodeless
standing wave with maximum average magnetization at the central units. This can be identified as a spin wave state, except for the minor upturn at the terminal units. Green filled circles
are associated to a state with _E_ = 11.6 meV and \(|S,{S}_{z}\rangle =|2,+1\rangle \), where the average magnetization shares similarities with both the edge and nodeless spin wave states.
EXTENDED DATA FIG. 6 THEORETICAL AND EXPERIMENTAL SPIN EXCITATION ENERGIES OF OPEN-ENDED AND CYCLIC TRIANGULENE SPIN CHAINS. A, Spin excitation energies calculated by ED of the BLBQ model
(\(J\) = 18 meV and \(\beta \) = 0.09) for oTSCs with _N_ = 2–16 (circles) and cTSCs with _N_ = 5, 6, 12, 13, 14, 15 and 16 (crosses) up to 50 meV. The size of the symbols accounts for the
spin spectral weight of the corresponding spin excitation. The lowest energy bulk excitation, as indicated for the _N_ = 16 cTSC, converges to the Haldane gap (9 meV) with increasing _N_. B,
Experimental spin excitation energies up to 50 meV for seventeen oTSCs with _N_ between 2 and 20, and eight cTSCs with _N_ = 5, 6, 12, 13, 14, 15, 16 and 47. The lowest energy bulk
excitation, indicated for the _N_ = 47 cTSC, converges to the Haldane gap (14 meV) with increasing _N_. Experimentally, starting from both _N_ = 16 oTSC and cTSC, convergence to the Haldane
gap is observed. Note the odd–even effect observed for the lowest energy excitation of cTSCs, seen both in theory and experiments. EXTENDED DATA FIG. 7 NON-CROSSING APPROXIMATION RESULTS FOR
THE MULTI-ORBITAL ANDERSON MODEL OF AN _N_ = 3 OPEN-ENDED TRIANGULENE SPIN CHAIN (_T_1 = −2.70 EV, _T_2 = 0 EV, _T_3 = −0.35 EV AND _U_ = 1.90|_T_1|) COUPLED TO THE SURFACE (_Γ_/Π = 13
MEV). A, Total spectral function of CAS(6,6) at different temperatures _T_ for the case of particle–hole symmetry. B, Orbital-resolved spectral function of CAS(6,6) for _T_ = 4.64 K and for
the particle–hole symmetric case. C, Detuning from particle–hole symmetry: total spectral function of CAS(6,6) for different values of δ_ε_ and _T_ = 4.64 K. D, Local spectral functions at
_T_ = 4.64 K for carbon sites of one of the outer triangulene units and the central triangulene unit (δ_ε_ = 200 meV). The inset shows a sketch of the _N_ = 3 oTSC with the two carbon sites
marked with the corresponding coloured filled circles. The spectral functions in individual panels are offset vertically for visual clarity. SUPPLEMENTARY INFORMATION SUPPLEMENTARY
INFORMATION Supplementary Figs. 1–49 and Supplementary Notes 1 and 2: additional STM and STS data, effect of extrinsic spin-orbit coupling on triangulenes, analytical solutions of the
Heisenberg and BLBQ models, materials and methods in solution synthesis and characterization, solution synthetic procedures, and NMR spectroscopy and high-resolution mass spectrometry of
chemical compounds. PEER REVIEW FILE RIGHTS AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Mishra, S., Catarina, G., Wu, F. _et al._ Observation of fractional
edge excitations in nanographene spin chains. _Nature_ 598, 287–292 (2021). https://doi.org/10.1038/s41586-021-03842-3 Download citation * Received: 30 April 2021 * Accepted: 20 July 2021 *
Published: 13 October 2021 * Issue Date: 14 October 2021 * DOI: https://doi.org/10.1038/s41586-021-03842-3 SHARE THIS ARTICLE Anyone you share the following link with will be able to read
this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative