ABSTRACT Spatial learning in teleost fish requires an intact telencephalon1, a brain region that contains putative analogues to components of the mammalian limbic system (for example,

hippocampus)2,3,4. However, cells fundamental to spatial cognition in mammals—for example, place cells (PCs)5,6—have yet to be established in any fish species. In this study, using tracking

microscopy to record brain-wide calcium activity in freely swimming larval zebrafish7, we compute the spatial information content8 of each neuron across the brain. Strikingly, in every

recorded animal, cells with the highest spatial specificity were enriched in the zebrafish telencephalon. These PCs form a population code of space from which we can decode the animal’s

analysis of neighbourhood distance between PCs across environments, we found evidence for a weakly preconfigured network in the telencephalon. The discovery of zebrafish PCs represents a

step forward in our understanding of spatial cognition across species and the functional role of the early vertebrate telencephalon. SIMILAR CONTENT BEING VIEWED BY OTHERS BRAIN-WIDE VISUAL

HABITUATION NETWORKS IN WILD TYPE AND _FMR1_ ZEBRAFISH Article Open access 16 February 2022 NOISE CORRELATIONS IN NEURAL ENSEMBLE ACTIVITY LIMIT THE ACCURACY OF HIPPOCAMPAL SPATIAL

REPRESENTATIONS Article Open access 25 July 2022 EARLY AND LATE PLACE CELLS DURING POSTNATAL DEVELOPMENT OF THE HIPPOCAMPUS Article Open access 21 November 2024 MAIN Animals generate an

internal map of their environment through spatial exploration6, integrating multiple sources of information including landmarks, geometry and self-motion9,10,11,12,13,14,15. Over half a

century of research in mammals has uncovered key computational building blocks of spatial cognition, beginning with the seminal discovery of place cells (PCs)5. Notably, PCs have been

comprehensively identified only in the hippocampus of birds16 and mammals5,17. In teleost fish, which shared a common ancestor with mammals around 450 million years ago18, the location or

even existence of the hippocampus is an area of active debate2,19, particularly given the lack of clear functional evidence for PCs20,21,22,23. Several methodological challenges may have

limited the discovery of PCs in fish. Electrophysiological recordings in freely moving adult fish have sampled only a small portion (under 1%) of cells in the telencephalon, a region

hypothesized to contain the functional analogue of the mammalian hippocampus1,2,3,19. Although brain-wide imaging is possible in larval zebrafish24,25, most studies have used tethered

preparations, which preclude naturalistic spatial exploration and can suppress spontaneous movement rate by roughly tenfold7. Mammalian studies have shown that PC activity is most robust

during continuous running26. Thus, the suppressed movement rate of tethered larval zebrafish may have been an obstacle in the search for PCs. To overcome these limitations we performed

brain-wide imaging in freely swimming larval zebrafish using tracking microscopy7,27, and systematically characterized the spatial information content8 of each recorded neuron. In contrast

to head direction cells and speed cells, which are both enriched in the fish rhombencephalon7,28,29, cells that encode spatial position (that is, PCs) are enriched in the fish telencephalon.

Collectively these PCs can be used to decode the animal’s spatial location. By projection of this population code onto a two-dimensional activity manifold, we observe untangling of spatial

representation across time, suggesting experience-dependent refinement of place codes. Through an extensive series of environmental manipulations, we find that zebrafish PCs potentially

integrate both allothetic and idiothetic information, flexibly remap to generate distinct spatial maps and exhibit some degree of preconfiguration30,31. Collectively these results suggest

that the compact neural network of the zebrafish telencephalon can generate functional units similar to mammalian PCs, and offer a potential window into the evolution of spatial cognition

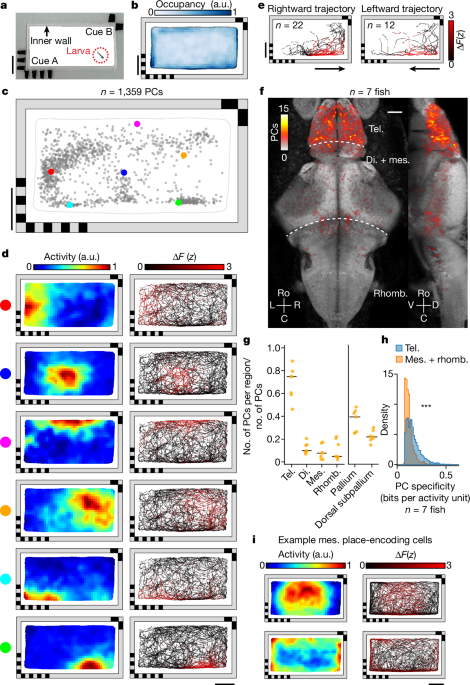
across vertebrate species. IDENTIFICATION OF CELLS ENCODING POSITIONAL INFORMATION We constructed a rectangular behavioural chamber (50 × 25 mm2) with landmark cues at two opposing corners

(Fig. 1a and Methods). A transparent, 1.5-mm-wide inner wall prevents the animal from directly contacting the landmarks. Larval zebrafish expressing pan-neuronal H2B-GCaMP6s (6–8 days post

fertilization) were placed in this chamber for 90 min of free exploration (Fig. 1b). During this time we recorded each animal’s brain-wide calcium activity at two volumes per second and then

extracted fluorescence across time _F_(_t_) for each cell centroid in the brain using non-negative matrix factorization (NMF)32 (Methods). Based on baseline-corrected neural activity

Δ_F_(_t_) and the position of the animal in space, we generated a two-dimensional spatial activity map for each cell, calculated its spatial information content normalized by its mean

activity (that is, spatial specificity)8 and identified the centre of mass (COM) of its place field (PF) (Fig. 1c,d and Methods). For identification of cells with significant spatial

specificity, we shuffled the activity of each cell 1,000 times by circular permutation (Methods). The shuffled data form a null distribution of spatial specificity for a given cell. A cell

was designated as a PC if its spatial specificity was significantly greater than the null distribution generated from its shuffled activity (_z_-score ≥ 5) and the distribution of spatial

specificity across all cells (_z_-score ≥ 3). With these significance criteria we identified 1,081 ± 329 (mean ± s.d.) PCs in each animal, with PFs distributed across the chamber (Fig. 1c,d,

Extended Data Fig. 1a and Methods). The majority of these cells fire uniquely at a single location whereas some show multiple PFs (Extended Data Fig. 1i–k). Using linear regression we

independently confirmed that the activity of the identified PCs is primarily predicted by the animal’s position in space rather than by other behavioural parameters such as heading or speed

(Extended Data Fig. 1b and Methods). Consistent with this, we find PC activity to be generally heading independent (Fig. 1e). Spatial position also accounts for a greater portion of activity

variance in PCs compared with non-PCs in the telencephalon (_P_ < 10−5, one-sided Mann–Whitney _U_-test; Extended Data Fig. 1c). The stability of spatial representation for a given cell

can be further quantified by measurement of the spatial correlation between two halves of the experiment. PCs have an average spatial correlation of 0.59 ± 0.19 (median ± s.d.) across the 90

 min experiment and are consistently activated on multiple traversals through the same spatial location (Extended Data Fig. 1d,e and Supplementary Video 1). We note that slow GCaMP sensor

kinetics combined with animal motion are likely to blur and enlarge each PF by at least 0.17–1.31 mm (Extended Data Fig. 1f–h and Methods). PCS ARE ENRICHED IN THE TELENCEPHALON OF LARVAL

ZEBRAFISH The anatomical distribution of spatial information in the brain is consistent across animals. We find that, in every animal, the telencephalon contains the highest number and

fraction of PCs (69 ± 14%, mean ± s.d.; Fig. 1f,g and Extended Data Fig. 2a–c), regardless of chamber geometry or landmarks, whereas telencephalic neurons consist of only 8 ± 1% (mean ± 

s.d.) of the recorded neurons on average. This enrichment of PCs in the telencephalon can also be observed by simply ranking cells across the brain according to their spatial specificity

(Extended Data Fig. 2d) or spatial information (Extended Data Fig. 2e). In every animal, cells with the highest-ranked spatial specificity are located primarily in the telencephalon (91 ± 

9%, mean ± s.d., for the top 100 cells). PCs that encode a given spatial location within the telencephalon are not clustered together anatomically (Extended Data Fig. 2g), with little

correlation between each cell pair’s anatomical distance and the similarity of their spatial activity maps (Extended Data Fig. 2h). Outside the telencephalon, cells with the highest spatial

specificity are located in a small number of bilaterally symmetric neuronal clusters near the boundary between the mesencephalon and rhombencephalon (Fig. 1f). However, the spatial

specificity or spatial information of these cells is significantly lower (_P_ < 10−5, one-sided Mann–Whitney _U_-test) than for those within the telencephalon (Fig. 1h and Extended Data

Fig. 2f). These non-telencephalic PCs appear to contain coarse-grained spatial information with larger PFs that often encompass the entire interior or border of the chamber (Fig. 1i),

whereas the telencephalon contains finer-scale spatial information that forms a population code of space. THE MAJORITY OF SPATIALLY SPECIFIC CELLS IN THE TELENCEPHALON ARE NOT CONSISTENT

WITH THE BVC MODEL A previous study has suggested that goldfish may use boundary vector cells (BVCs) rather than PCs for spatial navigation20, but no study of BVCs in zebrafish has yet been

conducted. BVCs are defined by two unique functional signatures33,34,35: (1) each BVC fires at a preferred allocentric heading and distance to a boundary, and (2) when a border at a given

BVC’s preferred heading is duplicated, its PF will also duplicate (Extended Data Fig. 3a). To test for BVCs, a movable wall was inserted and removed in the middle of an extended rectangular

chamber across three sessions (Extended Data Fig. 3b and Methods). Given the direction of wall insertion, we identified a set of candidate telencephalic cells (1,641 ± 238 cells with PFs

near the left or right wall of the chamber in session 1 (S1), mean ± s.d.), for which the BVC model predicts PF duplication in session 2 (S2) (Extended Data Fig. 3c and Methods). However, we

find that only a small percentage of all candidate telencephalic cells (4.77 ± 0.14%, mean ± s.d.) and candidate telencephalic PCs (4.14 ± 0.31%, mean ± s.d.) fit the BVC model (Extended

Data Fig. 3d), suggesting that, although BVCs exist in the zebrafish brain, they are distinct from PCs. TELENCEPHALIC PCS FORM A POPULATION CODE OF SPACE Collectively, telencephalic PCs span

spatial locations throughout the behavioural chamber, with high variance in the degree of spatial representation of each location across animals (Fig. 2a and Extended Data Fig. 4a,b), and

no apparent correlation between representational density and behavioural occupancy (Extended Data Fig. 4c,d). We applied a direct basis decoder36 to the population-level activity of PCs to

determine whether we could predict the animal’s physical location in space (Methods). To avoid circularity, decoding was performed only on held-out time points not included in spatial

activity map construction (Fig. 2, Extended Data Fig. 5 and Methods). This linear decoder is able to predict the animal’s spatial location to within 6.69 ± 2.34 mm (median ± s.d.) using

cells with the highest spatial specificity (up to the top 1,000) throughout the whole brain (Fig. 2b–e,h and Extended Data Fig. 5a). Using only telencephalic PCs, the decoder predicts

spatial position with a similar degree of accuracy (6.82 ± 2.05 mm, median ± s.d.), which significantly outperforms decoding from PCs in both mesencephalon and rhombencephalon (9.84 ± 2.89 

mm, median ± s.d.), cells in the optic tectum (11.63 ± 1.89 mm, median ± s.d.) and random cells across the brain (12.70 ± 2.30 mm, median ± s.d.) (Fig. 2e and Methods). The theoretical

baseline decoding error is 15.08 ± 2.30 mm (median ± s.d.) and the optimal time lag for the decoder is 2.5 s (Extended Data Fig. 5c). The decoder reaches peak performance using around 1,000 

cells with the highest spatial selectivity (Fig. 2f). However, because these cells may contain redundant encodings of position, we additionally demonstrate that, by selection of cells with

non-redundant PFs, a decoding accuracy of 5.41 ± 0.81 mm (mean ± s.d.) can be achieved with a minimal set of 25 PCs (Fig. 2g and Methods). TELENCEPHALIC PCS FORM A SPATIAL ACTIVITY MANIFOLD

THAT UNTANGLES OVER TIME Across a 90 min session we found subtle changes in spatial representation during the early (first 30 min) and late (final 30 min) periods (Fig. 3). To control for

potential differences in spatial coverage, we subsampled time points in both early and late periods to equalize their spatial coverage (Methods). When the population-level activity is

embedded in a two-dimensional Isomap37, the spatial manifold becomes more untangled across time (Fig. 3a and Supplementary Video 2). To quantify this we define a metric, neighbourhood

distance (Fig. 3b), that identifies for each time point _t__i_ the 30 nearest time points in the embedded two-dimensional manifold space and measures their average distance to _t__i_ in

physical space. From the early to late period, the distance relationships in the activity manifold increasingly resemble those in the physical chamber, resulting in a significant decrease in

neighbourhood distance (_P_ < 10−3 for six of seven animals, one-sided Mann–Whitney _U_-test; Fig. 3b and Supplementary Table 1). Neighbourhood distance computed directly from neural

activity without dimensionality reduction also shows a similar decrease across time (_P_ < 10−3 for six of seven animals, one-sided Mann–Whitney _U_-test; Supplementary Table 1).

Untangling of the spatial activity manifold is accompanied by a significant increase in spatial specificity (_P_ < 0.01 for seven of seven animals, one-sided Mann–Whitney _U_-test; Fig.

3c and Supplementary Table 1), a decrease in decoding error (_P_ < 10−5 for five of seven animals, one-sided Mann–Whitney _U_-test; Fig. 3d and Supplementary Table 1) and a decrease in PF

size (_P_ < 10−3 for six of seven animals, one-sided Wilcoxon signed-rank test; Fig. 3e and Supplementary Table 1). Untangling of the activity manifold, along with the increased spatial

specificity of individual cells (Fig. 3f), suggests refinement of the population code for spatial representation across time. IDIOTHETIC INFORMATION IS A MAJOR INPUT TO SPATIAL ACTIVITY MAPS

A hallmark of mammalian PCs is their ability to integrate information from both idiothetic and allocentric cues. Idiothetic information enables the animal to update its position in space

based on path integration whereas an allocentric reference frame (that is, combination of landmarks and geometric boundaries) orients, constrains and stabilizes the animal’s internal

position estimate13,14. To determine whether a non-visual source of information such as path integration significantly contributes to the spatial activity map, we adapted several classic

mammalian paradigms to larval zebrafish (Fig. 4 and Extended Data Fig. 6): (1) transition from light to dark (Fig. 4a–d), (2) removal of landmarks (Fig. 4e–h) and (3) morphing of

environmental boundaries (Fig. 4i–l). In all cases, if PCs are purely a read-out of visual patterns in the environments, then significant remapping should occur. Alternatively, because the

animal was not removed from the chamber during these manipulations (that is, path integration was not interrupted), if PCs can rely on idiothetic information, then partial or no remapping is

expected in all cases. Our results support the latter hypothesis (see below). TRANSITION FROM LIGHT TO DARK We recorded neural activity and behaviour for 60 min under bright diffuse

white-light illumination (7.05 µW mm−2) in a circular chamber (S1), followed by 60 min with no white-light illumination in S2 (Fig. 4a and Methods). We note that a localized blue excitation

spot (0.5 mm in radius) centred on the fish brain cannot be removed in these experiments due to its requirement for neural imaging (Methods). To quantify change in spatial representation we

compute three metrics: (1) PF correlation, which is the correlation of spatial activity maps between sessions, (2) PF shift, which is the change in the COM of PFs across sessions and (3)

population vector (PV) correlation, which is the correlation between population activity vectors at each spatial location (Methods). We found that PFs are retained despite substantial

changes in visual illumination (Fig. 4b,c), as shown by a PF correlation of 0.66 (median, with interquartile range (IQR) 0.51–0.77; Methods), PV correlation of 0.58 (IQR 0.45–0.68) and PF

shift of 3.38 mm (IQR 1.50–6.79 mm), all of which are not significantly different from control comparisons between the early and late periods of S1 (Fig. 4d; _P_ values per fish using

one-sided Wilcoxon signed-rank test are given in Supplementary Table 1). LANDMARK REMOVAL To enable landmark removal without interruption of path integration we created a movable wall

containing visual cues that can be remotely positioned (Fig. 4e). The wall was positioned with landmarks visible to the fish in S1 (75–90 min) and was then moved to hide the landmarks in S2

(60–100 min). We found that PFs are retained despite landmark removal (Fig. 4f,g), as shown by a PF correlation of 0.54 (IQR 0.36–0.67), PV correlation of 0.48 (IQR 0.37–0.58) and PF shift

of 3.61 mm (IQR 1.45–7.48 mm), which are comparable to within-session controls (see Fig. 4h, Extended Data Fig. 6a and Supplementary Table 1 for _P_ values). We did not observe a greater

change in PF correlation for cells with PFs near landmarks (Extended Data Fig. 7). MORPHING OF ENVIRONMENTAL BOUNDARIES Next we asked whether the retention of spatial tuning properties can

be explained by the interaction of idiothetic cues and boundary conditions, as previously observed in mammals38. To test this we created a morph chamber with eight flexibly connected

segments that can be remotely adjusted without removing the animal (Methods and Fig. 4i). We found that PFs mostly maintain their position relative to each other across sessions (Fig. 4j,k)

but not their absolute position in the chamber (Extended Data Fig. 8a and Supplementary Table 1). The absolute change in PF position across the two sessions is 8.41 mm (IQR 4.29–12.98 mm)

whereas the relative change in PF position (obtained following application of a non-rigid transformation of S2 spatial activity maps to match the shape of the S1 chamber; Methods) is 5.13 mm

(IQR 2.75–10.11 mm; Fig. 4l and Extended Data Figs. 6a and 8b). PF and PV correlations across sessions are similar to within-session controls (Fig. 4l, Extended Data Fig. 6a and

Supplementary Table 1). WHOLE-CHAMBER ROTATION AS A CONTROL FOR EXTRINSIC CUES To exclude the possibility that the retention of spatial maps in the above experiments is solely due to

extrinsic cues outside of the behaviour chamber (for example from the imaging room or microscope), we performed the following control. After an initial imaging session (S1, 90 min), we

rotated the entire chamber as a rigid body by 180° (S2, 60 min; Fig. 4m and Methods). Crucially, during this manipulation both the fish and chamber rotate together as one rigid body (that

is, allothetic cues within the chamber and idiothetic information remain aligned). If extrinsic cues are the dominant input to PCs, one would expect spatial activity maps to rotate by 0°; if

not, they should rotate by 180°. Our results strongly support the latter hypothesis (Fig. 4n–q). Direct comparison of spatial activity maps (assuming 0° rotation) across the two sessions

results in a PF correlation of −0.23 (IQR −0.44 to 0.03), PV correlation of 0.06 (IQR −0.1 to 0.2) and PF shift of 31.47 mm (IQR 15.59–39.49 mm) (Fig. 4p, Extended Data Fig. 6a and

Supplementary Table 1). By contrast, following the application of 180° rotation to the spatial activity map in S2, PF correlation increased to 0.55 (IQR 0.39–0.68), PV correlation increased

to 0.55 (IQR 0.41–0.66) and PF shift decreased to 4.52 mm (IQR 1.87–12.10 mm), all of which became indistinguishable from within-session controls (Fig. 4q, Extended Data Figs. 6a and 8b, and

Supplementary Table 1). ALLOCENTRIC VISUAL INFORMATION ENABLES RECOVERY OF SPATIAL ACTIVITY MAPS Next we asked whether, following interruption of path integration (for example, by removal

of the animal from the chamber), a larval zebrafish can recover its previous spatial map based on allothetic cues39,40. We performed a series of experiments with either complete or partial

retention of visual and geometric features across sessions (Fig. 5 and Extended Data Fig. 6): (1) no change in landmarks or geometry (Fig. 5a–d), (2) landmark removal without changing

geometric features (Fig. 5e–h) and (3) morphing of geometric boundaries without changing landmarks (Fig. 5i–l). We recorded for 60–90 min in S1, removed the animal from the chamber for

several minutes and then placed it in either the same chamber following cleaning (Methods) or a new chamber with partially altered landmarks or geometry for S2 (45–100 min). To interrupt

path integration, animals were returned to the chamber at a different location and heading from where they were removed. We found nearly complete or partial recovery of spatial maps in all

cases. NO CHANGE IN LANDMARKS OR GEOMETRIC FEATURES When animals were returned to the same chamber following removal or scrambling of any potential olfactory cues (Fig. 5a, Extended Data

Fig. 8f,g and Methods), we found that the spatial map is mostly maintained between S1 and S2 despite the interruption in path integration (Fig. 5b–d and Extended Data Fig. 6a), as shown by a

PF correlation of 0.40 (IQR 0.17–0.57), PV correlation of 0.36 (IQR 0.19–0.51) and PF shift of 5.05 mm (IQR 2.13–11.76 mm). PF shift was not significantly different from within-session

control in most animals, although PF and PV correlation showed small but significant decreases (Fig. 5d, Extended Data Fig. 6a and Supplementary Table 1). LANDMARK REMOVAL OR BOUNDARY

MORPHING Following landmark removal without changing chamber geometry, we found a PF correlation of 0.35 (IQR 0.16–0.50), PV correlation of 0.30 (IQR 0.16–0.44) and PF shift of 8.58 mm (IQR

4.17–17.79 mm; Fig. 5h), all of which show small but significant changes compared with within-session controls in most animals (Extended Data Fig. 6a and Supplementary Table 1). We found

similar partial recovery of the spatial map following geometric morphing without changing landmarks. In this case we performed non-rigid transformation of the spatial activity maps in S2 to

align the maps across sessions (Fig. 5l and Methods), resulting in a PF correlation of 0.44 (IQR 0.27–0.59), PV correlation of 0.42 (IQR 0.24–0.62) and PF shift of 6.77 mm (IQR 2.21–11.69 

mm) (Fig. 5l, Extended Data Figs. 6a and 8b, and Supplementary Table 1). CONFLICT BETWEEN SENSORY INPUTS If both self-motion and visual information are potential inputs to PCs, we can ask

which dominates when the two information streams come into conflict. To do this we created a chamber wall that can be remotely rotated without removal of fish or disassembly of the

water-sealed chamber (Fig. 5m and Methods). Unlike whole-chamber rotation (Fig. 4m), the fish itself is not rotated across sessions (45–90 min for S1 and 45–75 min for S2), but only the

walls of the chamber, along with the visual landmarks on the walls, undergo 180° rotation. If idiothetic information predominates over allothetic information, the spatial map in S2 should

directly correspond to that in S1; if the reverse is true, the spatial map in S2 should rotate by 180°. The result is intermediate between these two extremes (Fig. 5n–q). Direct comparison

of spatial maps across sessions results in a PF correlation of 0.38 (IQR 0.15–0.53), PV correlation of 0.37 (IQR 0.18–0.53) and PF shift of 6.85 mm (IQR 3.12–17.48 mm), all of which show

small but significant changes compared with within-session controls in most animals (Fig. 5p, Extended Data Fig. 6a and Supplementary Table 1). However, the application of 180° rotation to

the spatial map in S2 results in an even lower PF correlation of 0.05 (IQR −0.2 to 0.25) and PV correlation of 0.12 (IQR −0.1 to 0.39), and an even higher PF shift of 20.47 mm (IQR

12.31–36.23 mm) (Fig. 5q, Extended Data Figs. 6a and 8b, and Supplementary Table 1). Thus the spatial map in S2 shows greater direct (rather than 180° rotated) correspondence to that in S1,

suggesting that idiothetic information potentially predominates over allothetic visual information when the two information sources come into conflict. REPRESENTATIONAL FLEXIBILITY OF THE PC

NETWORK PCS DEMONSTRATE THE POTENTIAL FOR SIGNIFICANT REMAPPING ACROSS DISTINCT ENVIRONMENTS Mammalian PCs are notable for their representational flexibility10,40,41, while other spatial

cells exhibit more coherent shifts across environments42,43,44. To test this in zebrafish we recorded the animal in S1 (90 min), removed it from the chamber to interrupt path integration and

placed it in a new chamber with completely distinct geometry and visual features for S2 (60–80 min) (Fig. 6a–c). Following application of a non-rigid transformation to the spatial activity

maps in S2 for alignment of these across sessions (Methods), we found a PF correlation of 0.13 (IQR −0.13 to 0.36), PV correlation of 0.05 (IQR −0.07 to 0.21) and PF shift of 16.13 mm (IQR

7.96–26.83 mm), all of which are significantly different from within-session controls, which had a PF correlation of 0.56 (IQR 0.39–0.68), PV correlation of 0.58 (IQR 0.48–0.65) and PF shift

of 5.49 mm (IQR 2.03–12.46 mm) (Fig. 6d, Extended Data Figs. 6a and 8b, and Supplementary Table 1), demonstrating significant spatial remapping across distinct environments. RECOVERY OF A

PREVIOUSLY STORED MAP FOLLOWING REMAPPING Once remapping occurred and a new spatial map was generated, we asked whether larval zebrafish can recover the spatial map of a previously

encountered environment. In a three-session experiment, the animal was placed in chamber A (40–80 min), removed and placed in chamber B (30–60 min) and then returned to chamber A (40–60 min;

Extended Data Fig. 9a,b). We refer to this as an ABA experiment. Chambers A and B have a distinct arrangement of geometric features and landmarks. A non-rigid transformation was performed

on the spatial activity map in S2 to align maps across sessions (Methods). Following application of non-rigid transformation we found significant remapping between A and B, similar to the

experiment in Fig. 6a, as shown by a PF correlation of 0 (IQR −0.26 to 0.24), PV correlation of 0.01 (IQR −0.12 to 0.15) and PF shift of 15.94 mm (IQR 10.08–26.96 mm) (Extended Data Fig.

9c–e and Supplementary Table 1). After returning to chamber A, fish showed partial recovery of spatial maps as shown by a PF correlation of 0.28 (IQR 0.06–0.49), PV correlation of 0.22 (IQR

0.10–0.34) and PF shift of 9.27 mm (IQR 3.31–16.84 mm; Extended Data Fig. 9c–e and Supplementary Table 1). EVIDENCE FOR LATENT ENSEMBLE STRUCTURE ACROSS ENVIRONMENTS An active area of debate

is the extent to which pairwise relationships between PCs are retained during remapping and whether animals can use similar maps to generalize across distinct environments31,40. When both

environmental geometry and landmarks are altered, and path integration is interrupted, we find PF and PV correlation near 0 across sessions (Fig. 6d). Using these remapping experiments, we

then asked whether there are latent local or global spatial relationships that are maintained across sessions despite substantial remapping. First we assessed whether local neighbourhood

relationships between PCs are retained by computing the percentage of neurons that remain neighbours across sessions (Fig. 6e and Methods). To avoid the possibility of confounds due to

overlapping fluorescent signal between adjacent cells, we restricted the analysis to pairs of cells with a minimum anatomical distance of over 20 µm. In all animals the neighbour retention

percentages are significantly lower than controls (early versus late period of the same session, _P_ < 10−5, four of four fish, one-sided Wilcoxon signed-rank test; Supplementary Table

1), suggesting a significant disruption of neighbourhood relationships during remapping. However, the percentage of neurons that remain neighbours is also significantly higher than by random

chance (Fig. 6e; _P_ < 10−5, four of four fish, mean percentage of remaining neighbours compared with 1,000 random shuffles; Methods), suggesting that local relationships between neurons

are partially maintained. Second, we asked whether there are latent global relationships between spatial activity maps (for example, coherent PF rotations31). We synthetically applied 72 

potential rotations (in 5° increments; Methods) to the spatial activity map in S2 and then used non-rigid transformation to align spatial activity maps across sessions (Extended Data Fig.

8d). We identified the rotation that maximized the correlation between the two spatial activity maps and found this to be variable across the four animals (131, −147, −86 and −100°).

Application of optimal rotation and non-rigid transformation of S2 spatial activity maps slightly improved median PF correlation, PV correlation and PF shift, by 0.072 ± 0.036, 0.066 ± 0.032

and 3.35 ± 6.20 mm (all mean ± s.d.), respectively. Although the small improvement in PF correlation is higher than that expected by random chance (Extended Data Fig. 10, Methods and

Supplementary Table 1), PF and PV correlation and PF shift all remain significantly different than within-session controls (Extended Data Fig. 8c,e and Supplementary Table 1), suggesting

that global coherence between PCs is at most weakly maintained during remapping. DISCUSSION The previous lack of evidence for PCs outside of mammalian and avian species suggests either that

the neural architecture needed to generate PCs evolved following the emergence of land vertebrates5,16 or that PCs in species such as teleost fish have not yet been discovered, potentially

due to methodological limitations (for example, sparse recordings or tethered preparations). To overcome these challenges we recorded neural activity across the brain of freely swimming

larval zebrafish using tracking microscopy7, and identified a population of PCs that are enriched in the zebrafish telencephalon and collectively encode the animal’s position in space.

Zebrafish PCs exhibit two functional hallmarks of mammalian PCs: (1) multimodal integration of information and (2) flexible representation of the environment. First, to demonstrate that

zebrafish PCs potentially integrate multiple sources of sensory information13,14, we adapted some of the classic mammalian paradigms for manipulation of idiothetic or allothetic information

to larval zebrafish (for example, transition from light to dark, manipulation of environmental features with or without interruption of path integration). The results of these experiments

suggest that the multimodal integration property of PCs may indeed be conserved from early vertebrates to mammals. Second, a hallmark of mammalian PCs is their representational flexibility

(that is, the ability to remap) in response to complete environmental change or disorientation13,39,40,41. We found similar remapping of zebrafish PCs following a complete change in the

visual environment coupled with interrupted path integration, which supports the view that PCs form a flexible memory or prediction system. To fully determine the extent to which zebrafish

PCs are functionally analogous to mammalian PCs will require extensive future research. We have primarily focused on exposure to an initially new environment, and future studies will be

needed to investigate the storage capacity and stability of the PC network across greater spatial and temporal scales (for example, multiple environments, developmental stages and

experience-dependence changes across days and weeks). In addition, the PFs of zebrafish PCs are not completely uniformly distributed throughout the environment but can form clusters, and PCs

within a given cluster show weakly correlated activity across environments. This may support recent work in rodents suggesting that spatial tuning across the hippocampus is not entirely

independent but may form correlated assemblies30,31,40,45. Future studies combining behaviour, functional imaging and synaptic connectivity will be needed to understand the function and

neural basis of these weakly correlated ensembles. Lastly, BVCs, but not PCs, have been identified in the goldfish telencephalon20. By contrast, cells that truly fit the mammalian BVC model

constitute a small percentage of the zebrafish telencephalon. Although a significant number of larval zebrafish PCs have spatial tuning near boundaries, they may be more functionally

analogous to the high density of PCs observed near boundaries in juvenile rodents46,47. The differences between zebrafish and goldfish findings could have arisen from several sources. First,

the goldfish telencephalon has not been comprehensively recorded. Second, it is not yet entirely conclusive that all goldfish neurons with border activity are functionally closer to BVCs

than PCs, because some PCs can also exhibit PF duplications in parallel compartments48,49,50. Finally, it is possible that different fish species indeed rely on different spatial cells for

navigation. In the future, more comprehensive recordings and remapping experiments across a variety of fish and other non-mammalian species will be needed to answer these outstanding

questions. METHODS EXPERIMENTAL SET-UP SIMULTANEOUS BEHAVIOURAL AND NEURAL IMAGING BY TRACKING MICROSCOPY Tracking microscopy was performed as described in our previous study7. Motion

cancellation was performed by a custom three-axis motorized system, to be described elsewhere (Mohan et al., manuscript in preparation). To enable animal tracking, the behavioural chamber is

illuminated by four custom light strips consisting of narrow-angle, 850 nm infrared light-emitting diodes (LEDs; no. SFH4655-Z, Osram) that deliver infrared light to the chamber by total

internal reflection. Ambient white-light illumination in the behavioural chamber is provided by an array of wide-angle white LEDs (no. GW PSLM31.FM). For recording of neural activity, we

used DIFF microscopy to image a brain area of 1,013 × 764 × 150 µm3 at cellular resolution, a volume rate of 2 Hz and frame rate of 200 Hz, as described in our previous study7. The

performance and characteristics of the imaging system have been characterized in depth in our previous study7. CHAMBER CONSTRUCTION AND EXPERIMENT DESIGN Several constructions for the

chamber wall were used depending on the complexity of the experiment. The top and bottom of all behavioural chambers are made of glass to allow optical access from above and below7. Between

the glass plates, 1-mm-thick, gas-permeable PDMS walls (Sylgard 184, Dow Corning) were used to create a watertight rigid body as described previously7. PDMS chambers were cut using a

computer-controlled blade and finished by manual cutting. The chamber was filled with E3 water before fish loading (‘Fish loading, removal and reloading’). Following fish loading we gently

closed the chamber by sliding on a top coverslip. Excess fluid was removed to create a watertight seal between the PDMS and the two glass surfaces. Each imaging session lasted 45–100 min to

ensure sufficient spatial coverage of the arena (each experiment is described in more detail below). We did not include any fish in our analysis that was quiescent for more than 20 min

during the experiment. If not specified explicitly, all chambers were initially new to the fish. For whole-chamber-rotation experiments (Fig. 4m) and rectangle-to-circle experiments (Fig.

6a), the outer wall (1 mm thick) is made of translucent white PDMS cut into the desired chamber shape. Landmarks are constructed from black PDMS pieces embedded into the outer wall. A clear

PDMS inner wall (0.5 mm thick, 1.5 mm wide) placed alongside the outer wall prevents the fish from direct interaction with the outer wall or landmarks. For chamber-rotation experiments,

animals were first imaged for 90 min in the rectangular chamber (S1) and then the entire chamber was slowly rotated over 10–20 s as a rigid body without removing the animal (that is, the

chamber walls, ceiling, floor and fish all rotated together). Animals were then imaged for a further 60 min (S2). For experiments that required rotation of the chamber wall without removal

of the animal or disassembly of the chamber (Fig. 5m), an outer PDMS wall with a central square cut-out of 60 × 60 mm2 was used only for water-sealing the chamber. An inner chamber wall (of

distinct size and shape from the outer PDMS wall) was constructed from laser-etched plastic with embedded stainless steel pieces (grade 430), which enabled remote repositioning of the

plastic chamber wall using small magnets (3–5 mm in diameter) below the bottom glass of the chamber. Landmarks (when used) were painted onto the wall of the plastic chamber. The plastic

chamber wall was placed inside the square cut-out of the outer PDMS wall. Animal movement was restricted to within the plastic chamber walls. Given the flexibility of this chamber design, we

also used it for the experiments shown in Fig. 5a,e,i and Extended Data Fig. 9a. In the wall-rotation experiments we first recorded the animal for 45–90 min (S1) and then the entire chamber

assembly was removed from the microscope. Using small magnets underneath the bottom glass of the chamber, we then carefully rotated the chamber walls by 180° before replacing the chamber

assembly on the microscope. During this manipulation only the walls rotate but not the fish. Following wall rotation the animal was recorded for a further 45–75 min (S2). For wall-morphing

experiments (Fig. 4i) we constructed a morph chamber consisting of eight pieces of stainless steel (12 × 2 × 1 mm3) linked by a flexible ring of silicone (1 mm wide and 0.5 mm tall). The

stainless steel pieces can be remotely repositioned using small magnets below the bottom glass of the chamber (as described above), allowing flexible and gradual morphing of the chamber

wall. As described above, an outer PDMS wall with a central square cut-out of 60 × 60 mm2 was used only for water-sealing the chamber, and the morph chamber was placed inside the square

cut-out. Animal movement was restricted to within the morph chamber. We first arranged the morph chamber into a radially near-symmetric octagon and recorded the animal for 45–65 min (S1).

Using small magnets underneath the bottom glass of the chamber, we then morphed the chamber wall into an ellipse. During this manipulation we ensured that the walls did not make strong

physical contact with the fish. Following morphing, the animal was recorded for a further 45–70 min (S2). For border-insertion and -removal experiments (Extended Data Fig. 3b) we used a PDMS

chamber with an 84 × 15 mm2 central cut-out in which the animal was free to move. At the midpoint of the long axis of the chamber we created a hidden rectangular pocket (21.5 × 2 mm2)

containing a stainless steel rectangular bar (20 × 1.5 × 0.5 mm3). Using a small magnet, the stainless steel bar can either be inserted into the chamber (creating an extra border wall) or

hidden from the chamber. In S1 (45–95 min) the movable wall was hidden from the animal. Following S1, the movable wall was inserted into the interior of the chamber and the animal recorded

for 45–95 min (S2). Following S2, the movable wall was again retracted and hidden from the animal, and the animal recorded again for 45–90 min (S3). For the landmark-removal experiment (Fig.

4e) we used a PDMS chamber with a 25 × 25 mm2 central cut-out. On one edge of the chamber we created two additional PDMS pockets (100 × 2.5 mm2) that each contained a 70 × 2 × 0.5 mm3 white

(acrylic painted), stainless steel, rectangular bar. Landmarks (vertical black stripes) were painted on a portion of one of the stainless steel bars (Fig. 4e) whereas the opposing stainless

bar was completely white. In S1 (75–90 min), landmarks were positioned so as to be visible to the fish. Following S1, by applying small magnets to the bottom glass of the chamber, the

stainless steel piece with landmarks was remotely moved into the PDMS pocket, effectively hiding the landmarks from the animal within the chamber; the opposing stainless steel bar was not

moved. The animal was then recorded again for 60–100 min (S2). FISH LOADING, REMOVAL AND RELOADING For all experiments, fish were loaded into the chamber using a glass or plastic pipette.

For experiments with fish removal between S1 and S2 (Figs. 5a,e,i and 6a) we used the following procedure. Following the first 60–90 min recording (S1) the chamber was removed from the

microscope. The top coverslip of the chamber was loosened and then either partially or completely removed. The fish was then removed from the chamber with a glass or plastic pipette. In

between sessions, the chamber was thoroughly cleaned with soap and isopropanol and then pressure-rinsed for 2–5 min. For two fish (Extended Data Fig. 8g) we rotated the bottom glass relative

to the chamber walls without cleaning, to scramble any potential olfactory cues. We reloaded the fish into the chamber at a different heading and position from those at which the animal was

removed. Following fish loading, the chamber was again sealed with its top glass coverslip and transferred to the microscope for a second imaging session (45–100 min). For the ABA

experiment (Extended Data Fig. 9a) the same procedure was carried out to load the fish into the B chamber for S2, and to subsequently load the fish into the A chamber for S3. LIGHTS-ON/OFF

EXPERIMENT To study how PFs are influenced by the luminance of the environment we designed a light/dark protocol. Following 60 min of recording fish exploring the circular PDMS chamber we

turned off the white LEDs, providing visible illumination to the chamber. Turning off the white LEDs resulted in a luminance change from 7.05 to under 0.01 µW mm−2, measured at the centre of

the chamber. To ensure that the transition to lights off did not generate an aversive response, luminance was changed gradually over 1 min. Recording was then resumed for an additional 60 

min. We note that a small blue spotlight with a radius of 0.5 mm is always centred on the brain of the fish under all conditions, due to its requirement for neural imaging. We measured the

light scattering from this spotlight to be 0.14 µW mm−2 within 5 mm of the source. Light intensity measurements were performed using a photodiode-based optical power sensor with a known

detector area (no. S130C, Thorlabs). IMAGE REGISTRATION HIGH-RESOLUTION OFFLINE REGISTRATION OF FLUORESCENT BRAIN VOLUMES FOR EACH ANIMAL Each fluorescent image from the tracking microscope

was registered to a high-resolution reference brain volume collected from the same animal. An in-depth description and characterization of the registration pipeline was published in our

previous study7. Briefly, an initial coarse registration is obtained by optimization of a three-dimensional rigid transformation that maps the moving image to a (possibly tilted) plane

within the reference brain volume. This planar surface is then finely subdivided into a deformable surface that is locally adjusted within the reference volume using a regularized piecewise

affine transform. REGISTRATION TO A COMMON REFERENCE BRAIN ACROSS ANIMALS We use the Computational Morphometry Toolkit (CMTK)51 to register each animal to a common reference fish. An atlas

fish52 was selected to serve as the common reference brain. Each brain was registered onto the reference brain in a series of steps: initialization, rigid, full affine, warp. The coordinate

transformation for each individual cell was then saved. The command line commands are listed below: cmtk make_initial_affine --centers-of-mass moving_image fixed_image initial.list cmtk

registration --initial initial.list --nmi --dofs 6 --dofs 12 --nmi --exploration 8 --accuracy 0.8 -o affine.list moving_image fixed_image cmtk warp --nmi --threads 160 --jacobian-weight 0

--fast -e 18 --grid-spacing 100 --energy-weight 1e-1 --refine 4 --coarsest 10 --ic-weight 0 --output-intermediate --accuracy 0.5 -o warp.list affine.list cmtk reformatx --pad-out 0 -o

out_image --floating fixed_image moving_image warp.list cmtk streamxform warp.list <cell_coordinates.txt > cell_coordinates_registered.txt IMAGE ANALYSIS EXTRACTION OF NEURAL ACTIVITY

BY NMF Non-negative matrix factorization (NMF) separates each cell into two components—a spatial footprint and a time-varying activity component—as described in our previous study27.

Briefly, following registration, we applied constrained NMF32 to our whole-brain datasets with nuclear localized fluorescence. NMF was performed for each axial section of a given brain

volume. Our axial sections of the reference volume are separated by 2 µm and the average diameter of a zebrafish cell is approximately 5 µm; thus there can be double counting of centroids if

a cell spans more than one axial plane. Cell centroids were detected throughout the entire reference brain volume but were included in downstream analysis only if they were sampled in at

least 30% of time points throughout the imaging session. We merged these cell centroids belonging to the same cell based on close spatial proximity (horizontal distance 1.4 µm or less,

vertical distance 2 µm or less) and highly correlated activity (over 0.7). Following merging, the number of cells was 73,621 ± 10,558 (mean ± s.d.), decreasing by 28.4 ± 2.6% (mean ± s.d.)

across animals (_n_ = 6 fish). The fluorescence baseline for each merged cell was estimated using the tenth percentile within a 30 min sliding window. Baseline-corrected fluorescent traces

Δ_F_(_t_) were then obtained by subtraction of the estimated baseline from raw fluorescent traces. IDENTIFICATION OF PCS For identification of PCs we first generate a spatial activity map

for each neuron (see below), use this map to compute spatial information and specificity8 (see below), generate shuffled data by circular permutation to obtain a null distribution for

spatial specificity (see below) and, finally, compare the spatial specificity of each cell to the null distribution from shuffled activity and to the distribution of spatial specificity

across the brain (see below). The spatial information/specificity criteria for PC identification were originally defined by Skaggs et al.8. The criteria we use are similar to those in the

existing literature in both mammals and birds, for both electrophysiological and calcium imaging data16,53. A spatial activity map was generated for each neuron, representing the mean neural

activity at each spatial location. To calculate the spatial activity map the chamber was divided into square bins (side length 1.2 mm) and then the summed neural activity and occupancy time

were calculated for each bin. This resulted in two matrices: a summed neural activity matrix and an occupancy matrix (matrix entries correspond to spatial bins). We then applied a

boundary-constrained Gaussian filter (standard deviation one bin, with the boundary defined by the chamber boundary) to these two matrices. The spatial activity map was calculated by

dividing the filtered summed neural activity matrix by the filtered occupancy matrix to obtain the filtered average activity in each spatial bin. When the fish was stationary (speed below

0.1 mm s−1), the corresponding frames were not included in the calculation of the spatial activity map. For all experimental spatial activity maps (for example, for comparison of spatial

maps across sessions) we exclude the first 15 min following initial exposure to the environment in S1. For within-session control (comparison between the first and second halves of S1) we

separately generated spatial activity maps for the first and second halves of S1. The first 15 min were not excluded in the within-session control, to ensure sufficient coverage of the

environment by the fish trajectory. From the spatial activity map of each cell, spatial information can be used to quantify how much information is contained by that cell about the location

of the animal, in units of bits per second8. For each cell, spatial information _I_ was calculated as $$I=\sum _{x}\lambda \left(x\right){{\rm{lo}}g}_{2}\frac{\lambda \left(x\right)}{\lambda

}P(x),$$ where _x_ is a spatial bin, _P_(_x_) is the probability that the fish is in spatial bin _x_, _λ_(_x_) is the mean activity of the cell when the fish is in spatial bin _x_ and _λ_

is average neural activity, computed as \(\lambda ={\sum }_{x}\lambda (x)P(x)\). Based on the equation above, cells with high average neural activity tend to have higher spatial information.

To normalize for this we calculate specificity _s_ as $$s=\frac{I}{\lambda }.$$ In other words, specificity is spatial information divided by average neural activity, resulting in units of

bits per activity unit. Due to our baseline correction, bins occasionally have negative average activities. Such bins, as well as those with less than 1 s total occupancy time following

Gaussian filtering, were not included in the calculation of spatial information and specificity. To test the significance of the specificity of each cell we use circular permutation to

construct a null distribution. For each cell we define the set of valid timepoints as the frames in which neural activity was recorded and fish movement speed was above 0.1 mm s−1. A null

distribution for specificity is then estimated by measurement of specificity after circularly permuting the neural activity vector within the valid time points by 1,000 offsets (each offset

is 0.5 s, so it covers from −250 to +250 s). The specificity of a given cell is converted to a specificity _z_-score by subtracting the mean specificity of the null distribution and dividing

by the standard deviation of the null distribution. To test the significance of the specificity of a cell at the population level, a population specificity _z_-score is also calculated by

subtracting the mean specificity of all recorded cells and dividing by the standard deviation of the specificity of all recorded cells. To be classified as a place-encoding cell, a cell is

required to have a specificity _z_-score larger than or equal to 5, a population specificity _z_-score larger than or equal to 3 and a specificity value of over 0.01 bits per activity unit.

DEFINING PLACE FIELDS The place field (PF, or firing field) of each neuron is defined as the set of spatial bins with activity above 80% of peak activity (with peak defined as the 95th

percentile) of the spatial activity map. A more in-depth and systematic analysis of unimodal and multimodal PFs is described in Extended Data Fig. 1i–k, in which the activity threshold was

swept from 50 to 80%. The location of the PF is represented by its COM for cells with a single PF. For cells with multiple PFs (as distinct components in the map) we use the COM of the

component (over 20 bins, to avoid spurious PFs due to noise), with the highest peak activity (defined as the 95th percentile of the component) as the location of its primary PF. Only PCs

with a PF size of less than 30% of chamber size are included in maps of the distribution of PFs and in the analysis of PF shift. PFs are used only for analysis of PF shift and visualization

of PF location across an environment. All other analyses of PC activity, such as PF correlation, PV correlation, change in specificity and positional decoding, use the spatial activity map

directly. RIGID AND NON-RIGID REGISTRATION OF SPATIAL ACTIVITY MAPS ACROSS SESSIONS Experiments were conducted with various chambers, sometimes in varying orientations, sometimes before and

after morphing the chamber into different shapes. For comparison of spatial activity maps across these chambers we developed methods to register maps across sessions. When there was no

change in chamber wall geometry (for example, whole-chamber rotation), registration was performed by rotation and translation of the S2 activity map (that is, a rigid transformation) so that

activity in both sessions was represented in terms of the spatial bins of S1, thus facilitating comparisons (‘PV correlation, PF correlation and PF shift’). Otherwise we performed non-rigid

transformation to register spatial activity maps across sessions. Our strategy was first to establish a correspondence between the chamber walls of both sessions, then to map each spatial

bin of S2 to a set of spatial bins in S1 according to their distance to the wall anchor points, and finally to represent the activity of S2 in terms of the spatial bins of S1. Each of these

steps is described in greater detail below. First we detected the walls of the chambers in both sessions and defined a set of anchor points on the chamber walls. Because the precise number

of detected wall points could differ between sessions, we used linear interpolation to upsample the wall points of the session with fewer points, such that the number of anchor points was

the same across sessions. The correspondence between anchor points across sessions was established based on either landmarks (for example, the wall-morphing experiment with fish removal;

Fig. 5i) or the polar angle of the wall within the microscope reference frame in experiments with no clear match between geometry or landmarks (for example, rectangle-to-circle remapping

(Fig. 6a) and ABA remapping (Extended Data Fig. 9a)), or by systematic consideration of every rotation of the anchor points in S2 relative to S1 (Extended Data Figs. 8c,d and 10; ‘Non-rigid

transformation with the best rotation angle’). Next, for each spatial bin centre (_x_,_y_) in S2 we compute a corresponding location \(({x}^{{\prime} }\,,{y}^{{\prime} })\) in S1 using a COM

procedure. Specifically, for each anchor point \(({x}_{a},{y}_{a})\) in S2 we associate a weight \(1/{d}^{2}\), where _d_ is the distance between the anchor point \(({x}_{a},{y}_{a})\) and

the spatial bin centre (_x_,_y_) in S2. We then use the previously established wall correspondence between both sessions to transfer these weights to the anchor points in S1. The

corresponding location \(({x}^{{\prime} }\,,{y}^{{\prime} })\) in S1 is then defined as the COM of the S1 anchor points (that is, the weighted sum of the S1 anchor points divided by the sum

of the weights). Finally we represent the activity of S2 in terms of the spatial bins of S1. The computed location \(({x}^{{\prime} }\,,{y}^{{\prime} })\) in S1 is generally between the

spatial bin centres of the S1 activity map, so we identify the 4 × 4 spatial bins with bin centres (_x_,_y_) with \({\rm{floor}}({x}^{{\prime} })-1\le x\le {\rm{ceil}}\,({x}^{{\prime} })+1\)

and \({\rm{floor}}(\,y)-1\le y\le {\rm{ceil}}\,(\,y{\prime} )+1\). In this way we associate each S2 spatial bin with 4 × 4 spatial bins in S1. This procedure ensures that each S1 spatial

bin is associated with at least one S2 bin. We then average the activity of all S2 bins that are associated with a given spatial bin in S1, yielding a representation of the activity of S2 in

terms of the spatial bins of S1. NON-RIGID TRANSFORMATION WITH THE BEST ROTATION ANGLE Non-rigid transformation of the S2 maps described above is generally applied assuming a rotation angle

of 0° between sessions (for example, Figs. 4i, 5i and 6a). For systematic investigation of whether a coherent map rotation had occurred between sessions (Extended Data Fig. 8d), 72 

incremental rotations (covering 360°) were applied to the S2 anchor points followed by non-rigid registration as described above. The best rotation angle is identified by the maximum PF

correlation (‘PV correlation, PF correlation and PF shift’) across sessions. We refer to this procedure as ‘non-rigid transformation with the best rotation angle’. Note that this is also

done for the early–late control in Extended Data Fig. 8c,e. To test whether the improvement in PF correlation, from ‘non-rigid registration assuming an angle of 0°’ to ‘non-rigid

transformation with the best rotation angle’, is significant, we shuffle the cell identity in S2. Post shuffle, we then compare the improvement in PF correlation from non-rigid registration

assuming an angle of 0° with non-rigid transformation with the best rotation angle. This was repeated 1,000 times to generate a null distribution. The _P_ value in Extended Data Fig. 10 is

calculated by counting the percentage of shuffles in which the real data improve by less than the shuffle control. PV CORRELATION, PF CORRELATION AND PF SHIFT For comparison of

population-level activity across sessions, a population vector correlation (that is, PV correlation) was computed for each spatial bin that is shared across sessions. For each neuron we

first compute a Δ_F_/_F_ spatial activity map for each session. To do this we estimate a baseline fluorescent signal for each map by taking the mean of spatial bins with fluorescent signal

below the 20th percentile. The Δ_F_/_F_ of each spatial bin is then computed as follows: $$\frac{A-{\rm{baseline}}}{{\rm{baseline}}+c}$$ where _A_ is the mean fluorescent signal for a

spatial bin. A pseudocount _c_ is added when the baseline is below 10. For each spatial bin we obtained two vectors of population activity (one for each session). The length of the vector is

equal to the total number of telencephalic PCs identified from either session. Correlation between the two activity vectors yields the PV correlation for a given spatial bin. To determine

the similarity of spatial activity maps we computed the correlation between spatial activity maps (that is, PF correlation or spatial correlation). Correlation was performed on spatial bins

that are shared across both maps and normalized by the mean and variance of each map. All telencephalic cells identified as PCs in either session were used. To measure the extent of PF shift

across sessions, for each neuron we identified the COM of its PF in each session. We define PF shift as the distance between the COM of the cell’s PF in S1 and S2. Only cells with confined

PFs (firing field size less than 30% of chamber size; section ‘Defining place fields’) in both sessions are included for this analysis. For the within-session control we generate two

separate spatial activity maps corresponding to the early and late halves of S1. PV correlation, PF correlation and PF shift are computed from the within-session control spatial activity

maps using the procedure described above. For comparison with control we ensure that the same set of neurons (for PV correlation, PF correlation and PF shift) and spatial bins (for PV

correlation and PF correlation) are used. One-sided Wilcoxon signed-rank tests are used to measure whether PF correlation and PV correlation are significantly lower than control, and whether

PF shift is significantly higher than control. BLURRING OF THE SPATIAL ACTIVITY MAP Blurring is the broadening of a PF at a given point on its boundary in the radially outward direction.

For estimation of this blurring effect of PFs due to the speed of the fish, combined with calcium indicator dynamics, we compute an upper and a lower bound. The lower bound is computed by

assuming a 10 Hz firing rate and a speed of the mean minus standard deviation; the upper bound assumes a firing rate of 100 Hz with a speed of the mean plus standard deviation. Speed

distribution consists of pooled speed data from seven fish (Extended Data Fig. 1f). The data for the half-decay times for different firing rates are taken from ref. 54. The half-time of

temporal fluorescence decay is multiplied by the speed value to obtain the half-distance for spatial fluorescence decay (Extended Data Fig. 1g). Of this exponential spatial decay, the

distance needed for a decay down to 80% of starting value is computed (Extended Data Fig. 1h); this matches our definition of PF and is used as a blurring estimate. Based on the behavioural

data (Extended Data Fig. 1f) and calcium indicator kinetics, which both depend on firing rate54, we estimate the radius of the PFs to be spatially blurred by 0.17–1.31 mm. ISOMAP AND

QUANTIFICATION Isomap37 embedding was performed using Scikit-learn55 with ‘n_neighbors = 100’. A rectangular matrix representing the population activity of all telencephalic PCs in a span of

30 min was constructed, an Isomap manifold was fit to the data (with each point in the manifold representing the population activity at one time point) and finally a two-dimensional

embedding was extracted for visualization in Fig. 3a and computation in Fig. 3b. Because the implementation does not handle missing data, we filled in missing values in the activity trace

for individual cells with the nearest preceding available value. In the case of missing values at the beginning of the experiment, a backwards filling is applied. For Fig. 3a,b the early

(0–30 min) and late (60–90 min) windows of population activity data were fit separately and therefore have different two-dimensional embeddings. For Supplementary Video 2 we fit an Isomap

manifold to the final 30 min of imaging S1 (before chamber rotation; Fig. 4m) to establish stable axes for two-dimensional embedding, and then repeatedly transformed each window of 30 min of

population activity data into this embedding. Standard exclusion criteria based on movement were applied (spatial activity map in ‘Identification of PCs’). To quantify the relationship

between the two-dimensional manifold and the physical position of the fish we use neighbour distance, which quantifies the degree to which local neighbours in the manifold space are also

local neighbours in the physical space of the chamber. In a given 30 min time window we analyse each time point in the two-dimensional manifold space (the ‘seed point’) by selecting its 30 

nearest neighbours in the manifold space, then measuring the physical distance in the chamber between those 30 points and the seed point and averaging to obtain the mean physical neighbour

distance of the seed point. We then compute the overall average physical neighbour distance by averaging this across all time points in the manifold. As a baseline, for each seed point, 30 

random neighbours in the manifold are chosen and then physical neighbour distance is computed as before. For analyses comparing between two sessions, or between the early and late intervals

of a session (Fig. 3), the occupancy of each spatial bin was equalized by subsampling. That is, for each spatial bin, we identified the session or time interval having a lesser number of

time points and randomly subsampled from the session or time window with more time points, so that both time windows had the same number of time points in each spatial bin. DIRECT BASIS

DECODER The direct basis decoder36 is a linear decoder with no free parameters that predicts the animal’s position at each individual time point by a linear combination of the spatial

activity maps, weighted with the activity of the corresponding place-encoding cell. All decoding and map construction was performed only at those time points at which the fish was moving

(fish speed greater than 0.1 mm s−1). Even though no parameters had to be learned, it is still necessary to compute the spatial activity map of each cell. To avoid circularity between

computing the spatial activity map and testing the decoder we used a cross-validation scheme in which the neural data were divided into non-overlapping 1 min chunks. To test the decoder on

each 1 min chunk we first computed the spatial activity map without including the test chunk or its two neighbouring chunks. The predictions of all 1 min chunks were concatenated as the

prediction of the whole dataset. Decoder error was then computed as the mean distance between the predicted and actual position of the fish across the dataset. Spatial activity maps were

constructed as described above using spatial bins (side length 1.2 mm) and boundary-constrained Gaussian smoothing. Apart from the analysis shown in Extended Data Fig. 5c, the activity used

in this map construction is time shifted by 2 s relative to the location of the fish, to counteract potential calcium lag dynamics. All maps were standardized by mean and standard deviation.

To prepare the decoder, a 7.5 s boxcar average filter was applied to the activity and then maps of the most active 30% of cells were weighted by their respective activity and summed to form

the decoder map. This nonlinear thresholding step was designed to omit low-intensity signals that would contribute noise to the decoding. The decoder map was then normalized for density

differences in representation. To this end we calculated a representation histogram across all spatial bins, defined for each spatial bin as the number of PCs containing that bin in their

primary PF (Defining place fields). Because we found that the effect of representation density on decoding error was sublinear, we normalized the decoder map by the third root of the

representation histogram. The position estimate for each time point was then calculated by the COM of the 99th percentile of the decoder map. If not specified differently, 1,000 

telencephalic cells of the highest spatial tuning per animal were used for all decoding analyses. For selection of the top spatially tuned cells we ranked each telencephalic place-encoding

cell according to its specificity _z_-score and also according to its population specificity _z_-score, and then assigned its final rank according to the worse of the two ranks (Fig. 2f).

This allows for a fair comparison between fish that may have varying numbers of PCs (Fig. 1g). For selection of the minimum number of cells needed for good decoding, an iterative, greedy

algorithm was used (Fig. 2g). Starting with zero neurons, we find the single best neuron to add to the decoding set to minimize the resulting decoder error and then iteratively repeat this

same greedy selection procedure to grow the decoding set, one neuron at a time. For the analysis of decoder error by brain region (Fig. 2e), the 1,000 top spatially tuned cells were chosen

for each defined region (whole brain, telencephalon, mes- and rhombencephalon). The random cell population was randomly selected from cells with a population _z_-score less than 1, to

explicitly contain no PCs. We defined two baselines for evaluation of the decoder performance. For the uniform random baseline we measured the average decoder error of a decoder that outputs

random positions sampled uniformly from the chamber. This procedure was repeated 1,000 times, with the mean decoder error taken as the uniform random baseline. For the behaviour-informed

baseline we measured the average decoder error of a decoder that outputs the COM of fish positions in the chamber. For all analyses, if not specified differently, only the final 75 min of

each experiment were used for decoding. In the analysis of the decoder error as a function of number of cells included (Fig. 2f), the threshold for spatial tuning was gradually lowered until

10,000 cells were obtained (_n_ = 7 fish). The two fish with fewer than 10,000 recorded cells in the telencephalon were hence excluded from this analysis. To avoid circularity, for Fig. 3d

the shuffled specificity _z_-score and population _z_-score were calculated separately for the first and last 30 min of the experiments. Decoding for these two time windows was therefore

based on the respective top-ranked PCs within each window. We find that the non-redundant decoder starts to outperform the decoder using all cells from 17 cells onwards. The worse

performance of the decoder using all cells is a consequence of the simple linear decoder design, which values the information of all cells equally; hence, less specific neurons can influence

the decoder and slightly worsen the results. The advantages of this decoder, however, are the limited assumptions of the model, easy interpretability and impossibility of overfitting.

REGRESSION AND PREDICTION OF NEURAL ACTIVITY We used ordinary least-squares regression to measure how much of the variance in place-encoding cell activity can be explained by different

behavioural variables, including physical location, heading and speed. This is a much simpler model compared with previous work using a generalized linear model56. The behaviour variables

were discretized into bins, and an indicator function for each bin was added as a regressor in the model. The regression model can be summarized by the following formula: $${\lambda

}_{n}\left(t\right)={\mu }_{n}+\mathop{\sum }\limits_{i=1}^{L}{w}_{i,n}^{\left(x\right)}{x}_{i,t}+\mathop{\sum }\limits_{j=1}^{H}{w}_{j,n}^{\left(h\right)}{h}_{j,t}+\mathop{\sum

}\limits_{k=1}^{S}{w}_{k,n}^{\left(s\right)}{s}_{k,t}$$ where \({\lambda }_{n}\left(t\right)\) is the baseline-corrected neural activity for cell _n_ at time _t_, \({\mu }_{n}\) represents

baseline activity, \({w}_{i,n}^{(x)}{x}_{i,t}\) represents the contribution from the physical location of the fish, \({x}_{i,t}\) is the activity for spatial bin _i_ at time _t_, _L_ is the

number of spatial bins (15 × 8 = 120), \({w}_{j,n}^{\left(h\right)}{h}_{j,t}\) represents the contribution from the heading of the fish, \({h}_{j,t}\) is the activity for heading bin _j_ at

time _t_, _H_ is the number of heading bins (24), \({w}_{k,n}^{(s)}{s}_{k,t}\) represents the contribution from the speed of the fish, \({s}_{k,t}\) is the activity for speed bin _k_ at time

_t_ and _S_ = 24 is the number of speed bins. For comparison of contributions from spatial location, heading and speed, both individually and together, we tested ordinary least-squares

regression in four cases: \({\lambda }_{n}(t)={\mu }_{n}+{\sum }_{i=1}^{L}{w}_{i,n}^{(x)}{x}_{i,t}\) (that is, with only spatial indicator functions), \({\lambda }_{n}(t)={\mu }_{n}+{\sum

}_{j=1}^{H}{w}_{j,n}^{(h)}{h}_{j,t}\) (that is, with only heading indicator functions), \({\lambda }_{n}(t)={\mu }_{n}+{\sum }_{k=1}^{S}{w}_{k,n}^{(s)}{s}_{k,t}\) (that is, with only speed

indicator functions) and, finally, the complete equation shown above. All models included a weak L2 regularization on the parameters with a penalty coefficient of 1−10. For each regression

model we report the resulting distribution of _R_2 values across the telencephalic PCs shown in Extended Data Fig. 1b. Similarly, the distribution of _R_2 values across other telencephalic

cells is shown in Extended Data Fig. 1c. Standard exclusion criteria based on movement speed were applied (see spatial activity map in ‘Identification of PCs’). WHOLE-BRAIN PC MAPS Following

projection of the location of PCs from all fish to the same reference fish52, we accumulated all PCs into a three-dimensional histogram representing how many PCs were detected in each

three-dimensional bin within the reference volume. We then convolved the three-dimensional histogram with a spherical convolution mask of radius 5 µm, such that each place-encoding cell

contributes an increment of one count to all bins within a 5 µm radius. Maximum-intensity projections were then computed to visualize the anatomical distribution from multiple views (Fig.

1f). BVC MODEL To search for cells whose firing properties follow the BVC model34 we fitted a BVC model (see below) to candidate neurons in the telencephalon. The model predicts that the

activity of these cells, _f_, integrates each boundary point (represented in polar coordinates _r_ and _θ_ relative to the animal) according to $${\rm{\delta }}f=g(r,\theta ){\rm{\delta

}}\theta ,$$ where \(g(r,\theta )\) represents the firing rate relative to a preferred firing orientation _ϕ_ and distance _d_ from the boundary: $$g(r,\theta )=A\frac{\exp

\left[\frac{{-(r-d)}^{2}}{2{\sigma }_{{\rm{rad}}}^{2}}\right]}{\sqrt{2{\rm{\pi }}{\sigma }_{{\rm{rad}}}^{2}}}\frac{\exp \left[\frac{{-(\theta -\phi )}^{2}}{2{\sigma

}_{{\rm{ang}}}^{2}}\right]}{\sqrt{2{\rm{\pi }}{\sigma }_{{\rm{ang}}}^{2}}}+c.$$ Here, \({\sigma }_{{\rm{rad}}}\) and \({\sigma }_{{\rm{ang}}}\) are the width of radial and angular tuning,

respectively. Compared with the original model34, which treats \({\sigma }_{{\rm{rad}}}\) as a variable that linearly depends on _d_, we treat \({\sigma }_{{\rm{rad}}}\) as a constant to be

fit. _A_ is a scaling factor and _c_ is the baseline. Note that the bin size for spatial activity maps for this experiment is slightly smaller (side length 1.1 mm), to ensure sufficient

resolution for accurate detection and representation of the inserted wall. When fitting the model to spatial activity maps, we first normalize the map by its standard deviation. During the

fitting we constrain _d_ to be between 0 and 10 bins (assuming BVCs fire close to the boundary), _ϕ_ between −π and π, both \({\sigma }_{{\rm{rad}}}\) and \({\sigma }_{{\rm{ang}}}\) between

0 and 10, _A_ between 0 and 100 and _c_ between −10 and +10 activity units. To test whether the activity of a given neuron is predicted by the BVC model we performed a three-session

experiment—after a baseline session (45–95 min), an interior wall was introduced for S2 (45–95 min) and removed for S3 (45–95 min) (Extended Data Fig. 3b). We first identified all cells

passing a minimum specificity criterion (over 0.01 bits per activity unit for all three sessions). Given the orientation of the inserted wall, only cells with PFs parallel to the inserted

wall (from −45 to 45° or 135 to 225° in both S1 and S3) are suitable candidates for BVC analyses. We then fit the BVC model to the spatial activity maps of these candidate cells in S1 and

then used the fitted model to generate predicted activity maps across sessions (with or without wall insertion). We computed the Pearson correlation coefficient between the observed spatial

activity map of each session with the predicted activity map generated by the fitted model. To test the significance of the Pearson correlation coefficient we circularly permuted the

observed spatial activity maps approximately 1,100 times (same as the number of bins in the map) and recalculated the Pearson correlation coefficient for each permutation to construct the

null distribution for a one-sided shuffle test. Crucially, the BVC model predicts a duplication of PFs in S2. This duplicated firing field is expected to be absent in S1 and S3, which are

predicted to have the same spatial activity map. Thus, to be classified as a BVC, a cell has to be consistent with the BVC model in all three sessions: * 1. For S1, Pearson correlation

between the observed spatial activity map and model-predicted activity should be significantly higher relative to shuffle (_P_ < 0.05, one-sided shuffle test as described above). * 2. For

S2, Pearson correlation between the observed spatial activity map and model-predicted activity should be significantly higher relative to shuffle (_P_ < 0.05, one-sided shuffle test) and

the observed spatial activity map should have higher Pearson correlation with model-predicted activity with wall insertion than model-predicted activity without wall insertion. * 3. For S3,

the spatial activity map should return to the map observed in S1 (PF correlation between S1 and S3 should be significantly higher relative to shuffle; _P_ < 0.05, one-sided shuffle

test). NEIGHBOURHOOD ANALYSIS To quantify the degree to which potential clustering of PFs is maintained across sessions, we performed a neighbourhood analysis for each neuron (Fig. 6e).

First, for each neuron we ranked all other neurons by their PF correlation to the neuron of interest in S1. We define neurons with the highest PF correlation as neighbours, with a

systematically varied inclusion threshold from top 2% to top 100%. We define neighbour retention % as the number of neurons that remain neighbours in S2 divided by the number of original

neighbours in S1. The mean neighbour retention % across all telencephalic PCs from either session is then plotted. This analysis is also carried out separately for cells whose PF is close to

the edge (nearest distance of COM to edge 3 mm or less) and for cells whose firing field is away from the edge (nearest distance to edge greater than 3 mm). To avoid any potential

contribution from imperfect cell merging we restricted this analysis to pairs of cells with a minimum anatomical distance of over 20 µm. A one-sided Wilcoxon signed-rank test was used to

quantify whether neighbour retention % in the experiment was significantly worse than a within-session positive control (comparison between the early and late periods of S1). As a negative

control we shuffled the cell indices in the second session 1,000 times to randomize relationships between neurons. Post shuffle, we calculated mean neighbour retention % across all

telencephalic PCs from either session to generate a null distribution (that is, a shuffle control). A _P_ value is calculated by counting the percentage of shuffles in which the mean

neighbour retention % is higher than the shuffle control. For these significance tests we fixed the number of top correlated neighbours to 10%. SIGNIFICANCE TESTS FOR SAMPLE COMPARISON

Wilcoxon signed-rank tests were used for paired location comparisons with equal sample size. Mann–Whitney _U_-tests were used for unpaired location comparison. ANIMAL CARE AND TRANSGENIC

LINES Experiments were carried out in accordance with the Animal Welfare Office at the University of Tübingen and the Regierungspräsidium. All experiments in rectangular chambers, and ABA

experiments, used Tg(elavl3:H2B-GCaMP6s+/+) with nacre (mitfa−/−) at 6–9 days postfertilization. The remainder of the experiments used Tg(elavl3:H2B-GCaMP8s+/+ or GCaMP8s+/−) with nacre

(mitfa−/−) at 6–13 days postfertilization. In three of the rectangle-to-circle experiments the fish expressed an additional allele of Tg(elavl3:GCaMP6s). Fish were reared on a 14/10 h

light/dark cycle at 25 °C. They were maintained in sets of 30 in E3 water and fed dry food daily. COMPUTER HARDWARE FOR DATA ACQUISITION AND ANALYSIS The tracking microscope was controlled

by a rack-mounted, 12-core workstation with a Geforce RTX 3080 Ti graphics processing unit. Offline data analysis was performed using eight rack-mounted, 8- to 16-core Linux servers with

four graphics processing units each (Geforce RTX 3080 Ti, RTX 2080 Ti or GTX 1080 Ti), or at the Max Planck Computing and Data Facility (Raven, A100-SXM4). REPORTING SUMMARY Further

information on research design is available in the Nature Portfolio Reporting Summary linked to this article. DATA AVAILABILITY The data that support the findings of this study can be made

available from the corresponding authors on request. Source data are provided with this paper. CODE AVAILABILITY All analysis software was written in Julia 1.10 and CUDA C using the Julia

package ecosystem (Optim.jl, PyPlot.jl, PyCall.jl, Images.jl, Cairo.jl, HDF5.jl, CUDA.jl)57,58. Graphics processing was implemented for fish tracking, as well as for online and offline image

registration. Data analysis code is available online at https://github.com/RoLiLab/fish_place_cell_Yang_2024. CHANGE HISTORY * _ 13 SEPTEMBER 2024 A Correction to this paper has been

published: https://doi.org/10.1038/s41586-024-08009-4 _ REFERENCES * Rodríguez, F. et al. Spatial cognition in teleost fish: strategies and mechanisms. _Animals (Basel)_ 11, 2271 (2021).

PubMed  Google Scholar  * Briscoe, S. D. & Ragsdale, C. W. Evolution of the chordate telencephalon. _Curr. Biol._ 29, R647–R662 (2019). CAS  PubMed  PubMed Central  Google Scholar  *

Pandey, S., Moyer, A. J. & Thyme, S. B. A single-cell transcriptome atlas of the maturing zebrafish telencephalon. _Genome Res._ 33, 658–671 (2023). PubMed  PubMed Central  Google

Scholar  * Tanimoto, Y. et al. Transgenic tools targeting the basal ganglia reveal both evolutionary conservation and specialization of neural circuits in zebrafish. _Cell Rep._ 43, 113916

(2024). CAS  PubMed  Google Scholar  * O’Keefe, J. & Dostrovsky, J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. _Brain Res._ 34,

171–175 (1971). PubMed  Google Scholar  * O’Keefe, J. & Nadel, L. _The Hippocampus as a Cognitive Map_ (Oxford Univ. Press, 1978). * Kim, D. H. et al. Pan-neuronal calcium imaging with

cellular resolution in freely swimming zebrafish. _Nat. Methods_ 14, 1107–1114 (2017). CAS  PubMed  Google Scholar  * Skaggs, W. E., Mcnaughton, B. L., Gothard, K. M. & Markus, E. J.

Information theoretic approach to deciphering the hippocampal code. In _Advances in Neural Information Processing System_ 5 (eds. Hanson, S. J., Cowan, J. D. & Giles, C. J.) 1030–1037

(Morgan Kaufmann, 1993) . * O’ Keefe, J. & Burgess, N. Geometric determinants of the place fields of hippocampal neurons. _Nature_ 381, 425–428 (1996). ADS  PubMed  Google Scholar  *

Muller, R. U. & Kubie, J. L. The effects of changes in the environment on the spatial firing of hippocampal complex-spike cells. _J. Neurosci._ 7, 1951–1968 (1987). CAS  PubMed  PubMed

Central  Google Scholar  * Chen, G., King, J. A., Burgess, N. & O’Keefe, J. How vision and movement combine in the hippocampal place code. _Proc. Natl Acad. Sci. USA_ 110, 378–383

(2013). ADS  CAS  PubMed  Google Scholar  * Cheng, K. A purely geometric module in the rat’s spatial representation. _Cognition_ 23, 149–178 (1986). CAS  PubMed  Google Scholar  * Savelli,

F. & Knierim, J. J. Origin and role of path integration in the cognitive representations of the hippocampus: computational insights into open questions. _J. Exp. Biol._ 222, jeb188912

(2019). PubMed  PubMed Central  Google Scholar  * McNaughton, B. L., Battaglia, F. P., Jensen, O., Moser, E. I. & Moser, M. B. Path integration and the neural basis of the ‘cognitive

map’. _Nat. Rev. Neurosci._ 7, 663–678 (2006). CAS  PubMed  Google Scholar  * Lee, S. A., Vallortigara, G., Flore, M., Spelke, E. S. & Sovrano, V. A. Navigation by environmental

geometry: the use of zebrafish as a model. _J. Exp. Biol._ 216, 3693 (2013). PubMed  PubMed Central  Google Scholar  * Payne, H. L., Lynch, G. F. & Aronov, D. Neural representations of

space in the hippocampus of a food-caching bird. _Science_ 373, 343–348 (2021). ADS  CAS  PubMed  PubMed Central  Google Scholar  * Ulanovsky, N. & Moss, C. F. Hippocampal cellular and

network activity in freely moving echolocating bats. _Nat. Neurosci._ 10, 224–233 (2007). CAS  PubMed  Google Scholar  * Kumar, S. & Hedges, S. B. A molecular timescale for vertebrate

evolution. _Nature_ 392, 917–920 (1998). ADS  CAS  PubMed  Google Scholar  * Nieuwenhuys, R. The forebrain of Actinopterygians revisited. _Brain Behav. Evol._ 73, 229–252 (2009). PubMed 

Google Scholar  * Cohen, L., Vinepinsky, E., Donchin, O. & Segev, R. Boundary vector cells in the goldfish central telencephalon encode spatial information. _PLoS Biol._ 21, e3001747

(2023). CAS  PubMed  PubMed Central  Google Scholar  * Vinepinsky, E. et al. Representation of edges, head direction, and swimming kinematics in the brain of freely-navigating fish. _Sci.

Rep._ 10, 14762 (2020). ADS  CAS  PubMed  PubMed Central  Google Scholar  * Canfield, J. G. & Mizumori, S. J. Y. Methods for chronic neural recording in the telencephalon of freely

behaving fish. _J. Neurosci. Methods_ 133, 127–134 (2004). PubMed  Google Scholar  * Fotowat, H., Lee, C., Jun, J. J. & Maler, L. Neural activity in a hippocampus-like region of the

teleost pallium is associated with active sensing and navigation. _eLife_ 8, e44119 (2019). CAS  PubMed  PubMed Central  Google Scholar  * Ahrens, M. B., Orger, M. B., Robson, D. N., Li, J.

M. & Keller, P. J. Whole-brain functional imaging at cellular resolution using light-sheet microscopy. _Nat. Methods_ 10, 413–420 (2013). CAS  PubMed  Google Scholar  * Ahrens, M. B. et

al. Brain-wide neuronal dynamics during motor adaptation in zebrafish. _Nature_ 485, 471–477 (2012). ADS  CAS  PubMed  PubMed Central  Google Scholar  * McNaughton, B. L., Barnes, C. A.

& O’Keefe, J. The contributions of position, direction, and velocity to single unit activity in the hippocampus of freely-moving rats. _Exp. Brain Res._ 52, 41–49 (1983). CAS  PubMed 

Google Scholar  * Marques, J. C., Li, M., Schaak, D., Robson, D. N. & Li, J. M. Internal state dynamics shape brainwide activity and foraging behaviour. _Nature_ 577, 239–243 (2020). ADS

  CAS  PubMed  Google Scholar  * Petrucco, L. et al. Neural dynamics and architecture of the heading direction circuit in a vertebrate brain. _Nat. Neurosci_. 26, 765–773 (2023). * Severi,

K. E. et al. Neural control and modulation of swimming speed in the larval zebrafish. _Neuron_ 83, 692–707 (2014). CAS  PubMed  PubMed Central  Google Scholar  * Huszár, R., Zhang, Y.,

Blockus, H. & Buzsáki, G. Preconfigured dynamics in the hippocampus are guided by embryonic birthdate and rate of neurogenesis. _Nat. Neurosci._ 25, 1201–1212 (2022). PubMed  PubMed

Central  Google Scholar  * Kinsky, N. R., Sullivan, D. W., Mau, W., Hasselmo, M. E. & Eichenbaum, H. B. Hippocampal place fields maintain a coherent and flexible map across long

timescales. _Curr. Biol._ 28, 3578–3588 (2018). CAS  PubMed  PubMed Central  Google Scholar  * Friedrich, J. et al. Fast constrained non-negative matrix factorization for whole-brain calcium

imaging data. http://www.stat.columbia.edu/~johannes/docs/nips2015.pdf (2015). * Lever, C., Burton, S., Jeewajee, A., O’Keefe, J. & Burgess, N. Boundary vector cells in the subiculum of

the hippocampal formation. _J. Neurosci._ 29, 9771–9777 (2009). CAS  PubMed  PubMed Central  Google Scholar  * Barry, C. et al. The boundary vector cell model of place cell firing and

spatial memory. _Rev. Neurosci._ 17, 71–97 (2006). PubMed  PubMed Central  Google Scholar  * Solstad, T., Boccara, C. N., Kropff, E., Moser, M. B. & Moser, E. I. Representation of

geometric borders in the entorhinal cortex. _Science_ 322, 1865–1868 (2008). ADS  CAS  PubMed  Google Scholar  * Zhang, K., Ginzburg, I., McNaughton, B. L. & Sejnowski, T. J.

Interpreting neuronal population activity by reconstruction: unified framework with application to hippocampal place cells. _J. Neurophysiol._ 79, 1017–1044 (1998). CAS  PubMed  Google

Scholar  * Tenenbaum, J. B., De Silva, V. & Langford, J. C. A global geometric framework for nonlinear dimensionality reduction. _Science_ 290, 2319–2323 (2000). ADS  CAS  PubMed  Google

Scholar  * Lever, C., Wills, T., Cacucci, F., Burgess, N. & O’Keefe, J. Long-term plasticity in hippocampal place-cell representation of environmental geometry. _Nature_ 416, 90–94

(2002). ADS  CAS  PubMed  Google Scholar  * Knierim, J. J., Kudrimoti, H. S. & McNaughton, B. L. Place cells, head direction cells, and the learning of landmark stability. _J. Neurosci._

15, 1648–1659 (1995). CAS  PubMed  PubMed Central  Google Scholar  * Sanders, H., Wilson, M. A. & Gershman, S. J. Hippocampal remapping as hidden state inference. _eLife_ 9, e51140

(2020). PubMed  PubMed Central  Google Scholar  * Alme, C. B. et al. Place cells in the hippocampus: eleven maps for eleven rooms. _Proc. Natl Acad. Sci. USA_ 111, 18428–18435 (2014). ADS 

CAS  PubMed  PubMed Central  Google Scholar  * Fyhn, M., Hafting, T., Treves, A., Moser, M. B. & Moser, E. I. Hippocampal remapping and grid realignment in entorhinal cortex. _Nature_

446, 190–194 (2007). ADS  CAS  PubMed  Google Scholar  * Yoganarasimha, D., Yu, X. & Knierim, J. J. Head direction cell representations maintain internal coherence during conflicting

proximal and distal cue rotations: comparison with hippocampal place cells. _J. Neurosci._ 26, 622–631 (2006). Google Scholar  * Muessig, L. et al. Environment geometry alters subiculum

boundary vector cell receptive fields in adulthood and early development. _Nat. Commun._ 15, 982 (2024). ADS  CAS  PubMed  PubMed Central  Google Scholar  * Sharif, F., Tayebi, B., Buzsáki,

G., Royer, S. & Fernandez-Ruiz, A. Subcircuits of deep and superficial CA1 place cells support efficient spatial coding across heterogeneous environments. _Neuron_ 109, 363–376 (2021).

CAS  PubMed  Google Scholar  * Tan, H. M., Wills, T. J. & Cacucci, F. The development of spatial and memory circuits in the rat. _Wiley Interdiscip. Rev. Cogn. Sci._ 8, e1424 (2017).

Google Scholar  * Wills, T. J., Cacucci, F., Burgess, N. & O’Keefe, J. Development of the hippocampal cognitive map in preweanling rats. _Science_ 328, 1573–1576 (2010). ADS  CAS  PubMed

  PubMed Central  Google Scholar  * Skaggs, W. E. & McNaughton, B. L. Spatial firing properties of hippocampal CA1 populations in an environment containing two visually identical

regions. _J. Neurosci._ 18, 8455–8466 (1998). CAS  PubMed  PubMed Central  Google Scholar  * Grieves, R. M., Jenkins, B. W., Harland, B. C., Wood, E. R. & Dudchenko, P. A. Place field

repetition and spatial learning in a multicompartment environment. _Hippocampus_ 26, 118–134 (2016). PubMed  Google Scholar  * Spiers, H. J., Hayman, R. M. A., Jovalekic, A., Marozzi, E.

& Jeffery, K. J. Place field repetition and purely local remapping in a multicompartment environment. _Cereb. Cortex_ 25, 10–25 (2015). PubMed  Google Scholar  * Rohlfing, T. &

Maurer, C. R. Nonrigid image registration in shared-memory multiprocessor environments with application to brains, breasts, and bees. _IEEE Trans. Inf. Technol. Biomed._ 7, 16–25 (2003).

PubMed  Google Scholar  * Randlett, O. et al. Whole-brain activity mapping onto a zebrafish brain atlas. _Nat. Methods_ 1039–1046 (2015). * Gauthier, J. L. & Tank, D. W. A dedicated

population for reward coding in the hippocampus. _Neuron_ 99, 179–193 (2018). CAS  PubMed  PubMed Central  Google Scholar  * Chen, T.-W. et al. Ultrasensitive fluorescent proteins for

imaging neuronal activity. _Nature_ 499, 295–300 (2013). ADS  CAS  PubMed  PubMed Central  Google Scholar  * Pedregosa Fabian, et al. Scikit-learn: machine learning in Python. _J. Mach.

Learn. Res._ 12, 2825–2830 (2011). MathSciNet  Google Scholar  * Vinepinsky, E., Perchik, S. & Segev, R. A generalized linear model of a navigation network. _Front. Neural Circuits_ 14,

56 (2020). PubMed  PubMed Central  Google Scholar  * Bezanson, J., Edelman, A., Karpinski, S. & Shah, V. B. Julia: a fresh approach to numerical computing. _SIAM Rev. Soc. Ind. Appl.

Math._ 59, 65–98 (2017). MathSciNet  Google Scholar  * Besard, T., Foket, C. & De Sutter, B. Effective extensible programming: unleashing Julia on GPUs. _IEEE Trans. Parallel Distrib.

Syst._ 30, 827–841 (2019). Google Scholar  Download references ACKNOWLEDGEMENTS We thank R. Trivedi, S. Aimon, C. Heller, L. de Sardenberg Schmid and D. Cassidy Nolan for discussions and

feedback. This work was financially supported by the Max Planck Institute for Biological Cybernetics. FUNDING Open access funding provided by Max Planck Society. AUTHOR INFORMATION Author

notes * Lorenz Mammen Present address: Department of Neurobiology and Behavior, Cornell University, Ithaca, NY, USA * Meng Li Present address: Shanghai Institute of Microsystem and

Information Technology, Chinese Academy of Sciences, Shanghai, China * Meng Li Present address: INSIDE Institute for Biological and Artificial Intelligence, Shanghai, China AUTHORS AND

AFFILIATIONS * Max Planck Institute for Biological Cybernetics, Tuebingen, Germany Chuyu Yang, Lorenz Mammen, Byoungsoo Kim, Meng Li, Drew N. Robson & Jennifer M. Li * University of

Tuebingen, Tuebingen, Germany Chuyu Yang, Lorenz Mammen & Byoungsoo Kim Authors * Chuyu Yang View author publications You can also search for this author inPubMed Google Scholar * Lorenz

Mammen View author publications You can also search for this author inPubMed Google Scholar * Byoungsoo Kim View author publications You can also search for this author inPubMed Google

Scholar * Meng Li View author publications You can also search for this author inPubMed Google Scholar * Drew N. Robson View author publications You can also search for this author inPubMed 

Google Scholar * Jennifer M. Li View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS J.M.L. and D.N.R. conceived the project on identification

of cells with spatial information in the larval zebrafish brain. J.M.L., C.Y. and D.N.R. designed the behavioural chambers and experiments. J.M.L. and C.Y. collected the primary data. C.Y.

conducted the primary analysis related to spatial information, encoding, anatomical location, manifold structure and remapping, as well as data preprocessing. L.M. developed the direct basis

decoder and contributed to the design of the morph chamber and analysis of the manifold structure. B.K. contributed to data collection, data preprocessing and analysis for remapping

experiments and lights-off experiments. M.L. performed the preliminary analysis and initial identification of PCs using data from Marques et al.27. D.N.R. designed the software and hardware

for all imaging systems. C.Y., L.M. and B.K. contributed to all aspects of data analysis and manuscript preparation, with guidance from J.M.L. and D.N.R. CORRESPONDING AUTHORS Correspondence

to Drew N. Robson or Jennifer M. Li. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW  PEER REVIEW INFORMATION _Nature_ thanks the anonymous

reviewers for their contribution to the peer review of this work. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published

maps and institutional affiliations. EXTENDED DATA FIGURES AND TABLES EXTENDED DATA FIG. 1 PLACE CELL PROPERTIES. A, Example spatial activity maps at different locations in the chamber. B,

Modeling the relationship between activity and behavioral variables for telencephalic PCs. _R_² values of individual spatially tuned telencephalic cells after modeling their activity with

ordinary least squares regression (OLS, METHODS) using only the animal’s speed, heading, or two-dimensional position, as well as using all of them combined (n = 7 animals). C, Modeling the

relationship between activity and behavioral variables for other cells in the telencephalon. D, Activity traces (left) and spatial activity maps (right) for three example PCs. The time that

the fish spent inside the PF is marked in red. E, Statistics on the firing variability of PCs. One dot represents the mean and standard deviation of the peak activity across all traversals

of one PC. A traversal is defined as a stay inside the PF that is interrupted only by departures shorter than 5 s. Data pooled across 7 animals. F, Distribution of swimming speed from the

whole experiment from 7 animals, excluding quiescent time periods (swimming speed < 0.1 mm/s). G, Distribution of the estimated GCaMP6s fluorescence half decay distance in one linear

dimension, based on the data from F, and assuming decay half-times of 0.56 s (10 Hz firing rate) and 1.21 s (80 Hz firing rate). Vertical lines indicate the mean - std. dev. for the best

case and the mean + std. dev. for the worst case, based on the values of the distributions. H, Estimated actual PF blurring in one dimension based on an ideal PF with sharp edges (black

line, −2.5 mm to 2.5 mm) and the best and worst cases of half decay distances shown in G (blue and orange lines). PF size is determined by the set of spatial bins with activity above 80% of

the peak activity (with peak defined as 95th percentile) of the spatial activity map. Blurring to each side is 0.17 mm (best case) and 1.31 mm (worst case). I, Percentage of unimodal PCs as

a function of the threshold for defining the firing field. J, Spatial activity maps (left) and thresholded firing fields (right) at different thresholds for an example neuron with

consistently unimodal firing field (top), a neuron with consistently multimodal firing field (middle), and an ambiguous neuron (bottom) with unimodal or multimodal firing field depending on

the choice of threshold between 50% and 80%. K. More examples of neurons that are consistently unimodal (top) or consistently multimodal (bottom) as firing field threshold is swept between

50% and 80%. EXTENDED DATA FIG. 2 ANATOMICAL ANALYSIS OF PLACE CELLS. A, Fraction of cells within each brain region that are classified as PCs, shown for five differently shaped behavioral

chambers with or without landmarks: rectangle (Fig. 1a), asymmetric shape (Fig. 5a), square (Fig. 4e), octagon (Fig. 4i), and circle (Fig. 6a). B, Projections of telencephalic subdivisions:

pallium and subpallium. Masks imported from the Z-Brain-Atlas. C, Number of PCs in each brain region. Each animal is shown individually (orange dots, n = 7 animals) along with the median

across animals (black line). Tel., telencephalon; Mes., mesencephalon; Di., diencephalon; Rhomb., rhombencephalon. D, Anatomical distribution of cells that would be classified as PCs at

different spatial specificity thresholds, based on a population specificity z-score ≥ 1 (left), ≥ 3 (middle), and ≥ 5 (right). Summation of 7 animals overlaid on a reference brain. The black

bar indicates 50 μm. E, Anatomical distribution of cells that would be classified as PCs at different spatial information (SI) thresholds, based on a population SI z-score ≥ 1 (left), ≥ 3

(middle), and ≥ 5 (right). F, Comparison of SI for PCs found in the telencephalon and PCs found in the mesencephalon and rhombencephalon (left, n = 7 animals, _p_ = 1.1 × 10−98, one-sided

Mann–Whitney U test), as well as all PCs found in the whole brain (right, n = 7 animals). Since SI was calculated from calcium activity without attempting to convert to spikes/s, the SI

values reported here are proportional to classic SI, measured in bits/s, but with an unspecified constant of proportionality. G, Anatomical distribution of PCs (left) colored by their PF

locations (right). H, The relationship between anatomical distance and PF correlation. The solid line indicates the mean. The shaded region indicates the standard error of the mean. To avoid

any potential caveat of imperfect cell merging along the dorsal-ventral axis, only cell pairs from the same horizontal plane are plotted. To avoid overestimating correlation due to shared

measurement noise, adjacent cell pairs with NMF spatial footprints having any shared pixels are excluded (1.19% ± 0.54% of all cell pairs). EXTENDED DATA FIG. 3 BOUNDARY VECTOR CELL

ANALYSIS. A, Schematic of the boundary vector cell (BVC) model, adapted from Lever et al.33. A BVC reaches the highest firing rate when the animal is at its preferred firing orientation and

distance to the wall. B, Schematic of the experiment to test for BVCs in the larval zebrafish brain (METHODS). A wall hidden in the middle of the rectangular chamber is inserted between the

1st session (baseline) and the 2nd session of the experiment. Then the wall is removed again for the recording of the 3rd session of the experiment. The BVC model predicts that a BVC with a

preferred horizontal firing orientation would duplicate its firing field when a new wall is inserted. C, Procedure for identification of boundary vector cells. First, we identified suitable

candidate cells in the telencephalon with PFs parallel to the inserted wall (which could be PCs or non-PCs, left). We then fit the BVC model to the spatial activity maps of these candidate

cells in session 1 and used the fitted model to generate predicted activity maps across sessions (with or without wall insertion). We compare the actual spatial activity maps (left) and the

corresponding map predicted by the BVC model (right) to evaluate whether each cell is consistent with the BVC model. For each telencephalic candidate cell, the model is fit to the baseline

(1st session) and then used to predict the spatial activity map for the case of wall insertion or removal (2nd and 3rd sessions, METHODS). Top right shows an example neuron that is

consistent with the BVC model prediction. Bottom right shows an example of a neuron that does not follow the BVC model prediction. D, Additional examples of neurons that follow and do not

follow the BVC model prediction. EXTENDED DATA FIG. 4 SPATIAL REPRESENTATION AND OCCUPANCY. A, Distribution of telencephalic PFs encoding different locations in the behavioral arena (same as

Fig. 2a, n = 7 animals, median across animals is shown). To quantify the density of PFs across space, each spatial activity map was binarized. B, same as A, but showing the standard

deviation of spatial representation across the 7 animals. C, Spatial representation (top) and spatial occupancy (bottom) for two example fish. Representation and occupancy are both

normalized. D, Correlation between spatial representation and occupancy for 7 different animals. EXTENDED DATA FIG. 5 ADDITIONAL QUANTIFICATION OF DECODER ERROR. A, Distribution of decoder

error for 7 animals. Vertical lines indicate the median error (black line), the behavior-informed baseline (15.08 mm, dashed line), and the accessible length of the chamber’s long axis (47 

mm, dotted line). B, Replication of Fig. 2f but excluding from training the 2 min before and 2 min after the 1 min used for decoding (METHODS). The solid line indicates the mean, and the

shaded region indicates the standard deviation (the same applies to C). C, Decoder error as a function of timing shift between neural activity and animal position. EXTENDED DATA FIG. 6

SUMMARY OF SPATIAL ACTIVITY MAP CHANGES OF TELENCEPHALIC PLACE CELLS UNDER DIFFERENT ENVIRONMENTAL MANIPULATIONS. A, The median of PF correlation (top), PV correlation (middle), and PF shift

(bottom) for individual fish. Gray dots are comparisons between the early (1st half) and late (2nd half) stages of the 1st session. The red dots are comparisons made between the 1st session

and the 2nd session. Experiments from Figs. 4–6 are represented on the horizontal axis: chamber rotation (Fig. 4m), landmark removal (Fig. 4e), wall morphing (Fig. 4i), wall rotation (Fig.

5m), fish removal with no change in the chamber (Fig. 5a), landmark removal with fish removal (Fig. 5e), wall morphing with fish removal (Fig. 5i), and wall morphing with landmark removal

and fish removal (Fig. 6a). Data from the same fish are connected by gray lines. The results of statistical tests are marked for each fish separately (one-sided Wilcoxon signed-rank test,

*** for _p_ < 10−5, ** for _p_ < 0.001, * for _p_ < 0.01, n.s. for _p_ ≥ 0.01, see Supplementary Table 1 for exact _p_-values). B, The relationship between PF overlap and PF

correlation for different experiments. Each dot represents a PC. PF overlap is defined as the intersection over union of its PFs in the two sessions or between the early and late half of

session 1 (as control). Orange dots denote cells with significant PF correlation (one-sided shuffle test, _p_ < 0.05). Briefly, to test the significance of the PF correlation, we

circularly permuted (~ 1000 times, corresponding to the number of bins in the map) the observed spatial activity map of session 2 (or the 2nd half of session 1 in controls), and recalculated

the PF correlation across sessions for each permutation to construct the null distribution for a one-sided shuffle test. C, The dropout rates of PCs for individual fish (gray, within

session control; red, cross-session comparison, as defined in A). A dropout cell is defined as a cell that does not retain significant PF correlation between sessions and is only classified

as a PC in the first but not second session. EXTENDED DATA FIG. 7 PLACE FIELD CORRELATION VERSUS ENVIRONMENTAL FEATURES. Top, schematic of landmark removal experiment (Fig. 4e). Bottom, PF

correlation between recording sessions in the landmark removal experiment as a function of the distance of the PF (represented by its COM) to the landmark. Red line indicates mean values

after binning the data (n = 10 bins), red shaded region indicates standard deviation within bins. EXTENDED DATA FIG. 8 ADDITIONAL QUANTIFICATION OF MAP COMPARISONS. A, Summary of the changes

in telencephalic PCs by directly comparing the maps across two sessions in the microscope reference frame. Experiments from Fig. 4 and Fig. 5 are represented on the horizontal axis: chamber

rotation (Fig. 4m), landmark removal (Fig. 4e), wall morphing (Fig. 4i), wall rotation (Fig. 5m), fish removal with no change in the chamber (Fig. 5a), landmark removal with fish removal

(Fig. 5e), wall morphing with fish removal (Fig. 5i), and wall morphing with landmark removal and fish removal (Fig. 6a). From top to bottom are place field correlation (PF correlation),

population vector correlation (PV correlation), and the shift in the place field location (PF shift, METHODS). The union of telencephalic PCs from both sessions was used. The comparison

between the 1st and the 2nd sessions (red) is plotted against a reference comparison between the early (1st half) and late (2nd half) stages of the 1st session (black). Solid lines are the

mean distributions across all fish, and the shaded region indicates the standard deviation across all fish. Vertical dashed lines are the medians of the averaged distributions. B, similar to

A but after registering the maps from the 2nd session to the 1st session with reference to the chamber wall geometry and landmarks (METHODS). C, similar to B but the transformation is done

by finding the rotation of the reference anchor points that maximizes the mean PF correlation after registration (METHODS). D, The mean PF correlation as a function of the anchor rotation

angle used in the nonrigid transformation, for different experiments (METHODS). E, Summary of changes in the spatial activity maps of telencephalic PCs under different environmental

manipulations after applying the nonrigid transformation with the best rotation angle. The median of PF correlation, PV correlation, and PF shift are plotted for each fish. Red dots are

comparisons made between the 1st session and the 2nd session. Gray dots are reference comparisons made between the early (1st half) and late (2nd half) stages of the 1st session (also after

nonrigid transformation with the best rotation angle). The results of statistical tests are marked for each fish separately (one-sided Wilcoxon signed-rank test, *** for _p_ < 10−5, **

for _p_ < 0.001, * for _p_ < 0.01, n.s. for _p_ ≥ 0.01). See Supplementary Table 1 for exact _p_-values. F, Analysis of fish removal experiment as in Fig. 5d, but only for individual

fish where the olfactory cues were cleaned thoroughly before each recording session with soap and isopropanol. The results of statistical tests for different measures against a control

comparison between the early (1st half) and late (2nd half) period of the 1st session are shown for each fish (one-sided Wilcoxon signed-rank test, same for Extended Data Fig. 8g, fish 1 and

fish 2 corresponds to fish 1 and fish 2 in Supplementary Table 1). G, Analysis of fish removal experiment as in Fig. 5d, but only for individual fish where the bottom was rotated without

cleaning to scramble any potential olfactory cues (fish 1 and fish 2 correspond to fish 3 and fish 4 in Supplementary Table 1). See Supplementary Table 1 for exact _p_-values. EXTENDED DATA

FIG. 9 ABA EXPERIMENT. A, Schematic of ABA experiment. After the 1st recording session in an asymmetric chamber with landmarks, the fish was removed and transferred into a chamber with a

distinct arrangement of geometric features and landmarks for the 2nd recording session. For the 3rd recording session, the fish was removed and transferred back to the chamber that was used

in the 1st recording session (METHODS). B, Example animal trajectories in each session. C, Change in the distribution of telencephalic PCs with confined PFs, similar to Fig. 4b. Here, the

distributions are plotted separately for 1st session (top), 2nd session (middle), and 3rd session (bottom) for an example animal. Red boxes indicate the session where telencephalic PCs were

defined in each column. D, Example spatial activity maps as Fig. 4c. E, Summary of the changes in telencephalic PCs across the 1st and 2nd session, the 2nd and 3rd session, and the 1st and

3rd session. Similar to Fig. 4d, PF cor., PV cor., and PF shift were calculated for 4 fish. Each distribution uses the union of telencephalic PCs from the two sessions being compared. Grey

shaded regions show the distribution of each measurement, and black horizontal bars indicate medians. Each column is one fish. The results of statistical tests are marked on top of the

distributions being compared (one-sided Mann–Whitney U test, *** for _p_ < 10−5, ** for _p_ < 0.001, * for _p_ < 0.01, n.s. for _p_ ≥ 0.01, n.a. for not enough samples). The range

of sample sizes are provided on the right of each metric. See Supplementary Table 1 for exact _p_-values and exact sample sizes. EXTENDED DATA FIG. 10 WEAKLY COHERENT PLACE FIELD ROTATIONS

DURING REMAPPING. The increase in the median PF correlation (left), PV correlation (middle), and PF shift (right) are shown for 3 experiments: wall morphing without fish removal (Fig. 4i),

wall morphing with fish removal (Fig. 5i), and wall morphing with landmark removal and fish removal (Fig. 6a). Blue dots show the comparison of session 1 and session 2 after registration of

session 2 maps based on session 1 wall geometry and landmarks. Red dots show the comparison of session 1 and session 2 after registering session 2 maps to session 1 maps using the nonrigid

transformation with the best rotation angle. Data from the same fish are connected by gray lines. The observed improvement in PF correlation from map rotation was evaluated by a

non-parametric shuffle test (METHODS), applied to each fish individually: wall morphing without fish removal (1/4 fish, _p_ < 10−5, 3/4 fish, _p_ ≥ 0.01), wall morphing with fish removal

(1/3 fish, _p_ < 10−5, 2/3 fish, _p_ ≥ 0.01), and wall morphing with landmark removal and fish removal (2/4 fish, _p_ < 10−5, 1/4 fish, _p_ < 0.01, 1/4 fish, _p_ ≥ 0.01). See

Supplementary Table 1 for exact _p_-values. SUPPLEMENTARY INFORMATION SUPPLEMENTARY TABLE 1 _P_ values for all statistical tests. For all _P_ values of statistical tests, if not mentioned in

the figure legend they are provided in the table. REPORTING SUMMARY SUPPLEMENTARY VIDEO 1 Activity of three PCs over the course of one experiment. Fish trajectory is plotted in grey, and

cell activation (Δ_F_(_t_) greater than 3 s.d.) is shown as coloured dots (cyan, magenta and yellow representing the three cells). Activity is smoothed with a 2.5 s boxcar average filter.

SUPPLEMENTARY VIDEO 2 Activity manifold untangling over time. We fit an Isomap manifold to the final 30 min of imaging S1 (before chamber rotation; Fig. 4m) to establish stable axes for

two-dimensional embedding, and then repeatedly transformed each window of 30 min of population activity data into this embedding (Methods). SOURCE DATA SOURCE DATA FIG. 1 SOURCE DATA FIG. 2

SOURCE DATA FIG. 3 SOURCE DATA FIG. 4 SOURCE DATA FIG. 5 SOURCE DATA FIG. 6 RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International

License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source,

provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons

licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Yang, C., Mammen, L., Kim, B. _et al._ A population code for spatial representation

in the zebrafish telencephalon. _Nature_ 634, 397–406 (2024). https://doi.org/10.1038/s41586-024-07867-2 Download citation * Received: 24 October 2022 * Accepted: 23 July 2024 * Published:

28 August 2024 * Issue Date: 10 October 2024 * DOI: https://doi.org/10.1038/s41586-024-07867-2 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content:

Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative