Download PDF Article Open access Published: 12 April 2024 Inferring gene regulatory networks from single-cell multiome data using atlas-scale external data Qiuyue Yuan1 & Zhana Duren  ORCID:

orcid.org/0000-0003-4685-811X1  Nature Biotechnology volume 43, pages 247–257 (2025)Cite this article

56k Accesses

106 Altmetric

and RNA sequencing data, learning complex mechanisms from limited independent data points still presents a daunting challenge. Here we present LINGER (Lifelong neural network for gene

regulation), a machine-learning method to infer GRNs from single-cell paired gene expression and chromatin accessibility data. LINGER incorporates atlas-scale external bulk data across

diverse cellular contexts and prior knowledge of transcription factor motifs as a manifold regularization. LINGER achieves a fourfold to sevenfold relative increase in accuracy over existing

methods and reveals a complex regulatory landscape of genome-wide association studies, enabling enhanced interpretation of disease-associated variants and genes. Following the GRN inference

from reference single-cell multiome data, LINGER enables the estimation of transcription factor activity solely from bulk or single-cell gene expression data, leveraging the abundance of

available gene expression data to identify driver regulators from case-control studies.

multi-omics Article 26 June 2023 Single-cell multi-ome regression models identify functional and disease-associated enhancers and enable chromatin potential analysis Article Open access 21

March 2024 Gene regulatory network reconstruction: harnessing the power of single-cell multi-omic data Article Open access 19 October 2023 Main

GRNs1,2 are collections of molecular regulators that interact with each other and determine gene activation and silencing in specific cellular contexts. A comprehensive understanding of gene

regulation is fundamental to explain how cells perform diverse functions, how cells alter gene expression in response to different environments and how noncoding genetic variants cause

disease. GRNs are composed of transcription factors (TFs) that bind DNA regulatory elements to activate or repress the expression of target genes.

Inference of GRNs is a central problem2,3,4, and there have been many attempts to approach this issue2,5,6,7,8,9,10,11,12,13. Co-expression-based methods such as WGCNA14, ARACNe9 and GENIE3

(ref. 15) infer the TF–TG trans-regulation from gene expression by capturing the TF–TG covariation. Such networks have undirected edges, preventing distinction of direction from a TFA–TFB

edge. Moreover, co-expressions are interpreted as correlations rather than causal regulations16. Genome-wide measurements of chromatin accessibility, such as DNase-seq17 and assay for

transposase-accessible chromatin sequencing (ATAC-seq)18, locate REs, enabling TF–RE connections by motif matching and connecting REs to their nearby TGs19. However, TF footprint approaches

cannot distinguish within-family TFs sharing motifs. To overcome this limitation, we developed a statistical model, PECA20, to fit TG expression by TF expression and RE accessibility across

a diverse panel of cell types. However, the problem still has not been fully resolved because heterogeneity of cell types in bulk data limits the accuracy of inference.

The advent of single-cell sequencing technology has enabled highly accurate regulatory analysis at the level of individual cell types. Single-cell RNA sequencing (scRNA-seq) data enables

cell type-specific trans-regulation inference through co-expression analysis such as PIDC and SCENIC21,22,23,24,25,26,27,28,29,30. Single-cell sequencing assay for transposase-accessible

chromatin (scATAC-seq) can be used to infer trans-regulation, as in DeepTFni31. Many methods integrate unpaired scRNA-seq and scATAC-seq data to infer trans-regulation. Those methods,

including IReNA32, SOMatic33, UnpairReg34, CoupledNMF35,36, DC3 (ref. 36) and others37 link TFs to REs by motif matching and link REs to TGs using the covariation of RE–TG or physical base

pair distance. Recently, scJoint38 was developed to transfer labels from scRNA-seq to scATAC-seq data, which may enable improved cell GRN inference. Despite extensive efforts, GRN inference

accuracy has remained disappointingly low, marginally exceeding random predictions39.

Recent advances in single-cell sequencing40 provide opportunities to address these challenges41, exemplified by SCENIC+42. However, three major challenges persist in GRN inference. First,

learning such a complex mechanism from limited data points remains a challenge. Although single-cell data offers a large number of cells, most of them are not independent. Second,

incorporating prior knowledge such as motif matching into non-linear models is challenging. Third, inferred GRN accuracy assessed by experimental data is only marginally better than random

prediction39.

To overcome these challenges, we propose a method called LINGER (Lifelong neural network for gene regulation). This research paper contributes to the field of GRN inference in multiple ways.

First, LINGER uses lifelong learning, a previously defined concept43 that incorporates large-scale external bulk data, mitigating the challenge of limited data but extensive parameters.

Second, LINGER integrates TF–RE motif matching knowledge through manifold regularization, enabling prior knowledge incorporation into the model. Third, the accuracy of LINGER represents a

fourfold to sevenfold relative increase. Fourth, LINGER enables the estimation of TF activity solely from gene expression data, identifying driver regulators.

data to infer GRNs from single-cell multiome data

LINGER is a computational framework designed to infer GRNs from single-cell multiome data (Fig. 1 and Methods). Using count matrices of gene expression and chromatin accessibility along with

cell type annotation as input, it provides a cell population GRN, cell type-specific GRNs and cell-level GRNs. Each GRN contains three types of interactions, namely, trans-regulation

(TF–TG), cis-regulation (RE–TG) and TF-binding (TF–RE). Note that TF–TF interactions are included in TF–TG pairs but TF self-regulation, which is challenging to model without additional

data, is not considered. LINGER is distinguished by its ability to integrate the comprehensive gene regulatory profile from external bulk data. This is achieved through lifelong machine

learning, also called continuous learning. The concept of lifelong learning is that the knowledge learned in the past helps us learn new things with little data or effort44. Lifelong

learning has been proven to leverage the knowledge learned in previous tasks to learn the new task better45.

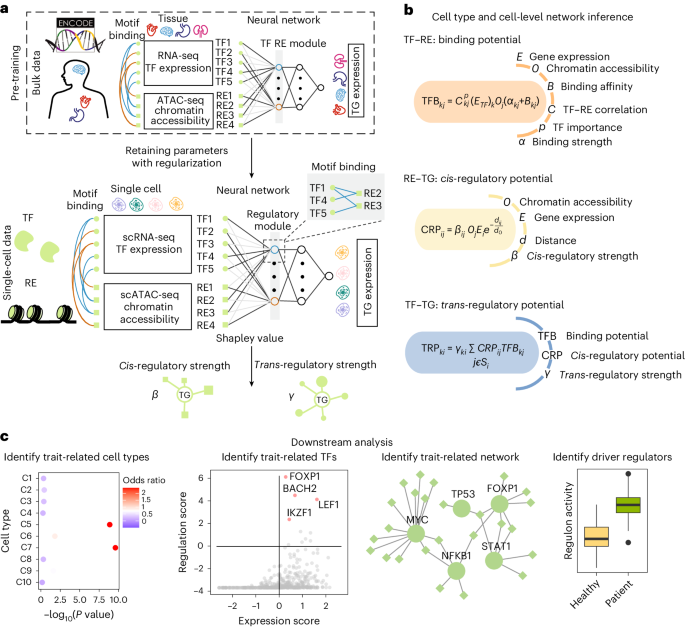
a, Schematic illustration of LINGER: a model predicting gene expression by TF expression and chromatin accessibility using a neural network model. LINGER pre-trains on the atlas-scale

external bulk data and retains parameters by lifelong learning. The population-level GRN is generated from the neural network using the Shapley value. b, Strategy for constructing cell

type-specific and cell-level GRNs. Cell type-specific and cell-level GRNs are inferred by an identical strategy, which combines consistent information across all cells, including regulatory

strength, motif binding affinity and RE–TG distance, with context-specific information on gene expression and chromatin accessibility. c, Downstream analyses enabled by LINGER-inferred GRNs,

including identifying complex regulatory landscape of GWAS traits and driver regulator identification.

LINGER leverages external data to enhance the inference from single-cell multiome data, incorporating three key steps: training on external bulk data, refining on single-cell data and

extracting regulatory information using interpretable artificial intelligence techniques. In our approach, we use a neural network model to fit the expression of TGs, taking as input TF

expression and the accessibility of REs. The second layer of the neural network model consists of weighted sums of TFs and REs, forming regulatory modules guided by TF–RE motif matching by

incorporating manifold regularization. This leads to the enrichment of TF motifs binding to REs that belong to the same regulatory module. First, we pre-train using external bulk data

obtained from the ENCODE project46, which contains hundreds of samples covering diverse cellular contexts, referred to as BulkNN.

For refinement on single-cell data, we apply elastic weight consolidation (EWC) loss, using bulk data parameters as a prior. The magnitude of parameter deviation is determined by the Fisher

information, which reflects the sensitivity of the loss function to parameter changes. In the Bayesian context, knowledge gained from the bulk data is the prior distribution, forming our

initial beliefs about the model parameters. As the model trains on new single-cell data, the posterior distribution is updated, combining the prior knowledge with the likelihood of the new

data. EWC regularization encourages the posterior to remain close to the prior, retaining knowledge while adapting, preventing excessive changes and ensuring a more stable learning

process47. After training the neural network model on single-cell data, we infer the regulatory strength of TF–TG and RE–TG interactions using the Shapley value, which estimates the

contribution of each feature for each gene. The TF–RE binding strength is generated by the correlation of TF and RE parameters learned in the second layer (Fig. 1a). LINGER then constructs

the cell type-specific and cell-level GRNs based on the general GRN and the cell type-specific profiles (Fig. 1b and Methods).

We will use independent datasets to validate the inference of GRN and then perform several downstream analyses: first, identification of the disease or trait-related cell type, TFs and GRN

combining genome-wide association studies (GWAS) data; second, constructing regulon activity on external expression data and identifying driver regulators as differentially active TFs (Fig.

1c).

To assess the performance of LINGER, we used a public multiome dataset of peripheral blood mononuclear cells (PBMCs) from 10× Genomics (see Methods for details). To investigate whether a

linear model is adequate for modeling gene expression or whether a non-linear model is necessary, we conducted a comparative analysis between two models. The first model employs an elastic

net to predict the expression of TG by TFs and REs. The second model, single-cell neural network (scNN), is a three-layer neural network model sharing LINGER’s architecture. We assessed the

gene expression prediction ability of the two models using fivefold cross-validation. We found that scNN modeled gene expression better than elastic net, with −log10P = 572.09, especially

for those substantial proportions of genes that show negative Pearson’s correlation coefficient (PCC) in elastic net predictions (−log10P = 1,060.17; Fig. 2a). This demonstrates that the

three-layer neural network model scNN outperforms the elastic net model in predicting gene expression.

a, Correlation between predicted and real gene expression, showing higher accuracy for scNN than elastic net. The x axis represents the PCC of genes predicted by elastic net and real gene

expression across cells, while the y axis gives the PCC for scNN. The points represent genes and the color of the points represents the density. The color of distribution in b–e indicates

the different methods: orange, LINGER; gray, elastic net; dark green, scNN; blue, BulkNN; light blue, PCC. Null hypothesis testing results in a t-statistic with an effect size of 53.46, df =

 15,659, −log10P = 572.09 and 95% confidence interval of [0.058, 0.063] from a two-sided paired t-test. b, Boxplot of the performance metric AUC for the predicted trans-regulatory strength

across all ground truth data. The ground truth data for b and c are putative targets of TFs from 20 ChIP–seq data points from blood cells (n = 20 independent samples). PCC denotes Pearson’s

correlation coefficient between the chromatin accessibility of RE and the expression of TG. Note that all boxplots in this study present minima and maxima, the smallest and largest value

that is not considered an outlier; center, median; bounds of box, 25th (Q1) to 75th (Q3) percentile; whiskers, 1.5 times the (Q3–Q1). In this study, we use the following convention for

symbols indicating statistical significance: ns, P > 0.05; *P ≤ 0.05; **P ≤ 0.01; ***P ≤ 0.001; ****P ≤ 0.0001. We hide the ns symbol when displaying significance levels. In detail, P = 8.32

 × 10−6 for LINGER and scNN, P = 8.57 × 10−5 for LINGER and BulkNN and P = 1.24 × 10−3 for LINGER and PCC. c, Boxplot of the performance metric AUPR ratio for the predicted trans-regulatory

strength. P values in b and c are from one-sided paired t-tests. In detail, P = 3.49 × 10−3 for LINGER and scNN, P = 2.13 × 10−4 for LINGER and BulkNN and P = 4.53 × 10−4 for LINGER and PCC.

d, AUC for cis-regulatory strength inferred by LINGER. The ground truth data for d and e are the variant-gene links from eQTLGen. We divide RE–TG pairs into different groups based on the

distance of the RE from the TSS of TG. e, AUPR ratio for cis-regulatory strength. f, Classification of the trans-dominant or cis-dominant gene. TFs contribute more to predicting the

expression of trans-dominant genes, while REs contribute more to cis-dominant genes. g, Probability of trans-dominant and cis-dominant being loss-of-function (LoF)-intolerant genes. Points

show estimated success probability from binomial distribution, at 0.26 and 0.09 for trans-dominant and cis-dominant, respectively. n = 317 and n = 693 independent sample size for

trans-dominant and cis-dominant, respectively. Data are presented as means ± 1.96 × s.d.

To show the utility and effectiveness of integrating external bulk data, we compared LINGER to scNN, BulkNN and PCC. To evaluate the performance of trans-regulatory strength, we collected

putative targets of TFs from chromatin immunoprecipitation followed by sequencing (ChIP–seq) data using a systematical standard (Methods) and, in total, obtained 20 data sets in blood cells

as ground truth48 (Supplementary Table 1). For each ground truth, we calculated the area under the receiver operating characteristic curve (AUC) and the area under the precision–recall curve

(AUPR) ratio (see Methods) by sliding the trans-regulatory predictions. Results show that scNN performs better than PCC and BulkNN. Compared to other methods, LINGER performs better, with a

significantly higher AUC (Fig. 2b) and AUPR ratio (Fig. 2c) across all ground truth data.

To validate the cis-regulatory inference of LINGER, we calculated the consistency of the cis-regulatory coefficients with expression quantitative trait loci (eQTL) studies that link genotype

variants to their TGs. We downloaded variant-gene links defined by eQTL in whole blood from GTEx49 and eQTLGen50 (Supplementary Table 2) as ground truth. As the distance between RE and TG

is important for the prediction, we divided RE–TG pairs into different distance groups. LINGER achieved a higher AUC and AUPR ratio than scNN in all different distance groups in eQTLGen

(Fig. 2d,e) as well as GTEx (Extended Data Fig. 1a,b). The above results show that LINGER improves the cis-regulatory and trans-regulatory strength inference by leveraging external data.

We next sought to investigate the dominant regulation for genes; that is, whether a gene is mainly regulated by cis-regulation or trans-regulation. To shed light on this question, we

compared the average of cis-regulatory and trans-regulatory strength Shapley values by a two-sided unpaired t-test and performed Bonferroni P value correction. Our findings reveal that most

genes exhibit no significant difference in cis-regulation and trans-regulation dominance. Specifically, 4.37% of genes are cis-regulation dominant, while 2.00% are trans-regulation dominant

(Fig. 2f). To discern evolutionary distinctions between trans-dominant and cis-dominant genes, we compared their strength of selection using pLI, which is an estimate of the ‘probability of

being loss of function intolerant’51. We observed that the percentage of selectively constrained genes with high pLI (>0.9) in the trans-dominant group was approximately three times higher

than that in the cis-dominant group (Fig. 2g). A previous study found that disease-associated genes from GWAS were enriched in selectively constrained genes, while eQTL genes were depleted

in selectively constrained genes52. These observations highlight the importance of the trans-regulatory network in understanding complex diseases. Functional enrichment analysis53 shows that

the cis-regulatory dominant genes were significantly enriched in 38 GTEx aging signatures (Supplementary Table 3), which aligns with the conclusion that chromatin accessibility alterations

occur in age-related macular degeneration54.

To gain an understanding of parameter sensitivity, we systematically evaluated the effects of TF–RE motif matching, cis-REs transcription start site (TSS) distance, activation function,

number of nodes in hidden layers and metacell-generating method on the scNN. Note that the sigmoid activation function would not improve the gene expression prediction but would improve the

GRN inference (Extended Data Fig. 2a). Using motif matching information by manifold regularization loss properly by setting the weight will improve the performance. Compared to 0, weight

0.01 improved the performance on 100% (Extended Data Fig. 2c) and 80% (Extended Data Fig. 2d) of ground truth data based on the AUC and AUPR ratio, respectively. The performance of weight 10

decreases compared to 0.01 (Extended Data Fig. 2c,d). To verify the robustness of our method to alternative metacell-generation approaches (see ‘PBMC 10× data’ in Methods), we used

metacells generated by the SEACells as a substitute for our original metacells. There were no significant differences in the performance between SEACells metacells and our original metacells

(two-sided paired t-test, P = 0.89; Extended Data Fig. 2e). Using REs within 1 Mb is the best across 200 kb, 500 kb, 1 Mb and 2 Mb (Extended Data Fig. 2f,g).

We evaluated LINGER’s capability for lifelong learning by leveraging additional data sources. We split the ENCODE data into two batches (ENCODE1, ENCODE2) and applied two rounds of

pre-training, then trained on PBMCs single-cell multiome data (ENCODE1+ENCODE2+sc). We compared the results with those obtained by using one batch of ENCODE data as pre-training

(ENCODE1+sc). Extended Data Fig. 2h shows that compared to single pre-training, the addition of the second round of pre-training improved the performance of TF–TG inference for 85.5% (17 out

of 20) and 75% (15 out of 20) of ChIP–seq data based on the AUC and AUPR ratio, respectively. This validates LINGER’s capability for continuous refinement through incremental learning from

diverse datasets.

We evaluated the cell type-specific GRN inference (Methods) of LINGER in PBMCs sc-multiome data as well as an in-silico mixture of H1, BJ, GM12878 and K562 cell lines from single-nucleus

chromatin accessibility and mRNA expression sequencing (SNARE-seq) data55. To assess TF–RE binding prediction, we used ChIP–seq data as ground truth, including 20 TFs from four cell types

within the blood and 33 TFs from the H1 cell line48 (Supplementary Table 4). The putative target of TF from the ChIP–seq data serves as ground truth for the trans-regulatory potential. For

the cis-regulatory potential, we incorporated promoter-capture Hi-C data of three primary blood cell types (Supplementary Table 5)56 and single-cell eQTL57, including six immune cell types

as ground truth for PBMCs.

To assess the TF–RE binding potential, we compared our method with TF–RE correlation (PCC) and motif binding affinity. For example, in naive CD4 T cells, LINGER achieves an AUC of 0.92 and

an AUPR ratio of 5.17 for ETS1, which is an improvement over PCC (AUC, 0.78; AUPR ratio, 2.71) and motif binding affinity (AUC, 0.70; AUPR ratio, 1.92) (Fig. 3a,e). For binding sites of MYC

in the H1 cell line, LINGER outperforms PCC and motif binding affinity-based predictions (Extended Data Fig. 3a,b). For all 20 TFs in PBMCs, LINGER consistently exhibits the highest AUC and

AUPR ratios, and the overall distributions are significantly higher than others in PBMCs (P ≤ 8.72 × 10−5; Fig. 3b,c and Supplementary Table 6). LINGER also outperforms other methods for H1

data (P ≤ 6.68 × 10−6; Extended Data Fig. 3c,d). Furthermore, we compared LINGER with a state-of-the-art method, SCENIC+42, which predicts TF–RE pairs from multiome single-cell data. Given

that SCENIC+ does not provide a continuous score for all REs, we used the F1 score as a measure of accuracy. Fig. 3d shows that LINGER performs better for all 20 TFs binding site

predictions.

a,e, Receiver operating characteristic curve and precision–recall curve of binding potential for ETS1 in naive CD4 T cells. The ground truth for a and e is the ChIP–seq data of ETS1 in naive

CD4+ T cells. The color in a–e represents the different methods used to predict TF–RE regulation. Orange, LINGER; green, PCC between the expression of TF and the chromatin accessibility of

RE; blue, motif binding affinity of TF to RE. b,c, Violin plot of the AUC and AUPR ratio values of binding potential across diverse TFs and cell types. The ground truth is the ChIP–seq data

for 20 TFs from different cell types in blood. The original data is in Supplementary Table 6. The null hypothesis testing in b, comparing the AUC of LINGER with PCC and binding, results in

t-statistics (one-sided paired t-test) with effect size, 8.99; df, 19; P = 1.42 × 10−8, 95% confidence intervals, [0.17, Inf] and effect size, 18.25; df, 19; P = 8.34 × 10−14; 95% confidence

intervals, [0.17, Inf], respectively. The null hypothesis testing in c, comparing the AUPR ratio of LINGER with PCC and binding, results in t-statistics (one-sided paired t-test) with

effect size, 4.65; df, 19; P = 8.72 × 10−5; 95% confidence intervals, [1.31, Inf] and effect size, 5.44, df, 19; P = 1.49 × 10−5; 95% confidence intervals, [1.51, Inf], respectively. d, The

performance metrics F1 score of binding potential. Each point represents ground truth data (n = 20 independent samples). The P values for d, h and k are based on one-sided paired t-tests.

f,g, AUC and AUPR ratio of cis-regulatory potential in naive CD4+ cells. The ground truth for f–h is promoter-capture Hi-C data. RE–TG pairs are divided into six distance groups ranging from

0–5 kb to 100–200 kb. PCC is calculated between the expression of TG and the chromatin accessibility of RE. Distance denotes the decay function of the distance to the TSS. Random denotes

the uniform distribution from 0 to 1. h, F1 score of cis-regulatory in naive CD4+ cells for LINGER and SCENIC+ (n = 9 independent samples). i,j, AUC and AUPR ratio of cis-regulatory

potential. The ground truth is eQTL data from six immune cell types. k, F1 score of cis-regulatory potential in naive B cells. The ground truth is eQTL data from naive B cells (n = 9

independent samples). This figure corresponds to the PBMC data.

To assess the cis-regulatory potential, we compared LINGER with four baseline methods, including distance-based methods, RE–TG correlation (PCC), random predictions, and SCENIC+. We divided

RE–TG pairs of Hi-C data into six distance groups ranging from 0–5 kb to 100–200 kb. In naive CD4 T cells, LINGER achieves AUC ranging from 0.66 to 0.70 (Fig. 3f) and AUPR ratio ranging from

1.81 to 2.16 (Fig. 3g) across all distance groups, while other methods are close to random. In other cell types, LINGER exhibits consistent superiority over the baseline methods (Extended

Data Fig. 3e–h). All eQTL pairs were considered positive labels owing to the insufficient pairs available for division into distance groups. In all cell types, the AUC and AUPR ratio of

LINGER are higher than the baseline methods (Fig. 3i,j). We also compared our method with SCENIC+, which outputs predicted RE–TG pairs without importance scores. We selected the same number

of top-ranking RE–TG pairs and calculated the F1 score using nine cutoffs corresponding to quantiles ranging from the 10th to the 90th percentile. As a result, LINGER attains significantly

higher F1 scores than SCENIC+ in all cell types (Fig. 3h and Extended Data Fig. 3i,j) based on Hi-C data. Taking eQTL as ground truth, the F1 score of LINGER is significantly higher than

SCENIC+ (Fig. 3k) and other cell types (Extended Data Fig. 3k–o).

To evaluate the accuracy of trans-regulatory potential, we chose GENIE3 (ref. 15) and PIDC21 for comparison based on the benchmarking literature of GRN inference from single-cell data39 that

we chose in previous work58 (see Methods). In addition, we compared LINGER with PCC and SCENIC+. For STAT1 in classical monocytes, LINGER improves the prediction performance, as evidenced

by an AUC of 0.76 versus 0.57–0.59 and an AUPR ratio of 2.60 versus 1.26–1.36 (Fig. 4a,b). A similar improvement is observed for CTCF in H1 (Extended Data Fig. 3p,q). The average AUPR ratio

across ground truth datasets for other methods was 1.17–1.29, 0.17–0.29 units above random prediction, whereas LINGER achieves 1.25 units above random prediction, indicating a fourfold to

sevenfold relative increase (Fig. 4d). Overall, LINGER consistently performs better than other methods for all 20 TFs in PBMCs, with a significantly higher AUC and AUPR ratio (P ≤ 9.49 × 

10−9; Fig. 4c,d and Supplementary Table 7). LINGER outperforms other competitors in the H1 cell line (P  ≤ 3.00 × 10−8; Extended Data Fig. 3r). Unlike GENIE3 and PIDC, which solely use

scRNA-seq data, our method effectively doubles the cell data by integrating both scRNA-seq and scATAC-seq. For a fairer comparison, we removed pre-training and used only half as many cells

as input (scNN_half). Comparing to other competitors showed that scNN_half continued to significantly outperform all other methods (Extended Data Fig. 2b). We also evaluated cell

type-specific trans-regulatory potential to predict direct differentially expressed genes (DEGs) under perturbation of the TF, using perturbation experiment data as ground truth. We

collected eight datasets for PBMCs (Supplementary Table 8) from the KnockTF database59. Extended Data Fig. 4a,b shows that LINGER outperforms all other methods (P ≤ 3.72 × 10−4).

Systematic benchmarking of cell type-specific trans-regulatory potential performance.

a,b, Receiver operating characteristic curve and precision–recall curve of trans-regulatory potential inference of STAT1 in classical monocytes. The ground truth data in a–d are putative

targets of TFs from ChIP–seq data for the corresponding cell types in PBMCs. c,d, Violin plot of AUC and AUPR ratio values of trans-regulatory potential performance across diverse TFs and

cell types. The original data is in Supplementary Table 7. The sample size for the one-sided paired t-test is 20. For c, −log10(P values) are 11.12, 7.72, 11,13 and 10.17 for GENIE3, PCC,

PIDC and SCENIC+, respectively. For d, −log10(P values) are 9.59, 8.02, 9.22 and 8.47, respectively. e, Uniform manifold approximation and projection (UMAP) of PBMCs including 14 cell types.

NK cells, natural killer cells; MAIT, mucosal-associated invariant T cells; DCs; dendritic cells. f, UMAP of RUNX1 expression across PBMCs. g, UMAP of cell level trans-regulatory potential

for RUNX1(TF)–SPI1(TG) across PBMCs. h, UMAP of cell level trans-regulatory potential for RUNX1(TF)–PRKCQ(TG) across PBMCs. i, Violin plot of cell level trans-regulatory potential from

different cell types. The sample size for each boxplot is the number of cells of each cell type, ranging from 98 to 1,848. This figure corresponds to the PBMCs.

The rationale for constructing a single-cell-level GRN is the same as a cell type-specific GRN, replacing the cell type-specific term with the single-cell term (Methods). We show the result

of trans-regulation, taking RUNX1 as an example. RUNX1 is critical for establishing definitive hematopoiesis60 and expresses at high levels in almost all PBMC cell types (Fig. 4e,f). RUNX1

regulates SPI1 in monocytes (classical, non-classical and intermediate) and myeloid dendritic cells (Fig. 4g,i), while regulates PRKCQ in CD56dim natural killer cells, effector CD8 T cells,

mucosal-associated invariant T cells, memory CD4 T cells, naive CD4 T cells and naive CD8 T cells (Fig. 4h,i). This example illustrates the capability of LINGER to visualize gene regulation

at the single-cell level.

GWASs have identified thousands of disease variants, but the active cells and functions involving variant-regulated genes remain largely unknown61. We integrate GWAS summary statistics and

cell type-specific GRN to identify the relevant cell types, key TFs and sub-GRN (Methods). We define a trait regulation score for TFs in each cell type, measuring the enrichment of GWAS

genes downstream of TFs. In trait-relevant cell types, TFs with high trait regulation scores should be expressed to perform their function. We identify the trait-relevant cell types by

assessing the concordance between TF expression and the trait regulation score.

In our specific study on inflammatory bowel disease (IBD), we collected the risk loci based on a GWAS meta-analysis of about 330,000 individuals from the NHGRI-EBI GWAS catalog62 for study

GCST9022555063. Figure 5a shows that in classical monocytes, trait regulation scores for the top-expressed TF are significantly higher than randomly selected TFs (P = 8.9 × 10−29, one-sided

unpaired t-test), while there is no significant difference for non-relevant cell types such as CD56dim natural killer cells. The most relevant cell types in PBMCs are monocytes and myeloid

dendritic cells (Fig. 5b). These findings align with previous studies linking monocytes to the pathogenesis of IBD64,65.

landscape.

a, Distribution of the number of TGs for top expression TFs and randomly selected TFs in classical monocytes (top) and CD56dim NK cells (bottom). The 100 top-expression TFs and 100 randomly

selected TFs are used to generate the distribution. b, Enrichment of IBD GWAS to cell types in PBMCs. The color of the bubbles corresponds to the odds ratio of the number of TGs between top

expression and randomly selected TFs. The x axis is the −log10(P value) from the one-sided unpaired t-test for the number of TGs between top expression and randomly selected TFs. c, Key

IBD-associated regulators in classical monocytes. The x axis is the z-score of the expression of TFs across all TFs. The y axis is the regulation score of TFs. The TFs in red are the

top-ranked TFs according to the summation of the expression level and regulation score. d, Enrichment of GWAS IBD genes among STAT1 targets in classical monocytes. The violin plot is

generated by randomly choosing 1,000 TFs; the number of overlapping genes for STAT1 is marked by a star. The different violin plots correspond to taking the top 200–5,000 genes as the TG for

each TF, respectively. e, Enrichment of DEGs between inflamed biopsies and non-inflamed biopsies among STAT1 targets in classical monocytes. The details are the same as in d. f, Sub-network

of IBD-relevant TFs from classical monocytes trans-regulatory network. The size of the TF or TG nodes corresponds to their degree in the network. The color of TF denotes the trait-relevant

score, and the color of TG denotes the −log10(P value) of GWAS SNP assigned to the gene. g, Cis-regulatory network at locus around SLC24A4. The interaction denotes significant RE–TG links,

and we use the location of the promoter to represent the gene.

We next identified key TFs by the sum of the expression level and trait regulation score. Figure 5c lists the top eight candidate TFs in classical monocytes. These TFs have been previously

reported to be associated with IBD in the literature. FOS can increase the risk of recurrence of IBD66; one variant identified in the IBD cohort is located at the exon of ETV6; IRF1 and ETV6

are key TFs with activity differences in IBD67; genes FOS, FOSB and JUN encode potent mediators of IBD68; CUX1 is induced in IBD69; and STAT1 epigenetically contribute to the pathogenesis

of IBD70.

To investigate the downstream targets of key TFs, we chose STAT1 as an example. Among the top 200 TGs regulated by STAT1 in classical monocytes, 67 of them overlap with the GWAS genes, which

is statistically significant with a P value of less than 0.01 based on a background distribution from a random selection of TFs (one-sided bootstrap hypothesis testing). The numbers of

overlapped TGs are all significant for the top 500, 1,000, 2,000 and 5,000 TGs (Fig. 5d). Apart from GWAS-relevant genes, we collected the DEGs between inflamed biopsies and non-inflamed

biopsies71 and we found that these DEGs significantly overlapped with the top-ranked TGs of STAT1 (one-sided bootstrap hypothesis testing; Fig. 5e). The lack of significant overlap between

DEGs and GWAS genes (P = 0.15, two-sided Fisher’s exact test) but the significant overlap of both DEGs and GWAS with the top-ranked TGs of STAT1 indicates the robustness and unbiased nature

of our method.

Finally, we extracted the sub-network of the eight candidate TFs from the classical monocyte trans-regulatory network for IBD (Fig. 5f). We also observed that the cis-regulatory network of

SLC24A4 (Fig. 5g), 46 kb from a risk single nucleotide polymorphism (SNP) rs11626366 (P = 7.4 × 10−3), is specifically dense in the IBD-relevant cell types, which shows the complex

regulatory landscape of disease genes across different cell types.

Researchers often identify DEGs between cases and controls using bulk or single-cell expression data, but the underlying regulatory drivers remain elusive. TF activity, focusing on the

DNA-binding component of TF proteins, is a more reliable metric than mRNA for identifying driver regulators. One feasible approach is to estimate TF activity based on the expression patterns

of downstream TGs, which necessitates the availability of an accurate GRN. Assuming that the GRN structure is consistent for the same cell type across individuals, we employed

LINGER-inferred GRNs from single-cell multiome data of a single individual to estimate the TF activity of other individuals using gene expression data alone from the same cell type. By

comparing TF activity between cases and controls, we identified driver regulators. This approach is valuable, as it leverages limited single-cell multiome data to estimate TF activity in

multiple individuals using only gene expression data (see Methods). We present two illustrative examples showcasing its utility.

Example 1: We collected the bulk gene expression data from 26 patients with acute myeloid leukemia (AML) and 38 healthy donors72. We calculated the TF activity for these samples based on the

LINGER-inferred cell population GRN from PBMCs and found that FOXN1 is significantly less active in patients with AML than in healthy donors, and it is not differentially expressed (Fig.

6a,b). In addition, we calculated the TF activity of the transcriptome profile (bulk RNA-seq data) of 671 individuals with AML73 and performed survival analysis, which indicated that

individuals with high FOXN1 activity level tend to have a higher survival probability (Fig. 6c). Furthermore, FOXN1 has been reported as a tumor suppressor74.

identification.

a, Violin plot of FOXN1 expression across healthy donors (n = 38 independent samples) and patients with AML (n = 26 independent samples), respectively. There is no significant difference in

the mean expression (two-sided unpaired t-test). b, Violin plot of regulon activity of FOXN1 across healthy donors (n = 38 independent samples) and patients with AML (n = 26 independent

samples), respectively (two-sided unpaired t-test, P = 0.035). c, AML survival by the regulon activity of FOXN1 (P value is from a two-sided log-rank test). d, The heatmap of regulon

activity and gene expression in response to TCR stimulation at 0 h and 8 h. Two-sided unpaired t-test for the difference in regulon activity, P = 0.0057 and P = 0.00081 for FOXK1 and NR4A1,

respectively; the P value for gene expression is >0.05. Heatmap is scaled by row. e, Heatmap of whole protein (wProtein) and phosphoproteomics (pProtein) expression in response to TCR

stimulation at 0 h, 2 h, 8 h and 16 h. There are two biological replicates, represented by a and b. The wProtein and pProtein expression of FOXK1 and NR4A1 is higher at 8 h than at 0 h. The

heatmap is scaled by row.

Example 2: We also present an example of the naive CD4+ T cell response upon T cell receptor (TCR) stimulation75, which induces T cell differentiation into various effector cells and

activates T lymphocytes. We calculated the TF activity based on the GRN of naive CD4+ T cells and identified differentially active regulators in response to TCR stimulation at 8 h versus 0 

h. FOXK2 and NR4A1 are activated at 8 h based on regulon activity (Fig. 6d), which is consistent with the whole proteomics and phosphoproteomics data (Fig. 6e)76. Other studies have also

shown that FOXK2 affects the activation of T lymphocytes77,78 and revealed the essential roles of NR4A1 in regulatory T cell differentiation79,80, suggesting that the identified TFs have

important roles in naive CD4+ T cell response upon TCR stimulation. However, FOXK2 and NR4A1 show no significant differences in expression at 8 h versus 0 h (Fig. 6d).

perturbation

We performed in silico perturbation to predict the gene expression after knocking out TFs. To do so, we changed the expression of an individual TF or combinations of TFs to zero and used the

predicted gene expression as the in silico perturbation gene expression. We used the expression difference before and after in silico perturbation to infer the TG. To assess the performance

of the prediction, we collected perturbation data for eight TFs in blood cells from the KnockTF59 database (Supplementary Table 8) as ground truth. We performed the in silico individual TF

perturbation of the eight TFs using LINGER. As a comparison, we performed identical computational perturbation experiments using the CellOracle81 and SCENIC+42 methods. The results, shown in

Extended Data Fig. 4c,d, demonstrate that LINGER is more accurate than the alternative approaches (P  ≤ 3.72 × 10−4).

To assess LINGER’s capability to infer differentiation behavior, we leveraged CellOracle81 as a downstream analytical tool. We used the LINGER-inferred GRN as an input to CellOracle. This

allowed us to investigate the capacity of LINGER-derived networks to recapitulate differentiation responses. Examining bone marrow mononuclear cell data82, which contains progenitor

populations, we performed an in silico knockout of GATA1, a known key regulator of erythroid and megakaryocytic differentiation83. CellOracle predictions based on the LINGER GRN showed that

GATA1 knockout shifted proerythroblasts to a megakaryocytic or erythroid progenitor state (Extended Data Fig. 4e), consistent with the functional role of GATA1 in inhibiting erythroblast

maturation. These results demonstrate that LINGER can not only predict gene expression under perturbation but also enable downstream characterizations of differentiation trajectories through

integration with complementary analytical frameworks like CellOracle.

LINGER is an neural network-based method that infers GRNs from paired single-cell multiomic data by incorporating bulk datasets and knowledge of TF–RE motif matching. Compared to existing

tools, LINGER achieves substantially higher GRN inference accuracy. A key innovation is lifelong machine learning to leverage diverse cellular contexts, continually updating the model as new

data emerge. This addresses historic challenges from limited single-cell datasets and vast parameter spaces hindering complex model fitting. LINGER’s lifelong learning approach has the

advantage of pre-training on bulk collections, allowing users to easily retrain the model for their own studies while capitalizing on publicly available resources without direct access.

Traditionally, GRN inference performance is assessed by gene expression prediction. However, the use of lifelong learning to leverage external data does not lead to improved gene expression

prediction but does improve the GRN inference. This finding challenges the traditional strategy of evaluating GRN inference solely based on gene expression prediction and highlights the

importance of considering the overall network structure and regulatory interactions.

The lifelong learning mechanism will encourage the model to retain prior knowledge from the bulk data when adapting to the new single-cell data. It is a tradeoff between retaining prior

knowledge and fitting new data. The flexibility of the variation in prior knowledge is not constrained when fitting the new data. The extent to which the final result deviates from the prior

knowledge depends on the loss incurred in fitting the new data. LINGER will learn this tradeoff automatically to obtain a maximized usage of the information from both

datasets.

LINGER is a computational framework to infer GRNs—pairwise regulation among TGs, REs and TFs—from single-cell multiome data. Overall, LINGER predicts gene expression by the TF expression and

chromatin accessibility of REs based on neural network models. The contribution of each feature is estimated by the Shapley value of the neural network models, enabling the inference of the

GRNs. To capture key information from the majority of tissue lineages, LINGER uses lifelong machine learning (continuous learning). Moreover, LINGER integrates motif binding data by

incorporating a manifold regularization into the loss function.

The inputs for full training of LINGER are external bulk and single-cell paired gene expression and chromatin accessibility data. However, we provided a bulk data pre-trained LINGER model so

that users can retrain it for their own single-cell data without accessing external bulk data. We collected paired bulk data—gene expression profiles and chromatin accessibility

matrices—from 201 samples from diverse cellular contexts84 from the ENCODE project46. Single-cell data are raw count matrices of multiome single-cell data (gene counts for RNA-seq and RE

counts for ATAC-seq). LINGER trains individual models for each gene using a neural network architecture that includes an input layer and two fully connected hidden layers. The input layer

has dimensions equal to the number of features, containing all TFs and REs within 1 Mb of the TSS for the gene to be predicted. The first hidden layer has 64 neurons with rectified linear

unit activation that can capture regulatory modules, each of which contains multiple TFs and REs. These regulatory modules are characterized by enriched motifs of the TFs on the

corresponding REs. The second hidden layer has 16 neurons with rectified linear unit activation. The output layer is a single neuron, which outputs a real value for gene expression

prediction.

We first construct neural network models based on bulk data, using the same architecture described above. We extract the TF expression matrix \({\widetilde{E}}_{{\rm{TF}}}\in

{{\mathbb{R}}}^{{N}_{{\rm{TF}}}\times {N}_{b}}\) from the bulk gene expression matrix \(\widetilde{E}\in {{\mathbb{R}}}^{{N}_{{\rm{TG}}}\times {N}_{b}}\), with \({N}_{{\rm{TG}}}\)

representing the number of genes, \({N}_{{\rm{TF}}}\) representing the number of TFs and \({N}_{b}\) representing the number of tissues. The loss function consists of mean squared error

(MSE) and L1 regularization, which, for the ith gene is:

}_{b}^{(i)}\right)=\frac{1}{{N}_{b}}\mathop{\sum }\limits_{n=1}^{{N}_{b}}{\left(\;f\left({({\tilde{E}}_{\rm{TF}})}_{\cdot ,n},{\tilde{O}}_{\cdot ,n}^{(i)},{\theta

}_{b}^{(i)}\right)-{\tilde{E}}_{in}\right)}^{2}{+}{\lambda }_{0}{\Vert {\theta }_{b}^{(i)}\Vert }_{1}$$

where \(\widetilde{O}\in {{\mathbb{R}}}^{{N}_{{\rm{RE}}}^{(i)}\times {N}_{b}}\) represents the chromatin accessibility matrix, with \({N}_{{\rm{RE}}}^{(i)}\) REs within 1 Mb of the TSS of

the ith gene, and \(f\left({\left({\widetilde{E}}_{{\rm{TF}}}\right)}_{\bullet ,n},{{\widetilde{O}}^{(i)}}_{\bullet ,n},{\theta }_{b}^{(i)}\right)\) is the predicted gene expression from the

neural network of sample n. The neural network is parametrized by a set of weights and biases, collectively denoted by \({\theta }_{b}^{(i)}\). The weight λ0 is a tuning parameter.

The loss function of LINGER is composed of MSE, L1 regularization, manifold regularization and EWC loss: \({{\mathcal{L}}}_{{\rm{LINGER}}}={{{\lambda }}_{1}{\mathcal{L}}}_{{\rm{MSE}}}\)

\(+{{\lambda }}_{2}{{\mathcal{L}}}_{L1}+{{\lambda }}_{3}{{\mathcal{L}}}_{{\rm{Laplace}}}+{{{\lambda }}_{4}{\mathcal{L}}}_{{\rm{EWC}}}\). \({{\mathcal{L}}}_{{\rm{Laplace}}}\) represents the

manifold regularization because a Laplacian matrix is used to generate this regularization term. The loss function terms correspond to gene i, and for simplicity, we omit subscripts \((i)\)

for the chromatin accessibility matrix (\(O\)), parameters for the bulk model (\({\theta }_{b}\)) and parameters for LINGER (\({\theta }_{l}\)).

MSE

}\limits_{n=1}^{{N}_{{\rm{sc}}}}{\left(f\left({\left({E}_{{\rm{TF}}}\right)}_{\bullet ,n},{O}_{\bullet ,n},{\theta }_{l}\right)-{E}_{{in}}\right)}^{2}$$

Here, \({E}_{{\rm{TF}}}\in {{\mathbb{R}}}^{{N}_{{\rm{TF}}}\times {N}_{{\rm{sc}}}}\) represents the TF expression matrix from the single-cell RNA-seq data, consisting of \({N}_{{\rm{sc}}}\)

cells; \(O\in {{\mathbb{R}}}^{{N}_{{\rm{RE}}}^{(i)}\times {N}_{{\rm{sc}}}}\) represents the RE chromatin accessibility matrix of the single-cell ATAC-seq data; \(E\in

{{\mathbb{R}}}^{{{N}_{{\rm{TG}}}\times N}_{{\rm{sc}}}}\) represents the expression of the genes across cells; and \({\theta }_{l}\) represents the parameters in the neural network. We use

metacells to train the models; therefore, \({N}_{{\rm{sc}}}\) is the number of cells from metacell data.

L1 regularization

Laplacian loss (manifold regularization)

We generate the adjacency matrix as: \({B}^{* }\in {{\mathbb{R}}}^{\left({N}_{{\rm{TF}}}+{N}_{{\rm{RE}}}^{(i)}\right)}\)\({\times \left({N}_{{\rm{TF}}}+{N}_{{\rm{RE}}}^{(i)}\right)}\), where

\({B}_{k,{N}_{{\rm{TF}}}+j}^{* }\) and \({B}_{{N}_{{\rm{TF}}}+j,k}^{* }\) represent the binding affinity of the TF \(k\) and the RE \(j\), which is elaborated in the following sections.

\({L}^{{\rm{Norm}}}\in {{\mathbb{R}}}^{\left({N}_{{\rm{TF}}}+{N}_{{\rm{RE}}}^{(i)}\right)\times \left({N}_{{\rm{TF}}}+{N}_{{\rm{RE}}}^{(i)}\right)}\) is the normalized Laplacian matrix based

on the adjacency matrix.

}_{l}^{\left(1\right)}\right)}^{T}{L}^{{\rm{Norm}}}{\theta }_{l}^{\left(1\right)}\right)$$

where \({\theta }_{l}^{\left(1\right)}\in {{\mathbb{R}}}^{\left({N}_{{\rm{TF}}}+{N}_{{\rm{RE}}}^{(i)}\right)\times 64}\) is the parameter matrix of the first hidden layer, which can capture

the densely connected TF–RE modules.

EWC loss. EWC constrains the parameters of the first layer to stay in a region of \({\theta }_{b}^{\left(1\right)}\), which is previously learned from the bulk data45. To do so, EWC uses MSE

between the parameters \({\theta }_{l}^{\left(1\right)}\) and \({\theta }_{b}^{\left(1\right)}\), weighted by the Fisher information, a metric of how important the parameter is, allowing

the model to protect the performance, both for single-cell data and bulk data45.

}_{l}\right)=\frac{1}{\left({N}_{{\rm{TF}}}+{N}_{{\rm{RE}}}\right)\times 64}\mathop{\sum }\limits_{i=1}^{{N}_{{\rm{TF}}}+{N}_{{\rm{RE}}}}\mathop{\sum

}\limits_{j}^{64}{F}_{{ij}}{\left({\theta }_{l}^{\left(1\right)}\right)}_{i,\;j}{\left({\theta }_{b}^{\left(1\right)}\right)}_{i,\;j}$$

where \(F\) is the fisher information matrix, which is detailed below, and \({\theta }_{l}^{\left(1\right)}\in {{\mathbb{R}}}^{\left({N}_{{\rm{TF}}}+K\right)\times 64}\) is the parameter

matrix of the first hidden layer.

To construct a normalized Laplacian matrix, we first generate the TF–RE binding affinity matrix for all REs from the single-cell ATAC-seq data. We extract the REs 1 Mb from the TSS for the

gene to be predicted. Let \({N}_{{\rm{RE}}}^{(i)}\) be the number of these REs and \(B\in {{\mathbb{R}}}^{{N}_{{\rm{TF}}}\times {N}_{{\rm{RE}}}^{(i)}}\) be the TF–RE binding affinity matrix,

where \({B}_{{kj}}\) represents the binding affinity for the TF \(k\) and RE \(j\). We construct a graph, taking TFs as the first \({N}_{{\rm{TF}}}\) nodes, REs as the remaining

\({N}_{{\rm{RE}}}^{\;(i)}\) nodes and binding affinity as the edge weight between TF and RE. The edge weights of TF–TF and RE–RE are set to zero. Then the adjacency matrix \({B}^{* }\in

{{\mathbb{R}}}^{\left({N}_{{\rm{TF}}}+{N}_{{\rm{RE}}}^{(i)}\right)\times \left({N}_{{\rm{TF}}}+{N}_{{\rm{RE}}}^{(i)}\right)}\) is defined as:

}=\\\left\{\begin{array}{l}{B}_{k,j-{N}_{{\rm{TF}}}},k\in \left\{1,2,\ldots ,{N}_{{\rm{TF}}}\right\},j\in \{{N}_{{\rm{TF}}}+1,{N}_{{\rm{TF}}}+2,\ldots

,{N}_{{\rm{TF}}}+{N}_{{\rm{RE}}}^{(i)}\}\\ {B}_{j,k-{N}_{{\rm{TF}}}},k\in \left\{{N}_{{\rm{TF}}}+1,{N}_{{\rm{TF}}}+2,\ldots ,{N}_{{\rm{TF}}}+{N}_{{\rm{RE}}}^{\;(i)}\right\},:j\in

\left\{1,2,\ldots ,{N}_{{\rm{TF}}}\right\}\\ 0,\qquad{\rm{else}}\end{array}\right.\end{array}$$

The Fisher information matrix is calculated based on the neural network trained on bulk data:

{\left({\theta }_{b}^{\left(1\right)}\right)}_{{ij}}}{{\mathcal{L}}}_{{\rm{MSE}}}\left({\widetilde{E}}_{{\rm{TF}}},\widetilde{O},{\widetilde{E}}_{i,\bullet },{\theta

}_{b}\right)\right)}^{2}\right]\\\quad\;\;\;=\displaystyle\frac{1}{{N}_{b}}\mathop{\sum }\limits_{n=1}^{{N}_{b}}{\left(\displaystyle\frac{\partial}{\partial {\left({\theta

}_{b}^{\left(1\right)}\right)}_{{ij}}}{\left(\frac{1}{{N}_{b}}f\left({\left({\widetilde{E}}_{{\rm{TF}}}\right)}_{\bullet ,n},{\widetilde{O}}_{\bullet ,n},{\theta

}_{b}\right)-{\widetilde{E}}_{{in}}\right)}^{2}\right)}^{2}\end{array}$$GRN inference by Shapley value

The Shapley value measures the contribution of features in a machine-learning model and is widely used in algorithms such as deep learning, graphical models and reinforcement learning85. We

use the average of absolute Shapley values across samples to infer the regulation strength of TF and RE to TGs, generating the RE–TG cis-regulatory strength and the TF–TG trans-regulatory

strength. Let \({\beta }_{{ij}}\) represent the cis-regulatory strength of RE \(j\) and TG i, and \({\gamma }_{{ki}}\) represent the trans-regulatory strength. To generate the TF–RE binding

strength, we use the weights from the input layer (TFs and REs) to all nodes in the second layer of the neural network model to embed the TF or RE. The TF–RE binding strength is calculated

by the PCC between the TF and RE based on this embedding. \({\alpha }_{{kj}}\) represents the TF–RE binding strength.

The TF–RE regulatory potential for a certain cell type is given by:

where \({\rm{TFB}}_{{kj}}\) is the TF–RE regulation potential of TF \(k\) and RE \(j\); \({s}_{k}\) is an importance score of TF \(k\) in the cell type to measure the preference of TF for

activating cell type-specific open chromatin regions (which will be described in ‘TF importance score’ below); \({C}_{{kj}}\) is the PCC of TF \(k\) and RE \(j\); \({O}_{j}\) is the average

chromatin accessibility across cells in the cell type; \({B}_{{kj}}\) is the binding affinity between TF \(k\) and RE \(j\); and \({\alpha }_{{kj}}\) is the TF–RE binding strength.

The RE–TG cis-regulatory potential is defined as:

where \({\rm{CRP}}_{{ij}}\) is the cis-regulatory potential of TG i and RE \(j\); \({\beta }_{{ij}}\) is the cis-regulatory strength of RE \(j\) and TG i; \({O}_{j}\) is the average

chromatin accessibility; \({E}_{i}\) is the average gene expression across cells in the cell type; \({d}_{{ij}}\) is the distance between genomic locations of TG i and RE \(j\); and

\({d}_{0}\) is a fixed value used to scale the distance, which is set to 25,000 in this paper.

The TF–TG trans-regulatory potential is defined as the cumulative effect of corresponding REs on the TG:

{S}_{i}}{\rm{TFB}}_{{kj}}{\rm{CRP}}_{{ij}}$$

where \({\gamma }_{{ki}}\) is the TF–TG trans-regulatory strength of TF \(k\) and TG i; \({S}_{i}\) is the set of REs within 1 Mb from the TSS for TG i; \({\rm{CRP}}_{{ij}}\) is the

cis-regulatory potential of TG i and RE \(j\); and \({\rm{TFB}}_{{kj}}\) is the TF–RE regulation potential of TF \(k\) and RE \(j\).

Cell-level GRNs are inferred by integrating information consistent across all cells, such as regulatory strength, binding affinity and RE–TG distance, with cell-level information, such as

gene expression and chromatin accessibility. This approach is similar to inferring cell type-specific GRNs, with the key difference that cell-level GRNs use cell-level TF expression

\({E}_{{\rm{TF}}}\), chromatin accessibility \(O\) and gene expression \(E\) rather than cell type-averaged data. This allows us to infer the network for each individual cell based on its

specific characteristics rather than grouping cells into predefined types.

To systematically identify TFs playing a pivotal role in controlling the chromatin accessibility of cell type, we introduce a TF importance score. The score is designed to measure the

preference of TFs for activating cell type-specific REs. The input is multiome single-cell data with known cell type annotations. There are four steps to generate the TF importance

score:

Motif enrichment. We perform the motif enrichment analysis86 to identify the motifs significantly enriched in the binding sites of the top 5,000 cell type-specific REs. We use the P value to

measure the significant level of motif enrichment.

TF–RE correlation. To avoid dropouts in single-cell data, we recover the original count matrix by an average of the observed count of nearby cells. We calculate PCC between the TF expression

and cell type-specific RE chromatin accessibility, with \({r}_{{kj}}\) representing the PCC of the TF \(k\) and the RE \(j\). To mitigate the bias in the distribution of TF expression and

REs chromatin accessibility so that the PCC is comparable across different TF–RE pairs, we permute the cell barcode in the gene expression data and then calculate, generating a background

PCC distribution for each TF–RE pair. We generate a z-score for \({r}_{{kj}}\),

where \({\mu }_{{kj}}\) and \({\sigma }_{{kj}}^{2}\) are the mean and the variance of the background PCC distribution between \({\rm{TF}}_{k}\) and \({\rm{RE}}_{j}\).

The co-activity score of the TF-motif pair. To pair TFs with their motifs, we match 713 TFs and 1,331 motifs, yielding 8,793 TF-motif pairs84. Let \(\left(k,m\right)\) denote the TF-motif

pair of TF \(k\) and motif \(m\). We then calculate a co-activity score for a TF-motif pair for \(\left(k,m\right)\), defined as the average z-score across cell type-specific REs with at

least one motif binding site. That is \({z}_{k,m}^{\;{co}}=\frac{1}{{N}_{m}}\sum _{j\in {\left\{{\rm{RE}}\;\right\}}_{m}}{z}_{{kj}}\), where \({\left\{{\rm{RE}}\right\}}_{m}\) is the set of

REs with the \(m\)-th motif binding; and \({N}_{m}=\left|{\left\{{\rm{RE}}\right\}}_{m}\right|\) is the number of REs in \({\left\{{\rm{RE}}\right\}}_{m}\).

TF importance score. The score of the TF-motif pair, \(\left(k,m\right)\), is given by:

{\rm{NA}}, & {\rm{otherwise}}\end{array}\right.$$

where \({p}_{m}\) is the P value of the \(m\)th motif from the motif-enrichment analysis and \({s}_{(k,m)}\) is the importance score of the TF-motif pair \((k,m)\). The TF importance score

for the TF \(k\) is the average TF-motif pair TF importance score across motifs, omitting NA:

\left\{{{m|s}}_{\left(k,m\right)}\ne {\rm{NA}}\right\}}{s}_{\left(k,m\right)}, & {\rm{if}}\,{N}_{\left(k,m\right)} > 0\\ 0, & {\rm{if}}\,{N}_{\left(k,m\right)}=0\end{array}\right.,$$

where \({N}_{(k,m)}=\left|\{{{m|s}}_{(k,m)}\ne {\rm{NA}}\}\right|\) is the number of the TF-motif pair of the TF \(k\), whose CECI score is not NA.

We download 713 TF position weight matrices for the known motifs from GitHub page of PECA284, which is collected from widely used databases including JASPAR, TRANSFAC, UniPROBE and Taipale.

Given a list of REs, we calculate the binding affinity score for each TF by motif scan using Homer86, as a quantitative measure of the strength of the interaction between TF and

RE20.

We identify the REs with motif binding by motif scan using Homer86.

Given that the choice of TFs for benchmarking may affect the final results, we use the following standard to collect all ChIP–seq data from the Cistrome database that satisfies the following

criteria.

The procedure for choosing ChIP–seq data for PBMC is as follows.

We downloaded all human TF ChIP–seq information, including 11,349 datasets.

We filtered samples that did not pass quality control, and 4,657 datasets remained.

We chose samples in blood tissue, and 609 datasets remained.

We filtered the cell line data that is not consistent with PBMC cell types, and 63 datasets remained.

We chose the TF expressed in single-cell data and with known motifs available, and 39 datasets remained.

We chose the experiments that were done in one of the 14 cell types detected in the PBMC data, and 20 datasets remained.

The procedure for choosing ChIP–seq data for the H1 cell line is as follows:

We downloaded all human TF ChIP–seq information, including 11,349 datasets.

We filtered samples that did not pass quality control, and 4,657 datasets remained.

We chose the H1 cell line, and 42 datasets remained.

We chose the TF expressed in single-cell data and with known motifs available, and 33 datasets remained.

The criteria for choosing ground truth from the KnockTF database is similar to ChIP–seq data.

The procedure for choosing knockdown data for PBMC is as follows.

We selected the molecular type as ‘TF’ and chose the ‘Peripheral_blood’ tissue type, with 21 cases remaining.

There are 11 datasets included in the PBMCs cell type in the single-cell data.

We chose the TF expressed in single-cell data and with known motifs available, and 8 datasets remained.

We download the PBMC 10K data from the 10× Genomics website (https://support.10xgenomics.com/single-cell-multiome-atac-gex/datasets). Note that it contains 11,909 cells, and the granulocytes

were removed by cell sorting of this dataset. We use the filtered cells by features matrix from the output of 10× Genomics software Cell Ranger ARC as input and perform the downstream

analysis. First, we perform weighted nearest neighbor analysis in Seurat (version 4.0)87, and it removes 1,497 cells. We also remove the cells that do not have surrogate ground truth and it

results in 9,543 cells. We generate metacells data by randomly selecting the square root of the number of cells in each cell type and averaging the expression levels and chromatin

accessibility of the 100 nearest cells to produce the gene expression and chromatin accessibility values of the selected cells. The metacells data were directly input into LINGER for

analysis.

To measure the accuracy of a predictor, we defined the AUPR ratio as the ratio of the AUPR of a method to that of a random predictor. For a random predictor, the AUPR equals the fraction of

positive samples in the dataset. The AUPR ratio is defined as \({\rm{AUPR}\frac{\#\,{sample}}{\#\,{real}\,{positive}}}\), representing the fold change of the accuracy of a predictor compared

to the random prediction.

We propose a method to integrate GWAS summary statistics data and cell type-specific GRNs to identify the relevant cell types, key TFs and sub-GRNs responsible for GWAS variants. To identify

relevant cell types, we first project the risk SNP identified from GWAS summary data to a gene. We then link the gene within the 200 kb region centering on the SNP and assign the most

significant P value of linked SNPs to each gene. In this study, the trait-related genes are defined as those with P < 0.01 after multiple testing adjustments. We then calculate a trait

regulation score for each TF in each cell type, measuring the enrichment of GWAS genes downstream of the TF based on the cell type-specific GRN. We choose 1,000 top-ranked genes according to

the trans-regulation as the TG of each TF and count the number of overlapping genes with trait-related genes. The enrichment of cell types to the GWAS traits is measured by a t-test

comparing the number of overlapping genes between the 100 top-expressed and 100 randomly chosen TFs.

To identify key TFs of GWAS traits, we combine the trait regulation score and the gene expression level of TFs in each cell type. The trait regulation score is the z-score of the number of

overlapping genes of a TF across all TFs. The expression level is also transformed to a z-score based on the gene expression. The final importance of key TFs is the summation of the

expression level and trait regulation score.

To measure the activity of each TF on the independent transcriptional profiles, we first constructed a TG set for each TF based on the corresponding GRN. We perform quantile normalization to

the trans-regulation score of each gene across all TFs. We then rank the genes for each TF and choose the top 1,000 genes as the target. Next, we use the R package AUCell22 to calculate

whether the TGs are enriched within the expressed genes for each sample, which defines the TF activity.

We compare LINGER’s performance of the trans-regulation prediction using PCC, SCENIC+, GENIE3 and PIDC as competitors to LINGER. Owing to the time-consuming nature of PIDC’s mutual

information-based algorithm, we used the 5,000 most variable genes as input. As a result, there are 9 TFs and 14 TFs in ground truth data left for PBMCs and the H1 cell line,

respectively.

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

The PBMC data used during this study was downloaded from the 10× Genomics website

(https://s3-us-west-2.amazonaws.com/10x.files/samples/cell-arc/1.0.0/pbmc_granulocyte_sorted_10k/pbmc_granulocyte_sorted_10k_fastqs.tar)40. SNARE-seq was downloaded from NCBI Gene Expression

Omnibus (https://www.ncbi.nlm.nih.gov/geo/) under accession number GSE126074 (ref. 55).

The software is available at GitHub88 (https://github.com/Durenlab/LINGER) and the Zenodo repository under the GPLv3 license89. We used Python and R for this study.

References Jacob, F. & Monod, J. On the regulation of gene activity. Cold Spring Harb. Symp. Quant. Biol. 26, 193–211 (1961).

CAS  Google Scholar 

Hecker, M., Lambeck, S., Toepfer, S., van Someren, E. & Guthke, R. Gene regulatory network inference: data integration in dynamic models—a review. BioSystems 96, 86–103 (2009).

CAS  PubMed  Google Scholar 

Thieffry, D., Huerta, A. M., Perez-Rueda, E. & Collado-Vides, J. From specific gene regulation to genomic networks: a global analysis of transcriptional regulation in Escherichia coli.

BioEssays 20, 433–440 (1998).

CAS  PubMed  Google Scholar 

Badia-i-Mompel, P. et al. Gene regulatory network inference in the era of single-cell multi-omics. Nat. Rev. Genet. 24, 739–754 (2023).

CAS  PubMed  Google Scholar 

Bansal, M., Gatta, D. G. & di Bernardo, D. Inference of gene regulatory networks and compound mode of action from time course gene expression profiles. Bioinformatics 22, 815–822 (2006).

CAS  PubMed  Google Scholar 

Wang, Y., Joshi, T., Zhang, X. S., Xu, D. & Chen, L. Inferring gene regulatory networks from multiple microarray datasets. Bioinformatics 22, 2413–2420 (2006).

CAS  PubMed  Google Scholar 

Iyer, A. S., Osmanbeyoglu, H. U. & Leslie, C. S. Computational methods to dissect gene regulatory networks in cancer. Curr. Opin. Syst. Biol. 2, 115–122 (2017).

Google Scholar 

Hempel, S., Koseska, A., Kurths, J. & Nikoloski, Z. Inner composition alignment for inferring directed networks from short time series. Phys. Rev. Lett. 107, 054101 (2011).

CAS  PubMed  Google Scholar 

Margolin, A. A. et al. ARACNE: an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinf. 7, S7 (2006).

Google Scholar 

Zou, M. & Conzen, S. D. A new dynamic Bayesian network (DBN) approach for identifying gene regulatory networks from time course microarray data. Bioinformatics 21, 71–79 (2005).

CAS  PubMed  Google Scholar 

Perrin, B. E. et al. Gene networks inference using dynamic Bayesian networks. Bioinformatics 19, 138–148 (2003).

Google Scholar 

Zhang, X. & Moret, B. M. E. Refining transcriptional regulatory networks using network evolutionary models and gene histories. Algorithms Mol. Biol. 5, 1 (2010).

PubMed  PubMed Central  Google Scholar 

Zhong, W. et al. Inferring regulatory networks from mixed observational data using directed acyclic graphs. Front. Genet. 11, 8 (2020).

CAS  PubMed  PubMed Central  Google Scholar 

Fuller, T. F. et al. Weighted gene coexpression network analysis strategies applied to mouse weight. Mammalian Genome 18, 463–472 (2007).

PubMed  PubMed Central  Google Scholar 

Huynh-Thu, V. A., Irrthum, A., Wehenkel, L. & Geurts, P. Inferring regulatory networks from expression data using tree-based methods. PLoS One 5, e12776 (2010).

PubMed  PubMed Central  Google Scholar 

Wang, Y. X. R. & Huang, H. Review on statistical methods for gene network reconstruction using expression data. J. Theor. Biol. 362, 53–61 (2014).

PubMed  Google Scholar 

Boyle, A. P. et al. High-resolution mapping and characterization of open chromatin across the genome. Cell 132, 311–322 (2008).

CAS  PubMed  PubMed Central  Google Scholar 

Buenrostro, J. D., Giresi, P. G., Zaba, L. C., Chang, H. Y. & Greenleaf, W. J. Transposition of native chromatin for fast and sensitive epigenomic profiling of open chromatin, DNA-binding

proteins and nucleosome position. Nat. Methods 10, 1213–1218 (2013).

CAS  PubMed  PubMed Central  Google Scholar 

Neph, S. et al. Circuitry and dynamics of human transcription factor regulatory networks. Cell 150, 1274–1286 (2012).

CAS  PubMed  PubMed Central  Google Scholar 

Duren, Z., Chen, X., Jiang, R., Wang, Y. & Wong, W. H. Modeling gene regulation from paired expression and chromatin accessibility data. Proc. Natl Acad. Sci. USA 114, E4914–E4923 (2017).

CAS  PubMed  PubMed Central  Google Scholar 

Chan, T. E., Stumpf, M. P. H. & Babtie, A. C. Gene regulatory network inference from single-cell data using multivariate information measures. Cell Syst. 5, 251–267.e3 (2017).

CAS  PubMed  PubMed Central  Google Scholar 

Aibar, S. et al. SCENIC: single-cell regulatory network inference and clustering. Nat. Methods 14, 1083–1086 (2017).

CAS  PubMed  PubMed Central  Google Scholar 

Matsumoto, H. et al. SCODE: an efficient regulatory network inference algorithm from single-cell RNA-seq during differentiation. Bioinformatics 33, 2314–2321 (2017).

PubMed  PubMed Central  Google Scholar 

Papili Gao, N., Ud-Dean, S. M. M., Gandrillon, O. & Gunawan, R. SINCERITIES: inferring gene regulatory networks from time-stamped single cell transcriptional expression profiles.

Bioinformatics 34, 258–266 (2018).

PubMed  Google Scholar 

Sanchez-Castillo, M., Blanco, D., Tienda-Luna, I. M., Carrion, M. C. & Huang, Y. A Bayesian framework for the inference of gene regulatory networks from time and pseudo-time series data.

Bioinformatics 34, 964–970 (2018).

CAS  PubMed  Google Scholar 

Hu, Y., Peng, T., Gao, L. & Tan, K. CytoTalk: de novo construction of signal transduction networks using single-cell transcriptomic data. Sci. Adv. 7, eabf1356 (2021).

CAS  PubMed  PubMed Central  Google Scholar 

Frankowski, P. C. A. & Vert, J. P. Gene regulation inference from single-cell RNA-seq data with linear differential equations and velocity inference. Bioinformatics 36, 4774–4780 (2020).

Google Scholar 

Specht, A. T. & Li, J. LEAP: constructing gene co-expression networks for single-cell RNA-sequencing data using pseudotime ordering. Bioinformatics 33, 764–766 (2017).

CAS  PubMed  Google Scholar 

Moerman, T. et al. GRNBoost2 and Arboreto: efficient and scalable inference of gene regulatory networks. Bioinformatics 35, 2159–2161 (2019).

CAS  PubMed  Google Scholar 

Zhang, S. et al. Inference of cell type-specific gene regulatory networks on cell lineages from single cell omic datasets. Nat. Commun. 14, 3064 (2023).

CAS  PubMed  PubMed Central  Google Scholar 

Li, H. et al. Inferring transcription factor regulatory networks from single-cell ATAC-seq data based on graph neural networks. Nat. Mach. Intell. 4, 389–400 (2022).

Google Scholar 

Jiang, J. et al. IReNA: integrated regulatory network analysis of single-cell transcriptomes and chromatin accessibility profiles. iScience 25, 105359 (2022).

CAS  PubMed  PubMed Central  Google Scholar 

Jansen, C. et al. Building gene regulatory networks from scATAC-seq and scRNA-seq using linked self organizing maps. PLoS Comput. Biol. 15, e1006555 (2019).

PubMed  PubMed Central  Google Scholar 

Yuan, Q. & Duren, Z. Integration of single-cell multi-omics data by regression analysis on unpaired observations. Genome Biol. 23, 160 (2022).

CAS  PubMed  PubMed Central  Google Scholar 

Duren, Z. et al. Integrative analysis of single-cell genomics data by coupled nonnegative matrix factorizations. Proc. Natl Acad. Sci. USA 115, 7723–7728 (2018).

CAS  PubMed  PubMed Central  Google Scholar 

Zeng, W. et al. DC3 is a method for deconvolution and coupled clustering from bulk and single-cell genomics data. Nat. Commun. 10, 4613 (2019).

PubMed  PubMed Central  Google Scholar 

Wang, Z. et al. Cell-type-specific gene regulatory networks underlying murine neonatal heart regeneration at single-cell resolution. Cell Rep. 33, 108472 (2020).

CAS  PubMed  PubMed Central  Google Scholar 

Lin, Y. et al. scJoint integrates atlas-scale single-cell RNA-seq and ATAC-seq data with transfer learning. Nat. Biotechnol. 40, 703–710 (2022).

CAS  PubMed  PubMed Central  Google Scholar 

Pratapa, A., Jalihal, A. P., Law, J. N., Bharadwaj, A. & Murali, T. M. Benchmarking algorithms for gene regulatory network inference from single-cell transcriptomic data. Nat. Methods 17,

147–154 (2020).

CAS  PubMed  PubMed Central  Google Scholar 

10× Genomics. PBMCs from C57BL/6 mice (v1, 150×150); single cell immune profiling dataset by Cell Ranger 3.1.0 (2019).

Duren, Z. et al. Regulatory analysis of single cell multiome gene expression and chromatin accessibility data with scREG. Genome Biol. 23, 114 (2022).

CAS  PubMed  PubMed Central  Google Scholar 

González-Blas, C. B. et al. SCENIC+: single-cell multiomic inference of enhancers and gene regulatory networks. Nat. Methods 20, 1355–1367 (2023).

Google Scholar 

Thrun, S. & Mitchell, T. M. Lifelong robot learning. Rob. Auton. Syst. 15, 25–46 (1995).

Google Scholar 

Chaudhri, Z. & Liu, B. Lifelong Machine Learning (Springer International Publishing, 2022).

Parisi, G. I., Kemker, R., Part, J. L., Kanan, C. & Wermter, S. Continual lifelong learning with neural networks: a review. Neural Netw. 113, 54–71 (2019).

PubMed  Google Scholar 

ENCODE Project Consortium. An integrated encyclopedia of DNA elements in the human genome. Nature 489, 57–74 (2012).

Google Scholar 

Kirkpatrick, J. et al. Overcoming catastrophic forgetting in neural networks. Proc. Natl Acad. Sci. USA 114, 3521–3526 (2017).

CAS  PubMed  PubMed Central  Google Scholar 

Liu, T. et al. Cistrome: an integrative platform for transcriptional regulation studies. Genome Biol. 12, R83 (2011).

CAS  PubMed  PubMed Central  Google Scholar 

Fairfax, B. P. et al. Innate immune activity conditions the effect of regulatory variants upon monocyte gene expression. Science 343, 1246949 (2014).

PubMed  PubMed Central  Google Scholar 

Võsa, U. et al. Large-scale cis- and trans-eQTL analyses identify thousands of genetic loci and polygenic scores that regulate blood gene expression. Nat. Genet. 53, 1300–1310 (2021).

PubMed  PubMed Central  Google Scholar 

Lek, M. et al. Analysis of protein-coding genetic variation in 60,706 humans. Nature 536, 285–291 (2016).

CAS  PubMed  PubMed Central  Google Scholar 

Mostafavi, H., Spence, J. P., Naqvi, S. & Pritchard, J. K. Systematic differences in discovery of genetic effects on gene expression and complex traits. Nat. Genet. 55, 1866–1875 (2023).

CAS  PubMed  Google Scholar 

Kuleshov, M. V. et al. Enrichr: a comprehensive gene set enrichment analysis web server 2016 update. Nucleic Acids Res. 44, W90–W97 (2016).

CAS  PubMed  PubMed Central  Google Scholar 

Wang, J. et al. ATAC-seq analysis reveals a widespread decrease of chromatin accessibility in age-related macular degeneration. Nat. Commun. 9, 1364 (2018).

PubMed  PubMed Central  Google Scholar 

Chen, S., Lake, B. B. & Zhang, K. High-throughput sequencing of the transcriptome and chromatin accessibility in the same cell. Nat. Biotechnol. 37, 1452–1457 (2019).

CAS  PubMed  PubMed Central  Google Scholar 

Javierre, B. M. et al. Lineage-specific genome architecture links enhancers and non-coding disease variants to target gene promoters. Cell 167, 1369–1384.e19 (2016).

CAS  PubMed  PubMed Central  Google Scholar 

Yazar, S. et al. Single-cell eQTL mapping identifies cell type-specific genetic control of autoimmune disease. Science 376, eabf3041 (2022).

CAS  PubMed  Google Scholar 

Duren, Z. et al. Sc-compReg enables the comparison of gene regulatory networks between conditions using single-cell data. Nat. Commun. 12, 4763 (2021).

CAS  PubMed  PubMed Central  Google Scholar 

Feng, C. et al. KnockTF: a comprehensive human gene expression profile database with knockdown/knockout of transcription factors. Nucleic Acids Res. 48, D93–D100 (2020).

CAS  PubMed  Google Scholar 

Satpathy, A. T. et al. Runx1 and Cbfβ regulate the development of Flt3+ dendritic cell progenitors and restrict myeloproliferative disorder. Blood 123, 2968–2977 (2014).

CAS  PubMed  PubMed Central  Google Scholar 

Jagadeesh, K. A. et al. Identifying disease-critical cell types and cellular processes by integrating single-cell RNA-sequencing and human genetics. Nat. Genet. 54, 1479–1492 (2022).

CAS  PubMed  PubMed Central  Google Scholar 

Sollis, E. et al. The NHGRI-EBI GWAS Catalog: knowledgebase and deposition resource. Nucleic Acids Res. 51, D977–D985 (2023).

CAS  PubMed  Google Scholar 

Mize, T.J. & Evans, L. M. Examination of a novel expression-based gene-SNP annotation strategy to identify tissue-specific contributions to heritability in multiple traits. Eur. J. Hum.

Genet. 263, 32 (2024).

Google Scholar 

Anderson, A. et al. Monocytosis is a biomarker of severity in inflammatory bowel disease: analysis of a 6-year prospective natural history registry. Inflamm. Bowel Dis. 28, 70–78 (2022).

PubMed  Google Scholar 

Aschenbrenner, D. et al. Deconvolution of monocyte responses in inflammatory bowel disease reveals an IL-1 cytokine network that regulates IL-23 in genetic and acquired IL-10 resistance. Gut

70, 1023–1036 (2021).

CAS  PubMed  Google Scholar 

Wang, X., Guo, R., Lv, Y. & Fu, R. The regulatory role of Fos related antigen-1 in inflammatory bowel disease. Mol. Med. Rep. 17, 1979–1985 (2018).

CAS  PubMed  Google Scholar 

Nowak, J. K. et al. Characterisation of the circulating transcriptomic landscape in inflammatory bowel disease provides evidence for dysregulation of multiple transcription factors including

NFE2, SPI1, CEBPB, and IRF2. J. Crohns Colitis 16, 1255–1268 (2022).

PubMed  PubMed Central  Google Scholar 

Broom, O. J., Widjaya, B., Troelsen, J., Olsen, J. & Nielsen, O. H. Mitogen activated protein kinases: A role in inflammatory bowel disease? Clin. Exp. Immunol. 158, 272–280 (2009).

CAS  PubMed  PubMed Central  Google Scholar 

Darsigny, M., St-Jean, S. & Boudreau, F. Cux1 transcription factor is induced in inflammatory bowel disease and protects against experimental colitis. Inflamm. Bowel Dis. 16, 1739–1750

(2010).

PubMed  Google Scholar 

Yu, Y. L. et al. STAT1 epigenetically regulates LCP2 and TNFAIP2 by recruiting EP300 to contribute to the pathogenesis of inflammatory bowel disease. Clin. Epigenetics 13, 127 (2021).

CAS  PubMed  PubMed Central  Google Scholar 

Hu, S. et al. Inflammation status modulates the effect of host genetic variation on intestinal gene expression in inflammatory bowel disease. Nat. Commun. 12, 1122 (2021).

CAS  PubMed  PubMed Central  Google Scholar 

Stirewalt, D. L. et al. Identification of genes with abnormal expression changes in acute myeloid leukemia. Genes Chromosomes Cancer 47, 8–20 (2008).

CAS  PubMed  Google Scholar 

Bottomly, D. et al. Integrative analysis of drug response and clinical outcome in acute myeloid leukemia. Cancer Cell 40, 850–864.e9 (2022).

CAS  PubMed  PubMed Central  Google Scholar 

Ji, X., Ji, Y., Wang, W. & Xu, X. Forkhead box N1 inhibits the progression of non-small cell lung cancer and serves as a tumor suppressor. Oncology Lett. 15, 7221–7230 (2018).

Google Scholar 

Yang, K. et al. T Cell exit from quiescence and differentiation into Th2 cells depend on raptor-mTORC1-mediated metabolic reprogramming. Immunity 39, 1043–1056 (2013).

CAS  PubMed  PubMed Central  Google Scholar 

Tan, H. et al. Integrative proteomics and phosphoproteomics profiling reveals dynamic signaling networks and bioenergetics pathways underlying T cell activation. Immunity 46, 488–503 (2017).

CAS  PubMed  PubMed Central  Google Scholar 

Blanchett, S., Boal-Carvalho, I., Layzell, S. & Seddon, B. NF-κB and extrinsic cell death pathways—entwined do-or-die decisions for T cells. Trends Immunol. 42, 76–88 (2021).

CAS  PubMed  Google Scholar 

Oh, H. & Ghosh, S. NF-κB: roles and regulation in different CD4+ T-cell subsets. Immunol. Rev. 252, 41–51 (2013).

PubMed  PubMed Central  Google Scholar 

Sekiya, T. et al. Essential roles of the transcription factor NR4A1 in regulatory T cell differentiation under the influence of immunosuppressants. J. Immunol. 208, 2122–2130 (2022).

CAS  PubMed  Google Scholar 

Fassett, M. S., Jiang, W., D’Alise, A. M., Mathis, D. & Benoist, C. Nuclear receptor Nr4a1 modulates both regulatory T-cell (Treg) differentiation and clonal deletion. Proc. Natl Acad. Sci.

USA 109, 3891–3896 (2012).

CAS  PubMed  PubMed Central  Google Scholar 

Kamimoto, K. et al. Dissecting cell identity via network inference and in silico gene perturbation. Nature 614, 742–751 (2023).

CAS  PubMed  PubMed Central  Google Scholar 

Lance, C. et al. Multimodal single cell data integration challenge: results and lessons learned. Preprint at bioRxiv https://doi.org/10.1101/2022.04.11.487796 (2022).

Shivdasani, R. A. Molecular and transcriptional regulation of megakaryocyte differentiation. Stem Cells 19, 397–407 (2001).

CAS  PubMed  Google Scholar 

Duren, Z., Chen, X., Xin, J., Wang, Y. & Wong, W. H. Time course regulatory analysis based on paired expression and chromatin accessibility data. Genome Res. 30, 622–634 (2020).

CAS  PubMed  PubMed Central  Google Scholar 

Rozemberczki, B. et al. The Shapley value in machine learning. Preprint at https://doi.org/10.48550/arXiv.2202.05594 (2022).

Heinz, S. et al. Simple combinations of lineage-determining transcription factors prime cis-regulatory elements required for macrophage and B cell identities. Mol. Cell 38, 576–589 (2010).

CAS  PubMed  PubMed Central  Google Scholar 

Hao, Y. et al. Integrated analysis of multimodal single-cell data. Cell 184, 3573–3587 (2021).

CAS  PubMed  PubMed Central  Google Scholar 

Qiuyue Y. & Duren Z. Predicting gene regulatory networks from single cell multiome data using atlas-scale external data. GitHub https://github.com/Durenlab/LINGER (2022).

Qiuyue Y. & Duren Z. Predicting gene regulatory networks from single cell multiome data using atlas-scale external data. Zendo https://zenodo.org/records/10639041 (2024).

Download references

The authors are supported by National Institutes of Health grants P20 GM139769 and R35 GM150513. The language in the text has been polished by GPT-3.5 and Grammarly.

Author informationAuthors and Affiliations Center for Human Genetics, Department of Genetics and Biochemistry, Clemson University, Greenwood, SC, USA

Qiuyue Yuan & Zhana Duren

AuthorsQiuyue YuanView author publications You can also search for this author inPubMed Google Scholar

Zhana DurenView author publications You can also search for this author inPubMed Google Scholar

Z.D. conceived the LINGER method. Z.D. and Q.Y. designed the analytical approach. Q.Y. performed the data analysis. Q.Y. wrote the software. Q.Y. and Z.D. wrote, revised and contributed to

the final manuscript. The authors read and approved the final manuscript.

Corresponding author Correspondence to Zhana Duren.

The authors declare no competing interests.

Nature Biotechnology thanks Marc Sturrock, Ricard Argelaguet and Olivier Gandrillon for their contribution to the peer review of this work.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

performance of cis-regulatory strength inferred by LINGER taking eQTL data for GTEx as ground truth.

A. AUC for cis-regulatory strength inferred by LINGER. The ground truth for A and B is the variant-gene links from GTEx. We divide RE-TG pairs into different groups based on the distance of

RE and the TSS of TG. B. AUPR ratio for cis-regulatory strength.

A. Sensitivity of neural network structure and active function. B. Violin plot of AUC and AUPR ratio values of trans-regulatory potential performance across diverse TFs and cell types (n=20

independent sample). One-sided paired t-test result in -log10P-value 10.73, 7.11, 10.85, and 9.61 compared with GENIE3, PCC, PIDC, and SCENIC+ in terms of AUC, respectively. For AUPR ratio,

-log10P-values are 8.94, 7.03, 8.48, and 7.57, respectively. C, D. Bar plot of AUC and AUPR ratio difference of different motif matching weight. The upper and lower figures refer to the

difference in weight 0.01 to 0 and 0.01 to 10. The x-axis of C, D, and H refers to the ground truth data named by the TF name and Cistrome database ID. E. Scatter plot of AUC of original

metacells and SEACells metacells as input. Each point refers to each ChIP-seq ground truth data. F, G. Box plot of AUPR ratio and AUC of defining regulatory element within different TSS

distances from 200 Kb to 2 Mb (n = 20 independent sample). Two-sided paired t-test result in p-value 0.055(2 Mb and 1 Mb), 0.088(2 Mb and 500 Kb), 0.028(2 Mb and 200 Kb), 0.025(1 Mb and 500

Kb), 0.0056(1 Mb and 200 Kb), and 0.70(500 Kb and 200 Kb) in terms of AUC. For AUPR ratio, p-values are 0.0017(2 Mb and 1 Mb), 0.093(2 Mb and 500 Kb), 0.12(2 Mb and 200 Kb), 0.00048(1 Mb and

500 Kb), 0.00075(1 Mb and 200 Kb), and 0.64(500 Kb and 200 Kb). H. Bar plot of AUC and AUPR ratio difference of two rounds pre-train and single round pre-train.

Systematic benchmarking of cell type-specific GRN.

A, B. ROC curve and PR curve of binding potential for MYC in H1 cell line. The ground truth for A to D is the ChIP-seq data of MYC in the H1 cell line. The color in A to D represents the

different competitors to predict TF-RE regulation. Orange represents LINGER, green represents PCC between the expression of TF and the chromatin accessibility of RE, and blue represents

motif binding affinity of TF to RE. C, D. Violin plot of AUC and AUPR ratio values of binding potential across diverse TFs. The ground truth is ChIP-seq data for 33 TFs (n=33 independent

sample). One-sided paired t-test is performed to test whether there is significant difference. In C, -log10P-values are 11.36 and 12.27 compared with PCC and TFBS, respectively. In D, -log

P-values are 6.21 and 5.18, respectively. E, F. AUC and AUPR ratio of cis-regulatory potential in naïve CD8 T cells. The ground truth for E to J is promoter capture HiC data. RE-TG pairs are

divided into six distance groups ranging from 0-5k to 100-200 kb. PCC is calculated between the expression of TG and the chromatin accessibility of RE. Distance denotes the decay function

of the distance to the TSS. Random denotes the uniform distribution. G, H. AUC and AUPR ratio of cis-regulatory potential in naïve B cells. I, J. F1 score of cis-regulatory in naïve CD8 T

cells and naïve B cells for LINGER and SCENIC+. P-values are from one-sided paired t-test with n=9 independent sample. K to O, F1 score of cis-regulatory potential in classical monocytes,

effector CD8 T cells, memory B cells, non-classical monocytes, and plasmacytoid DC cells for LINGER and SCENIC+. The ground truth is eQTL data (n=9 independent sample). P-values are from

one-sided paired t-test. P, Q. ROC curve and PR curve of trans-regulatory potential inference of CTCF in H1 cell line. The ground truth of P to R is putative targets of TFs from ChIP-seq

data in the H1 cell line. R Violin plot of AUC and AUPR ratio values of trans-regulatory potential performance across diverse TFs in H1 cell line (n=33 independent sample). One-sided

unpaired t-test result in -log10P-value 15.89, 15.64, 16.36, and 15.54 compared with GENIE3, PCC, PIDC, and SCENIC+ in terms of AUC, respectively. For AUPR ratio, -log10P-values are 11.01,

10.64, 11.20, and 11.17, respectively.

A, B. Violin plot of AUC and AUPR ratio values of trans-regulatory potential performance across diverse TFs and cell types for PBMCs. The ground truth of A to D is 8 experimental

perturbation data from KnockTF database (n=8 independent sample). One-sided paired t-test are performed to test the difference. For AUC, -log10P-values are 3.74, 3.43, 3.64, and 3.86

compared with GENIE3, PCC, PIDC, and SCENIC+, respectively. For AUPR ratio, -log10P-values are 3.36, 2.14, 1.69 and 1.80, respectively. C, D. Box plot of AUC and AUPR ratio values of in

silico perturbation predicted target gene. P-values are from one-sided paired t-test with 8 independent samples. E. Differentiation behavior prediction on BMMC data after knocking out

GATA1.

Table 1: Information of ground truth data for the trans-regulation and TF–RE binding potential for PBMC data. Table 2: Details of eQTL data as ground truth for the cis-regulation for PBMCs.

Table 3: Functional enrichment of cis-regulatory dominant gene. Table 4: Ground truth data for the trans-regulation and TF-RE binding potential for H1 cell line. Table 5: Details of Hi-C

data as ground truth for the cis-regulation for PBMCs. Table 6: Details of Fig. 3b,c Table 7: Details of Fig. 4c,d. Table 8: Ground truth data information of the trans-regulation for PBMC

data from the KnockTF database.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or

format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or

other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in

the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the

copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and permissions

About this articleCite this article Yuan, Q., Duren, Z. Inferring gene regulatory networks from single-cell multiome data using atlas-scale external data. Nat Biotechnol 43, 247–257 (2025).

https://doi.org/10.1038/s41587-024-02182-7

Download citation

Received: 04 August 2023

Accepted: 26 February 2024

Published: 12 April 2024

Issue Date: February 2025

DOI: https://doi.org/10.1038/s41587-024-02182-7

Share this article Anyone you share the following link with will be able to read this content:

Get shareable link Sorry, a shareable link is not currently available for this article.

Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative