ABSTRACT Accurate identification of _in vivo_ nonlinear, anisotropic mechanical properties of the aortic wall of individual patients remains to be one of the critical challenges in the field

of cardiovascular biomechanics. Since only the physiologically loaded states of the aorta are given from _in vivo_ clinical images, inverse approaches, which take into account of the

unloaded configuration, are needed for _in vivo_ material parameter identification. Existing inverse methods are computationally expensive, which take days to weeks to complete for a single

patient, inhibiting fast feedback for clinicians. Moreover, the current inverse methods have only been evaluated using synthetic data. In this study, we improved our recently developed

obtained and subjected to planar biaxial tests. Relatively close matches were achieved for the _in vivo_-identified and _ex vivo_-fitted stress-stretch responses. It is hoped that further

development of this inverse approach can enable an accurate identification of the _in vivo_ material parameters from _in vivo_ image data. SIMILAR CONTENT BEING VIEWED BY OTHERS AN INVERSE

METHOD FOR MECHANICAL CHARACTERIZATION OF HETEROGENEOUS DISEASED ARTERIES USING INTRAVASCULAR IMAGING Article Open access 18 November 2021 MULTIMODALITY IMAGING-BASED CHARACTERIZATION OF

REGIONAL MATERIAL PROPERTIES IN A MURINE MODEL OF AORTIC DISSECTION Article Open access 08 June 2020 CHARACTERIZING VARIABILITY IN PASSIVE MYOCARDIAL STIFFNESS IN HEALTHY HUMAN LEFT

VENTRICLES USING PERSONALIZED MRI AND FINITE ELEMENT MODELING Article Open access 14 February 2025 INTRODUCTION Accurate identification of _in vivo_ nonlinear, anisotropic mechanical

properties of the vessel wall of individual patients has long been regarded as one of the critical challenges in the field of cardiovascular biomechanics1. Magnetic resonance imaging (MRI)2,

ultrasound3,4 and computed tomography (CT)5 imaging techniques have been utilized to perform _in vivo_ wall motion analyses. For example, MRI2 and ultrasound3,4 studies of ascending

thoracic aortic aneurysm (TAA) patients have highlighted disparities between the dilated and non-dilated ascending aorta mechanics. However, such direct measurements of _in vivo_ aortic wall

deformation can only provide insight on TAA mechanical behaviors within the measured physiologic pressure range5 (usually between 80 mmHg–120 mmHg), whereas aneurysm rupture/dissection

usually occurs under elevated arterial pressures (e.g., about 300 mmHg) brought on by extreme emotional or physical stress6. Thus, patient-specific TAA rupture analysis could benefit from

estimating the full _in vivo_ elastic properties using a constitutive model, which, consequently, can be utilized to predict TAA mechanical response at various loading conditions. Recently,

some studies7,8 derived linearized stiffness from _ex vivo_ biaxial tests and showed that the stiff aneurysms are prone to rupture. This linearized metric can provide a simple and

clinically-relevant way to roughly predict diameter/stretch-based rupture potential. The distribution of linearized stiffness has been measured on TAA from multiphase CT scans9,10. However,

rupture analysis may benefit more from identification of nonlinear hyperelastic properties. For instance, the maximum curvature point of strain-stress curve has been shown to be the most

important feature that is predictive of the aorta wall strength in machine learning models11,12. By extracting nonlinear properties from multiphase CT scans, it is feasible to derive

intrinsic features such as the maximum curvature point, which may be used to estimate wall strength. Eventually, rupture risk prediction could be achieved by determining when the

stress/stretch applied to the tissue exceeds its strength/extensibility13. Since the unloaded state of arteries is unknown, it is challenging to inversely estimate hyperelastic constitutive

parameters from _in vivo_ deformed geometries. To simplify such inverse computation, the geometry of arteries is often assumed as a perfect tube. Based on this assumption, Schulze-Bauer and

Holzapfel14 estimated Fung-type material parameters, Masson _et al_., Olsson and Klarbring, Stålhand15,16,17,18 estimated material parameters using the constitutive model proposed by

Holzapfel _et al_.19 and geometrical parameters, Smoljkić _et al_.20 identified the Gasser–Ogden-Holzapfel (GOH) model21 parameters. To account for the irregularity of patient-specific

geometries, inverse finite element (FE) simulations are often used in the identification of _in vivo_ hyperelastic properties from multi-phase clinical images. Optimization-based FE-updating

approaches were proposed, in which the optimal set of material parameters is identified by updating the material parameters in the FE simulations to minimize a pre-defined error function.

Using these strategies, Liu _et al_.22 estimated parameters of the modified Mooney-Rivlin model from carotid artery MRI data. The optimization problem can be much more challenging when

estimating anisotropic model parameters, since different hyperelastic parameters are coupled nonlinearly in their contributions to the structural response. Wittek _et al_.23,24 developed two

approaches to identify _in vivo_ GOH model parameters of the abdominal aorta from 4D ultrasound data based on mixed stochastic-deterministic optimization. A total of 7400 iterations23 and

43,500–86,900 iterations24 were needed to reach the optimal set of parameters in their approaches, resulting in a computational time of 1~2 weeks. Such high computational cost could inhibit

a practical use of the methods, particularly in a clinical setting requiring fast feedback to clinicians. To expedite the identification process, our group has recently proposed the

multi-resolution direct search (MRDS) approach25, which was designed to improve the searching algorithm, and the computation time was reduced to 1~2 days with less than 1000 iterations.

However, these studies23,24,25,26 relied on numerically-generated data to validate the approaches. In this study, _in vivo_ nonlinear anisotropic material properties of the aortic wall were

estimated from clinical 3D gated CT images of two ascending thoracic aortic aneurysm (ATAA) patients. The MRDS approach25 was improved in this study in the following aspects: (1) without

having to iteratively recover the unloaded configuration, the generalized prestressing algorithm (GPA)27 is implemented to directly account for the pre-stress state. Thus, the material

parameter identification process is expected to be significantly accelerated; (2) rigid motions of the ascending aorta due to heart movements are removed using the rigid iterative closest

point (ICP) registration algorithm28,29; and (3) to obtain the diastolic-to-systolic displacement field, non-rigid ICP registration30 and thin-plate spline (TPS) fitting31 algorithms are

used to establish mesh correspondence between the two phases. For comparison, corresponding surgically-resected aortic wall tissue samples were obtained and subjected to planar biaxial tests

to extract their experimentally-derived material properties. The estimated material properties were compared with the experimentally-derived material properties. MATERIALS AND METHODS IMAGE

DATA AND CORRESPONDING TISSUE SPECIMENS With Institutional Review Board (IRB) approvals, aortic tissue specimens from two patients (Patient 1: a 67 year-old male; Patient 2: a 68 year-old

female) with ascending thoracic aortic aneurysm (ATAA) who underwent surgical repair was obtained from the Emory University Hospital, Atlanta, GA. The 10-phase preoperative ECG-gated CT data

and systolic and diastolic blood pressure levels were obtained prior to the intervention. A complete waiver of HIPAA authorization and informed consent was granted by the Emory IRB. All

data was collected retrospectively and de-identified and all methods were performed in accordance with the relevant guidelines and regulations. The CT images had a scan matrix size of 256 × 

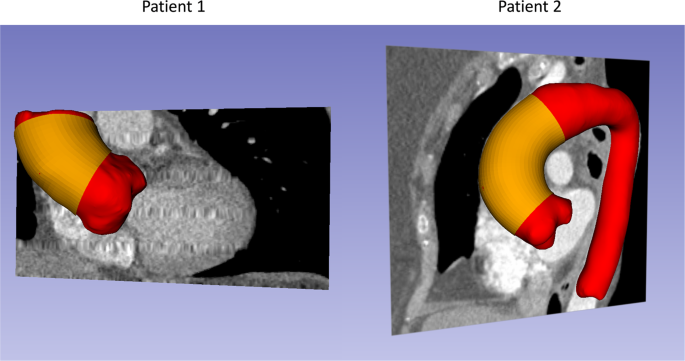
256, in-plane pixel size of 0.75 mm × 0.75 mm and slice thickness of 1 mm. Unfortunately, only part of ATAA of Patient 1 was imaged from the multiphase CT data. For each patient, the

systolic and diastolic aorta geometries (Fig. 1, depicted in red) were reconstructed following our established protocol32. Wall thickness of the aorta can be obtained from high resolution CT

images according to Shang _et al_.33. The thickness values were measured at 16 locations (Fig. 2) from cross-sectional planes of the ATAA segment (Figs 1 and 2, depicted in yellow) in the

systolic phase. For each patient, surgically-excised aneurysmal tissue were dissected into 2~3 square-shaped specimens (2 specimens for Patient 1 and 3 specimens for Patient 2) for biaxial

tensile tests. For one square-shaped specimen, the wall thickness values were measured at 3 equally-spaced locations along the diagonal line. After image segmentation, each aorta geometry

was represented by a triangular mesh. For each patient, since the diastolic aorta geometry Ω_dia_ and systolic aorta geometry Ω_sys_ have different numbers of nodes and elements, the

displacement field from diastole to systole cannot be directly calculated. To obtain the displacement field, mesh correspondence between diastolic and systolic phases needs to be

established. Herein, non-rigid ICP registration30 and TPS fitting31 algorithms were applied to find a nonlinear coordinate transform _T_ from the template geometry Ω_dia_ to the target

geometry Ω_sys_, such that the distance between Ω_sys_ and the transformed template geometry _T_(Ω_dia_) is minimized (Fig. 3(A,B)). Please refer to Amberg _et al_.30 for details of the

registration method. The geometries of ATAA segment at diastolic phase were remeshed with quadrilateral elements (Fig. 1, yellow) using our previous remeshing algorithm34. Using the

transform _T_, the quad ATAA meshes were transformed onto the surface of the ATAA segment at systolic phase (Fig. 3(C)). Thus, we obtained diastolic and systolic quad meshes of the ATAA with

mesh correspondence. CONSTITUTIVE MODEL Following our previous studies25,26, the Gasser-Ogden-Holzapfel (GOH) model21 was used to model the mechanical response of the aortic wall tissue. In

this model, tissues are assumed to be composed of a matrix material with two families of embedded fibers, each of which has a preferred direction. The fiber directions can be mathematically

described using two unit vectors. The strain energy function can be expressed by $$\Psi ={C}_{10}({\bar{I}}_{1}-3)+\frac{{k}_{1}}{2{k}_{2}}\mathop{\sum

}\limits_{i=1}^{2}[exp\{{k}_{2}{[\kappa {\bar{I}}_{1}+(1-3\kappa ){\bar{I}}_{4i}-1]}^{2}\}-1]+\frac{1}{D}[\frac{{J}^{2}-1}{2}-\,{\rm{l}}{\rm{n}}\,J]$$ (1) where _C_10 is a material parameter

to describe the matrix material. _k_1 is a positive material parameter that has the same dimension of stress, while _k_2 is a dimensionless parameter. The deviatoric strain invariant

\({\bar{I}}_{1}\) is used to characterize the matrix material, and the deviatoric strain invariant \({\bar{I}}_{4i}\) is used to characterize the fiber families. \({\bar{I}}_{4i}\) is equal

to squares of the stretches in the fiber directions._κ_ is used as a dispersion parameter describing the distribution of fiber orientation. When _κ_ = 0, the fibers are perfectly aligned.

When _κ_ = 0.33, the fibers are randomly distributed, and the material becomes isotropic. _D_ is a fixed constant enforcing the material incompressibility (_D_ = 1 × 10−5). The mean fiber

directions were assumed symmetric with respect to the circumferential axis of the local coordinate system. The parameter _θ_ defines the angle between one of the mean local fiber direction

and the circumferential axis of the local coordinate system. Thus, the five material parameters (_C_10, _k_1, _k_2, _κ_, _θ_) in this model need to be estimated. THE INVERSE METHOD FOR _IN

VIVO_ MATERIAL PARAMETER IDENTIFICATION We assume that the aortic wall is quasi-static at diastole and systole, respectively. The flowchart for constitutive parameter identification is

demonstrated in Fig. 4. By using our modified multi-resolution direct search (MRDS) approach25 based on finite element (FE) updating, averaged material parameters throughout the ascending

aorta were estimated from the _in vivo_ systolic and diastolic ATAA geometries. Briefly, in the FE-updating scheme, with an initial guess of material parameters, (1) the pre-stresses

associated with the systolic geometry are recovered by the generalized prestressing algorithm (GPA)27 implemented in FE simulation, (2) the geometry is depressurized to diastolic phase

\({\Omega }_{dia}^{FE}\) in FE simulation, and (3) using the multi-resolution direct search (MRDS) strategy, the estimated material parameters are iteratively adjusted to minimize the

average node-to-node error ε_dia_ between the FE-deformed diastolic geometry \({\Omega }_{dia}^{FE}\) and the _in vivo_ CT-derived diastolic geometry Ω_dia_. This optimization process yields

the optimal set of identified material parameters. We define the objective function, which measures the average node-to-node error _ε__dia_ between ICP registered \({\Omega }_{dia}^{FE}\)

and Ω_dia_ $${\varepsilon }_{dia}({\Omega }_{dia}^{FE},{\Omega }_{dia})=\frac{1}{N}\mathop{\sum }\limits_{n=1}^{N}||{{\boldsymbol{X}}}_{dia,n}^{FE}-{{\boldsymbol{X}}}_{dia,n}||$$ (2) where

\({{\boldsymbol{X}}}_{dia,n}^{FE}\) is the coordinates of the _n_th node on \({\Omega }_{dia}^{FE}\); _n_ is the node index and _N_ is the number of nodes; ||■|| denotes 3D Euclidean norm.

The FE simulations were performed in ABAQUS using C3D8H solid elements, and the mesh sensitivity analysis was performed in our previous work35. In the FE simulations, the boundary nodes were

only allowed to move in the radial directions. The node-to-node error ε_dia_ can be decomposed into two components: (1) rigid body motions (translation and rotation) and (2) strain. Due to

the heart movements during the cardiac cycles (as can be observed in Fig. 3(C)), the boundaries of FE-deformed diastolic geometry \({\Omega }_{dia}^{FE}\) may not align with the boundaries

of the _in vivo_ CT-derived diastolic geometry Ω_dia_, and the rigid body motions between the two phases are not negligible. With the current boundary conditions, the rigid motions can

result in large residuals in the objective function, and hence the error caused by strain could be overwhelmed. Thus, during each iteration of the material parameter identification, rigid

ICP registration algorithm28,29 is applied to \({\Omega }_{dia}^{FE}\) to remove rigid motions with respect to Ω_dia_ before calculating the average node-to-node error ε_dia_. In general,

the GOH model21 has coupled material parameters, and the optimization problem in Eq. (2) is nonlinear, multivariate and non-convex, which causes the _in vivo_ material parameter

identification difficulty known as the local optima. Different combinations of _C_10, _k_1, _k_2, _κ_ and _θ_ in the GOH model may result in very similar mechanical responses. For the

optimization methods that directly search the material parameter space, this coupling effect can produce numerous local optima. Gradient-based optimization approaches may not guarantee a

global optimum. Mixed stochastic-deterministic approaches are typically used23,24 where material parameters are randomly initialized for the gradient-based optimization approaches. However,

by directly searching the material parameter space, these approaches usually require a large number of iterations and may take weeks to complete23,24. In this study, we utilized our recently

developed MRDS strategy25 to accelerate the optimization process. In the MRDS approach25, a new search space, derived from the stress-stretch curves using principal component analysis

(PCA), instead of the material parameter space, was used for the search of best material properties. The new PCA-based curve shape space is decomposed into multi-resolution representations,

from coarse to fine. Instead of searching using the gradient of the objective function, the MRDS searches in the new PCA space at different resolutions and identifies the best curve shape

match. Hence, to obtain the multiple resolution representations, the PCA space is represented by PCA parameter-candidates with multiple resolutions (note that PCA space parameters are

different from the material parameters). In our previous study25, four resolutions were built: In the first, second, third and fourth resolutions, a total of 12, 117, 1197 and 10529

parameter-candidates were selected, respectively. The parameter-candidates at one resolution are linked to the nearby parameter-candidates at adjacent resolutions according to the Euclidean

distance. The MRDS strategy follows the links between multi-resolutions: a parameter-candidate with the lowest value of the objective function (Eq. (2)) is selected by searching the first

resolution; following the links of the selected parameter-candidate, a new search begins at the next resolution. Consequently, the MRDS approach searches the discrete PCA space from the

first (lowest) resolution to the last (highest) resolution, and the best parameter-candidate, which yields the lowest value of the objective function (Eq. (2)), can be eventually identified.

BIAXIAL TESTING PROTOCOLS Stress-controlled biaxial tensile tests were performed on corresponding surgically-resected tissue samples of the two patients. Frozen tissue samples were

submerged in a 37 °C water bath until totally defrosted, following the two-stage slow thawing method to remove the cryopreserving agent36. The samples were trimmed into 2~3 square-shaped

specimens (2 specimens for Patient 1 and 3 specimens for Patient 2) with a side length of 20~25 mm. Each specimen was subjected to biaxial tension with the circumferential (θ) and

longitudinal (_z_) directions aligned with the primary axes of the biaxial test fixture. A stress-controlled biaxial testing protocol was used37,38. _P_ denotes the first Piola–Kirchhoff

stress, and the ratio _P_θ:_P__z_ was kept constant. Each tissue specimen was preconditioned for at least 40 continuous cycles with _P_θ:_P__z_ = 1:1 to minimize tissue hysteresis. Seven

successive protocols were performed using ratios \({P}_{{\rm{\theta }}}:{P}_{z}=0.75:1,0.5:1,\,0.3:1,\,1:1,\,1:0.75,\,1:0.5,\,1:0.3\). The GOH model parameters for each specimen were

obtained by fitting the biaxial stretch-stress response in MATLAB. To obtain material parameters that approximately represent an average response, the stretch-stress data for all specimens

from the same patient was fitted simultaneously. ETHICAL APPROVAL The study was approved by the Georgia Tech and Emory University Institutional Review Boards. RESULTS WALL THICKNESS AND

BLOOD PRESSURES The wall thickness values from _in vivo_ and _ex vivo_ measurements are shown in Table 1. Diastolic and systolic blood pressures for the two patients are reported in Table 2.

The blood pressure levels were measured at the time of the patients’ visits for CT scans. _IN VIVO_-IDENTIFIED AND _EX VIVO_-FITTED MATERIAL PROPERTIES The improved MRDS approach can be

completed in 1~2 hours with less than 100 FE iterations using a quad-core CPU with 32GB memory. The _in vivo_-identified and _ex vivo_-fitted material parameters are shown in Table 3, where

the difference in material parameters can be clearly seen. The difference is anticipated mainly due to the highly coupled material parameters - leading to local optima in the optimization

process (Section 2.3). The coefficient of determination (R2) values between the _ex vivo_-experimental and _ex vivo_-fitted stress/strain data are also reported in Table 3. A more

informative way for comparing material properties obtained from the inverse method and experiments, is to plot the stress-stretch curves computed from material parameters. We use _σ_θ and

_λ_θ to denote the circumferential stress and stretch, _σ_z and _λ_z to denote the longitudinal stress and stretch. Thus, stress-stretch curves are plotted using the _in vivo-_identified

_and ex vivo-_fitted material parameters with three _λ_θ:_λ_z ratios, namely three protocols: (1) in the circumferential strip biaxial protocol, fixing _λ_z = 1 while increasing _λ_θ; (2) in

the equi-biaxial protocol, keeping the ratio _λ_θ:_λ_z = 1:1; (3) in the longitudinal strip biaxial protocol, fixing _λ_θ = 1 while increasing _λ_z. The stress-stretch curves determined by

the estimated parameters were compared with the stress-stretch curves derived from biaxial data. As plotted in Fig. 5, the two specimens of Patient 1 demonstrate almost identical

stretch-stress response, whereas the three tissue specimens of Patient 2 show different stress-stretch responses, which indicate that the material properties are heterogeneously distributed.

Mean absolute percentage error (MAPE) is computed to measure the goodness-of-fit between _in vivo_-identified and _ex vivo-_fitted average curve (_ex vivo_-all). For both patients, the

average response show relatively good agreements with the identified stretch-stress curves. To further compare the biaxial stretch-stress response, using the _in vivo_-identified material

parameters, the stress _σ_θ or _σ_Z values can be obtained at various values of stretch _λ_θ and _λ_z, which creates the response surfaces, by assuming a plane stress state and

incompressible condition. Hence, the stretch-stress response surfaces for _in vivo_-identified and _ex vivo_-fitted average material response can be visualized in Fig. 6. Relatively close

matches were achieved between the _in vivo_-identified and _ex vivo_-fitted response surfaces. To compare linearized response in the circumferential direction within the physiological range,

we computed pressure-strain modulus as defined in Martin _et al_.5 from image-derived geometries and FE-deformed geometries, respectively. _Ex vivo_-derived pressure-strain modulus can also

be obtained using the same FE simulation setup (Section 2.3) with _ex vivo_-fitted average material parameters. The results are shown in Table 4, which show that close matches are achieved

between the image-derived and FE-predicted the pressure-strain moduli. For Patient 2, the difference between FE-predicted and _ex vivo_-derived pressure-strain modulus may be explained by

the deviation of curve slop in the physiological range (Fig. 5(G)). COMPARISON OF THE IMAGE-DERIVED AND FE-DEFORMED GEOMETRIES The objective function (Eq. (2)) was minimized by the MRDS

approach for the two patients, which measures the node-to-node error between the image-derived and the FE-deformed (using _in vivo_-identified material parameters) diastolic geometries. The

image-derived and the FE-deformed diastolic geometries are plotted in Fig. 7. For comparison, we also compute the node-to-surface error defined by Eqs (2) and (3) of our previous work Liu

_et al_.25. The errors are reported in Table 5. It is worth noting that, in general, the averaged node-to-node error is larger than the averaged node-to-surface error25. The relatively large

value of node-to-node error for Patient 2 may be explained by heterogeneity of the material properties and wall thickness. In other words, deformations between the diastolic and systolic

phases of Patient 2 cannot be fitted well using one set of material parameters. Hence, the diastolic-to-systolic displacement fields of image-derived and FE-deformed geometries are compared

as follows. For a node on the image-derived diastolic geometry Ω_dia_ and the corresponding node on the image-derived systolic geometry Ω_sys_, the displacement magnitude of a node is

defined as $${d}_{dia-sys}^{(n)}({{\boldsymbol{X}}}_{dia,n},{{\boldsymbol{X}}}_{sys,n})=||{{\boldsymbol{X}}}_{sys,n}-{{\boldsymbol{X}}}_{dia,n}||$$ (3) where \(\,{{\boldsymbol{X}}}_{sys,n}\)

is the coordinates of the _n_th node on Ω_sys_. The averaged displacement magnitude between the diastolic and systolic geometries, \({d}_{dia-sys}\) can also be obtained. Similarly, we can

compute the FE-derived displacement magnitude \({d}_{dia-sys}^{FE,(n)}({{\boldsymbol{X}}}_{dia,n}^{FE},{{\boldsymbol{X}}}_{sys,n})\) between the FE-deformed diastolic geometry \({\Omega

}_{dia}^{FE}\) and the image-derived systolic geometry Ω_sys_. Thus, the averaged displacement magnitude \({d}_{dia-sys}^{FE}\) can be calculated. The displacement fields for the two

patients are plotted in Fig. 8. As expected, for Patient 2, the image-derived displacement fields are significantly heterogeneous comparing to the FE-derived displacement fields, while

Patient 1 demonstrates only minor difference. DISCUSSION Despite the discrepancy in numerical values of the constitutive parameters, the inverse method and experiments achieved relatively

good agreement in the biaxial stress-stretch curves and response surfaces. The averaged node-to-surface errors between the FE-deformed and the image-derived geometries were 0.41 mm and 0.77 

mm for Patients 1 and 2, respectively, which are less than or equal to the size of a voxel (0.75 × 0.75 × 1 mm). This marks, to our knowledge, the first study that directly estimate _in

vivo_ nonlinear, anisotropic material properties of the ATAA from gated CT scans with comparisons to experimental data of planar biaxial tests. Trabelsi _et al_.39 utilized _in vitro_

experimental bulge inflation test for inverse method validation. However, the study39 assumed isotropic constitutive behavior of ATAA and a linear relation between the aorta volume and the

material parameters. In this study, the improved MRDS approach does not require such assumptions and can handle anisotropic tissue response. The computational efficiency is further improved

by the modified MRDS approach. This is mainly because that the computationally-expensive iterative method34,40 for recovering unloaded configuration is avoided by using the GPA method27. The

improved MRDS approach can be completed in 1~2 hours with less than 100 FE iterations, using a quad-core CPU with 32GB memory, whereas the original MRDS method25 took 1~2 days using the

same computation power. The diastolic-to-systolic displacement field, which establishes mesh correspondence between diastolic and systolic phases, is often required by the material parameter

identification schemes such as the virtual field method41 and the stress-matching26,42 or strain-matching method23,24. This requirement can be satisfied in _in vitro_ experiments by

tracking physical markers or tracking speckle patterns in ultrasound images43. CT is routinely used for imaging ascending aorta because of its large field of view44. However, CT images do

not have distinct image texture patterns for tracking individual points on the aortic wall, and therefore the absence of diastolic-to-systolic displacement field poses a critical challenge

for material parameter identification using CT data. In the original MRDS approach25, because the objective was based on geometry-matching, the use of node-to-surface objective function

eliminates the need for mesh correspondence. In the improved version of MRDS, mesh correspondence was established using the non-rigid ICP registration30 and TPS fitting31 algorithms. Thus,

the improved MRDS can support different identification schemes24,26 and material properties can be estimated from the gated CT data. Because ECG-gated CT are not routinely performed for

ATAA, we only acquired the multiphase CT data and tissue samples of two patients. In addition, only part of ATAA of Patient 1 was imaged from the multiphase CT data, so the identification

are restricted on a small segment for Patient 1 (Fig. 1). Hence, the current inverse approach needs more validation cases before clinical application. The discrepancies between the _in vivo_

identified and _ex vivo_ fitted material parameter could be attributed to the following sources. (1) The experimental and physiological (diastolic and systolic) stretch values are shown in

Fig. 9. The physiological stretch values (with pre-stretch/pre-stress considered) were computed from the GPA method in Section 2.3. It is worth noting that, the stretch ratios are different

under experimental and physiological conditions, which indicates that the biaxial experimental data can only partially capture the physiological conditions. A constitutive model that can

characterize the biaxial experimental data well may have to extrapolate its predication under some physiological conditions. (2) The aorta may undergoes rhythmic active contraction _in vivo_

during the cardiac cycle45. However, active contractions generated by the smooth muscle cells are not considered by the constitutive model in this study. The surgically-resected tissues may

only demonstrate passive _ex vivo_ behavior. This could be a source of discrepancy between the _in vivo_ and _ex vivo_ properties. (3) The blood pressure levels were measured at the time of

the patients’ visits for CT scans. Unfortunately, their blood pressures were not obtained simultaneously with the ECG-gated CT scans. (4) The external supports from pulmonary arteries and

vena cava could alter the stress distribution within the aorta. Since the supporting forces are unknown, it could be a source of discrepancy between the _ex vivo_ and _in vivo_ properties.

Note that there is no rigid (or high stiffness) structure (e.g. rib cage) that contacts the aorta, it is likely that the external supports from the pulmonary arteries/vena cava would not

have significant impact on the loading bearing of the aorta. (5) In the FE simulations, the boundary nodes were only allowed to move in the radial directions. To validate this boundary

condition, we plotted the FE-deformed (after ICP) versus image-derived diastolic geometries. From Fig. 7, close matches can be observed for the proximal and distal boundaries. (6) Heart

motions could induce unknown axial forces/stresses in the aorta. However, using the current displacement boundary condition, the reaction forces at the proximal and distal ends required for

the static equilibrium were calculated by the FEA. Because of different pressure loading conditions, the boundary forces are different for diastole and systole. Therefore, the axial stresses

are also different at diastolic and systolic phases and are dependent on the patient-specific geometry and blood pressure levels. The similarities of identified material parameters between

the two patients could be explained by the similarities of the pressure-strain modulus (Table 4). It is unlikely that the similarities is due to constraint or initial values in the

optimization. Unlike gradient-based optimization, in the MRDS, the parameter space is represented by a finite number of parameter-candidates prior to the optimization process. Therefore, the

optimization always starts with the same parameter-candidates in the first level (12), and there is only a limited number of (10529) of possible solutions in the MRDS. The identified

parameters were automatically determined by the MRDS algorithm. The upper and lower bounds used for sampling the parameter-candidates are shown in our previous study25, they are far from the

identified parameters in this study. In addition, there is no bound or constraint during the MRDS optimization process. In this study, the constitutive parameter identification was based on

the following two main assumptions. (1) It is known that the aortic tissue properties are heterogeneously distributed46,47, material properties of the inner curvature region may be

different from those of the outer curvature region. The wall thickness may also has spatial variation across the ATAA, heterogeneity of wall thickness and material heterogeneity could be

correlated48. In the current inverse method, we only considered a simplified case, where the averaged _in vivo_ wall thickness was used, and the averaged hyperleastic behavior of the aorta

segment was identified. The stress-stretch data in this study (Fig. 5) also suggests material heterogeneity. The discrepancy in Figs 5 and 6 may be attributed to location-dependent material

property distribution. As shown in Fig. 8, the displacement field explained by the FE simulation is smoother than the image-derived displacement field, which indicates an averaging effect

when assuming homogenous properties. (2) We assume that residual stresses have minimal impact on the material parameter identification, since a study49 suggested that the inclusion of

residual stress in the model has little effect on estimated material properties. Our recent work50 also demonstrated that the transmural mean stress is independent of the residual stress.

CONCLUSION To identify _in vivo_ nonlinear anisotropic material properties of the ATAA, we have improved our original MRDS approach, thus computation time cost is further reduced and mesh

correspondence can be established. The improved MRDS approach was applied to pre-operative gated CT scans of two ATAA patients. For comparison, surgically-excised tissue samples were

obtained for experimental planar biaxial tests. Relatively close match was achieved in terms of the _in vivo_-identified and _ex vivo_-fitted stress-stretch response. Our results are

preliminary, but encouraging. It is hoped that further development of this approach can enable an accurate identification of the _in vivo_ material properties from gated CT data, which

currently is a critical challenge in the field of cardiovascular biomechanics. DATA AVAILABILITY All relevant data are within the paper. REFERENCES * Taylor, C. A. & Figueroa, C. A.

Patient-Specific Modeling of Cardiovascular Mechanics. _Annual Review of Biomedical Engineering_ 11, 109–134, https://doi.org/10.1146/annurev.bioeng.10.061807.160521 (2009). Article  CAS 

PubMed  PubMed Central  Google Scholar  * Bieging, E. T. _et al_. _In vivo_ three-dimensional MR wall shear stress estimation in ascending aortic dilatation. _J Magn Reson Imaging_ 33,

589–597, https://doi.org/10.1002/jmri.22485 (2011). Article  PubMed  Google Scholar  * Koullias, G. _et al_. Mechanical deterioration underlies malignant behavior of aneurysmal human

ascending aorta. _J Thorac Cardiovasc Surg_ 130, 677–683, https://doi.org/10.1016/j.jtcvs.2005.02.052 (2005). Article  PubMed  Google Scholar  * Wittek, A. _et al_. Cyclic three-dimensional

wall motion of the human ascending and abdominal aorta characterized by time-resolved three-dimensional ultrasound speckle tracking. _Biomechanics and Modeling in Mechanobiology_ 15,

1375–1388, https://doi.org/10.1007/s10237-016-0769-2 (2016). Article  PubMed  Google Scholar  * Martin, C., Sun, W., Primiano, C., McKay, R. & Elefteriades, J. Age-dependent ascending

aorta mechanics assessed through multiphase CT. _Ann Biomed Eng_ 41, 2565–2574, https://doi.org/10.1007/s10439-013-0856-9 (2013). Article  PubMed  Google Scholar  * Hatzaras, I. S. _et al_.

Role of Exertion or Emotion as Inciting Events for Acute Aortic Dissection. _American Journal of Cardiology_ 100, 1470–1472, https://doi.org/10.1016/j.amjcard.2007.06.039 (2007). Article 

PubMed  Google Scholar  * Duprey, A., Trabelsi, O., Vola, M., Favre, J.-P. & Avril, S. Biaxial rupture properties of ascending thoracic aortic aneurysms. _Acta Biomaterialia_ 42,

273–285, https://doi.org/10.1016/j.actbio.2016.06.028 (2016). Article  PubMed  Google Scholar  * Martin, C., Sun, W., Pham, T. & Elefteriades, J. Predictive biomechanical analysis of

ascending aortic aneurysm rupture potential. _Acta Biomaterialia_ 9, 9392–9400, https://doi.org/10.1016/j.actbio.2013.07.044 (2013). Article  PubMed  Google Scholar  * Farzaneh, S.,

Trabelsi, O. & Avril, S. Inverse identification of local stiffness across ascending thoracic aortic aneurysms. _Biomechanics and Modeling in Mechanobiology_ 18, 137–153,

https://doi.org/10.1007/s10237-018-1073-0 (2019). Article  PubMed  Google Scholar  * Farzaneh, S., Trabelsi, O., Chavent, B. & Avril, S. Identifying Local Arterial Stiffness to Assess

the Risk of Rupture of Ascending Thoracic Aortic Aneurysms. _Annals of Biomedical Engineering_ 47, 1038–1050, https://doi.org/10.1007/s10439-019-02204-5 (2019). Article  PubMed  Google

Scholar  * Luo, Y., Fan, Z., Baek, S. & Lu, J. Machine learning–aided exploration of relationship between strength and elastic properties in ascending thoracic aneurysm. _International

Journal for Numerical Methods in Biomedical Engineering_ 34, e2977, https://doi.org/10.1002/cnm.2977 (2018). Article  MathSciNet  PubMed  Google Scholar  * He, X., Ferrara, A., Luo, Y.,

Auricchio, F. & Lu, J. In _2019 ASME Summer Biomechanics_, _Bioengineering_, _and Biotransport Conference_ (Seven Springs, Pennsylvania, 2019). * Campobasso, R. _et al_. Evaluation of

Peak Wall Stress in an Ascending Thoracic Aortic Aneurysm Using FSI Simulations: Effects of Aortic Stiffness and Peripheral Resistance. _Cardiovascular Engineering and Technology_ 9,

707–722, https://doi.org/10.1007/s13239-018-00385-z (2018). Article  PubMed  Google Scholar  * Schulze-Bauer, C. A. J. & Holzapfel, G. A. Determination of constitutive equations for

human arteries from clinical data. _Journal of Biomechanics_ 36, 165–169, https://doi.org/10.1016/S0021-9290(02)00367-6 (2003). Article  CAS  PubMed  Google Scholar  * Stålhand, J.

Determination of human arterial wall parameters from clinical data. _Biomechanics and Modeling in Mechanobiology_ 8, 141–148, https://doi.org/10.1007/s10237-008-0124-3 (2009). Article 

PubMed  Google Scholar  * Olsson, T. & Klarbring, J. S. A. Modeling initial strain distribution in soft tissues with application to arteries. _Biomechanics and Modeling in

Mechanobiology_ 5, 27–38, https://doi.org/10.1007/s10237-005-0008-8 (2006). Article  CAS  PubMed  Google Scholar  * Masson, I., Boutouyrie, P., Laurent, S., Humphrey, J. D. & Zidi, M.

Characterization of arterial wall mechanical behavior and stresses from human clinical data. _Journal of Biomechanics_ 41, 2618–2627, https://doi.org/10.1016/j.jbiomech.2008.06.022 (2008).

Article  PubMed  PubMed Central  Google Scholar  * Masson, I. _et al_. Carotid artery mechanical properties and stresses quantified using _in vivo_ data from normotensive and hypertensive

humans. _Biomechanics and Modeling in Mechanobiology_ 10, 867–882, https://doi.org/10.1007/s10237-010-0279-6 (2011). Article  PubMed  Google Scholar  * Holzapfel, G. A., Gasser, T. C. &

Ogden, R. W. A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models. _Journal of elasticity and the physical science of solids_ 61, 1–48,

https://doi.org/10.1023/a:1010835316564 (2000). Article  MathSciNet  MATH  Google Scholar  * Smoljkić, M., Vander Sloten, J., Segers, P. & Famaey, N. Non-invasive, energy-based

assessment of patient-specific material properties of arterial tissue. _Biomechanics and Modeling in Mechanobiology_ 14, 1045–1056, https://doi.org/10.1007/s10237-015-0653-5 (2015). Article

  PubMed  Google Scholar  * Gasser, T. C., Ogden, R. W. & Holzapfel, G. A. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. _Journal of The Royal

Society Interface_ 3, 15–35, https://doi.org/10.1098/rsif.2005.0073 (2006). Article  Google Scholar  * Liu, H. _et al_. Using _In Vivo_ Cine and 3D Multi-Contrast MRI to Determine Human

Atherosclerotic Carotid Artery Material Properties and Circumferential Shrinkage Rate and Their Impact on Stress/Strain Predictions. _Journal of Biomechanical Engineering_ 134,

011008-011008-011009, https://doi.org/10.1115/1.4005685 (2012). Article  Google Scholar  * Wittek, A. _et al_. _In vivo_ determination of elastic properties of the human aorta based on 4D

ultrasound data. _Journal of the Mechanical Behavior of Biomedical Materials_ 27, 167–183, https://doi.org/10.1016/j.jmbbm.2013.03.014 (2013). Article  PubMed  Google Scholar  * Wittek, A.

_et al_. A finite element updating approach for identification of the anisotropic hyperelastic properties of normal and diseased aortic walls from 4D ultrasound strain imaging. _Journal of

the Mechanical Behavior of Biomedical Materials_ 58, 122–138, https://doi.org/10.1016/j.jmbbm.2015.09.022 (2016). Article  PubMed  Google Scholar  * Liu, M., Liang, L. & Sun, W.

Estimation of _in vivo_ mechanical properties of the aortic wall: A multi-resolution direct search approach. _J Mech Behav Biomed Mater_ 77, 649–659,

https://doi.org/10.1016/j.jmbbm.2017.10.022 (2017). Article  PubMed  PubMed Central  Google Scholar  * Liu, M., Liang, L. & Sun, W. A new inverse method for estimation of _in vivo_

mechanical properties of the aortic wall. _J Mech Behav Biomed Mater_ 72, 148–158, https://doi.org/10.1016/j.jmbbm.2017.05.001 (2017). Article  PubMed  PubMed Central  Google Scholar  *

Weisbecker, H., Pierce, D. M. & Holzapfel, G. A. A generalized prestressing algorithm for finite element simulations of preloaded geometries with application to the aorta. _International

Journal for Numerical Methods in Biomedical Engineering_ 30, 857–872, https://doi.org/10.1002/cnm.2632 (2014). Article  PubMed  Google Scholar  * Besl, P. J. & McKay, N. D. A method for

registration of 3-D shapes. _IEEE Transactions on Pattern Analysis and Machine Intelligence_ 14, 239–256, https://doi.org/10.1109/34.121791 (1992). Article  Google Scholar  * Chen, Y. &

Medioni, G. In _Proceedings_. 1991 _IEEE International Conference on Robotics and Automation_. vol. 2723, 2724–2729 (1991). * Amberg, B., Romdhani, S. & Vetter, T. In 2007 _IEEE

Conference on Computer Vision and Pattern Recognition_. 1–8 (2007). * Duchon, J. Splines minimizing rotation-invariant semi-norms in Sobolev spaces. In Schempp W., Zeller K. (eds)

Constructive Theory of Functions of Several Variables. Lecture Notes in Mathematics, vol. 571. Springer, Berlin, Heidelberg (1977). https://doi.org/10.1007/BFb0086566. Chapter  Google

Scholar  * Wang, Q. _et al_. Dimensional Analysis of Aortic Root Geometry During Diastole Using 3D Models Reconstructed from Clinical 64-Slice Computed Tomography Images. _Cardiovascular

Engineering and Technology_ 2, 324–333, https://doi.org/10.1007/s13239-011-0052-8 (2011). Article  Google Scholar  * Shang, E. K. _et al_. Validation of semiautomated and locally resolved

aortic wall thickness measurements from computed tomography. _Journal of Vascular Surgery_ 61, 1034–1040, https://doi.org/10.1016/j.jvs.2013.11.065 (2015). Article  PubMed  Google Scholar  *

Liang, L., Liu, M., Martin, C., Elefteriades, J. A. & Sun, W. A machine learning approach to investigate the relationship between shape features and numerically predicted risk of

ascending aortic aneurysm. _Biomechanics and Modeling in Mechanobiology_ 16, 1519–1533, https://doi.org/10.1007/s10237-017-0903-9 (2017). Article  PubMed  PubMed Central  Google Scholar  *

Martin, C., Sun, W. & Elefteriades, J. Patient-specific finite element analysis of ascending aorta aneurysms. _American Journal of Physiology - Heart and Circulatory Physiology_ 308,

1306–1316 (2015). Article  Google Scholar  * Bia, D. _et al_. Cryopreservation procedure does not modify human carotid homografts mechanical properties: an isobaric and dynamic analysis.

_Cell and Tissue Banking_ 7, 183–194, https://doi.org/10.1007/s10561-005-0655-0 (2006). Article  PubMed  Google Scholar  * Sun, W., Sacks, M. S. & Scott, M. J. Effects of Boundary

Conditions on the Estimation of the Planar Biaxial Mechanical Properties of Soft Tissues. _Journal of Biomechanical Engineering_ 127, 709–715, https://doi.org/10.1115/1.1933931 (2005).

Article  PubMed  Google Scholar  * Pham, T., Martin, C., Elefteriades, J. & Sun, W. Biomechanical characterization of ascending aortic aneurysm with concomitant bicuspid aortic valve and

bovine aortic arch. _Acta Biomaterialia_ 9, 7927–7936, https://doi.org/10.1016/j.actbio.2013.04.021 (2013). Article  CAS  PubMed  PubMed Central  Google Scholar  * Trabelsi, O., Duprey, A.,

Favre, J.-P. & Avril, S. Predictive Models with Patient Specific Material Properties for the Biomechanical Behavior of Ascending Thoracic Aneurysms. _Annals of Biomedical Engineering_

44, 84–98, https://doi.org/10.1007/s10439-015-1374-8 (2016). Article  PubMed  Google Scholar  * Bols, J. _et al_. A computational method to assess the _in vivo_ stresses and unloaded

configuration of patient-specific blood vessels. _Journal of Computational and Applied Mathematics_ 246, 10–17, https://doi.org/10.1016/j.cam.2012.10.034 (2013). Article  MathSciNet  MATH 

Google Scholar  * Avril, S., Badel, P. & Duprey, A. Anisotropic and hyperelastic identification of _in vitro_ human arteries from full-field optical measurements. _Journal of

Biomechanics_ 43, 2978–2985, https://doi.org/10.1016/j.jbiomech.2010.07.004 (2010). Article  PubMed  Google Scholar  * Zhao, X., Chen, X. & Lu, J. Pointwise Identification of Elastic

Properties in Nonlinear Hyperelastic Membranes—Part II: Experimental Validation. _Journal of Applied Mechanics_ 76, 061014-061014-061018, https://doi.org/10.1115/1.3130810 (2009). Article 

ADS  CAS  Google Scholar  * Compas, C. B. _et al_. Radial Basis Functions for Combining Shape and Speckle Tracking in 4D Echocardiography. _IEEE Transactions on Medical Imaging_ 33,

1275–1289, https://doi.org/10.1109/TMI.2014.2308894 (2014). Article  PubMed  PubMed Central  Google Scholar  * van Disseldorp, E. M. J. _et al_. Influence of limited field-of-view on wall

stress analysis in abdominal aortic aneurysms. _Journal of Biomechanics_ 49, 2405–2412, https://doi.org/10.1016/j.jbiomech.2016.01.020 (2016). Article  PubMed  Google Scholar  * Sahibzada,

N. _et al_. Rhythmic Aortic Contractions Induced by Electrical Stimulation _In Vivo_ in the Rat. _Plos One_ 10, e0130255, https://doi.org/10.1371/journal.pone.0130255 (2015). Article  CAS 

PubMed  PubMed Central  Google Scholar  * Iliopoulos, D. C. _et al_. Regional and directional variations in the mechanical properties of ascending thoracic aortic aneurysms. _Medical

Engineering & Physics_ 31, 1–9, https://doi.org/10.1016/j.medengphy.2008.03.002 (2009). Article  Google Scholar  * Sassani, S. G., Tsangaris, S. & Sokolis, D. P. Layer- and

region-specific material characterization of ascending thoracic aortic aneurysms by microstructure-based models. _Journal of Biomechanics_ 48, 3757–3765,

https://doi.org/10.1016/j.jbiomech.2015.08.028 (2015). Article  PubMed  Google Scholar  * Bersi, M. R., Bellini, C., Humphrey, J. D. & Avril, S. Local variations in material and

structural properties characterize murine thoracic aortic aneurysm mechanics. _Biomechanics and Modeling in Mechanobiology_ 18, 203–218, https://doi.org/10.1007/s10237-018-1077-9 (2019).

Article  PubMed  Google Scholar  * Labrosse, M. R., Beller, C. J., Mesana, T. & Veinot, J. P. Mechanical behavior of human aortas: Experiments, material constants and 3-D finite element

modeling including residual stress. _Journal of Biomechanics_ 42, 996–1004, https://doi.org/10.1016/j.jbiomech.2009.02.009 (2009). Article  PubMed  Google Scholar  * Liu, M. _et al_. On the

computation of _in vivo_ transmural mean stress of patient-specific aortic wall. _Biomechanics and Modeling in Mechanobiology_, https://doi.org/10.1007/s10237-018-1089-5 (2018). Article 

Google Scholar  Download references ACKNOWLEDGEMENTS This study is supported in part by American Heart Association (AHA) 18TPA34230083 and National Center for Advancing Translational

Sciences of the National Institutes of Health under Award Number UL1TR002378. Minliang Liu is supported by an AHA predoctoral fellowship 19PRE34430060. AUTHOR INFORMATION AUTHORS AND

AFFILIATIONS * Tissue Mechanics Laboratory, The Wallace H. Coulter Department of Biomedical Engineering, Georgia Institute of Technology and Emory University, Atlanta, GA, USA Minliang Liu, 

Liang Liang, Fatiesa Sulejmani, Xiaoying Lou & Wei Sun * Emory University School of Medicine, Atlanta, GA, USA Xiaoying Lou, Glen Iannucci, Edward Chen & Bradley Leshnower *

Department of Computer Science, University of Miami, Coral Gables, FL, USA Liang Liang Authors * Minliang Liu View author publications You can also search for this author inPubMed Google

Scholar * Liang Liang View author publications You can also search for this author inPubMed Google Scholar * Fatiesa Sulejmani View author publications You can also search for this author

inPubMed Google Scholar * Xiaoying Lou View author publications You can also search for this author inPubMed Google Scholar * Glen Iannucci View author publications You can also search for

this author inPubMed Google Scholar * Edward Chen View author publications You can also search for this author inPubMed Google Scholar * Bradley Leshnower View author publications You can

also search for this author inPubMed Google Scholar * Wei Sun View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS Conceptualization: M.L. and

W.S.; Formal analysis: M.L.; Investigation: M.L., L.L. and W.S.; Methodology: M.L. and L.L.; Project administration: M.L. and W.S.; Resources: F.S., X.L., G.I., E.C. and B.L.; Supervision:

W.S.; Visualization: M.L.; Writing – original draft: M.L.; Writing – review & editing: M.L., L.L., F.S., X.L., G.I., E.C., B.L. and W.S. CORRESPONDING AUTHOR Correspondence to Wei Sun.

ETHICS DECLARATIONS COMPETING INTERESTS Dr. Wei Sun is a co-founder and serves as the Chief Scientific Advisor of Dura Biotech. He has received compensation and owns equity in the company.

The other authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and

institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing,

adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons

license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a

credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted

use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT

THIS ARTICLE CITE THIS ARTICLE Liu, M., Liang, L., Sulejmani, F. _et al._ Identification of _in vivo_ nonlinear anisotropic mechanical properties of ascending thoracic aortic aneurysm from

patient-specific CT scans. _Sci Rep_ 9, 12983 (2019). https://doi.org/10.1038/s41598-019-49438-w Download citation * Received: 18 February 2019 * Accepted: 24 August 2019 * Published: 10

September 2019 * DOI: https://doi.org/10.1038/s41598-019-49438-w SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a

shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative