ABSTRACT For a broad class of input-output maps, arguments based on the coding theorem from algorithmic information theory (AIT) predict that simple (low Kolmogorov complexity) outputs are

exponentially more likely to occur upon uniform random sampling of inputs than complex outputs are. Here, we derive probability bounds that are based on the complexities of the inputs as

well as the outputs, rather than just on the complexities of the outputs. The more that outputs deviate from the coding theorem bound, the lower the complexity of their inputs. Since the

number of low complexity inputs is limited, this behaviour leads to an effective lower bound on the probability. Our new bounds are tested for an RNA sequence to structure map, a finite

OF HUMAN LANGUAGE WITH BAYESIAN PROGRAM INDUCTION Article Open access 30 August 2022 INTRODUCTION Deep links between physics and theories of computation1,2 are being increasingly exploited

to uncover new fundamental physics and to provide novel insights into theories of computation. For example, advances in understanding quantum entanglement are often expressed in

sophisticated information theoretic language, while providing new results in computational complexity theory such as polynomial time algorithms for integer factorization3. These connections

are typically expressed in terms of Shannon information, with its natural analogy with thermodynamic entropy. There is, however, another branch of information theory, called algorithmic

information theory (AIT)4, which is concerned with the information content of individual objects. It has been much less applied in physics (although notable exceptions occur, see5 for a

recent overview). Reasons for this relative lack of attention include that AIT’s central concept, the Kolmogorov complexity _K__U_(_x_) of a string _x_, defined as the length of the shortest

program that generates _x_ on an optimal reference universal Turing machine (UTM) _U_, is formally uncomputable due to its link to the famous halting problem of UTMs6 — see7 for technical

details. Moreover, many important results, such as the invariance theorem which states that for two UTMs _U_ and _W_, the Kolmogorov complexities \({K}_{U}(x)={K}_{W}(x)+{\mathcal{O}}(1)\)

are equivalent, hold asymptotically up to \({\mathcal{O}}(1)\) terms that are independent of _x_, but not always well understood, and therefore hard to control. Another reason applications

of AIT to many practical problems have been hindered can be understood in terms of hierarchies of computing power. For example, one of the oldest such categorisations, the Chomsky

hierarchy8, ranks automata into four different classes, of which the UTMs are the most powerful, and finite state machines (FSMs) are the least. Many key results in AIT are derived by

exploiting the power of UTMs. Interestingly, if physical processes can be mapped onto UTMs, then certain properties can be shown to be uncomputable9,10. However, many problems in physics are

fully computable, and therefore lower on the Chomsky hierarchy than UTMs. For example, finite Markov processes are equivalent to FSMs, and RNA secondary structure (SS) folding algorithms

can be recast as context-free grammars, the second level in the hierarchy. Thus, an important cluster of questions for applications of AIT revolve around extending its methods to processes

lower in computational power than UTMs. To explore ways of moving beyond these limitations and towards practical applications, we consider here one of the most iconic results of AIT, namely

Levin’s coding theorem11 (see also the work of Solomonoff12 who had a version of the a priori distribution), which predicts that upon randomly chosen programs (e.g. a binary string program

constructed by coin flips), the probability _P__U_(_x_) that a universal Turing machine (UTM) generates output _x_ can be bounded as \({2}^{-K(x)}\le P(x)\le {2}^{-K(x)+{\mathcal{O}}(1)}\).

Technically, because we require the programs of the Turing machine to be prefix-free, we restrict ourselves to what are called prefix Turing machines. Given this profound prediction of a

general exponential bias towards simplicity (low Kolmogorov complexity) one might have expected widespread study and applications in science and engineering. This has not been the case

because the theorem unfortunately suffers from the general issues of AIT described above. Nevertheless, it has recently been shown13,14 that a related exponential bias towards low complexity

outputs obtains for a range of non-universal input-output maps _f_: _I_ → _O_ that are lower on the Chomsky hierarchy than UTMs. In particular, an upper bound on the probability _P_(_x_)

that an output obtains upon uniform random sampling of inputs, $$P(x)\le {2}^{-a\widetilde{K}(x)-b}\ $$ (1) was recently derived13 using a computable approximation \(\widetilde{K}(x)\) to

the Kolmogorov complexity of _x_, typically calculated using lossless compression techniques. Here _a_ and _b_ are constants that are independent of _x_ and which can often be determined

from some basic information about the map. The so-called _s_implicity bias bound (1) holds for computable maps _f_ where the number of inputs _N__I_ is much greater than the number of

outputs _N__O_ and the map _f_ is simple, meaning that asymptotically \(K(f)+K(n)\ll K(x)+{\mathcal{O}}(1)\) for a typical output _x_, where _n_ specifies the size of _N__I_, e.g. _N__I_ = 

2_n_. It is important to distinguish the map _f_ (which we assume is simple) and the initial conditions15, i.e. a program for _x_ (which may or may not be simple). Equation (1) typically

works better for larger _N__I_ and _N__O_. Approximating the true Kolmogorov complexity also means that the bound shouldn’t work for maps where a significant fraction of outputs have

complexities that are not qualitatively captured by compression based approximations. For example many pseudo random-number generators are designed to produce outputs that appear to be

complex when measured by compression or other types of Kolmogorov complexity approximations. Yet these outputs must have low _K_(_x_) because they are generated by relatively simple

algorithms with short descriptions. Nevertheless, it has been shown that the bound (1) works remarkably well for a wide class of input-output maps, ranging from the sequence to RNA secondary

structure map, to systems of coupled ordinary differential equations, to a stochastic financial trading model, to the parameter-function map for several classes of deep neural

networks13,16,17. The simplicity bias bound (1) predicts that high _P_(_x_) outputs will be simple, and that complex outputs will have a low _P_(_x_). But, in sharp contrast to the full AIT

coding theorem, it doesn’t have a lower bound, allowing low \(\widetilde{K}(x)\) outputs with low _P_(_x_) that are far from the bound. Indeed, this behaviour is generically observed for

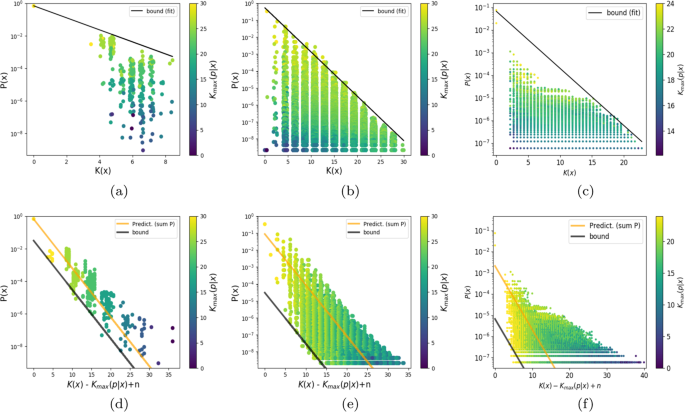
many (non-universal) maps13,16 (see also Fig. 1), but should not be the case for UTMs that obey the full coding theorem. Understanding the behaviour of outputs far from the bound should shed

light on fundamental differences between UTMs and maps with less computational power that are lower on the Chomsky hierarchy, and may open up avenues for wider applications of AIT in

physics. RESULTS With this challenge in mind, we take an approach that contrasts with the traditional coding theorem of AIT or with the simplicity bias bound, which only consider the

complexity of the outputs. Instead, we derive bounds that also take into account the complexity of the inputs that generate a particular output _x_. While this approach is not possible for

UTMs, since the halting problem means one cannot enumerate all inputs4, and so averages over input complexity cannot be calculated, it can be achieved for non-UTM maps. Among our main

results, we show that the further outputs are from the simplicity bias bound (1), the lower the complexity of the set of inputs. Since, by simple counting arguments, most strings are

complex4, the cumulative probability of outputs far from the bound is therefore limited. We also show that by combining the complexities of the output with that of the inputs, we can obtain

better bounds on and estimates of _P_(_x_). Whether such bounds nevertheless have real predictive power needs to be tested empirically. Because input based bounds typically need exhaustive

sampling, full testing is only possible for smaller systems, which restricts us here to maps where finite size effects may still play a role13. We test our bounds on three systems, the

famous RNA sequence to secondary structure map (which falls into the context-free class in the Chomsky hierarchy), here for a relatively small size with length _L_ = 15 sequences, a finite

state transducer (FST), a very simple input-output map that is lowest on the Chomsky hierarchy8, with length _L_ = 30 binary inputs, and finally the parameter-function map16,17 of a

perceptron18 with discretized weights to allow complexities of inputs to be calculated. The preceptron plays a key role in deep learning neural network architectures19. Nevertheless, as can

be seen in Fig. 1(a–c) all three maps exhibit simplicity bias predicted by Eq (1), even if they are relatively small. In ref. 13, much cleaner simplicity bias behaviour can be observed for

larger RNA maps, but these are too big to exhaustively sample inputs. Similarly, cleaner simplicity bias behaviour occurs for the undiscretised perceptron17, but then it is hard to analyse

the complexity of the inputs. Figure 1(a–c) shows that the complexity of the input strings that generate each output _x_ decreases for further distances from the simplicity bias bound. This

is the kind of phenomenon that the we will attempt to explain. To study input based bounds, consider a map _f_: _I_ → _O_ between _N__I_ inputs and _N__O_ outputs that satisfies the

requirements for simplicity bias13. Let _f_(_p_) = _x_, where _p_ is some input program _p_ ∈ _I_ producing output _x_ ∈ _O_. For simplicity let _p_ ∈ {0, 1}_n_, so that all inputs have

length _n_ and _N__I_ = 2_n_ (this restriction can be relaxed later). Define _f_−1(_x_) to be the set of all the inputs that map to _x_, so that the probability that _x_ obtains upon

sampling inputs uniformly at random is $$P(x)=\frac{| \,{f}^{-1}(x)| }{{2}^{n}}\ $$ (2) Any arbitrary input _p_ can be described using the following \({\mathcal{O}}(1)\) procedure13:

Assuming _f_ and _n_ are given, first enumerate all 2_n_ inputs and map them to outputs using _f_. The index of a specific input _p_ within the set _f_ −1(_x_) can be described using at most

\({{\rm{\log }}}_{2}(| \,{f}^{-1}(x)| )\) bits. In other words, this procedure identifies each input by first finding the output _x_ it maps to, and then finding its label within the set

_f_ −1(_x_). Given _f_ and _n_, an output _x_ = _f_(_p_) can be described using \(K(x| \,f,n)+{\mathcal{O}}(1)\) bits13. Thus, the Kolmogorov complexity of _p_, given _f_ and _n_ can be

bounded as: $$K(p| \,f,n)\le K(x| \,f,n)+{{\rm{\log }}}_{2}(| \,{f}^{-1}(x)| )+{\mathcal{O}}(1).$$ (3) We note that this bound holds in principle for all _p_, but that it is tightest for

\({K}_{\max }(p| x)\equiv {\max }_{p}\{K(p| \,f,n)\}\) for _p_ ∈ _f_ −1(_x_). More generally, we can expect these bounds to be fairly tight for the maximum complexity \({K}_{\max }(p|

\,f,n)\) of inputs due to the following argument. First note that $${K}_{\max }(p| \,f,n)\ge {{\rm{\log }}}_{2}(| \,{f}^{-1}(x)| )+{\mathcal{O}}(1)$$ (4) because any set of | _f_ −1(_x_)|

different elements must have strings of at least this complexity. Next, $$K(x| \,f,n)\le K(p| \,f,n)+{\mathcal{O}}(1)$$ (5) because each _p_ can be used to generate _x_. Therefore: $$\max

(K(x| \,f,n),{{\rm{\log }}}_{2}(| \,{f}^{-1}(x)| ))\le {K}_{\max }(p| \,f,n)+{\mathcal{O}}(1),$$ (6) so the bound (3) cannot be too weak. In the worst case scenario, where \({K}_{\max }(p|

n)\approx {{\rm{\log }}}_{2}(| \,{f}^{-1}(x)| )\approx K(x| \,f,n)\), the right hand side of the bound (3) is approximately twice the left hand side (up to additive \({\mathcal{O}}(1)\)

terms). It is tighter if either _K_(_x_| _f_, _n_) is small, or if _K_(_x_| _f_, _n_) is big relative to \({{\rm{\log }}}_{2}(| \,{f}^{-1}(x)| )\). As is often the case for AIT predictions,

the stronger the constraint/prediction, the more likely it is to be observed in practice, because, for example, the \({\mathcal{O}}(1)\) terms are less likely to drown out the effects. By

combining with Eq. (2), the bound (3) can be rewritten in two complementary ways. Firstly, a lower bound on _P_(_x_) can be derived of the form: $$P(x)\ge {2}^{-K(x| f,n)-[n-K(p|

f,n)]+{\mathcal{O}}(1)}$$ (7) ∀ _p_ ∈ _f_ −1(_x_) which complements the simplicity bias upper bound (1). This bound is tightest for \({K}_{\max }(p| n)\). In ref. 13 it was shown that

\(P(x)\le {2}^{-K(x| f,n)+{\mathcal{O}}(1)}\) by using a similar counting argument to that used above, together with a Shannon-Fano-Elias code procedure. Similar results can be found in

standard works4,20. A key step is to move from the conditional complexity to one that is independent of the map and of _n_. If _f_ is simple, then the explicit dependence on _n_ and _f_ can

be removed by noting that since \(K(x)\le K(x| \,f,n)+K(\,f)+K(n)+{\mathcal{O}}(1)\), and \(K(x| \,f,n)\le K(x)+{\mathcal{O}}(1)\) then \(K(x| \,f,n)\approx K(x)+{\mathcal{O}}(1)\). In Eq.

(1) this is further approximated as \(K(x| \,f,n)+{\mathcal{O}}(1)\approx a\widetilde{K}(x)+b\), leading to a practically useable upper bound. The same argument can be used to remove

explicit dependence on _n_ and _f_ for _K_(_p_| _f_, _n_). If we define a maximum randomness deficit \({\delta }_{\max }(x)=n-{K}_{\max }(p| n)\), then this tightest version of bound (7) can

be written in a simpler form as $$P(x)\ge {2}^{-a\widetilde{K}(x)+b-{\delta }_{\max }(x)+{\mathcal{O}}(1)}$$ (8) In Fig. 1(d–f) we plot this lower bound for all three maps studied.

Throughout the paper, we use a scaled complexity measure, which ensures that \(\widetilde{K}(x)\) ranges between ≈0 and ≈_n_ bits, for strings of length _n_, as expected for Kolmogorov

complexity. See Methods for more details. When comparing the data in Fig. 1(d–f) to Fig. 1(a–c), it is clear that including the input complexities reduces the spread in the data for RNA and

the FST, although for the perceptron model the difference is less pronounced. This success suggests using the bound (8) as a predictor \(P(x)\approx {2}^{-K(x| f,n)-{\delta }_{\max }(x)}\),

with the additional constraint that ∑_x__P_(_x_) = 1 to normalise it. As can be seen in Fig. 1(d–f), this simple procedure works reasonably well, showing that the input complexity provides

additional predictive power to estimate _P_(_x_) from some very generic properties of the inputs and outputs. A second, complimentary way that bound (3) can be expressed is in terms of how

far _P_(_x_) differs from the simplicity bias bound (1): $$[{{\rm{\log }}}_{2}({P}_{0}(x))-{{\rm{\log }}}_{2}(P(x))]\le [n-K(p| \,f,n)]+{\mathcal{O}}(1)$$ (9) where \({P}_{0}(x)={2}^{-K(x|

f,n)}\approx {2}^{-a\widetilde{K}(x)+b}\) is the upper bound (1) shown in Fig. 1(a–c). For a random input _p_, with high probability we expect \(K(p| \,f,n)=n+{\mathcal{O}}(1)\)4. Thus, Eqs.

(7) and (9) immediately imply that large deviations from the simplicity bias bound (1) are only possible with highly non-random inputs with a large randomness deficit \({\delta }_{\max

}(x)\). In Fig. 2(a–c) we directly examine bound (9), showing explicitly the prediction that a drop of probability _P_(_x_) by Δ bits from the simplicity bias bound (1) corresponds to a Δ

bit randomness deficit in the set of inputs. Simple counting arguments can be used to show that the number of non-random inputs is a small fraction of the total number of inputs21. For

example, for binary strings of length _n_, with _N__I_ = 2_n_, the number of inputs with complexity _K_ = _n_ − _δ_ is approximately 2−_δ__N__I_. If we define a set \({\mathcal{D}}(f)\) of

all outputs _x__i_ that satisfy \(({{\rm{\log }}}_{2}({P}_{0}({x}_{i}))-{{\rm{\log }}}_{2}({P}_{({x}_{i})}))\ge \Delta \), i.e. the set of all outputs for which \({{\rm{\log }}}_{2}P(x)\) is

at least Δ bits below the simplicity bias bound (1), then this counting argument leads to the following cumulative bound: $$\sum _{x\in {\mathcal{D}}(f)}P(x)\le {2}^{-\Delta

+1+{\mathcal{O}}(1)}$$ (10) which predicts that, upon randomly sampling inputs, most of the probability weight is for outputs with _P_(_x_) relatively close to the upper bound. There may be

many outputs that are far from the bound, but their cumulative probability drops off exponentially the further they are from the bound because the number of simple inputs is exponentially

limited. Note that this argument is for a cumulative probability over all inputs. It does not predict that for a given complexity _K_(_x_), that the outputs should all be near the bound. In

that sense this lower bound is not like that of the original coding theorem which holds for any output _x_. See the Supplementary Information for an alternative derivation of this bound.

Bound (10) does not need an exhaustive enumeration to be tested. In Fig. 3 we show this bound for a series of different maps, including many maps from13. The cumulative probability weight

scales roughly as expected, implying that most of the probability weight is relatively close to the bound (at least on a log scale). What is the physical nature of these low complexity, low

probability outputs that occur far from the bound? They must arise in one way or another from the lower computational power of these maps, since they don’t occur in the full AIT coding

theory. Low complexity, low probability outputs correspond to output patterns which are simple, but which the given computable map is not good at generating. In RNA it is easy to construct

outputs which are simple but will have low probability. Compare two _L_ = 15 structures _S_1 = ((.(.(...).).)). and _S_2 = .((.((...)).))., which are both symmetric and thus have a

relatively low complexity _K_(_S_1) = _K_(_S_2) = 21.4. Nevertheless they have a significant difference in probability, _P_(_S_2)∕_P_(_S_1) ≈ 560 because _S_1 has several single bonds, which

is much harder to make according to the biophysics of RNA. Only specially ordered input sequences can make _S_1, in other words they are simple, with \({K}_{\max }(p| n)=8.6\). By contrast,

the inputs of _S_2 are much higher at \({K}_{\max }(p| n)=21.4\) because they need to be constrained less to produce this structure. This example illustrates how the system specific details

of the RNA map can unfavourably bias away from some outputs due to a system specific constraint. Similar examples of system specific constraint for the FST and perceptron can be found in

the SI. We hypothesise that such low complexity, low probability structures highlight specific non-universal aspects of the maps, and extra information (in the form of a reduced set of

inputs) are needed to generate such structures. DISCUSSION In conclusion, it is striking that bounds based simply on the complexity of the inputs and outputs can make powerful and general

predictions for such a wide range of systems. Although the arguments used to derive them suffer from the well known problems – e.g. the presence of uncomputable Kolmogorov complexities and

unknown \({\mathcal{O}}(1)\) terms – that have led to the general neglect of AIT in the physics literature, the bounds are undoubtably successful. It appears that, just as is found in other

areas of physics, these relationships hold well outside of the asymptotic regime where they can be proven to be correct. This practical success opens up the promise of using such AIT based

techniques to derive other results for computable maps from across physics. Many new questions arise. Can it be proven when the \({\mathcal{O}}(1)\) terms are relatively unimportant? Why do

our rather simple approximations to _K_(_x_) work? It would be interesting to find maps where these classical objections to the practical use of AIT are important. There may also be

connections between our work and finite state complexity22 or minimum description length23 approaches. Progress in these domains should generate new fundamental understandings of the physics

of information. METHODS RNA SEQUENCE TO SECONDARY STRUCTURE MAPPING RNA is made of a linear sequence of 4 different kinds of nucleotides, so that there are _N__I_ = 4_L_ possible sequences

for any particular length _L_. A versatile molecule, it can store information, as messenger RNA, or else perform catalytic or structural functions. For functional RNA, the three-dimensional

(3D) structure plays an important role in its function. In spite of decades of research, it remains difficult to reliably predict the 3D structure from the sequence alone. However, there are

fast and accurate algorithms to calculate the so-called secondary structure (SS) that determines which base binds to which base. Given a sequence, these methods typically minimize the

Turner model24 for the free-energy of a particular bonding pattern. The main contributions in the Turner model are the hydrogen bonding and stacking interactions between the nucleotides, as

well as some entropic factors to take into account motifs such as loops. Fast algorithms based on dynamic programming allow for rapid calculations of these SS, and so this mapping from

sequences to SS has been a popular model for many studies in biophysics. In this context, we view it as an input-output map, from _N__I_ input sequences to _N__O_ output SS structures. This

map has been extensively studied (see e.g.25,26,27,28,29,30,31,32,33) and provided profound insights into the biophysics of folding and evolution. Here we use the popular Vienna package26 to

fold sequences to structures, with all parameters set to their default values (e.g. the temperature _T_ = 37°_C_). We folded all _N__I_ = 415 ≈ 109 sequences of length 15, into 346

different structures which were the free-energy minimum structures for those sequences. The number of sequences mapping to a structure is often called the _neutral set size_. The structures

can be abstracted in standard dot-bracket notation, where brackets denote bonds, and dots denote unbonded pairs. For example, ...((. . . .))..... means that the first three bases are not

bonded, the fourth and fifth are bonded, the sixth through ninth are unbonded, the tenth base is bonded to the fifth base, the eleventh base is bonded to the fourth base, and the final four

bases are unbounded. To estimate the complexity of an RNA SS, we first converted the dot-bracket representation of the structure into a binary string _x_, and then used the complexity

estimator described below to estimate its complexity. To convert to binary strings, we replaced each dot with the bits 00, each left-bracket with the bits 10, and each right-bracket with 01.

Thus an RNA SS of length _n_ becomes a bit-string of length 2_n_. As an example, the following _n_ = 15 structure yields the displayed 30-bit string $$..(((...)))....\to

000010101000000001010100000000$$ Because we are interested in exhaustive calculations, we are limited to rather small RNA sequence lengths. This means that finite-size effects may play an

important role. In13, we compared the simplicity bias bound (1) from the main text to longer sequences where only partial sampling can be achieved, and showed much clearer simplicity bias is

evident in those systems. FINITE STATE TRANSDUCER Finite state transducers (FSTs) are a generalization of finite state machines that produce an output. They are defined by a finite set of

states \({\mathcal{S}}\), finite input and output alphabets \({\mathcal{I}}\) and \({\mathcal{O}}\), and a transition function \(T:{\mathcal{S}}\times {\mathcal{I}}\to {\mathcal{S}}\times

{\mathcal{O}}\) defining, for each state, and input symbol, a next state, and output symbol. One also needs to define a distinguished state, \({S}_{0}\in {\mathcal{S}}\), which will be the

initial state, before any input symbol has been read. Given an _input sequence_ of _L_ input symbols, the system visits different states, and simultaneously produces an _output sequence_ of

_L_ output symbols. FST form a popular toy system for computable maps. They can express any computable function that requires only a finite number of memory, and the number of states in the

FSTs offers a good parameter to control the complexity of the map. The class of machines we described above is also known as Mealy machines34. If one restricts the transition function to

only depend on the current state, one obtains Moore machines35. If one considers the input sequence to a Moore machine to be stochastic, it immediately follows that its state sequence

follows a Markov chain, and its output sequence is a Markov information source. Therefore, FSTs can be used to model many stochastic systems in nature and engineering, which can be described

by finite-state Markov dynamics. FSTs lie in the lowest class in the Chomsky hierarchy. However, they appear to be biased towards simple outputs in a manner similar to Levin’s coding

theorem. In particular, Zenil _et al_.14 show evidence of this by correlating the probability of FSTs and UTMs producing particular outputs. More precisely, they sampled random FSTs with

random inputs, and random UTMs with random inputs, and then compared the empirical frequencies with with individual output strings are obtained by both families, after many samples of

machines and inputs. For both types of machines, simple strings were much more likely to be produced than complex strings. We use randomly generated FSTs with 5 states. The FSTs are

generated by uniformly sampling complete initially connected DFAs (where every state is reachable from the initial state, and the transition function is defined for every input) using the

library FAdo36, which uses the algorithm developed by Almeida _et al_.37. Output symbols are then added to each transition independently and with uniform probability. In our experiments, the

inputs are binary strings and the outputs are binary strings of length _L_ = 30. The outputs for the whole set of 2_L_ input strings are computed using the HFST library

(https://hfst.github.io/). Not all FSTs show bias, but we have observed that all those that show bias show simplicity bias, and have the same behavior as that shown in Fig. 1 for low

complexity - low probability outputs. We can see why some simple outputs will occur with low probability by considering system specific details of the FST. For an FST, an output of length

_n_ which is _n_/2 zeros followed by _n_/2 ones is clearly simple, but we find that it has a low probability. We can understand this intuitively as follows. Producing such a string requires

the "counting” up to _n_/2 to know when to switch output, and counting requires a memory that grows with _n_, while FSTs have finite memory. We can also prove that, for instance, an FST

that only produces such strings (for any _n_) is impossible. The set of possible strings that an FST can produce comprises a regular language, as constructed by using the output symbols at

each transition as input symbols, giving us a non-deterministic finite automaton. Finally, using the pumping lemma38, it is easy to see that this family of strings isn’t a regular language.

PERCEPTRON The perceptron18 is the simplest type of artificial neural network. It consists of a single linear layer, and a single output neuron with binary activation. Because modern deep

neural network architectures are typically made of many layers of perceptrons, this simple system is important to study17. In this paper we use perceptrons with Boolean inputs and

discretized weights. For inputs _x_ ∈ {0, 1}_n_, the discretized perceptron uses the following parametrized class of functions: $${f}_{w,b}(x)={\bf{1}}(w\cdot x+b),$$ where _w_ ∈ {−_a_, _a_ 

+ _δ_, …, _a_ − _δ_, _a_}_n_ and _b_ ∈ { − _a_, _a_ + _δ_, …, _a_ − _δ_, _a_} are the weight vector and bias term, which take values in a discrete lattice with _D_ := 2_a_/_δ_ + 1 possible

values per weight. We used _D_ = 2_k_, so that each weight can be represented by _k_ bits, and _a_ = (2_k_ − 1)/2, so that _δ_ = 1. Note that rescaling all the weights _w_ and the bias _b_

by the same fixed constant wouldn’t change the family of functions. To obtain the results in Fig. 1, for which _n_ = 7, we represented the weights and bias with _k_ = 3 bits. We exhausitvely

enumerated all 23(7+1) possible values of the weights and vectors, and we counted how many times we obtained each possible Boolean function on the Boolean hypercube {0, 1}7. The weight-bias

pair was represented using 3 × (7 + 1) = 24 bits. A pair (_w_, _b_) is an input to the parameter-function map of the perceptron. The complexity of inputs to this map can therefore be

approximated by computing the Lempel-Ziv complexity of the 24-bit representation of the pair (_w_, _b_). In Fig. 4, we compare the simplicity bias of a perceptron with real-valued weights

and bias, sampled from a standard Normal distribution, to the simplicity bias of the perceptron with discretized weights. We observe that both display similar simplicity bias, although the

profile of the upper bound changes slightly. For the perceptron we can also understand some simple examples of low complexity, low probability outputs. For example, the function with all 0s

except a 1, for the inputs (1, 0, 0, 0, 0, 0, 0) and (0, 1, 0, 0, 0, 0, 0) has a similar complexity to the function which only has 1s at the inputs (1, 0, 0, 0, 0, 0, 0) and (0, 1, 1, 1, 1,

1, 1). However, the latter has much lower probability. One can understand this because if we take the dot product of a random weight vector _w_ with two different inputs _x_1 and _x_2, the

results have correlation given _x_1 ⋅ _x_2∕(||_x_1||||_x_2||). Therefore we expect the input (0, 1, 1, 1, 1, 1, 1) to be correlated to more other inputs, than (0, 1, 0, 0, 0, 0, 0), so that

the probability of it having a different value than the majority of inputs (as is the case for the second function) is expected to be significantly lower. METHODS TO ESTIMATE COMPLEXITY

\(\TILDE{{\BOLDSYMBOL{K}}}{\BOLDSYMBOL{(}}{\BOLDSYMBOL{X}}{\BOLDSYMBOL{)}}\) There is a much more extensive discussion of different ways to estimate the Kolmogorov complexity in the

supplementary information of13 and16. Here we use compression based measures, and as in these previous papers, we these are based on the 1976 Lempel Ziv (LZ) algorithm39, but with some small

changes: $${C}_{LZ}(x)=\left\{\begin{array}{ll}{{\rm{\log }}}_{2}(n), & x={0}^{n}\ {\rm{or}}\ {1}^{n}\\ {{\rm{\log

}}}_{2}(n)[{N}_{w}({x}_{1}\,...{x}_{n})+{N}_{w}({x}_{n}\,...{x}_{1})]/2, & \,{\rm{otherwise}}\,\end{array}\right.$$ (11) Here _N__w_(_x_) is the number of code words found by the LZ

algorithm. The reason for distinguishing 0_n_ and 1_n_ is merely an artefact of _N__w_(_x_) which assigns complexity _K_ = 1 to the string 0 or 1, but complexity 2 to 0_n_ or 1_n_ for _n_ ≥ 

2, whereas the Kolmogorov complexity of such a trivial string actually scales as \({{\rm{\log }}}_{2}(n)\), as one only needs to encode _n_. In this way we ensure that our _C__L__Z_(_x_)

measure not only gives the correct behaviour for complex strings in the \({{\rm{lim}}}_{n\to \infty }\), but also the correct behaviour for the simplest strings. In addition to the

\({{\rm{\log }}}_{2}(n)\) correction, taking the mean of the complexity of the forward and reversed strings makes the measure more fine-grained, since it allows more values for the

complexity of a string. Note that _C__L__Z_(_x_) can also be used for strings of larger alphabet sizes than just 0/1 binary alphabets. To directly test the input based measures we typically

need fairly small systems, where the LZ based measure above may show some anomalies (see also the supplementary information of13 for a more detailed description). Thus, for such small

systems, or when comparing different types and sizes of objects (e.g. RNA SS and RNA sequences) a slightly different scaling may be more appropriate, which not only accounts for the fact

that _C__L__Z_(_x_) > _n_ for strings of length _n_, but also the lower complexity limit may not be ~0, which it should be (see also the discussion in the supplementary information of13).

Hence we use a different rescaling of the complexity measure $$\widetilde{K}(x)={{\rm{\log }}}_{2}({N}_{O})\cdot \frac{{C}_{LZ}(x)-\min ({C}_{LZ}(x))}{\max ({C}_{LZ}(x))-\min

({C}_{LZ}(x))}$$ (12) which will now range between \(0\le \widetilde{K}(x)\ \le \ {{\rm{\log }}}_{2}({N}_{O})=n\) if for example _N__O_ = 2_n_. For large objects, this different scaling will

reduce to the simpler one, because \(\max ({C}_{LZ}(x))\gg \min ({C}_{LZ}(x))\). We note that there is nothing fundamental about using LZ to generate approximations to true Kolmogorov

complexity. Many other approximations could be used, and their merits may depend on the details of the problems involved. For further discussion of other complexity measures, see for example

the supplementary information of refs. 13,16. DATA AVAILABILITY The data that support the findings of this work are available from the corresponding authors upon request. REFERENCES *

Mezard, M. & Montanari, A.  _Information, physics, and computation_ (Oxford University Press, USA, 2009). * Moore, C. & Mertens, S.  _The nature of computation_ (OUP Oxford, 2011). *

Shor, P. W.  Algorithms for quantum computation: Discrete logarithms and factoring. In _Proceedings 35th annual symposium on foundations of computer science_, 124–134 (Ieee, 1994). * Li, M.

& Vitanyi, P.  _An introduction to Kolmogorov complexity and its applications_ (Springer-Verlag New York Inc, 2008). * Devine, S.  Algorithmic information theory: Review for physicists

and natural scientists (2014). * Turing, A. M. On computable numbers, with an application to the entscheidungsproblem. _J. of Math_ 58, 5 (1936). MATH  Google Scholar  * Shen, A., Uspensky,

V. A. & Vereshchagin, N.  _Kolmogorov complexity and algorithmic randomness_, vol. 220 (American Mathematical Soc., 2017). * Chomsky, N. Three models for the description of language.

_Information Theory, IRE Transactions on_ 2, 113–124 (1956). Article  Google Scholar  * Lloyd, S. Quantum-mechanical computers and uncomputability. _Physical review letters_ 71, 943 (1993).

Article  ADS  CAS  Google Scholar  * Cubitt, T. S., Perez-Garcia, D. & Wolf, M. M. Undecidability of the spectral gap. _Nature_ 528, 207–211 (2015). Article  ADS  CAS  Google Scholar  *

Levin, L. Laws of information conservation (nongrowth) and aspects of the foundation of probability theory. _Problemy Peredachi Informatsii_ 10, 30–35 (1974). ADS  Google Scholar  *

Solomonoff, R. J. A formal theory of inductive inference. part i. _Information and control_ 7, 1–22 (1964). Article  MathSciNet  Google Scholar  * Dingle, K., Camargo, C. Q. & Louis, A.

A. Input-output maps are strongly biased towards simple outputs. _Nature communications_ 9, 761 (2018). Article  ADS  Google Scholar  * Zenil, H., Badillo, L., Hernández-Orozco, S. &

Hernández-Quiroz, F. Coding-theorem like behaviour and emergence of the universal distribution from resource-bounded algorithmic probability. _International Journal of Parallel, Emergent and

Distributed Systems_ 34, 161–180 (2019). Article  Google Scholar  * Chibbaro, S., Rondoni, L. & Vulpiani, A. Reductionism, emergence and levels of reality. _Springer, Berlin. by SWISS

FEDERAL INSTITUTE OF TECHNOLOGY ZURICH (ETH) on_  3, 17 (2014). * Pérez, G. V., Louis, A. A. & Camargo, C. Q. Deep learning generalizes because the parameter-function map is biased

towards simple functions. empharXiv preprint arXiv:1805.08522 (2018). * Mingard, C.  _et al_.  Neural networks are a priori biased towards Boolean functions with low entropy. _Arxiv preprint

arXiv:1909.11522_ (2019). * Rosenblatt, F. The perceptron: a probabilistic model for information storage and organization in the brain. _Psychological review_ 65, 386 (1958). Article  CAS 

Google Scholar  * LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. _nature_ 521, 436 (2015). Article  ADS  CAS  Google Scholar  * Gács, P.  _Lecture notes on descriptional complexity

and randomness_ (Boston University, Graduate School of Arts and Sciences, Computer Science Department, 1988). * Chaitin, G. Information-theoretic computation complexity. _IEEE Transactions

on Information Theory_ 20, 10–15 (1974). Article  MathSciNet  Google Scholar  * Calude, C. S., Salomaa, K. & Roblot, T. K. Finite state complexity. _Theoretical Computer Science_ 412,

5668–5677 (2011). Article  MathSciNet  Google Scholar  * Grünwald, P. and Roos, T. Minimum description length revisited. _arXiv preprint arXiv:1908.08484_ (2019). * Mathews, D. H. _et al_.

Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of rna secondary structure. _Proceedings of the National Academy of Sciences_ 101,

7287–7292 (2004). Article  ADS  CAS  Google Scholar  * Schuster, P., Fontana, W., Stadler, P. & Hofacker, I. From sequences to shapes and back: A case study in RNA secondary structures.

_Proceedings: Biological Sciences_ 255, 279–284 (1994). CAS  Google Scholar  * Hofacker, I. _et al_. Fast folding and comparison of RNA secondary structures. _Monatshefte für Chemie/Chemical

Monthly_ 125, 167–188 (1994). Article  CAS  Google Scholar  * Fontana, W. Modelling evo-devo’ with RNA. _BioEssays_ 24, 1164–1177 (2002). Article  CAS  Google Scholar  * Cowperthwaite, M.,

Economo, E., Harcombe, W., Miller, E. & Meyers, L. The ascent of the abundant: how mutational networks constrain evolution. _PLoS computational biology_ 4, e1000110 (2008). Article  ADS

  MathSciNet  Google Scholar  * Aguirre, J., Buldú, J. M., Stich, M. & Manrubia, S. C. Topological structure of the space of phenotypes: the case of rna neutral networks. _PloS ONE_ 6,

e26324 (2011). Article  ADS  CAS  Google Scholar  * Schaper, S. & Louis, A. A. The arrival of the frequent: how bias in genotype-phenotype maps can steer populations to local optima.

_PloS one_ 9, e86635 (2014). Article  ADS  Google Scholar  * Wagner, A.  _Robustness and evolvability in living systems_ (Princeton University Press Princeton, NJ:, 2005). * Wagner, A.  _The

Origins of Evolutionary Innovations: A Theory of Transformative Change in Living Systems_ (Oxford University Press, 2011). * Dingle, K., Schaper, S. & Louis, A. A. The structure of the

genotype-phenotype map strongly constrains the evolution of non-coding RNA. _Interface focus_  5, 20150053 (2015). * Holcombe, M. and Holcombe, W.  _Algebraic automata theory_, vol. 1

(Cambridge University Press, 2004). * Moore, E. F. Gedanken-experiments on sequential machines. _Automata studies_ 34, 129–153 (1956). MathSciNet  Google Scholar  * Almeida, A., Almeida, M.,

Alves, J., Moreira, N. & Reis, R.  Fado and guitar: tools for automata manipulation and visualization. In _International Conference on Implementation and Application of Automata_, 65–74

(Springer, 2009). * Almeida, M., Moreira, N. & Reis, R. Enumeration and generation with a string automata representation. _Theoretical Computer Science_ 387, 93–102 (2007). Article 

MathSciNet  Google Scholar  * Rabin, M. O. & Scott, D. Finite automata and their decision problems. _IBM journal of research and development_ 3, 114–125 (1959). Article  MathSciNet 

Google Scholar  * Lempel, A. & Ziv, J. On the complexity of finite sequences. _Information Theory, IEEE Transactions on_ 22, 75–81 (1976). Article  MathSciNet  Google Scholar  * Vilar,

J., Kueh, H., Barkai, N. & Leibler, S. Mechanisms of noise-resistance in genetic oscillators. _Proceedings of the National Academy of Sciences of the United States of America_ 99, 5988

(2002). Article  ADS  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS K.D. acknowledges partial financial support from the Kuwait Foundation for the Advancement of Sciences (KFAS)

grant number P115-12SL-06. G.V.P. acknowledges financial support from EPSRC through grant EP/G03706X/1. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Centre for Applied Mathematics and

Bioinformatics, Department of Mathematics and Natural Sciences, Gulf University for Science and Technology, Hawally, 32093, Kuwait Kamaludin Dingle * Rudolf Peierls Centre for Theoretical

Physics, University of Oxford, Parks Road, Oxford, OX1 3PU, United Kingdom Kamaludin Dingle, Guillermo Valle Pérez & Ard A. Louis Authors * Kamaludin Dingle View author publications You

can also search for this author inPubMed Google Scholar * Guillermo Valle Pérez View author publications You can also search for this author inPubMed Google Scholar * Ard A. Louis View

author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS K.D. and A.A.L. conceived the project. K.D., A.A.L. and G.V.P. derived the theoretical results.

K.D. performed the numerical calculations for RNA, and G.V.P. performed the numerical calculations for the finite state transducer and the perceptron. K.D., G.V.P. and A.A.L. wrote the

paper. CORRESPONDING AUTHOR Correspondence to Ard A. Louis. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION. RIGHTS AND

PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any

medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The

images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not

included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly

from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Dingle, K., Pérez,

G.V. & Louis, A.A. Generic predictions of output probability based on complexities of inputs and outputs. _Sci Rep_ 10, 4415 (2020). https://doi.org/10.1038/s41598-020-61135-7 Download

citation * Received: 12 November 2019 * Accepted: 16 February 2020 * Published: 10 March 2020 * DOI: https://doi.org/10.1038/s41598-020-61135-7 SHARE THIS ARTICLE Anyone you share the

following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer

Nature SharedIt content-sharing initiative