ABSTRACT In this work, we observe the behavior of a hybrid nanofluidic model containing nanodiamonds and silica nanoparticles. The nanofluid propagates through a catheterized tapered artery

with three distinct configurations: converging tapered, non-tapered and diverging tapered arteries. In order to assess the rheological properties of the blood, the third-grade non-Newtonian

fluid is employed in the flow model such that the Newtonian versus non-Newtonian effects are revealed. The system of equations governing the flow is modeled under magnetic field and with

heat transfer, then solved in a closed form using the perturbation approach for the pertinent parameters. The interpretations of the physical variables of interest, such as the velocity,

biomedicine. SIMILAR CONTENT BEING VIEWED BY OTHERS BIOLOGICAL STRUCTURAL STUDY OF EMERGING SHAPED NANOPARTICLES FOR THE BLOOD FLOW IN DIVERGING TAPERED STENOSED ARTERIES TO SEE THEIR

APPLICATION IN DRUG DELIVERY Article Open access 17 January 2024 COMPUTATIONAL STUDY OF EFFECT OF HYBRID NANOPARTICLES ON HEMODYNAMICS AND THERMAL TRANSFER IN RUPTURED ARTERIES WITH

PATHOLOGICAL DILATION Article Open access 11 June 2024 CONCENTRIC BALLOONED CATHETERIZATION TO THE FRACTIONAL NON-NEWTONIAN HYBRID NANO BLOOD FLOW THROUGH A STENOSED ANEURYSMAL ARTERY WITH

HEAT TRANSFER Article Open access 14 October 2021 INTRODUCTION Diamond nanoparticles, often known as nanodiamonds (NDs), are particles with a size of less than 100 nm. They have a particle

size that is thousands of times smaller than human hair1. Nanodiamonds are quickly gaining traction as viable carriers for several therapies through drug delivery since they have a

customizable surface, high biocompatibility and a wide surface area that allows for the hybridization of compounds such as medicines and genes in extra- and intracellular delivery. Many

studies have significantly contributed to the improvement of NDs by utilizing their diverse characteristics for biological purposes2. Due to the ability of NDs to shuttle drugs through the

blood–brain barrier, Alawadi et al.3 successfully investigated the loading of amlodipine onto NDs opening the doors for the delivery of other drugs into the brain. Owing to the

neuroprotective effects of the NDs, various neuroprotective remedies depend upon NDs such as those that treat Alzheimer’s and Parkinson’s diseases4. Li et al.5 shed some light on NDs being a

member of nanocarbon family that can be used in biomedical and bioengineering applications. In 2016, Tasi et al.6 investigated the interaction of the mice blood as well as the impact of the

surface modification of NDs in the optimization of ND-blood interaction. Their findings support the safety of NDs in organisms, as well as the potential of using them without affecting the

physiological conditions of blood. Chen and Zhang7 presented some insights into important topics about NDs and their potential developments in various applications. It was seen that due to

the diamond's exceptional mechanical strength, vertically aligned diamond nanostructures are predicted to outperform other forms of vertical nanostructures in applications requiring

mechanical force. It has been noticed by Masys et al.8 that hydrogenated NDs have hydrophilic traits so that the molecules of water get attracted to particular sites at the surface. The

hydrophilic characteristic was confirmed by Chauhan et al.1 where NDs were noticed to be excellent carriers of drugs and can be used in chronic disorders. In addition, it has been

highlighted by Namdar and Nafisi9 that the nontoxicity of NDs along with their great potential in being absorbed through the skin due to their size make them a good choice for skin care

products. The latter property has been taken to a higher level when some investigators researched the capability of NDs in treating superficial malignant tumors such the skin cancer,

melanoma10,11. Silica nanoparticles, SiNPs, are used to contain contrast agent particles such as organic dyes, gold nanoparticles and iron oxide, and they serve an essential auxiliary

function in medical imaging. Nowadays, drug-delivery systems through red blood cells along with developed nanomedicines are attracting great interests of researchers12,13. It has been said

that SiNPs are not hazardous up to a concentration of 100 mg/mL if the particle size is 100 nm as seen by Meng et al.14. They are further an excellent choice for controlled release of

medicinal drugs thanks to their enormous surface area, pore capacity and great stability. There are natural sources to extract silica from such as sugarcane, coffee husk, rice husk, corn cob

and much more15. Worth mentioning that SiNPs have been recently introduced in fighting SARS-Cov-2 by depositing silver nanocluster/silica on a mask to reduce infection to zero16. There are

three types of SiNPs: solid, mesoporous and nonporous. Silica nanoparticles have become essential in the transport of medicines and genetic material due to their physical and chemical

stability as well as their well-defined hydrophilic surface and the ability to shield pharmaceuticals from aggressive immune responses17. The hydrophilic nature of particles can also be

utilized to alter the particles by surface adsorption of surfactants or short chain polymers via electrostatic attractions and hydrogen bonding18. Blood, which is composed of plasma, white

and red cells, may be considered one of nature's most essential multi-segment mixes. It can be considered as the third-grade non-Newtonian fluid19. In the latter work and with the use

of the least squares approach, the authors studied the blood flow including nanoparticles via porous blood arteries in the presence of a magnetic field and heat transfer. Their results

revealed that there is a huge change in the velocity distribution as a result of an increase in the Brownian and thermophoresis parameters. Parida and Padhy20 investigated numerically the

third-grade fluid flow, representing the blood, in a porous conduit with heat transfer and uniform transverse magnetic field. They found out that the fluid temperature is enhanced as a

result of a diffusion in heat within the conduit. In 2013, Baoku et al.21 researched the impact of heat and mass transfer along with magnetic effects and partial slip on a third-grade fluid

flow in an infinite vertical insulated plate with suction along the boundary layer. It was seen that when the porous plate is insulated, the magnetic field strength is reduced with an

enhanced temperature. Sobamowo et al.22 used the Runge–Kutta Fehlberg procedure and shooting method to discuss the impact of thermal radiation and magnetic field of a third-grade fluid

between two disks in a porous space. It was concluded that the rate of heat transfer is increased as a result to an increase in the radiation parameter. Rahbari et al.23 considered the blood

as a third-grade fluid and investigated the inclusion of nanoparticles within the flow with magnetic effect through a porous artery. They discovered that the nanoparticles concentration

increases as a result of an increase in the thermophoresis number. For more information about the inclusion of non-Newtonian fluids with magnetic effect and/or thermal effect through various

physiological applications, readers are referred to Refs.24,25,26,27 and to the references therein. Taking the aforementioned considerations and restrictions into account, we intend to

study the effects arising from adding diamonds and silica nanoparticles to a flow field where blood is represented with a third-grade fluid. The flow is inspected through a catheterized

tapered artery with three distinct configurations: converging tapered, non-tapered and diverging tapered arteries. For more tackled biological applications, we take the magnetic field and

heat transfer into considerations and test the impact of all pertinent parameters on the flow rheology. Since the hybridity of both nanoparticles, diamonds and silica, has not been

investigated, according to our knowledge, we wish to harness such nanoparticles in investigating their impact when incorporated in various types of conduits. It is expected that the current

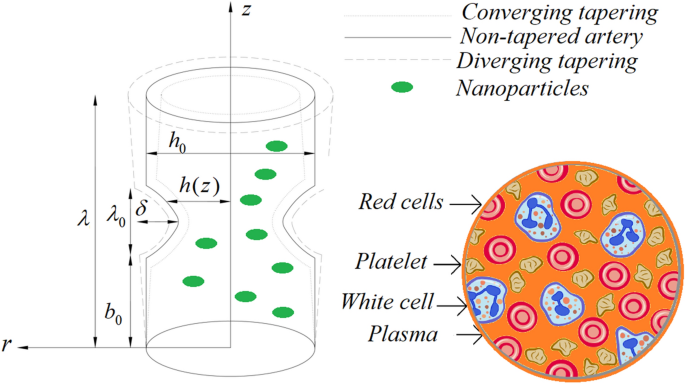
study will aid in developing future nanoscale drug carriers in biological systems. MATHEMATICAL AND PHYSICAL MODELING OF THE BLOOD FLOW Consider a catheterized tapered artery having length

\(\lambda\) filled with hybrid third-grade nanofluid in the presence of diamond and silica nanoparticles. The third-grade nanofluid is considered as blood with incompressible and

irrotational features. The third-grade nanofluid is electrically conducting due to the strong influence of an extrinsic magnetic field. The system of cylindrical polar coordinates \(\left(

{r,\theta ,z} \right)\) is considered, whereas _r_ is located in the radial direction, _z_ is located along the flow direction and \(\theta\) is located along the circumferential direction.

Furthermore, the third-grade nanofluid propagates in the presence of heat transfer phenomena where \(\tilde{T}_{{{\text{ref}}}}\) is the temperature at the artery and \(\tilde{T}_{1}\) is

the temperature at the endoscopic wall. The mathematical form of the proposed geometry is described as: $$ h(z) = \left\{ \begin{gathered} \left( {h_{0} + z\xi } \right)\left[ {1 -

\frac{{n^{{\frac{n}{n - 1}}} \delta }}{{\lambda_{0}^{n} h_{0} \left( {n - 1} \right)}}\left\{ {\lambda_{0}^{n - 1} \left( {z - b_{0} } \right) - \left( {z - b_{0} } \right)^{n} } \right\}}

\right],\quad b_{0} < z \le b_{0} \lambda_{0} , \hfill \\ \left( {h_{0} + z\xi } \right)\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad

\quad \quad \quad \quad \quad \quad \quad {\text{otherwise}} \hfill \\ \end{gathered} \right. $$ (1) where \(\delta\) represents the height of the stenosis which is situated at \(z = b_{0} +

\frac{{\lambda_{0} }}{{n^{{\left( {n - 1} \right)/n}} }}\), \(h_{0}\) is the radius of the non-tapered artery in a non-stenotic part, \(\xi = \tan \psi\) is the tapering parameter, i.e.,

\(\psi\) is the tapering angle where non-tapered artery is at \(\psi = 0\), diverging tapered artery is at \(\psi > 0\) and converging tapered artery at is at \(\psi < 0\). Also,

\(\lambda_{0}\) is the length of the stenosis, \(n \ge 2\) represents the configuration of the constriction profile which belongs to shape parameter in which symmetric stenosis can be

obtained for \(n = 2\), and \(b_{0}\) shows the location of the stenosis as shown in Fig. 1. The equations governing the flow model can then be written as $$ \nabla \cdot

{\tilde{\mathbf{V}}} = 0, $$ (2) $$ \rho_{hnf} \left( {\frac{{\partial {\tilde{\mathbf{V}}}}}{\partial t} + {\tilde{\mathbf{V}}} \cdot \nabla {\tilde{\mathbf{V}}}} \right) = \nabla \cdot

\overline{\xi } + {\text{J}} \times {\text{B}} + \left( {\rho \beta } \right)_{hnf} g\left( {\tilde{T} - \tilde{T}_{{{\text{ref}}}} } \right), $$ (3) where \({\tilde{\mathbf{V}}}\) has the

components of velocity, \({\text{B}}\) is the magnetic field, \({\text{J}}\) is the current density, \({\text{J}} \times {\text{B}} = - \sigma_{hnf} B_{0}^{2} {\tilde{\mathbf{V}}}\),

\(\sigma_{hnf}\) is the electrical conductivity of hybrid nanofluid, \(B_{0}\) is the applied magnetic field, \(\beta_{hnf}\) denotes the thermal expansion coefficient, \(\tilde{T}\) is the

nanofluid temperature, \(g\) the accelaration due to gravity, \(T_{{{\text{ref}}}}\) is the reference temperature, \(\rho_{hnf}\) represents the density of hybrid nanofluid, \(k\) is the

porosity parameter, \(\mu_{hnf}\) is the viscosity of the hybrid nanofluid, the subscript \(hnf\) represents the hybrid nanofluid and \(\overline{\xi }\) is the stress tensor for the

third-grade fluid model and is defined as: $$ \overline{\xi } = - p{\text{I + }}\mu_{hnf} D_{1} + \alpha_{1} D_{2} + \alpha_{2} D_{1}^{2} + \beta_{1} D_{3} + \beta_{1} \left[ {D_{1} D_{2} +

D_{2} D_{1} } \right] + \beta_{3} \left( {{\text{tr}}D_{1}^{2} } \right)D_{1} , $$ (4) where \(p{\text{I}}\) denotes the pressure, \(\mu_{hnf}\) is the viscosity coefficient, \(\left(

{\alpha_{n} ,\beta_{n} } \right)\)’_s_ is the material moduli, \({D}_{1},{D}_{2}\) and \({D}_{3}\) are the first three Rivlin-Erickson tensors that are described as $$ D_{1} = G + G^{T}

,\;{\text{and}}\;D_{m} = \dot{D}_{m - 1} + D_{m - 1} G + G^{T} D_{m - 1} ,\quad m = 2,3 $$ (5) where \(G=grad(v)\), \(v\) is the velocity components, \(T\) in superscript denotes the

transpose of the matrix and the dot represents the material time differentiation. The temperature equation under the presence of viscous dissipation and joule heating reads as $$ \left(

{\frac{{\partial \tilde{T}}}{\partial t} + {\tilde{\mathbf{V}}} \cdot \nabla \tilde{T}} \right) = \frac{{\kappa_{hnf} }}{{\left( {\rho C_{p} } \right)_{hnf} }}\nabla \cdot \left( {\nabla

\tilde{T}} \right) + \frac{{{\text{J}} \cdot {\text{J}}}}{{\left( {\rho C_{p} } \right)_{hnf} \sigma_{hnf} }} + \frac{{\overline{\xi }}}{{\left( {\rho C_{p} } \right)_{hnf} }} \cdot \nabla

{\tilde{\mathbf{V}}}, $$ (6) where \(\kappa_{hnf}\) and \(\left( {\rho C_{p} } \right)_{hnf}\) characterize the thermal conductivity and the heat capacity of the hybrid nanofluid,

respectively. The thermo-physical properties of density, heat capacity, dynamic viscosity, thermal conductivity, thermal expansion coefficient and electric conductivity are defined in the

following equations: * i Density: $$ \begin{gathered} \rho_{nf} = \rho_{f} \left[ {1 - \Phi_{1} } \right] + \Phi_{1} \rho_{np1} , \hfill \\ \rho_{hnf} = \left[ {1 - \Phi_{2} } \right]\left\{

{\rho_{f} \left[ {1 - \Phi_{1} } \right] + \Phi_{1} \rho_{np1} } \right\}, \hfill \\ \end{gathered} $$ (7) * ii Heat capacity: $$ \begin{gathered} \left( {\rho C_{p} } \right)_{nf} = \left[

{1 - \Phi_{1} } \right]\left( {\rho C_{p} } \right)_{f} + \Phi_{1} \left( {\rho C_{p} } \right)_{np1} , \hfill \\ \left( {\rho C_{p} } \right)_{hnf} = \left[ {1 - \Phi_{2} } \right]\left\{

{\left[ {1 - \Phi_{1} } \right]\left( {\rho C_{p} } \right)_{f} + \Phi_{1} \left( {\rho C_{p} } \right)_{np1} } \right\}\Phi_{2} \left( {\rho C_{p} } \right)_{np2} . \hfill \\ \end{gathered}

$$ (8) * iii Dynamic viscosity: $$ \begin{gathered} \mu_{nf} = \frac{{\mu_{f} }}{{\left[ {1 - \Phi_{1} } \right]^{2.5} }}, \hfill \\ \mu_{hnf} = \frac{{\mu_{f} }}{{\left[ {1 - \Phi_{1} }

\right]^{2.5} \left[ {1 - \Phi_{2} } \right]^{2.5} }}. \hfill \\ \end{gathered} $$ (9) * iv Thermal conductivity: $$ \begin{gathered} \kappa_{nf} = \kappa_{f} \times \left[

{\frac{{\kappa_{np1} + 2\kappa_{f} - 2\Phi_{1} \left( {\kappa_{f} - \kappa_{np1} } \right)}}{{\kappa_{np1} + 2\kappa_{f} + \Phi_{1} \left( {\kappa_{f} - \kappa_{np1} } \right)}}} \right],

\hfill \\ \kappa_{hnf} = \kappa_{nf} \times \left[ {\frac{{\kappa_{np2} + 2\kappa_{nf} - 2\Phi_{2} \left( {\kappa_{nf} - \kappa_{np2} } \right)}}{{\kappa_{np2} + 2\kappa_{nf} + \Phi_{2}

\left( {\kappa_{nf} - \kappa_{np2} } \right)}}} \right]. \hfill \\ \end{gathered} $$ (10) * v Thermal expansion coefficient: $$ \begin{gathered} \left( {\rho \beta } \right)_{nf} = \left[ {1

- \Phi_{1} } \right]\left( {\rho \beta } \right)_{f} + \Phi_{1} \left( {\rho \beta } \right)_{np1} , \hfill \\ \left( {\rho \beta } \right)_{hnf} = \left[ {1 - \Phi_{2} } \right]\left\{

{\left[ {1 - \Phi_{1} } \right]\left( {\rho \beta } \right)_{f} + \Phi_{1} \left( {\rho \beta } \right)_{np1} } \right\} + \Phi_{2} \left( {\rho \beta } \right)_{np2} . \hfill \\

\end{gathered} $$ (11) * vi Electric conductivity: $$ \begin{gathered} \sigma_{nf} = \sigma_{f} \times \left[ {\frac{{\sigma_{np1} \left( {1 + 2\Phi_{1} } \right) + 2\sigma_{f} \left( {1 -

\Phi_{1} } \right)}}{{\sigma_{np1} \left( {1 - \Phi_{1} } \right) + \sigma_{f} \left( {2 + \Phi_{1} } \right)}}} \right], \hfill \\ \sigma_{hnf} = \sigma_{nf} \times \left[

{\frac{{\sigma_{np2} \left( {1 + 2\Phi_{2} } \right) + 2\sigma_{f} \left( {1 - \Phi_{2} } \right)}}{{\sigma_{np2} \left( {1 - \Phi_{2} } \right) + \sigma_{f} \left( {2 + \Phi_{2} }

\right)}}} \right]. \hfill \\ \end{gathered} $$ (12) where \({\Phi }_{1}\) and \({\Phi }_{2}\) represent the nanoparticle volume fraction, and \(np1\) and \(np2\) represent the nanoparticles

of diamond and silica, respectively. LUBRICATION APPROACH The proposed governing equation are modelled using the lubrication approach. Therefore, in order to obtain the proposed model in

the dimensionless form and the scaled variables are defined as: $$ \begin{gathered} \tilde{r} = \frac{r}{{R_{0} }},\;\tau = \frac{{\lambda_{0} \tau }}{{R_{0} }},\;\tilde{v} =

\frac{{\lambda_{0} }}{{u_{{{\text{ave}}}} \delta }}v,\;\tilde{R} = \frac{R}{{R_{0} }},\;\tilde{p} = \frac{{R_{0}^{2} }}{{u_{{{\text{ave}}}} \lambda_{0} \mu }}p, \hfill \\ \tilde{z} =

\frac{z}{{R_{0} }},\;T = \frac{{\tilde{T} - \tilde{T}_{{{\text{ref}}}} }}{{\tilde{T}_{1} - \tilde{T}_{{{\text{ref}}}} }},\;\tilde{\delta } = \frac{\delta }{{R_{0} }},\;\lambda =

\frac{L}{{\lambda_{0} }},\;\tilde{u} = \frac{u}{{u_{{{\text{ave}}}} }}. \hfill \\ \end{gathered} $$ (13) where \(u_{{{\text{ave}}}}\) is the averaged velocity of the whole tube over a whole

section. Using Eq. (13) into Eqs. (4–6), we obtain the dimensionless equations as (after removing the tilde): $$ \frac{\partial p}{{\partial z}} = \frac{1}{r}\frac{\partial }{\partial

r}\left[ {r\frac{\partial w}{{\partial r}}\left( {C_{1} + \zeta \left( {\frac{\partial w}{{\partial r}}} \right)^{2} } \right)} \right] - C_{2} M^{2} w + G_{r} C_{3} T, $$ (14) $$

\frac{{C_{4} }}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial T}{{\partial r}}} \right) + B_{m} C_{2} M^{2} w^{2} + B_{m} \left[ {C_{1} \left( {\frac{\partial u}{{\partial r}}}

\right)^{2} + \zeta \left( {\frac{\partial u}{{\partial r}}} \right)^{4} } \right], $$ (15) where \(\zeta\) is the third-grade fluid parameter, _Ec_ is the Eckert number, _M_ is the Hartmann

number, \(Gr\) is the thermal Grashof number and Pr is the Prandtl number. They are defined as $$ \begin{gathered} \zeta = \frac{{2u_{{{\text{ave}}}}^{2} \left( {\beta_{2} + \beta_{3} }

\right)}}{{\mu_{f} R_{0}^{2} }},\;Ec = \frac{{u_{{{\text{ave}}}}^{2} }}{{\left( {\tilde{T}_{1} - \tilde{T}_{{{\text{ref}}}} } \right)\left( {C_{p} } \right)_{f} }},\;M = \sqrt

{\frac{{\sigma_{f} }}{{\mu_{f} }}} B_{0} R_{0} , \hfill \\ \Pr = \frac{{\left( {\rho C_{p} } \right)_{f} \upsilon_{f} }}{{\kappa_{f} }},\;G_{r} = \frac{{\left( {\tilde{T}_{1} -

\tilde{T}_{{{\text{ref}}}} } \right)\left( {\rho \beta } \right)_{f} gR_{0}^{2} }}{{\mu_{f} u_{{{\text{ave}}}} }},\;B_{m} = Ec \times \Pr . \hfill \\ \end{gathered} $$ (16) Here, _B__m_ is

the Brinkman number and the reaming parameters \({C}_{1},{C}_{2},{C}_{3}\) and \({C}_{4}\) are defined as: $$ C_{1} = \frac{{\mu_{hnf} }}{{\mu_{f} }},\;C_{2} = \frac{{\sigma_{hnf}

}}{{\sigma_{f} }},\;C_{3} = \frac{{\left( {\rho \beta } \right)_{hnf} }}{{\left( {\rho \beta } \right)_{f} }},\;C_{4} = \frac{{\kappa_{hnf} }}{{\kappa_{f} }}, $$ (17) The boundary conditions

in dimensionless form are defined as: $$ \left\{ \begin{gathered} w^{\prime} = T^{\prime} = 0\quad \quad {\text{at }}r = 0, \hfill \\ w = 0, T = 0 \, \quad {\text{at }}r = R. \hfill \\

\end{gathered} \right. $$ (18) SERIES SOLUTIONS USING PERTURBATION APPROACH The formulated Eqs. (14–15) are nonlinear, therefore exact solutions are not possible for such cases. We will

employ a perturbation approach to obtain the series solutions. More details on the proposed methodology is given in the references28,29. The perturbation scheme for the formulated equations

are defined as $$ \hbar \left( {\overline{w},\varepsilon } \right) = \left( {1 - \varepsilon } \right)\left[ {\Theta \left( {\overline{w}} \right) - \Theta \left( {w_{0} } \right)} \right] +

\varepsilon \left[ {\Theta \left( {\overline{w}} \right) + \frac{\zeta }{{C_{1} r}}\left( {\frac{{\partial \overline{w}}}{\partial r}} \right)^{3} + \frac{\zeta }{{C_{1} }}\frac{\partial

}{\partial r}\left( {\frac{{\partial \overline{w}}}{\partial r}} \right)^{3} - \frac{{C_{2} }}{{C_{1} }}M^{2} \overline{u} + G_{r} \frac{{C_{3} }}{{C_{1} }}\overline{T} - \frac{1}{{C_{1}

}}\frac{dp}{{dz}}} \right], $$ (19) $$ \hbar \left( {\overline{T},\varepsilon } \right) = \left( {1 - \varepsilon } \right)\left[ {\Theta \left( {\overline{T}} \right) - \Theta \left( {T_{0}

} \right)} \right] + \varepsilon \left[ {\Theta \left( {\overline{T}} \right) + \frac{{B_{m} }}{{C_{4} }}\left( {C_{1} \left( {\frac{\partial u}{{\partial r}}} \right)^{2} + \zeta \left(

{\frac{\partial u}{{\partial r}}} \right)^{4} } \right) + \frac{{C_{2} M^{2} B_{m} }}{{C_{4} }}\overline{w}^{2} } \right], $$ (20) where \(\varepsilon\) is the artificial embedded parameter.

The form of linear operator is chosen as $$ \Theta = \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial }{\partial r}} \right). $$ (21) In view of Eqs. (18) and (21), the

appropriate initial guess is defined as $$ w_{0} = T_{0} = \frac{{r^{2} - R^{2} }}{4}. $$ (22) Defining the expansion $$ \overline{w} = \overline{w}_{0} + \varepsilon \overline{w}_{1} +

\varepsilon^{2} \overline{w}_{2} + \ldots , $$ (23) $$ \overline{T} = \overline{T}_{0} + \varepsilon \overline{T}_{1} + \varepsilon^{2} \overline{T}_{2} + \ldots , $$ (24) ZEROTH ORDER

SYSTEM At zeroth order, we obtain the following set of differential equations $$ \Theta \left( {\overline{w}_{0} } \right) - \Theta \left( {w_{0} } \right) = 0, $$ (25) $$ \Theta \left(

{\overline{T}_{0} } \right) - \Theta \left( {T_{0} } \right) = 0, $$ (26) The solutions of the latter equations can be written as $$ \overline{w}_{0} = \overline{T}_{0} = \frac{{r^{2} -

R^{2} }}{4}. $$ (27) FIRST ORDER SYSTEM \(\LEFT( \VAREPSILON \RIGHT)\) At first order, we obtain the following set of differential equations $$ \Theta \left( {\overline{w}_{1} } \right) +

\Theta \left( {w_{0} } \right) + \frac{\zeta }{{C_{1} r}}\left( {\frac{{\partial \overline{w}_{0} }}{\partial r}} \right)^{3} + \frac{\zeta }{{C_{1} }}\frac{\partial }{\partial r}\left(

{\frac{{\partial \overline{w}_{0} }}{\partial r}} \right)^{3} - \frac{{C_{2} }}{{C_{1} }}M^{2} \overline{w}_{0} + G_{r} \frac{{C_{3} }}{{C_{1} }}\overline{T}_{0} - \frac{1}{{C_{1}

}}\frac{dp}{{dz}}, $$ (28) $$ \Theta \left( {\overline{T}_{1} } \right) + \Theta \left( {T_{0} } \right) + \frac{{B_{m} }}{{C_{4} }}\left( {C_{1} \left( {\frac{{\partial \overline{w}_{0}

}}{\partial r}} \right)^{2} + \zeta \left( {\frac{{\partial \overline{w}_{0} }}{\partial r}} \right)^{4} } \right) + \frac{{C_{2} M^{2} B_{m} }}{{C_{4} }}\overline{w}_{0}^{2} , $$ (29) The

solutions of the above equations can be written as $$ \overline{w}_{1} = - \frac{{\left( {r^{2} - R^{2} } \right)\left( {16C_{1} - 16dp/dz + A3G_{r} r^{2} - C_{2} M^{2} r^{2} - 3C_{3} G_{r}

R^{2} + 3C_{2} M^{2} R^{2} + 2r^{2} \zeta + 2R^{2} \zeta } \right)}}{{64C_{1} }}, $$ (30) $$ \overline{T}_{1} = - \frac{{\left( {r^{2} - R^{2} } \right)\left[ {288C_{4} + B_{m} \left(

{18C_{1} \left( {r^{2} + R^{2} } \right) + C_{2} M^{2} \left( {2r^{4} - 7r^{2} R^{2} + 11R^{4} } \right) + 2\left( {r^{4} + r^{2} R^{2} + R^{4} } \right)\zeta } \right)} \right]}}{{1152C_{4}

}}, $$ (31) SECOND ORDER SYSTEM \(\LEFT( {\VAREPSILON^{2} } \RIGHT)\) At second order, we obtain the following set of differential equations $$ \Theta \left( {\overline{w}_{2} } \right) +

\frac{3\zeta }{{C_{1} r}}\left( {\frac{{\partial \overline{w}_{0} }}{\partial r}} \right)^{2} \left( {\frac{{\partial \overline{w}_{1} }}{\partial r}} \right) + \frac{\zeta }{{C_{1}

}}\frac{\partial }{\partial r}\left\{ {\left( {\frac{{\partial \overline{w}_{1} }}{\partial r}} \right)\left( {\frac{{\partial \overline{w}_{0} }}{\partial r}} \right)^{2} } \right\} -

\frac{{C_{2} }}{{C_{1} }}M^{2} \overline{w}_{1} + G_{r} \frac{{C_{3} }}{{C_{1} }}\overline{T}_{1} , $$ (32) $$ \Theta \left( {\overline{T}_{2} } \right) + \frac{{B_{m} }}{{C_{4} }}\left(

{2C_{1} \frac{{\partial \overline{w}_{0} }}{\partial r}\frac{{\partial \overline{w}_{1} }}{\partial r} + 4\zeta \left( {\frac{{\partial \overline{w}_{0} }}{\partial r}} \right)^{3}

\frac{{\partial \overline{w}_{1} }}{\partial r}} \right) + \frac{{2C_{2} M^{2} B_{m} }}{{C_{4} }}\overline{w}_{1} \overline{w}_{0} . $$ (33) The solutions of the latest equations can be

written as $$ \begin{gathered} \overline{w}_{2} = \frac{{\left( {r^{2} - R^{2} } \right)}}{{36864C_{1}^{2} C_{4} }}\left[ {16C_{1}^{2} C_{3} B_{m} G_{r} \left( {r^{4} + r^{2} R^{2} - 8R^{4}

} \right) + 16C_{4} \left\{ {C_{2}^{2} M^{4} \left( {r^{4} - 8r^{2} R^{2} + 19R^{4} } \right)} \right.} \right. \hfill \\ \quad \quad \; + C_{2} M^{2} \left( {36dp/dz\left( {r^{2} - 3R^{2} }

\right) - C_{3} G_{r} \left( {r^{4} - 8r^{2} R^{2} + 19R^{4} } \right) - 20r^{4} \zeta + 34r^{2} R^{2} \zeta + 52R^{4} \zeta } \right) \hfill \\ \quad \quad \; + 18\zeta \left. {\left( { -

12dp/dz\left( {r^{2} + R^{2} } \right) + C_{3} G_{r} \left( {r^{4} - 2r^{2} R^{2} - 2R^{4} } \right) + 2\left( {r^{4} + r^{2} R^{2} + R^{4} } \right)\zeta } \right)} \right\} \hfill \\ \quad

\quad { + }C_{1} \left\{ { - 576C_{4} \left( {C_{2} M^{2} \left( {r^{2} - 3R^{2} } \right) - 6\left( {r^{2} + R^{2} } \right)\zeta } \right) + C_{3} G_{r} \left\{ {576C_{4} \left( {r^{2} -

3R^{2} } \right)} \right.} \right. \hfill \\ \left. {\left. {\left. {\quad \quad \; + B_{m} \left( {C_{2} M^{2} \left( {r^{6} - 7r^{4} R^{2} + 29r^{2} R^{4} - 59R^{6} } \right) + \left(

{r^{6} + r^{4} R^{2} + r^{2} R^{4} - 15R^{6} } \right)\zeta } \right)} \right\}} \right\}} \right], \hfill \\ \end{gathered} $$ (34) $$ \begin{gathered} \overline{T}_{2} = \frac{{B_{m}

\left( {r^{2} - R^{2} } \right)}}{{73728C_{1} C_{4} }}\left[ {2304C_{1}^{2} \left( {r^{2} + R^{2} } \right) + C_{2}^{2} M^{4} \left( { - 9r^{6} + 71r^{4} R^{2} - 181r^{2} R^{4} + 251R^{6} }

\right)} \right. \hfill \\ \quad \quad \; - 64C_{1} \left\{ { - 2C_{2} M^{2} r^{4} + 7C_{2} M^{2} r^{2} R^{2} - 29C_{2} M^{2} R^{4} + 36dp/dz\left( {r^{2} + R^{2} } \right) + C_{3} G_{r} }

\right. \hfill \\ \quad \quad \;\left. { \times \left( { - 2r^{4} + 7r^{2} R^{2} + 7R^{4} } \right) - 12r^{4} \zeta - 12r^{2} R^{2} \zeta - 12R^{4} \zeta } \right\} + 4\zeta \left\{ { -

128dp/dz\left( {r^{4} + r^{2} R^{2} + R^{4} } \right)} \right. \hfill \\ \quad \quad \; + \left. {C_{3} G_{r} \left( {9r^{6} - 23r^{4} R^{2} - 23r^{2} R^{4} - 23R^{6} } \right) + 18\left(

{r^{6} + r^{4} R^{2} + r^{2} R^{4} + R^{6} } \right)\zeta } \right\} \hfill \\ \quad \quad \; + C_{2} M^{2} \left\{ { - 128dp/dz\left( {2r^{4} - 7r^{2} R^{2} + 11R^{4} } \right) + C_{3}

G_{r} \left( {9r^{6} - 71r^{4} R^{2} + 181r^{2} R^{4} - 251R^{6} } \right)} \right. \hfill \\ \quad \quad \;\left. {\left. { + 6\left( { - 3r^{6} + 13r^{4} R^{2} + r^{2} R^{4} + 49R^{6} }

\right)\zeta } \right\}} \right], \hfill \\ \end{gathered} $$ (35) The approximate series solutions can be written as $$ w = \mathop {\lim }\limits_{\varepsilon \to 1} \overline{w} =

\overline{w}_{0} + \overline{w}_{1} + \overline{w}_{2} + \ldots , $$ (36) $$ T = \mathop {\lim }\limits_{\varepsilon \to 1} \overline{T} = \overline{T}_{0} + \overline{T}_{1} +

\overline{T}_{2} + \ldots , $$ (37) The flux (_Q_) can be computed with the help of following expression $$ Q = 2\mathop \smallint \limits_{0}^{R} ru\left( {r,z} \right){\text{d}}r. $$ (38)

The expression of impedance can be computed utilizing the above expression (38), thus, we have $$ I_{m} = \frac{1}{Q}\int\limits_{0}^{L} {\left( { - \frac{dp}{{dz}}} \right)} {\text{d}} z.

$$ (39) SIGNIFICANCE OF THE STUDY In this section, we are going to investigate the plotted graphs for the most important physical variables versus the parameters of interest. Results have

been computed on the basis of the following parametric values: \({G}_{r}=5,\zeta =1,{B}_{m}=5,\delta =0.3,{\Phi }_{1}=0.1,{\Phi }_{1}=0.15\) and \(M=0.5\). In addition, Table 1 presents the

thermo-physical values of blood, diamond and silica for the numerical computations. The analytical and numerical results are performed based on the symbolic computational software,

Mathematica. VELOCITY MECHANISM Figures 2, 3, 4, 5 and 6 reveal the dependency of the velocity distribution on the thermal Grashof number \(Gr\), third-grade fluid parameter \(\zeta\),

magnetic parameter _M_, height of stenosis \(\delta\) and nanoparticle volume fraction \({\Phi }_{1}\) and \({\Phi }_{2}\). Figure 2 represents the behaviour of velocity profile with various

values of \(Gr\) for converging, non-tapered and diverging arteries. It is noticed that \(Gr\) reduces the flow greatly until _r_ = 0.5 before the behaviour is reversed with an increase in

\(Gr\). Such reduction in flow velocity might be attributed to Lorentz force that opposes the flow. It is seen that for the converging artery, the flow is accelerated more than that of the

non-tapered and diverging ones until _r_ = 0.5 before the difference does not seem to be very effective after that for progressive values of \(Gr\). Figure 3 elucidates the behaviour of

velocity distribution with higher values of \(\zeta\). It is depicted that \(\zeta\) has the same effect of the flow field as does \(Gr\). Figure 4 illustrates the impact of _M_ on the

velocity distribution along the different proposed conduits. It is observed that _M_ accelerates the flow for various values of the pertinent parameters until _r_ = 0.5 after which the flow

is seen slightly decelerating for progressive values of _M_. Figure 5 presents the behaviour of the velocity profile along the various arteries for progressive values of \(\delta\) where it

is seen that \(\delta\) has the exact same effect on the flow field as does _M_. Figure 6 illustrates the behaviour of the flow due to enhanced values of \({\Phi }_{1}\) and \({\Phi }_{2}\)

where it is seen that the converging artery attains higher velocity distribution than that of the non-tapered and diverging ones until mid-artery. It is also observed that \({\Phi }_{1}\)

and \({\Phi }_{2}\) causes a reduction in the flow velocity till almost midway of all the segments after which the effect is weakly increasing. TRAPPING MECHANISM Figures 7, 8, 9 and 10 are

plotted to investigate the trapping as an important mehcanism in nanofluid flows that visualizes different trajectories. Ordinarily, trapping represents the development of inwardly

circulating free eddy currents in the blood that are surrounded by streamlines. This mechanism is critical in biology because it assists in the development of blood clots and the harmful

migration of bacteria. Figures 7, 8, 9 and 10 are plotted to illustrate the physical impact of pertinent parameters on the streamlines across the flow. It is seen from Fig. 7 that by

increasing the third-grade fluid parameter \(\zeta ,\) the number of trapped boluses increases while their size decreases. Figure 8 elucidates the impact of \(Gr\) on the trapped region.

Results show a drastic change in the shape and size of trapped region with an increase in \(Gr\). The circulated region decreases then vanishes with progressive values of \(Gr\). Figure 9

illustrates the effect of _M_ on the streamlines with different values of parameters under consideration. It is notied that increasing _M_ implies to a significant reduction in the number of

circulating streamlines. It is shown from Fig. 10 that the impact of \({\Phi }_{1}\) and \({\Phi }_{2}\) is to decrease the number of circulating streamlines greatly along with increasing

the size of trapped bolus to a great extent. TEMPERATURE PROFILE Figures 11, 12, 13 and 14 depict the behaviour of the temperature distribution against the governing flow parameters. Figure 

11 observes the effect of \({B}_{m}\) on the temperature profile for the converging, non-tapered and diverging arteries. It is noticed that \({B}_{m}\) has an increasing effect on the flow

temperature. It is also seen that the temperature of the converging artery attains smaller values than that of the non-tapered and diverging arteries. Figure 12 is plotted to describe the

behaviour of temperature with increasing _M_ where is seen that the temperature increases steadily with an increase in M across the flow field for all arteries. Figures 13 and 14 illustrate

the behaviour of the temperature profile for all arteries against enhanced values \({\Phi }_{1}\), \({\Phi }_{2}\) and \(\zeta\). It is observed from both figures that \({\Phi }_{1}\),

\({\Phi }_{2}\) and \(\zeta\) enhance the temperature distribution across the flow greatly. It is also noticed that the diverging artery has the highest temperature profile across all

arteries. Further, it is seen from Fig. 14 that the temperature of Newtonian fluid is smaller than that if non-Newtonian one across the arteries. IMPEDANCE PROFILE Figures 15, 16, 17 and 18

are plotted to present the effect of _M_, _Gr_, \(\zeta\), \({\Phi }_{1}\) and \({\Phi }_{2}\) on the impedance _I__m_ that is plotted against \(\delta\) for various values of the pertinent

parameters. Figure 15 shows that the impedance profile is greatly enhanced with progressive values of \(\zeta\). It is noticed from Fig. 16 that _Gr_ has the exact same effect on _I__m_ as

does \(\zeta\). It is generally noticed that with both _M_ and _Gr_, the converging artery’s impedance attains the least values among the non-tapered and diverging ones. Figures 17 and 18

describe the behaviour of _I__m_ with \(\zeta\), \({\Phi }_{1}\) and \({\Phi }_{2}\) where it is seen that these parameters boost _I__m_ to a great extent for any value for the other

parameters under consideration. It is also shown that the converging artery has the least impedance than do the non-tapered and diverging arteries. Further, it is seen from Fig. 17 that the

impedance of Newtonian fluid is smaller than that of the non-Newtonian one. WALL SHEAR STRESS Figure 19, 20, 21 and 22 reveal the impact of \({\Phi }_{1}\), \({\Phi }_{2}\), \(\zeta\), _M_

and _Gr_ on the wall shear stress with sundry values of the other parameters on interest. It is obvious that all the parameters’ impact on the wall shear stress is to reduce it steadily. It

is also seen that the wall shear stress attains the highest values for the converging artery than that of the non-tapered and diverging ones with enhanced values of \(\zeta\) and _M_ as seen

in Figs. 20 and 21. Inversely, Figs. 19 and 22 show that the wall shear stress attains the least values with increasing \({\Phi }_{1}\), \({\Phi }_{2}\) and _Gr_ for any value of the other

parameters of interest. OBSERVATIONS In the proposed work, we aim to study the behavior of a hybrid nanofluid model with nano-diamonds and silica through a catheterized tapered artery with

three distinct configurations: converging tapered, non-tapered and diverging tapered arteries. The third-grade fluid is used to represent the flow model. Magnetic field and with heat

transfer are also taken into consideration and the governing system of equations is then solved in a closed form using the perturbation approach. The interpretation of the physical variables

of interest is explained. The most important findings are as follows: * i. The flow decelerates with an increase of thermal Grashof number and this is attributed to Lorentz force. * ii. The

volume fraction of nanoparticles causes a reduction in the flow velocity till almost midway of all the segments of the arteries. * iii. The magnetic parameter is seen to significantly

reducing the number of circulating streamlines. * iv. The diverging artery has the highest temperature profile across all arteries. * v. The third-grade fluid parameter enhances the

temperature distribution across the flow greatly. * vi. The converfing artery’s impedance attains the least values among the non-tapered and diverging ones. * vii. The wall shear stress

increases steadily with an increase in the nanoparticles’ volume fraction, magnetic parameter, thermal Grashof number and third-grade parameter. * viii. The impedance and temperature of the

Newtonian fluid are smaller than these of the non-Newtonian one. DATA AVAILABILITY All data generated or analyzed during this study are included in this published article. REFERENCES *

Chauhan, S., Jain, N. & Nagaich, U. Nanodiamonds with powerful ability for drug delivery and biomedical applications: Recent updates on in vivo study and patents. _J. Pharm. Anal._

10(1), 1–12. https://doi.org/10.1016/j.jpha.2019.09.003 (2020). Article  PubMed  Google Scholar  * Vul, A. Y., Dideikin, A. T., Aleksenskii, A. E. & Baidakova, M. V. Detonation

nanodiamonds: Synthesis, properties and applications. _RSC Nanosci. Nanotechnol._ 31, 27–48 (2014). Article  CAS  Google Scholar  * Alawdi, S. H., Eidi, H., Safar, M. M. & Abdel-Wahhab,

M. A. Loading amlodipine on diamond nanoparticles: A novel drug delivery system. _Nanotechnol. Sci. Appl._ 12, 47–53. https://doi.org/10.2147/NSA.S232517 (2019). Article  CAS  PubMed  PubMed

Central  Google Scholar  * Saraf, J., Kalia, K., Bhattacharya, P. & Tekade, R. K. Growing synergy of nanodiamonds in neurodegenerative interventions. _Drug Discov. Today_ 24(2),

584–594. https://doi.org/10.1016/j.drudis.2018.10.012 (2019). Article  CAS  PubMed  Google Scholar  * Li, H. C. _et al._ The hemocompatibility of oxidized diamond nanocrystals for biomedical

applications. _Sci. Rep._ 3, 3044. https://doi.org/10.1038/srep03044 (2013). Article  PubMed  PubMed Central  Google Scholar  * Tsai, L. W. _et al._ Nanodiamonds for medical applications:

Interaction with blood in vitro and in vivo. _Int. J. Mol. Sci._ 17(7), 1111. https://doi.org/10.3390/ijms17071111 (2016). Article  CAS  PubMed  PubMed Central  Google Scholar  * Chen, X.

& Zhang, W. Diamond nanostructures for drug delivery, bioimaging, and biosensing. _Chem. Soc. Rev._ 46, 734–760. https://doi.org/10.1039/C6CS00109B (2016). Article  ADS  Google Scholar 

* Masys, S., Rinkevicius, Z. & Tamuliene, J. Computational study on the electronic _g_-tensors of hydrophilic and hydrophobic nanodiamonds interacting with water. _J. Chem. Phys._ 152,

144302. https://doi.org/10.1063/5.0001485 (2020). Article  ADS  CAS  PubMed  Google Scholar  * Namdar, R. & Nafisi, S. Nanodiamond applications in skin preparations. _Drug Discov. Today_

23(5), 1152–1158. https://doi.org/10.1016/j.drudis.2018.04.006 (2018). Article  CAS  PubMed  Google Scholar  * Ansari, S. A. _et al._ Role of nanodiamonds in drug delivery and stem cell

therapy. _Iran. J. Biotechnol._ 14(3), 130–141. https://doi.org/10.15171/ijb.1320 (2016). Article  PubMed  PubMed Central  Google Scholar  * Bei, D., Meng, J. & Youan, B. B. Engineering

nanomedicines for improved melanoma therapy: progress and promises. _Nanomedicine_ 5(9), 1385–1399. https://doi.org/10.2217/nnm.10.117 (2010). Article  CAS  PubMed  Google Scholar  * Pei, Q.

_et al._ Light-activatable red blood cell membrane-camouflaged dimeric prodrug nanoparticles for synergistic photodynamic/chemotherapy. _ACS Nano_ 12, 1630–1641 (2018). Article  CAS  PubMed

  Google Scholar  * Peng, H. _et al._ Biomimetic mesoporous silica nanoparticles for enhanced blood circulation and cancer therapy. _ACS Appl. Bio Mater._ 3(11), 7849–7857 (2020). Article 

CAS  PubMed  Google Scholar  * Meng, H. _et al._ Engineered design of mesoporous silica nanoparticles to deliver doxorubicin and P-glycoprotein siRNA to overcome drug resistance in a cancer

cell line. _ACS Nano_ 4(8), 4539–4550 (2010) (PMID: 20731437; PMCID: PMC3899722). Article  CAS  PubMed  PubMed Central  Google Scholar  * Prabha, S., Durgalakshmi, D., Rajendran, S. &

Lichtfouse, E. Plant-derived silica nanoparticles and composites for biosensors, bioimaging, drug delivery and supercapacitors: A review. _Environ. Chem. Lett._ 19, 1667–1691.

https://doi.org/10.1007/s10311-020-01123-5 (2021). Article  CAS  PubMed  Google Scholar  * Balagna, C., Perero, S., Percivalle, E., Nepita, E. V. & Ferraris, M. Virucidal effect against

coronavirus SARS-CoV-2 of a silver nanocluster/silica composite sputtered coating. _Open Ceram._ 1, 100006. https://doi.org/10.1016/j.oceram.2020.100006 (2020). Article  CAS  Google Scholar

  * Biju, V. Chemical modifications and bioconjugate reactions of nanomaterials for sensing, imaging, drug delivery and therapy. _Chem. Soc. Rev._ 43(3), 744–764.

https://doi.org/10.1039/c3cs60273g (2014) (PMID: 24220322). Article  CAS  PubMed  Google Scholar  * Jana, S. C. & Jain, S. Dispersion of nanofillers in high performance polymers using

reactive solvents as processing aids. _Polymer_ 42(16), 6897–6905. https://doi.org/10.1016/S0032-3861(01)00175-6 (2001). Article  CAS  Google Scholar  * Usman, M., Mohyud, D. S. T., Zubair,

T., Hamid, M. & Wang, W. Fluid flow and heat transfer investigation of blood with nanoparticles through porous vessels in the presence of magnetic field. _J. Algorithms Comput. Technol._

13, 1–15. https://doi.org/10.1177/1748301818788661 (2019). Article  MathSciNet  Google Scholar  * Parida, M. & Padhy, S. Numerical study of MHD flow of a third grade fluid in a

non-Darcian porous channel. _Int. J. Pure Appl. Math._ 118(3), 651–665. https://doi.org/10.12732/ijpam.v118i3.13 (2018). Article  Google Scholar  * Baoku, I. G., Olajuwon, B. I. &

Mustapha, A. O. Heat and mass transfer on a MHD third grade fluid with partial slip flow past an infinite vertical insulated porous plate in a porous medium. _Int. J. Heat Fluid Flow_ 40,

81–88. https://doi.org/10.1016/j.ijheatfluidflow.2013.01.016 (2013). Article  Google Scholar  * Sobamowo, M. G., Yinusa, A. A. & Aladenusi, S. T. Impacts of magnetic field and thermal

radiation on squeezing flow and heat transfer of third grade nanofluid between two disks embedded in a porous medium. _Heliyon_ 6(5), e03621 (2020). Article  CAS  PubMed  PubMed Central 

Google Scholar  * Rahbari, A., Fakour, M., Hamzehnezhad, A., Vakilabadi, M. A. & Ganji, D. D. Heat transfer and fluid flow of blood with nanoparticles through porous vessels in a

magnetic field: A quasi-one dimensional analytical approach. _Math. Biosci._ 283, 38–47 (2017). Article  MathSciNet  CAS  PubMed  MATH  Google Scholar  * Abdelsalam, S. I. & Zaher, A. Z.

Leveraging elasticity to uncover the role of Rabinowitsch suspension through a wavelike conduit: Consolidated blood suspension application. _Mathematics_ 9(16), 1–25.

https://doi.org/10.3390/math9162008 (2021). Article  Google Scholar  * Abdelsalam, S. I., Velasco-Hernández, J. X. & Zaher, A. Z. Electromagnetically modulated self-propulsion of

swimming sperms via cervical canal. _Biomech. Model. Mechanobiol._ 20, 861–878. https://doi.org/10.1007/s10237-020-01407-3 (2021). Article  PubMed  Google Scholar  * Bhatti, M. M., Marin,

M., Zeeshan, A. & Abdelsalam, S. I. Editorial: Recent trends in computational fluid dynamics. _Front. Phys._ 8, 593111 (2020). Article  Google Scholar  * Eldesoky, I. M., Abdelsalam, S.

I., El-Askary, W. A. & Ahmed, M. M. The integrated thermal effect in conjunction with slip conditions on peristaltically induced particle fluid transport in a catheterized pipe. _J.

Porous Media_ 23(7), 695–713 (2020). Article  Google Scholar  * He, J. H. Homotopy perturbation technique. _Comput. Methods Appl. Mech. Eng._ 178(3–4), 257–262 (1999). Article  ADS 

MathSciNet  MATH  Google Scholar  * He, J. H. Homotopy perturbation method: A new nonlinear analytical technique. _Appl. Math. Comput._ 135(1), 73–79 (2003). Article  MathSciNet  MATH 

Google Scholar  * Khan, U., Zaib, A., Khan, I., Baleanu, D. & Nisar, K. S. Enhanced heat transfer in moderately ionized liquid due to hybrid MoS2/SiO2 nanofluids exposed by nonlinear

radiation: Stability analysis. _Crystals_ 10(2), 142 (2020). Article  CAS  Google Scholar  Download references FUNDING Open access funding provided by The Science, Technology &

Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Basic Science, Faculty of Engineering, The British

University in Egypt, Al-Shorouk City, Cairo, 11837, Egypt Sara I. Abdelsalam * College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao, 266590,

Shandong, China M. M. Bhatti Authors * Sara I. Abdelsalam View author publications You can also search for this author inPubMed Google Scholar * M. M. Bhatti View author publications You can

also search for this author inPubMed Google Scholar CONTRIBUTIONS Conceptualization: S.I.A. and M.M.B.; Formal analysis: S.I.A. and M.M.B.; Investigation: S.I.A. and M.M.B.; Methodology:

M.M.B.; Resources: S.I.A.; Software: M.M.B.; Supervision: S.I.A; Validation: S.I.A. and M.M.B.; Visualization: S.I.A. and M.M.B.; Writing—original draft: S.I.A. and M.M.B.; Writing—review

& editing: S.I.A. and M.M.B. CORRESPONDING AUTHOR Correspondence to Sara I. Abdelsalam. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL

INFORMATION PUBLISHER'S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS

This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as

long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third

party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the

article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the

copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Abdelsalam, S.I., Bhatti,

M.M. Unraveling the nature of nano-diamonds and silica in a catheterized tapered artery: highlights into hydrophilic traits. _Sci Rep_ 13, 5684 (2023).

https://doi.org/10.1038/s41598-023-32604-6 Download citation * Received: 29 December 2022 * Accepted: 30 March 2023 * Published: 07 April 2023 * DOI:

https://doi.org/10.1038/s41598-023-32604-6 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative