ABSTRACT The aim of this study is to examine the analog/RF performance characteristics of graphene nanoribbon (GNR) field-effect transistors (FETs) using a novel technique called underlap

engineering. The study employs self-consistent atomistic simulations and the non-equilibrium Green's function (NEGF) formalism. Initially, the optimal underlap length for the GNR-FET by

device has been determined evaluating the ON-current (_I__ON_) to OFF-current (_I__OFF_) ratio, which is a critical parameter for digital applications. Subsequently, the impact of underlap

engineering on analog/RF performance metrics has been analyzed and conducting a comprehensive trade-off analysis considering parameters such as intrinsic-gain, transistor efficiency, and

underlap effect demonstrates the highest transconductance (_g__m_) and cut-off frequency (_f__T_). Finally, a linearity analysis has been conducted to compare the optimized GNR-FET device

with the conventional GNR-FET device without the underlap effect. SIMILAR CONTENT BEING VIEWED BY OTHERS TRADE-OFF ANALYSIS BETWEEN GM/ID AND FT OF GNR-FETS WITH SINGLE-GATE AND DOUBLE-GATE

DEVICE STRUCTURE Article Open access 03 May 2024 ANALOG AND RF PERFORMANCE OPTIMIZATION FOR GATE ALL AROUND TUNNEL FET USING BROKEN-GAP MATERIAL Article Open access 29 October 2022

DIRAC-SOURCE DIODE WITH SUB-UNITY IDEALITY FACTOR Article Open access 26 July 2022 INTRODUCTION In recent decades, there has been a notable decrease in the size of transistors, moving from

micrometers to nanometers, driven by the well-known Moore’s Law1,2. However, as the demand for advanced electronic devices continues to rise, the size limitations of silicon-based

transistors have become increasingly challenging, and there will eventually be physical limits to further miniaturization. The main obstacle in this regard is the occurrence of short-channel

effects (SCE), such as leakage current, subthreshold swing (SS), drain-induced barrier lowering (DIBL), and velocity saturation, which are consequences of decreasing the distance between

the source and drain3,4,5. In recent times, researchers have actively pursued extensive research to explore novel materials that could overcome these limitations. Subsequently, graphene has

emerged as a highly significant material that has captured significant attention in the field of electronic devices. This is primarily due to its abundant availability and cost-effective

attributes, making it an exceptionally attractive option for various electronic applications6. Graphene, consisting of a single layer of carbon atoms, has positioned itself as an

exceptionally promising material for future semiconductor devices, especially in high-frequency applications. This is primarily attributed to its remarkable properties, including outstanding

thermal conductivity, high saturation velocity, flexibility, impressive mechanical strength, and superior carrier mobility7,8,9,10,11. Moreover, graphene's exceptional mobility

characteristics make it an excellent candidate for flexible and radio frequency (RF) device applications12,13. In addition to its advantageous characteristics, at relatively short channels,

the lack of band gaps in graphene results poor current ON/OFF ratio (ION/IOFF). Thus, graphene nanoribbon (GNR) needs to be made to use graphene as a device, and the device based on graphene

is known as a graphene nanoribbon (GNR) field-effect transistor (FET)14,15. Various approaches have been explored to enhance the electrical performance of GNR-based FETs. These methods

include utilizing different gate-oxide dielectric materials, channel doping, dimensional scaling, selecting gate materials with specific work functions, and introducing vacancy defects on

the channel16,17,18,19,20,21,22,23,24,25. However, there is still significant room for investigation, particularly in the area of channel-length engineering. Previous studies have

demonstrated that implementing a gate-underlap structure can improve leakage current, subthreshold swing (SS), and current ON/OFF ratio26. The introduction of underlap architectures helps in

reducing short-channel effects (SCEs) by adjusting the effective channel length of the device27. It also mitigates fringing capacitance28 and Gate Induced Drain Leakage (GIDL)29, resulting

in reduced switching power and improved suitability for logic applications. However, the underlap between the gate and the source or drain leads to an increase in channel resistance, which

diminishes the ON-current and adversely affects device performance. To address this issue, an asymmetric underlap structure, where the underlap is applied on the drain side, is preferred30.

Despite these advancements, the existing methods for enhancing the analog/RF performance of FETs remain inadequate. As a result, recent studies have focused on improving the analog/RF

performance of GNR-FETs. This motivates further investigation into the analog and RF performance characteristics of GNR-FETs with underlap structures. Notably, there is a lack of prior

research examining the analog/RF performance behavior of GNR-FETs employing the asymmetric underlap mechanism. This research study focuses on examining the impact of underlap engineering on

analog/RF parameters in GNR-FETs for low-power applications. To achieve this objective, the non-equilibrium Green's function (NEGF) methodology is employed to investigate the

figure-of-merits (FOMs) related to analog and RF performance in GNR-FET devices with varying underlap lengths. Key parameters such as the gain frequency product (GFP) and gain transfer

frequency product (GTFP) are analyzed, as they are crucial for circuit design and high-speed switching applications. The findings of this study can serve as a valuable resource for

researchers involved in the design of novel GNR-FETs that exhibit superior performance compared to conventional FETs. Moreover, it is expected that this research will inspire further

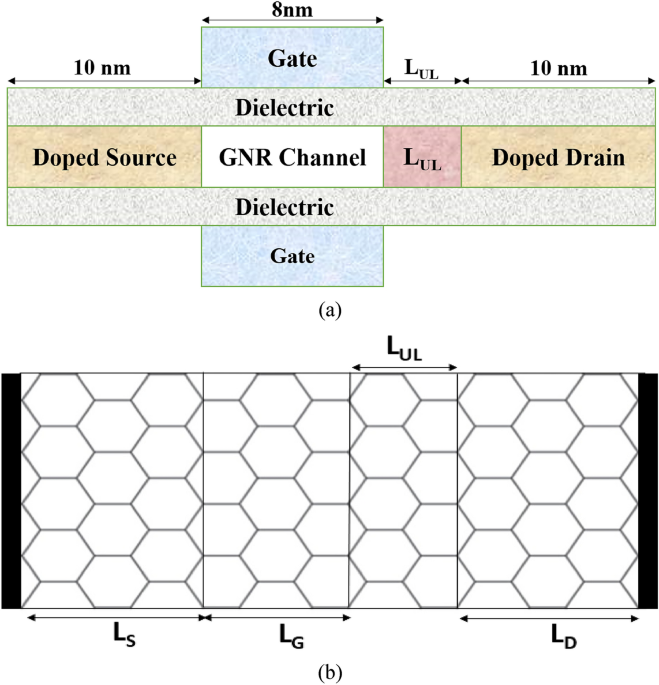
exploration of the application potential of GNR-FETs in diverse multidimensional contexts. DEVICE STRUCTURE AND SIMULATION METHODOLOGY Figure 1a and b illustrate the cross-sectional view and

top view, respectively, of the simulated 12-armchair double-gated (DG) GNR-FET with underlap engineering. The channel and the source/drain are formed by a 1.37 nm-wide 2D graphene sheet.

The lattice constant in GNR is 2.46 Å, and the carbon–carbon (C–C) bond length (d) is 1.42 Å. Our focus on 12-armchair GNRs stems from previous research suggesting that a bandgap of 0.6 eV

and an effective mass of 0.064 _m__0_31,32,33, where _m__0_ represents the free mass of an electron, are essential for achieving optimal performance. The top and bottom gate oxide layers are

composed of _HfO__2_. We vary the underlap length from 0-nm to 10-nm, incrementing by 2-nm. The source and drain regions are doped with n-type dopants, while the underlap and channel length

(_L__G_ = 8 nm)26 are intrinsic regions. The simulations are conducted with a fixed drain-to-source voltage (_V__DS_) at a temperature of 300 K. The parameters used in the device simulation

are presented in Table 1. To accomplish the objective, the NanoTCAD ViDES atomistic device simulator perform all simulations within the non-equilibrium Green's function (NEGF)

framework34. The tight-binding approximation is used to describe the interactions between individual carbon atoms in a graphene nanoribbon (GNR) at an atomic level. These interactions

specifically involve the C–C atoms and are limited to the nearest neighboring atoms. In the NEGF approach, first-of-all, an appropriate Hamiltonian matrix for the channel is taken into

account. The simulation employed a 2-band Hamiltonian, expressed as follows35,36: $$H\left(k\right)=\left[\begin{array}{cc}{E}_{B}& tf(k)\\ {tf(k)}^{*}& {E}_{A}\end{array}\right],$$

(1) the parameters EA and EB represent the energy levels at the top of the valence band and the bottom of the conduction band, respectively. These can be expressed as EB—EA = EG, where EG is

the bandgap. Here, only one atomic orbital and the primitive unit cell comprises only one atom is considered, which leads to the formation of a single energy band. In this simulation, the

in-plane hopping parameter, denoted as t, has a value of 2.7 eV31. $$f\left(k\right)={e}^{j{k}_{y}d}+{e}^{-j{k}_{y}d/2}\mathrm{cos}\left(\sqrt{3}{k}_{x}d/2\right).$$ (2) After defining the

Hamiltonian matrix, Green's function is calculated as Ref.37: $$ G\left( E \right) = \left[ {EI - H - \sum_{S} - \sum_{D} } \right]^{ - 1} , $$ (3) which is examined by referencing

earlier work38. After performing the Green's function calculation, the Schrödinger equation is solved with an open boundary condition to obtain the electron and hole concentrations.

Subsequently, the electron density is calculated using Newton–Raphson iteration method. Ultimately, the Landauer formula37 is employed to compute the drain current (_I__D_). In Green’s

function equation, _E_, _I_, _H_, \(\sum_{D}\) and \(\sum_{S}\) represent energy, identity matrix, material Hamiltonian, and self-energy matrix at drain and source terminals, respectively.

RESULTS AND DISCUSSION To begin the analysis, the current simulator is calibrated to correspond to the device structure presented in Ref.39. Figure 2 demonstrates that obtained simulations

are in good agreement with previous research findings. Once the correctness of the simulation with the above-described methodology has been established, an underlap is introduced in the body

of the GNR-FET at the drain end to assess the impact of Asymmetric underlap (UL) length on the performance of GNR-FET devices. It is important to clarify that whenever UL is mentioned

unless explicitly stated otherwise, it refers to the default Asymmetric UL of drain extension. OPTIMIZATION OF UNDERLAP LENGTH After confirming the accuracy, the impact of UL engineering on

the transfer characteristics of GNR-FETs is examined. Figure 3 depicts the impact of UL length in the _I__D_ as a function of gate-to-source voltage (_V__GS_) of GNR-FETs in which the

underlap length is varied from 0-nm to 10-nm with a step-size of 2-nm to get an optimized underlap state. The optimized state of the device is achieved by utilizing digital performance FOM,

ON-current to OFF-current ratio. The _I__D_ values for the ON-state and OFF-state are examined at _V__DS_ = 0.3 V, _V__GS_ = 0.8 V, and _V__DS_ = 0.3 V, _V__GS_ = 0 V, respectively. It is

observed from Fig. 4 that a significant amount of DIBL is present in the device with low underlap length, which implies a larger _I__OFF_. When the underlap length increases, the DIBL

decreases, resulting in a reduced _I__OFF_ without considerably lowering _I__ON_. As a result, the _I__ON__/I__OFF_ ratio increases. The Underlap length eventually rises to a level where

DIBL is no longer important. As a result, a small change in the _I__OFF_ is seen as underlap increases. However, raising the underlap raises the total resistance of the channel, which

dramatically reduces the _I__ON_ after some point. As a result, _I__ON__/I__OFF_ begins to decline. Figure 5 depicts the surface potential plot of the simulated structure for various

underlap lengths. It is observed from Fig. 5 that the induced inversion charge of the device rises as the underlap length of the device increases. As a result, the potential barrier in the

UL region is enhanced. Following the observation of the surface potential curve, the effects of UL engineering on the transmission window for carrier transmission are investigated. Figure 6

depicts the transmission probability variation with energy, and it is observed that with the increase of UL length of the device, the transmission probability curve decreases, which results

smaller drain current39. From the above graphs and discussion, it is clear that the optimal underlap point is achieved at a UL length of 6-nm. Henceforth, an UL length of up to 6-nm is

elected for further analysis and compare the results with a conventional GNR-FET device having zero underlap gap between the gate and drain regions. ANALOG PERFORMANCE The analog performance

FOMs of the GNR-FET device are discussed in this section. The parameters investigated and analyzed here are as follows: the transconductance (_g__m_), transconductance generation factor

(TGF), output resistance (_r__0_), and intrinsic gain (_A__V_). The parameters _g__m_ and TGF are expressed as follows: $${g}_{m}= \frac{\partial {I}_{D}}{\partial {V}_{GS}}$$ (4)

$$TGF=\frac{{g}_{m}}{{I}_{D}}$$ (5) Figure 7 depicts the changes in _g__m_ concerning_ V__GS_, where it is observed that initially _g__m_ increases rapidly with gate voltage and finally

appears to peak and then decreases. This rising and falling tendency in _g__m_ is due to the _I__D_ variation of the device with _V__GS_. It is evident that the device with UL = 6-nm has a

lower _g__m_. It is because of degraded mobility in the channel due to increased channel resistance with UL engineering. The TGF is another crucial factor for analog applications. The

concept of TGF refers to the effective utilization of drain current in achieving a desirable _g__m_ value. A higher TGF value suggests that the device is well-suited for low-power amplifier

designs. Figure 7 depicts the variation of TGF with respect to _V__GS_. It is observed from Fig. 7 that the TGF curve improves with UL structure at low _V__GS_, although there is no

substantial improvement with high _V__GS_. Moreover, the maximum value of TGF is obtained with the UL = 6-nm structure due to the lower _I__D_ in the GNR-FET with the UL effect. The

intrinsic gain (_A__V_) is another significant FOM for analog operation. The _A__V_ should be as high as possible for optimal analog performance. The _A__V_ can be defined and calculated as

follows: $${A}_{V}= {g}_{m}{r}_{0}$$ (6) It is clear from the above equation that _A__V_ depends on the device’s _r__0_ and _g__m_. Thus, understanding the variation of _r__0_ is required

before studying _A__V_. It is observed from Fig. 8 that _r__0_ increases with UL engineering. This is due to the enlargement in channel resistance with underlap length. As the channel

resistance increases, the conductivity of the channel decreases. As a result, _r__0_ increases with underlap length. Figure 8 depicts the effect of underlap engineering on _A__V_. It is

evident from Fig. 8 that initially _A__V_ increases, eventually appears at peak value, and then decreases. The initial rise in _A__V_ can be attributed to the dominance of _g__m_ over

_r__0_. As the gate voltage increases, the value of _g__m_ approaches a constant value for shorter period of _V__GS_, after which it decreases, while _r__0_ keeps decreasing, leading to a

Bell-shaped _A__V_ curve. RF PERFORMANCE To evaluate the effectiveness and feasibility of underlap on RF applications of devices, two essential RF FOMs; gate capacitance (_C__G_), and

cut-off frequency (_f__T_) are analyzed in this section. The _C__G_ of a device is an essential FOM for with RF applications. The _C__G_ of a device can be calculated as the ratio between

the change in charge carrier concentration and the change in _V__GS_. The variation of _C__G_ with respect to _V__GS_ and underlap effect is shown in Fig. 9, and it is observed that with the

introduction of underlap effect, the gate capacitance of the device rises. The peak value of _C__G_ without UL mechanism is observed as 1.46 fF, whereas, with UL engineering of 6-nm, the

maximum value of capacitance is 2.25 fF. One of the crucial factors in determining a device’s RF performance is the cut-off frequency (_f__T_). The frequency at which the current gain is

equal to 0-dB is known as _f__T_. The _f__T_ is calculated by the following expression: $${f}_{T}={g}_{m}/2\pi {C}_{G}$$ (7) Figure 10 shows the _f__T_ variation with _I__D_ for GNR-FET

devices. According to Eq. (7), the _f__T_ depends on _g__m_ to _C__G_ ratio; And the GNR-FETs with UL structure has a smaller value of _g__m_ and a larger value of _C__G_. Hence, it is

obvious that _f__T_ will decrease in devices with UL mechanism compared to a device with no underlap effect. In the design of analog circuits, achieving a balance between device efficiency,

bandwidth, and intrinsic gain is a critical factor. Trade-off analysis can be utilized to identify the optimal operating point by examining several metrics, including the gain frequency

product (GFP) and gain transconductance frequency product (GTFP). GFP, which is calculated as GFP = (\({g}_{m}{r}_{0}\))_ f__T_, is a significant property for operational amplifiers employed

in high-frequency applications40. Figure 11 depicts GFP variation with _V__GS_. The underlap effect produces the maximum value of GFP, while at low and high _V__GS_, the GFP with no

underlap effect has a higher value. However, to determine the best operating point for analog circuits, it is more critical to consider how device efficiency, inherent gain, and frequency

can be traded off. As a result, GTFP is evaluated. A higher GTFP value enables the circuit designer to adjust gain, transconductance, and cut-off frequency to achieve the optimal operating

region41. The GTFP is defined as the product of GFP and TGF. Figure 12 shows the variation of GTFP with _V__GS_. It is observed that the GTFP value is highest for the GNR-FET device with

underlap engineering, due to its higher transistor efficiency and output resistance. IMPACT OF SYMMETRIC UNDERLAP LENGTH In this section, we analyze the impact of symmetric underlap length

on the transfer characteristics of the device and compare it with the optimized asymmetric Source/Drain extension. Specifically, we consider the optimized asymmetric underlap length as UL = 

6-nm and a symmetric underlap of 6-nm for our comparison. Figure 13 illustrates the impact of asymmetric underlap (UL) length and symmetric underlap (SUL) length on the _I__D_ concerning the

_V__GS_ of GNR-FETs. It is evident from Fig. 13 that the drive current decreases, while the off-current increases considerably in SUL 6-nm compared to UL 6-nm underlap. This is due to the

significant influence of series resistance in the region of operation. In a SUL DG FET, there exists a swapping between on-current and fringing capacitance. While utilizing the underlap

engineering can decrease parasitic capacitance, it also results in higher source/drain resistances30. To make it viable for system-on-chip applications, where analog and digital circuits

coexist on the same integrated circuit, efforts should be directed towards identifying the optimized device with the highest on–off current ratio. LINEARITY ANALYSIS Linearity is a crucial

requirement in RF applications42. To achieve a distortion-free output signal with minimal intermodulation and higher-order harmonics, MOS devices with high linearity are essential.

Non-linearity in this context is typically associated with higher-order transconductance, representing higher-order derivatives of a transistor’s transfer characteristics. In this study,

several metrics, namely _g__m2_, _g__m3_, VIP2 and IIP343 are used to assess RF linearity of an asymmetric underlap length near the channel-drain junction, and compare it with the device

without underlap. We will begin by focusing on the impact of higher-order transconductance FOMs, specifically _g__m2_ and _g__m3_, which can introduce non-linearity by interfering with the

fundamental frequency. To address this non-linearity, _g__m3_ is considered the dominant parameter compared to _g__m2_. The even-order harmonics in circuits can be effectively mitigated

through balanced topologies, making the impact of _g__m2_ manageable in maintaining high linearity. On the contrary, _g__m3_ proves to be highly unpredictable, thus imposing lower limits on

distortion. Consequently, minimizing the amplitudes of _g__m2_ and _g__m3_ to the greatest extent possible is crucial to achieving high linearity in RF applications. The transconductance of

the second order (_g__m2_) and the transconductance of the third order (_g__m3_). The _g__m2_ and _g__m3_ are determined as Ref.44: $${g}_{m2} = \frac{\partial {g}_{m1}}{\partial {V}_{GS}}$$

(8) $${g}_{m3} = \frac{\partial {g}_{m2}}{\partial {V}_{GS}}$$ (9) If a device has a greater peak value of _g__mn_ at a lower _V__GS_ compared to another device, it is considered to have

better linearity45. Figure 14 displays the variation of _g__m2_, while Fig. 15 depicts the variation of _g__m3_ with _V__GS_ for GNR-FET devices under study. It is interesting to note from

Figs. 14 and 15 that conventional and UL GNR-FET devices have first peak values of _g__m2_ and _g__m3_ at the same _V__GS_. Therefore, in order to determine the device with the best

linearity among those under consideration, further investigation of linearity parameters such as VIP2 and IIP3 is required. VIP2 is utilized to evaluate distortion characteristics based on

dc parameters. Improved linearity performance and reduced distortion operation are attained with higher values of VIP2 and IIP3. The IIP3 represents the input power level at which

extrapolation results in the first-order power being equal to the third-order power. Having a high IIP3 value allows for enhanced linearity performance operation. The VIP2 and IIP3 is given

by Refs.42,43: $$VIP2=4*\frac{{g}_{m1}}{{g}_{m3}}$$ (10) $$IIP3=\frac{2}{3 {g}_{m3}}\frac{{g}_{m1}}{{R}_{S}}$$ (11) where RS represents source resistance. For most RF applications, RS = 50 Ω

is considered. The variation of VIP2 with _V__GS_ is shown in Fig. 16. It can be observed from the figure that the device without underlap architecture exhibits a higher VIP2 value when

compared to the UL design. Figure 17 shows the variation of IIP3 as a function of _V__GS_. It is observed from Fig. 17 that the device without UL engineering has the maximum value of IIP3.

Therefore, the GNR FET without UL structure is more linear in compared to the GNT FET devices with underlap architecture. CONCLUSION In this study, the optimization of the underlap length

and the comparative analysis of analog and RF FOMs for the GNR-FET device is performed. The study examines the impact of underlap structure on the drain side of the GNR channel in analog and

RF applications, comparing it to an ideal device without underlap in the GNR channel. The optimized device with underlap structure demonstrates notable enhancements, including a 102%

increase in _I__ON__/I__OFF_ ratio and a 12.33% decrease in DIBL compared to the conventional GNR-FET device without underlap. Similarly, GNR-FETs with underlap structures exhibit a 38.49%

increase in TGF and a 54.32% increase in intrinsic gain compared to conventional GNR-FET devices. The results also highlight significant changes in RF performance metrics, with a 53.41%

increase in gate capacitance, a 11.48% increase in GFP, and an 22.78% increase in GTFP. However, the cut-off frequency of the GNR-FETs is reduced by 43.3% compared to the ideal GNR-FET

device. Therefore, underlap engineering in GNR-FETs is particularly advantageous for analog circuit applications where high transistor efficiency (TGF), gain, GFP, and GTFP are of primary

importance. This approach enables a balance of device efficiency, gain and frequency, making it well-suited for medium to high-frequency applications. However, for RF performance and

stability, the device without underlap is preferable. Consequently, the discussed parameters exhibit high sensitivity to the underlap structure of GNR-FETs, and the underlap mechanism can be

utilized to regulate the performance of double-gate GNR-FETs based on specific application requirements. DATA AVAILABILITY The data that support the findings of this study are available

from the corresponding author, [[email protected]], upon reasonable request. REFERENCES * Ferain, I., Colinge, C. A. & Colinge, J. P. Multigate transistors as the future of classical

metal–oxide–semiconductor field-effect transistors. _Nature_ 479, 310–316. https://doi.org/10.1038/nature10676 (2011). Article  ADS  PubMed  CAS  Google Scholar  * Assad, F., Ren, Z.,

Vasileska, D., Datta, S. & Lundstrom, M. On the performance limits for Si MOSFETs: A theoretical study. _IEEE Trans. Electron Devices_ 47, 232–240. https://doi.org/10.1109/16.817590

(2000). Article  ADS  CAS  Google Scholar  * Rawat, A., Gupta, A. K. & Rawat, B. Performance projection of 2-D material-based CMOS inverters for sub-10-nm channel length. _IEEE Trans.

Electron Devices_ 68, 3622–3629. https://doi.org/10.1109/TED.2021.3072880 (2021). Article  ADS  CAS  Google Scholar  * F. D’Agostino, D. Quercia, Short-Channel Effects in MOSFETs,

Introduction to VLSI design (EECS 467), 2000. * Anvarifard, M. K. & Nirmal, D. Creation of step-shaped energy band in a novel double-gate GNRFET to diminish ambipolar conduction. _IEEE

Trans. Electron Devices_ 68, 2549–2555. https://doi.org/10.1109/TED.2021.3069442 (2021). Article  ADS  CAS  Google Scholar  * Novoselov, K. S. _et al._ Electric field effect in atomically

thin carbon films. _Science_ 306, 666–669. https://doi.org/10.1126/science.1102896 (2004). Article  ADS  PubMed  CAS  Google Scholar  * Geim, A. K. N. & Novoselov, K. S. The rise of

graphene. _Nat. Mater._ 6, 183–191. https://doi.org/10.1038/nmat1849 (2007). Article  ADS  PubMed  CAS  Google Scholar  * Rumyantsev, S. _et al._ Electrical and noise characteristics of

graphene field-effect transistors: Ambient effects and noise sources. _J. Phys. Condens. Matter_ 22, 395302. https://doi.org/10.1088/0953-8984/22/39/395302 (2010). Article  PubMed  CAS 

Google Scholar  * Palacios, T., Hsu, A. & Wang, H. Applications of graphene devices in RF communications. _IEEE Commun. Mag._ 48, 122–128. https://doi.org/10.1109/MCOM.2010.5473873

(2010). Article  Google Scholar  * Schwierz, F. Graphene transistors. _Nat. Nanotechnol._ 5, 487–496. https://doi.org/10.1038/nnano.2010.89 (2010). Article  ADS  PubMed  CAS  Google Scholar

  * Du, X. _et al._ Approaching ballistic transport in suspended graphene. _Nat. Nanotechnol._ 3, 491–495. https://doi.org/10.1038/nnano.2008.199 (2008). Article  ADS  PubMed  CAS  Google

Scholar  * Kim, S. _et al._ Realization of a high mobility dual-gated graphene field effect transistor with Al2O3 dielectric. _Appl. Phys. Lett._ 94, 062107.

https://doi.org/10.1063/1.3077021 (2009). Article  ADS  CAS  Google Scholar  * Novoselov, K. S. _et al._ Two-dimensional gas of massless Dirac fermions in graphene. _Nature_ 438, 197–200.

https://doi.org/10.1038/nature04233 (2005). Article  ADS  PubMed  CAS  Google Scholar  * Rawat, B. & Paily, R. Performance evaluation of bilayer graphene nanoribbon tunnel FETs for

digital and analog applications. _IEEE Trans. Nanotechnol._ 16, 411–416. https://doi.org/10.1109/TNANO.2017.2675939 (2017). Article  ADS  CAS  Google Scholar  * Banadaki, Y. M. &

Srivastava, A. Investigation of the width-dependent static characteristics of graphene nanoribbon field effect transistors using non-parabolic quantum-based model. _Solid-State Electron._

111, 80–90. https://doi.org/10.1016/j.sse.2015.05.003 (2015). Article  ADS  CAS  Google Scholar  * Wang, X. _et al._ Electrically configurable graphene field effect transistor with a graded

potential gate. _Nano Lett._ 15, 3212–3216. https://doi.org/10.1021/acs.nanolett.5b00396 (2015). Article  ADS  PubMed  CAS  Google Scholar  * Saremi, M. _et al._ Modeling of lightly doped

drain and source graphene nanoribbon field effect transistors. _Superlattices Microstruct._ 60, 67–72. https://doi.org/10.1016/j.spmi.2013.04.013 (2013). Article  ADS  CAS  Google Scholar  *

Tamersit, K. Performance enhancement of an ultra-scaled double-gate graphene nanoribbon tunnel field-effect transistor using channel doping engineering: Quantum simulation study. _Int. J.

Electron. Commun. (AEÜ)_ 122, 153287. https://doi.org/10.1016/j.aeue.2020.153287 (2020). Article  Google Scholar  * Anvarifard, M. K., Ramezani, Z. & Amir Ghoreishi, S. A ballistic

transport nanodevice based on graphene nanoribbon FET by enhanced productivity for both low-voltage and radio-frequency scopes. _ECS J. Solid State Sci. Technol._ 11, 061008.

https://doi.org/10.1149/2162-8777/ac77ba (2022). Article  ADS  Google Scholar  * Eshkalak, M. A., Faez, R. & Haji-Nasiri, S. A novel graphene nanoribbon field effect transistor with two

different gate insulators. _Physica E Low-Dimensional Syst. Nanostruct._ 66, 133–139. https://doi.org/10.1016/j.physe.2014.10.021 (2015). Article  ADS  CAS  Google Scholar  * Maedeh Akbari,

E. & Anvarifard, M. K. A novel graphene nanoribbon FET with an extra peak electric field (EFP-GNRFET) for enhancing the electrical performances. _Phys. Lett. A_ 381, 1379.

https://doi.org/10.1016/j.physleta.2017.02.032 (2017). Article  ADS  CAS  Google Scholar  * Ouyang, Y., Yoon, Y. & Guo, J. Scaling behaviors of graphene nanoribbon FETs: A

three-dimensional quantum simulation study. _IEEE Trans. Electron Devices_ 54, 2223–2231. https://doi.org/10.1109/TED.2007.902692 (2007). Article  ADS  CAS  Google Scholar  * Mencarelli, D.

& Pierantoni, L. Analysis of the metal work function dependence of charge transfer in contacted graphene nanoribbons. _Nanomat. Nanotech._ 2, 1. https://doi.org/10.5772/54995 (2012).

Article  CAS  Google Scholar  * Ramezani, Z. & Ali, A. O. Dual metal gate tunneling field effect transistors based on MOSFETs: A 2-D analytical approach. _Superlattices Microstruct._

113, 41–56. https://doi.org/10.1016/j.spmi.2017.09.042 (2018). Article  ADS  CAS  Google Scholar  * Chang, S. _et al._ Effects of vacancy defects on graphene nanoribbon field effect

transistor. _Micro Nano Lett._ 8, 816–821. https://doi.org/10.1049/mnl.2013.0457 (2013). Article  CAS  Google Scholar  * Tamersit, K., Ramezani, Z. & Amiri, I. S. Improved performance of

sub-10-nm band-to-band tunneling n-i-n graphene nanoribbon field-effect transistors using underlap engineering: A quantum simulation study. _J. Phys. Chem. Solids_ 160, 110312.

https://doi.org/10.1016/j.jpcs.2021.110312 (2022). Article  CAS  Google Scholar  * Trivedi, V. P. & Fossum, J. G. Nanoscale FinFETs with gate–source/drain underlap. _IEEE Trans. Electron

Devices_ 52, 56–62. https://doi.org/10.1109/TED.2004.841333(410) (2005). Article  ADS  Google Scholar  * Bansal, A., Paul, B. C. & Roy, K. Modeling and optimization of fringe

capacitance of nanoscale DGMOS devices. _IEEE Trans. Electron Devices_ 52, 256–262. https://doi.org/10.1109/TED.2004.842713 (2005). Article  ADS  CAS  Google Scholar  * Sachid, A. _et al._

Gate fringe-induced barrier lowering in underlap FinFET structures and its optimization. _IEEE Electron Device Lett._ 29, 128–130. https://doi.org/10.1109/LED.2007.911974 (2008). Article 

ADS  CAS  Google Scholar  * Koley, K. _et al._ Subthreshold analog/RF performance of underlap DG FETs with asymmetric source/drain extensions. _Microelectron. Reliab._ 52, 2572–2578.

https://doi.org/10.1016/j.microrel.2012.06.110 (2012). Article  Google Scholar  * Son, Y.-W. _et al._ Energy gaps in graphene nanoribbons. _Phys. Rev. Lett._ 97, 216803.

https://doi.org/10.1103/PhysRevLett.97.216803 (2006). Article  ADS  PubMed  CAS  Google Scholar  * Fiori, G. & Iannaccone, G. Simulation of graphene nanoribbon field-effect transistors.

_IEEE Electron Device Lett._ 28, 760–762. https://doi.org/10.1109/LED.2007.901680 (2007). Article  ADS  CAS  Google Scholar  * Sako, R., Hosokawa, H. & Tsuchiya, H. Computational study

of edge configuration and quantum confinement effects on graphene nanoribbon transport. _IEEE Electron Device Lett._ 32, 6–8. https://doi.org/10.1109/LED.2010.2086426 (2011). Article  ADS 

CAS  Google Scholar  * NanoTCAD ViDES, March, 2022. http://vides.nanotcad.com/vides. * T. K. Agarwal, Device-circuit co-design of 2D material based devices for future electronics, ARENBERG

DOCTORAL SCHOOL Faculty of Engineering Science, (2018). * Lovarelli, G., Calogero, G., Fiori, G. & Iannaccone, G. Multiscale pseudoatomistic quantum transport modeling for van der Waals

heterostructures. _Phys. Rev. Appl._ 18, 034045. https://doi.org/10.1103/PhysRevApplied.18.034045 (2022). Article  ADS  CAS  Google Scholar  * Datta, S. Nanoscale device modeling: The

Green’s function method. _Superlattice Microstruct._ 28, 253–278. https://doi.org/10.1006/spmi.2000.0920 (2000). Article  ADS  CAS  Google Scholar  * Nazari, A., Faez, R. & Shamloo, H.

Modeling comparison of graphene nanoribbon field effect transistors with single vacancy defect. _Superlattices Microstruct._ 97, 28–45. https://doi.org/10.1016/j.spmi.2016.06.008 (2016).

Article  ADS  CAS  Google Scholar  * Yoon, Y. _et al._ Performance comparison of graphene nanoribbon FETs with Schottky contacts and doped reservoirs. _IEEE Trans. Electron Devices_ 55,

2314–2323. https://doi.org/10.1109/TED.2008.928021 (2008). Article  ADS  CAS  Google Scholar  * Mohapatra, S. K. _et al._ The performance measure of GS-DG MOSFET: An impact of metal gate

work function. _Nanosci. Nanotechnol._ 5, 025002. https://doi.org/10.1088/2043-6262/5/2/025002 (2014). Article  CAS  Google Scholar  * Pratap, Y. _et al._ Performance evaluation and

reliability issues of junctionless CSG MOSFET for RFIC design. _IEEE Trans. Device Mater. Reliab._ 14, 418–425. https://doi.org/10.1109/TDMR.2013.2296524 (2014). Article  CAS  Google Scholar

  * Kaya, S. Wei Ma, optimization of RF linearity in DG-MOSFETs. _IEEE Electron Device Lett._ 25, 308–310. https://doi.org/10.1109/LED.2004.826539 (2004). Article  ADS  CAS  Google Scholar 

* Kumar, S. P. _et al._ Device linearity and intermodulation distortion comparison of dual material gate and conventional AlGaN/GaN high electron mobility transistor. _Microelectron.

Reliab._ 53, 587–596. https://doi.org/10.1016/j.microrel.2010.09.033 (2011). Article  CAS  Google Scholar  * Kondekar, P. N. _et al._ Design and analysis of polarity controlled electrically

doped tunnel FET with bandgap engineering for analog/RF applications. _IEEE Trans. Electron Devices_ 64, 412–418. https://doi.org/10.1109/TED.2016.2637638 (2017). Article  ADS  CAS  Google

Scholar  * Tripathy, M. R. _et al._ III-V/Si staggered heterojunction based source-pocket engineered vertical TFETs for low power applications. _Superlattices Microstruct._ 142, 106494.

https://doi.org/10.1016/j.spmi.2020.106494 (2020). Article  CAS  Google Scholar  Download references AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Electronics Engineering, IIT

Dhanbad, Dhanbad, 826004, India Md Akram Ahmad & Jitendra Kumar Authors * Md Akram Ahmad View author publications You can also search for this author inPubMed Google Scholar * Jitendra

Kumar View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS M.A.A.: Analysis, Writing- original draft. J.K.: Conceptualization, Supervision.

CORRESPONDING AUTHOR Correspondence to Md Akram Ahmad. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a

Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit

to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are

included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons

licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of

this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Ahmad, M.A., Kumar, J. The understanding of the impact of

efficiently optimized underlap length on analog/RF performance parameters of GNR-FETs. _Sci Rep_ 13, 13872 (2023). https://doi.org/10.1038/s41598-023-40711-7 Download citation * Received: 28

May 2023 * Accepted: 16 August 2023 * Published: 24 August 2023 * DOI: https://doi.org/10.1038/s41598-023-40711-7 SHARE THIS ARTICLE Anyone you share the following link with will be able to

read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing

initiative