ABSTRACT This paper aims to increase the Unmanned Aerial Vehicle's (UAV) capacity for target tracking. First, a control model based on fuzzy logic is created, which modifies the

UAV's flight attitude in response to the target's motion status and changes in the surrounding environment. Then, an edge computing-based target tracking framework is created. By

deploying edge devices around the UAV, the calculation of target recognition and position prediction is transferred from the central processing unit to the edge nodes. Finally, the latest

Vision Transformer model is adopted for target recognition, the image is divided into uniform blocks, and then the attention mechanism is used to capture the relationship between different

the traditional proportional-integral-derivative (PID) method, from 5.2 s of the traditional PID to 4.2 s. The average tracking error is reduced by 15%, from 0.8 m of traditional PID to 0.68

 m. Meanwhile, in the case of environmental change and target motion change, this algorithm shows better robustness, and the fluctuation range of tracking error is only half of that of

traditional PID. This shows that the fuzzy logic control theory is successfully applied to the UAV target tracking field, which proves the effectiveness of this method in improving the

target tracking performance. SIMILAR CONTENT BEING VIEWED BY OTHERS OPTIMAL FUZZY-PID CONTROLLER DESIGN FOR OBJECT TRACKING Article Open access 08 April 2025 BINOCULAR STEREO VISION-BASED

RELATIVE POSITIONING ALGORITHM FOR DRONE SWARM Article Open access 27 January 2025 AN EFFICIENT VISUAL SERVO TRACKER FOR HERD MONITORING BY UAV Article Open access 07 May 2024 INTRODUCTION

Unmanned Aerial Vehicle (UAV) is leading innovations in many fields1,2,3. From military to civilian, from environmental monitoring to search and rescue, UAV has become a multifunctional

tool, providing unprecedented convenience and opportunities for people4. In this potential field, UAV target tracking, as one of the key issues, has received extensive attention5,6,7. Its

possible applications include help managing resources and responding to disasters, as well as increasing the effectiveness with which military missions are carried out8. However, with the

diversification of UAV application scenarios and the constant change of target environment, the existing control methods and tracking algorithms are facing increasingly severe

challenges9,10. In the field of UAV target tracking, the traditional proportional-integral-derivative (PID) control method, as one of the most used control methods, has achieved remarkable

success in some scenes, but its coping ability in complex and uncertain environments is gradually limited11,12,13. Traditional PID control methods are usually based on the linear model of

the target system, which performs well in some simple cases14. However, with the increasing complexity and diversity of the target environment, it is often difficult for linear models to

accurately describe the dynamic characteristics of real systems, which leads to the lack of adaptability of traditional PID controllers15. The standard PID technique may result in

significant performance fluctuation and even instability when it is necessary to swiftly adjust to changes in the environment and target motion16,17,18. In addition, target recognition and

position prediction, as the key links to achieve efficient target tracking, are also facing great challenges19. With the expansion of UAV application field, the target may have more

diversity, and there may be problems such as occlusion and illumination change, which makes target recognition more complicated20,21,22. Meanwhile, the accurate prediction of the target

position requires more efficient algorithms to meet the requirements of real-time and accuracy while ensuring the tracking accuracy23. Traditional prediction methods are often difficult to

deal with uncertainty and nonlinearity, which further limits the performance of target tracking. In order to address the above issues, a control model based on fuzzy logic is created that

may dynamically modify the flight attitude of the UAV in response to the target's motion state and environmental changes, leading to more adaptable and reliable target tracking. In

addition, the concept of edge computing is introduced. By deploying edge devices around the UAV, the calculation of target recognition and position prediction is transferred from the central

processing unit to the edge nodes to reduce the calculation load and improve the real-time performance. In order to realize accurate target recognition, the latest Vision Transformer model

is adopted to divide the image into uniform blocks, and the attention mechanism is used to capture the relationship between different blocks, thus realizing real-time image analysis. In this

paper, a key algorithm of Visual Attention Converter Model is adopted for target recognition. The model divides the image into uniform blocks and captures the relationship among different

blocks by using attention mechanism, thus realizing real-time image analysis, thus achieving excellent performance in target recognition. The structure of the model includes the following

steps: CNN extracts the feature representation of the image, generates a query vector to ask questions about the block, generates a key vector to identify the important information of the

block, and converts the feature representation into a value vector containing the feature information of the block. Through the query and the calculation of attention weight matrix of key

sum, the relationship among different blocks is determined, and the feature representations of each block are weighted and merged, and finally sent to the classifier for target

classification and recognition. This model can focus on the part related to the target in the image and improve the accuracy of target recognition. In addition, the position prediction

method based on particle filter algorithm is also adopted. In this algorithm, in the initial stage of particle swarm optimization, a group of particles are randomly generated, each particle

represents the possible target position, and then the state of each particle is updated according to the motion model of the target to reflect the change of the current position of the

target. Through the measurement updating stage, the weights of particles are updated by using sensor data or other measurement information to make them more in line with the actual

measurement values. Finally, the weights are normalized and resampled to get the final target position estimation. The algorithm can combine historical data and real-time sensor information,

gradually adjust the particle distribution, and estimate the target position more accurately, which is very effective for dealing with nonlinear motion models and environmental changes.

This paper has made innovative progress in the field of UAV target tracking. Firstly, a target tracking algorithm based on fuzzy logic control is proposed. By introducing type II fuzzy logic

control, the upper and lower fuzzy controllers are successfully constructed, thus reducing the computational complexity. Compared with the traditional control method, the algorithm is

superior in dealing with complex and fuzzy inputs, and improves the robustness of the system to uncertainty. Secondly, the edge computing framework is innovatively integrated. By performing

tasks such as image processing, target detection and position prediction on edge devices, the computational burden of the central processing unit is effectively reduced, and the response

speed of the system to target changes is improved. Although the introduction of edge computing framework may bring some system complexity, experiments show that this method significantly

reduces the execution time of the algorithm and provides a feasible solution for the real-time performance of UAV target tracking. In addition, the visual attention conversion model is

introduced and applied to target recognition. Through the application of image segmentation and attention mechanism, the real-time analysis of the target-related areas is successfully

realized, the accuracy of target recognition is improved, and a relatively low computational complexity is maintained. This provides more accurate target recognition support for UAV target

tracking. Most importantly, the performance of the proposed method in different scenarios and wind speed conditions is fully verified in the experiment. By comparing the traditional PID

algorithm, CNN, DQN and MPC, it is proved that the algorithm proposed in this paper has achieved remarkable advantages in average target acquisition time, average tracking error and

robustness. This series of innovations makes this paper have important theoretical and practical value in improving the real-time performance of UAV target tracking. LITERATURE REVIEW The

widespread use of UAV technology in numerous industries has advanced noticeably in recent years. Among them, Siyal et al.24 developed and tested a model for UAV target tracking. Chen et

al.25 described the importance of visual management to the risk management of UAV project. The study by Chinthi-Reddy et al.26 changed the privacy paradigm from safeguarding users and

restricted areas from malicious UAV to safeguarding and hiding the sensitive information of UAV, and three privacy protection target tracking strategies based on shortest path, random

location, and virtual location were suggested. Upadhyay et al.27 proposed a unique collaborative method based on computer vision, which was used to track the target according to the specific

position of interest in the image. This method provides users with free choice to track any target in the image and form a formation around it, which improves the tracking accuracy of UAV.

Birds and UAVs both have innate flight mechanisms and behavioural patterns, according to Liu et al.28. In this study, a target classification approach was put forth using the radar

trajectory to derive the target motion features. The suggested method's efficacy was confirmed by the real bird surveillance radar system installed in the airport area, which was used

to categorize targets in the new feature space using the random forest model. A real-time UAV tracking system was suggested by Hong et al.29 that employed a 5G network to send UAV monitoring

photos to the cloud and a machine learning algorithm to detect and track numerous targets. This study modified the network topology of the target detector YOLO4 to address the challenges in

UAV identification and tracking, and it achieved a tracking accuracy of 35.69%. Dogru & Marques30 proposed a ground air target detection system using lidar, which relied on sparse

detection instead of dense point clouds, and its purpose was not only to detect, but also to estimate their motion and actively track. Qamar et al.31 proposed an autonomous method using deep

reinforcement learning for group navigation. Meanwhile, a new island policy optimization model was introduced to deal with multiple dynamic targets, making the group more dynamic. In

addition, a new reward function for robust group formation and target tracking was designed to learn complex group behavior. In the research of UAV target tracking, many methods have been

proposed and verified in practical application. But there are still some limitations and unresolved problems. Firstly, the performance fluctuation and lack of adaptability of traditional PID

control method in complex environment limit its effect in practical application. Secondly, the target recognition algorithm is difficult to maintain stable recognition performance in

various complex scenes, which affects the stability of the whole tracking process. Thirdly, the existing methods of position prediction are not satisfactory in the face of uncertainty, and

more efficient algorithms are needed to improve the prediction accuracy. In order to fill these gaps, this paper adopts fuzzy logic control theory and combines it with advanced technologies

such as edge calculation, visual attention converter model and particle filter algorithm. RESEARCH METHODOLOGY DESIGN OF FUZZY LOGIC CONTROL MODEL The movement state of the target and the

change of the environment have an important influence on the control of the flight attitude of the UAV. The advantage of fuzzy logic control is that it can handle fuzzy input and output and

realize more accurate control strategy. In this paper, a control model based on fuzzy logic is proposed, and an interval II fuzzy controller is adopted to realize the precise control of the

flight attitude of unmanned aerial vehicle (UAV). Compared with the traditional PID control method, the fuzzy controller can handle the fuzzy input and output more flexibly to realize a more

accurate control strategy. Traditional PID control relies on a set of fixed proportional, integral and differential gains, which makes it less adaptable to the target movement and dynamic

changes of the environment. On the contrary, the interval type II fuzzy controller proposed in this paper dynamically adjusts its control strategy according to fuzzy input, which can make

more flexible and detailed control decisions. In addition, the traditional PID method often faces difficulties when the target moves at high speed and the motion mode changes suddenly. In

this paper, the experimental results of different scenarios (Section "Experimental process") show that the fuzzy logic control model is superior to the traditional PID method in

average target capture time and tracking error, highlighting its superiority in dealing with complex situations. The moving state of the target and the shifting environment have a

significant impact on how an UAV controls its flight attitude. The advantage of fuzzy logic control is that it can deal with fuzzy input and output to realize more accurate control strategy.

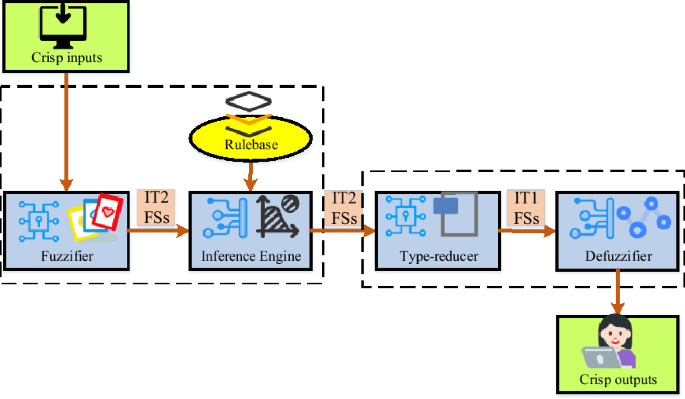
Type II fuzzy logic controller (control flow is shown in Fig. 1), as a method to realize control decision in fuzzy and uncertain environment, consists of five key parts (fuzzy controller,

rule base, reasoning engine, reducer and defuzzifier), and each part plays an important role. Among them, the input of fuzzy controller is the relative distance between the target center and

the image center, and the output is the yaw angle of UAV. In the UAV target tracking system, the upper interval II fuzzy controller and the lower speed fuzzy controller cooperate with each

other to realize the accurate control of UAV yaw angle and speed. The upper controller pays attention to the yaw angle of UAV to ensure that the direction of UAV is consistent with the

target direction; The lower speed fuzzy controller is responsible for controlling the forward speed of UAV in order to track the target at an appropriate speed and keep the correct

direction. The outputs of these two controllers are yaw angle and speed control commands, which are used by UAV to realize real-time tracking of ground moving targets. The relative distance

between the target center and the image center is used as input to build IT2 in the UAV target tracking system developed in this paper due to the relatively straightforward computation of

interval type II fuzzy control theory. The frame diagram for the designed interval type II fuzzy controller for UAV is shown in Fig. 2. In the UAV target tracking system of Fig. 2, the upper

interval type II fuzzy controller and the lower velocity fuzzy controller cooperate with each other to realize the accurate control of the yaw angle and velocity of the UAV. This control

strategy enables UAV to track moving targets on the ground efficiently. The upper interval type II fuzzy controller focuses on controlling the yaw angle of the UAV to ensure that the

orientation of the UAV is consistent with the target direction. At the same time, the lower speed controller is responsible for controlling the forward speed of the UAV. The output of the

upper controller is the yaw angle, which guides the flight attitude of the UAV in order to aim at the target correctly. The lower speed fuzzy controller controls the speed of the UAV so that

it can track the target at an appropriate speed while maintaining the correct orientation. The output of the speed controller is the speed command of the UAV, which adjusts the power system

of the UAV to achieve the accuracy and stability of target tracking. These two controllers output yaw angle and speed control commands, which the UAV uses to track the moving target on the

ground in real time. However, the UAV must return to the image feedback phase after completing the control instructions in order to guarantee the tracking accuracy. The controller's

input is the difference in the target position coordinates from the image's center point. This offset reflects the position of the target relative to the center and provides the

controller with the knowledge of the target position. In this way, the whole system forms a closed-loop control loop, and the UAV constantly adjusts according to the feedback information,

thus realizing the continuous tracking of the ground moving target. Fuzzy sets and fuzzy logic rules in fuzzy control are used to determine the yaw angle and speed control strategy of UAV

according to the fuzzy values of inputs (\(\Delta x\) and \(\Delta y\)). For example, fuzzy set E corresponds to the fuzzy set of horizontal offsets \(\Delta x\), while fuzzy sets F and G

correspond to the fuzzy sets of yaw angle and speed, respectively. Fuzzy logic rules are designed based on practical experience and control requirements, and the yaw angle and speed control

strategy of the output are determined according to the input fuzzy values. Through these fuzzy rules, the flight attitude of UAV can be accurately controlled to effectively track the moving

target on the ground. Among them, fuzzification is a technology that maps real and accurate physical values to fuzzy sets. In this way, fuzzy controllers can better deal with uncertainties.

In this system, the upper branch controller pays attention to the yaw angle of the UAV. Its input is the horizontal offset ∆x between the target center and the image center, and its output

is the yaw angle Yaw of the UAV. At the same time, the lower speed fuzzy controller controls the speed of the UAV. Its input is the vertical offset ∆y between the target and the image

center, and its output is the speed v of the UAV. Kx, ky, kyaw and kv represent horizontal and vertical offsets, respectively, and quantization factors of output variables yaw and v. output

variables yaw and v represent the yaw angle and speed of the UAV. These definitions are expressed by equations: $${k}_{x}=\Delta x/{x}_{c}$$ (1) $${k}_{y}=\Delta y/{y}_{c}$$ (2)

$${k}_{yaw}=yaw/\frac{\pi }{3}$$ (3) $${k}_{v}=v/2$$ (4) In fuzzy control, set the relative distance between the target position and the image center as \(\Delta x\), and define the fuzzy

set according to the input and output of fuzzy control. input variables \(\Delta x\) and \(\Delta y\) respectively represent the horizontal and vertical deviations between the target center

and the image center. The fuzzy sets corresponding to the input variables ∆x and ∆y are E = {NB, NS, MM, PS, PB}, which correspond to {negative big, negative small, zero, positive small,

positive big} respectively. For the output variable yaw, the fuzzy set is F = {LB, LS, ZO, RS, RB}, which means {large left turn, small left turn, no rotation, small right turn, and large

right turn}. The fuzzy set of the output variable V is G = {GB, GS, ZO, BS, BB}, corresponding to {fast forward, slow forward, motionless, slow backward, fast backward}. In the control

process, after the UAV executes the control command, it returns to the image feedback step to re-detect the target and obtain the new position coordinates. The offset between the target

position and the image center is used as the input of the controller and enters the closed-loop control loop. The core idea of this system is to track the moving target on the ground in

constant adjustment, and the UAV automatically makes accurate attitude and speed adjustment in actual flight through fuzzy controller. According to the general control experience and mission

requirements of UAV, a set of IT2 system is designed, which contains five key fuzzy rules to control the yaw angle of UAV. The form of fuzzy reasoning is: $${R}^{1}:IF\Delta \;x \;is

\;NB,THEN \;yaw \;is \;LB$$ (5) $${R}^{2}:IF\Delta \;x \;is \;NS,THEN \;yaw \;is \;LS$$ (6) $${R}^{3}:IF\Delta \;x \;is \;MM,THEN \;yaw \;is \;ZO$$ (7) $${R}^{4}:IF\Delta \;x \;is \;PS,THEN

\;yaw \;is \;RS$$ (8) $${R}^{5}:IF\Delta \;x \;is \;PB,THEN \;yaw \;is \;RB$$ (9) The reasoning method of these fuzzy rules is based on practical experience: when the horizontal offset ∆x is

negative, the UAV will perform a left turn. The greater the absolute value of ∆x, the greater the deflection angle of UAV. Similarly, when ∆x is positive, the UAV will turn right. In the

fuzzy control model, a fuzzy inference engine is used to deal with fuzzy logic rules and determine the output yaw angle and speed control commands. According to the input fuzzy values and

fuzzy rules in the rule base, the fuzzy reasoning engine calculates the output fuzzy values through the reasoning process, and converts the fuzzy values into certain control commands through

the defuzzifier. In this way, the fuzzy control model can accurately control the flight attitude of UAV, thus effectively tracking the moving target on the ground. In order to ensure the

stability of the rule base, five rules are also set to adjust the speed of the UAV. These rules are based on the following principles: when the vertical offset ∆y is negative, the UAV will

move forward. The greater the absolute value of ∆y, the faster the speed of the UAV. The specific expression of these rules is as follows: $${R}^{1}:IF\Delta \;y \;is \;NB,THEN \;v \;is

\;GB$$ (10) $${R}^{2}:IF\Delta \;y \;is \;NS,THEN \;v \;is \;GS$$ (11) $${R}^{3}:IF\Delta \;y \;is \;MM,THEN \;v \;is \;ZO$$ (12) $${R}^{4}:IF\Delta \;y \;is \;PS,THEN \;v \;is \;BS$$ (13)

$${R}^{5}:IF\Delta \;y \;is \;PB,THEN \;v \;is \;BB$$ (14) Equations 10–14 are a series of fuzzy rules adopted by the control logic, which are used to determine the speed control strategy of

the UAV according to the vertical offset (\(\Delta y\)) between the target position and the image center. The concrete expression is as follows: If \(\Delta y\) is NB (negative big), the

velocity \(v\) of UAV is GB (fast forward). This means that when the target is far away from the center of the image and moves down, the UAV will move forward at a faster speed to catch up

with the target. If \(\Delta y\) is NS (negative small), the velocity \(v\) of UAV is GS (slow forward). When the target moves down but deviates less from the center of the image, the UAV

will move forward at a slower speed to track the target properly. If \(\Delta y\) is MM (medium), the velocity \(v\) of UAV is ZO (keep still). When the target is aligned with or very close

to the center of the image, the UAV will remain still to maintain a stable tracking state. If \(\Delta y\) is PS (positive small), the velocity \(v\) of UAV is BS (backward slow). When the

target moves upward but deviates less from the center of the image, the UAV will move backward at a slower speed to adjust the distance from the target appropriately. If \(\Delta y\) is PB

(positive big), then the velocity \(v\) of UAV is BB (quickly backward). This means that when the target moves upward and is far away from the center of the image, the UAV will move backward

at a faster speed to adjust the distance from the target. The inference engine process is described as: $${E}_{\Delta x}\times {E}_{\Delta y}\to F\times G$$ (15) Finally, the fuzzy set

obtained in the descending process is analytically calculated to obtain the determined output value, and the output variables yaw and v are obtained by the central set defuzzification

method. TARGET TRACKING FRAMEWORK BASED ON EDGE COMPUTING In this paper, a target tracking framework based on edge computing is proposed, aiming at improving the accuracy and speed of UAV

target tracking by optimizing the effectiveness of target recognition and position prediction calculation. The goal of the edge computing-based target tracking framework is to increase the

accuracy and speed of UAV target tracking by optimizing the effectiveness of target recognition and position prediction calculations. In Fig. 3, the precise frame structure is displayed. In

Fig. 3, in this framework, the strategy of edge computing is adopted, and some computing tasks are transferred from the central processing unit to the edge devices. The central processing

unit is still responsible for coordinating the overall system and advanced decision-making, while the edge devices are responsible for image processing, target detection and position

prediction. The edge device contains an image sensor, which is used to collect the image data of the flight area. These image data are processed by the target detection module in the edge

device, and the target in the image is identified by advanced target detection algorithm. The identified target information is employed in the position prediction module, which forecasts the

target's position using particle filter and other methods. People can lighten the load on the central processing unit and enhance the response time and real-time performance of the

entire system by doing image processing and location prediction on edge devices. Target tracking operations can be carried out by UAVs more effectively, particularly when a real-time

response is required. Figure 4 depicts the specific target tracking method based on edge computation. In Fig. 4, the process is divided into six steps. First, the UAV is equipped with camera

equipment to obtain image data of the flight area regularly. Then the image data is transmitted to the surrounding edge devices for processing. These edge devices are equipped with

high-performance computing resources, which can process and analyze images in the near field. Edge devices use advanced target detection algorithms to extract target information from images.

This is helpful to identify the position and characteristics of the target quickly and accurately. Then, using particle filter and other algorithms, the edge device predicts the position of

the target based on historical data and sensor information. This provides an important basis for UAV to formulate appropriate control strategy. Finally, the edge equipment generates

corresponding control instructions according to the position and motion state of the target, including yaw angle and speed. The UAV receives the control instructions sent by the edge

equipment and performs corresponding flight actions to track the target. APPLICATION OF VISUAL ATTENTION CONVERTER MODEL IN TARGET RECOGNITION The visual attention conversion model aims to

simulate the working mode of human visual system and improve the accuracy of target recognition by paying attention to important parts in the image. Firstly, the model divides the image into

uniform blocks, and then uses attention mechanism to calculate the relationship between blocks to determine which blocks contain important target information. By weighting and fusing the

features of different blocks, the target recognition of the whole image is finally realized. The schematic diagram of the model is shown in Fig. 5: In Fig. 5, the input image is the image

data acquired by the UAV. The input image is extracted by convolutional neural network (CNN) to get the feature representation of the image. Then the feature representation is transformed to

get the query vector, which is used to ask questions about the block. Similarly, the feature representation is also transformed to get the key vector, which is used to identify the

important information of the block. The feature representation is also converted into a value vector, which contains the feature information of the block. Then the attention weight matrix is

calculated by query, key, and value, which determines the relationship between different tiles. Based on the attention weight, the features of each block are weighted and merged to get the

overall feature representation. The final feature representation is sent to the classifier for target classification and recognition, that is, to judge whether there is a specific target in

the image. This model can focus on the part related to the target in the image and improve the accuracy of target recognition. The input image is represented as \(I\), and the feature

representation of the image is extracted by CNN and other methods. The extracted feature image is divided into \(N\) uniform blocks, and each block is denoted as \({B}_{i}\). The attention

weight of each block \({B}_{i}\) is calculated to determine its importance in the whole image. By using attention mechanism, the characteristics of each block are compared with those of its

surrounding blocks to capture the relationship between different blocks. The calculation formula of attention weight matrix \({A}_{i}\) is as follows:

$${A}_{i}={\text{softmax}}({Q}_{i}{K}_{i}^{T}){V}_{i}$$ (16) \({Q}_{i}\), \({K}_{i}\) and \({V}_{i}\) represent query, key and numerical vector respectively. According to the attention

weight, the features of each block are weighted and fused to get the feature representation of the whole image. This process can be expressed by the following equation:

$${F}_{final}=\sum_{i=1}^{N}{A}_{i}{B}_{i}$$ (17) \({F}_{final}\) is the final feature representation of the whole image. Through this visual attention conversion model, real-time image

analysis can be realized in the target recognition task, and the accuracy of target recognition can be improved. POSITION PREDICTION BASED ON PARTICLE FILTER ALGORITHM Particle filter

algorithm plays a key role in UAV target tracking. Particle filter algorithm is used to predict the target position in this paper, which is a state estimation technology based on Monte Carlo

method. The algorithm randomly samples a group of particles in the state space, and updates the weights of these particles according to the system dynamics model and sensor measurement

information, thus realizing the estimation of the target position. The basic theory of particle filter algorithm is based on Bayesian filtering principle. In the problem of target tracking,

it is hoped to estimate the state of the target based on the previous observation data and the system dynamic model and the new observation data obtained by the sensor. Particle filter

algorithm approximates the posterior probability distribution of target state by randomly sampling a group of particles in state space. These particles represent the possible target states

and are updated and optimized according to the dynamic model of the system to reflect the evolution process of the target states. The measurement information of the sensor is used to correct

the weight of particles, so that the particles consistent with the sensor data have higher weight, thus better estimating the position of the target. The modeling analysis of particle

filter algorithm includes the establishment of system dynamic model and sensor model. The system dynamic model describes the evolution law of the target state with time, which is usually

expressed by the state transition equation. Sensor model describes the error characteristics of sensor measurement and the relationship between target state and sensor observation, which is

usually expressed by observation equation. These models are the key components of particle filter algorithm, which directly affect the performance and accuracy of the algorithm. Figure 6 is

the detailed process of particle filter algorithm in position prediction: The steps and processes of the particle filter algorithm in Fig. 6 include: Initializing particle swarm: At the

beginning of the algorithm, a group of particles are randomly generated, and each particle represents a possible target position. These particles are evenly distributed in the flight area.

The equation of state of particles at any time is shown in Eqs. (18) and (19):

$$x(t)={\text{f}}({\text{x}}\left({\text{t}}-1\right),{\text{u}}\left({\text{t}}\right),{\text{w}}\left({\text{t}}\right))$$ (18) \(x(t)\) is the state at time \(t\).

\({\text{u}}\left({\text{t}}\right)\) is the control input, and \({\text{w}}\left({\text{t}}\right)\) is the state noise. This equation describes how the target moves from one state to

another in motion. Next is the measurement updating phase, which uses sensor data or other measurement information to update the weight of each particle. Measurement update is simulated by

observation equation: $$y(t)={\text{h}}({\text{x}}\left({\text{t}}\right),{\text{e}}\left({\text{t}}\right))$$ (19) \(y(t)\) is the measured value. \({\text{h}}\) is the observation

equation, and \({\text{e}}\left({\text{t}}\right)\) is the measurement noise. This equation represents how the observed values are generated by the current state of the target. By comparing

the measured value with the state of each particle, the weight of each particle can be calculated. Usually, the weight is expressed by probability density function (such as Gaussian

distribution), and the higher the weight, the more likely the particles are to represent the real target position. Then comes the weight normalization stage, which standardizes the weights

of all particles to ensure that they form a probability distribution. This is done to facilitate subsequent resampling operations. This is followed by a resampling phase, in which particles

are sampled according to their weights. The higher the weight, the greater the probability of particles being selected, thus realizing the balance and concentration of particles. Finally,

the position estimation stage, in which the position of the target is estimated by weighted average of the resampled particles. Generally, the weighted average method is adopted, i.e. Eq.

(20): $$\widehat{x}(t)=\sum_{i=1}^{N}{w}_{i}{x}_{i}(t)$$ (20) \(\widehat{x}(t)\) is the estimation of the target position. \(N\) is the number of particles. \({w}_{i}\) is the weight of the

\(i\) th particle, and \({x}_{i}(t)\) is the state of the ith particle at time \(t\). Through this series of steps, the particle filter algorithm can combine historical data and real-time

sensor information to gradually adjust the distribution of particles, thus achieving accurate prediction of the target position. This method is very effective for dealing with nonlinear

motion models and environmental changes, and provides strong support for UAV to achieve accurate target tracking. In the above equation, \(x(t)\) is the state at time \(t\).

\({\text{u}}\left({\text{t}}\right)\) is the control quantity, and \({\text{w}}\left({\text{t}}\right)\) and \({\text{e}}\left({\text{t}}\right)\) are the state noise and observation noise

respectively. State noise is a random variable that describes the uncertainty or external interference in the system model. It represents the unmodeled factors or random disturbances that

may exist in the process of state transition. State noise is usually represented by symbol \({\text{w}}\left({\text{t}}\right)\), where t stands for time step. Observation noise is a random

variable that describes the uncertainty or measurement error in the observation model. It represents the difference between the observed value and the real value or the error in the

measurement process. Observation noise is usually represented by symbol \({\text{e}}\left({\text{t}}\right)\), where t represents time step. In particle filter, state noise and observation

noise are used to simulate the uncertainty of system and observation. By introducing these noises, the randomness in the actual system and observation process can be modeled more accurately,

thus improving the accuracy of state estimation. Equation (17) describes the state transition, and Eq. (18) is the observation equation. Motion model update: Update each particle's

state to reflect the target's current position change in accordance with the target's motion model. This step updates the position and velocity of each particle according to the

motion model. Measurement update: use sensor data or other measurement information to update the weight of particles. This step is used to adjust the weight of particles to make them more in

line with the actual measured values. The closer the particle is to the sensor data, the higher its weight. Weight normalization: Normalize the updated particle weights to ensure that they

form a probability distribution, which is convenient for subsequent resampling operations. Resampling: resample according to the weight of particles. In the resampling process, particles

with higher weight will be copied more, while particles with lower weight may be deleted to achieve the purpose of balancing and concentrating particles. Position estimation: The final

position estimation is calculated based on the resampled particles. Weighted average is usually used, that is, the position of particles is multiplied by their corresponding weights, and

then the weighted positions of all particles are added to get the predicted position. Through particle filter algorithm, UAV can combine historical data and real-time sensor information to

gradually adjust the distribution of particles to estimate the target position more accurately. This method is very effective for dealing with nonlinear motion model and environmental

changes, and can provide high-precision target position prediction, which provides strong support for UAV to achieve accurate target tracking. EXPERIMENTAL PROCESS The target tracking

algorithm and fuzzy logic control theory are used in this paper's studies to assess the effectiveness of UAVs in tracking targets. The parameter Settings used in the experiment are

shown in Table 1: Table 1 shows that during the experiment, the image resolution of 1920*1080 is used for data acquisition. The experiment of each scene includes the evaluation of the

performance of UAV target tracking algorithm. By carrying camera equipment, the image data of the flight area can be obtained regularly. These image data are transmitted to peripheral

devices, which are equipped with high-performance computing resources and are responsible for image processing, target detection and position prediction. The data processing program first

identifies the target from the image through the advanced target detection algorithm, and then uses the visual attention conversion model for real-time image analysis. The position

information of the target is transmitted to the particle filter algorithm for position prediction. Finally, the edge device generates corresponding control instructions, including yaw angle

and speed, and transmits them to the UAV to track the target. In this paper, DJI Phantom 4 Pro is selected as the UAV model used in the experiment. In order to improve the real-time

performance of UAV target tracking, a target tracking algorithm based on fuzzy logic control is adopted, which combines edge computing framework and visual attention conversion model. In

order to evaluate the performance of the algorithm, a series of experiments are carried out, covering different scenes and motion modes. The experimental setup includes three different

scenes: A- fast target movement, B- complex environment change and C- movement pattern change. Ten experiments were carried out in each scene to evaluate the performance of different control

algorithms. The comparison algorithm includes the traditional PID control algorithm. Scenario A-Fast target movement: In this scenario, the UAV target moves rapidly, and the tracking

ability of the control algorithm under high-speed moving targets was tested. Scenario B-Complex Environment Change: In this scenario, the UAV tracks the target with obstacles and environment

changes, and tests the robustness of the control algorithm in complex environment. Scene C-Motion mode change: In this scene, the target changes motion mode, from uniform motion to sudden

change of direction, and tests the adaptability of the control algorithm to different motion modes. RESULTS AND DISCUSSION PERFORMANCE OF THIS ALGORITHM IN DIFFERENT SCENARIOS In each scene

of the experimental part, fuzzy logic controller is used to track the target. When selecting the parameters of fuzzy logic controller, the influence of target moving speed and environmental

change on control performance is mainly considered. The selection of membership function parameters is based on the analysis of target speed and environmental changes in the actual sports

scene, and the parameters of rule base are set according to experience and experimental data to ensure the good performance of the algorithm in different scenes. In order to compare the

optimal setting of parameters in this paper, the specific contents of benchmark parameters, parameter setting 1 and parameter setting 2 are shown. Benchmark parameters: membership function

parameters: \(\Delta y\) is NB: triangular membership function with parameters (a = 0, b = 5, c = 10). \(\Delta y\) is NS: triangular membership function with parameters (a = 3, b = 8, c = 

13). \(\Delta y\) is MM: triangular membership function with parameters (a = 8, b = 13, c = 18). \(\Delta y\) is PS: triangular membership function with parameters (A = 13, B = 18, C = 23).

\(\Delta y\) is PB: triangular membership function with parameters (a = 18, b = 23, c = 28). Rule base parameters: there are five fuzzy rules, as follows: \({{\text{R}}}^{1}:\mathrm{IF

\Delta \;y \;is \;NB},\mathrm{THEN \;v \;is \;GB}\);\({{\text{R}}}^{2}:\mathrm{IF \Delta \;y \;is \;NS},\mathrm{THEN \;v \;is \;GS};\)  \({{\text{R}}}^{3}:\mathrm{IF \Delta \;y \;is

\;MM},\mathrm{THEN \;v \;is \;ZO}\);\({{\text{R}}}^{4}:\mathrm{IF \Delta \;y \;is \;PS},\mathrm{THEN \;v \;is \;BS}\);\({{\text{R}}}^{5}:\mathrm{IF \Delta \;y \;is \;PB},\mathrm{THEN \;v

\;is \;BB}\). Parameter setting 1: membership function parameters: \(\Delta y\) is NB: triangular membership function with parameters (a = 0, b = 6, c = 12). \(\Delta y\) is NS: triangular

membership function with parameters (a = 4, b = 9, c = 14). \(\Delta y\) is MM: triangular membership function with parameters (A = 9, B = 14, C = 19). \(\Delta y\) is PS: triangular

membership function with parameters (A = 14, B = 19, C = 24). \(\Delta y\) is PB: triangular membership function with parameters (a = 19, b = 24, c = 29). Rule base parameters: remain

unchanged, the same as the benchmark parameters. Parameter setting 2: membership function parameters: \(\Delta y\) is NB: triangular membership function with parameters (a = 0, b = 4, c = 

10). \(\Delta y\) is NS: triangular membership function with parameters (a = 3, b = 7, c = 12). \(\Delta y\) is MM: triangular membership function with parameters (a = 7, b = 12, c = 17).

\(\Delta y\) is PS: triangular membership function with parameters (A = 12, B = 17, C = 22). \(\Delta y\) is PB: triangular membership function with parameters (a = 17, b = 22, c = 28). Rule

base parameters: remain unchanged, the same as the benchmark parameters. In this paper, three different scenes (A, B, C) are designed to simulate different environmental conditions and

target motion patterns. The specific features are as follows: Scene A: High-speed moving target. In this scene, the target moves at high speed, and the challenge is to capture and track the

target quickly and accurately. Scene B: Complex environment. There are complex environmental changes in this scene, such as obstructions and light changes. The challenge is to maintain the

stability and accuracy of target tracking in the complex environment. Scene C: Dynamic mode change. In this scene, the motion mode of the target is constantly changing, and the challenge is

to capture and track the target in time under different modes. Figures 7, 8 and 9 demonstrate how the algorithm based on this paper performs in various settings. In the experiments of

different scenes, by comparing the performance of the fuzzy logic control and target tracking algorithm proposed in this paper with the traditional PID algorithm, a series of remarkable

experimental results have been obtained. In Figs. 7, 8, 9, in Scenario A, with the increase of the number of experiments, the performance of the algorithm is remarkable under high-speed

target movement. The average target capture time is gradually stabilized at about 4.2 s, which proves that the algorithm can effectively capture the target in a relatively short time in a

rapidly moving target situation. At the same time, the average tracking error is about 0.68 m, which shows the consistency of the algorithm for target position prediction. The robustness

index is stable at about 0.84, which shows that the algorithm can maintain relatively stable performance in the face of high-speed target movement and has good adaptability to target

movement changes. In scenario B, with the increase of the number of experiments, the algorithm performs well in complex environment. The average target capture time tends to be stable at

about 4.0 s, which shows that the algorithm can capture targets quickly in the face of large-scale environmental changes. The average tracking error is stable at about 0.65 m, which shows

the accuracy of the algorithm for the target position. The robustness index is stable at about 0.87, which shows that the algorithm has excellent stability in dealing with complex

environmental changes and can adapt to different environmental conditions. In Scenario C, it is observed the excellent performance of the algorithm. The average target capture time is stable

at about 4.3 s, which shows that the algorithm can capture the target quickly when dealing with the change of motion mode. The average tracking error is stable at about 0.70 m, which

indicates the stability of the algorithm for the target position. The robustness index is stable at about 0.83, which shows that the algorithm has excellent robustness when facing the change

of target motion mode and can adapt to different motion modes. The experimental results of UAV performance under different wind speeds are shown in Table 2: Table 2 shows the experimental

results of UAV performance under different wind speeds when other natural environmental conditions are unchanged. It shows that the average target capture time is 3.8 s and the average

tracking error is 0.72 m when the maximum wind speed is 12.1 m/s (No.1). This shows that under extreme weather conditions, the target tracking algorithm proposed in this paper can quickly

capture the target in a relatively short time, and shows a low error in the accuracy of target tracking. Secondly, when the maximum wind speed is 9.6 m/s (No.2), the average target capture

time is slightly increased to 4.1 s, and the average tracking error is 0.67 m. This shows that the algorithm can still effectively capture the target at high wind speed, and the tracking

accuracy remains at a high level although the capture time is slightly increased. Finally, under the condition that the maximum wind speed is 4.9 m/s (No.3), the average target capture time

is 4.5 s, and the average tracking error is 0.69 m. Even at relatively low wind speed, the algorithm can still capture the target stably and maintain high tracking accuracy. These

experimental results show that the method proposed in this paper can effectively deal with different wind speeds and has good performance. This further verifies the effectiveness and

robustness of this method in practical application, especially in the face of different meteorological environments, which can maintain reliable target tracking performance. PERFORMANCE

COMPARISON OF SIMILAR ALGORITHMS The performance of the traditional PID control algorithm, CNN algorithm, Deep Q-Network (DQN) algorithm based on deep reinforcement learning, Model

Predictive Control (MPC) algorithm based on classical control theory, and target tracking algorithm based on fuzzy logic control theory in this paper is compared in various scenarios in

order to further validate the performance of the algorithm. The results are shown in Figs. 10, 11, 12: In Figs. 10, 11, 12, the tracking algorithm in this paper has excellent performance in

various scenarios. Compared with the traditional PID control method, CNN, DQN and MPC, the algorithm in this paper shows obvious advantages in many performance indexes. Firstly, in terms of

target capture time, compared with the traditional PID algorithm, the experimental results show that the average target capture time is shortened by about 12–20%. This indicates that the

technique presented in this paper offers clear advantages in the rate at which the target is captured, enabling the UAV to track and locate the target more quickly. Meanwhile, compared with

other similar algorithms, this algorithm also shows faster response speed in the average target capture time, which further strengthens the advantages of its real-time performance. Secondly,

in terms of average tracking error, this algorithm also performs well. Compared with the traditional PID algorithm, CNN, DQN and MPC, the average tracking error of this algorithm is

decreasing in different scenarios, and the decreasing range is about 13–18%. This demonstrates that the algorithm presented in this paper can more accurately estimate and maintain the

UAV's distance from the target, resulting in more accurate target tracking. Finally, the algorithm in this paper also exhibits higher stability in comparison in terms of robustness. In

a variety of settings, this method's robustness index (standard deviation) is typically lower than that of the conventional PID algorithm, CNN, DQN, and MPC. This demonstrates how the

method in this paper can maintain more dependable and consistent tracking performance while minimizing the fluctuation of tracking error under various environmental conditions and target

motion variations. Through these detailed and specific experimental results, the performance of the target tracking algorithm proposed in this paper can be comprehensively evaluated in

different situations. In the performance comparison experiment, this paper compares the parameter settings of traditional PID control algorithm, CNN algorithm, DQN algorithm and MPC

algorithm, and analyses the sensitivity. The following are the results of sensitivity analysis: According to Table 3, the performance of benchmark parameters, parameter setting 1 and

parameter setting 2 are compared for the method in this paper. The results show that parameter setting 2 is slightly better than other settings in average target acquisition time and average

tracking error, and the robustness index is also improved to 0.86. This shows that the performance of the algorithm can be slightly improved by adjusting the parameters of the fuzzy logic

controller under the given experimental conditions. For the traditional PID algorithm, parameter setting 1 and parameter setting 2 are also compared. In terms of average target acquisition

time and average tracking error, parameter setting 1 performs slightly better, while the robustness index performs slightly worse. However, compared with the method in this paper, the

performance of the traditional PID algorithm is generally poor, showing a long average target acquisition time and a large average tracking error. For CNN algorithm, DQN algorithm and MPC

algorithm, the comparison of parameter setting 1 and parameter setting 2 is also made. The results show that these algorithms are relatively stable under different parameter settings, but

compared with this method and traditional PID algorithm, their performance is generally poor, with longer average target acquisition time and larger average tracking error. In order to

verify the reliability and validity of the experimental results, the experimental data are statistically analyzed and hypothesis tested. T-test is carried out on many experimental data in

each scene, and the statistical significance of the experimental results can be determined by calculating the p value, thus verifying the superiority of the method in different scenes. The

hypothesis test results of this algorithm in different scenarios are shown in Table 4: According to Table 4, in different scenes, the method in this paper shows significant differences in

average target acquisition time and robustness index, while there are significant differences in average tracking error in some scenes, but there are no significant differences in other

scenes. This further supports the superiority of this method in different scenarios, especially in terms of target capture time and robustness. In order to evaluate the performance of the

method proposed in this paper more comprehensively, it is compared with three latest research methods published recently. Specifically, the research of Zatout et al.32, de Koning and

Jamshidnejad33 and Tsitses et al.34 are selected, which respectively involve fuzzy logic and particle swarm optimization, mixed control of model prediction and fuzzy logic, and autonomous

UAV bridge landing system based on fuzzy logic. The specific numerical comparison results of different methods on various performance indexes are shown in Table 5: In Table 5, the average

target capture time of this method is relatively low, which is 4.17 s. Compared with other methods, such as Zatout et al. (2022) and de Koning and Jamshidnejad (2023), it is shortened by

0.63 s and 1.03 s respectively, which shows that this method is more rapid and efficient in capturing targets. Compared with the method of Tsitses et al. (2024), this method is slightly

longer by 0.33 s, but the difference is not obvious. The average tracking error of this method is 0.68 m, which is 0.07 m and 0.14 m lower than that of Zatout et al. (2022) and de Koning and

Jamshidnejad (2023), respectively, showing higher tracking accuracy. Compared with the method of Tsitses et al. (2024), the error of this method is similar, but slightly lower by 0.04 m.

The robustness index of this method is 0.85, which is 0.06 and 0.04 percentage points higher than that of Zatout et al. (2022) and Tsitses et al. (2024) respectively, showing stronger

robustness. However, compared with the method of de Koning and Jamshidnejad (2023), the robustness index of this method is slightly lower by 0.1 percentage point. To sum up, this method

shows relatively good performance in average target acquisition time, average tracking error and robustness index, and surpasses other research methods in many aspects. DISCUSSION The

methods to improve real-time performance mentioned in this paper include target tracking algorithm based on fuzzy logic control, edge computing framework, and visual attention conversion

model. In order to explore the computational complexity and real-time performance of these methods, this paper discusses them with the research of four related scholars. Pham et al.35

pointed out that fuzzy logic control was more suitable for dealing with complex and fuzzy input than traditional control methods, which improved the robustness of the system to

uncertainties. However, fuzzy logic control may increase the computational complexity when dealing with large-scale input. In this paper, a fuzzy controller with upper and lower layers was

constructed by introducing type II fuzzy logic control, which effectively reduced the computational complexity. This design took into account the movement state of the target and the change

of the environment, and realized the real-time adjustment of the flight attitude of the UAV through the cooperation of two fuzzy controllers. Zhang et al.36 applied the edge computing

framework in UAV target tracking, which reduced the computational burden of the central processing unit and improved the response speed of the system to target changes. Edge devices were

responsible for image processing, target detection and position prediction, thus reducing data transmission delay. Although the deployment of edge computing framework may introduce some

system complexity, the experimental results showed that this method effectively reduced the execution time of the algorithm and improves the real-time performance of UAV target tracking. El

Hamidi et al.37 applied the visual attention conversion model in the field of target recognition, and realized the real-time analysis of the target-related areas by blocking the image and

using the attention mechanism. This model can improve the accuracy of target recognition while maintaining low computational complexity. In this paper, the visual attention conversion model

was applied to target recognition, and real-time image analysis was realized by analyzing the relationship between image blocks. This provided more accurate target recognition support for

UAV target tracking. In previous studies, Zare et al.38 found that the particle filter algorithm had certain influence on real-time performance. Particle filter algorithm can provide

high-precision prediction of target position through initialization, motion model update, measurement update, weight normalization and resampling. However, because the increase of the number

of particles may cause computational burden, it was necessary to balance the computational complexity and real-time performance in the implementation of the algorithm. To sum up, through

the comprehensive discussion of the research results of the above scholars, the conclusion can be drawn: In the method of improving real-time performance, fuzzy logic control reduces the

computational complexity by introducing type II fuzzy logic control. The edge computing framework improves the real-time performance by reducing the burden on the central processing unit.

The visual attention conversion model takes into account both computational complexity and accuracy when realizing real-time image analysis. The particle filter algorithm needs to find a

balance between accuracy and computational burden. These studies provide beneficial enlightenment for improving real-time performance, but the influence of various factors still needs to be

considered comprehensively in specific applications. CONCLUSION The purpose of this paper is to enhance UAV target tracking performance. Fuzzy logic is used to create a control model that

can modify the flying attitude of a UAV in real time in response to changes in the environment and target motion states. This model shows superior target capturing ability and stability in

all scenarios. Meanwhile, a target tracking framework based on edge computing is constructed. By distributing the computing tasks such as target recognition and position prediction to the

edge devices, the burden of the central processing unit is effectively reduced, and the real-time performance and efficiency are improved. Finally, the latest visual attention converter

model is used to divide the image into uniform blocks, and the relationship between different blocks is captured by attention mechanism, which realizes more accurate target recognition and

provides reliable input for tracking. However, it is worth noting that there are still some limitations in this method. First, although it shows good performance in experiments under

different scenes and wind speed conditions, the robustness of the algorithm may be affected in some special or extreme environments, such as extreme weather or high-intensity interference.

Future work can further study and improve the robustness of the algorithm in extreme environments. Secondly, the experimental results under different wind speeds are preliminarily discussed,

but the influence of wind speed changes on the real-time performance of the algorithm is not analyzed in detail. Future research can further explore the performance of the algorithm under

the condition of dynamic wind speed to understand its reliability in practical application more comprehensively. Looking forward to the future work, people can consider further optimizing

the computational complexity of the algorithm to improve the real-time performance. Meanwhile, combined with cutting-edge technologies such as deep learning, the accuracy of target detection

and tracking is further improved, thus further improving the performance of the overall system. In addition, expanding the experimental range and introducing more performance experiments in

specific application scenarios will help to verify the applicability and universality of the algorithm more comprehensively. Generally speaking, the UAV target tracking method proposed in

this paper shows good performance in the experiment, but it still needs to be further verified in special environment and further improved in achieving higher performance and wide

applicability. Future research work will be devoted to solving these limitations and promoting the development of this field to better meet the needs of practical applications. DATA

AVAILABILITY All data generated or analysed during this study are included in this published article and its supplementary information files. REFERENCES * Lee, D. H. CNN-based single object

detection and tracking in videos and its application to drone detection. _Multimed. Tools Appl._ 80(26–27), 34237–34248 (2021). Article  Google Scholar  * Yeom, S. Long distance ground

target tracking with aerial image-to-position conversion and improved track association. _Drones_ 6(3), 55 (2022). Article  Google Scholar  * Balamurugan, N. M. _et al._ DOA tracking for

seamless connectivity in beamformed IoT-based drones. _Comput. Stand. Interfaces_ 79, 103564 (2022). Article  Google Scholar  * Yeom, S. & Nam, D. H. Moving vehicle tracking with a

moving drone based on track association. _Appl. Sci._ 11(9), 4046 (2021). Article  CAS  Google Scholar  * Wu, Y. & Low, K. H. Route coordination of uav fleet to track a ground moving

target in search and lock (sal) task over urban airspace. _IEEE Internet Things J._ 9(20), 20604–20619 (2022). Article  Google Scholar  * Gong, J. _et al._ Comparison of radar signatures

from a hybrid VTOL fixed-wing drone and quad-rotor drone. _Drones_ 6(5), 110 (2022). Article  Google Scholar  * Petrolo, R. _et al._ ASTRO: A system for off-grid networked drone sensing

missions. _ACM Trans. Internet Things_ 2(4), 1–22 (2021). Article  Google Scholar  * Zou, J. T. & Dai, X. Y. The development of a visual tracking system for a drone to follow an

omnidirectional mobile robot. _Drones_ 6(5), 113 (2022). Article  Google Scholar  * Pavliv, M. _et al._ Tracking and relative localization of drone swarms with a vision-based headset. _IEEE

Robot. Autom. Lett._ 6(2), 1455–1462 (2021). Article  Google Scholar  * Barbary, M. _et al._ Extended drones tracking from ISAR images with doppler effect and orientation based robust

sub-random matrices algorithm. _IEEE Trans. Veh. Technol._ 71(12), 12648–12666 (2022). Article  Google Scholar  * Lin, Y. _et al._ Multiple object tracking of drone videos by a

temporal-association network with separated-tasks structure. _Remote Sens._ 14(16), 3862 (2022). Article  ADS  Google Scholar  * Pardhasaradhi, B. & Cenkeramaddi, L. R. GPS spoofing

detection and mitigation for drones using distributed radar tracking and fusion. _IEEE Sens. J._ 22(11), 11122–11134 (2022). Article  ADS  Google Scholar  * Azar, A. T. _et al._ Drone deep

reinforcement learning: A review. _Electronics_ 10(9), 999 (2021). Article  Google Scholar  * Tullu, A., Hassanalian, M. & Hwang, H. Y. Design and implementation of sensor platform for

uav-based target tracking and obstacle avoidance. _Drones_ 6(4), 89 (2022). Article  Google Scholar  * Valianti, P. _et al._ Multi-agent coordinated close-in jamming for disabling a rogue

drone. _IEEE Trans. Mobile Comput._ 21(10), 3700–3717 (2021). Article  Google Scholar  * Na, K. I., Choi, S. & Kim, J. H. Adaptive target tracking with interacting heterogeneous motion

models. _IEEE Trans. Intell. Transp. Syst._ 23(11), 21301–21313 (2022). Article  Google Scholar  * Barbary, M. & Abd ElAzeem, M. H. Drones tracking based on robust cubature

Kalman-TBD-multi-Bernoulli filter. _ISA Trans._ 114, 277–290 (2021). Article  PubMed  Google Scholar  * Zhou, W., Li, J. & Zhang, Q. Joint communication and action learning in

multi-target tracking of UAV swarms with deep reinforcement learning. _Drones_ 6(11), 339 (2022). Article  Google Scholar  * Park, Y. & Kim, Y. Circumnavigation of multiple drones under

intermittent observation: An integration of guidance, control, and estimation. _Int. J. Aeronaut. Space Sci._ 23(2), 423–433 (2022). Article  Google Scholar  * Unal, G. Visual target

detection and tracking based on Kalman filter. _J. Aeronaut. Space Technol._ 14(2), 251–259 (2021). Google Scholar  * Zhang, P. _et al._ Agile formation control of drone flocking enhanced

with active vision-based relative localization. _IEEE Robot. Automat. Lett._ 7(3), 6359–6366 (2022). Article  Google Scholar  * Zigelman, R. _et al._ A bio-mimetic miniature drone for

real-time audio based short-range tracking. _PLoS Computat. Biol._ 18(3), e1009936 (2022). Article  CAS  Google Scholar  * Zhu, P. _et al._ Detection and tracking meet drones challenge.

_IEEE Trans. Pattern Anal. Mach. Intell._ 44(11), 7380–7399 (2021). Article  Google Scholar  * Siyal, S. _et al._ They can’t treat you well under abusive supervision: Investigating the

impact of job satisfaction and extrinsic motivation on healthcare employees. _Ration. Soc._ 33(4), 401–423 (2021). Article  Google Scholar  * Chen, D., Wawrzynski, P. & Lv, Z. Cyber

security in smart cities: A review of deep learning-based applications and case studies. _Sustain. Cities Soc._ 66, 102655 (2021). Article  Google Scholar  * Chinthi-Reddy, S. R. _et al._

DarkSky: Privacy-preserving target tracking strategies using a flying drone. _Veh. Commun._ 35, 100459 (2022). Google Scholar  * Upadhyay, J., Rawat, A. & Deb, D. Multiple drone

navigation and formation using selective target tracking-based computer vision. _Electronics_ 10(17), 2125 (2021). Article  Google Scholar  * Liu, J., Xu, Q. Y. & Chen, W. S.

Classification of bird and drone targets based on motion characteristics and random forest model using surveillance radar data. _IEEE Access_ 9, 160135–160144 (2021). Article  Google Scholar

  * Hong, T. _et al._ A real-time tracking algorithm for multi-target UAV based on deep learning. _Remote Sens._ 15(1), 2 (2022). Article  ADS  Google Scholar  * Dogru, S. & Marques, L.

Drone detection using sparse lidar measurements. _IEEE Robot. Automat. Lett._ 7(2), 3062–3069 (2022). Article  Google Scholar  * Qamar, S. _et al._ Autonomous drone swarm navigation and

multitarget tracking with island policy-based optimization framework. _IEEE Access_ 10, 91073–91091 (2022). Article  Google Scholar  * Zatout, M. S. _et al._ Optimisation of fuzzy logic

quadrotor attitude controller–particle swarm, cuckoo search and BAT algorithms. _Int. J. Syst. Sci._ 53(4), 883–908 (2022). Article  ADS  Google Scholar  * de Koning, C. & Jamshidnejad,

A. Hierarchical integration of model predictive and fuzzy logic control for combined coverage and target-oriented search-and-rescue via robots with imperfect sensors. _J. Intell. Robot.

Syst._ 107(3), 40 (2023). Article  Google Scholar  * Tsitses, I. _et al._ A fuzzy-based system for autonomous unmanned aerial vehicle ship deck landing. _Sensors_ 24(2), 680 (2024). Article

  ADS  PubMed  PubMed Central  Google Scholar  * Pham, D. A. & Han, S. H. Design of combined neural network and fuzzy logic controller for marine rescue drone trajectory-tracking. _J.

Marine Sci. Eng._ 10(11), 1716 (2022). Article  Google Scholar  * Zhang, Y., Pan, M. & Han, Q. Joint sensor selection and power allocation algorithm for multiple-target tracking of

unmanned cluster based on fuzzy logic reasoning. _Sensors_ 20(5), 1371 (2020). Article  ADS  PubMed  PubMed Central  Google Scholar  * El Hamidi, K. _et al._ Neural network and

fuzzy-logic-based self-tuning PID control for quadcopter path tracking. _Stud. Inform. Control_ 28(4), 401–412 (2019). Article  Google Scholar  * Zare, M., Pazooki, F. & Haghighi, S. E.

Quadrotor UAV position and altitude tracking using an optimized fuzzy-sliding mode control. _IETE J. Res._ 68(6), 4406–4420 (2022). Article  Google Scholar  Download references

ACKNOWLEDGEMENTS Supported by the Science and Technology Project of State Grid Co., Ltd. (project Code: 520234220001 Project name: research on AI+ UAV Inspection system based on Edge

Computing). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * State Grid Beijing Economics Research Institute, Beijing, 100055, China Cong Li, Wenyi Zhao, Li Ju & Hongyu Zhang * State Grid

Beijing Electric Power Company, Beijing, 100031, China Liuxue Zhao Authors * Cong Li View author publications You can also search for this author inPubMed Google Scholar * Wenyi Zhao View

author publications You can also search for this author inPubMed Google Scholar * Liuxue Zhao View author publications You can also search for this author inPubMed Google Scholar * Li Ju

View author publications You can also search for this author inPubMed Google Scholar * Hongyu Zhang View author publications You can also search for this author inPubMed Google Scholar

CONTRIBUTIONS C.L., W.Z., L.Z., L.J. and H.Z. contributed to conception and design of the study. C.L. organized the database. L. Z. performed the statistical analysis. C.L., W.Z. wrote the

first draft of the manuscript. L.J. and H.Z. wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version. CORRESPONDING AUTHOR

Correspondence to Wenyi Zhao. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE Springer Nature remains neutral

with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION. RIGHTS AND PERMISSIONS OPEN ACCESS This article

is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any

medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed

material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are

included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and

your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this

licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Li, C., Zhao, W., Zhao, L. _et al._ Application of fuzzy logic

control theory combined with target tracking algorithm in unmanned aerial vehicle target tracking. _Sci Rep_ 14, 18506 (2024). https://doi.org/10.1038/s41598-024-58140-5 Download citation *

Received: 13 November 2023 * Accepted: 26 March 2024 * Published: 09 August 2024 * DOI: https://doi.org/10.1038/s41598-024-58140-5 SHARE THIS ARTICLE Anyone you share the following link

with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt

content-sharing initiative KEYWORDS * Unmanned aerial vehicle target tracking * Edge computing * Fuzzy logic control * Vision transformer model * Particle filter algorithm