ABSTRACT Mechanical failure of biological nanostructures due to sustained force application has been studied in great detail. In contrast, fatigue failure arising from repeated application

of subcritical stresses has received little attention despite its prominent role in engineering and potentially biology. Here, paclitaxel-stabilized microtubules are up to 256 times bent

into sinusoidal shapes of varying wavelength and the frequency of breaking events are observed. These experiments allow the calculation of fatigue life parameters for microtubules. Repeated

buckling due to 12.5% compression–equal to the compression level experienced by microtubules in contracting cardiomyocytes – results in failure after in average 5 million cycles, whereas at

LIVING CELLS Article 29 June 2023 MYOSIN AND \(\UPALPHA\)-ACTININ REGULATION OF STRESS FIBER CONTRACTILITY UNDER TENSILE STRESS Article Open access 29 May 2023 INTRODUCTION Nanomechanical

studies of biological structures have delivered important biophysical insights which advanced our understanding of cell biology1. In particular, the characterization of the mechanical

properties of cytoskeletal filaments, such as actin filaments and microtubules, has attracted great interest due to their prominent roles in cell mechanics2,3,4, but also increasingly as

scaffolds and motile agents for hybrid nanodevices5,6,7,8. From the initial measurements of their rigidity9,10,11, over indentation12,13 and breaking6,14 experiments to the recent discovery

of their self-healing capabilities15, cytoskeletal filaments have revealed a surprising complexity in their mechanical properties. For example, the breaking rate of microtubules increases

exponentially with increasing curvature16, a fact which can be understood based on mechanochemical principles17 and which affects the organization of the microtubule cytoskeleton18. However,

microtubules in vitro and in vivo do not only experience constant or increasing loads which cause breaking, but also the repeated application of subcritical stresses. The repeated

application of subcritical stresses leads to materials fatigue in macroscopic systems19, where each stress cycle can cause the incremental growth of cracks leading ultimately to fracture of

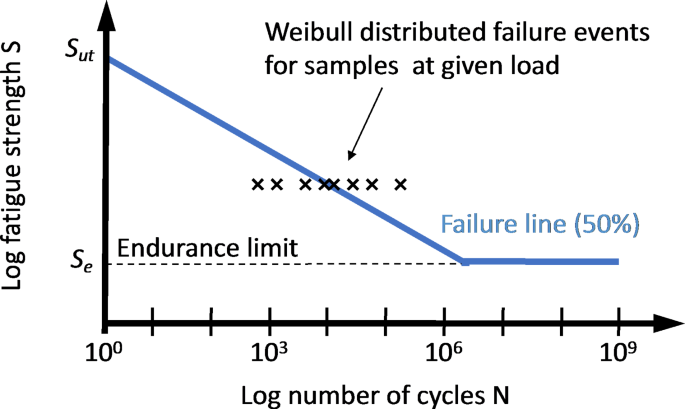
the part and failure of the system. The fatigue properties of a material are typically characterized using an S-N diagram, where the average number of stress cycles until failure is related

to the applied stress (Fig. 1). While application of the ultimate stress leads to failure in a single stress cycle, decreasing the stress below the ultimate stress typically leads to a large

increase in the number of cycles before failure is observed19. Some materials exhibit an endurance limit, that is, a stress level below which failure is not observable anymore. Here we aim

to experimentally measure the S-N diagram for paclitaxel-stabilized, fluorescently labeled microtubules by repeatedly buckling straight microtubules into sinusoidal shapes. This is

accomplished by tethering microtubules via kinesin motor proteins to a flexible polydimethylsiloxane (PDMS) substrate, which is stretched and relaxed by external actuators20. Each

relaxation-stretch cycle of the pre-stretched PDMS substrate results in a buckling-straightening cycle of the microtubules immobilized on it. The integrity of the microtubules after the

completion of up to 256 cycles was observed using fluorescence microscopy. Repeated bending of microtubules into reproducible sinusoidal shapes was accomplished using a

“micro-stretcher”20,21 which actuates a two-dimensional elastic film of PDMS used as substrate to immobilize the microtubules via kinesin-1 motor proteins bound to the substrate

(pre-stretched to 100% strain). The ATTO 488-labeled microtubules are largely aligned with the axis of stretching by shear flow during their initial interaction with the kinesin-covered PDMS

surface. Continuous purging of the experimental chamber with humid N2 minimized evaporation and photodamage over several hours of observation with fluorescence microscopy22. The buffer

solution did not contain ATP or ADP in order to attach the microtubules to the kinesin in the strongly bound rigor state (Fig. 2a). RESULTS The experiment proceeded by repeatedly relaxing

and stretching the pre-stretched PDMS at a strain rate of 0.004 s−1 (with 1 s intervals between each motion), which causes microtubules to buckle into sinusoidal waves and straighten again

(Fig. 2b,c). Variations in the kinesin density on the surface lead to variations in buckling amplitude along each microtubule. By analyzing small segments of each microtubule and determining

the curvature of each segment individually, we can investigate the breaking rate for a specific curvature16. The sinusoidal shape of the buckled microtubule prevents the build-up of

internal stresses between protofilaments described by Pampaloni et al. for bending microtubules with increasing length11, so that the effective persistence length is expected to be small and

on the order of 0.2 mm as for very short microtubules. The extent of buckling is controlled by the degree of compression relative to the initial pre-stretched state of the PDMS substrate23.

Since our current experimental setup allows compressive strain of up to 40%, we chose compression levels of 10.0%, 12.5%, 20.0%, 30.0% and 40.0%, requiring cycle completion times between 52

 s (10.0%) and 202 s (40.0%). Images of the microtubules were captured after specific numbers of stretch cycles (1, 2, 4, 8, 16, 32, 64, 256; Fig. 2c). Breakage or damage of a microtubule

was visually identified by a non-uniformity in the fluorescence signal of a microtubule (Fig. 2c). In some cases, the breaks on the microtubules that were not observable in the buckled state

became visible in the stretched state. At the highest compression level of 40.0%, a single compression already creates breakage along the microtubules, which becomes more clearly visible

after the microtubules are returned to the stretched state (Supplementary Fig. S1). At lower compression levels, a single cycle was insufficient to break the microtubules (Supplementary Fig.

 S1). At 10.0%, even 256 cycles did not disrupt the microtubules. We therefore analyzed in detail 1 to 8 cycles for a compression level of 20.0% and 1 to 256 cycles for a compression level

of 12.5%. All microtubules were identified and divided into 0.5 μm long segments for which the curvature after compression was determined. The segment length was chosen because it is optimal

for determining the curvature16. Specific segments repeatedly experienced the same level of curvature (Fig. 3). Breaking events were identified by close examination by eye and associated

with specific segments. The microtubule segments at risk and the microtubule segments experiencing a break were grouped into curvature bins (0–0.5, 0.5–1, …, 2.5–3 μm−1) as shown in Table 1,

because the curvature determines the local breaking rate16. The number of microtubule segments at risk and the number of new microtubule segments breaking allows the calculation of the

logarithm of the complement of the breaking probabilities (the survival probability) as a function of the logarithm of the cycle number (Fig. 4). The breaking probability exhibits the

expected strong dependence on the curvature and increases roughly linearly with the logarithm of the cycle number. For example, for the 20.0% compression level and after 8 cycles, the

breaking probability increases from 0.009 over 0.04 to 0.08 for the 0.0–0.5, 0.5–1.0 and 1.0–1.5 μm−1 curvature bins, respectively. However, the survival curves for the 12.5% and 20.0%

compression levels do not overlap, as one would expect if curvature and cycle number are the only determinants of survival. The absence of a consistent trend for the different curvature

conditions points towards a significant stochastic variability between experiments. To reduce stochastic effects, we therefore pool the different curvature bins and calculate a survival

curve for each compression level (Fig. 5) and model it as a Weibull distribution24,25: $$\:{P}_{S}\left(N\right)={e}^{-{\left(N/b\right)}^{a}}$$ (1) For our experiments, the shape and scale

coefficients a and b were determined as 0.39 ± 0.03 and 107 for 12.5% compression, and 0.83 ± 0.11 and 103 for 20.0% compression, respectively. From these fits the number of cycles N50 at

which 50% of the segments are broken can be extrapolated to be 5 × 106 for 12.5% compression and 103 for 20.0% compression. DISCUSSION In our previous work16, we determined the rate of

breaking of a smoothly gliding microtubule as 0.4 ± 0.1 mm−1 min−1, and found that the breaking rate increases 250-fold from that value in an exponential fashion as the curvature increases

from zero to 2.5 μm−1. Given that the time to complete a compression and relaxation cycle is 62 s for a compression level of 12.5% and 102 s for a compression level of 20% and the 0.5 μm

segment length, we expect to a segment bent to an average curvature of 0.25 μm−1 to break after 10 cycles with a probability of 0.3% for 12.5% compression and 0.5% for 20% compression. These

breaking probabilities should increase by a factor of 3 as the curvature is increased by 0.5 μm−1. The experimentally determined survival probabilities (the complement of the breaking

probabilities) shown in Fig. 4 match these expectations derived from our previous analysis of microtubule breaking reasonably well. Because the observed curvatures are below the level of 2.5

 μm−1 up to which we previously found a consistent exponential increase in the microtubule breaking rate16, we assume here that the obtained two data points (12.5% and 20.0%) are in the

linearly declining part of the S-N curve before a potential endurance limit is reached. Clearly, more data points at low compression levels obtained with a method allowing observation of a

larger number of cycles are needed in future work, so that this assumption can be further tested. The N50 value of 5 × 106 for 12.5% compression seems to suggest that breaking due to

mechanical fatigue becomes negligible for almost all experimental situations. However, it is important to remember that the large numerical values of N50 simply results from the chosen

segment length (0.5 μm). As Weibull discussed for the breaking of a chain consisting of several links24, a microtubule consisting of several segments will have a survival probability given

by the product of the survival probabilities of each segment. The survival probability of a microtubule with m segments is therefore:

$$\:{P}_{S}\left(N,m\right)={e}^{-m{\left(N/b\right)}^{a}}$$ (2) To determine the failure line given by the number of cycles at which 50% of the microtubules survive, one sets PS equal to

0.5 and solves for N, finding that N50(m) = N50(1)/m1/a. For a 10 μm microtubule with 20 segments, N50 would be reduced by a factor 20^(1/a), that is by a factor of 2000 for a compression

level of 12.5% and a factor of 40 for a compression level of 20.0%. Therefore, 50% of all microtubules would be expected to break somewhere after only 3000 (12.5%) or 30 cycles (20.0%

compression). While we here treat the segments as independent from each other, the complex biomechanics of a microtubule can make the breaking probability of a segment dependent on the state

of adjacent segments as described in our previous work16, where we found that it matters for the breaking process if a highly curved segment is at the center or the end of a bending

microtubule due to a varying degree of internal stress redistribution. In the compression method used here, the sinusoidal shape of the bent microtubules yields a periodic stress

distribution repeating every few micrometers. In this situation, the alternating bending prevents correlations beyond a distance of one wavelength. It therefore makes sense to consider 20–50

 μm long microtubules (Fig. 1c) as consisting of independent segments and account for the variable lengths of the microtubules by dividing them into different numbers of segments. The

numbers determined here for the parameters a, b and N50 represent averages over all assumed curvatures for a segment of length 0.5 μm, and the parameters applying to longer segments or

entire microtubules can be calculated as described above. Notably, the buckling of a microtubule into a roughly sinusoidal shape is representative of several biological situations26,27. The

fatigue strength (Basquin) exponent B relating the stress amplitude σa to the cycle number N50 according to σa ~ N50B can be estimated as -0.054±0.009, if the stress amplitude is assumed to

be proportional to the maximal curvature of a buckled microtubule. Assuming a sinusoidal shape, the maximal curvature determined by the amplitude divided by the square of the wavelength and

is approximately proportional to the compression level21,23. The fatigue strength exponent B is then given by:

$$\:B=\text{l}\text{o}\text{g}(20\%/12.5\%)/\text{l}\text{o}\text{g}({N}_{50}^{20\%}/{N}_{50}^{12.5\%})$$ (3) which yields the value stated above for \(\:{N}_{50}^{20\%}={10}^{3}\) and

\(\:{N}_{50}^{12.5\%}={5\times\:10}^{6}\). For comparison, the Basquin exponent for most metals is in the range of -0.05 to -0.12 and for some polymer nanocomposites in the range of − 0.08

to − 0.1519,28. This indicates that the fatigue life time increases roughly as expected if the stress on the microtubule is reduced. The two values, (5 × 106; 12.5%) and (103; 20.0%),

determined for the S-N curve allow in principle an extrapolation to the point at which 50% of the microtubule segments break in a single cycle, which is a compression level of 30%±20%. In

our experiments, even at a compression level of 40.0% not half of all – not even half of all the highly curved – segments are broken (Supplementary Fig. S1). Given the large error bar of the

extrapolated compression level, it is statistically quite possible that the true required compression level for 50% breaking in one cycle exceeds 40% and is not accessible to our

experimental method. Repeated buckling of microtubules has particular relevance in the context of cardiac myocytes, where recent studies have highlighted the significant contribution of

microtubules to the mechanical properties in contracting cardiomyocytes4,29,30. Robison et al. demonstrated that microtubules of cardiomyocytes buckle during contraction due to their

attachment to the z-disks4. At the peak of contraction, the cardiomyocyte is shortened by 13% suggesting a comparison with our 12.5% compression data point, where a stress life of 5 million

cycles, equivalent to about a month in the life of a human heart, has been determined. Curvature-induced breaking is an phenomenon observed in vivo suggesting that microtubule repair

mechanisms as reviewed by Thery and Blanchoin are essential to sustain heart function3,31. It has to be noted though that posttranslational modifications, such as acetylation, regulate

microtubule stability in cells32, so that the parameters measured here for paclitaxel-stabilized microtubules may be altered in specific cellular contexts. Combining the approaches for

imaging microtubule self-repair mechanisms developed by Thery et al. with techniques allowing cyclical deformation such as the present method can provide additional insights in the future17.

Our experimental work can, of course, only describe nature and not explain it. Fatigue testing in silico pioneered by Barsegov et al. has the potential to provide explanations by making the

dynamic evolution of cracks in the microtubule lattice visible13,33. While nanoindentation simulations model events on a timescale of milliseconds commensurate with AFM nanoindentation

experiments34, their numerical results cannot be directly compared to our experiments conducted on a time scale of minutes and a different, but more biologically relevant mode of force

application, that is cyclic bending35,36. The main message from these data is that the number of microtubule breaking events for a population of microtubule segments does not increase in

proportion to the number of stress cycles when the microtubules are loaded to only a subcritical level. Instead, the number of cycles required to create a given number of new breaks keeps

increasing (Table 1; Fig. 4), which means that the breaking probability per cycle decreases rapidly with additional cycles. This contradicts the simple picture of mechanochemistry where each

loading cycle would lead to a constant probability of bond breaking. Similar to fatigue failure at the macroscale where cracks are often initiated at randomly distributed preexisting defect

sites19, it originates in the variability of the microtubule segments under observation, which exhibit a variety of lattice defects31,37. Similar to the fatigue behavior at the macroscale,

small reductions in the stress level (here from 20.0% compression to 12.5% compression) have large effects on the number of stress cycles a microtubule can withstand. CONCLUSION From a

broader perspective, fatigue failure and its various aspects can be considered as a specific case of reliability theory. Gavrilov and Gavrilova highlighted the conceptual connections between

biological aging and technical failure, and suggested that the characteristic time course of biological aging arises from a network of components with a preexisting random distribution of

flaws, whereas technical failure follows a different time course due to the initial flawlessness of the system38. The microtubule is an interesting object in this context due to its variable

content in mechanical defects created during its assembly10 and its ability to self-repair31. This suggests that a further exploration of microtubule fatigue failure could be fascinating.

EXPERIMENTAL SECTION/METHODS PREPARATION OF FLUORESCENTLY LABELED MICROTUBULES Tubulin was purified from fresh porcine brain using a high-concentration PIPES buffer (1 M PIPES, 20 mM EGTA,

10 mM MgCl2; pH adjusted to 6.8 using KOH)39. The purified tubulin was labeled with the ATTO 488 fluorescent dye with a labeling ratio of 1.0 as determined from the absorbance of tubulin at

280 nm and ATTO-488 fluorescent dye at 500 nm40. 56 µM tubulin (80% ATTO 488-labeled tubulin and 20% non-labeled tubulin) was polymerized to microtubules in the presence of 5 mM GTP, 20 mM

MgCl2, and 25% dimethyl sulfoxide in BRB80 (80 mM PIPES, 1 mM MgCl2, and 1 mM EGTA, pH 6.8) at 37 °C for 30 min. Microtubules were stabilized using 50 µM paclitaxel in BRB80. EXPRESSION AND

PURIFICATION OF KINESIN We expressed and purified recombinant conventional kinesin-1 construct consisting of human kinesin (residues 1-573) as described previously with partial

modification41,42. PREPARATION OF THE FLOW CELL We used PDMS film with a thickness of 0.05 mm as an elastic substrate to prepare the flow cell. The relaxation and stretch cycles were

performed using a previously developed micro-stretcher consisting of a base plate containing a computer-controlled stretcher/compressor and a cover plate20,21. First, the PDMS film with

approximate dimension 4.0 × 5.0 × 0.05 mm3 (L×W×T) was fixed horizontally on the stretcher. Then the film was elongated 100% by applying tensile force with the computer-controlled stretcher.

This pre-stretched PDMS film was masked with two 18 × 18 cover glasses, leaving a narrow channel for use as a flow cell. The channel was exposed to etching with a plasma etcher (6–8 Pa, 8 

mA, 4 min) to increase the hydrophilicity prior to each experiment. The flow cell was then incubated for 5 min with 10 µL of 50 nM kinesin in buffer A (80 mM PIPES, 40 mM NaCl, 1 mM EGTA, 1

mM MgCl2, 0.65 mM DTT, 1.3 mg/mL casein, 13 mM paclitaxel; pH 6.8) and washed with buffer A. Next, 20 µL of paclitaxel-stabilized, ATTO-488-labeled microtubule solution (280 nM tubulin) was

introduced by flowing the solution from one end and holding filter paper to the other end of the channel which ensured that the microtubules are aligned parallel to the stress axis and

incubated for 5 min, followed by washing with buffer A. This results in microtubules bound to the PDMS substrate via interaction with kinesin with a parallel alignment relative to the

stretch axis. The micro-stretcher chamber was then sealed, and humid nitrogen gas was continuously purged through until the observation finished. The concentration of the kinesin was the

same in all experiments. REPETITIVE CYCLES OF RELAXATION-STRETCHING OF PDMS The pre-stretched PDMS was relaxed by a chosen strain (10.0, 12.5, 20.0, 40.0% of the pre-stretched length) to

compress the microtubule attachment points and sinusoidally buckle the microtubules. The choice of the strain level was limited by our observation system, which allows up to 40.0%

compression of the PDMS from its pre-stretched length. Repetitive cycles of relaxation and stretching were carried out until breakage of the microtubules was observed. The number of applied

repetitive cycles were chosen as power of 2, that is, 20, 21, 22, … 28. During each set of repetitive cycles PDMS was relaxed and then returned to the initial stretch, always operating with

a strain rate of 0.004 s−1 and a 1 s gap between movements. Microtubules were imaged after each motion (compression or stretching) was completed. Breaking events were identified by visually

inspecting the fluorescence signal along each microtubule and identifying inhomogeneities. After the prescribed number of compression and stretching cycles was completed, the substrate was

stretched by an additional 2.5% and imaged. This revealed additional breaks (22 for 12.5% compression and 140 for 20.0% compression) which were not included in the analysis, because it was

not clear when these breaks occurred and it was not assured that the breaks were a result of compression only and not the final 2.5% stretching. GENERATION OF SURVIVAL CURVES AND ESTIMATION

OF N50 VALUES Survival curves were constructed using the Kaplan Meier estimator; the survival probability, _S(j)_, after a set of _j_ compression cycles can be written down as the product.

$$\:S\left(j\right)={\prod\:}_{i\le\:j}(1-\frac{{d}_{i}}{{r}_{i}})$$ (4) where _d__i_ the number of breaking events during _i_ cycles and _r__i_ denotes the number of microtubules at risk

during i cycles. Pointwise standard errors of survival probabilities were estimated using Greenwood’s formula:

$$\:{\sigma\:}^{2}\left(j\right)=S{\left(j\right)}^{2}{\sum\:}_{i\le\:j}\left(\frac{{d}_{i}}{{r}_{i}({r}_{i}-{d}_{i})}\right)$$ (5) where _σ(j)_ is the pointwise standard error for the

estimate of the survival probability _S(j)_. The number of cycles required to break 50% of the microtubules N50 was estimated by fitting the following model:

$$\:{\text{log}}_{10}S\left(j\right)=\frac{{\text{log}}_{10}\left(0.5\right)-b}{\gamma\:}\cdot\:{\text{log}}_{10}\left(j\right)+b$$ (6) where the equation is parametrized such that b is an

intercept term and γ corresponds to the \(\:{\text{log}}_{10}{N}_{50}\). The above equation is fit using least squares regression with the σ(j) derived from Eq. (5) used as weights. Fitting

is conducted using the _nls_ function from the R ‘stats’ package. Standard errors from the fit for _γ_ are reported as error bars. DATA AVAILABILITY The original experimental recording used

as the basis of this study are available at: https://doi.org/10.5061/dryad.6hdr7sr3v. REFERENCES * Ingber, D. E., Wang, N. & Stamenovic, D. Tensegrity, cellular biophysics, and the

mechanics of living systems. _Rep. Prog Phys._ 77, 046603 (2014). Article  ADS  MathSciNet  PubMed  PubMed Central  Google Scholar  * Arai, Y. et al. Tying a molecular knot with optical

tweezers. _Nature_. 399, 446–448 (1999). Article  ADS  CAS  PubMed  Google Scholar  * Odde, D. J., Ma, L., Briggs, A. H., DeMarco, A. & Kirschner, M. W. Microtubule bending and breaking

in living fibroblast cells. _J. Cell. Sci._ 112, 3283–3288 (1999). Article  CAS  PubMed  Google Scholar  * Robison, P. et al. Detyrosinated microtubules buckle and bear load in contracting

cardiomyocytes. _Science_. 352, aaf0659 (2016). Article  PubMed  PubMed Central  Google Scholar  * Saper, G. & Hess, H. Synthetic systems powered by Biological Molecular Motors. _Chem.

Rev._ 120, 288–309 (2020). Article  CAS  PubMed  Google Scholar  * Kabir, A. M. R., Sada, K. & Kakugo, A. Breaking of buckled microtubules is mediated by kinesins. _Biochem. Biophys.

Res. Commun._ 524, 249–254 (2020). Article  CAS  PubMed  Google Scholar  * Månsson, A. The potential of myosin and actin in nanobiotechnology. _J. Cell. Sci._ 136, (2023). * van Delft, F. C.

M. J. M. et al. Roadmap for network-based biocomputation. _Nano Futur_. 6, 032002 (2022). Article  ADS  Google Scholar  * Gittes, F., Mickey, B., Nettleton, J. & Howard, J. Flexural

rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. _J. Cell. Biol._ 120, 923–934 (1993). Article  CAS  PubMed  Google Scholar  * Janson, M. E. &

Dogterom, M. A. Bending Mode Analysis for growing microtubules: evidence for a velocity-dependent rigidity. _Biophys. J._ 87, 2723–2736 (2004). Article  ADS  CAS  PubMed  PubMed Central 

Google Scholar  * Pampaloni, F. et al. Thermal fluctuations of grafted microtubules provide evidence of a length-dependent persistence length. _Proc. Natl. Acad. Sci. U S A_. 103,

10248–10253 (2006). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Kis, A. et al. Nanomechanics of microtubules. _Phys. Rev. Lett._ 89, 248101 (2002). Article  ADS  CAS  PubMed

  Google Scholar  * Kononova, O. et al. Tubulin Bond Energies and Microtubule Biomechanics determined from Nanoindentation in Silico. _J. Am. Chem. Soc._ 136, 17036–17045 (2014). Article 

CAS  PubMed  PubMed Central  Google Scholar  * Jiang, N., Bailey, M. E., Burke, J. & Ross, J. L. Dima, R. I. Modeling the effects of lattice defects on microtubule breaking and healing.

_Cytoskeleton (Hoboken)_. 74, 3–17 (2017). Article  CAS  PubMed  Google Scholar  * Schaedel, L. et al. Microtubules self-repair in response to mechanical stress. _Nat. Mater._ 14, 1156–1163

(2015). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Tsitkov, S. et al. The rate of microtubule breaking increases exponentially with curvature. _Sci. Rep._ 12, 20899 (2022).

Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Beyer, M. K. & Clausen-Schaumann, H. Mechanochemistry: the mechanical activation of covalent bonds. _Chem. Rev._ 105,

2921–2948 (2005). Article  CAS  PubMed  Google Scholar  * Bicek, A. D. et al. Anterograde microtubule transport drives microtubule bending in LLC-PK1 epithelial cells. _Mol. Biol. Cell._ 20,

2943–2953 (2009). Article  CAS  PubMed  PubMed Central  Google Scholar  * Suresh, S. _Fatigue of Materials_ (Cambridge University Press, 1998). * Kabir, A. M. R. et al. Biomolecular motor

modulates mechanical property of microtubule. _Biomacromolecules_. 15, 1797–1805 (2014). Article  CAS  PubMed  Google Scholar  * Kabir, A. M. R. et al. Buckling of microtubules on a 2D

Elastic Medium. _Sci. Rep._ 5, 17222 (2015). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Kabir, A. M. R., Inoue, D., Kakugo, A., Kamei, A. & Gong, J. P. Prolongation of

the active lifetime of a biomolecular motor for in vitro motility assay by using an inert atmosphere. _Langmuir_ 27, 13659–13668 (2011). Article  CAS  PubMed  Google Scholar  * Nasrin, S. R.

et al. Regulation of Biomolecular-Motor-Driven Cargo Transport by microtubules under mechanical stress. _ACS Appl. Bio Mater._ 3, 1875–1883 (2020). Article  CAS  PubMed  Google Scholar  *

Weibull, W. A statistical distribution function of wide applicability. _J. Appl. Mech._ (1951). * Hostettler, N., Cohades, A. & Michaud, V. Statistical fatigue investigation and failure

prediction of a Healable Composite System. _Front. Mater._ 7, 561852 (2020). Article  Google Scholar  * Brangwynne, C. P. et al. Microtubules can bear enhanced compressive loads in living

cells because of lateral reinforcement. _J. Cell. Biol._ 173, 733–741 (2006). Article  CAS  PubMed  PubMed Central  Google Scholar  * Tang-Schomer, M. D., Patel, A. R., Baas, P. W., Smith,

D. H. & Smith, D. Mechanical breaking of microtubules in axons during dynamic stretch injury underlies delayed elasticity, microtubule disassembly, and axon degeneration. _FASEB J._ 24,

1401–1410 (2010). Article  CAS  PubMed  PubMed Central  Google Scholar  * Wang, G. T., Liu, H. Y., Saintier, N. & Mai, Y. W. Cyclic fatigue of polymer nanocomposites. _Eng. Fail. Anal._

16, 2635–2645 (2009). Article  CAS  Google Scholar  * Caporizzo, M. A., Chen, C. Y., Salomon, A. K., Margulies, K. B. & Prosser, B. L. Microtubules provide a viscoelastic resistance to

myocyte motion. _Biophys. J._ 115, 1796–1807 (2018). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Uchida, K., Scarborough, E. A. & Prosser, B. L. Cardiomyocyte

microtubules: control of mechanics, transport, and remodeling. _Annu. Rev. Physiol._ 84, 257–283 (2022). Article  CAS  PubMed  Google Scholar  * Théry, M. & Blanchoin, L. Microtubule

self-repair. _Curr. Opin. Cell. Biol._ 68, 144–154 (2021). Article  PubMed  Google Scholar  * Xu, Z. et al. Microtubules acquire resistance from mechanical breakage through intralumenal

acetylation. _Science_ 356, 328–332 (2017). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Maksudov, F., Kliuchnikov, E., Marx, K. A., Purohit, P. K. & Barsegov, V.

Mechanical fatigue testing in silico: dynamic evolution of material properties of nanoscale biological particles. _Acta Biomater._ 166, 326–345 (2023). Article  CAS  PubMed  Google Scholar 

* Schaap, I. A. T., Carrasco, C., de Pablo, P. J., MacKintosh, F. C. & Schmidt, C. F. Elastic Response, Buckling, and instability of microtubules under Radial Indentation. _Biophys. J._

91, 1521–1531 (2006). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Hess, H., Howard, J. & Vogel, V. A Piconewton Forcemeter assembled from microtubules and Kinesins.

_Nano Lett._ 2, 1113–1115 (2002). Article  ADS  Google Scholar  * Clausen-Schaumann, H., Seitz, M., Krautbauer, R. & Gaub, H. E. Force spectroscopy with single bio-molecules. _Curr.

Opin. Chem. Biol._ 4, 524–530 (2000). Article  CAS  PubMed  Google Scholar  * Reid, T. A., Coombes, C. & Gardner, M. K. Manipulation and quantification of microtubule lattice integrity.

_Biol. Open._ 6, 1245–1256 (2017). CAS  PubMed  PubMed Central  Google Scholar  * Gavrilov, L. A. & Gavrilova, N. S. Reliability theory of aging and longevity. in Handbook of the Biology

of Aging 3–42 (Elsevier, (2005). * Castoldi, M. & Popov, A. V. Purification of brain tubulin through two cycles of polymerization- depolymerization in a high-molarity buffer. _Protein

Exp. Purif._ 32, 83–88 (2003). Article  CAS  Google Scholar  * Peloquin, J., Komarova, Y. & Borisy, G. Conjugation of fluorophores to tubulin. _Nat. Methods_ 2, 299–303 (2005). Article 

CAS  PubMed  Google Scholar  * Fujimoto, K. et al. Colocalization of quantum dots by reactive molecules carried by motor proteins on polarized microtubule arrays. _ACS Nano_ 7, 447–455

(2013). Article  CAS  PubMed  Google Scholar  * Nasrin, S. R., Kabir, A. M. R. & Kakugo, A. Cargo Transport by Microtubule-Associated motor protein along mechanically deformed

microtubules. In _Methods in Molecular Biology_ vol. 2430 291–302 (Humana Press Inc., 2022). Download references ACKNOWLEDGEMENTS N.M.B.K. gratefully acknowledges support through an

International Fellowship for Research in Japan by the Japan Society for the Promotion of Science (JSPS). S.R.N., A.K. and H.H. were supported by grant RGP0026_2021 from the Human Frontiers

Science Program, grant JPNP20006, commissioned by the Future AI and Robot Technology Research and Development Project from the New Energy and Industrial Technology Development Organization

(NEDO), Grant-in-Aid for Scientific Research on Innovative Areas “Molecular Engine” JP18H05423, Grant-in-Aid for Scientific Research (A) JP21H04434, and Grant-in-Aid for Challenging Research

(Pioneering) JP17K19211. S.R.N. was supported by Grant-in-Aid for Early-Career Scientists 22K18165 and JSPS Postdoctoral Fellowships for Research in Japan (Standard). J.B.R. and H.H. were

supported by NSF grant 2230116. AUTHOR INFORMATION Author notes * These authors contributed equally: Syeda Rubaiya Nasrin and Neda M. Bassir Kazeruni. AUTHORS AND AFFILIATIONS * Division of

Physics and Astronomy, Graduate School of Science, Kyoto University, Kitashirakawa-Oiwake-Cho, Sakyo-ku, Kyoto, 606-8502, Japan Syeda Rubaiya Nasrin & Akira Kakugo * Department of

Biomedical Engineering, Columbia University, 1210 Amsterdam Avenue, New York, NY, 10027, USA Neda M. Bassir Kazeruni, Juan B. Rodriguez III, Stanislav Tsitkov & Henry Hess * Department

of Biological Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA Stanislav Tsitkov Authors * Syeda Rubaiya Nasrin View author publications You can also search for this

author inPubMed Google Scholar * Neda M. Bassir Kazeruni View author publications You can also search for this author inPubMed Google Scholar * Juan B. Rodriguez III View author publications

You can also search for this author inPubMed Google Scholar * Stanislav Tsitkov View author publications You can also search for this author inPubMed Google Scholar * Akira Kakugo View

author publications You can also search for this author inPubMed Google Scholar * Henry Hess View author publications You can also search for this author inPubMed Google Scholar

CONTRIBUTIONS A.K. and H.H. conceptualized and designed the study. A.K. supervised the experiments, S.R.N., J.B.R., S.T., A.K. and H.H. wrote the manuscript, S.R.N. and N.M.B.K. conducted

the experiments. N.M.B.K. and J.B.R. analyzed the experiments. S.T. performed the statistical analysis. CORRESPONDING AUTHORS Correspondence to Akira Kakugo or Henry Hess. ETHICS

DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in

published maps and institutional affiliations. ELECTRONIC SUPPLEMENTARY MATERIAL Below is the link to the electronic supplementary material. SUPPLEMENTARY MATERIAL 1 RIGHTS AND PERMISSIONS

OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or

format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or

other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in

the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the

copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Nasrin, S.R., Bassir

Kazeruni, N.M., Rodriguez, J.B. _et al._ Mechanical fatigue in microtubules. _Sci Rep_ 14, 26336 (2024). https://doi.org/10.1038/s41598-024-76409-7 Download citation * Received: 26 February

2024 * Accepted: 14 October 2024 * Published: 01 November 2024 * DOI: https://doi.org/10.1038/s41598-024-76409-7 SHARE THIS ARTICLE Anyone you share the following link with will be able to

read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing

initiative KEYWORDS * Fatigue failure * Fatigue strength exponent * Microtubule * Tubulin * Mechanobiology