ABSTRACT To investigate the reasonable calculation value of the transverse design bending moment of a long-span cantilever box girder bridge deck under vehicle load, the plate beam model and

beam element frame model were established according to the concept of load effective distribution width in the Chinese highway specifications. The local finite element model and full bridge

model of a long-cantilever plate were established using the plate-shell element. The practical calculation formula and finite element analysis of the transverse bending moment of a bridge

deck were studied. The results showed that the transverse bending moment of the long-cantilever plate calculated using Baider Bahkt formula slightly deviated from the calculated value of the

Article Open access 27 February 2025 A NUMERICAL ANALYSIS OF BUCKLE CABLE FORCE OF CONCRETE ARCH BRIDGE BASED ON STRESS BALANCE METHOD Article Open access 21 July 2022 STUDY ON DYNAMIC

RESPONSES AND IMPACT FACTORS OF LONG SPAN DECK TYPE CFST ARCH BRIDGE UNDER VEHICLE LOADS Article Open access 13 May 2025 INTRODUCTION The top slab between the webs of a box girder and the

cantilever plate is commonly called the bridge deck. A reasonable design of bridge decks is a concern of many bridge researchers and designers. Currently, the research on the bridge deck of

box girders mainly focuses on the fatigue problem of composite structures, but the research on the wheel load effective distribution width and transverse bending moment of box girders under

vehicle loads remains insufficient. The wheel load transverse distribution width is mainly calculated based on current highway specifications1,2, and relevant provisions are mainly obtained

from the study of the bridge deck of T-shaped beams. The box girder and T-shaped beam have notably different cross sections, the internal forces of the bridge deck deviate from the actual

conditions as calculated using the plate-beam method and the Sawko formula stipulated in highway specifications. This discrepancy results in an unreasonable design of the box girder bridge

deck, thereby directly impacting its safety, toughness, and durability. In the calculation of bridge decks, the wheel load should first be determined. According to the Specifications for

Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts (JTG 3362 − 2018, China), the wheel load value is determined according to the concept of effective

distribution width, and the calculation model of a bridge deck is a simply supported plate-beam per unit width. The advantage of this provision is that the calculation process of the bridge

deck is simple, clear, and easy for engineers to operate. Although the elastic plate theory is used to consider the bearing effect of the bridge deck, there is a large deviation in the

results of the highway specification methods and finite element calculation. Li HJ et al.3 discussed the influence of the support type in the bridge deck calculation on the transverse

bending moment value. A reasonable determination of the wheel load effective distribution width is the key to the transverse bending moment calculation of bridge decks. Xu LP et al.4 applied

the energy analogy principle and used the G-M methods to calculate the wheel load effective distribution width on the top slab of the box girder. Fang Z et al.5,6,7 experimentally studied

the wheel load effective distribution width of reinforced concrete box girder. Cheng XY et al.8 studied the wheel load effective distribution width of the single-box double-cell box girder,

analyzed the transversal internal force of the box girder using an expanded-continuous-plate, and believed that the bending moment at the fulcrum of the bridge deck could be taken as 0.5

times the value at the mid-span of the simply supported plate-beam. Zhao P et al.9,10 studied the wheel load effective distribution width of corrugated steel webs and believed that the

calculated value of highway specifications was more conservative than the finite element calculation value and test value. Qiao P et al.11 calculated the wheel load effective distribution

width of multi-cell box girders according to that of single-cell box girders, and the error did not exceed 10%. The cantilever plate of box girders generally has a large length along the

longitudinal direction of the girder, which is much longer than the cantilever length along the horizontal direction. Based on these factors, the design bending moment of the top slab

obtained according to the highway specification calculation will be very different from the actual situation. Although the highway specifications (JTG 3362 − 2018) have revised the

provisions on the calculation of the design transverse bending moment of cantilever plates, Sawko formula is used for long cantilever plates. However, Sawko formula is only used for

cantilever plates with equal thickness, which is inconsistent with the actual situation of cantilever plates with variable thickness. Bakht B et al.12 developed an empirical formula to

calculate cantilever plates with variable thickness, which is more consistent with the actual situation than Sawko’s formula. This work verifies this situation through a numerical example.

Reference13,14,15 analyzed the transverse bending moment of cantilever plates through finite element methods and studied the effects of the cantilever plate length, thickness, and other

factors on the internal force distribution. Based on the finite element analysis, Zhang G et al.16,17 analyzed the wheel load effective distribution width and bending moment of a cantilever

plate using sub-model technology and believed that the application scope of Sawko formula for calculating the bending moment of a cantilever plate was small, which actually showed that the

error of Sawko formula for calculating variable thickness cantilever plate was too large. The calculation of the bridge deck is generally based on the analysis of the elastic stage. Fang Z

et al.18 extended the calculation of the wheel load effective distribution width of the cantilever plate to the plastic stage. When a wheel load acts on the end of the cantilever plate, the

effective distribution width is 1.58 times that of the elastic stage. The above studies have a consensus on the research of bridge decks, and the calculation of bridge decks in the current

specification is notably different from the actual situation because of the reasonable selection of support of bridge decks, spatial mechanical characteristics of cantilever plates, and

other factors. Therefore, considering the differences in mechanical models of bridge deck calculation, influence of the anti-collision wall on the wheel load effective distribution width,

and other factors, this work used the finite element methods to establish the simply supported plate-beam model, beam element frame model per unit width, and plate-shell element box girder

model to analyze the calculation of the transverse bending moment of the bridge deck. This calculation supplements the calculation of the bending moment of the box girder bridge deck in the

highway specifications and enriches the research on the calculation of the bending moment of cantilever plates in box girders. Taking the actual bridge as the research object, the results

and conclusions can be used as a reference for the design and calculation of box girder bridge decks. PROVISIONS FOR BRIDGE DECK CALCULATION AND RELEVANT EMPIRICAL FORMULAS PROVISIONS OF

HIGHWAY SPECIFICATIONS The specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts(JTG 3362 − 2018, china) is hereinafter referred to as

highway specifications. According to the provisions on the calculation of the bridge deck, the bending moment of the bridge deck connected with the beam rib as a whole can be calculated

according to the simplified method. _M_0 is the mid-span bending moment value1,2 of the simply supported plate with the same span. At the fulcrum, the design bending moment value is _M_ = − 

0.7_M_0. At the mid-span, _M_ = + 0.7_M_0 (when the ratio of the plate thickness to the beam rib height is equal to or greater than 1/4); _M_ = + 0.5_M_0(when the ratio of the plate

thickness to the beam rib height is less than 1/4). When calculating the bending moment of the bridge deck, one first determines the wheel load effective distribution width of the vehicle

load. For a one-way slab, the calculation of the wheel load effective distribution width on the bridge deck is detailed in the highway specifications1,2. See the highway specifications for

the model of the vehicle load. When the wheel is on the cantilever plate of the box girder, the old specification stipulates that when _l_c is not greater than 2.5 m, the wheel load

distribution width _a_, which is perpendicular to the cantilever plate span, is calculated according to _a_ = (_a_1 + 2_h_) + 2_l_c, and _l_c is the distance from the outer edge of the

pavement to the outer edge of the web plate with the wheel landing size parallel to the cantilever plate span direction, _h_ is the pavement thickness, _a_1 is the wheel landing dimension

perpendicular to the plate span direction. When _l_c is greater than 2.5 m, _a_ = 0.8(_a_1 + 2_h_) + 1.6_l_c. According to the current specifications, the transverse bending moment of the

long cantilever plate is calculated according to Sawko formula. PRACTICAL CALCULATION FORMULA FOR LONG CANTILEVER PLATE OF BOX GIRDER The calculation of cantilever plates of bridge decks is

complex. Various practical calculation methods are based on the following assumptions4: (1) The root of the cantilever plate is fixed on the beam rib, and the beam rib has a much greater

bending stiffness than the cantilever plate of the box girder. (2) To calculate the transverse bending moment of a cantilever plate under live load, the calculated width of the cantilever

plate can be determined according to the concept of load transverse distribution width of a beam. Because the long cantilever plate is considered to have infinite width along the

longitudinal direction of the bridge, the value calculated using the simply supported plate-beam model has a large deviation. The bending moment of the long cantilever plate is often

calculated using Sawko formula and Baider Bahkt formula, among others. Sawko formula is mainly applicable to long cantilever plates with equal thickness and is written as follows:

$$\:{m}_{x}=\:-\:\frac{P}{\pi\:}\:{A}^{{\prime\:}}\frac{1}{ch\left(\frac{y{A}^{{\prime\:}}}{{l}_{0}}/\frac{\xi\:}{{l}_{0}}\right)}$$ (1) where _P_ is the concentrated load;

\(\:{A}^{{\prime\:}\:}\)is a parameter that can be obtained from a look-up table; \(\:\xi\:\:\)is the distance from the concentrated load to the root of the cantilever plate;

\(\:{l}_{0\:}\)is the calculated width of the cantilever plate; and \(\:{m}_{x}\) is the bending moment per unit width at the root of the cantilever plate. Baider Bahkt formula is mainly

used to calculate cantilever plates with variable thicknesses with an edge beam. The formula is as follows:

$$\:{m}_{x}=\:-\:\frac{P}{\pi\:}\:{A}^{{\prime\prime\:}}\frac{1}{ch\left(\frac{{A}^{{\prime\prime\:}}y}{\xi\:-x}\right)}$$ (2) Where \(\:{A}^{{\prime\prime\:}}\) is a parameter that can be

obtained from a look-up table. There are great deviations in the calculation results of other practical formulas, which will not be listed in this work. BRIDGE DECK BENDING MOMENT

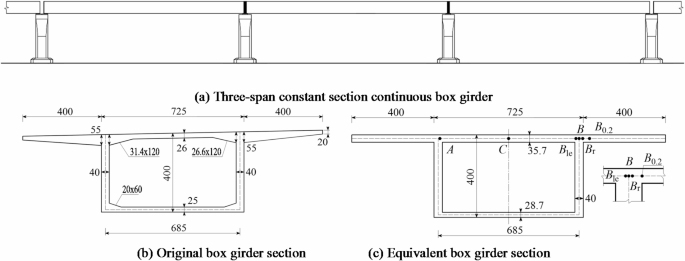
CALCULATION AND WHEEL LOAD EFFECTIVE DISTRIBUTION WIDTH In this work, an actual project was used to investigate the calculation of the bridge deck. Donghai Bridge connects Shanghai and

Yangshan port. One continuous unit is a three-hole 70-m continuous box girder bridge with equal cross sections, as shown in Fig. 1(a). The load is specified in the General Specifications for

the Design of Highway Bridges and Culverts (JTG D60-2015, China); the material modulus of elasticity is _E_ = 35 GPa, Poisson’s ratio is _µ_ = 0, the pavement thickness is 0.15 m, the

reinforced concrete unit weight is 27 kN/m3, and the anti-collision wall width is 0.5 m. To facilitate the use of plate-shell element modeling and theoretical analysis and calculation of box

girders, the box girder section in Fig. 1(b) is simplified. Under the condition of constant section area, the thicknesses of the top slab, cantilever plate, and bottom slab were adjusted,

as shown in Fig. 1(c). In the figure, _A_ is the bending moment calculation point of the left fulcrum of the top slab, _C_ is the point of the mid-span, _B_le is the point of the right

fulcrum, _B_r is the point of the cantilever plate on the right side of point _B_, and _B_0.2 is the point at the root of the cantilever plate. After the wheel load effective distribution

width had been calculated, a 1-m-wide strip was taken to calculate as the simply supported plate-beam, and the bending moment of the bridge deck specified in the highway specification was

obtained. Then, the design and checking calculation of the bridge deck were performed. WHEEL LOAD EFFECTIVE DISTRIBUTION WIDTH OF TOP AND CANTILEVER PLATE OF BOX GIRDER The lane division of

bridge deck of box girder is shown in Fig. 2(a). It is divided into left and right according to the driving direction. From right to left, three standard lanes were designed. In the

cantilever plate calculation, the vehicle load near the anti-collision wall at 0.50 m is the actual vehicle load transverse distribution. In the top slab calculation, the right rear wheel of

the vehicle load is located in the mid-span of the top slab, which is the most unfavorable position of the vehicle load calculated the top slab bending moment. The vehicle load in Fig. 2(a)

only shows the position of the rear-axle and mid-axle. Figure 2(b) shows a schematic of the load and bending moment calculation points of a bridge deck. According to the provisions of the

highway specifications (JTG 3362 − 2018), Table 1 lists the calculation results of the wheel load effective distribution width of the bridge deck. In this project example, the load

distribution width formed by the mid-axle of the vehicle load does not overlap with the rear-axle. BENDING MOMENT CALCULATION OF TOP AND CANTILEVER PLATE BASED ON BEAM ELEMENT BENDING MOMENT

OF TOP SLAB OF BOX GIRDER The dead load of the top and cantilever plate with a width of 1 m along the longitudinal direction of the bridge is 10.64 kN/m. According to the requirements of

highway specifications, Fig. 3 shows the bending moment calculation diagram of the box girder top slab. Under the combined action of the dead load and vehicle load, bending moment _M_0 = 

96.97 kN·m of the mid-span section of a simply supported plate-beam in Fig. 3 was obtained. According to the highway specifications, the bending moment at the top slab fulcrum of the box

girder is _M_ = 67.88 kN·m, and the bending moment at the mid-span is _M_= 48.49 kN·m. In the above calculation, the highway specifications consider the elastic constraint of simply

supported strips1,2. Considering the actual constraint of the top slab of the box girder, a 1-m-wide beam segment was taken to establish the beam element frame model with web and bottom slab

by using the MIDAS general finite element software. The bottom plate of the model was simply supported, and the dead load and vehicle load were calculated as shown in Fig. 3. the beam

element frame model was shown in Fig. 4. At this time, it is most advantageous to obtain the maximum bending moment in the mid-span of the top slab by arranging the vehicle load only in the

mid-span of the top slab. If the vehicle load is arranged on the cantilever plate, the bending moment at the mid-span of the top slab will decrease, and the bending moment at the top slab

fulcrum will not greatly change due to the unloading of the web. Therefore, when the vehicle load is located in the mid-span of the top slab, it is the most unfavorable position for

calculating the bending moment in the mid-span of the top slab. Under the combined action of the dead load and vehicle load, the bending moment in the mid-span of the top slab is 16.47 kN·m,

and the maximum bending moment at the top slab fulcrum is 86.29 kN·m. Table 2 compares the bending moment values calculated using the highway specifications formula and beam element frame

model for the top slab of the box girder. The bending moment of the top slab is generated by the dead load and vehicle load. The bending moment at the mid-span of the top slab is 48.49 kN·m

if calculated according to the highway specifications formula and 16.47 kN·m if calculated using the beam element frame model. If the bridge deck is designed according to the specification

calculation value, it is much more conservative and safer than the design based on the beam element frame model. The beam element frame model yields a greater bending moment at the

supporting point of the top slab than the highway specifications. Based on the wheel load effective distribution width and local uniform load on the bridge deck, the formula of the highway

specifications yields a larger bending moment value deviation at the mid-span and fulcrum of the top slab compared with the beam element frame model. BENDING MOMENT OF CANTILEVER PLATE OF

BOX GIRDER When the cantilever plate acts on the vehicle load, the impact of the anti-collision wall on the vehicle load transverse distribution should be considered. Table 1 lists the wheel

load effective distribution width affected by the anti-collision wall on the cantilever plate according to the highway specifications. When the vehicle load is simultaneously arranged in

Lanes 1 and 3, the vehicle load of Lane 1 has an unloading effect on the bending moment of the mid-span section of the top slab but an increasing effect on the bending moment of the fulcrum

section. Figure 4 shows the bending moment of the top and cantilever plate caused by the dead load and vehicle load calculated using the beam element frame model. The bending moment at the

mid-span of the top slab is 12.97 kN·m, the maximum bending moment at the fulcrum is 92.87 kN·m, the bending moment at the root of the cantilever plate is 142.71 kN·m, and the bending moment

at the intersection of the centerline of the cantilever plate and web is 157.48 kN·m. If the vehicle load is only arranged on Lane 1, the bending moment of the cantilever plate will remain

unchanged, and the bending moment of the mid-span section of the top slab will decrease. For the analysis and calculation of the cantilever plate of the box girder, the arrangement of the

vehicle load only on Lane 1 is the most unfavorable situation. When the edge of the outer wheel of the vehicle load is flush with the edge of the cantilever plate, and there is no impact of

the anti-collision wall, the bending moment at the root of the cantilever plate has the maximum value in the same case. At this time, _l_c is taken as 4 m. The bending moment at the root of

the cantilever plate of the box girder was calculated using the beam element frame model, and the bending moment generated by the vehicle load plus dead load was 148.03kN·m, as listed in

Table 2. According to the influence of anti-collision walls or not, the calculated deviation of the bending moment at the root of the cantilever plate is − 3.59%, and there is little

difference between the two conditions. Based on the concept of effective distribution width of the wheel load, using the simply supported plate-beam and beam element frame model, the

calculated bending moment of the cantilever plate cannot reflect the real bending moment of a long cantilever plate. For the long cantilever slab with _l_c greater than 2.5 m in the highway

specifications, the root bending moment value should be calculated using Sawko formula. BENDING MOMENT OF CANTILEVER PLATE CALCULATED BY PLATE-SHELL ELEMENT AND PRACTICAL FORMULA NO IMPACT

OF ANTI-COLLISION WALL The impact of the anti-collision wall was not considered to obtain the maximum bending moment at the root of the cantilever plate. The bending moment at the root of

the cantilever plate was calculated according to the beam theory, which masked the influence of an infinite-width plate on the bending moment. Then, the shell-63 element in ANSYS and plate

element in Midas were used to establish the local finite element model of the cantilever plate, which was compared with the bending moment obtained using the calculation formula in the

highway specifications. When the plate-shell element was used for modeling and analysis, the root of the cantilever plate was consolidated. The current highway specifications do not explain

the arrangement of vehicle load in the longitudinal direction of the cantilever slab. According to the old specifications, a vehicle is arranged on the cantilever slab for loading. Under a

dead load, the theoretical bending moment at the root of the cantilever plate is 96 kN·m/m. The bending moment generated by the rear-axle of the vehicle load alone is 100.914 kN·m/m, and the

bending moment generated by the arrangement of a vehicle is 104.737 kN·m/m. The bending moment on the calculation section generated by the mid-axle and front-axle of the vehicle only

increases by 3.823 kN·m/m. Using ANSYS shell-63 element modeling and calculation, the bending moments at the root of the cantilever plate caused by the vehicle load are 98.7 kN·m/m when only

the rear-axle is arranged and 103.56 kN·m/m when one vehicle is arranged. The bending moment generated by the mid-axle and front-axle only increases by 4.86 kN·m/m. Table 3 lists specific

data. When the right edge of the wheel of the mid-axle and rear-axle of the vehicle load is flush with the edge of the cantilever plate, the bending moment at the root of the cantilever

plate when only the rear-axle of the vehicle load is loaded is less than the value of the entire vehicle load, and the two models yield only small deviations from each other. In practice,

due to the impact of the anti-collision wall, there is a distance between the outer wheel edge of the vehicle and the edge of the cantilever plate. Therefore, considering the impact of the

anti-collision wall, the bending moment at the root of the cantilever plate was calculated. IMPACT OF ANTI-COLLISION WALL The cast-in-situ anti-collision wall at the cantilever plate end of

the constant cross-section continuous beam bridge is equivalent to the cantilever plate with a side beam, and it is reasonable to use Baider Bahkt formula for calculation. Baider Bahkt

formula, Sawko formula, MADIS plate element, and ANSYS shell-63 element were used to calculate the transverse bending moment at the root of the cantilever plate, and the vehicle load was

included in the effects of the rear-axle, mid-axle, and front-axle. The height of the root of the cantilever plate was 0.55 m, the height of the side beam of the free edge of the cantilever

plate was 1.05 m, and the length of the cantilever plate was 4 m. Considering the impact of the anti-collision wall, Fig. 5 shows the finite element model and internal force nephogram of the

cantilever plate. Table 3 lists the root bending moment of the cantilever plate calculated using various methods. For the bending moment at the root of the cantilever plate with an

anti-collision wall, if the calculated value of Baider Bahkt formula is taken as the standard, the calculated value deviation of the plate element is 2.32%, the deviation of the shell

element is 1.30%, and the deviation of Sawko formula is 7.72%. The highway specifications recommend using Sawko formula to calculate the bending moment at the root of the cantilever plate,

which will result in a large deviation. The local model of a plate-shell element considers the spatial effect of a vehicle load, so it is consistent with the calculated value of Baider Bahkt

formula, and the deviation is small. ANALYSIS OF CALCULATION RESULTS OF BENDING MOMENT AT THE ROOT OF CANTILEVER PLATE We arranged the entire vehicle and considered the impact of an

anti-collision wall when the vehicle load was arranged laterally. The bending moment value at the root of cantilever plate calculated by the local model of plate-shell element, by the

formula of highway specifications, by the practical formula of cantilever plate were listed in Table 3. The frame model of the beam element was used for analysis according to the method of

the specifications. When the plate-shell element analysis is used, the cantilever plate root is consolidated, the opposite side is free, a hole is taken along the longitudinal direction of

the bridge for modeling, and the two sides perpendicular to the consolidation side are simply supported. As listed in Table 3, the calculated value of Baider Bahkt formula is standard. The

deviation of the calculated value of the plate-shell element is very small. ANSYS yields a consistent value with Baider Bahkt formula. The deviation between the calculated value of the beam

element frame model based on the concept of effective distribution width in the highway specifications and that of Baider Bahkt formula is − 21.94%. The highway specifications recommend

using Sawko formula to calculate the internal force of a long cantilever plate, but from the comparison in this work, Baider Bahkt formula has better accuracy. Using the plate-shell element,

the anti-collision wall has a greater impact on the bending moment of the cantilever plate than the impact considered in the beam element frame model. REASONABLE FINITE ELEMENT MODEL FOR

INTERNAL FORCE CALCULATION OF BRIDGE DECK OF BOX GIRDER The bending moment of the top slab of the box girder under the vehicle load was calculated based on the calculation concept of the

highway specifications, and the calculation results are different from the finite element values. The results show differences among the calculated values of Sawko formula, Baider Bahkt

formula, and the plate-shell element in the calculation of the bending moment of the cantilever plate of a long box girder, Sawko formula is not optimal for the calculation of bending moment

of cantilever plate of long box girder. In the finite element modeling analysis, the arrangement of the mid-axle and front-axle of the vehicle load hardly affects the transverse bending

moment of the bridge deck generated by the rear-axle. For the finite element modeling analysis of a bridge deck, this work studies whether to use the local model or the full bridge model.

The plate element was used to establish a 70-m simply supported box girder, a 70-m fixed-end box girder, and a 3 × 70-m continuous box girder with constant cross-section. The vehicle load

was arranged to calculate the transverse bending moment of the bridge deck at the mid-span section of the box girder. The three-span continuous girder was taken as the value of the mid-span

section of the mid-span hole for comparative analysis. Figure 6 shows part of the established plate element model. Table 4 lists the calculation results. Case 1 refers to loading only the

rear-axle load during the vehicle load calculation; case 2 refers to loading the rear-axle and mid-axle load; and case 3 refers to loading the rear-axle, mid-axle, and front-axle load. In

the calculation of a three-span continuous beam, one vehicle load is arranged along each longitudinal hole of the bridge. The location of the bending moment calculation point is shown in

Fig. 2. The layout of the vehicle load considers the impact of an anti-collision wall. As listed in Table 4, the bending moment caused by vehicle load at point _B_r is 85.374 kN·m/m only

according to the modeling calculation of the simply supported box girder. If only the bending moment caused by the vehicle rear-axle load is 80.895 kN·m/m, the deviation is 5.25%, and the

bending moment of the cantilever plate caused by the vehicle load mid-axle and front-axle is relatively small. According to the calculation of the fixed-end box girder, there is little

change compared with the calculation results of the simply supported box girder. The bending moment of the cantilever plate at the mid-span section of the mid-hole is calculated according to

the three-span continuous box girder when the vehicle load is distributed in two adjacent spans, the bending moment value is 85.379 kN·m/m, and the change is small. The calculation of the

transverse bending moment of the bridge deck of the long-span cantilever box girder, which simplifies the continuous beam into a single-span simply supported beam or a single-span fixed-end

beam, hardly affects the calculation of the transverse bending moment of the mid-span section, but the effect on the vicinity of the beam end is not negligible. In the design of box girders,

there are often diaphragms with large stiffness at the beam end. It is safe to take the calculated value of the mid-span section of the box girder as the design value of the bending moment

of the bridge deck. Therefore, to simplify the calculation of bridge decks, the more complex multi-span continuous box girder can be modeled and calculated as a simple supported box girder

with the same single span. The transverse bending moment of the bridge deck caused by vehicle loads satisfies the accuracy requirements of engineering design. The interaction of vehicle

loads on adjacent spans of long-span continuous beams is small. From the calculation of this example, the bending moment of the bridge deck generated by the rear-axle load of the vehicle in

the calculation section has reached the design requirements, and the influence of the mid-axle and front-axle load of the vehicle can be ignored. When the beam element model based on the

concept of the vehicle load effective distribution width in the highway specifications calculates the bending moment of the bridge deck, the top-slab bending moment at the fulcrum and

mid-span is notably different from the actual value. STUDY ON REASONABLE DESIGN BENDING MOMENT VALUE OF BRIDGE DECK OF BOX GIRDER For the calculation of a three-span continuous box girder

bridge deck, according to the concept of the effective distribution width of vehicle loads in the highway specifications calculated by the beam element, plate-shell element modeling, and

full bridge model modeling, and Baider Bahkt formula, and other practical calculation formulas were used in this work. Considering the end restraint of a box girder, the arrangement of

vehicle loads along the longitudinal direction of the bridge, impact of an anti-collision wall, and whether the impact of the mid-axle and front-axle is considered for the vehicle load, a

reasonable design value of the bending moment of bridge deck was studied based on comparative analysis. CALCULATION VALUE OF BENDING MOMENT OF TOP SLAB OF BOX GIRDER Based on the concept of

effective distribution width in the highway specifications, Table 5 lists the bending moments at each calculation point of the bridge deck calculated using beam theory. Using the calculation

formula of the highway specifications, the bending moment of the bridge deck calculated according to the simply supported plate-beam cannot accurately reflect the constraint of the web

plate on the bridge deck, which results in an unreasonable bending moment calculation. Therefore, a beam element frame model was established to calculate the bending moment of the bridge

deck by loading the vehicle load only on the top slab. Although the bending moment at the fulcrum calculated using the simply supported plate-beam model according to the highway

specifications is similar to that at point _B_le, the bending moment at the mid-span of the top slab is very different. Considering the vehicle load on the top and cantilever plate and the

impact of the anti-collision wall, the bending moment of the bridge deck was calculated. Because of the unloading effect of the vehicle load on the cantilever plate, the bending moment in

the mid-span of the top slab decreased, whereas the bending moment at the fulcrum increased. If the bending moment of the top slab is designed by multiplying coefficient in the highway

specifications, there will be a deviation from the actual situation. Table 5 shows that according to the concept of vehicle load effective distribution width in the highway specifications,

the simply supported plate-beam model to calculate the bending moment of the top slab does not obtain ideal results and masks the characteristics of the spatial stress of the box girder.

Thus, the finite element model of the plate element full bridge was established. The vehicle load is loaded on the top slab of the box girder and cantilever plate at the same time. Table 6

shows the bending moments of _A_, _B_le, _C_, and other points of the bridge deck caused by the dead load and vehicle load. The full bridge space model of the plate element has a higher

calculation accuracy and a larger bending moment value on the cantilever plate than the frame model of the beam element. Figure 7 compares the bending moments at each calculation point of

the bridge deck obtained using different methods. The ordinate represents the bending moment calculation methods. The bending moment at point _C_ and calculation result of the frame model of

the beam element are relatively small, and the highway specifications and finite element model of the entire bridge yield similar values. The top-slab bending moment at the fulcrum,

calculation results of the beam element frame model, and results of the full bridge finite element model have little deviations, and the results of the highway specifications are small.

Therefore, the design bending moment of the top slab of the box girder according to the calculation value of the highway specifications is unsafe at the fulcrum and too conservative at the

mid-span of the top slab. Footnote of Fig. 7. In the vertical coordinate, 1, 2, and 3 represent the full bridge model with a plate element using the simply supported beam model, fixed-end

beam model, and continuous beam model, respectively; 4 is the calculation using the beam element frame model (vehicle load acting on the top and cantilever plate); 5 is the calculated result

according to the highway specifications; and 6 is the beam element frame model (only the top slab acts on the vehicle load). CALCULATION VALUE OF BENDING MOMENT OF CANTILEVER PLATE OF BOX

GIRDER Tables 5, 6 and 7 show the bending moments at points _B_r and _B_0.2 on the cantilever plate of a box girder. The bending moments at _B_r are − 157.48 kN·m/m when the anti-collision

wall has an impact and − 161.51 kN·m/m when the anti-collision wall has no impact according to the concept of the vehicle load effective distribution width in the highway specifications and

as calculated using the beam element frame model. The full bridge plate element model yields a greater value than the beam element. For example, the value calculated according to the full

bridge model of the simply supported beam is − 190.513 kN·m/m. For the bending moment at point _B_0.2, the bending moment calculated using the full bridge model of a simply supported beam is

− 169.303 kN·m/m; the calculation values of the full bridge model of a fixed-end beam and a continuous beam are very close to this value, which is less than the bending moment at _B_r. The

finite element full bridge model yields a greater value than the beam element frame model and a smaller value than the local model of the plate element and practical formula. Table 7 shows

the bending moment at _B_0.2 calculated using the local model of the plate element of a cantilever plate, and Using the practical calculation formula of a long cantilever plate. Because the

local model of the cantilever plate cannot consider the unloading effect of the web, the calculated value is larger than that of the entire bridge model. For the bending moment of the

cantilever plate, Fig. 8 compares the results obtained using different methods and calculation models. The plate-shell element and Baider Bahkt formula yield relatively similar bending

moments at the root of the cantilever plate, whereas the calculation results of Sawko formula, which is recommended by the highway specifications, and the calculation results of the beam

element frame model have large deviations. For the bending moment calculation of the long cantilever plate, Baider Bahkt formula is more reasonable than Sawko formula. CONCLUSIONS Through

the calculation and research on the bending moment of the bridge deck of an engineering example, considering the constraints at the end of the box girder, impact of the anti-collision wall

on the transverse layout of the vehicle load, longitudinal layout of the vehicle load along the bridge, and whether it is necessary to consider the impact of the mid-axle and front-axle of a

vehicle on the calculation results of the rear-axle load, the following conclusions were obtained: (1) When the box girder with a long-span cantilever plate, a large beam height, and a

ratio of plate thickness to beam-rib height less than 1/4, the value of the mid-span bending moment of the top slab calculated by the highway specifications formula was closed to the value

by the finite element model of the full bridge, but the value calculated using the beam element frame model is relatively small. The top slab bending moment at the fulcrum, calculation value

of the full bridge finite element model, and calculation value of the beam element frame model have small deviations, but the calculation value of the highway specifications has large

deviations. The top slab bending moment calculated according to the highway specifications can be appropriately reduced at the mid-span and increased at the fulcrum. (2) In the calculation

of the bending moment at the root of a long cantilever plate of a box girder under a vehicle load, Baider Bahkt formula yields a value consistent with that obtained using the shell-63

element. In particular, Baider Bahkt formula results in deviations of 1.3%, 2.32%, and 7.72% from the values of the shell-63 element, plate element, and Sawko formula, respectively. The

calculated value of the beam element that according to the concept of the effective width of load distribution is quite different from the calculated value of Baider Bahkt formula. (3) For

the calculation of the bending moment at the root of the cantilever plate of the box girder, the value calculated by the full bridge model of the box girder is smaller than that calculated

by the local model of the cantilever plate, and is larger than that calculated by the beam element frame model based on the concept of the effective distribution width of the vehicle load.

Although the difference between the practical formula and the local model of the cantilever plate is small, the local model of the cantilever plate cannot consider the unloading effect of

the web, and the full bridge model is more in line with the actual situation. (4) For this example project, when we calculated the bending moment of a long-span cantilever box girder bridge

deck, the mid-axle and front-axle of vehicle load hardly affected the calculation results of the rear-axle load. The calculation of the transverse bending moment of the bridge deck in the

mid-span of a continuous beam can be decomposed into the modeling calculation of a simply supported beam with the same single span, the deviation is small, and the accuracy satisfies the

needs of the actual project. The constraint conditions of the box girder hardly affect the calculated transverse bending moment of the bridge deck in the mid-span. In the calculation of the

transverse bending moment of the cantilever plate, the impact of an anti-collision wall on the lateral distribution of the vehicle load should be considered. DATA AVAILABILITY All data

generated or analysed during this study are included in this published article. REFERENCES * JTG 3362 – 2018. Specifications for design of highway reinforced concrete and prestressed

concrete bridges and culverts[S] . Beijing: China Communication Press, 2018.  Google Scholar  * JTG D60-2015. General specifications for design of highway bridges and culverts[S]. Beijing:

China Communication Press, 2015. * Li, H. J. Review on special issues in prestressed concrete box girders with corrugated steel webs[J]. Journal of Basic Science and Engineering, 26(2):

440–454. https://doi.org/CNKI:SUN:YJGX.0.2018-02-020 (2018). * Xu, L. P., Hu, S. D. & Du, G. H. Application of G–M method in analysing the deck of box girders[J]. Journal of Tongji

University, 28(3): 353–358. https://doi.org/CNKI:SUN:TJDZ.0.2000-03-023 (2000). * Fang, Z. & Zhang, Z. T. Research on the effective distribution width of transverse forces of reinforced

concrete box beam[J]. China Journal of Highway and Transport, 14(1): 35 – 38. https://doi.org/10.3321/j.issn:1001-7372.2001.01.008 (2001). * Fang, Z. & Zhang, Z. T. The effective

distribution width of the transverse internal force in R-C box girders with varied section[J]. _J. Hunan University(Natural Sciences)_. 30 (6): 82–85.

https://doi.org/10.3321/j.issn:1000-2472.2003.06.022 (2003). Article  MATH  Google Scholar  * Fang, Z., Cao, Q. & Zheng, H. Plastic analysis of transverse effective width of top slabs in

reinforced concrete box-girders[J]. China Journal of Highway and Transport, 30(10): 45 – 52. https://doi.org/CNKI:SUN:ZGGL.0.2017-10-007 (2017). * Cheng, X. Y. Effective width in

calculation of transverse internal force of box girder with twin-cells [J]. _J. Hunan University: Nat. Sci._ 13 (1), 34–39 . https://doi.org/CNKI:SUN:HNDX.0  (1986). MathSciNet  MATH  Google

Scholar  * Zhao, P., Rong, X. L. & Ye, J. S. Research on the lateral effective width of composite box-girders with corrugated steel webs[J]. _J. Hunan University(Natural Sciences)_. 43

(7), 105–110. https://doi.org/10.3969/j.issn.1674-2974.2016.07.014 (2016). Article  MATH  Google Scholar  * Zhao, P. et al. Research on transverse load bearing behavior of variable

cross-section PC composite continuous box girder with corrugated steel webs[J]. _Bridge Constr._ 53 (2), 90–97. https://doi.org/10.20051/j.issn.1003-4722.2023.02.012 (2023). Article  MATH 

Google Scholar  * Qiao, P. et al. Analysis of single-box multi-cell composite box girder with corrugated steel webs due to transverse force[J]. _Eng. Mech._ 37 (9), 161–172.

https://doi.org/10.6052/j.issn.1000-4750.2019.10.0627 (2020). Article  MATH  Google Scholar  * Bakht, B. et al. Analysis of cantilever decks of thin-walled box girder bridges[J]. Journal of

Structure Engineering, 118(3): 873 – 874. https://doi.org/10.1061/(asce)0733-9445(1992)118:3(873) (1992). * Shih, T. C. & Jiang, Z. G. Analysis of cantilever decks of thin-walled box

girder bridge[J]. _J. Struct. Egineering_. 116 (9), 2410–2418. https://doi.org/10.1061/(ASCE)0733-9445(1990)116:9(2410) (1990). Article  MATH  Google Scholar  * Cheung, M. S. & Chan, M.

Y. T. Finite strip evaluation of effective flange width of bridge girders[J]. _Can. J. Civ. Eng._ 5 (2), 174–185. https://doi.org/10.1139/l78-022 (1978). Article  MATH  Google Scholar  * Ma,

H. D. & Zhang, Y. H. Finite element analysis for long cantilever slab of box girders[J]. _J. Lanzhou Jiaotong Univ._ 28 (6), 60–62. https://doi.org/10.3969/j.issn.1001-4373.2009.06.015

(2009). Article  MATH  Google Scholar  * Zhang, G., Wang, X. M. & He, S. H. Space numeric simulation of concrete box bridge cantilever plate[J]. _J. Wuhan Univ. Technol. (Transportation

Science & Engineering)_. 31 (3), 434–437. https://doi.org/10.3963/j.issn.2095-3844.2007.03.016 (2007). Article  MATH  Google Scholar  * Zhang, G., He, S. H. & Wang, X. M. Calculation

method for cantilever slab of concrete box girder[J]. _J. Chang’an University(Natural Sci. Edition)_. 27 (6), 58–62. https://doi.org/10.3321/j.issn:1671-8879.2007.06.013 (2007). Article 

MATH  Google Scholar  * Fang, Z., Zheng, H. & Liu, S. Y. Plastic analysis of the lateral effective width of cantilever slabs of reinforced concrete box-girders[J]. China Civil

Engineering Journal, 45(3): 35–41. https://doi.org/CNKI:SUN:TMGC.0.2012-03-007 (2012). Download references ACKNOWLEDGEMENTS The work described in this paper was supported by grants from the

Gansu Provincial Department of Education: University Teachers’ Innovation Fund (Grant No. 2024B-140), and the Lanzhou City University Doctoral Research Fund (Grant No. LZCU-BS2022-09), and

the Discipline Construction Project of Lanzhou City University. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Civil Engineering, Lanzhou City University, Lanzhou, 730070, China

Zhaonan Wang * School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou, 730070, China Ruizheng Wang Authors * Zhaonan Wang View author publications You can also search for this

author inPubMed Google Scholar * Ruizheng Wang View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS Zhaonan Wang conducted the theoretical

calculations and analysis of this article, and Ruizheng Wang created the charts for this article. This article was jointly completed by Zhaonan Wang and Ruizheng Wang. I would like to

declare that the work described was original research that has not been published previously, and not under consideration for publication elsewhere, in whole or in part. CORRESPONDING AUTHOR

Correspondence to Zhaonan Wang. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral

with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons

Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give

appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission

under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons

licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit

http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Wang, Z., Wang, R. Research on calculation of transverse bending moment of

deck of box girder with long-span and long cantilever. _Sci Rep_ 15, 3486 (2025). https://doi.org/10.1038/s41598-025-87723-z Download citation * Received: 15 August 2024 * Accepted: 21

January 2025 * Published: 28 January 2025 * DOI: https://doi.org/10.1038/s41598-025-87723-z SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get

shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative KEYWORDS * Bridge

engineering * Transverse bending moment * Long cantilever plate * Wheel load effective distribution width * Vehicle load