ABSTRACT Critical slowing down of the dynamics of a system near bifurcation points leads to long recovery times towards stable states in response to perturbations. Analogously, for systems

initially in an unstable state, the relaxation also becomes slow near bifurcation points. Here we explore the onset of self-sustained oscillations in a sideband-driven electromechanical

resonator, when the zero-amplitude state changes from stable to unstable. As the system moves away from the unstable zero-amplitude state due to thermal fluctuations, the vibration amplitude

increases exponentially with time until nonlinear effects limit the growth and the system settles into stable self-sustained vibrations. We show that the first passage time for the

exponential rise exhibit power law scaling with the distance to either the supercritical or subcritical Hopf bifurcation point with exponent of − 1. SIMILAR CONTENT BEING VIEWED BY OTHERS

NOISE-INDUCED SWITCHING FROM A SYMMETRY-PROTECTED SHALLOW METASTABLE STATE Article Open access 26 June 2020 NONLINEAR INTERACTIONS BETWEEN VIBRATION MODES WITH VASTLY DIFFERENT

EIGENFREQUENCIES Article Open access 16 August 2023 TOPOLOGICAL PHASE LOCKING IN STOCHASTIC OSCILLATORS Article Open access 24 May 2025 INTRODUCTION The dynamics of a system become slow when

the stability of its state changes across a bifurcation point. Starting from a stable state, the time required for the recovery from perturbations diverges approaching the critical point.

Systems experiencing critical slow down have been explored in various theoretical and experimental settings1,2,3,4,5. It has been proposed that the increase in either the recovery time or

the variance can serve as a warning signal for the approach of a critical threshold6,7. If the system parameter is changed further beyond the critical value, the state changes from stable to

unstable. Fluctuations initiate the relaxation away from the unstable state. The interplay between fluctuations and relaxation plays an important role in many non-equilibrium systems such

as supercooled liquids8, superfluorescence9 and buildup of laser oscillations10. Similar to the critical slow down in the recovery of stable states, the relaxation away from unstable states

is also expected to become slow near a critical point. In situations where the control parameter is continuously swept across the critical point, it has been found that bifurcation of the

system is delayed due to the slow dynamics, leading to hysteresis11,12,13,14,15. Near the critical point, the system does not follow the stationary state in a quasi-static manner. Decreasing

the sweep rate only reduces but does not completely eliminate the hysteresis2. Delayed bifurcations have been studied in a wide range of systems, from lasers2,16 to chemical reactions17.

Alternatively, the control parameter can be discontinuously changed so that the state becomes unstable abruptly. Scaling theories18 and other formalisms19,20,21 were developed to analyze the

transient behavior of the relaxation towards a final stable state. Early experiments measured the relaxation as a function of time in a laser10 and an electronic oscillator22 when the

system changed from stable to unstable. More recently, experiments on particles in a parametrically driven magneto-optical trap23 studied the relaxation at different distances from a

bifurcation point. From the decay of the population at the trap center, the relaxation time was extracted. The relaxation time was found to follow a power law dependence on the drive

frequency detuning from the bifurcation point, with scaling exponent close to 1. Furthermore, the passage time distribution for a particle to arrive at a specific boundary in phase space was

shown to be non-Gaussian with a long tail. This experiment involved a single vibrational mode near a pitchfork bifurcation where two stable states and one unstable state merge together.

While the slowing down near bifurcation points is universal, the dependence on the distance to the bifurcation point is expected to depend on the type of bifurcation. Such generic behavior

resembles scaling laws near phase transitions24 or percolations25 where the critical exponents depend on general system properties such as the dimensionality and the symmetries rather than

the specifics of interactions, as well as the scaling of the Lyapunov exponent in dissipative dynamical systems undergoing period doubling bifurcations from periodic to chaotic behaviors26.

In this paper, we report measurements of the slow onset of self-sustained oscillations induced by dynamical backaction in a sideband-driven micromechanical resonator27. The resonator has two

vibrational modes with significantly different resonant frequencies and decay constants. In the absence of external drive and noise, the system is in a zero-amplitude state where the

vibration amplitudes of both modes are zero. Nonlinear coupling between the two modes creates sidebands around the resonant frequency of the higher mode. Parametric modulation is applied to

the upper sideband, at the sum frequency of the two modes. By controlling the frequency of this sideband drive, the zero-amplitude state is changed from stable to unstable. Thermal

fluctuations are amplified so that the vibration amplitudes of both modes increase exponentially. Eventually, nonlinear effects limit the amplitude increase so that both modes settle into

stable self-sustained vibrations. Unlike the pitchfork bifurcation studied in single mode parametric oscillators23, here the self-sustained oscillations in the two nonlinearly coupled modes

are limit cycles that emerge out of Hopf bifurcations. With the onset of vibrations simultaneously out of two modes, the bifurcation is also qualitatively different from Hopf bifurcations

previously studied in single-mode systems10,22. In our system, there are two Hopf bifurcation points. We demonstrate that the buildup of vibrations slows down significantly when the

parametric modulation frequency approaches either bifurcation point. The inverse rate of exponential buildup as well as the mean and the standard deviation of the first passage time, defined

as the time it takes for the amplitude to reach a chosen threshold amplitude, diverge with distance to the bifurcation point. We measure power law dependence with exponent close to − 1.

Furthermore, we show that the first passage time is random and follows a non-Gaussian distribution. METHODS PARAMETRICALLY DRIVEN TWO-MODE ELECTROMECHANICAL SYSTEM Measurements were

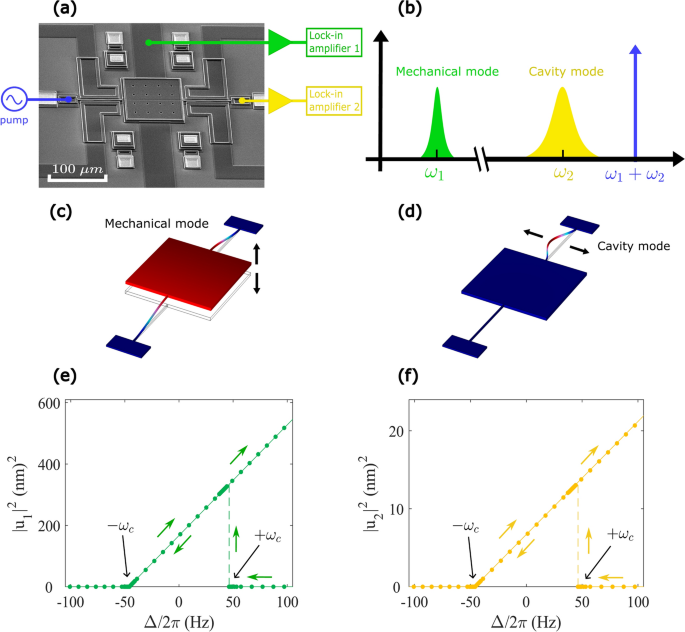
performed on a micromechanical resonator placed inside the vacuum can of a cryogenic probe at < 10–5 torr submerged in liquid helium at 4 K. As shown in Fig. 1a, the resonator consists of

a movable silicon square plate (100 μm × 100 μm) with thickness of 3.5 μm suspended on opposite sides by two beams. The beams are 80 μm and 75 μm long respectively, with identical widths of

1.3 μm and identical thickness of 2 μm. Both beams are covered by 30 nm of gold. The experiment involves two vibration modes (Fig. 1b). In mode 1 (the mechanical mode), the entire plate

vibrates in the direction normal to the substrate due to bending of the two beams, as shown in Fig. 1c. The resonance frequency ω1/2π and damping constant Γ1/2π of mode 1 are 47,030.7 Hz and

0.48 Hz respectively. For the second mode, the shorter beam vibrates in-plane (Fig. 1d) at resonance frequency ω2/2π of 1,867,195.4 Hz. With a damping constant Γ2/2π (36.2 Hz) much higher

than Γ1/2π, mode 2 serves as a phonon cavity mode28 when the system is subjected to driving at its sideband, analogous to photon cavity modes in cavity optomechanics29,30. The resonance

frequencies and damping constants are measured from the linear responses. We apply small probe ac voltages to electrodes near the plate or the beam to generate periodic electrostatic forces

that excite forced vibrations of each mode. The displacement of the plate for mode 1 is detected via the time variations in the capacitance as the gap between the plate and the underlying

electrode changes. For mode 2, vibrations are measured through the current induced by the back electromotive force when the beam moves in a direction perpendicular to the magnetic field of 5

 T. Nonlinear coupling between the two modes is induced by the change in the tension of the beam as it deforms. Self-sustained oscillations are excited when the nonlinear coupling between

the two modes is modulated at the upper sideband of the cavity mode, at a frequency \({\omega }_{F}\) close to the sum frequency (\({\omega }_{1}+{\omega }_{2}\)), by an ac pump current that

generates a periodic Lorentz force that deforms the beam. The effects of the resonant modulation on the coupled modes are described by the equations of motion: $$\left\{

{\begin{array}{*{20}l} {\ddot{q}_{1} + \omega_{1}^{2} q_{1} + 2\Gamma_{1} \dot{q}_{1} + \frac{{\gamma_{1} }}{{m_{1} }}q_{1}^{3} + \frac{\gamma }{{m_{1} }}q_{1} q_{2}^{2} = \frac{F}{{m_{1}

}}q_{2} \cos \left( {\omega_{F} t} \right),} \\ {\ddot{q}_{2} + \omega_{2}^{2} q_{2} + 2\Gamma_{2} \dot{q}_{2} + \frac{{\gamma_{2} }}{{m_{2} }}q_{2}^{3} + \frac{\gamma }{{m_{2} }}q_{2}

q_{1}^{2} = \frac{F}{{m_{2} }}q_{1} \cos \left( {\omega_{F} t} \right),} \\ \end{array} } \right.$$ (1) where _q__1,2_ denotes the displacements of the plate and the midpoint of the beam,

respectively. _m__i_ and \({\gamma }_{i}\) are the effective mass and the coefficient of the Duffing nonlinearity of mode i (i = 1, 2). The last terms on the left-hand side of Eq. (1)

originate from the dispersive coupling of the two modes, with coupling energy \(\frac{1}{2}{\gamma q}_{1}^{2}{q}_{2}^{2}.\) _F_ represents the amplitude of the sideband pumping that

corresponds to a term \(-F{q}_{1}{q}_{2}\mathit{cos}\left({\omega }_{F}t\right),\) in the Hamiltonian. We choose the pump frequency \({\omega }_{F}\) to be close to \({\omega }_{1}+ {\omega

}_{2}\) (Fig. 1b), so that the pump detuning frequency \(\Delta ={\omega }_{F}-{(\omega }_{1}+{\omega }_{2})\) is much smaller than \({\omega }_{F}\). \({q}_{1}\) and \({q}_{2}\) oscillates

at \({\omega }_{1}\) and \({\omega }_{2}\) respectively, with amplitudes and phases that only vary slowly. Hence we convert \({q}_{\text{1,2}}\) into slowly varying complex vibration

amplitudes \({u}_{\text{1,2}}\) using the relations \({q}_{1}={u}_{1}{e}^{i{\omega }_{1}t}+c.c.\), \({q}_{2}={u}_{2}{e}^{i\left[{\omega }_{F}-{\omega }_{1}\right]t}+c.c.\). Applying the

rotating wave approximation, we obtain the equations of motion of \({u}_{\text{1,2}}\) in the rotating frame: $$\left\{ {\begin{array}{*{20}l} {\dot{u}_{1} + \Gamma_{1} u_{1} -

i\frac{{3\gamma_{11} }}{{2\omega_{1} }}u_{1} \left| {u_{1} } \right|^{2} - i\frac{{\gamma_{12} }}{{\omega_{1} }}u_{1} \left| {u_{2} } \right|^{2} = \frac{{F_{1} }}{{4i\omega_{1} }}u_{2}^{*}

,} \hfill \\ {\dot{u}_{2} + \left( {\Gamma_{2} + i\Delta } \right)u_{2} - i\frac{{3\gamma_{22} }}{{2\omega_{2} }}u_{2} \left| {u_{2} } \right|^{2} - i\frac{{\gamma_{21} }}{{\omega_{2}

}}u_{2} \left| {u_{1} } \right|^{2} = \frac{{F_{2} }}{{4i\omega_{2} }}u_{1}^{*} ,} \hfill \\ \end{array} } \right.$$ (2) where \(\gamma_{11} = 1.91 \times 10^{22}\) rad2 s−2 m−2,

\(\gamma_{22} = 7.38 \times 10^{25}\) rad2 s−2 m−2, \(\gamma_{12} = 8.41 \times 10^{22}\) rad2 s−2 m−2 and \(\gamma_{21} = 1.26 \times 10^{25}\) rad2 s−2 m−2. We used pump current amplitude

of 133 μA that corresponds to _F__1_ = 2.13 × 107 N kg−1 m−1 and _F__2_ = 3.18 × 109 N kg−1 m−1. The relations between the parameters in Eq. (2) and the system parameters are described in

Ref.27. Equation (2) can also be obtained using the method of multiple scales to the first order31. When the vibration amplitudes are small, the terms involving _γ__11_, _γ__22_, _γ__12_ and

_γ__21_ in Eq. (2) become negligible. In our resonator, Γ2 far exceeds Γ1. Mode 2 acts as a thermal reservoir for mode 1. After a short transient, both \(\left|

{{\raise0.7ex\hbox{${\dot{u}_{1} }$} \!\mathord{\left/ {\vphantom {{\dot{u}_{1} } {u_{1} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${u_{1} }$}}} \right|\) and \(\left|

{{\raise0.7ex\hbox{${\dot{u}_{2} }$} \!\mathord{\left/ {\vphantom {{\dot{u}_{2} } {u_{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${u_{2} }$}}} \right|\) become small compared to \(\left(

{\Gamma_{2}^{2} + \Delta^{2} } \right)^{1/2}\), so that it is valid to apply the adiabatic approximation to set \(\dot{u}_{2}\) to zero. If \(\Delta = 0\), it follows from the second

equation in Eq. (2) that \(u_{2} \approx \frac{{F_{2} }}{{4i\omega_{2} \Gamma_{2} }}u_{1}^{*}.\) By substituting \(u_{2}\) back into the first equation, we find that mode 1 can be described

by an effective damping \({\Gamma }_{1} - F_{1} F_{2} /16\omega_{1} \omega_{2} {\Gamma }_{2}\). As the pump power increases, the effective damping of mode 1 decreases, while its effective

temperature increases. Eventually the effective damping drops below zero. The zero-amplitude state becomes unstable. Thermal fluctuations are amplified. The vibration amplitude of mode 1

grows while mode 2 follows mode 1 adiabatically. Ultimately, the growth of amplitude is limited by the nonlinearities and both modes settle into stable self-sustained oscillations. Figure 1e

and f plot the square of the steady state amplitude of self-sustained oscillations in modes 1 and 2 respectively as a function of the pump frequency detuning \(\Delta\). We measure the

vibration amplitudes using two lockin amplifiers referenced to the self-sustained oscillation frequencies of the two modes. The bifurcation frequencies are at Δ = ± \(\omega_{c}\), where

\(\omega_{c}\)/2π = 45.18 Hz is determined by fitting the measured response to theory27. Identification of \(\omega_{c}\) also allows us to determine the product F1F2, as described in

Ref.27. When Δ < − \(\omega_{c}\), there is only one stable state at zero amplitude. A supercritical Hopf bifurcation occurs at Δ = − \(\omega_{c}\) as the zero-amplitude state becomes

unstable and self-sustained oscillations emerge. The steady state oscillation amplitude increases with Δ. At Δ = \(\omega_{c}\), the zero-amplitude state becomes stable again in a

subcritical Hopf bifurcation. As Δ is swept up and down, the system displays bistability and hysteresis that was studied in detail in a previous experiment27. RESULTS AND DISCUSSION SLOW

BUILDUP OF SELF-SUSTAINED OSCILLATIONS NEAR BIFURCATION POINTS Next, we measure the buildup of self-sustained oscillations as the zero-amplitude state is changed abruptly from stable to

unstable. We maintain the amplitude of the pump constant and choose a target pump detuning frequency Δm with − ωc < Δm < ωc. In this range of Δm, the self-sustained oscillations are

stable while the zero-amplitude state is unstable. The pump current amplitude of 133 μA is chosen to give a sufficiently large ωc so that Δm can be varied over a wide frequency range, while

keeping the effects of ohmic heating small. Figure 2a and b show the time profile of Δ during one buildup event for two different target values of Δm. To prepare the system in the unstable

state, Δ is first tuned to Δm − Δs where Δs/2π = 500 Hz. This pump detuning frequency is smaller than − ωc so that the system settles into the zero-amplitude state that is the only stable

state. At time t = 0 s, Δ is suddenly changed to Δm so that the zero-amplitude state becomes unstable. The vibration amplitude and the phase of both modes are measured using lockin

amplifiers as a function of time. This process is then repeated to record multiple build-up events. Figure 2c plots the buildup of amplitude of mode 2 as a function of time for Δm/2π = 40 

Hz. For mode 1, the amplitude also builds up in a similar fashion, with mode 2 adiabatically following mode 1. The measurement was repeated multiple times and three of the records are shown.

We analyze the buildup by dividing the process into three parts18. The first stage starts at t = 0 s. Deviations from the unstable state are small. Due to thermal fluctuations, the system

undergoes diffusion about the origin in the rotating frame. In our experiment, the detection sensitivity is not sufficient to resolve the vibrations at this stage. The fluctuations near t = 

0 s in Fig. 2c represent noise in the detection circuit instead of the actual thermomechanical motion of the vibrational mode. As the mean square distance from the unstable state accumulates

due to the thermomechanical motion, the vibration amplitude begins to grow exponentially in time in stage two. This rise becomes observable when the vibration amplitude exceeds our

detection sensitivity. The time at which the vibration amplitude reaches a measurable level is random, so that the data shown in Fig. 2c are shifted laterally from each other. Nevertheless,

the rate of exponential increase is identical for different buildup events. This observation is consistent with the notion that motion in the second regime is largely deterministic, albeit

with a random time shift that is determined by fluctuations in the initial regime18. As explained in more detail later, the build-up rate can be obtained by the eigenvalues of the linearized

equation of motion about the unstable state. Eventually, at the final stage the nonlinear terms in the equation of motion becomes important and the vibration amplitude saturates. Figure 2e

shows three records from numerical simulations using the same system parameters and the same time profile of Δ as the measurements in Fig. 2c. The results from numerical simulations display

a similar build-up rate as the measurements. Random time shifts due to fluctuations can also be identified. One notable difference between Fig. 2c and e is that the initial thermomechanical

motion at small amplitudes can be observed in simulations, whereas such motion is buried by detection noise in experiments. We further note that the phase of self-sustained oscillations is

arbitrary. The three events shown in Fig. 2c exhibit different vibration phase upon saturation of the amplitude. Exponential increase followed by saturation has been observed in other

systems32. Our study focuses on the random starting time of the second stage of exponential rise, as well as the scaling relations near the bifurcation points. We measure the buildup rate,

defined as the rate of exponential rise of the vibration amplitude in the second stage of the buildup process. The dependence of the buildup rate on Δm is shown in Fig. 2d and the

corresponding simulation results in Fig. 2f. One representative buildup event is shown for each of five different values of Δm. By fitting to the region of the measured exponential rise, the

buildup rate is extracted and plotted as a function of Δm as solid squares in Fig. 2g. The buildup rate approaches zero near the bifurcation points ± ωc and attains a maximum at Δm/2π = 0 

Hz. We calculate the buildup rate using Eq. (2). In stages 1 and 2 of the building process, the vibration amplitudes are small so that the nonlinear terms can be neglected. In the absence of

noise, the equation of motion in the rotating frame simplifies to: $$\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {\dot{u}_{1} } \\ {\dot{u}_{2}^{*} } \\ \end{array} } \right] =

\left[ {\begin{array}{*{20}c} { - \Gamma_{1} } & {\frac{{F_{1} }}{{4i\omega_{1} }}} \\ { - \frac{{F_{2} }}{{4i\omega_{2} }}} & { - \Gamma_{2} + i\Delta_{m} } \\ \end{array} }

\right]\left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2}^{*} } \\ \end{array} } \right],} \\ \end{array}$$ (3) where \({\Delta }\) in Eq. (2) is replaced by \(\Delta_{m}\). The

diagonalization of the 2 × 2 matrix above gives two eigenvalues $$\begin{array}{*{20}c} {\lambda_{ \pm } = - \frac{1}{2}\left[ {\Gamma_{1} + \Gamma_{2} - i\Delta_{m} \mp \sqrt {\left(

{\Gamma_{1} - \Gamma_{2} + i\Delta_{m} } \right)^{2} + \frac{{F_{1} F_{2} }}{{4\omega_{1} \omega_{2} }}} } \right].} \\ \end{array}$$ (4) The imaginary parts of \(\lambda_{ \pm }\) determine

the frequency of vibrations of the two modes in the rotating frame. With the real part of \(\lambda_{+}\) being positive, the amplitude of the associated normal mode grows exponentially in

time and vice versa for \(\lambda_{ - }\) that has a negative real part. The solid line in Fig. 2g shows the dependence of \(\lambda_{ + }\) on Δm given by Eq. (4) with no fitting

parameters, as \(\Gamma_{1,2}\) and \(\omega_{1,2}\) are already determined by the linear response of the two modes to a periodic force when they are not coupled by the parametric

modulation, while the product F1F2, is obtained from the bifurcation frequencies ± \(\omega_{c}\)27. There is good agreement between measurement and theory for the buildup rate. At each Δm,

we record multiple buildup events in a manner similar to Fig. 2c. From each event, we extract the first passage time12 for the vibration amplitude to reach a threshold that we choose to be

30% of the final amplitude of stable self-sustained oscillations. In Fig. 2h, the circles are from measurements and the solid line represents numerical simulations using Eq. (3) including

thermal noise added to both modes. The mean first passage time attains minimum at Δm/2π = 0 Hz and increases with |Δm|. Unlike the inverse buildup rate that remains constant for fixed Δm,

the first passage time varies randomly for each buildup event. The stochastic nature indicates that thermal fluctuations play an important role at the initial stage of the buildup process.

For t < 0 s, the system fluctuates about the origin due to thermal noise but stays close to it. The fluctuations do not accumulate because the zero-amplitude state is stable so that

motion is confined. At time just before t = 0 s, the displacement from the origin is random. The zero-amplitude state suddenly becomes unstable at t = 0 s. Subsequently, fluctuations in the

displacement due to thermal noise accumulate so that the mean square displacement from the origin increases with time. Initially, effects of thermal fluctuations dominate. At sufficiently

large amplitudes, the linear terms in the equations of motion take over and give rise to the exponential buildup. As the crossover from diffusion to exponential buildup takes place at random

time, the first passage time to cross the threshold is also random. The hollow circles in Fig. 2h are the standard deviation of the first passage times measured in experiment. While the

first passage time includes contributions from the buildup rate, choosing other values of threshold does not affect the conclusions of this paper, provided that the threshold lies within the

region of exponential increase and also above our detection limit. For stable states, the critical slow down of the recovery of a system from perturbations has been extensively

studied1,2,3,4,5 in various systems. Here we place our resonator near the unstable state and find that the buildup of oscillations also slows down upon approaching a bifurcation point. For

the data point closest to the subcritical bifurcation in Fig. 2g, the buildup rate is 0.0018 Hz, slower than the damping constant of mode 1 by a factor of 88. Compared to the fastest buildup

rate at Δm/2π = 0 Hz, it is 270 times smaller. Numerical simulations show that the mean first passage time also diverges at the bifurcation point. In our experiment, the longest first

passage time measured is 67.7 s, much longer than the inverse of the damping constants. SCALING RELATIONS NEAR BIFURCATION POINTS Next, we investigate how the build-up rate and the first

passage time scales with distance to the bifurcation points for our two-mode system near the Hopf bifurcations. Figure 3a shows the buildup rate near the subcritical Hopf bifurcation at

\({\Delta }_{m} = \omega_{c}\) in log–log scale. The squares are the measured values and the straight line is a linear fit with slope of \(1.00 \pm 0.013\). Figure 3b plots the mean and

standard deviation of the first passage time as squares and hollow circles respectively. Linear fits yield slopes of \(- 0.95 \pm 0.012\) and \(- 0.93 \pm 0.027\) respectively. The absolute

values of the exponents of the power law in Fig. 3a and b are close to one. Figure 3c and d are similar plots near the supercritical Hopf bifurcation at \({\Delta } = - \omega_{c}\). The

fitted slopes are \(1.03 \pm 0.020\), \(- 0.91 \pm 0.019\) and \(- 0.98 \pm 0.042\) respectively. In Fig. 3, the error bars are calculated from measuring 200 buildup events for each

\({\Delta }_{m}\). The uncertainty in the buildup rate is mostly due to noise in the detection circuit, as the rate of exponential rise of the amplitude is expected to be the same for all

the events. On the other hand, the uncertainty in the mean first passage time represents the inherent stochastic nature of the relaxation from the unstable state initiated by thermal motion

of the system. Our measurement shows that the mean and standard deviation of the first passage time as well as the inverse buildup rate are inversely proportional to the distance to the

bifurcation point for Hopf bifurcations involving two nonlinearly coupled modes. Apart from the mean and standard deviation of the first passage time, its distribution also exhibits

interesting behavior. The shape of the distribution is asymmetric and non-Gaussian. Figure 4a shows the distribution of the first passage time close to a bifurcation point, at pump frequency

of 5.18 Hz from the subcritical bifurcation. Figure 4b shows the distribution far away from the bifurcation points, at \(\Delta_{m} = 0\) Hz. The distributions display long tails that

extend to large values of the first passage time. This observation is consistent with the notion that the relaxation from an unstable state are generally not described by Gaussian

distributions18,23 beyond the initial stage. Determination of the exact form of the distribution of the first passage time in our two-mode system is beyond the scope of this paper. It is an

interesting problem that warrants further theoretical analysis. CONCLUSION We reported measurement of the slow onset of self-sustained oscillations of a sideband-driven micromechanical

resonator near the supercritical or subcritical Hopf bifurcation. As the distance from the bifurcation point decreases, both the mean and the standard deviation of the first passage time as

well as the inverse rate of exponential buildup diverge. The dependence on the distance from the bifurcation point is of the form of a power law with exponent of − 1 for both the

supercritical and subcritical Hopf bifurcations. We measure a buildup rate slower than the damping constant of mode 1 by a factor of 88. The distribution of first passage time is shown to be

non-Gaussian. Scaling behaviors typically depend only on the type of bifurcation. Other oscillatory systems that undergo Hopf bifurcations are expected to display the same scaling of the

first passage time and exponential buildup rate near the bifurcations as we report in this paper. The slowing down of the buildup near bifurcation points is generic and occurs in systems

undergoing other types of bifurcations. For example, a parametrically driven magneto-optical trap exhibits pitchfork bifurcation where two stable states and one unstable state merge

together. The relaxation time of particle population at the center of the trap23 was shown to depend inversely on distance to the bifurcation point. Whether other types of bifurcations

exhibit scaling behaviors similar to Hopf or pitchfork bifurcations is an interesting topic for further investigation. Our system of two nonlinear coupled modes in a micromechanical

resonator provides a well-characterized platform for studying the interplay between fluctuations and relaxation. System parameters are well-controlled and maintained stable over long periods

of time, facilitating the comparison of measurements with theoretical predictions. The ability to control the rate of buildup may prove useful to sensing or timing applications that utilize

self-sustained oscillations in mechanical resonators. METHODS NUMERICAL SIMULATIONS Thermal noise exerts a stochastic force of \(\xi_{i} \left( t \right)\) on mode i (i = 1, 2)33 that

satisfies: $$\langle{\xi_{i} \left( t \right)\xi_{j} \left( {t^{\prime}} \right)\rangle = 4D_{i} {\Gamma }_{i} \delta_{ij} \delta \left( {t - t^{\prime}} \right),}$$ (5) where the intensity

of the noise _D__i_ is given by \(m_{i} k_{B} T\). With the effects of thermal noise taken into account, Eq. (1) is modified to $$\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c}

{\ddot{q}_{1} + \omega_{1}^{2} q_{1} + 2\Gamma_{1} \dot{q}_{1} + \frac{{\gamma_{1} }}{{m_{1} }}q_{1}^{3} + \frac{\gamma }{{m_{1} }}q_{1} q_{2}^{2} = \frac{F}{{m_{1} }}q_{2} \cos \left(

{\omega_{F} t} \right) + \frac{{\xi_{1} \left( t \right)}}{{m_{1} }}} \\ {\ddot{q}_{2} + \omega_{2}^{2} q_{2} + 2\Gamma_{2} \dot{q}_{2} + \frac{{\gamma_{2} }}{{m_{2} }}q_{2}^{3} +

\frac{\gamma }{{m_{2} }}q_{2} q_{1}^{2} = \frac{F}{{m_{2} }}q_{1} \cos \left( {\omega_{F} t} \right) + \frac{{\xi_{2} \left( t \right)}}{{m_{2} }}} \\ \end{array} } \right.} \\ \end{array}

.$$ (6) Numerical simulations are based on Eq. (6). \(\xi_{1,2} \left( t \right)\) are generated as white Gaussian noise, the power density of which is adjusted according to Eq. (5). The

frequency of the drive is changed in exactly the same manner as in the experiments (Fig. 2a,b). The temperature T of the system is estimated to be ~ 52 K from the thermomechanical vibrations

induced by \(\xi_{1} \left( t \right)\) in the absence of sideband driving: $$\frac{1}{2}m_{1} \omega_{1}^{2} \langle q_{1}^{2}\rangle= \frac{1}{2}k_{B} T.$$ (7) T is higher than the

temperature of the liquid helium surrounding the chamber due to the Joule heating of the pump current. DATA AVAILABILITY The results of our research will be available upon request sent to

the corresponding author. REFERENCES * Kramer, J. & Ross, J. Stabilization of unstable states, relaxation, and critical slowing down in a bistable system. _J. Chem. Phys._ 83, 6234–6241

(1985). Article  ADS  CAS  Google Scholar  * Tredicce, J. R. et al. Critical slowing down at a bifurcation. _Am. J. Phys._ 72, 799–809 (2004). Article  ADS  Google Scholar  * Scheffer, M. et

al. Anticipating critical transitions. _Science_ 338, 344–348 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Yang, C. J. et al. Critical slowing down near a magnetic quantum phase

transition with fermionic breakdown. _Nat. Phys._ 19, 1605 (2023). Article  CAS  PubMed  PubMed Central  Google Scholar  * Zhang, W. Q., Wu, Y. D., Qiu, X. Z., Nan, J. & Li, X. P.

Subexponential critical slowing-down at a Floquet time-crystal phase transition. _Phys. Rev. B_ 108, 014307 (2023). Article  ADS  CAS  Google Scholar  * Scheffer, M. et al. Early-warning

signals for critical transitions. _Nature_ 461, 53–59 (2009). Article  ADS  CAS  PubMed  Google Scholar  * Diks, C., Hommes, C. & Wang, J. X. Critical slowing down as an early warning

signal for financial crises?. _Empir. Econ._ 57, 1201–1228 (2019). Article  Google Scholar  * Wong, Y. M. & Meijer, P. H. E. Simple extension of Suzukis scaling approach to the onset

time of an unstable state: Application to supercooled liquid. _Phys. Rev. A_ 26, 611–616 (1982). Article  ADS  CAS  Google Scholar  * Haake, F., Haus, J., King, H., Schroder, G. &

Glauber, R. Delay-time statistics and inhomogeneous line broadening in superfluorescence. _Phys. Rev. Lett._ 45, 558–561 (1980). Article  ADS  CAS  Google Scholar  * Arecchi, F. T.,

Degiorgio, V. & Querzola, B. Time-dependent statistical properties of the laser radiation. _Phys. Rev. Lett._ 19, 1168 (1967). Article  ADS  CAS  Google Scholar  * Vandenbroeck, C. &

Mandel, P. Delayed bifurcations in the presence of noise. _Phys. Lett. A_ 122, 36–38 (1987). Article  ADS  Google Scholar  * Stocks, N. G., Mannella, R. & McClintock, P. V. E. Influence

of random fluctuations on delayed bifurcations: The case of additive white noise. _Phys. Rev. A_ 40, 5361–5369 (1989). Article  ADS  CAS  Google Scholar  * Zeghlache, H., Mandel, P. &

Van den Broeck, C. Influence of noise on delayed bifurcations. _Phys. Rev. A_ 40, 286–294 (1989). Article  ADS  CAS  Google Scholar  * Baer, S. M., Erneux, T. & Rinzel, J. The slow

passage through a Hopf-bifurcation: Delay, memory effects, and resonance. _SIAM J. Appl. Math._ 49, 55–71 (1989). Article  MathSciNet  Google Scholar  * Cantisán, J., Yanchuk, S., Seoane, J.

M., Sanjuán, M. A. F. & Kurths, J. Rate and memory effects in bifurcation-induced tipping. _Phys. Rev. E_ 108, 024203 (2023). Article  ADS  MathSciNet  PubMed  Google Scholar  *

Scharpf, W. et al. Experimental-observation of a delayed bifurcation at the threshold of an argon-laser. _Opt. Commun._ 63, 344–348 (1987). Article  ADS  CAS  Google Scholar  * Strizhak, P.

& Menzinger, M. Slow passage through a supercritical Hopf bifurcation: Time-delayed response in the Belousov–Zhabotinsky reaction in a batch reactor. _J. Chem. Phys._ 105, 10905–10910

(1996). Article  ADS  CAS  Google Scholar  * Suzuki, M. Anomalous fluctuation and relaxation in unstable systems. _J. Stat. Phys._ 16, 477 (1977). Article  ADS  Google Scholar  * Haake, F.,

Haus, J. W. & Glauber, R. Passage-time statistics for the decay of unstable equilibrium states. _Phys. Rev. A_ 23, 3255–3271 (1981). Article  ADS  MathSciNet  Google Scholar  *

Depasquale, F., Tartaglia, P. & Tombesi, P. New expansion technique for the decay of an unstable state. _Phys. Rev. A_ 25, 466–471 (1982). Article  ADS  CAS  Google Scholar  * Colet, P.,

De Pasquale, F., Caceres, M. O. & San Miguel, M. Theory for relaxation at a subcritical pitchfork bifurcation. _Phys. Rev. A_ 41, 1901–1911 (1990). Article  ADS  CAS  PubMed  Google

Scholar  * Arecchi, F. T. & Politi, A. Transient fluctuations in the decay of an unstable state. _Phys. Rev. Lett._ 45, 1219–1222 (1980). Article  ADS  CAS  Google Scholar  * Moon, G. et

al. Relaxation of an unstable state in parametrically excited cold atoms. _Phys. Rev. E_ 84, 036217 (2011). Article  ADS  Google Scholar  * Stanley, H. _Introduction to Phase Transitions

and Critical Phenomena_ (Oxford University Press, 1971). Google Scholar  * Stauffer, D. Scaling theory of percolation clusters. _Phys. Rep._ 54, 1–74 (1979). Article  ADS  Google Scholar  *

Huberman, B. A. & Rudnick, J. Scaling behavior of chaotic flows. _Phys. Rev. Lett._ 45, 154–156 (1980). Article  ADS  MathSciNet  Google Scholar  * Sun, F., Dong, X., Zou, J., Dykman, M.

I. & Chan, H. B. Correlated anomalous phase diffusion of coupled phononic modes in a sideband-driven resonator. _Nat. Commun._ 7, 12694 (2016). Article  ADS  CAS  PubMed  PubMed Central

  Google Scholar  * Mahboob, I., Nishiguchi, K., Okamoto, H. & Yamaguchi, H. Phonon-cavity electromechanics. _Nat. Phys._ 8, 387–392 (2012). Article  CAS  Google Scholar  * Kippenberg,

T. J. & Vahala, K. J. Cavity optomechanics: Back-action at the mesoscale. _Science_ 321, 1172–1176 (2008). Article  ADS  CAS  PubMed  Google Scholar  * Aspelmeyer, M., Kippenberg, T. J.

& Marquardt, F. Cavity optomechanics. _Rev. Mod. Phys._ 86, 1391–1452 (2014). Article  ADS  Google Scholar  * Nayfeh, A. H. _Introduction to Perturbation Techniques_ (Wiley, 1993).

Google Scholar  * Bergeot, B., Almeida, A., Gazengel, B., Vergez, C. & Ferrand, D. Response of an artificially blown clarinet to different blowing pressure profiles. _J. Acoust. Soc.

Am._ 135, 479–490 (2014). Article  ADS  PubMed  Google Scholar  * Risken, H. _The Fokker–Planck Equation_ 2nd edn. (Springer, 1996). Book  Google Scholar  Download references

ACKNOWLEDGEMENTS This work is supported by the Research Grants Council of Hong Kong SAR, China (Project Nos. 16301421 and 16304219). We thank M. I. Dykman for useful discussions. AUTHOR

INFORMATION AUTHORS AND AFFILIATIONS * Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China B. Zhang, P. Y. Chan, X. Dong, F.

Sun & H. B. Chan * William Mong Institute of Nano Science and Technology, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China B. Zhang, P. Y.

Chan, X. Dong, F. Sun & H. B. Chan Authors * B. Zhang View author publications You can also search for this author inPubMed Google Scholar * P. Y. Chan View author publications You can

also search for this author inPubMed Google Scholar * X. Dong View author publications You can also search for this author inPubMed Google Scholar * F. Sun View author publications You can

also search for this author inPubMed Google Scholar * H. B. Chan View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS H.B.C. conceived the idea

of the work. B.Z., X.D and F.S. made the sample and performed the measurements. B.Z., X.D, F.S. and P.Y.C. analyzed the data. All authors co-wrote and edited the paper. CORRESPONDING AUTHOR

Correspondence to H. B. Chan. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with

regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons

Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give

appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission

under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons

licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit

http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Zhang, B., Chan, P.Y., Dong, X. _et al._ Slow onset of self-sustained

oscillations in a fluctuating sideband-driven electromechanical resonator. _Sci Rep_ 15, 18965 (2025). https://doi.org/10.1038/s41598-025-98844-w Download citation * Received: 21 August 2024

* Accepted: 15 April 2025 * Published: 30 May 2025 * DOI: https://doi.org/10.1038/s41598-025-98844-w SHARE THIS ARTICLE Anyone you share the following link with will be able to read this

content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative

KEYWORDS * Bifurcations * Critical slow down * Self-sustained oscillations * Micromechanical and nanomechanical oscillators