ABSTRACT Degenerate minima in momentum space—valleys—provide an additional degree of freedom that can be used for information transport and storage. Notably, such minima naturally exist in

the band structure of transition metal dichalcogenides (TMDs). When these atomically thin crystals interact with intense laser light, the second harmonic generated (SHG) field inherits

special characteristics that reflect not only the broken inversion symmetry in real space but also the valley anisotropy in reciprocal space. The latter is present whenever there exists a

valley population imbalance (VPI) between the two valleys and affects the polarization state of the detected SHG. In this work, it is shown that the temperature-induced change of the SHG

intensity polar diagrams at low temperatures and is attributed to the VPI-induced SHG. SIMILAR CONTENT BEING VIEWED BY OTHERS GIANT VALLEY-ZEEMAN COUPLING IN THE SURFACE LAYER OF AN

INTERCALATED TRANSITION METAL DICHALCOGENIDE Article 19 January 2023 NONLINEAR VALLEY SELECTION RULES AND ALL-OPTICAL PROBE OF BROKEN TIME-REVERSAL SYMMETRY IN MONOLAYER WSE2 Article Open

access 07 January 2025 EXCITON-TO-TRION CONVERSION AS A CONTROL MECHANISM FOR VALLEY POLARIZATION IN ROOM-TEMPERATURE MONOLAYER WS2 Article Open access 15 October 2020 INTRODUCTION

Conventional optoelectronics is based on the manipulation of electronic charge with light, for information transport, storage, and readout. In electronic systems with degenerate minima in

their band structure—valleys—an additional degree of freedom that labels those minima, i.e., the valley index, can serve as the information carrier. Such a possibility has opened an

alternative field of electronics, namely valleytronics, which enables the processing of additional information within the same physical space1,2,3. Specifically, the valley index can be

mapped to a pseudospin that, similar to the response of a spin to magnetic fields, is affected by the Berry curvature of the bands4,5. In transition metal dichalcogenides (TMDs), the valley

pseudospin is coupled to the electron spin6 to give rise to selection rules that allow the excitation of carriers in specific valleys only when light of suitable helicity is used7,8,9. More

specifically, the excitation and control of carriers is achieved by circularly polarized light that populates only one of the two valleys. Interestingly, the polarization is transferred to

and subsequently measured in the emitted (one- and two-photon) photoluminescence (PL)10,11,12. Such measurements are used to indirectly probe the population imbalance in different valleys.

Several other phenomena, associated with the existence of valleys and related with time reversal symmetry, have been reported in atomically thin crystals with hexagonal structure and

corresponding degenerate (but inequivalent) K and K′ valleys in the hexagonal Brillouin zone. For example, in the presence of external fields, the valley imbalance may generate valley

currents that give rise to valley Hall conductivity13,14. In addition, when linearly polarized light is used for excitation, superpositions of excitons in different valleys are created and

one can measure valley coherence15,16. Valley injection and transport may be used to create a valley filter, i.e., a means to populate a single valley and therefore induce valley

polarization. Serial combination of two such filters acts as a valley valve that can be externally controlled17,18. Moreover, although intervalley scattering is suppressed in ideal crystals,

there are recent reports of intervalley collective modes in the presence of unequal valley populations19. In all the aforementioned cases, the common underlying physical principle is the

population imbalance between different valleys. This is reasonable considering that polarization and transport effects are associated with charge separation and local variations in the

chemical potential, respectively. Hence, they directly reflect the crystal symmetries in both real and momentum space. In real space, the charge is locally accumulated around the atomic

positions, whereas in momentum space, the carriers occupy states in the vicinity of high symmetry points within the hexagonal Brillouin zone. Interestingly, both polarization and transport

effects can be examined by analyzing the second-order nonlinear optical response of atomically thin crystals. Recently, SHG spectroscopy has been highly appreciated as a powerful tool to

study two-dimensional (2D) TMDs20,21,22,23,24,25,26,27. Owing to the vanishing thickness of these thin crystals, phase-matching conditions are readily satisfied and thus the second-order

nonlinear susceptibility, _χ_(2), is large28. Under the D3h point group symmetry of TMD crystals, the _χ_(2) tensor exhibits non-vanishing elements for odd-layer TMDs in 2H configuration and

for arbitrary-layered in 3R stacking geometry28. These elements are not independent but are inter-related through: \(\chi _{xxx}^{(2)} = - \chi _{xyy}^{(2)} = - \chi _{yyx}^{(2)} = - \chi

_{yxy}^{(2)} = \chi _{{\mathop{\rm{int}}} }^{(2)}\) where _x_ denotes the crystal mirror symmetry axis, i.e., the armchair direction, _y_ is the zig-zag direction and \(\chi _{{\mathrm

{int}}}^{(2)}\) is the nonzero element of the intrinsic second-order susceptibility tensor. In addition, both SHG intensity and polarization have been found to reveal information about the

main crystallographic axis20,21,25,26, grain boundaries29,30, stacking sequence, twist angle24,27, number of layers, and crystal homogeneity26. Indeed, the ability to control the

polarization state of the SHG signal enables the extraction of additional information from a single measurement, since the second-order response is determined by a third rank susceptibility

tensor31; therefore, measurements at higher order of response enable access to a larger number of independent quantities of a system32,33. Recent theoretical studies suggest that the

second-order optical response is also a useful tool to probe the electronic configuration of 2D crystals32,34,35. This is possible due to the symmetry characterizing the hexagonal Brillouin

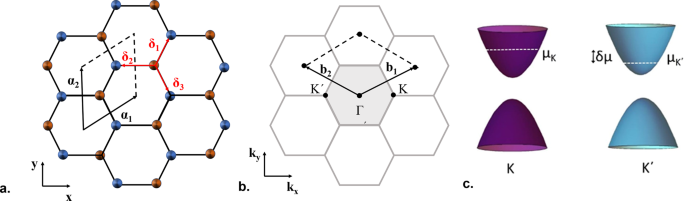
zone in momentum space. Similarly to the alternating atoms at the corners of the hexagon in real space, characterized by the D3h symmetry of the trigonal prismatic structure with Bernal

stacking (Fig. 1a), in momentum space the alternating K and K′ points also result in D3h symmetry, reflecting the trigonal warping of electrons in the vicinity of high symmetry points (Fig.

1b)36. Besides, the conduction and valence band states at the corners of the hexagonal Brillouin zone are formed by hybridization of the transition metal _d-_orbitals with the chalcogen

_p_-orbitals and therefore are strongly localized in the metal atom plane37,38,39. A direct consequence of this effect is the possibility for such crystals to produce valley-induced SHG,

additionally to the intrinsic second-order response. As a result, in the presence of population imbalance between the two valleys, additional elements in the second-order nonlinear optical

susceptibility tensor become nonzero32,34,35,40. Therefore, we have: \(\chi _{yyy}^{(2)} = - \chi _{yxx}^{(2)} = - \chi _{xxy}^{(2)} = - \chi _{xyx}^{(2)} = \chi _{{\mathrm {vpi}}}^{(2)}\),

where \(\chi _{\mathrm {vpi}}^{(2)}\) is the nonzero element of the valley population imbalance (VPI)-induced second-order susceptibility tensor. VPI can be either induced10,40 or emerge

spontaneously41 and depending on the way it is created, it reflects different aspects of the electronic system. For instance, when circularly polarized light is used for excitation, only one

of the two valleys is populated and the spin-valley polarization is transferred to the detected one- or two-photon PL15. In contrast, for linearly polarized light, a superposition of

excitons in the K and K′ valleys is created and one can measure valley coherence16. Even at equilibrium, i.e., valley population balance, there is a small, but finite probability that an

electron will be transferred to the adjacent valley, while at the same time flipping its spin, thus perturbing the balance. In this last case, access to the degree of VPI would reveal

information about the intrinsic valley relaxation time41. In this work, we take advantage of the temperature dependence of polarization-resolved SHG (PSHG) to account for the VPI in

atomically thin TMDs. Notably, since the VPI defines the difference between the valley populations, \(\delta n = n_K - n_{K^\prime }\), it also reflects the chemical potential difference,

_δμ_, between the two valleys (Fig. 1c). Hence, in the presence of imbalance, the additional valley-induced contribution to the SHG that is intrinsically generated by the TMD crystal, can be

estimated as $$I_{\mathrm {SHG}}^{\mathrm {VPI}}\sim \delta n^2\sim \delta \mu ^2$$ (1) with the corresponding contribution to the second-order nonlinear susceptibility being proportional

to the chemical potential difference, i.e., \(\chi _{\mathrm {vpi}}^{(2)}\sim \delta \mu\)34,35,41. Accordingly, local variations in the chemical potential affect the SHG induced by the VPI

and thus can be probed by nonlinear optical experiments40. More importantly, and in contrast to the intrinsic nonlinear optical response of 2D TMDs, the valley-induced SHG is sensitive to

temperature variations. Based on this, we here vary the temperature of a 2D TMD crystal and the corresponding changes in the SHG intensity are used to probe the intervalley chemical

potential difference and therefore the VPI. We consider an electromagnetic field that is normally incident to a 2D TMD sample with polarization parallel to the sample plane, at an angle _φ_

(Fig. 2a); the crystal armchair direction is oriented at an angle _θ_. Here we implement the experiment proposed by Hipolito and Pereira32, in which a quarter-wave plate is placed before the

sample with its fast axis at an angle _α_. Using a half-wave plate we control the orientation _φ_ of the fundamental linear polarization, while a linear polarizer placed before the detector

at an angle _ζ_, selects suitable SHG components. All angles are measured with respect to the laboratory _X_-axis. The linear polarization of the excitation changes to elliptical as the

beam passes through the quarter-wave plate whose axis has an offset of 5° with respect to the polarization axis. Such a configuration provides the means for an asymmetric population of the

two valleys40. An accurate description of the polarization state of the fundamental field incident to the sample and the SHG field emerging from the 2D crystal entails the use of the Jones

formalism and is presented in detail in the Supplementary Eqs. (1)–(10). PSHG imaging was performed in 78–300 K temperature range using a fs laser-scanning microscope coupled with a liquid

nitrogen cryogenic system (Fig. 2b; see also “Methods”). The infrared laser beam is guided into an inverted microscope, while its polarization is controlled by properly rotating half- and

quarter-wave plates. A pair of galvanometric mirrors enables raster-scanning of the sample, which is placed inside a continuous flow cryostat. The SHG signal from the sample passes through a

rotating linear polarizer and is collected in reflection geometry. Different rotation speeds of the optical elements allows control over the angles _φ_, _α_ and _ζ_. The armchair direction

_θ_ can be determined with the same experimental setup26. For the PL measurements, a micro-PL setup was used to collect PL in a backscattering geometry (see also “Methods”). Emitted light

was dispersed by a single monochromator equipped with a multichannel CCD detector. Following the excitation, the emitted PL spectra were analyzed as _σ_+ and _σ_− using a combination of

quarter-wave plate and linear polarizer placed in front of the spectrometer entrance slit. Α cryogenic system was coupled with the optical setups to perform temperature-dependent second

harmonic and spin-valley polarization measurements in a range of temperatures from 78 up to 300 K. Application of nonlinear optics for a crystal with D3h symmetry in the presence of VPI

yields the SHG field emerging from the crystal as42,43 $$\left( {\begin{array}{*{20}{c}} {P_x^{2\omega }} \\ {P_y^{2\omega }} \end{array}} \right) \sim \left( {\begin{array}{*{20}{c}} {\chi

_{{\mathrm {int}}}^{(2)}\left( {E_x^2 - E_y^2} \right) - 2\chi _{{\mathrm {vpi}}}^{(2)}E_xE_y} \\ { - \chi _{{\mathrm {vpi}}}^{(2)}\left( {E_x^2 - E_y^2} \right) - 2\chi _{{\mathrm

{int}}}^{(2)}E_xE_y} \end{array}} \right).$$ (2) Here \(\chi _{{\mathrm {int}}}^{(2)}\) and \(\chi _{{\mathrm {vpi}}}^{(2)}\) correspond to the intrinsic and induced due to VPI contributions

to the second-order response, respectively. This means that the SHG intensity reaching the detector depends on four angles, namely _φ_, _θ_, _α_, _ζ_, corresponding to the effects of

excitation linear polarization, crystal orientation, quarter-wave plate, and analyzer, respectively (Fig. 2). In this case, the detected SHG intensity is given by

$$\begin{array}{l}I_{2\omega } = {\rm{A}}\left[ {\cos \left( {2\alpha + \zeta - 3\theta } \right) - \kappa \,{\mathrm{sin}}\left( {2\alpha + \zeta - 3\theta } \right)} \right]^2\\ + \,\,

\left[ {\kappa \cos \left( {2\alpha + \zeta - 3\theta } \right) + {\mathrm{sin}}\left( {2\alpha + \zeta - 3\theta } \right)} \right]^2 \, \sin ^2\left[ {2\left( {\alpha - \varphi } \right)}

\right],\end{array}$$ (3) where _κ_ denotes the magnitude of VPI-induced to intrinsic susceptibility ratio $$\kappa = \frac{{|\chi _{\mathrm {vpi}}^{(2)}|}}{{|\chi _{{\mathrm

{int}}}^{(2)}|}}$$ (4) and _A_ is a multiplication factor that depends on the amplitude of the field and the intrinsic second-order susceptibility. The ratio _κ_ can be extracted upon

fitting the experimentally measured PSHG intensity with Eq. (3) and reflects the degree of VPI. In our experiment, the optical elements are controlled using motorized stages synchronized to

rotate in phase giving rise to a six-petal pattern for the PSHG intensity (see also Fig. S6). RESULTS AND DISCUSSION TEMPERATURE-DEPENDENT IMAGING OF VPI WS2 samples were prepared with

mechanical exfoliation and characterized using Raman mapping (see “Methods”). Figure 3a shows an optical image of the sample where the monolayer (1L) region is indicated. In order to

quantify the VPI, we fit the experimentally measured SHG intensity at each temperature with Eq. (3) to extract the dimensionless parameter _κ_. For 300 K, in particular, we assume that the

valley-induced SHG is negligible (_κ_ = 0) and use the same equation to determine the armchair orientation _θ_. As shown in Fig. 3b, c, the SHG intensity as well as the VPI mapping of WS2 at

78 K appear to be relatively uniform across the sample area yielding a value of _κ_ = 0.1. However, several points of the flake boundaries correspond to increased or decreased _κ_ values,

most probably originating from local field effects that affect the electron distribution in the valleys, hence the VPI. In Fig. 3d–i we present polar plots of the SHG emerging from the same

monolayer region as a function of the excitation field polarization angle, for temperatures ranging from 78 to 300 K. The effect of low temperature is to preserve VPI by hindering the

relaxation processes due to scarcity of phonons44; this effect is readily imprinted onto the PSHG patterns. As a consequence, as the temperature rises the PSHG intensity becomes

progressively lower (see also Fig. 4), indicating the suppression of VPI. The asymmetry in the size of the lobes in the polar diagrams stems from the well-known effect of polarization

scrabbling due to the use of dichroic mirror in front of the microscope objective45. A forward detection geometry would produce polar diagrams with symmetric lobes. However, such a

configuration was not possible in our case, since the experiments were performed inside a cryostat and the sample had to be placed on a non-transparent substrate. Thus, the asymmetry in the

lobes, which is the same for all examined temperatures and pixels, is a known systematic error due to the use of dichroic mirror and affects only the quality of fitting and not our main

observation, i.e., the rotation of the polar pattern with temperature. This is readily shown in the Supplementary Video where the polar diagrams taken from every pixel of a large image

exhibit the same rotation with lowering temperature. All polar diagrams presented in our work were taken from a single pixel from an image consisting of 500 × 500 pixels with pixel dwell

time of ~1 μs. The experimental data (red spheres)—obtained from representative monolayer regions of interest—are fitted with Eq. (3) (blue line) and the theoretically predicted features of

the polar patterns32 are indeed identified: (a) increase in intensity at low temperatures where we expect larger values of population imbalance, (b) rotation of the low-temperature polar

diagram—with respect to the ambient temperature one—as it can no longer be exclusively associated with the armchair direction. These features are summarized in Fig. 4a, where the fitted SHG

polar diagrams for the minimum and maximum temperature are compared. The rotation of the polar pattern at low temperature originates from the additional elements in the second-order

susceptibility tensor that have to be taken into account in the presence of VPI. The monotonic decrease of the SHG with temperature (Fig. 4b) is reflected in the temperature dependence of

_κ_-ratio (Fig. 4c). For comparison, we present in Fig. 4d the degree of spin-valley polarization as a function of temperature for the neutral and charged excitons, obtained from PL

measurements performed in the same sample (see also Supplementary Fig 2). It is evident that the degrees of VPI and spin-valley polarization both exhibit a monotonic reduction with

temperature. We attribute both effects to the balancing of the populations in different valleys at elevated temperatures. In order to further validate our method, we examined another flake

of exfoliated WS2, comprising monolayer, few-layer and bulk regions (Fig. 5a). The SHG intensity from the monolayer region at 78 K is higher than the multilayer one, as it is clearly shown

in Fig. 5b. In contrast, the VPI, depicted in Fig. 5c in terms of the parameter _κ_, is higher in the few-layer region. This is actually expected, since there is an additional contribution

to the valley-induced SHG from the extra layers. PL measurements also demonstrate a higher degree of valley polarization in the few-layer region compared to the monolayer one (Supplementary

Fig. 5), further supporting the increased value of _κ_ due to the additional layers46,47. Finally, we present polar diagrams of PSHG intensity at different temperatures for monolayer (Fig.

5d–f) and few-layer regions (Fig. 5g–i). The experimental data (red spheres)—obtained from representative regions of interest—are fitted with Eq. (3) (blue line) and the fingerprints of VPI

are again identified: Similar to the single layer case presented previously, as the temperature rises from 78 to 200 K, the maximum SHG intensity decreases and the polar diagram is rotated.

The PSHG method for imaging VPI can be applied simultaneously to different atomically thin crystals. For instance, within the same field of view one can image the VPI of adjacent crystalline

areas consisting of different 2D TMD flakes as demonstrated in Fig. 6, showing the WS2 flake presented above together with a WSe2 monolayer in the same field of view (Fig. 6a). Juxtaposing

the SHG from the WS2 and WSe2 monolayers, we observe that the latter exhibits increased intensity at the excitation wavelength we have used (1030 nm) (Fig. 6b). On the contrary, the VPI

imaging (Fig. 6c) and histogram (Fig. 6d) in terms of the parameter _κ_ reveal that WS2 is found to have slightly higher _κ_ values. Notably, apart from a quantification of the VPI, the

method presented here provides an optical way to determine the monolayer nature of a TMD crystal and discriminate regions consisting of different TMDs. In conclusion, we have presented an

all optical nonlinear method based on PSHG that enables the quantification and imaging of VPI in 2D TMDs. The demonstrated approach relies in analyzing the temperature-dependent changes in

the PSHG intensity pattern as a function of the incident polarization angle. Fitting of the experimental data with a nonlinear optics model reveals the susceptibility ratio _κ_ between the

intrinsic and valley-induced second-order response of the TMD crystal. The PSHG-based method is suitable for large crystalline areas containing various 2D TMDs either adjacent or in stacked

geometry. Considering that VPI is the fundamental physical principle behind a plethora of phenomena, including valley polarization, valley coherence, valley Hall conductivity and valley

filtering, its quantification is of great importance for advances in the field of valleytronics. We envisage the work presented herein as a significant step towards this effort. METHODS

SAMPLE PREPARATION Polydimethylsiloxane films (PDMS) were fabricated from 10:1 mixing ratio of SYLGARD 182 Silicone Elastomer Kit with heat cure at 80 °C for 2 h. WS2 and WSe2 bulk crystals,

purchased from HQ Graphene, were mechanically exfoliated on the PDMS films placed on microscope glass slides48,49. Monolayers of these crystals were realized under an optical microscope and

characterized with Raman spectroscopy. Then, the glass slides with PDMS films containing the monolayers were mounted on a XYZ micromechanical stage, placed under a coaxially illuminated

microscope. The WS2 and WSe2 monolayers were transferred on Si/SiO2 (285 nm) substrate using viscoelastic stamping50. OPTICAL SPECTROSCOPY MEASUREMENTS We used a micro-PL setup with a ×50

objective and appropriate filters and incorporated a liquid nitrogen-cooled cryostat to collect PL in a backscattering geometry. Emitted light was dispersed by a single monochromator

equipped with a multichannel CCD detector. For optical spectroscopy measurements we used a combined μ-PL setup. A Mitutoyo ×50 lens (NA: 0.42, _f_ = 200 mm) was used to focus the excitation

beam onto the sample, down to ~1 μm size. The samples were held inside a continuous flow cryostat (ST500, Jannis, USA); their exact position was controlled by a XYZ mechanical translation

stage (PT3, Thorlabs, USA) and the excitation procedure was continuously monitored via a CCD optical setup. Following the excitation, the emitted PL signal passes through a long pass filter

to eliminate the emission of the laser. The PL spectra were analyzed as _σ_+ and _σ_− using a combination of a quarter-wave plate (liquid crystal) and a linear polarizer placed in front of

the spectrometer entrance slit. TEMPERATURE-DEPENDENT MEASUREMENTS Α cryogenic system has been coupled with the optical setup to perform temperature-dependent second harmonic and spin-valley

polarization measurements in a range of temperatures from 78 up to 300 K. The cryogenic system consists of the liquid nitrogen-cooled cryostat (ST500, Janis, USA), the transfer line

(Standard Flexible Transfer Line, Janis, USA), a liquid nitrogen 20lt storage dewar (Janis, USA), a temperature controller, a mechanical pump, and a turbo pump. RAMAN CHARACTERIZATION Raman

characterization was employed to verify the monolayer character of the samples. A Nicolet Almega XR μRaman analysis system (Thermo Scientific Instruments, Waltham MA USA) was used. The

excitation wavelength was 473 nm and characterization was performed under ambient conditions. A set of data was collected from several regions across the WS2 and WSe2 monolayer areas

(Supplementary Figs. 3a and 4a). Exposure time, laser intensity, and number of acquisitions were kept constant for all experiments. There is a variation in the intensity of different areas

in the monolayer (Supplementary Figs 3b and 4b). For WS2, analysis of the peak positions of the two most prominent Raman vibrational modes A1′ (out of plane) and E′ (in plane) is an

indicator of the monolayer character of the sample. In all cases, the difference was ranging from 59 to 61 cm−1, which confirms the existence of the monolayer in all studied areas

(Supplementary Fig. 3c). Similarly for WSe2, E′ (in plane) vibrational mode is positioned around 249 cm−1 and A1 (out of plane) vibrational mode is at 260 cm−1 (Supplementary Fig. 4c). Raman

mapping revealed a difference of 11 cm−1, which also indicates monolayer thickness for WSe2. Finally, Raman characterization of the WS2 sample comprising monolayer, few-layer, and bulk

areas (Supplementary Fig. 5a) was performed at liquid nitrogen conditions, with an excitation energy of 543 nm. The corresponding Raman spectra for the three areas (Supplementary Figs 5d–f)

suggest that they comprise one, two to three, and above six layers, respectively. POLARIZATION-RESOLVED SECOND HARMONIC GENERATION IMAGING PSHG imaging was performed using an fs laser

raster-scanning microscope coupled with a liquid nitrogen cryogenic system (ST500, Janis, USA) (Fig. 2b). The laser beam from a diode-pumped Yb:KGW fs oscillator (1030 nm, 70–90 fs, 76 MHz,

Pharos-SP, Light Conversion, Lithuania) is guided into an inverted microscope (modified Axio Observer Z1, Carl Zeiss, Germany). In order to control the polarization of the fundamental field,

we use two motorized rotation stages of high accuracy (0.1°) (M-060.DG, Physik Instrumente, Karlsruhe, Germany), holding a half-wave plate (QWPO-1030-10-2, CVI Laser, USA) and a

quarter-wave plate (QWPO-1030-10-4, CVI Laser, USA). A pair of galvanometric mirrors (6215H, Cambridge Technology, Bedford, MA, USA) directs the beam into the microscope, enabling

raster-scanning of the stationary sample placed inside a continuous flow cryostat (ST500, Janis, USA). Then, a pair of lenses forming a telescope suitably expands the beam to fill the back

aperture of the microscope objective lens (×50, 0.55 NA, M Plan Apo, Mitutoyo, Japan). Given that the cryostat is not permeable, we collect the SHG in the backward (epi-) direction, with the

same objective used for excitation and a short-pass dichroic mirror (DMSP805R, Thorlabs, USA) at the microscope turret box. The SHG signal is then filtered by suitable short-pass

(FF01-680/SP, Semrock, Rochester, NY, USA) and narrow bandpass filters (FF01-514/3, Semrock, Rochester, NY, USA), to separate it from fundamental and absorption-induced radiation. Finally,

SHG passes through a linear polarizer (LPVIS100-MP, ThorLabs, USA) placed on a third motorized rotation stage in front of the detector, which is based on a PMT module (H9305-04, Hamamatsu,

Hamamatsu City, Japan). Coordination of PMT recordings with the galvanometric mirrors for the image formation, as well as the movements of all motors, is carried out using LabView (National

Instruments, USA). DATA AVAILABILITY The data that support the findings of this study are available from the corresponding authors upon reasonable request. REFERENCES * Akinwande, D.,

Petrone, N. & Hone, J. Two-dimensional flexible nanoelectronics. _Nat. Commun._ 5, 5678 (2014). Article  CAS  Google Scholar  * Mak, K. F. & Shan, J. Photonics and optoelectronics of

2D semiconductor transition metal dichalcogenides. _Nat. Photonics_ 10, 216–226 (2016). Article  CAS  Google Scholar  * Schaibley, J. R. et al. Valleytronics in 2D materials. _Nat. Rev.

Mater._ 1, 16055 (2016). Article  CAS  Google Scholar  * Xiao, D., Yao, W. & Niu, Q. Valley-contrasting physics in graphene: magnetic moment and topological transport. _Phys. Rev. Lett._

99, 236809 (2007). Article  CAS  Google Scholar  * Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. _Nat. Phys._ 10, 343–350

(2014). Article  CAS  Google Scholar  * Xiao, D., Liu, G. B., Feng, W. X., Xu, X. D. & Yao, W. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides.

_Phys. Rev. Lett._ 108, 196802 (2012). Article  CAS  Google Scholar  * Mak, K. F., Xiao, D. & Shan, J. Light-valley interactions in 2D semiconductors. _Nat. Photonics_ 12, 451–460

(2018). Article  CAS  Google Scholar  * Cheng, J. et al. Chiral selection rules for multi-photon processes in two-dimensional honeycomb materials. _Opt. Lett._ 44, 2141–2144 (2019). Article

  CAS  Google Scholar  * Xiao, J. et al. Nonlinear optical selection rule based on valley-exciton locking in monolayer WS2. _Light. Sci. Appl._ 4, e366 (2015). Article  CAS  Google Scholar 

* Mak, K. F., He, K., Shan, J. & Heinz, T. F. Control of valley polarization in monolayer MoS2 by optical helicity. _Nat. Nanotechnol._ 7, 494 (2012). Article  CAS  Google Scholar  * He,

K. et al. Tightly bound excitons in monolayer WSe2. _Phys. Rev. Lett._ 113, 026803 (2014). Article  CAS  Google Scholar  * Wang, G. et al. B. Giant enhancement of the optical

second-harmonic emission of WSe2 monolayers by laser excitation at exciton resonances. _Phys. Rev. Lett._ 114, 097403 (2015). Article  CAS  Google Scholar  * Song, Z. et al. Tunable valley

polarization and valley orbital magnetic moment Hall effect in honeycomb systems with broken inversion symmetry. _Sci. Rep._ 5, 13906 (2015). Article  Google Scholar  * Lundt, N. et al.

Optical valley Hall effect for highly valley-coherent exciton-polaritons in an atomically thin semiconductor. _Nat. Nanotechnol._ 14, 770–775 (2019). Article  CAS  Google Scholar  * Jones,

A. M. et al. Optical generation of excitonic valley coherence in monolayer WSe2. _Nat. Nanotechnol._ 8, 634–638 (2013). Article  CAS  Google Scholar  * Hao, K. et al. Direct measurement of

exciton valley coherence in monolayer WSe2. _Nat. Phys._ 12, 677–682 (2016). Article  CAS  Google Scholar  * Neumann, A. et al. Opto-valleytronic imaging of atomically thin semiconductors.

_Nat. Nanotechnol._ 12, 329–334 (2017). Article  CAS  Google Scholar  * Luo, Y. K. et al. Opto-valleytronic spin injection in monolayer MoS2/few-layer graphene hybrid spin valves. _Nano

Lett._ 17, 3877–3883 (2017). Article  CAS  Google Scholar  * Zyuzin, A. A. & Zyuzin, A. Y. U. Spin and valley waves in Dirac semimetals with population imbalance. _Phys. Rev. B_ 100,

121402(R) (2019). Article  Google Scholar  * Malard, L. M., Alencar, T. V., Barboza, A. P. M., Mak, K. F. & de Paula, A. M. Observation of intense second harmonic generation from MoS2

atomic crystals. _Phys. Rev. B_ 87, 201401 (2013). Article  CAS  Google Scholar  * Kumar, N. et al. Second harmonic microscopy of monolayer MoS2. _Phys. Rev. B_ 87, 161403 (2013). Article 

CAS  Google Scholar  * Li, Y. L. et al. Probing symmetry properties of few-layer MoS2 and hBN by optical second-harmonic generation. _Nano Lett._ 13, 3329–3333 (2013). Article  CAS  Google

Scholar  * Clark, D. J. et al. Strong optical nonlinearity of CVD-grown MoS2 monolayer as probed by wavelength-dependent second-harmonic generation. _Phys. Rev. B_ 90, 121409 (2014). Article

  CAS  Google Scholar  * Hsu, W. T. et al. Second harmonic generation from artificially stacked transition metal dichalcogenide twisted bilayers. _ACS Nano_ 8, 2951–2958 (2014). Article  CAS

  Google Scholar  * David, S. N. et al. Rapid, all-optical crystal orientation imaging of two-dimensional transition metal dichalcogenide monolayers. _Appl. Phys. Lett._ 107, 111902 (2015).

Article  CAS  Google Scholar  * Psilodimitrakopoulos, S. et al. Ultrahigh-resolution nonlinear optical imaging of the armchair orientation in 2D transition metal dichalcogenides. _Light.

Sci. Appl._ 7, 18005 (2018). Article  CAS  Google Scholar  * Psilodimitrakopoulos, S. et al. Twist angle mapping in layered WS2 by polarization-resolved second harmonic generation. _Sci.

Rep._ 7, 14285 (2019). Article  CAS  Google Scholar  * Zhao, M. et al. Atomically phase-matched second-harmonic generation in a 2D crystal. _Light. Sci. Appl._ 5, e16131 (2016). Article  CAS

  Google Scholar  * Yin, X. et al. Edge nonlinear optics on a MoS2 atomic monolayer. _Science_ 344, 488–490 (2014). Article  CAS  Google Scholar  * Karvonen, L. et al. Rapid visualization of

grain boundaries in monolayer MoS2 by multiphoton microscopy. _Nat. Commun._ 8, 15714 (2017). Article  CAS  Google Scholar  * Haussühl, S. _Physical Properties roof Crystals_ (Wiley,

Weinheim, 2007). Book  Google Scholar  * Hipolito, F. & Pereira, V. M. Second harmonic spectroscopy to optically detect valley polarization in 2D materials. _2D Mater._ 4, 021027

[039501] (2017). Google Scholar  * McIver, J. W., Hsieh, D., Steinberg, H., Jarillo-Herrero, P. & Gedik, N. Control over topological insulator photocurrents with light polarization.

_Nat. Nanotechnol._ 7, 96–100 (2011). Article  CAS  Google Scholar  * Golub, L. E. & Tarasenko, S. A. Valley polarization induced second harmonic generation in graphene. _Phys. Rev. B_

90, 201402(R) (2014). Article  CAS  Google Scholar  * Wehling, T. O., Huber, A., Lichtenstein, A. I. & Katsnelson, M. I. Probing of valley polarization in graphene via optical

second-harmonic generation. _Phys. Rev. B_ 91, 041404(R) (2015). Article  CAS  Google Scholar  * Wang, G. et al. Excitons in atomically thin transition metal dichalcogenides. _Rev. Mod.

Phys._ 90, 021001 (2018). Article  CAS  Google Scholar  * Li, T. & Galli, G. Electronic properties of MoS2 nanoparticles. _J. Phys. Chem. C_ 111, 16192–16196 (2007). Article  CAS  Google

Scholar  * Zhu, Z. Y., Cheng, Y. C. & Schwingenschlögl, U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. _Phys. Rev. B_ 84,

153402 (2011). Article  CAS  Google Scholar  * Kormányos, A. et al. k·p theory for two-dimensional transition metal dichalcogenide semiconductors. _2D Mater._ 2, 022001 (2015). Article  CAS

  Google Scholar  * Ho, Y. W. et al. Measuring valley polarization in transition metal dichalcogenides with second-harmonic spectroscopy. _ACS Photonics_ 7, 925–931 (2020). Article  CAS 

Google Scholar  * Goryca, M., Wilson, N. P., Dey1, P., Xu, X. & Crooker, S. A. Detection of thermodynamic “valley noise” in monolayer semiconductors: access to intrinsic valley

relaxation time scales. _Sci. Adv._ 5, eaau489 (2019). * Boyd, R. W. _Nonlinear Optics._ 3rd edn (Academic Press, San Diego, 2008). Google Scholar  * Maragkakis, G. M. et al. Imaging the

crystal orientation of 2D transition metal dichalcogenides using polarization-resolved second-harmonic generation. _Opto-Electron. Adv._ 2, 190026 (2019). CAS  Google Scholar  * Paradisanos,

I. et al. Prominent room temperature valley polarization in WS2/graphene heterostructures grown by chemical vapor deposition. _Appl. Phys. Lett._ 116, 203102 (2020). Article  CAS  Google

Scholar  * Chou, C.-K. et al. Polarization ellipticity compensation in polarization second-harmonic generation microscopy without specimen rotation. _J. Biomed. Opt._ 13, 014005 (2008).

Article  CAS  Google Scholar  * Nayak, P. K. et al. Robust room temperature valley polarization in monolayer and bilayer WS2. _Nanoscale_ 8, 6035–6042 (2016). Article  CAS  Google Scholar  *

Zhu, B. et al. Anomalously robust valley polarization and valley coherence in bilayer WS2. _Proc. Natl Acad. Sci. USA_ 111, 11606–11611 (2014). Article  CAS  Google Scholar  * Frisenda, R.

et al. Recent progress in the assembly of nanodevices and van der Waals heterostructures by deterministic placement of 2D materials. _Chem. Soc. Rev._ 47, 53–68 (2018). Article  CAS  Google

Scholar  * Jayasena, B. & Melkote, S. N. An investigation of PDMS stamp assisted mechanical exfoliation of large area graphene. _Procedia Manuf._ 1, 840–853 (2015). Article  Google

Scholar  * Castellanos-Gomez, A. et al. Deterministic transfer of two-dimensional materials by all-dry viscoelastic stamping. _2D Mater._ 1, 011002 (2014). Google Scholar  Download

references ACKNOWLEDGEMENTS We would like to acknowledge financial support by the Hellenic Foundation for Research and Innovation (HFRI) under the “First Call for HFRI Research Projects to

support Faculty members and Researchers and the procurement of high-cost research equipment grant” (Project No. HFRI-FM17-3034). This research has been co-financed by the European Union and

Greek national funds through the Operational Program Competitiveness, Entrepreneurship and Innovation, under the call European R & T Cooperation-Grant Act of Hellenic Institutions that

have successfully participated in Joint Calls for Proposals of European Networks ERA NETS (National project code: GRAPH-EYE T8ΕΡΑ2-00009 and European code: 26632, FLAGERA). Support by the

European Research Infrastructure NFFA-Europe, funded by the EC’s H2020 framework program for research and innovation under grant agreement no. 654360, is also gratefully acknowledged. AUTHOR

INFORMATION AUTHORS AND AFFILIATIONS * Institute of Electronic Structure and Laser-Foundation for Research and Technology-Hellas, Heraklion, 70013, Greece Leonidas Mouchliadis, Sotiris

Psilodimitrakopoulos, George Miltos Maragkakis, Ioanna Demeridou, George Kourmoulakis, Andreas Lemonis, George Kioseoglou & Emmanuel Stratakis * Physics Department, University of Crete,

Heraklion, 71003, Greece George Miltos Maragkakis, Ioanna Demeridou & Emmanuel Stratakis * Department of Materials Science and Technology, University of Crete, Heraklion, 71003, Greece

George Kourmoulakis & George Kioseoglou Authors * Leonidas Mouchliadis View author publications You can also search for this author inPubMed Google Scholar * Sotiris Psilodimitrakopoulos

View author publications You can also search for this author inPubMed Google Scholar * George Miltos Maragkakis View author publications You can also search for this author inPubMed Google

Scholar * Ioanna Demeridou View author publications You can also search for this author inPubMed Google Scholar * George Kourmoulakis View author publications You can also search for this

author inPubMed Google Scholar * Andreas Lemonis View author publications You can also search for this author inPubMed Google Scholar * George Kioseoglou View author publications You can

also search for this author inPubMed Google Scholar * Emmanuel Stratakis View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS L.M., S.P., E.S.,

and G. Kioseoglou planned the project; S.P., L.M., and G.M.M. designed the experiment; S.P., G.M.M., and I.D. conducted the optical experiments; L.M., S.P., and G.M.M. conducted the data

analysis; A.L. provided technical support; L.M. elaborated the theoretical model; G. Kourmoulakis prepared the samples; E.S. and G. Kioseoglou guided the research. All authors contributed to

the discussion and preparation of the manuscript. CORRESPONDING AUTHORS Correspondence to Leonidas Mouchliadis or Emmanuel Stratakis. ETHICS DECLARATIONS COMPETING INTERESTS The authors

declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION SUPPLEMENTARY VIDEO RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International

License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source,

provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons

license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Mouchliadis, L., Psilodimitrakopoulos, S., Maragkakis, G.M. _et al._ Probing valley

population imbalance in transition metal dichalcogenides via temperature-dependent second harmonic generation imaging. _npj 2D Mater Appl_ 5, 6 (2021).

https://doi.org/10.1038/s41699-020-00183-z Download citation * Received: 17 June 2020 * Accepted: 25 November 2020 * Published: 04 January 2021 * DOI:

https://doi.org/10.1038/s41699-020-00183-z SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative