ABSTRACT Liquid-liquid phase separation of protein solutions has regained heightened attention for its biological importance and pathogenic relevance. Coarse-grained models are limited when

explaining residue-level effects on phase equilibrium. Here we report phase diagrams for γ-crystallins using atomistic modeling. The calculations were made possible by combining our FMAP

method for computing chemical potentials and Brownian dynamics simulations for configurational sampling of dense protein solutions, yielding the binodal and critic temperature (_T_c). We

obtain a higher _T_c for a known high-_T_c γ-crystallin, γF, than for a low-_T_c paralog, γB. The difference in _T_c is corroborated by a gap in second virial coefficient. Decomposition of

FOR BIOMOLECULAR PHASE SEPARATION WITH NEAR-QUANTITATIVE ACCURACY Article 22 November 2021 EXPANDING THE MOLECULAR GRAMMAR OF POLAR RESIDUES AND ARGININE IN FUS PHASE SEPARATION Article 07

February 2025 THERMODYNAMIC FORCES FROM PROTEIN AND WATER GOVERN CONDENSATE FORMATION OF AN INTRINSICALLY DISORDERED PROTEIN DOMAIN Article Open access 21 September 2023 INTRODUCTION

Liquid–liquid phase separation of proteins has been studied intensively in recent years, because the resulting biomolecular condensates both mediate a host of cellular processes ranging from

transcription to stress regulation and also are prone to disease-linked aggregation1,2,3. Most of the attention has been focused on intrinsically disordered proteins (IDPs) or proteins with

long disordered regions, in part due to the strong tendency of such proteins to undergo phase separation4,5,6,7,8,9,10,11. This tendency arises from the fact that intrinsic disorder allows

the proteins to easily form multivalent interactions that drive phase separation12. Ironically, phase separation was first observed on structured proteins, including γ-crystallins13,14,

which are present in the eye lens of animals at high concentrations. For structured proteins, the formation of multivalent interactions that drive phase separation requires high

concentrations12. Consequently the phase separation of structured proteins is characterized by a high saturation concentration and/or a low critical temperature (_T_c), both of which pose

difficulties for experimental studies. Whereas the sequence determinants for the phase separation of disordered proteins are well studied5,7,10,11, our understanding of this crucial issue

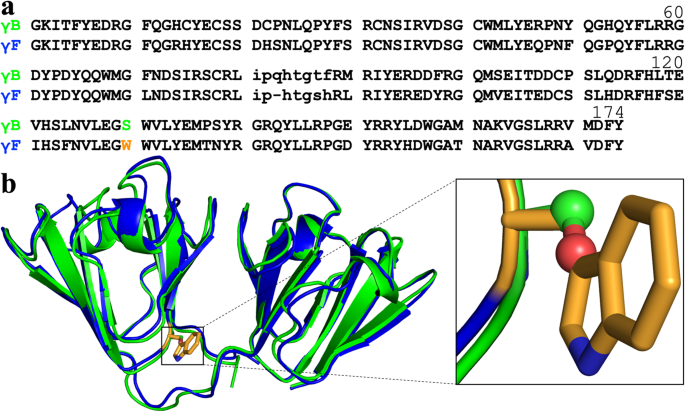
lags for structured proteins. Up to six highly homologous γ-crystallins each have been identified in bovine, rat, and human lenses15,16,17 (Fig. 1a and Supplementary Fig. 1a). According to

their _T_c values for phase separation, they can be divided into two groups: one, represented by bovine γB, has _T_c below 10 °C; the other, represented by bovine γF, has _T_c around body

temperature14,18,19. High-_T_c γ-crystallins are present at a higher level in the lens nucleus than in the cortex, contributing to the gradient in refractive index14,18. Phase separation of

γ-crystallins may lead to cataract, and is suppressed by other components, such as β-crystallins20. When a rat lens was cooled, phase separation was observed, in a phenomenon known as cold

cataract21. The effects of several cataract-causing point mutations on phase separation have been studied; the resulting changes in _T_c, e.g., by R14C (in the presence of a reducing agent

to prevent disulfide crosslinking) and E107A of human γD were small22,23. Given the 82% sequence identity between bovine γB and γF (Fig. 1a), the large gap between their _T_c values is

astounding and prompted the question about its sequence determinants14. The first structural comparison between these two proteins24 also showed high similarity [Fig. 1b; 0.19 Å

root-mean-square-deviation (RMSD) for all backbone atoms]; the authors suggested differences in crystal contact and loop (residues 116–122) conformation as possible causes for the _T_c gap.

Based on sequence comparison, Broide et al. 19 proposed the amino acid substitutions at positions 22 and 47 as potential, 15 as possible, and 163 as less likely determinants. Norledge et al.

 15 noted that these previous attempts were hampered by inaccurate sequences, because the γ-crystallins studied were isolated from bovine lenses and collected as different fractions, and

their sequences were not verified. They attributed the _T_c gap to differences in overall surface charges, including a higher Arg/Lys ratio and a higher His content in the high-_T_c group.

However, this attempt had a handicap of its own, i.e., the classification of human and rat γD as high-_T_c; subsequent studies have shown that both human and rat γD, just like bovine γD19,

belong to the low-_T_c group22,25. Augusteyn et al. 26 measured the tryptophan fluorescence quenching of different bovine γ-crystallins fractions. Commenting on the latter study, Norledge et

al. 15 noted that “their division of the bovine γ-crystallins into two groups on the basis of the tryptophan fluorescence coincides with the division into two groups on the basis of phase

separation behavior,” and attributed the ready fluorescence quenching of the high-_T_c group to an exposed Trp residue, at position 130 (Fig. 1b). Yet, they did not link Trp130 with high

_T_c. The binodals, i.e., the temperature dependence of protein concentrations in the coexisting dilute and dense phases, measured in ref. 19 for bovine γ-crystallins have motivated a number

of computational studies. Dorsaz et al. 27 used spherical particles interacting via a square-well potential to model γ-crystallins. Kastelic et al. 28 extended such a model to have

interaction sites located on the spherical surface. Coarse-grained models are becoming successful in reproducing the effects of large sequence variations (e.g., substitutions of all Tyr

residues by Phe) on the phase equilibria of IDPs6,8,9, but quantitative prediction for the effect of a point mutation seems beyond the reach of these models, especially for structured

proteins. Recognizing the limitation of these simplified models, we developed a method called FMAP, or fast Fourier transform (FFT)-based modeling of atomistic protein-protein interactions,

and demonstrated its feasibility for studying phase separation for γ-crystallins and other proteins29 (see Supplementary Note 1 and Supplementary Fig. 2). The power of FFT enables FMAP to

handle a vast amount of computation required for determining the binodal of an atomistic protein. The FFT-based approach has also been used to compute the second virial coefficients30, which

are an indicator of the critical temperature31. Here we combine FMAP with Brownian dynamics simulations for configurational sampling of dense protein solutions to determine the binodals of

bovine γB and γF and identify the origin of their _T_c gap. Our residue-specific decomposition of inter-protein interactions and sequence analysis reveal the substitution from Ser in γB to

Trp in γF at position 130 (Fig. 1b) as the major contributor to the _T_c gap. This work demonstrates a computational approach to map phase equilibrium to amino-acid sequence for structured

proteins and opens the possibility for designing mutations to alter phase equilibrium. RESULTS FFT-BASED METHOD, FMAPΜ, ENABLES CALCULATION OF THE CHEMICAL POTENTIALS OF Γ-CRYSTALLINS The

chemical potential \(\mu\) is the free energy on a per-molecule basis. For a protein solution, the dependence of the chemical potential on protein concentration (\(\rho\)) allows the

determination of the binodal12,32. \(\mu\) can be decomposed into $$\mu ={\mu }_{{{{{{\rm{id}}}}}}}+{\mu }_{{{{{{\rm{ex}}}}}}}$$ (1) The ideal part \({\mu }_{{{{{{\rm{id}}}}}}}\) is the

chemical potential of an ideal solution, where the protein molecules have no interactions at all, and is the same as the counterpart of an ideal gas, $${\mu

}_{{{{{{\rm{id}}}}}}}={k}_{{{{{{\rm{B}}}}}}}T{{{{{\rm{ln}}}}}}(\rho /{\rho }_{0})$$ (2) where \({k}_{{{{{{\rm{B}}}}}}}\) is Boltzmann’s constant, \(T\) is absolute temperature, and \({\rho

}_{0}\) is an arbitrary reference concentration. The excess part \({\mu }_{{{{{{\rm{ex}}}}}}}\) accounts for interactions between the protein molecules in the solution. While low

concentration decreases \({\mu }_{{{{{{\rm{id}}}}}}}\) (as dictated by Eq. [2]), intermolecular interactions at high protein concentrations can decrease \({\mu }_{{{{{{\rm{ex}}}}}}}\). Two

coexisting phases must have the same chemical potential. So the simple reason that a protein solution undergoes phase separation is that \({\mu }_{{{{{{\rm{id}}}}}}}\) favors the dilute

phase whereas \({\mu }_{{{{{{\rm{ex}}}}}}}\) favors the dense phase, leading to equality in chemical potential between the phases. One way to formulate \({\mu }_{{{{{{\rm{ex}}}}}}}\) is

through the introduction of a test protein, which is identical to the protein molecules in the solution, including experiencing the same intermolecular interactions, but does not affect the

protein solution in any way. If we treat each protein molecule as rigid, then the position and orientation of the protein molecule allow the positions of all its atoms to be specified. Let

\({{{{{\bf{R}}}}}}\) and \({{{{{\boldsymbol{\Omega }}}}}}\), respectively, be the position and orientation of the test protein, \({{{{{\bf{X}}}}}}\) be the configurations of the protein

molecules in the solution, and \(U\left({{{{{\bf{X}}}}}},{{{{{\boldsymbol{\Omega }}}}}},{{{{{\bf{R}}}}}}\right)\) be the interaction energy between the test protein and the protein solution,

then the excess chemical potential is given by33 $${e}^{-\beta {\mu }_{{{{{{\rm{ex}}}}}}}}=\left\langle {e}^{-\beta U\left({{{{{\bf{X}}}}}},{{{{{\boldsymbol{\Omega

}}}}}},{{{{{\bf{R}}}}}}\right)}\right\rangle$$ (3) where \(\beta =1/{k}_{{{{{{\rm{B}}}}}}}T\) and \(\left\langle \cdots \right\rangle\) signifies averaging over \({{{{{\bf{X}}}}}}\),

\({{{{{\boldsymbol{\Omega }}}}}}\), and \({{{{{\bf{R}}}}}}\). For proteins modeled at the atomistic level, the evaluation of \({\mu }_{{{{{{\rm{ex}}}}}}}\) requires a vast amount of

computation, involving sampling over \({{{{{\bf{X}}}}}}\), \({{{{{\boldsymbol{\Omega }}}}}}\), and \({{{{{\bf{R}}}}}}\). For example, the sampling over \({{{{{\bf{R}}}}}}\) entails placing

the test protein (with a particular orientation \({{{{{\boldsymbol{\Omega }}}}}}\)) into numerous positions inside a protein solution (with a particular configuration \({{{{{\bf{X}}}}}}\)),

as illustrated in Fig. 2a. Our FFT-based method, here termed FMAPμ, accelerates the averaging over \({{{{{\bf{R}}}}}}\) and thereby makes the evaluation of \({\mu }_{{{{{{\rm{ex}}}}}}}\)

feasible29. Our interaction energy function is comprised of additive contributions from all pairs of atoms between any two protein molecules. The contribution from each pair of atoms _i_ and

_j_ has three terms29,34:

$${u}_{{ij}}({r}_{{ij}})={u}_{{ij}}^{{{{{{\rm{st}}}}}}}({r}_{{ij}})+{s}_{1}{u}_{{ij}}^{{{{{{\rm{n}}}}}}-{{{{{\rm{a}}}}}}}({r}_{{ij}})+{s}_{2}{u}_{{ij}}^{{{{{{\rm{elec}}}}}}}({r}_{{ij}})$$

(4) where \({r}_{{ij}}\) is the interatomic distance. The steric term is $${u}_{{ij}}^{{{{{{\rm{st}}}}}}}({r}_{{ij}})=\left\{\begin{array}{cc}{{\infty }},&{r}_{{ij}} \, < \,({\sigma

}_{{ii}}+{\sigma }_{{jj}})/2\\ 0,&{{{{{\rm{otherwise}}}}}}\end{array}\right.$$ (5) where \({\sigma }_{{ii}}/2\) denotes the hard-core radius of atom \(i\). The nonpolar attraction term,

including van der Waals and hydrophobic interactions, has the form of a Lennard-Jones potential, $${u}_{{ij}}^{{{{{{\rm{n}}}}}}-{{{{{\rm{a}}}}}}}({r}_{{ij}})=4{\epsilon

}_{{ij}}\left[{\left(\frac{{\sigma }_{{ij}}}{{r}_{{ij}}}\right)}^{12}-{\left(\frac{{\sigma }_{{ij}}}{{r}_{{ij}}}\right)}^{6}\right]$$ (6) where \({\epsilon }_{{ij}}\) denotes the magnitude

of the \(i-j\) attraction, \({\sigma }_{{ij}}\) is the distance at which the nonpolar interaction energy is zero. As in our previous studies29,34, we used AMBER parameters for \({\epsilon

}_{{ij}}\) and \({\sigma }_{{ij}}\), along with a scaling parameter \({s}_{1}\) = 0.16. The electrostatic term has the form of a Debye-Hückel potential,

$${u}_{{ij}}^{{{{{{\rm{elec}}}}}}}({r}_{{ij}})=332\mathop{\sum }\limits_{{ij}}\frac{{q}_{i}{q}_{j}}{\varepsilon {r}_{{ij}}}{e}^{-\kappa {r}_{{ij}}}$$ (7) where \({q}_{i}\) is the partial

charge on atom \(i\), \(\varepsilon\) is the dielectric constant, and \(\kappa\) is the Debye screening parameter. We introduced a scaling factor \({s}_{2}\) = 1.6 to account for effects

such as possible reduction in the dielectric constant in dense protein solutions29. The sampling of protein configurations (\({{{{{\bf{X}}}}}}\)) was implemented by Brownian dynamics (BD)

simulations35. 30–450 γB or γF molecules were started in a cubic box of side length 324 Å, resulting in concentrations from 31 to 461 mg/ml that span the experimentally relevant range (see

Fig. 3f inset below). The pair distribution function calculated from the BD simulations matches with that expected from the pair interaction energy (Supplementary Fig. 3). From these

simulations, we took 2000 configurations at 10-ns intervals to implement FMAPμ. To sample \({{{{{\boldsymbol{\Omega }}}}}}\), we generated 500 random orientations for the test protein.

Lastly the sampling over \({{{{{\bf{R}}}}}}\) was realized by discretizing the BD simulation box with a 0.6-Å resolution in each dimension, resulting in a total of 5403 = 1.57464 × 108 grid

points. So altogether we obtained 1.57464 × 1014 interaction energies to calculate \({\mu }_{{{{{{\rm{ex}}}}}}}\) at each protein concentration. In Fig. 2b, c, we display the \({\mu

}_{{{{{{\rm{ex}}}}}}}\) results for γB and γF over the aforementioned concentration range and at temperatures from −2 °C to 50 °C. Several features at low temperatures are worth noting.

First, attractive interactions dominate the Boltzmann average of Eq. [3], and hence \({\mu }_{{{{{{\rm{ex}}}}}}}\) is negative. Second and most interestingly, γF \({\mu

}_{{{{{{\rm{ex}}}}}}}\) is more negative than γB \({\mu }_{{{{{{\rm{ex}}}}}}}\). For example, at \(T\) = −2 °C and \(\rho\) = 400 mg/ml, \(\beta {\mu }_{{{{{{\rm{ex}}}}}}}\) is −2.3 ± 0.1

for γB but decreases to −3.0 ± 0.2 for γF. The difference in \({\mu }_{{{{{{\rm{ex}}}}}}}\) reflects stronger attractive interactions in the γF solution, and translates into a higher _T_c.

So the raw \({\mu }_{{{{{{\rm{ex}}}}}}}\) results already capture the key difference between γB and γF in phase equilibrium. Third, \({\mu }_{{{{{{\rm{ex}}}}}}}\) initially decreases with

increasing concentration, because more and more molecules can participate in attractive interactions. For example, for γB at \(T\) = −2 °C, \(\beta {\mu }_{{{{{{\rm{ex}}}}}}}\) decreases

from −1.27 ± 0.02 at 123 mg/ml to −2.3 ± 0.1 at 400 mg/ml. However, with further increase in concentration, \({\mu }_{{{{{{\rm{ex}}}}}}}\) starts to turn over, as molecules experience steric

repulsion. Lastly, at the lowest temperatures, the values of \({\mu }_{{{{{{\rm{ex}}}}}}}\) can suffer large uncertainties, as illustrated by the \({\beta \mu }_{{{{{{\rm{ex}}}}}}}\) value

−4.7 (+2.6/−0.7) of γB at −2 °C and 277 mg/ml. The numerical uncertainties arise from the general difficulty of sampling the lowest energy region of any molecular system (e.g., ref. 4). As

the temperature is raised, steric interactions become important even at lower protein concentrations, thereby elevating the entire \({\mu }_{{{{{{\rm{ex}}}}}}}\) curve. At _T_ = 50 °C,

\({\mu }_{{{{{{\rm{ex}}}}}}}\) is positive even at the lowest concentration 31 mg/ml for γB and first becomes positive at 184 mg/ml for γF. In this situation, true for all temperatures above

_T_c, no dense phase can achieve equal stability as a would-be dilute phase and thus no phase separation is possible. At the limit of _T_ → ∞, only the steric term survives in the Boltzmann

average of Eq. [3]; the resulting excess chemical potential, \({\mu }_{{{{{{\rm{ex}}}}}}}^{{{{{{\rm{st}}}}}}}\), is related to the fraction, \({f}_{{{{{{\rm{CF}}}}}}}\), of test-protein

placements that are free of steric clashes with protein molecules in the solution. This relation is given by Eq. [9] in Computational Methods. The clash-free fraction can be obtained

accurately at any temperature. As shown in Supplementary Fig. 4, the \({f}_{{{{{{\rm{CF}}}}}}}\) results of γB and γF are very close to each other, and, at high concentrations, are

orders-of-magnitude higher than the counterpart obtained by replacing Lennard-Jones particles with γB molecules, as we did in 201629. The BD simulations here, with an atomistic energy

function, capture the ability of protein molecules to form intricate clusters stabilized by preferential interactions, leaving more voids to place the test protein. The excessively low

\({f}_{{{{{{\rm{CF}}}}}}}\), along with limited sampling in \({{{{{\boldsymbol{\Omega }}}}}}\), in our 2016 study is responsible for the narrow binodal obtained there. BINODALS DETERMINED

FROM CONCENTRATION DEPENDENCE OF CHEMICAL POTENTIAL SHOW HIGHER _T_ C FOR ΓF THAN FOR ΓB We developed a procedure to mitigate numerical uncertainties of \({\mu }_{{{{{{\rm{ex}}}}}}}\)

manifested at low temperatures. This procedure is based on the observation that the cumulative distribution function (CDF) of the interaction energy

\(U\left({{{{{\bf{X}}}}}},{{{{{\boldsymbol{\Omega }}}}}},{{{{{\bf{R}}}}}}\right)\) is exponential for over 10 orders of magnitude, covering nearly the entire negative range of \(U\)

(Supplementary Fig. 5a, b). The procedure involves fitting the logarithm of the CDF to a linear function of \(U\) in an intermediate region of \(U\) (Supplementary Fig. 5a, b) and then

extrapolating to a minimum energy \({U}_{{{\min }}}\) (Supplementary Figs. 5a, b and 636). As illustrated in Fig. 3a, the corrected \({\mu }_{{{{{{\rm{ex}}}}}}}\), by modeling the CDF in the

low interaction energy region, is now free of the large variations of the original \({\mu }_{{{{{{\rm{ex}}}}}}}\). We then add the ideal part to the corrected \({\mu }_{{{{{{\rm{ex}}}}}}}\)

and perform an equal-area construction29,32 (Fig. 3b) to obtain the concentrations in the coexisting dilute and dense phases. By connecting the coexisting concentrations from different

temperatures, we obtain the binodal (Fig. 3c). The equal-area construction also yields the spinodal, which defines a range of concentrations in which the system is thermodynamically

unstable. As shown in Fig. 3c, the computed binodal and spinodal for γB both match well with the experimental counterparts from ref. 37. The computation yields a critical temperature of

approximately 4 °C for γB. At _T_ = −2 °C, the computed spinodal concentrations for γB are 123 mg/ml at the lower end and 400 mg/ml at the higher end. In Fig. 3d, we display a slice of a

configuration of the γB solution at these concentrations. Both illustrate the intricate clusters noted above, which again are stabilized by preferential interactions. At the higher

concentration, the average number of interaction partners per molecule is higher, leading to a more negative \({\mu }_{{{{{{\rm{ex}}}}}}}\) as presented above. In Fig. 3e, we compare the

original and corrected \({\mu }_{{{{{{\rm{ex}}}}}}}\) for γF at −2 °C, along with the corresponding results for γB that have already been shown in Fig. 3a. Again, \({\mu

}_{{{{{{\rm{ex}}}}}}}\) is more negative for γF than for γB. Finally, in Fig. 3f, we present the computed binodal for γF, which exhibits a higher _T_c, ~10 °C, relative to the counterpart

for γB. Similar increases in _T_c from γB to γF are predicted when other acceptable values of the scaling factors \({s}_{1}\) and \({s}_{2}\) are applied in the energy function (Eq. [4])

(Supplementary Note 1 and Supplementary Fig. 7). Though moving in the correct direction relative to the γB _T_c, the predicted γF _T_c significantly underestimates the experimental value of

~39 °C19. A MORE NEGATIVE SECOND VIRIAL COEFFICIENT FOR ΓF CORROBORATES ITS HIGHER _T_ C Whereas the excess chemical potential \({\mu }_{{{{{{\rm{ex}}}}}}}\) is determined by the

interactions among all the protein molecules in a solution, the second virial coefficient \({B}_{2}\) is determined by the interaction between a pair of protein molecules. When \({\mu

}_{{{{{{\rm{ex}}}}}}}\) is expanded as a Taylor series in \(\rho\) (see Eq. [19] in Computational Methods), the first-order coefficient is twice of \({B}_{2}\). \({B}_{2}\) can be an

indicator of the critical temperature31. A more negative \({B}_{2}\) corresponds to a higher _T_c. We have adapted the FFT-based approach to derive FMAPB2 as a very robust method for

computing second virial coefficients30. The resulting \({B}_{2}\) values of γB and γF over a wide temperature range are shown as solid curves in Fig. 4a. It is clear that γF has a more

negative \({B}_{2}\), therefore supporting a higher _T_c. The computed \({B}_{2}\) values for γB match well with the experimental data of ref. 38 (Fig. 4a inset). Vliegenthart and

Lekkerkerker31 found an empirical rule, \({B}_{2}({T}_{{{{{{\rm{c}}}}}}})/{V}_{{{{{{\rm{st}}}}}}}\approx -6\), for spherical particles with a steric core and attractive rim, where

\({V}_{{{{{{\rm{st}}}}}}}\) denotes the volume of the steric core. We can use the steric version of \({B}_{2}\), \({B}_{2}^{{{{{{\rm{st}}}}}}}\), obtained when only the steric term is kept

in the interaction energy function, to define the steric volume: \({V}_{{{{{{\rm{st}}}}}}}\equiv {B}_{2}^{{{{{{\rm{st}}}}}}}/4\). The critical temperatures predicted by the

Vliegenthart-Lekkerkerker rule are 0 °C for γB and 6 °C for γF, resulting in the same gap in _T_c as determined from the binodals (Fig. 3f). The virial coefficients determined by FMAPB2 are

also close to those, displayed as circles, derived from the first-order coefficient of a truncated Taylor expansion of \({\mu }_{{{{{{\rm{ex}}}}}}}\) (Eq. [19]). RESIDUE-SPECIFIC

DECOMPOSITION OF PAIR INTERACTION ENERGY REVEALS THE S130W SUBSTITUTION AS THE MAIN CAUSE FOR _T_ C DIFFERENCE To identify the γB-to-γF substitutions responsible for the increase in _T_c, we

decomposed the pair interaction energies of γB or γF molecules. Such decomposition has been used previously to reveal residues important for phase separation39. In Fig. 5, we display the

differences between corresponding residues of γF and γB in their contributions to the respective pair interaction energies. The six positions that make the greatest contributions to the

lower pair interaction energy of γF are, in descending order: 128, 130, 84, 79, 127, and 21. The differences in energetic contributions at all these positions are beyond the cutoff set at

mean – 3 × SD. γB and γF have the same amino acids at five of these positions: Asp21, Arg79, His84, Leu127, and Glu128. The only position that involves a change in amino acids is 130, from

Ser in γB to Trp in γF. Therefore the decomposition reveals the S130W substitution as the main cause for strengthening intermolecular interactions, leading to the higher _T_c of γF. To

verify the role of the S130W substitution, we modeled the W-to-S mutation in γF and the reverse mutation in γB, and calculated their effects. As shown in Fig. 4a, the γFW130S mutant largely

mimics γB in \({B}_{2}\), with only slight undershooting of its magnitude at low temperatures. The γBS130W mutation partially recovers the large negative \({B}_{2}\) of γF. Similar

descriptions apply to the effects of the two mutations on residue-specific decomposed pair interaction energies. As shown in Supplementary Fig. 8a, the γF – γFW130S differences in

residue-specific contribution are similar to the γF–γB counterparts (Fig. 5). In particular, at Asp21 and Glu128 along with position 130, the γF–γFW130S differences exceed the mean – 3 × SD

cutoff. On the other hand, the γBS130W mutant does not quite recover the pair interaction energy of γF; only the γBS130W–γB difference in residue-specific contribution at position 130

exceeds the mean – 3 × SD cutoff (Supplementary Fig. 8b). As the ultimate test of the role of the S130W substitution, we determined the binodals of the γFW130S and γBS130W mutants (Fig. 4b).

The binodal of the γFW130S mutant is close to that of γB, while the binodal of the γBS130W mutant comes close to that of γF. ΓB INTERACTIONS ARE MORE ISOTROPIC WHEREAS ΓF INTERACTIONS MORE

PREFERENTIALLY INVOLVE TRP130 To provide further insight into the S130W substitution, we analyzed the poses with the lowest pair interaction energies from FMAPB2 calculations. We label one

partner of the pair as the central copy and the other partner as the test protein. The poses of the low-energy pairs are displayed in Fig. 6a for γB and 6b for γF. The central copy is

rendered in cartoon or surface and the test protein represented by a dot at its center of geometry, one for each low-energy pose. We define a molecular frame, with the _z_ axis parallel to

its inter-domain interface and the _y_ axis pointing from the C-terminal domain to the N-terminal domain. The view in Fig. 6a, b is into the negative _x_ axis of the central copy. A 360°

view of Fig. 6a, b is presented in Supplementary Movies 1 and 2. In the top left panels of Fig. 6a, b, we display the 1000 lowest-energy poses. For both γB and γF, the test protein tends to

concentrate in positions facing residue 130 of the central copy, but this tendency is stronger for γF. We clustered the 1000 poses and present the large clusters (≥20 members) in the top

right panels of Fig. 6a, b. Each cluster is represented by a sphere and an arrow. The sphere has a radius proportional to the cluster size and is centered at the pose with the lowest energy

in that cluster; the arrow is along the _z_ axis of the molecular frame of the test protein in the latter pose. Both γB and γF have seven large clusters. For γB, six of the seven clusters

are around residue 130 and the seventh cluster is at the back of the central copy; together the seven clusters account for 30% of the 1000 low-energy poses. For γF, all the seven clusters

are around residue 130 and collect 47% of the 1000 lowest-energy poses, indicating a much stronger preference for residue 130 to be an interaction site. We also display the cluster

representatives by their molecular structures in the top right panels of Fig. 6a, b. As further illustrated in Supplementary Fig. 9a, the two partner γF molecules prefer a parallel relative

orientation, but the γB pairs prefer a perpendicular orientation. Moreover, while γF pairs have a strong tendency to form interfaces that bury the Trp130 residues in both partner molecules,

γB Ser130 can be either inside or outside the interfaces of the low-energy pairs. Trp has the bulkiest sidechain, possessing the potential for hydrophobic, cation–π, amido–π, π–π, and

hydrogen bonding interactions. The roles of Trp-mediated cation-π interactions in the folding stability of structured proteins and binding stability of IDPs are well recognized40,41. In

contrast, Ser has only a short polar sidechain, with interaction limited to hydrogen bonding. In γ-crystallin structures, residue 130 is located at the foot of the inter-domain cleft (Fig. 

1b). In interfaces that bury the Trp130 residues in both partners, Trp130 in one partner can interact with surface residues around Trp130 of the other partner, including Asp21, Arg79,

Leu127, and Glu128 (Supplementary Fig. 9b). In contrast, for γB, Ser130 has limited ability to form these interactions even when buried in an interface; instead other interactions, such as

between Arg153 in one partner and Glu150 of the other partner, stabilize the interface (Supplementary Fig. 9c). The foregoing structural differences between γB and γF in their respective

pairs can now explain the energetic differences in Fig. 5. γF pairs form interfaces where both Trp130 residues are buried; interactions between Trp130 on one side and Asp21, Arg79, His84,

Leu127, and Glu128 on the opposite side result in the negative energy values at these residues. γB pairs can form alternative interfaces, which explain the positive energy values at Arg153

and Asp156. While the interfaces in the representatives of the large clusters are energetically favorable, it is important to point out that γB or γF can form numerous other binary

interfaces. A fuller picture is presented when all clusters with at least two members are included (bottom right panels of Fig. 6a, b). Poses start to populate the rest of the surface of the

central copy. An even fuller picture is reached when all poses with pair energies below -6 kcal/mol are included (bottom left panels of Fig. 6a, b). For γF, although Trp130 is a preferred

interaction site, many other sites can also participate in intermolecular interactions, allowing the formation of clusters beyond a dimer in a concentrated solution and thereby leading to

phase separation. This scenario is illustrated well using the Trp130-Trp130 distance between two neighboring γF molecules. The distribution of Trp130-Trp130 distances in low-energy pairs,

weighted by the Mayer function, exhibits a high peak around 10 Å (Supplementary Fig. 9d), reflecting the Trp130-Trp130 interface noted above. Trp130-Trp130 distances in γF clusters formed in

the dense phase (as captured by BD simulations) still show a peak around 10 Å (Supplementary Fig. 9e), indicating that Trp130-Trp130 interfaces are also formed to stabilize the clusters.

However, beyond this peak, Trp130-Trp130 distances exhibit a broad distribution, indicating the participation of other interfaces. In comparison, Ser130-Ser130 interfaces have a reduced

tendency to form in low-energy γB pairs (Supplementary Fig. 9d) and play a reduced role in γB clusters (Supplementary Fig. 9e). GRANTHAM’S DISTANCE BETWEEN LOW AND HIGH-_T_ C Γ-CRYSTALLINS

ALSO SINGLES OUT THE S130W SUBSTITUTION We calculated Grantham’s distance42 between the low-_T_c group (γA, γB, γC, and γD) and the high-_T_c group (γE and γF) at each position along the

sequence alignment in Supplementary Fig. 1a. Grantham’s distance measures the physicochemical difference between the side chains of two amino acids. Its square is a weighted sum of squared

differences in three properties: group composition, polarity, and molecular volume. The residual Grantham distance, defined as the difference between inter-group and intra-group distances,

is displayed as a red curve in Fig. 5. The values exceed the cutoff of mean +3 × SD at three positions: 22, 111, and 130. In Supplementary Fig. 1b, we specifically compare the amino acids of

the 15 γ-crystallins at each of these three positions. At position 22, the low-_T_c group contains three unique amino acids: Asn, Cys, and His whereas the high-_T_c group contains only His.

Therefore the two groups share the amino acid His at position 22. A similar situation occurs at position 111, where the two groups share the amino acid Ser. Only at position 130, the two

groups do not share any amino acid: the low-_T_c group contains Cys and Ser, whereas the high-_T_c group contains Trp and Tyr, which are both aromatic. The analysis using Grantham’s distance

thus singles out the substitutions at position 130 as involving the greatest physicochemical difference between the low and the high-_T_c groups, from a short sidechain to an aromatic

sidechain. The sequence logo around position 130 is shown as an inset in Fig. 5, illustrating the divergence at position 130 and consensus at neighboring positions. HIGH-_T_ C Γ-CRYSTALLINS

COLLECTIVELY HAVE MORE NEGATIVE VIRIAL COEFFICIENTS THAN LOW-_T_ C Γ-CRYSTALLINS The energetic differences presented above between γB and γF not only are not limited to the Protein Data Bank

(PDB) structures chosen for the calculations but also extend to other low and high-_T_c γ-crystallins. We expanded the FMAPB2 calculations to 13 other PDB structures (Fig. 7). Together the

15 structures cover six different γ-crystallins; 10 of these structures are in the low-_T_c group and the remaining five are in the high-_T_c group. The \({B}_{2}/{V}_{{{{{{\rm{st}}}}}}}\)

values are −1.3 ± 0.5 (mean ± SD) for the low-_T_c group and −2.1 ± 0.3 for the high-_T_c group. The high-_T_c group has a very significantly lower mean \({B}_{2}\) (_P_ value = 0.002 in

unpaired _t_ test), consistent with a much higher _T_c. DISCUSSION Based on extensive sequential, structural, and energetic analyses, we have identified a Ser to Trp substitution at position

130 as the main cause for the difference in _T_c between γB and γF. This identification finally provides a solution to the question first raised by Siezen et al. 14 nearly 40 years ago.

More broadly, our study demonstrates that it is now possible to quantitatively account for the contributions of individual residues to the energetics of phase separation for structured

proteins. Such quantitative characterization enables us not only to understand how sequence determines phase equilibrium but also to design sequences with the critical temperature altered in

a desired direction. Trp (or Tyr) as an amino acid that promotes phase separation has been well-recognized for IDPs5,7,10. Here we show that a substitution from Ser to Trp has a major role

in raising the _T_c of a structured protein. In IDPs, a Trp can take advantage of their flexibility to form a variety of intermolecular interactions including hydrophobic, cation–π, amido–π,

π–π, and hydrogen bonding. In structured proteins, the same potential for intermolecular interactions is open to a Trp when we consider the fact that the dense phase is stabilized by

nonspecific intermolecular association that can occur in countless ways. Whereas the effect of an S-to-W mutation could be context-dependent for IDP, it may be much more so in a structured

protein. For example, an S-to-W mutation in a buried site (assuming that the protein structure remains stable), is expected to have little effect on phase separation because the residue does

not participate in intermolecular interactions. Moreover, not all exposed S-to-W mutations are created equal. An S-to-W mutation at a site where low-energy pairs are unlikely to form may

have only a modest effect, but an S-to-W mutation at a preferential binding site, such as at the foot of the inter-domain cleft of γ-crystallins (Fig. 6), is likely to promote phase

separation. The S130P mutation of human γD abolished heat-induced aggregation43, possibly by promoting dimers that hide the residue-130 sites in both monomers and thus prevent further

aggregation. We conclude that the significant contribution of the S130W substitution to γF _T_c derives from not only the physicochemical differences between the two amino acids but also

from the strategic location of residue 130 on the protein surface. While both IDPs and structured proteins can undergo phase separation, it has been recognized that IDPs more readily do so

than structured proteins12. In essence, the flexibility of IDPs makes it easier for them to form intermolecular interactions that stabilize the dense phase. In contrast, structured proteins

require high concentrations for a given protein molecule to interact with a sufficient number of partner molecules in order to make the dense phase stable. As a result, the dense-phase

concentration of a structured protein is much higher than the counterpart of a typical IDP, corresponding to a much broader binodal. One indication of this concentration difference is the

much higher dense-phase viscosities of structured or multi-domain proteins relative to IDPs44. For γB and γF, the dense-phase concentrations are 400–500 mg/ml, or around 20 mM19. Atomistic

modeling presented here captures well the countless ways that proteins can form intermolecular interactions in the dense phase and thereby can recapitulate the broad binodals. By exploiting

the power of FFT, our approach has overcome the challenge presented by the vast amount of computation required for determining the binodal of an atomistic protein. Still, the approach has

significant room for improvement, including the accuracy of the interaction energy function and the treatment of protein flexibility. These limitations most likely account for the present

underestimation of the _T_c gap between γF and γB. Binodals are sensitive to energy functions and thus hold great potential for their parameterization. For example, our current energy

function may underestimate the distinction between Arg and Lys. A substitution from Lys to Arg at position 163 could contribute to the high _T_c of γF15,19; such substitutions in Antarctic

toothfish γ-crystallins have indeed been found to have a significant effect on _T_c45. Our preliminary calculation using the Rosetta all-atom energy function46, which is widely used in

protein docking and design and more sophisticated than our energy function, shows a wider gap between γF and γB in binary interaction energies (Supplementary Note 1 and Supplementary Fig. 

10). As for protein flexibility, an important step forward may be sidechain repacking in response to the approach of other protein molecules. Our preliminary study, by using RosettaDock47 to

carry out sidechain repacking, indeed shows a further widening of the energy gap between γF and γB (Supplementary Note 1 and Supplementary Fig. 10). Alternatively, using a preselected

library of protein structures in simulations48 and for chemical potential calculations also seems a promising direction. As an initial test of this idea, we calculated the \({B}_{2}\) value

by averaging over multiple structures from the PDB for a given γ-crystallin (Supplementary Note 1 and Supplementary Fig. 11). These average \({B}_{2}\) values show the expected gap between

the low and high-_T_c groups, now with a higher confidence level since it is based on multiple structures. COMPUTATIONAL METHODS PROTEIN STRUCTURE PREPARATION The structures of the

γ-crystallins were from PDB entries 1AMM for bovine γB49 and 1A45 for bovine γF15. PDB2PQR50 was used to add hydrogens and assign AMBER charges, with protonation states assigned according to

PROPKA51 at pH 7. The net charge is 0 for γB and +1 for γF. Additionally, 13 other high-resolution (2.3 Å or better) γ-crystallin X-ray structures were downloaded from the PDB and similarly

processed (see Fig. 7 for PDB names). The S130W mutation of γB was modeled by grafting the sidechain of Trp130 in γF after structure alignment using all backbone atoms. The newly introduced

Trp130 sidechain clashed with the nearby Arg147 sidechain, and so these two sidechains were refined by steepest-descent energy minimization in UCSF Chimera52. The W130S mutation of γF was

similarly modeled. Four of the five human γD structures (other than 1HK0) contained single or double mutations; each of the mutated sidechains was reverted to the wild-type sidechain, by

grafting the corresponding sidechain in 1HK0 (after structure alignment using backbone atoms of the residue in question plus two neighboring residues in either direction) and then energy

minimization. Unless otherwise indicated, the ionic strength was 0.24 M, modeling 100 mM phosphate buffer at pH 7.1 in experimental studies of γ-crystallin phase separation19. BROWNIAN

DYNAMICS (BD) SIMULATIONS The simulation of diffusional association package (SDA, version 7.2.2)35 was used to generate protein configurations at multiple concentrations. The simulation box

was a cube with a side length of 324 Å; periodic boundary conditions were imposed. The number (_N_) of proteins inside the box was 30 or a higher multiple, all the way to 450, covering a

concentration range of 31–461 mg/ml. For initial configurations, the protein molecules were oriented randomly and placed at the positions of Lennard-Jones particles from previous

simulations29. The effective charges derived from solving the Poisson-Boltzmann equation (with van der Waals surface as the dielectric boundary) using APBS53 were used for electrostatic

solvation energy calculation54. The temperature was 300 K. The interaction energy between protein molecules consists of Coulomb interaction, electrostatic solvation, hydrophobic solvation,

and soft-core repulsion. Default parameter values were used except for the last term, for which we reduced the scaling factor by fourfold (from 0.0156 to 0.0039). The latter value allowed

for a good match with FMAPB2 in pair correlation functions (Supplementary Fig. 3). After 1 μs equilibration, snapshots were collected at 10-ns intervals for the next 20 μs, totaling 2000

snapshots. Depending on the protein number _N_, the BD simulations took 5–330 h on 16 cores in two Intel(R) Xeon(R) CPU E5-2650 2.6 GHz CPUs. FMAPΜ CALCULATIONS The interaction energy

function is specified by Eqs. [4] to [7]. A cutoff of 12 Å was imposed for calculating interactions between two atoms. For a given configuration \({{{{{\bf{X}}}}}}\) of the protein solution

and a given orientation \({{{{{\boldsymbol{\Omega }}}}}}\) of the test protein, the interaction energy \(U\left({{{{{\bf{X}}}}}},\,{{{{{\boldsymbol{\Omega

}}}}}}{{{{{\boldsymbol{,}}}}}}\,{{{{{\bf{R}}}}}}\right)\) when placing the position \({{{{{\bf{R}}}}}}\) of test protein at any of the 5403 = 1.57464 × 108 points on a cubic grid was

calculated using FMAP29,32,34. For each protein concentration, the calculation was repeated 2000 × 500 = 106 times, combining 2000 protein configurations with 500 orientations of the test

protein. These calculations took about 3500 h per protein concentration on 16 cores in two Intel(R) Xeon(R) E5-2650 2.6 GHz CPUs. The excess chemical potential is finally determined

according to Eq. [3]. For a given \({{{{{\bf{X}}}}}}\) and a given \({{{{{\boldsymbol{\Omega }}}}}}\), FMAP returns the number of grid points where the test protein experiences steric clash

and the interaction energies at all the clash-free grid points. The latter grid points constitute the clash-free fraction, \({f}_{{{{{{\rm{CF}}}}}}}\). The value of

\({f}_{{{{{{\rm{CF}}}}}}}\) is very stable with respect to the change in \({{{{{\bf{X}}}}}}\) or \({{{{{\boldsymbol{\Omega }}}}}}\)55\({{{{{\rm{;}}}}}}\) therefore we can treat

\({f}_{{{{{{\rm{CF}}}}}}}\) as a constant and pool the clash-free interaction energies from the 106 combinations of \({{{{{\bf{X}}}}}}\) and \({{{{{\boldsymbol{\Omega }}}}}}\), leading to

$${e}^{-\beta {\mu }_{{{{{{\rm{ex}}}}}}}}=\frac{{f}_{{{{{{\rm{CF}}}}}}}}{{M}_{{{{{{\rm{CF}}}}}}}}\mathop{\sum }\limits_{m=1}^{{M}_{{{{{{\rm{CF}}}}}}}}{e}^{-\beta

U\left({{{{{\bf{X}}}}}},{{{{{\boldsymbol{\Omega }}}}}},{{{{{\bf{R}}}}}}\right)}$$ (8) where \({M}_{{{{{{\rm{CF}}}}}}}\) is the total number of clash-free interaction energies. The maximum

possible value of \({M}_{{{{{{\rm{CF}}}}}}}\) is 1.57464 × 1014. We refer to this formulation of the excess chemical potential as “raw-sum”. In the hypothetical limit of _T_ → ∞, we can set

\(\beta\) to 0 in the right-hand side of Eq. [8] and obtain $${e}^{-\beta {\mu }_{{{{{{\rm{ex}}}}}}}^{{{{{{\rm{st}}}}}}}}={f}_{{{{{{\rm{CF}}}}}}}$$ (9) CALCULATING \({{{{{{\BOLDSYMBOL{\MU

}}}}}}}_{{{{{{\BF{EX}}}}}}}\) OVER A RANGE OF TEMPERATURES Results for \({\mu }_{{{{{{\rm{ex}}}}}}}\) over a range of temperatures are needed to determine the binodal. Instead of repeating

the above FMAPμ calculations at different temperatures, we calculated the interaction energies once at 298 K and then merely changed \(\beta\) when carrying out the sum over the Boltzmann

factors (Eq. [8]). This shortcut assumes that the interaction energy function is temperature-independent and that the same BD configurations can be used for FMAPμ calculations at different

temperatures. We did not save the individual interaction energies, which could be up to 1.6 × 1014 in total number, but binned them into a histogram in very fine bins (width \(\Delta\) at

0.016 kcal/mol). We did save all the configurations with interaction energies lower than −8 kcal/mol for further analysis. The raw sum in Eq. [8] can now be expressed as $${e}^{-\beta {\mu

}_{{{{{{\rm{ex}}}}}}}}=\frac{{f}_{{{{{{\rm{CF}}}}}}}}{{M}_{{{{{{\rm{CF}}}}}}}}\mathop{\sum }\limits_{U={U}_{{{\min }}}}^{{U}_{{{\max }}}}H(U){e}^{-\beta U}$$ (10) where \(H(U)\) is the

number of interaction energies in the bin centered at \(U\); and \({U}_{{{\min }}}\) and \({U}_{{{\max }}}\), respectively, are the minimum and maximum interaction energies. Note that the

Boltzmann factor \({e}^{-\beta U}\) is a decaying function of \(U\) whereas \(H(U)\) is expected to be a growing function of \(U\) as \(U\) increases from \({U}_{{{\min }}}\). Depending on

whether the rate of decay is lower or higher than the rate of growth, the product, \(H(U){e}^{-\beta U}\), is either a growing or decaying function of \(U\). The rate of decay of

\({e}^{-\beta U}\) depends on temperature. For high temperatures, \(H(U){e}^{-\beta U}\) is a growing function of \(U\); hence its values at \(U\) near \({U}_{{{\min }}}\) contribute little

to the sum in Eq. [10] and the inaccuracy in \(H(U)\) near \({U}_{{{\min }}}\) does not cause serious numerical errors in \({\mu }_{{{{{{\rm{ex}}}}}}}\). However, at low temperatures,

\(H(U){e}^{-\beta U}\) is a decaying function of \(U\); then this inaccuracy in \(H(U)\) can result in significant uncertainties in \({\mu }_{{{{{{\rm{ex}}}}}}}\), as illustrated by the

result for γB at 277 mg/ml and −2 °C (Fig. 2b). We not only saved the total interaction energies but also the separate terms (i.e., nonpolar attraction and electrostatic) in a histogram

form. These data allowed us to quickly produce chemical potentials and other results when we changed the values of the scaling factors \({s}_{1}\) and \({s}_{2}\). MODELING

\({{{{{\BOLDSYMBOL{H}}}}}}({{{{{\BOLDSYMBOL{U}}}}}})\) NEAR \({{{{{{\BOLDSYMBOL{U}}}}}}}_{{{{{{\BF{MIN }}}}}}}\) AS A POWER LAW DISTRIBUTION WITH AN UPPER BOUND To mitigate the

aforementioned uncertainties in \({\mu }_{{{{{{\rm{ex}}}}}}}\), we modeled \(H(U)\) in the low interaction energy region. We observed that the (unnormalized) cumulative distribution function

(CDF) $$C(U)=\mathop{\sum }\limits_{{U}^{{\prime} }\ge {U}_{{{\min }}}}^{U}H({U}^{{\prime} })$$ (11) has an exponential dependence on the interaction energy (e.g., Supplementary Fig. 5a, b)

$$C\left(U\right)=A{e}^{\alpha U},{U}_{{{\min }}}\le U \, < \,0$$ (12) for over 10 orders of magnitude, covering nearly the entire negative range of \(U\). The values of \(\alpha\) range

from 2.1 to 1.5 (decreasing with increasing protein concentration), comparable to the value, 1.7, of \(\beta\) at 298 K. Correspondingly, the histogram function has the form

$$H\left(U\right)=\frac{{dC}(U)}{{dU}}$$ (13a) $$=A\alpha {e}^{\alpha U},{U}_{\min }\,\le \,U \, < \,0$$ (13b) A variable change $$x={e}^{-\beta U}$$ (14) turns \(H\left(U\right)\) into a

power law distribution: $$J(x)\equiv H(U)\frac{{dU}}{{dx}}$$ (15a) $$=A\left(\frac{\alpha }{\beta }\right){e}^{-\left(\frac{\alpha }{\beta }+1\right)x},1 \, < \, x\le b$$ (15b) where

$$b={e}^{-\beta {U}_{\min }}$$ (16) is the upper bound of \(x\) in the power law distribution. Instead of using an exact power law distribution in \(x\), we fit the logarithm of the CDF to a

linear function of \(U\) using the local linear regression program loess in the R package (http://cran.r-project.org/; with degree = 1 for linear regression and span = 0.75 as the fraction

of data points for locally weighted fitting). The fit was limited to a portion of the CDF bounded below by CDF = 104 and above by \(U\) = −4 kcal/mol (Supplementary Fig. 5a, b). The fit

function was then extrapolated to \(U={U}_{\min }\). The determination of \({U}_{\min }\) is described next. One possible estimate for \({U}_{\min }\) is the observed lowest interaction

energy, but such an estimate is subject to significant statistical uncertainties. A more robust method for estimating the upper bound \(b\) (equal to the Boltzmann factor of \({U}_{\min }\))

in a power law distribution was developed recently36. In this method, one calculates the mean value of the largest observed \(x\) among replicate samples of a given size and then fits the

dependence of the mean largest value on sample size to a function. To apply this method, we divided the full list of clash-free interaction energies into blocks, each of which was generated

from a fixed number (\({M}_{{{{{{\rm{ori}}}}}}}\)) of test-protein orientations. Each block is a replicate sample. The block size \({M}_{{{{{{\rm{ori}}}}}}}\) is effectively a measure of

sample size; the number of interaction energies for a single test-protein orientation is actually up to 2000 × 1.57464 × 108 = 3.1 × 1011. The total number of orientations in our

calculations was 500 (denoted as \({M}_{{{{{{\rm{tot}}}}}}}\)); \({M}_{{{{{{\rm{ori}}}}}}}\) could be any factor of \({M}_{{{{{{\rm{tot}}}}}}}\), including 1, 2, 4, 5, 10, 20, 25, 50, 100,

125, 250, 500. The number of blocks, or replicate samples, was then \({M}_{{{{{{\rm{rep}}}}}}}={M}_{{{{{{\rm{tot}}}}}}}/{M}_{{{{{{\rm{ori}}}}}}}\). For each block, the lowest interaction

energy was found; the average of the block-specific lowest interaction energies was then evaluated to yield the mean lowest interaction energy, \({\widehat{U}}_{\min }\), for a given block

size \({M}_{{{{{{\rm{ori}}}}}}}\). The dependence of \({\widehat{U}}_{\min }\) on \({M}_{{{{{{\rm{ori}}}}}}}\) was finally fit to $${\widehat{U}}_{\min }={U}_{\min

}+\frac{E}{1+{({M}_{{{{{{\rm{ori}}}}}}}/D)}^{\delta }}$$ (17) where \({U}_{\min }\), \(D\), \(E\), and \(\delta\) are fitting parameters, with \(\delta\) restricted to [0.6. 1]36. To reduce

variations in the fit values of \({U}_{\min }\), we simultaneously fit the \({\widehat{U}}_{\min }\) data of a protein at different concentrations to Eq. [17] and treated \(D\) as a global

parameter. Fitting was done by calling the least_squares function in scipy (https://scipy.org/), with the trust region reflective algorithm as the method of minimization. In addition to

obtaining \({\widehat{U}}_{\min }\) from the FMAP output, we also took the 50 configurations with the lowest FMAP interaction energies from each test-protein orientation and recalculated the

exact interaction energies by an atom-based method56, thereby yielding a second set of \({\widehat{U}}_{\min }\) results. The fitting to Eq. [17] is illustrated in Supplementary Fig. 6. The

resulting \({U}_{\min }\) values are presented in Supplementary Fig. 5c, d, where one can see that the FMAP and atom-based methods gave very similar results. To further smooth \({U}_{\min

}\) as a function of the protein concentration, we assumed the endpoint of the CDF extrapolation to have the following dependence on the clash-free fraction at the given protein

concentration: $${{{{{\rm{CDF}}}}}}\left({U}_{\min }\right)=B{{f}_{{{{{{\rm{CF}}}}}}}}^{\gamma }$$ (18) With the coefficient \(B\) chosen to be 1 and the exponent \(\gamma\) chosen to be

0.25, Eq. [18] closely models the \({U}_{\min }\) results obtained according to Eq. [17], as shown in Supplementary Fig. 5c, d. So finally we used Eq. [18] to determine \({U}_{\min }\)

values for ending the CDF extrapolation. The resulting \({\mu }_{{{{{{\rm{ex}}}}}}}\) is now a smooth function of the protein concentration (e.g., Fig. 3a), free of large variations caused

by a single outlying low interaction energy. Such outliers can be identified by a large (>1.0 kcal/mol) deviation from the expected \(U\) when the fit function for the CDF is extrapolated

to CDF = 1 (Supplementary Fig. 5b inset). The \({U}_{\min }\) values obtained according to Eq. [17] in cases with such outliers are displayed as open symbols in Supplementary Fig. 5c. In

short, we applied local linear regression to a portion of the CDF (above CDF = 104) and then extrapolated down to the lower bound given by Eq. [18]. In calculating \({\mu

}_{{{{{{\rm{ex}}}}}}}\), the extrapolated CDF was used between the lower bound and CDF = 104, but the original CDF was used above CDF = 104. DETERMINING BINODAL AND SPINODAL Once \({\mu

}_{{{{{{\rm{ex}}}}}}}\) is calculated as described above for a range of protein concentrations at a given temperature, we fit it to a fifth-order polynomial29: $$\beta {\mu

}_{{{{{{\rm{ex}}}}}}}=\mathop{\sum }\limits_{l=1}^{5}{b}_{l}{\rho }^{l}$$ (19) This fit makes it easier to determine the binodal and spinodal. Equation [19] is a truncated Taylor expansion;

in a full expansion (related to the virial expansion of the osmotic pressure), the first-order coefficient, \({b}_{1}\), is twice the second virial coefficient \({B}_{2}\). Adding the ideal

part (Eqs. [1] and [2]) yields the full chemical potential \(\mu\). Below the critical temperature, the dependence of \(\mu\) on \(\rho\) contains a nonmonotonic part (known as the van der

Waals loop) for finite-sized systems such as the protein solutions modeled here (see Fig. 3b). A horizontal line that bisects the van der Waals loop with equal areas below and above

(equal-area construction) yields the concentrations of the protein in two coexisting phases. That is, the inner and outer intersections define the concentrations in the dilute and dense

phases, respectively. By connecting the coexistence concentrations at a series of temperatures, one obtains the binodal. Moreover, the concentrations at the two extrema of the van der Waals

loop define the bounds of a concentration range in which the system is thermodynamically unstable. By connecting the extremum concentrations at a series of temperatures, one obtains the

spinodal. Further details of polynomial fit and equal-area construction are found in ref. 32. A web server implementing these steps is at https://zhougroup-uic.github.io/LLPS/. FMAPB2

CALCULATIONS AND RELATED ANALYSES The second virial coefficient \({B}_{2}\) is determined by the interaction energy between a pair of protein molecules. Let

\({U}_{1}\left({{{{{\bf{R}}}}}},{{{{{\boldsymbol{\Omega }}}}}}\right)\) be the pair interaction energy, then30 $${B}_{2}=-\frac{V}{2}\left\langle

f\left({{{{{\bf{R}}}}}},{{{{{\boldsymbol{\Omega }}}}}}\right)\right\rangle$$ (20) where \(V\) is the volume in which the average over \({{{{{\bf{R}}}}}}\) is carried out, and

\(f\left({{{{{\bf{R}}}}}},{{{{{\boldsymbol{\Omega }}}}}}\right)\) is the Mayer function: $$f\left({{{{{\bf{R}}}}}},{{{{{\boldsymbol{\Omega }}}}}}\right)={e}^{-\beta

{U}_{1}\left({{{{{\bf{R}}}}}},{{{{{\boldsymbol{\Omega }}}}}}\right)}-1$$ (21) We calculated \({B}_{2}\) also by an FFT-based method called FMAPB230. The setup of FMAPB2 is identical to that

of FMAPμ, but now the periodic box contains a single molecule, i.e., the central copy. The interaction energy function (see Eqs. [4] to [7]) and other details of FMAPB2 are the same as

described above for FMAPμ calculations, with the following exceptions. The side length of the periodic box was ~200 Å. The test-protein orientations were generated from 68,760 rotation

matrices that uniformly and deterministically sample the full orientation space, with a 6° angle between successive rotation matrices57. The large number of test-protein orientations makes

the \({B}_{2}\) results highly robust (with a 3% difference in γB \({B}_{2}\) at 25 °C when the test-protein orientation space was sampled at 4° intervals, involving 232,020 rotation

matrices). In addition to the histogram of pair interaction energies, configurations with interaction energies lower than -6 kcal/mol were saved for further analysis. We further analyzed the

pair intermolecular interactions of the 1000 lowest-energy configurations using the atom-based method. Specifically, the pair interaction energy was decomposed into the contributions from

the individual residues of the test protein interacting with the whole central copy. Because the test protein and the central copy are the same molecules, we also carried out the

decomposition in the opposite way, i.e., with the central copy decomposed into individual residues and the test protein treated as a whole. For a given residue, the results were first

averaged over the 1000 lowest-energy configurations and then over these two ways of decomposition. We clustered the 1000 lowest-energy configurations by using the ligand-RMSD as the distance

measure. Ligand-RMSD is the root-mean-square-deviation between two poses of the test protein after superposition on the central copy. We used a ligand-RMSD cutoff of 10 Å to define

clusters. In each cluster, all members have ligand-RMSDs ≤ the cutoff from one member. CALCULATIONS WITH THE ROSETTA ENERGY FUNCTION AND WITH SIDECHAIN REPACKING We used RosettaDock47

(Rosetta version 3.13; https://www.rosettacommons.org/) on the 1000 lowest-energy poses from FMAPB2 calculations for γB and γF. We first wanted to see how the Rosetta all-atom energy

function46 may separate γF from γB in pair interaction energy. For this purpose, we applied a single round of energy minimization (option -dock_min) and saved the resulting pair interaction

energies. We then wanted to see how sidechain repacking may affect the pair interaction energies. For this purpose, we carried out a refinement of the energy-minimized poses by preventing

translation and rotation (movement magnitudes set to 0) but allowing sidechain repacking (option -use_input_sc and options -ex1 and -ex2aro, recommended by Rosetta). Up to ten tries of

sidechain repacking were applied to obtain a negative interaction energy. If the interaction energies were positive in all the ten tries, the value from the last try was saved. AVERAGING

\({{{{{{\BOLDSYMBOL{B}}}}}}}_{{{{{{\BOLDSYMBOL{2}}}}}}}\) OVER A PRESELECTED LIBRARY OF STRUCTURES As another option to model protein flexibility in \({B}_{2}\) calculations, we allowed the

central copy and the test protein to each sample a preselected library of _n_ structures, resulting in _n_ × _n_ pairs of structures. For each pair, a calculation was carried out using

FMAPB2339, which is the same as FMAPB230 except that the central copy and the test protein were allowed to take different structures. The final average \({B}_{2}\) was taken as the

arithmetic mean of the _n_ × _n_ FMAPB23 results. For each particular γ-crystallin (e.g., rat γE), the library consisted of all the high-resolution X-ray structures in the PDB; all the

processed structures contained residues 1–174 (bovine γB numbering) and the same sequence. GRANTHAM’S DISTANCE BETWEEN LOW AND HIGH-_T_ C GROUPS OF Γ-CRYSTALLINS There are 12 sequences in

the low-_T_c group and 3 sequences in the high-_T_c group (Supplementary Fig. 1a); correspondingly there are 66 Grantham distances in the low-_T_c group, 3 such distances in the high-_T_c

group, and 36 such distances between the two groups, at each position along the sequence. We first calculated the mean values of the intra or inter-group distances, then subtracted the

greater of the two intra-group mean distances from the inter-group mean distance, yielding the residual inter-group Grantham distance. Gln83 of γB aligns to a gap in 11 of the 15 sequences;

we set the residual Grantham distance at this position to 0. REPORTING SUMMARY Further information on research design is available in the Nature Portfolio Reporting Summary linked to this

article. DATA AVAILABILITY All data generated or analyzed during this study are included in this published article (and its supplementary data files). The source data for all the plots

presented in figures are deposited in GitHub at https://github.com/hzhou43/g-crystallins. CODE AVAILABILITY Data analysis procedures were described under Computational Methods. Sample codes

for calculating chemical potentials by FMAP are deposited at https://github.com/hzhou43/MiMB_simulations/tree/main/FMAP. A web server for generating binodals from chemical potentials is at

https://zhougroup-uic.github.io/LLPS/. REFERENCES * Cho, W. K. et al. Mediator and RNA polymerase II clusters associate in transcription-dependent condensates. _Science_ 361, 412–415 (2018).

CAS  PubMed  PubMed Central  Google Scholar  * Kroschwald, S. et al. Different material states of pub1 condensates define distinct modes of stress adaptation and recovery. _Cell Rep._ 23,

3327–3339 (2018). CAS  PubMed  Google Scholar  * Alberti, S. & Dormann, D. Liquid-liquid phase separation in disease. _Annu. Rev. Genet._ 53, 171–194 (2019). CAS  PubMed  Google Scholar

  * Dignon, G. L., Zheng, W., Best, R. B., Kim, Y. C. & Mittal, J. Relation between single-molecule properties and phase behavior of intrinsically disordered proteins. _Proc. Natl Acad.

Sci. USA_ 115, 9929–9934 (2018). CAS  PubMed  PubMed Central  Google Scholar  * Wang, J. et al. A molecular grammar governing the driving forces for phase separation of prion-like RNA

binding proteins. _Cell_ 174, 688–699 e616 (2018). CAS  PubMed  PubMed Central  Google Scholar  * Das, S., Lin, Y.-H., Vernon, R. M., Forman-Kay, J. D. & Chan, H. S. Comparative roles of

charge, _π_, and hydrophobic interactions in sequence-dependent phase separation of intrinsically disordered proteins. _Proc. Natl Acad. Sci. USA_ 117, 28795–28805 (2020). CAS  PubMed 

PubMed Central  Google Scholar  * Martin, E. W. et al. Valence and patterning of aromatic residues determine the phase behavior of prion-like domains. _Science_ 367, 694–699 (2020). CAS 

PubMed  PubMed Central  Google Scholar  * Tesei, G., Schulze, T. K., Crehuet, R. & Lindorff-Larsen, K. Accurate model of liquid–liquid phase behavior of intrinsically disordered proteins

from optimization of single-chain properties. _Proc. Natl Acad. Sci. USA_ 118, e2111696118 (2021). CAS  PubMed  PubMed Central  Google Scholar  * Joseph, J. A. et al. Physics-driven

coarse-grained model for biomolecular phase separation with near-quantitative accuracy. _Nat. Comput. Sci._ 1, 732–743 (2021). PubMed  PubMed Central  Google Scholar  * Bremer, A. et al.

Deciphering how naturally occurring sequence features impact the phase behaviours of disordered prion-like domains. _Nat. Chem._ 14, 196–207 (2022). CAS  PubMed  Google Scholar  * Ruff, K.

M. et al. Sequence grammar underlying the unfolding and phase separation of globular proteins. _Mol. Cell_ 82, 3193–3208.e3198 (2022). CAS  PubMed  Google Scholar  * Zhou, H. X., Nguemaha,

V., Mazarakos, K. & Qin, S. Why do disordered and structured proteins behave differently in phase separation? _Trends Biochem. Sci._ 43, 499–516 (2018). CAS  PubMed  PubMed Central 

Google Scholar  * Tanaka, T., Ishimoto, C. & Chylack, L. T. Jr. Phase separation of a protein-water mixture in cold cataract in the young rat lens. _Science_ 197, 1010–1012 (1977). CAS 

PubMed  Google Scholar  * Siezen, R. J., Fisch, M. R., Slingsby, C. & Benedek, G. B. Opacification of gamma-crystallin solutions from calf lens in relation to cold cataract formation.

_Proc. Natl Acad. Sci. USA_ 82, 1701–1705 (1985). CAS  PubMed  PubMed Central  Google Scholar  * Norledge, B. V., Hay, R. E., Bateman, O. A., Slingsby, C. & Driessen, H. P. Towards a

molecular understanding of phase separation in the lens: a comparison of the X-ray structures of two high Tc gamma-crystallins, gammaE and gammaF, with two low Tc gamma-crystallins, gamma B

and gamma D. _Exp. Eye Res._ 65, 609–630 (1997). CAS  PubMed  Google Scholar  * den Dunnen, J. T., Moormann, R. J. M., Lubsen, N. H. & Schoenmakers, J. G. G. Concerted and divergent

evolution within the rat γ-crystallin gene family. _J. Mol. Biol._ 189, 37–46 (1986). Google Scholar  * Meakin, S. O., Du, R. P., Tsui, L.-C. & Breitman, M. L. γ-Crystallins of the human

eye lens: expression analysis of five members of the gene family. _Mol. Cell Biol._ 7, 2671–2679 (1987). CAS  PubMed  PubMed Central  Google Scholar  * Siezen, R. J., Wu, E., Kaplan, E. D.,

Thomson, J. A. & Benedek, G. B. Rat lens gamma-crystallins. Characterization of the six gene products and their spatial and temporal distribution resulting from differential synthesis.

_J. Mol. Biol._ 199, 475–490 (1988). CAS  PubMed  Google Scholar  * Broide, M. L., Berland, C. R., Pande, J., Ogun, O. O. & Benedek, G. B. Binary-liquid phase separation of lens protein

solutions. _Proc. Natl Acad. Sci. USA_ 88, 5660–5664 (1991). CAS  PubMed  PubMed Central  Google Scholar  * Wang, Y., Lomakin, A., McManus, J. J., Ogun, O. & Benedek, G. B. Phase

behavior of mixtures of human lens proteins gamma D and Beta B1. _Proc. Natl Acad. Sci. USA_ 107, 13282–13287 (2010). CAS  PubMed  PubMed Central  Google Scholar  * Lo, W. K. Visualization

of crystallin droplets associated with cold cataract formation in young intact rat lens. _Proc. Natl Acad. Sci. USA_ 86, 9926–9930 (1989). CAS  PubMed  PubMed Central  Google Scholar  *

Pande, A. et al. Molecular basis of a progressive juvenile-onset hereditary cataract. _Proc. Natl Acad. Sci. USA_ 97, 1993–1998 (2000). CAS  PubMed  PubMed Central  Google Scholar  *

Banerjee, P. R., Pande, A., Patrosz, J., Thurston, G. M. & Pande, J. Cataract-associated mutant E107A of human gammaD-crystallin shows increased attraction to alpha-crystallin and

enhanced light scattering. _Proc. Natl Acad. Sci. USA_ 108, 574–579 (2011). CAS  PubMed  Google Scholar  * White, H. E., Driessen, H. P., Slingsby, C., Moss, D. S. & Lindley, P. F.

Packing interactions in the eye-lens. Structural analysis, internal symmetry and lattice interactions of bovine gamma IVa-crystallin. _J. Mol. Biol._ 207, 217–235 (1989). CAS  PubMed  Google

Scholar  * Cinar, S., Cinar, H., Chan, H. S. & Winter, R. Pressure-sensitive and osmolyte-modulated liquid-liquid phase separation of eye-lens gamma-crystallins. _J. Am. Chem. Soc._

141, 7347–7354 (2019). CAS  PubMed  Google Scholar  * Augusteyn, R. C., Chandrasekher, G., Ghiggino, K. P. & Vassett, P. Probing the microenvironments of tryptophan residues in the

monomeric crystallins of the bovine lens. _Biochim. Biophys. Acta_ 1205, 89–96 (1994). CAS  PubMed  Google Scholar  * Dorsaz, N., Thurston, G. M., Stradner, A., Schurtenberger, P. &

Foffi, G. Phase separation in binary eye lens protein mixtures. _Soft Matter_ 7, 1763–1776 (2011). CAS  Google Scholar  * Kastelic, M., Kalyuzhnyi, Y. V., Hribar-Lee, B., Dill, K. A. &

Vlachy, V. Protein aggregation in salt solutions. _Proc. Natl Acad. Sci. USA_ 112, 6766–6770 (2015). CAS  PubMed  PubMed Central  Google Scholar  * Qin, S. & Zhou, H. X. Fast method for

computing chemical potentials and liquid-liquid phase equilibria of macromolecular solutions. _J. Phys. Chem. B_ 120, 8164–8174 (2016). CAS  PubMed  PubMed Central  Google Scholar  * Qin, S.

& Zhou, H. X. Calculation of second virial coefficients of atomistic proteins using fast fourier transform. _J. Phys. Chem. B_ 123, 8203–8215 (2019). CAS  PubMed  PubMed Central  Google

Scholar  * Vliegenthart, G. A. & Lekkerkerker, H. N. W. Predicting the gas-liquid critical point from the second virial coefficient. _J. Chem. Phys._ 112, 5364–5369 (2000). CAS  Google

Scholar  * Mazarakos, K., Qin, S. & Zhou, H. X. Calculating binodals and interfacial tension of phase-separated condensates from molecular simulations with finite-size corrections.

_Methods Mol. Biol._ 2563, 1–35 (2023). PubMed  Google Scholar  * Widom, B. Some Topics in the theory of fluids. _J. Chem. Phys._ 39, 2808–2812 (1963). CAS  Google Scholar  * Qin, S. &

Zhou, H. X. Further development of the FFT-based method for atomistic modeling of protein folding and binding under crowding: optimization of accuracy and speed. _J. Chem. Theory Comput._

10, 2824–2835 (2014). CAS  PubMed  PubMed Central  Google Scholar  * Martinez, M. et al. SDA 7: A modular and parallel implementation of the simulation of diffusional association software.

_J. Comput. Chem._ 36, 1631–1645 (2015). CAS  PubMed  PubMed Central  Google Scholar  * Zhou, H. X. Power law in a bounded range: Estimating the lower and upper bounds from sample data. _J.

Chem. Phys._ 158, 191103 (2023). CAS  PubMed  PubMed Central  Google Scholar  * Thomson, J. A., Schurtenberger, P., Thurston, G. M. & Benedek, G. B. Binary liquid phase separation and

critical phenomena in a protein/water solution. _Proc. Natl Acad. Sci. USA_ 84, 7079–7083 (1987). CAS  PubMed  PubMed Central  Google Scholar  * Bucciarelli, S. et al. Extended law of

corresponding states applied to solvent isotope effect on a globular protein. _J. Phys. Chem. Lett._ 7, 1610–1615 (2016). CAS  PubMed  Google Scholar  * Ahn, S. H. et al. Characterizing

protein kinase A (PKA) subunits as macromolecular regulators of PKA RIalpha liquid-liquid phase separation. _J. Chem. Phys._ 154, 221101 (2021). CAS  PubMed  PubMed Central  Google Scholar 

* Gallivan, J. P. & Dougherty, D. A. Cation-π interactions in structural biology. _Proc. Natl Acad. Sci. USA_ 96, 9459–9464 (1999). CAS  PubMed  PubMed Central  Google Scholar  * Song,

J., Ng, S. C., Tompa, P., Lee, K. A. W. & Chan, H. S. Polycation-π interactions are a driving force for molecular recognition by an intrinsically disordered oncoprotein family. _PLoS

Comput. Biol._ 9, e1003239 (2013). CAS  PubMed  PubMed Central  Google Scholar  * Grantham, R. Amino acid difference formula to help explain protein evolution. _Science_ 185, 862–864 (1974).

CAS  PubMed  Google Scholar  * Serebryany, E. & King, J. A. The betagamma-crystallins: native state stability and pathways to aggregation. _Prog. Biophys. Mol. Biol._ 115, 32–41 (2014).

CAS  PubMed  PubMed Central  Google Scholar  * Ghosh, A., Kota, D. & Zhou, H. X. Shear relaxation governs fusion dynamics of biomolecular condensates. _Nat. Commun._ 12, 5995 (2021).

CAS  PubMed  PubMed Central  Google Scholar  * Bierma, J. C. et al. Controlling liquid-liquid phase separation of cold-adapted crystallin proteins from the Antarctic toothfish. _J. Mol.

Biol._ 430, 5151–5168 (2018). CAS  PubMed  Google Scholar  * Alford, R. F. et al. The Rosetta all-atom energy function for macromolecular modeling and design. _J. Chem. Theory Comput._ 13,

3031–3048 (2017). CAS  PubMed  PubMed Central  Google Scholar  * Gray, J. J. et al. Protein–protein docking with simultaneous optimization of rigid-body displacement and side-chain

conformations. _J. Mol. Biol._ 331, 281–299 (2003). CAS  PubMed  Google Scholar  * Majumdar, B. B. et al. Role of conformational flexibility in monte carlo simulations of many-protein

systems. _J. Chem. Theory Comput_ 15, 1399–1408 (2019). CAS  PubMed  Google Scholar  * Kumaraswamy, V. S., Lindley, P. F., Slingsby, C. & Glover, I. D. An eye lens protein-water

structure: 1.2 A resolution structure of gammaB-crystallin at 150 K. _Acta Crystallogr. D. Biol. Crystallogr._ 52, 611–622 (1996). CAS  PubMed  Google Scholar  * Dolinsky, T. J., Nielsen, J.

E., McCammon, J. A. & Baker, N. A. PDB2PQR: an automated pipeline for the setup of Poisson-Boltzmann electrostatics calculations. _Nucleic Acids Res._ 32, W665–W667 (2004). CAS  PubMed

  PubMed Central  Google Scholar  * Olsson, M. H., Sondergaard, C. R., Rostkowski, M. & Jensen, J. H. PROPKA3: consistent treatment of internal and surface residues in empirical pKa

predictions. _J. Chem. Theory Comput._ 7, 525–537 (2011). CAS  PubMed  Google Scholar  * Pettersen, E. F. et al. UCSF Chimera-a visualization system for exploratory research and analysis.

_J. Comput. Chem._ 25, 1605–1612 (2004). CAS  PubMed  Google Scholar  * Baker, N. A., Sept, D., Joseph, S., Holst, M. J. & McCammon, J. A. Electrostatics of nanosystems: application to

microtubules and the ribosome. _Proc. Natl Acad. Sci. USA_ 98, 10037–10041 (2001). CAS  PubMed  PubMed Central  Google Scholar  * Gabdoulline, R. R. & Wade, R. C. Effective charges for

macromolecules in solvent. _J. Phys. Chem._ 100, 3868–3878 (1996). CAS  Google Scholar  * Nguemaha, V., Qin, S. & Zhou, H. X. Transfer free energies of test proteins into crowded protein

solutions have simple dependence on crowder concentration. _Front. Mol. Biosci._ 6, 39 (2019). CAS  PubMed  PubMed Central  Google Scholar  * Qin, S., Zhou, H. X. An FFT-based method for

modeling protein folding and binding under crowding: benchmarking on ellipsoidal and all-atom crowders. _J. Chem. Theory Comput._ 9, 4633–4643 (2013). * Mitchell, J. C. Sampling rotation

groups by successive orthogonal images. _SIAM J. Sci. Comput._ 30, 525–547 (2008). Google Scholar  * Thompson, J. D., Gibson, T. J., Higgins, D. G. Multiple sequence alignment using ClustalW

and ClustalX. _Curr. Protoc. Bioinformatics_ Chapter 2, 2.3.1-2.3.22 (2003). * Flyvbjerg, H. & Petersen, H. G. Error estimates on averages of correlated data. _J. Chem. Phys._ 91,

461–466 (1989). CAS  Google Scholar  Download references ACKNOWLEDGEMENTS This work was supported by National Institutes of Health Grant GM118091. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS

* Department of Chemistry, University of Illinois Chicago, Chicago, IL, 60607, USA Sanbo Qin & Huan-Xiang Zhou * Department of Physics, University of Illinois Chicago, Chicago, IL,

60607, USA Huan-Xiang Zhou Authors * Sanbo Qin View author publications You can also search for this author inPubMed Google Scholar * Huan-Xiang Zhou View author publications You can also

search for this author inPubMed Google Scholar CONTRIBUTIONS S.Q. and H.X.Z. designed research, conducted research, analyzed data, and wrote manuscript. CORRESPONDING AUTHOR Correspondence

to Huan-Xiang Zhou. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Communications Biology_ thanks Marina Guenza and

the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Gene Chong. A peer review file is available. ADDITIONAL INFORMATION

PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION PEER REVIEW FILE

SUPPLEMENTARY INFORMATION DESCRIPTION OF SUPPLEMENTARY MATERIALS SUPPLEMENTARY MOVIE 1 SUPPLEMENTARY MOVIE 2 REPORTING SUMMARY RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed

under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate

credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article

are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and

your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this

licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Qin, S., Zhou, HX. Atomistic modeling of liquid-liquid phase

equilibrium explains dependence of critical temperature on γ-crystallin sequence. _Commun Biol_ 6, 886 (2023). https://doi.org/10.1038/s42003-023-05270-7 Download citation * Received: 02 May

2023 * Accepted: 22 August 2023 * Published: 29 August 2023 * DOI: https://doi.org/10.1038/s42003-023-05270-7 SHARE THIS ARTICLE Anyone you share the following link with will be able to

read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing

initiative