ABSTRACT The success of deep learning in various applications depends on task-specific architecture design choices, including the types, hyperparameters, and number of layers. In

computational biology, there is no consensus on the optimal architecture design, and decisions are often made using insights from more well-established fields such as computer vision. These

may not consider the domain-specific characteristics of genome sequences, potentially limiting performance. Here, we present GenomeNet-Architect, a neural architecture design framework that

automatically optimizes deep learning models for genome sequence data. It optimizes the overall layout of the architecture, with a search space specifically designed for genomics.

baselines. SIMILAR CONTENT BEING VIEWED BY OTHERS A COMMUNITY EFFORT TO OPTIMIZE SEQUENCE-BASED DEEP LEARNING MODELS OF GENE REGULATION Article Open access 11 October 2024 AN AUTOMATED

FRAMEWORK FOR EFFICIENTLY DESIGNING DEEP CONVOLUTIONAL NEURAL NETWORKS IN GENOMICS Article 15 March 2021 DEEPC: PREDICTING 3D GENOME FOLDING USING MEGABASE-SCALE TRANSFER LEARNING Article 12

October 2020 INTRODUCTION Deep learning (DL) techniques have been shown to achieve exceptional performance on a wide range of machine learning (ML) tasks, especially when large training

sets are available1. These techniques have been applied to a variety of challenges in bioinformatics2,3,4. For different ML problems and data modalities, different neural architectures have

emerged that perform well in their respective domains, such as convolutional neural networks (CNN) for images or recurrent neural networks (RNN) for text. Architectural design choices are

often made based on the experience of researchers and trial and error5,6,7,8,9,10,11,12,13. However, the optimal design and arrangement of these layers are highly domain-specific,

problem-dependent, and computationally expensive to evaluate. Besides expert-driven design, it has therefore become increasingly popular to apply systematic approaches to finding neural

network configurations, such as automated neural architecture search (NAS)14. The number of possible configurations of even small neural networks is very large, as the number of decisions to

be made grows exponentially, and most practical NAS algorithms therefore impose various constraints on the search space. To efficiently perform NAS for ML tasks in genomics, it is essential

to identify DL network architecture designs for genomic sequence analysis that are widely recognized in the literature. These designs often start with one or several convolutional layers,

followed by a global pooling layer, and conclude with a series of fully connected layers6,7,9,11. Recurrent layers offer an alternative to convolutional or global pooling layers. Their

ability to propagate information across sequences allows recurrent layers to effectively summarize data, comparable to pooling layers. While numerous works in genomics use RNN

layers15,16,17,18,19, one example is _Seeker_8, an RNN-based model that employs an LSTM layer for bacteriophage detection. Furthermore, by stacking them sequentially, integrating

convolutional and recurrent layers enhances model capability. For instance, the model developed by Wang et al.20 demonstrates this approach by placing an RNN on top of a convolutional layer,

followed by two fully connected layers. A similar configuration is utilized in the DanQ model21, showcasing the effectiveness of combining recurrent and convolutional layers. One way to

approach NAS is to consider it as a hyperparameter optimization (HPO) problem. Hyperparameters (HPs) are configuration settings that determine how an ML model works. In the context of DL,

typical HPs are the choice of the gradient descent algorithm and its learning rate. However, the choice of neural network layers and their configuration can also be considered as HPs. NAS is

then equivalent to optimizing HPs that define different architectures. A popular class of optimization algorithms used for HPO is model based optimization (MBO), also called Bayesian

optimization22. It iteratively evaluates HP configurations and selects new configurations to try based on knowledge of which configurations have worked well in the past. This is done by

fitting a regression model, the so-called surrogate model, to the observed performance values. New evaluations are made by considering the “exploration-exploitation tradeoff”: new

configurations should be tried if their expected performance is high (exploitation), or if the model’s uncertainty about their performance is high (exploration). MBO-based methods such as

BANANAS23 have been shown to outperform methods based on other optimization paradigms such as ENAS24 (which uses reinforcement learning) or DARTS25 (which uses gradient descent). The quality

of the configurations evaluated by MBO increases gradually as the optimization progresses. The first configurations evaluated, which constitute the initial design, are randomly sampled from

the search space without using any prior knowledge. By anticipating that early configurations are unlikely to perform as well as later ones, and by devoting fewer resources to their

evaluation, it is possible to reduce the cost of the overall optimization process. Algorithms that speed up optimization by using cheaper approximations of the target objective are called

multi-fidelity (MF) optimization algorithms. A simple way to approximate the performance of a DL model is to stop training the model after a certain amount of time, even though the model

performance has not fully converged26. While there are libraries that perform NAS on genome datasets27, we are not aware of any methods that use efficient multi-fidelity or MBO methods

specifically for genome datasets. MBO has been used in the past to tune specifically designed genomic DL models28, but only to optimize specific HPs, not as a general NAS framework. No

general-purpose MBO-based NAS framework provides a search space specifically modified to fit genome sequence data; in fact, many focus on 2D image data instead. In this work, we present

GenomeNet-Architect, which optimizes DL network architectures by repeatedly constructing new network configurations, training networks based on these configurations on a given dataset, and

evaluating the performance of the resulting models by predicting on held-out test data. It uses MBO as an efficient black-box optimization method, combined with a multi-fidelity approach

that increases model training time after some initial optimization progress has been made. Unlike other general-purpose NAS frameworks, GenomeNet-Architect uses a search space specifically

for genome data. It is made up of neural architectures and HP setups that build on top of and generalize various architectures for the genome data that have been successfully applied in the

past. This approach allows us to efficiently explore a large space of possible network architectures and identify those that perform well for genome-related tasks, creating architectures

that outperform expert-guided architectures. Our method can be used for a variety of DL tasks on genome sequence data, such as genome-level, loci-level, or nucleotide-level classification

and regression. RESULTS GENOMENET-ARCHITECT USES AN EFFICIENT GLOBAL OPTIMIZATION METHOD GenomeNet-Architect provides a predefined search space of hyperparameters (HPs) that are used to

construct different network architectures. It needs to be given a specific ML task on genome sequence data. In our framework, we use model-based optimization (MBO)22 to jointly tune the

network layout and HPs, and generate a specific architecture that works well on the given task. The result of the optimization process itself is a specific HP configuration that works well

for the given task. The resulting architecture can be trained and evaluated on the given data, as well as used to make predictions on new data. However, the resulting architecture can also

be used for other tasks that are similar to the task for which it was optimized. It is therefore possible to perform a single optimization run to solve multiple genome sequence DL tasks.

GENOMENET-ARCHITECT USES A SEARCH SPACE THAT COVERS THE MOST COMMON LAYER TYPES AND HYPERPARAMETER SETTINGS The search space of GenomeNet-Architect is based on our literature analysis of

successful architectures developed for genome data, such as DeepVirFinder6, ViraMiner7, Seeker8, CHEER9, Fiannaca (CNN model)10, PPR-Meta11, and an adapted version of RC-ResNet-1812. A

common type of architecture consists of convolutional layers followed by global pooling and fully connected layers6,7,9,11. An alternative to pooling, which also aggregates information

across the entire sequence, is the use of recurrent (RNN) layers. Inspired by these common patterns observed in many networks successfully applied to genome data, we build a template for an

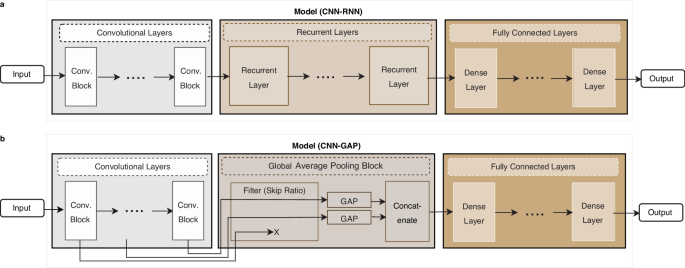
architecture consisting of three stages (Fig. 1): (i) a stage of stacked convolutional layers operating on one-hot encoded input sequences, (ii) a stage for embedding the sequential output

data of the convolutional layers into a vector representation, using either global average pooling (GAP) (in a setup that we call the CNN-GAP model) or a stack of recurrent layers (which we

call the CNN-RNN model), and (iii) a fully connected neural network stage operating on the embedded values. Some of the properties we search over include the network layout, such as the

number and size of convolutional, dense, and recurrent layers. Other HPs that we searched over influence the training process, such as the optimizer, and the behavior of specific layers,

such as the dropout rate, the activation functions, and the batch normalization constant (Table 1). By introducing multiple HPs that influence the final layout of the model, our framework

covers many successful architectures from the literature, while also making it possible to find architectures that have not yet been implemented. While the provided search space is our

recommendation, our method also supports defining a custom search space, e.g. allowing more layers, or including GMP instead of GAP. Our HPs cover both the overall architecture of the

network (e.g., number of convolutional layers) and the setup of individual layers (e.g., the CNN kernel size). Having different HPs for each layer individually would introduce HP

dependencies, which would make the optimization problem more difficult. Therefore, we use a setup where only the first and last layers are directly parameterized. _f_0 and _f__end_, for

example, specify the number of filters of the first and last convolutional layer. The setup of the intermediate layers is interpolated based on the first and last layers (see Methods for

more details). MODEL CONFIGURATIONS ARE INITIALLY EVALUATED WITH SHORTER RUNTIMES FOR MORE EFFICIENT SEARCH SPACE EXPLORATION Several challenges arise when optimizing DL architectures on

complex data modalities such as genomics. First, for complex tasks, the time required for a single model to converge to a solution makes it impractically slow to optimize over a large search

space such as the one we have designed. A simple way to speed up model evaluation would be to limit the time for which each proposed model is trained, even if models do not converge within

a given timeframe, because models that perform well early in model fitting will continue to perform well after more training epochs26. While this reduces the time spent on individual

evaluations, the resulting models can only approximate the true performance of a given HP configuration. Smaller models (which have fewer parameters and therefore converge faster) may

falsely appear to be superior to larger models that run slower, complete fewer epochs, and cannot converge in the given time limit. However, the models trained for only a short time are

still informative about which parts of the search space are more likely to contain models that perform well. We can therefore use them in a “warm start” method that speeds up the

optimization process. This works by only partially evaluating initial configuration proposals at first, and using the resulting data about which HPs tend to perform well for short evaluation

times to help determine which configurations are later evaluated for longer training times29. GenomeNet-Architect first runs the MBO with a fixed, low setting for the model training time

_t_ = _t_1. After a given number of optimization iterations, a new MBO run is started with a higher training time setting _t_ = _t_2, where the surrogate model contains the performance

result data for _t_ = _t_1 as a “warm start”. The optimization procedure can be restarted several times with higher values of _t__n_ using all previous points evaluated at times _t_1, ...,

_t__n_−1 as warm start data. Our experiments started with _t_1 = 2 h and then continued with _t_2 = 6 h (Fig. 2a). Longer times were also tried, but did not lead to sufficient improvement to

justify the additional resources required (Supplementary Note 1). Models evaluated after increasing the training time have higher performance than randomly sampled models at the beginning,

showing that the information learned from models trained for a short time is useful for building models trained for a longer time. GENOMENET-ARCHITECT MAKES USE OF PARALLEL RESOURCES

GenomeNet-Architect parallelizes the HP tuning process across multiple GPUs to reduce the overall optimization time. There are a variety of multi-point proposal techniques that allow MBO to

evaluate several different HP configurations simultaneously30. A particularly straightforward method is to use the UCB (upper confidence bound) infill criterion31: Given a parameter _λ_, it

uses the mean prediction of the surrogate model and adds _λ_ times the model’s uncertainty, thereby giving an optimistic bias to regions that have high uncertainty and therefore potential

for improvement. By sampling multiple instances of the _λ_-parameter from an exponential distribution32, effectively making different tradeoffs between exploration and exploitation, one can

generate different point propositions to be evaluated simultaneously. It is used by our method because, despite its simplicity, it is one of the best-performing MBO parallelization

methods30. In addition to parallelizing individual MBO runs, we also identify setups that are likely to lead to different optimal configurations, and whose optimization can therefore be run

independently and in parallel: Which HP settings are optimal, such as specific kernel sizes or number of filters, may vary for different sequence lengths. Similarly, optimal values may

differ for CNN-GAP and CNN-RNN, and they may also change depending on whether residual blocks are used. Therefore, the optimization proceeds in a fully crossed design of these choices: The

length of the training mini-sequence (in our experiments we investigated both 150 nt, 250 nt, and 10,000 nt), the architecture (CNN-GAP or CNN-RNN), and whether residual connections are

used. These optimization runs are independent of each other and can be run in parallel. GENOMENET-ARCHITECT FINDS MODELS THAT OUTPERFORM EXPERT-DESIGNED BASELINE MODELS IN THE VIRAL

IDENTIFICATION TASK GenomeNet-Architect demonstrated superior performance on the virus classification task compared to other deep learning (DL) and non-deep learning methods that we selected

as baselines, effectively distinguishing between sequences originating from bacterial chromosomes, prokaryotic viruses (referred to as bacteriophages) and eukaryotic viruses (referred to as

viral non-phage DNA). We have tested the effectiveness of GenomeNet-Architect against baselines for classification at the read-level (150 nt long sequences) and at the contig-level (10,000

nt) separately. At the read level, GenomeNet-Architect reduces the class-balanced misclassification rate, i.e., the misclassification rate averaged over all classes, by 19%, while having 83%

fewer parameters and achieving 67% faster inference time compared to the best DL baseline (Fiannaca10) and outperforms k-mer-based and alignment-based approaches for sequence classification

(Fig. 3a, Supplementary Table 2). At the contig-level, the best model found by our method achieves a class-balanced misclassification rate of 1.21%, outperforming the best baseline (1.36%)

while being 82% smaller. GenomeNet-Architect also finds a model that performs comparably to the baseline (1.41%) while having a factor of 117 times fewer parameters (Fig. 3b, Supplementary

Table 1). For a fair comparison, we trained and validated all DL baseline models on the same dataset and dataset splits. Additionally, we standardized the configuration by adapting the

output layer of each model and employing multi-class cross-entropy as the loss function, aligning with our models to facilitate three-class classification. This approach allows for a direct

comparison of algorithmic improvements. We show the best configuration found for this classification task using 10,000 nt sequences (red lines), as well as the top 10% configurations (solid

circles) in front of all evaluated configurations (transparent circles) (Fig. 2b) and a diagram visualizing the optimized architecture for the classification task using 150 nt (Fig. 2c). We

also analyzed the performance of the optimized model stratified by the degree of genomic differences to the training data. Our findings show that it consistently outperforms the Fiannaca

baseline, demonstrating that GenomeNet-Architect’s performance does not come from overfitting on sequences that occur in the training dataset (Supplementary Fig. 1). The superior performance

persists even when reads are simulated with the Illumina read error profile, underscoring the tool’s effectiveness across diverse genomic sequencing challenges (Supplementary Fig. 2).

GENOMENET-ARCHITECT IDENTIFIES MODELS THAT OUTPERFORM EXPERT-DESIGNED BASELINES IN THE PATHOGENICITY DETECTION TASK To further validate the versatility of GenomeNet-Architect, we extended

our experiments to a second task: pathogen detection in bacteria, specifically to distinguish between pathogenic and non-pathogenic sequences in human hosts. We aligned our evaluation with

the baseline values reported in the study of Bartoszewicz et al.13, utilizing the same search space for the viral classification task and hyperparameter optimization stage, where models are

optimized for 2 h. We also fine-tuned the pre-trained DNABERT33 (6-mer model), using the suggested hyperparameter settings given for fine-tuning on the method’s GitHub page. We added it as

an additional baseline for this task to make our benchmark more comprehensive. GenomeNet-Architect’s optimized models outperform all baseline models, showing substantial improvement in

pathogenicity detection (up to 11% improvement, see Fig. 4). Additionally, we adapted the models originally optimized for the viral classification (initially optimized for sequences of 150

nt, CNN-RNN-6h, and CNN-GAP-6h) by adjusting the input size to 250 nt to evaluate how well performance of an architecture optimized for one task transfers to a different task and conditions.

These architectures are renamed to have “VC” (short for viral classification) as a suffix. The comparable performance of “VC” models to models detected by GenomeNet-Architect on this

dataset “GAP-CNN” and “GAP-RNN” shows good transfer between related tasks on genome data (Fig. 4). To enhance the predictive accuracy and robustness, we explored the efficacy of ensemble

approaches, a technique that combines multiple model predictions, akin to the approach presented in Bartoszewicz et al.13, merging RC-LSTM and RC-CNN models into an RC-CNN + LSTM ensemble.

Our experiments with ensemble models, including GAP + RNN-VC, GAP + RNN, and the 4-model ensemble combining both CNN-RNN and CNN-GAP variants, demonstrate a notable decrease in

misclassification rates. Specifically, the 4-model ensemble reduced misclassification rates by 11% compared to the RC-CNN + LSTM baseline, with a single model improvement of 8% for

CNN-GAP-VC versus RC-CNN. DISCUSSION GenomeNet-Architect defines an HP configuration search space for neural architectures that extends and generalizes successful genome data architectures

from the past. This adaptable search space is coupled with an efficient black-box optimization method that can generate more optimal network architectures for genome-related tasks compared

to expert-designed architectures. With GenomeNet-Architect, researchers can identify better models when applying DL to genomic datasets. The search space used by GenomeNet-Architect leads to

resulting architectures that are similar to other models used in the literature, and the individual components of the resulting architecture therefore have similar interpretations. The

convolutional layer can be thought of as a pattern-matching method that encodes the presence of motifs in short subsequences. The global pooling layer then aggregates the information about

specific patterns within the entire sequence. A global average pooling (GAP) layer measures the relative frequency of these patterns, as opposed to the encoding of the presence of individual

patterns that are recorded in some models that use global max-pooling (GMP). Models using RNNs, on the other hand, are able to predict outcomes based on the spatial relationships between

different patterns and can learn long-term dependencies8,34. The following fully connected layers are used to learn complex relationships between detected patterns and can be used in both

GAP and RNN-based models20. The _DeepVirFinder_6 model is an architecture that uses pooling, with a convolutional layer, followed by a global max-pooling layer and a fully connected layer.

The _ViraMiner_7 model builds on the DeepVirFinder model and proposes two branches called frequency and pattern branches, using either GAP (frequency branch) or GMP (pattern branch) after

separate convolutional layers. In both branches, a fully connected layer follows, after which their output vectors are concatenated. Finally, another fully connected layer classifies whether

a 300 nt sequence is human or viral DNA. Since Tampuu et al.7 showed that the GAP alone achieves higher performance than the GMP alone, we did not include GMP in our search space. Another

similarly structured architecture for viral classification is the _CHEER_ model9. In this model, reads from 250 nt sequences are fed into four different convolutional layers with different

kernel sizes: 3, 7, 11, and 15. Global max-pooling layers follow each convolutional layer, after which the paths are concatenated. Similar to other architectures, multiple fully connected

layers follow the concatenation. DeepMicrobes is another RNN-based DL model developed for viral identification. The model consists of a 12-mer embedding layer, a bidirectional LSTM layer, a

self-attention layer, and several fully connected layers. The convolutional layer in this model learns local representations, and the recurrent layer can learn long-term dependencies within

these local representations in a sequential manner. Although DL models based on raw nucleotide sequences are common, there are also alternatives. One example is _Fiannaca-CNN_10, which is a

model for bacterial classification. The model uses the number of k-mer occurrences as input, which is fed into convolutional layers followed by max-pooling layers and fully connected layers.

We used _k_ = 7 (7-mers) in our experiments because they show that the highest accuracy is achieved using this HP. Another example is _PPR-Meta_11, which is used to classify if the sequence

is a plasmid, chromosome, or phage. The input to the model is both one-hot encoded nucleotides and 3-mers. In addition, the reverse-complements of the original inputs are concatenated to

the original sequence for both inputs. The model consists of two different three convolutional layers, the outputs of which are global average pooled, concatenated, and fed into a fully

connected layer. There are also max-pooling and batch-normalization layers after the first two convolutional layers. Our HPO results provide valuable insight into the design and training of

architectures for specific tasks and datasets. For example, increasing the kernel size, number of filters, and layers in convolutional networks can substantially increase both the number of

trainable parameters and memory requirements, resulting in a trade-off. Many existing models, such as DeepVirFinder6, ViraMiner7 or CHEER9, are limited to a single (or multiple but

parallelized, not sequential) convolutional layer with a large kernel size (up to ~15) and a large number of filters ( ~ 1000). Although PPR-Meta11 proposes a deeper model (3 sequential

convolutional layers), it compensates by reducing the kernel size (down to 3). Our HPO framework has discovered an architecture that performs better on viral classification in terms of

accuracy: deeper (7 convolutional layers) with a smaller number of filters in the final convolutional layers (as low as 30). In examining model architectures that perform well across two

datasets and three different sequence lengths, we sought to identify common trends and patterns in their architecture designs. Our analysis reveals that architectures with GAP layers

typically incorporate more convolutional layers (5 to 7, as opposed to 1 to 5 in RNN models) and more fully connected layers (1 or 2, vs. 0 or 1) (Supplementary Table 1). The preference for

GAP layers is likely due to their function in aggregating information learned by convolutional layers through averaging over the sequence, instead of learning representations by optimizing

its own weights. Compared to CNN-RNN models, CNN-GAP models mainly use fully connected layers to integrate long-range information. Furthermore, LSTM layers are consistently preferred to GRU

layers. Our findings also indicate a general avoidance of multiple recurrent layers, while bidirectional RNN layers are preferred over unidirectional ones. In terms of training

hyperparameters, the optimized learning rate is typically between 10−3 and 10−4 with the Adam35 optimizer more commonly chosen over alternatives like Adagrad36, Rmsprop, and SGD37. It is

important to note, however, that these trends are observations and may not universally apply to every dataset or task. Therefore, we recommend running GenomeNet-Architect on the specific

dataset and task in question to tailor the model architecture for optimal performance in each unique scenario. The results of the 10,000 nt setting in contrast to the 150 nt setting are

noteworthy in that there is a much smaller improvement in accuracy over the baselines in the 10,000 nt setting. This is because the viral identification task becomes “too easy” at 10,000

nucleotides, leaving little room for improvement. In such settings, where relatively simple models already perform sufficiently well, it may not be worth the considerable computational

overhead of finding a specialized architecture. METHOD HYPERPARAMETER SEARCH SPACE The hyperparameter space used for optimization is listed in Table 1 and described in more detail here. The

first part of the model constructed by GenomeNet-Architect consists of a sequence of convolutional blocks (Fig. 1), each of which consists of convolutional layers. The number of blocks

(_N__cb_) and the number of layers in each block (_s__cb_) is determined by the HPs _n__cb_ and _n__c_ in the following way: _N__cb_ is directly set to _n__cb_ unless _n__c_ (which relates

to the total number of convolutional layers) is less than that. Their relation is therefore $${N}_{{cb}}=\left\{\begin{array}{cc}{n}_{c},&{{if} \, {n}_{c}\le {n}_{{cb}}}\\ {n}_{{cb}},

&{otherwise}\end{array}\right.$$ _s__cb_ is calculated by rounding the ratio of the _n__c_ hyperparameter to the actual number of convolutional blocks _N__cb_:

$${s}_{{cb}}={round}\left(\frac{{n}_{c}}{{N}_{{cb}}}\right).$$ This results in _n__c_ determining the approximate total number of convolutional layers while satisfying the constraint that

each convolutional block has the same (integer) number of layers. The total number of convolutional layers is then given by $${N}_{c}={N}_{{cb}}\times {s}_{{cb}}.$$ _f_0 and _f__end_

determine the number of filters in the first or last convolutional layers, respectively. The number of filters in intermediate layers is interpolated exponentially. If residual blocks are

used, the number of filters within each convolutional block needs to be the same, in which case the number of filters changes block-wise. Otherwise, each convolutional layer can have a

different number of filters. If there is only one convolutional layer, ⌈_f_0⌉ is used as the number of filters in this layer. Thus, the number of filters for the _i__th_ convolutional layer

is: $${f}_{i}=\left\lceil {f}_{0}\times {\left(\frac{{f}_{{end}}}{{f}_{0}}\right)}^{j\left(i\right)}\right\rceil,\,j\left(i\right)=\left\{\begin{array}{cc}\left\lfloor

\frac{i}{{s}_{{cb}}}\right\rfloor \times \frac{1}{{N}_{{cb}}-1}, & {if} \, res\_block\\ \frac{i}{{N}_{c}-1}, & {otherwise}\end{array}\right..$$ The kernel size of the convolutional

layers is also exponentially interpolated between _k_0 and _k__end_. If the model has only one convolutional layer, the kernel size is set to ⌈_k_0⌉. The kernel size of the convolutional

layer _i_ is: $${k}_{i}=\left\lceil{k}_{0}\times {\left(\frac{{k}_{{end}}}{{k}_{0}}\right)}^{\frac{i}{{N}_{c}-1}}\right\rceil.$$ The convolutional layers can use dilated convolutions, where

the dilation factor increases exponentially from 1 to _d__end_ within each convolutional block. Using “_REM_” as the remainder operation, the dilation factor for each layer is then:

$${d}_{i}=\left\lceil{d}_{{end}}^{\,\left(\left\lfloor i\,{{{{{\boldsymbol{rem}}}}}}\,{s}_{{cb}}\right\rfloor \right)/\left({s}_{{cb}}-1\right)}\right\rceil.$$ We apply max-pooling after

convolutional layers, depending on the total max-pooling factor pend. Max pooling layers of stride and a kernel size of 2 or the power of 2 are inserted between convolutional layers so that

the sequence length is reduced exponentially along the model. pend represents the approximate value of total reduction in the sequence length before the output of the convolutional part is

fed into the last GAP layer or into the RNN layers depending on the model type. For CNN-GAP, outputs from multiple convolutional blocks can be pooled, concatenated, and fed into a fully

connected network. Out of _N__cb_ outputs, the last _min_(1, ⌈(1 − _r__s_) × _N__cb_⌉) of them are fed into global average pooling layers, where _r__s_ is the skip ratio hyperparameter.

HYPERPARAMETER OPTIMIZATION PROCESS GenomeNet-Architect uses the mlrMBO software38 with a Gaussian process model from the DiceKriging R package39 configured with a Matérn-3/2 kernel40 for

optimization. It uses the UCB31 infill criterion, sampling _λ_ from an exponential distribution as a batch proposal method32. In our experiment, we proposed three different configurations

simultaneously in each iteration. For both tasks, we trained the proposed model configurations for a given amount of time and then evaluated them afterwards on the validation set. For each

architecture (CNN-GAP and CNN-RNN) and for each sequence length of the viral classification task (150 nt and 10,000 nt), the best-performing model configuration found within the optimization

setting (2 h, 6 h) was saved and considered for further evaluation. For the pathogenicity detection task, we only evaluated the 2 h optimization. For each task and sequence length value,

the first _t_ = _t_1 (2 h) optimization evaluated a total of 788 configurations, parallelized on 24 GPUs, and ran for 2.8 days (wall time). For the viral classification task, the

warm-started _t_ = _t_2 (6 h) optimization evaluated 408 more configurations and ran for 7.0 days for each sequence length value. During HPO, the number of samples between model validation

evaluations was set dynamically, depending on the time taken for a single model training step. It was chosen so that approximately 20 validation evaluations were performed for each model in

the first phase (_t_ = 2 h), and approximately 100 validation evaluations were performed in the second phase (_t_ = 6 hours). In the first phase, the highest validation accuracy found during

model training was used as the objective value to be optimized. In the second phase, the second-highest validation accuracy found in the last 20 validation evaluations was used as the

objective value. This was done to avoid rewarding models with a very noisy training process with performance outliers. The batch size of each model architecture is chosen to be as large as

possible while still fitting into GPU memory. To do this, GenomeNet-Architect performs a binary search to find the largest model that still fits in the GPU and subtracts a 10% safety margin

to avoid potential training failures. ARCHITECTURE EVALUATION AND BENCHMARKS For the viral classification task, the training and validation samples are generated by randomly sampling FASTA

genome files and splitting them into disjoint consecutive subsequences from a random starting point. A batch size that is a multiple of 3 (the number of target classes) is used, and each

batch contains the same number of samples from each class. Since we work with datasets that have different quantities of data for each class, this effectively oversamples the minor classes

compared to the largest class. The validation set performance was evaluated at regular intervals after training on a predetermined number of samples, set to 6,000,000 for the 150 nt models

and 600,000 for the 10,000 nt models. The evaluation used a subsample of the validation set equal to 50% of the training samples seen between each validation. During the model training, the

typical batch size was 1200 for the 150 nt models, and either 120, 60, or 30 for the 10,000 nt models. Unlike during training and validation, the test set samples were not randomly generated

by selecting random FASTA files. Instead, test samples were generated by iterating through all individual files, and using consecutive subsequences starting from the first position. For the

pathogenicity detection task, the validation performance was evaluated at regular intervals on the complete set, specifically once after training on 5,000,000 samples. The batch size of

1000 was used for all models, except for GAP-RNN, as it was not possible with the memory of our GPU. For this model, a batch size of 500 was used. For both tasks, we chose a learning rate

schedule that automatically reduced the learning rate by half if the balanced accuracy did not increase for 3 consecutive evaluations on the validation set. We stopped the training when the

balanced accuracy did not increase for 10 consecutive evaluations. This typically corresponds to stopping the training after 40/50 evaluations for the 150 nt models, 25/35 evaluations for

the 10,000 nt models for the viral classification tasks, and 5/15 evaluations for the pathogenicity detection task. To evaluate the performance of the architectures and HP configurations,

the models proposed by GenomeNet-Architect were trained until convergence on the training set; convergence was checked on the validation set. The resulting models were then evaluated on a

test set that was not seen during optimization. DATASETS For the viral classification task, we downloaded all complete bacterial and viral genomes from GeneBank and RefSeq using the genome

updater script (https://github.com/pirovc/genome_updater) on 04-11-2020 with the arguments -d “genbank,refseq” -g “bacteria”/”viral” -c “all” and -l “Complete Genome”. To filter out possible

contamination consisting of plasmids and bacteriophages, we removed all genomes from the bacteria set with more than one chromosome. Filtering out plasmids due to their inconsistent and

poor annotations in databases avoids introducing substantial noise in sequence and annotation since they can be incorrectly included or excluded in genomes. We used the taxonomic metadata to

split the viral set into eukaryotic or prokaryotic viruses. Overall this resulted in three subgroups: bacteria, prokaryotic bacteriophages, and eukaryotic viruses (referred to as non-phage

viruses, Table 2). To assess the model’s generalization performance, we subset the genomes into training, validation, and test subsets. We used the “date of publishing” metadata to split the

data by publication time, with the training data consisting mostly of genomes published before 2020, and the validation and test data consisting of more recently published genomes. Thus,

when applied to newly sequenced DNA, the classification performance of the models on yet unknown data is estimated. For smaller datasets, using average nucleotide identity information (ANI)

generated with tools such as Mashtree41 to perform the splits can alternatively be used to avoid overlap between training and test data. The training data was used for model fitting, the

validation data was used to estimate generalization performance during HPO and to check for convergence during final model training, and the test data was used to compare final model

performance and draw conclusions. The test data was not seen by the optimization process. The training, validation and test sets represent approximately 70%, 20%, and 10% of the total data,

respectively. The number of FASTA files in the sets and the number of non-overlapping samples in sets of the viral classification task are listed in Table 2. Listed is the number of

different non-overlapping sequences that could theoretically be extracted from the datasets, were they split into consecutive subsequences. However, whenever the training process reads a

file again, e.g. in a different epoch, the starting point of the sequence to be sampled is randomized, resulting in a much larger number of possible distinct (though overlapping) samples.

Because the size of the test set is imbalanced, we report class-balanced measures, i.e. measures calculated for each class individually and then averaged over all classes. For the

pathogenicity classification task, we downloaded the dataset from https://zenodo.org/records/367856313. Specifically, the used training files are nonpathogenic_train.fasta.gz,

pathogenic_train.fasta.gz, the used validation files are pathogenic_val.fasta.gz, nonpathogenic_val.fasta.gz, and the used test files are nonpathogenic_test_1.fasta.gz,

nonpathogenic_test_2.fasta.gz, pathogenic_test_1.fasta.gz, pathogenic_test_2.fasta.gz. REPORTING SUMMARY Further information on research design is available in the Nature Portfolio Reporting

Summary linked to this article. DATA AVAILABILITY The data for the virus identification task is available under

https://research.bifo.helmholtz-hzi.de/downloads/deepg_refpacks/architect_training_data.tar.gz. Data for the pathogen detection task is taken from a study of Bartoszewicz et al.13

https://zenodo.org/records/3678563 as mentioned in the Datasets subsection. Source data for figures can be found in Supplementary Data 1 as well as on https://github.com/GenomeNet/Architect

(https://doi.org/10.5281/zenodo.10889923). CODE AVAILABILITY The code, available at https://github.com/GenomeNet/Architect, enables users to apply the optimization process across various

datasets and tasks. It is based on our R library deepG (deepg.de) and can therefore be adapted to a variety of genomics tasks that are supported by it. It uses the TensorFlow backend and can

be made to run in parallel on multi-GPU-machines and compute clusters through the batchtools42 R package. CHANGE HISTORY * _ 23 MAY 2024 A Correction to this paper has been published:

https://doi.org/10.1038/s42003-024-06318-y _ REFERENCES * LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. _Nature_ 521, 436–444 (2015). Article  CAS  PubMed  Google Scholar  *

AlQuraishi, M. AlphaFold at CASP13. _Bioinformatics_ 35, 4862–4865 (2019). Article  CAS  PubMed  PubMed Central  Google Scholar  * Ronneberger, O., Fischer, P. & Brox, T. U-Net:

Convolutional Networks for Biomedical Image Segmentation. in _Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015_ 234–241 (Springer International Publishing, 2015). *

Daoud, M. & Mayo, M. A survey of neural network-based cancer prediction models from microarray data. _Artif. Intell. Med._ 97, 204–214 (2019). Article  PubMed  Google Scholar  *

Patterson, J. & Gibson, A. _Deep Learning: A Practitioner’s Approach_. (‘O’Reilly Media, Inc.’ 2017). * Ren, J. et al. Identifying viruses from metagenomic data using deep learning.

_Quant. Biol._ 8, 64–77 (2020). Article  CAS  PubMed  PubMed Central  Google Scholar  * Tampuu, A., Bzhalava, Z., Dillner, J. & Vicente, R. ViraMiner: Deep learning on raw DNA sequences

for identifying viral genomes in human samples. _PLoS One_ 14, e0222271 (2019). Article  CAS  PubMed  PubMed Central  Google Scholar  * Auslander, N., Gussow, A. B., Benler, S., Wolf, Y. I.

& Koonin, E. V. Seeker: alignment-free identification of bacteriophage genomes by deep learning. _Nucleic Acids Res._ 48, e121 (2020). Article  CAS  PubMed  PubMed Central  Google

Scholar  * Shang, J. & Sun, Y. CHEER: HierarCHical taxonomic classification for viral mEtagEnomic data via deep learning. _Methods_ 189, 95–103 (2021). Article  CAS  PubMed  Google

Scholar  * Fiannaca, A. et al. Deep learning models for bacteria taxonomic classification of metagenomic data. _BMC Bioinformatics_ 19, 198 (2018). Article  PubMed  PubMed Central  Google

Scholar  * Fang, Z. et al. PPR-Meta: a tool for identifying phages and plasmids from metagenomic fragments using deep learning. _Gigascience_ 8, giz066 (2019). Article  PubMed  PubMed

Central  Google Scholar  * Bartoszewicz, J. M., Nasri, F., Nowicka, M. & Renard, B. Y. Detecting DNA of novel fungal pathogens using ResNets and a curated fungi-hosts data collection.

_Bioinformatics_ 38, ii168–ii174 (2022). Article  PubMed  Google Scholar  * Bartoszewicz, J. M., Seidel, A., Rentzsch, R. & Renard, B. Y. DeePaC: predicting pathogenic potential of novel

DNA with reverse-complement neural networks. _Bioinformatics_ 36, 81–89 (2019). Article  Google Scholar  * Elsken, T., Metzen, J. H., & Hutter, F. Neural architecture search: A survey.

_J. Machine Learn. Res._ 20, 1–21 (2019). * Eraslan, G., Avsec, Ž., Gagneur, J. & Theis, F. J. Deep learning: new computational modelling techniques for genomics. _Nat. Rev. Genet._ 20,

389–403 (2019). Article  CAS  PubMed  Google Scholar  * Koumakis, L. Deep learning models in genomics; are we there yet? _Comput. Struct. Biotechnol. J._ 18, 1466–1473 (2020). Article  CAS 

PubMed  PubMed Central  Google Scholar  * Boža, V., Brejová, B. & Vinař, T. DeepNano: Deep recurrent neural networks for base calling in MinION nanopore reads. _PLoS One_ 12, e0178751

(2017). Article  PubMed  PubMed Central  Google Scholar  * Cao, R. et al. ProLanGO: Protein Function Prediction Using Neural Machine Translation Based on a Recurrent Neural Network.

_Molecules_ 22, 1732 (2017). Article  PubMed  PubMed Central  Google Scholar  * Shen, X., Jiang, C., Wen, Y., Li, C. & Lu, Q. A brief review on deep learning applications in genomic

studies. Front. Syst. Biol., 2, 877717 (2022). * Wang, R., Zang, T. & Wang, Y. Human mitochondrial genome compression using machine learning techniques. _Hum. Genomics_ 13, 49 (2019).

Article  PubMed  PubMed Central  Google Scholar  * Quang, D. & Xie, X. DanQ: a hybrid convolutional and recurrent deep neural network for quantifying the function of DNA sequences.

_Nucleic Acids Res._ 44, e107 (2016). Article  PubMed  PubMed Central  Google Scholar  * Snoek, J., Larochelle, H. & Adams, R. P. Practical bayesian optimization of machine learning

algorithms. _Adv. Neural Inf. Process. Syst_. 25, (2012). * White, C., Neiswanger, W., & Savani, Y. Bananas: Bayesian optimization with neural architectures for neural architecture

search. In Proceedings of the AAAI conference on artificial intelligence (Vol. 35, No. 12, pp. 10293–10301) (2021). * Pham, H., Guan, M., Zoph, B., Le, Q. & Dean, J. Efficient Neural

Architecture Search via Parameters Sharing. 80, 4095–4104 (2018). * Liu, H., Simonyan, K. & Yang, Y. DARTS: Differentiable Architecture Search. _arXiv [cs.LG]_ (2018). * Li, L.,

Jamieson, K., DeSalvo, G., Rostamizadeh, A. & Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. _arXiv [cs.LG]_ (2016). * Zhang, Z., Park, C. Y.,

Theesfeld, C. L. & Troyanskaya, O. G. An automated framework for efficiently designing deep convolutional neural networks in genomics. _Nat. Machine Intell._ 3, 392–400 (2021). Article 

Google Scholar  * Kelley, D. R. et al. Sequential regulatory activity prediction across chromosomes with convolutional neural networks. _Genome Res._ 28, 739–750 (2018). Article  CAS  PubMed

  PubMed Central  Google Scholar  * Booker, A. J. et al. A rigorous framework for optimization of expensive functions by surrogates. _Struct. Optimization_ 17, 1–13 (1999). Article  Google

Scholar  * Bischl, B., Wessing, S., Bauer, N., Friedrichs, K. & Weihs, C. MOI-MBO: Multiobjective Infill for Parallel Model-Based Optimization. in _Learning and Intelligent Optimization_

173–186 (Springer International Publishing, 2014). * Srinivas, N., Krause, A., Kakade, S. M. & Seeger, M. Gaussian Process Optimization in the Bandit Setting: No Regret and Experimental

Design. _arXiv [cs.LG]_ (2009). * Hutter, F., Hoos, H. H. & Leyton-Brown, K. Parallel Algorithm Configuration. in _Learning and Intelligent Optimization_ 55–70 (Springer Berlin

Heidelberg, 2012). * Ji, Y., Zhou, Z., Liu, H. & Davuluri, R. V. DNABERT: pre-trained Bidirectional Encoder Representations from Transformers model for DNA-language in genome.

_Bioinformatics_ https://doi.org/10.1093/bioinformatics/btab083. (2021). * Liang, Q., Bible, P. W., Liu, Y., Zou, B. & Wei, L. DeepMicrobes: taxonomic classification for metagenomics

with deep learning. _NAR Genom. Bioinform._ 2, lqaa009 (2020). Article  PubMed  PubMed Central  Google Scholar  * Kingma, D. P. & Ba, J. Adam: A Method for Stochastic Optimization.

_arXiv [cs.LG]_ (2014). * Stochastic Optimization. Adaptive Subgradient Methods for. https://www.jmlr.org/papers/volume12/duchi11a/duchi11a.pdf (2011). * Robbins, H. & Monro, S. A

Stochastic Approximation Method. _Ann. Math. Stat._ 22, 400–407 (1951). Article  Google Scholar  * Bischl, B. et al. mlrMBO: A Modular Framework for Model-Based Optimization of Expensive

Black-Box Functions. _arXiv [stat.ML]_ (2017). * Roustant, O., Ginsbourger, D. & Deville, Y. DiceKriging, DiceOptim: Two R Packages for the Analysis of Computer Experiments by

Kriging-Based Metamodeling and Optimization. _J. Stat. Softw._ 51, 1–55 (2012). Article  Google Scholar  * Genton, M. G., Cristianini, N., Shawe-Taylor, J. & Williamson, R. Classes of

kernels for machine learning: A statistics perspective. https://www.jmlr.org/papers/volume2/genton01a/genton01a.pdf?ref=https://githubhelp.com. * Katz, L. S. et al. Mashtree: a rapid

comparison of whole genome sequence files. _J. Open Source Softw_. 4, 44 (2019). * Lang, M., Bischl, B. & Surmann, D. batchtools: Tools for R to work on batch systems. _J. Open Source

Softw._ 2, 135 (2017). Article  Google Scholar  Download references ACKNOWLEDGEMENTS This work was funded in part by the German Federal Ministry of Education and Research (BMBF) under Grant

No. 01IS18036A and under GenomeNet Grant No. 031L0199A/031L0199B and by the Deutsche Forschungsgemeinschaft DFG EXC 2155. P.C.M. received funding from the German Research Foundation (Grant

number 405892038). X.-Y.T. received funding from the German Center for Infection Research (DZIF) TI BBD. C.H. received funding from NIH U19AI110820. FUNDING Open Access funding enabled and

organized by Projekt DEAL. AUTHOR INFORMATION Author notes * These authors jointly supervised this work: Philipp C. Münch, Martin Binder. AUTHORS AND AFFILIATIONS * Department of Statistics,

LMU Munich, Munich, Germany Hüseyin Anil Gündüz, Julia Moosbauer, Xiao-Yin To, Mina Rezaei, Bernd Bischl & Martin Binder * Munich Center for Machine Learning, Munich, Germany Hüseyin

Anil Gündüz, Julia Moosbauer, Xiao-Yin To, Mina Rezaei, Bernd Bischl & Martin Binder * Department for Computational Biology of Infection Research, Helmholtz Center for Infection

Research, 38124, Braunschweig, Germany René Mreches, Gary Robertson, Xiao-Yin To, Alice C. McHardy & Philipp C. Münch * Braunschweig Integrated Centre of Systems Biology (BRICS),

Technische Universität Braunschweig, Braunschweig, Germany René Mreches, Gary Robertson, Xiao-Yin To, Alice C. McHardy & Philipp C. Münch * Department of Biostatistics, Harvard School of

Public Health, Boston, MA, USA Eric A. Franzosa, Curtis Huttenhower & Philipp C. Münch * German Centre for Infection Research (DZIF), partner site Hannover Braunschweig, Braunschweig,

Germany Alice C. McHardy & Philipp C. Münch Authors * Hüseyin Anil Gündüz View author publications You can also search for this author inPubMed Google Scholar * René Mreches View author

publications You can also search for this author inPubMed Google Scholar * Julia Moosbauer View author publications You can also search for this author inPubMed Google Scholar * Gary

Robertson View author publications You can also search for this author inPubMed Google Scholar * Xiao-Yin To View author publications You can also search for this author inPubMed Google

Scholar * Eric A. Franzosa View author publications You can also search for this author inPubMed Google Scholar * Curtis Huttenhower View author publications You can also search for this

author inPubMed Google Scholar * Mina Rezaei View author publications You can also search for this author inPubMed Google Scholar * Alice C. McHardy View author publications You can also

search for this author inPubMed Google Scholar * Bernd Bischl View author publications You can also search for this author inPubMed Google Scholar * Philipp C. Münch View author publications

You can also search for this author inPubMed Google Scholar * Martin Binder View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS H.A.G., M.B.,

and P.C.M. designed the study and experiments. H.A.G. was responsible for coding the baselines and optimized architectures, and for training, evaluating, and analyzing them. H.A.G. drafted

the initial manuscript. R.M. and J.M. contributed to code development. M.B. was the main developer of the hyperparameter optimization code and the multi-fidelity approach used. M.B. also

supervised and contributed to the model code, and ran the model-based optimization experiments to find optimal architectures. G.R. provided computational resources and support. E.A.F. and

C.H. contributed to virus identification and benchmarking. M.R., A.C.M., B.B., and X.-Y.T. provided valuable feedback and input throughout the project. The project was supervised by M.B. and

P.C.M. All authors contributed to the writing of the manuscript. CORRESPONDING AUTHORS Correspondence to Philipp C. Münch or Martin Binder. ETHICS DECLARATIONS COMPETING INTERESTS The

authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Communications Biology_ thanks the anonymous reviewers for their contribution to the peer review of this work.

Primary Handling Editors: Gene Chong and Luke R. Grinham. A peer review file is available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to

jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION PEER REVIEW FILE SUPPLEMENTARY INFORMATION DESCRIPTION OF ADDITIONAL SUPPLEMENTARY FILES

SUPPLEMENTARY DATA 1 REPORTING SUMMARY RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing,

adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons

licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a

credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted

use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT

THIS ARTICLE CITE THIS ARTICLE Gündüz, H.A., Mreches, R., Moosbauer, J. _et al._ Optimized model architectures for deep learning on genomic data. _Commun Biol_ 7, 516 (2024).

https://doi.org/10.1038/s42003-024-06161-1 Download citation * Received: 08 February 2023 * Accepted: 08 April 2024 * Published: 30 April 2024 * DOI:

https://doi.org/10.1038/s42003-024-06161-1 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative