Play all audios:
ABSTRACT Reinforcement learning (RL) has become a proven method for optimizing a procedure for which success has been defined, but the specific actions needed to achieve it have not. Using a
method we call ‘controlled online optimization learning’ (COOL), we apply the so-called ‘black box’ method of RL to simulated annealing (SA), demonstrating that an RL agent based on
proximal policy optimization can, through experience alone, arrive at a temperature schedule that surpasses the performance of standard heuristic temperature schedules for two classes of
Hamiltonians. When the system is initialized at a cool temperature, the RL agent learns to heat the system to ‘melt’ it and then slowly cool it in an effort to anneal to the ground state; if
the system is initialized at a high temperature, the algorithm immediately cools the system. We investigate the performance of our RL-driven SA agent in generalizing to all Hamiltonians of
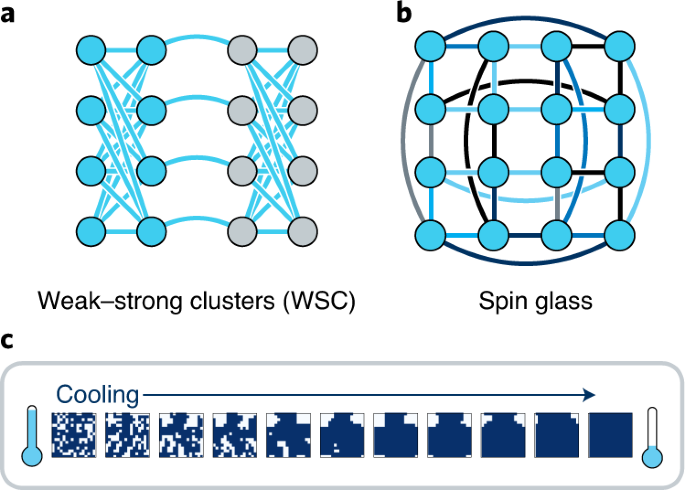
a specific class. When trained on random Hamiltonians of nearest-neighbour spin glasses, the RL agent is able to control the SA process for other Hamiltonians, reaching the ground state with
a higher probability than a simple linear annealing schedule. Furthermore, the scaling performance (with respect to system size) of the RL approach is far more favourable, achieving a
performance improvement of almost two orders of magnitude on _L_ = 142 systems. We demonstrate the robustness of the RL approach when the system operates in a ‘destructive observation’ mode,
an allusion to a quantum system where measurements destroy the state of the system. The success of the RL agent could have far-reaching impacts, from classical optimization, to quantum
annealing and to the simulation of physical systems. Access through your institution Buy or subscribe This is a preview of subscription content, access via your institution ACCESS OPTIONS
Access through your institution Access Nature and 54 other Nature Portfolio journals Get Nature+, our best-value online-access subscription $32.99 / 30 days cancel any time Learn more
Subscribe to this journal Receive 12 digital issues and online access to articles $119.00 per year only $9.92 per issue Learn more Buy this article * Purchase on SpringerLink * Instant
access to full article PDF Buy now Prices may be subject to local taxes which are calculated during checkout ADDITIONAL ACCESS OPTIONS: * Log in * Learn about institutional subscriptions *
Read our FAQs * Contact customer support SIMILAR CONTENT BEING VIEWED BY OTHERS OPTIMIZING QUANTUM ANNEALING SCHEDULES WITH MONTE CARLO TREE SEARCH ENHANCED WITH NEURAL NETWORKS Article 14
March 2022 SEARCHING FOR SPIN GLASS GROUND STATES THROUGH DEEP REINFORCEMENT LEARNING Article Open access 09 February 2023 COHERENT QUANTUM ANNEALING IN A PROGRAMMABLE 2,000 QUBIT ISING
CHAIN Article 15 September 2022 DATA AVAILABILITY The test datasets necessary to reproduce these findings are available at https://doi.org/10.5281/zenodo.3897413. CODE AVAILABILITY The code
necessary to reproduce these findings is available at https://doi.org/10.5281/zenodo.3897413. REFERENCES * Kirkpatrick, S., Gelatt, C. D. & Vecchi, M. P. Optimization by simulated
annealing. _Science_ 220, 671–680 (1983). MathSciNet MATH Google Scholar * Barahona, F. On the computational complexity of Ising spin glass models. _J. Phys. A_ 15, 3241–3253 (1982).
MathSciNet Google Scholar * Sherrington, D. & Kirkpatrick, S. Solvable model of a spin-glass. _Phys. Rev. Lett._ 35, 1792–1796 (1975). Google Scholar * Ising, E. Beitrag zur Theorie
des Ferromagnetismus. _Zeitschrift Phys._ 31, 253–258 (1925). MATH Google Scholar * Onsager, L. Crystal statistics. I. A two-dimensional model with an order–disorder transition. _Phys.
Rev._ 65, 117–149 (1944). MathSciNet MATH Google Scholar * Ferdinand, A. E. & Fisher, M. E. Bounded and inhomogeneous Ising models. I. Specific-heat anomaly of a finite lattice.
_Phys. Rev._ 185, 832–846 (1969). Google Scholar * Lucas, A. Ising formulations of many NP problems. _Front. Phys._ 2, 1–14 (2014). Google Scholar * Hastings, B. Y. W. K. Monte Carlo
sampling methods using Markov chains and their applications. _Biometrika_ 57, 97–109 (1970). MathSciNet MATH Google Scholar * Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller,
A. H. & Teller, E. Equation of state calculations by fast computing machines. _J. Chem. Phys._ 21, 1087–1092 (1953). MATH Google Scholar * Kirkpatrick, S. Optimization by simulated
annealing: quantitative studies. _J. Stat. Phys._ 34, 975–986 (1984). MathSciNet Google Scholar * van Laarhoven, P. J. M. & Aarts, E. H. L. Simulated Annealing: Theory and Applications
(Springer, 1987). * Stander, J. & Silverman, B. W. Temperature schedules for simulated annealing. _Stat. Comput._ 4, 21–32 (1994). Google Scholar * Heim, B., Rønnow, T. F., Isakov, S.
V. & Troyer, M. Quantum versus classical annealing of Ising spin glasses. _Science_ 348, 215–217 (2015). MathSciNet MATH Google Scholar * Bounds, D. G. New optimization methods from
physics and biology. _Nature_ 329, 215–219 (1987). Google Scholar * Farhi, E. et al. A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem. _Science_
292, 472–475 (2001). MathSciNet MATH Google Scholar * Hen, I. & Young, A. P. Solving the graph-isomorphism problem with a quantum annealer. _Phys. Rev. A_ 86, 042310 (2012). Google
Scholar * Boixo, S. et al. Evidence for quantum annealing with more than one hundred qubits. _Nat. Phys._ 10, 218–224 (2014). Google Scholar * Bian, Z. et al. Discrete optimization using
quantum annealing on sparse Ising models. _Front. Phys._ 2, 1–10 (2014). Google Scholar * Venturelli, D., Marchand, D. J. J. & Rojo, G. Quantum annealing implementation of job-shop
scheduling. Preprint at https://arxiv.org/pdf/1506.08479.pdf (2015). * Ray, P., Chakrabarti, B. K. & Chakrabarti, A. Sherrington–Kirkpatrick model in a transverse field: absence of
replica symmetry breaking due to quantum fluctuations. _Phys. Rev. B_ 39, 11828–11832 (1989). Google Scholar * Martoňák, R., Santoro, G. E. & Tosatti, E. Quantum annealing by the
path-integral Monte Carlo method: the two-dimensional random Ising model. _Phys. Rev. B_ 66, 094203 (2002). Google Scholar * Santoro, G. E. Theory of quantum annealing of an Ising spin
glass. _Science_ 295, 2427–2430 (2002). Google Scholar * Finnila, A., Gomez, M., Sebenik, C., Stenson, C. & Doll, J. Quantum annealing: a new method for minimizing multidimensional
functions. _Chem. Phys. Lett._ 219, 343–348 (1994). Google Scholar * Kadowaki, T. & Nishimori, H. Quantum annealing in the transverse Ising model. _Phys. Rev. E_ 58, 5355–5363 (1998).
Google Scholar * Harris, R. et al. Experimental demonstration of a robust and scalable flux qubit. _Phys. Rev. B_ 81, 134510 (2010). Google Scholar * Harris, R. et al. Experimental
investigation of an eight-qubit unit cell in a superconducting optimization processor. _Phys. Rev. B._ 82, 024511 (2010). Google Scholar * Johnson, M. W. et al. Quantum annealing with
manufactured spins. _Nature_ 473, 194–198 (2011). Google Scholar * McGeoch, C. C. & Wang, C. Experimental evaluation of an adiabiatic quantum system for combinatorial optimization. In
_Proceedings of the ACM International Conference on Computing Frontiers_, _CF_ ’_13_, Vol. 23, 1–11 (ACM, 2013). * Ikeda, K., Nakamura, Y. & Humble, T. S. Application of quantum
annealing to nurse scheduling problem. _Sci. Rep._ 9, 12837 (2019). Google Scholar * Dickson, N. G. et al. Thermally assisted quantum annealing of a 16-qubit problem. _Nat. Commun._ 4, 1903
(2013). MathSciNet Google Scholar * Okada, S., Ohzeki, M. & Tanaka, K. Efficient quantum and simulated annealing of Potts models using a half-hot constraint. _J. Phys. Soc. Jpn_ 89,
094801 (2020). Google Scholar * Battaglia, D. A., Santoro, G. E. & Tosatti, E. Optimization by quantum annealing: lessons from hard satisfiability problems. _Phys. Rev. E_ 71, 066707
(2005). Google Scholar * Tsukamoto, S., Takatsu, M., Matsubara, S. & Tamura, H. An accelerator architecture for combinatorial optimization problems. _Fujitsu Sci. Technical J._ 53, 8–13
(2017). Google Scholar * Inagaki, T. et al. A coherent Ising machine for 2,000-node optimization problems. _Science_ 354, 603–606 (2016). Google Scholar * Leleu, T., Yamamoto, Y.,
McMahon, P. L. & Aihara, K. Destabilization of local minima in analog spin systems by correction of amplitude heterogeneity. _Phys. Rev. Lett._ 122, 040607 (2019). Google Scholar *
Tiunov, E. S., Ulanov, A. E. & Lvovsky, A. I. Annealing by simulating the coherent Ising machine. _Opt. Express_ 27, 10288–10295 (2019). Google Scholar * Farhi, E., Goldstone, J. &
Gutmann, S. A quantum approximate optimization algorithm. Preprint at https://arxiv.org/pdf/1411.4028.pdf (2014). * Farhi, E., Goldstone, J., Gutmann, S. & Zhou, L. The quantum
approximate optimization algorithm and the Sherrington–Kirkpatrick model at infinite size. Preprint at https://arxiv.org/pdf/1910.08187.pdf (2019). * Sutton, R. & Barto, A.
_Reinforcement Learning_: _An Introduction_ 2nd edn (MIT Press, 2018). * Berner, C. et al. Dota 2 with large scale deep reinforcement learning. Preprint at
https://arxiv.org/pdf/1912.06680.pdf (2019). * Zhang, Z. et al. Hierarchical reinforcement learning for multi-agent MOBA Game. Preprint at https://arxiv.org/pdf/1901.08004.pdf (2019). *
Vinyals, O. et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. _Nature_ 575, 350–354 (2019). Google Scholar * Mnih, V. et al. Playing Atari with deep
reinforcement learning. Preprint at https://arxiv.org/pdf/1312.5602.pdf (2013). * Silver, D. et al. Mastering the game of Go with deep neural networks and tree search. _Nature_ 529, 484–489
(2016). Google Scholar * Silver, D. et al. Mastering the game of Go without human knowledge. _Nature_ 550, 354–359 (2017). Google Scholar * Silver, D. et al. A general reinforcement
learning algorithm that masters chess, shogi and Go through self-play. _Science_ 362, 1140–1144 (2018). MathSciNet MATH Google Scholar * Agostinelli, F., McAleer, S., Shmakov, A. &
Baldi, P. Solving the Rubik’s cube with deep reinforcement learning and search. _Nat. Mach. Intell._ 1, 356–363 (2019). Google Scholar * Akkaya, I. et al. Solving Rubik’s cube with a robot
hand. Preprint at https://arxiv.org/pdf/1910.07113.pdf (2019). * Schulman, J., Wolski, F., Dhariwal, P., Radford, A. & Klimov, O. Proximal policy optimization algorithms. Preprint at
https://arxiv.org/pdf/1707.06347.pdf (2017). * Hill, A. et al. Stable Baselines (2018); https://github.com/hill-a/stable-baselines * Brockman, G. et al. OpenAI Gym. Preprint at
https://arxiv.org/pdf/1606.01540.pdf (2016). * Schulman, J., Levine, S., Abbeel, P., Jordan, M. & Moritz, P. Trust region policy optimization. In _Proceedings of the 32nd_ _International
Conference on Machine Learning_ 1889–1897 (ICML, 2015). * Kakade, S. & Langford, J. Approximately optimal approximate reinforcement learning. In _Proceedings of the 19th International
Conference on Machine Learning_ 267–274 (ICML, 2002). * Hochreiter, S. & Schmidhuber, J. Long short-term memory. _Neural Comput._ 9, 1735–1780 (1997). Google Scholar * Aramon, M. et al.
Physics-inspired optimization for quadratic unconstrained problems using a Digital Annealer. _Front. Phys._ 7 (2019); https://doi.org/10.3389/fphy.2019.00048 * Bunyk, P. I. et al.
Architectural considerations in the design of a superconducting quantum annealing processor. _IEEE Trans. Appl. Superconductivity_ 24, 1–10 (2014). Google Scholar * Liers, F., Jünger, M.,
Reinelt, G. & Rinaldi, G. in _New Optimization Algorithms in Physics_ Vol. 4, 47–69 (Wiley, 2005). * Jünger, M. Spin glass server; https://informatik.uni-koeln.de/spinglass/ * Wang, F.
& Landau, D. P. Efficient, multiple-range random walk algorithm to calculate the density of states. _Phys.Rev. Lett._ 86, 2050–2053 (2001). Google Scholar Download references
ACKNOWLEDGEMENTS I.T. acknowledges support from NSERC. K.M. acknowledges support from Mitacs. We thank B. Krayenhoff for valuable discussions in the early stages of the project and thank M.
Bucyk for reviewing and editing the manuscript. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * 1QB Information Technologies (1QBit), Vancouver, British Columbia, Canada Kyle Mills & Pooya
Ronagh * University of Ontario Institute of Technology, Oshawa, Ontario, Canada Kyle Mills & Isaac Tamblyn * Vector Institute for Artificial Intelligence, Toronto, Ontario, Canada Kyle
Mills & Isaac Tamblyn * Institute for Quantum Computing (IQC), Waterloo, Ontario, Canada Pooya Ronagh * Department of Physics and Astronomy, University of Waterloo, Waterloo, Ontario,
Canada Pooya Ronagh * National Research Council Canada, Ottawa, Ontario, Canada Isaac Tamblyn Authors * Kyle Mills View author publications You can also search for this author inPubMed
Google Scholar * Pooya Ronagh View author publications You can also search for this author inPubMed Google Scholar * Isaac Tamblyn View author publications You can also search for this
author inPubMed Google Scholar CONTRIBUTIONS All authors contributed to the ideation and design of the research. K.M. developed and ran the computational experiments and wrote the initial
draft of the the manuscript. P.R. and I.T. jointly supervised this work and revised the manuscript. CORRESPONDING AUTHORS Correspondence to Kyle Mills, Pooya Ronagh or Isaac Tamblyn. ETHICS
DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in
published maps and institutional affiliations. RIGHTS AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Mills, K., Ronagh, P. & Tamblyn, I. Finding the ground
state of spin Hamiltonians with reinforcement learning. _Nat Mach Intell_ 2, 509–517 (2020). https://doi.org/10.1038/s42256-020-0226-x Download citation * Received: 04 March 2020 *
Accepted: 05 August 2020 * Published: 07 September 2020 * Issue Date: September 2020 * DOI: https://doi.org/10.1038/s42256-020-0226-x SHARE THIS ARTICLE Anyone you share the following link
with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt
content-sharing initiative