ABSTRACT Rapid ice loss is facilitated by sliding over beds consisting of reworked sediments and erosional products, commonly referred to as till. The dynamic interplay between ice and till

reshapes the bed, creating landforms preserved from past glaciations. Leveraging the imprint left by past glaciations as constraints for projecting future deglaciation is hindered by our

incomplete understanding of evolving basal slip. Here, we develop a continuum model of water-saturated, cohesive till to quantify the interplay between meltwater percolation and till

mobilization that governs changes in the depth of basal slip under fast-moving ice. Our model explains the puzzling variability of observed slip depths by relating localized till deformation

LARGE-SCALE BED WEAKENING IN GREENLAND Article 27 July 2022 ANTARCTIC BASAL ENVIRONMENT SHAPED BY HIGH-PRESSURE FLOW THROUGH A SUBGLACIAL RIVER SYSTEM Article 27 October 2022 THE IMPACT OF

GLACIERS ON MOUNTAIN EROSION Article 18 May 2021 INTRODUCTION The Intergovernmental Panel on Climate Change ascribes the largest uncertainty in future sea level rise to the ice dynamics of

our two ice sheets, Greenland and Antarctica1. Most of this uncertainty arises from specifying meaningful boundary conditions at both the base of the land ice and its seaward margins2. While

ice-ocean interactions have received considerable attention over recent years3,4,5, our ability to predict the evolution of basal conditions underneath the ice sheets remains limited. The

debate over the evolution of basal conditions is closely tied to the question of where basal slip is accommodated. The fast speed of the ice leaves little doubt that motion is facilitated

primarily by localized basal slip rather than distributed deformation inside the ice, but observations of where slip occurs provide conflicting evidence. Field observations range from basal

slip occurring almost exclusively at the ice-bed interface6,7, to partial slip at the ice-bed interface combined with shallow deformation within the upper portion of the till8,9, and deep

basal slip meters below the ice-bed interface10,11. Interestingly, the depth of basal slip can vary by several meters even at the same field site as in the case of Black Rapids Glacier,

Alaska9,10. Observations hence suggest that the depth of basal slip is a dynamic variable that evolves in time. The mechanical coupling between the ice and bed determines if till is

mobilized beneath the ice-bed interface12,13,14,15,16. Coupling could emerge, for example, from protruding clasts lodged in the basal ice that plough through the uppermost bed

sediment17,18,19,20,21,22, and from regelation infiltration incorporating the upper till bed into the basal ice through freeze-on23. The depth of basal slip in the till bed determines both

the rate and the volume of till transport, and directly influences the pace at which a glacier or ice stream reshapes its bed24,25,26,27. The landforms emerging from this reshaping process

alter ice motion and till deformation by locally changing the bed slopes, rerouting subglacial water28,29,30 and, potentially, creating barriers to ice transport31. Leveraging the

information imprinted in till and landforms deposited from past glaciations32,33 to inform models of current and future deglaciation, requires understanding the feedback between ice motion,

till deformation and water storage and drainage. The seemingly inconsistent observations of basal deformation across space and time mean that our understanding of the dominant subglacial

processes is incomplete, shedding doubt on the reliability of predictive models. The goal of this paper is to advance our fundamental understanding of the physical processes that contribute

to the dynamics of subglacial beds as reflected in existing, seemingly inconsistent observations of basal deformation. We hypothesize that the variability in observational evidence reflects

different dynamic regimes arising from the complex interplay between ice, melt-water and till in the subglacial environment. We test this hypothesis by deriving a continuum model for

water-saturated subglacial till that is consistent with laboratory measurements of a near-plastic till rheology16,34,35,36. Our model builds on recent advances in continuum descriptions of

dense, granular behavior by Henann and Kamrin37 and integrates it with progress in understanding the coupling of water flux through granular media at the scale of individual grains38,39,40.

THE GRANULAR MECHANICS OF COHESIVE, WATER-SATURED TILL Over the past two decades, many granular mechanics models have shifted towards statistical approaches41 and away from classical solid

mechanics42. The main advance provided by this line of thinking is the ability to represent non-local effects, which represent deformation in places where the granular medium is not strictly

at the yield stress but deforms due to interactions with failing patches nearby. These non-local interactions dominate deformation in granular shear zones43,44,45 such as those under

fast-moving ice. In the non-local granular fluidity (NGF) model by Henann and Kamrin37, a _fluidity_ field variable accounts for the non-local effects on deformation. Microscopically,

fluidity is related to velocity fluctuations in the granular medium46. The original non-local fluidity model accurately describes the strain distribution in a variety of experimental

settings37, but it assumes a dry, cohesionless granular medium. In the subglacial context, in-situ measurements document significant temporal variations in both water pressure and shear

strain rates6,8,10,47. These variations result from both internal till dynamics48 and external water input49, highlighting that meltwater is a crucial component of the overall dynamics. In

the current study, we capture the interplay between till strength and water percolation by incorporating effective stress and pore-pressure diffusion that depends on porosity and

permeability38,39. We also consider cohesion in subglacial tills, which tends to increase with clay content50, by adding a strength contribution from cohesion to the model. We refer to our

model as the cohesive non-local granular fluidity model with pore fluid (CNGF-PF). Contrary to the intense computational costs of our previous particle-scale model (e.g.51,52), the CNGF-PF

model is a continuum model that is sufficiently efficient to allow coupling to numerical ice-dynamics models. Following37, we assume that till is in the critical state throughout the domain,

implying that average porosity does not change as a function of granular deformation. The critical state assumption is likely justified, particularly underneath fast-moving ice16. To test

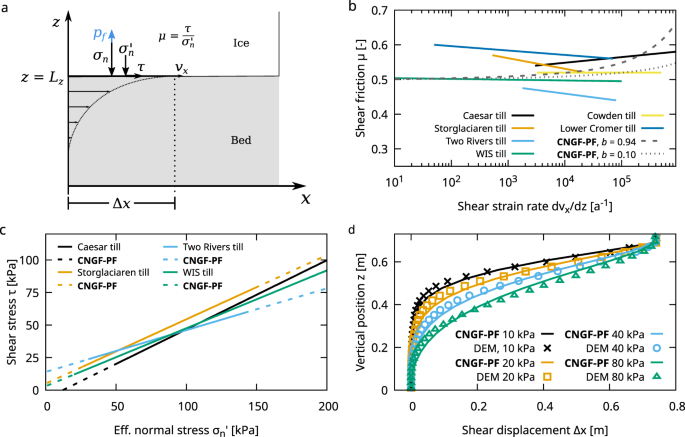
the ability of our model to reproduce the range of observed behavior in the field, we shear the modeled till with idealized boundary conditions that represent end members of the ice-bed

coupling (Fig. 1a). Speed-controlled conditions are typical for laboratory shear experiments, and represent a subglacial setting where changes in bed friction do not immediately alter the

ice flow velocity because the force balance includes other prominent terms such as topography or shear stress in the lateral margins. Specifically, the interfacial shear velocity at the base

may vary over time, but is not dependent on the local basal resistance contributed by subglacial friction. An example of this limit is Storglaciären Glacier, Sweden, where subglacial strain

rates and surface velocities are largely uncorrelated, at least at the place and time of measurement by Hooke et al.8. Similarly, the slip speed of several outlet glaciers in Greenland show

little sensitivity to variations in meltwater production53. In contrast, stress-controlled simulations approximate conditions where ice flow velocity responds to changes in subglacial

strain rate directly. Whillans Ice Stream, West Antarctica is an example of this setting, where a low surface slope and low driving stress results in stick-slip movement54. Evidently, most

real glacier settings shift along the spectrum spanned between the two limits, depending on how important basal friction is to the overall stress balance. RESULTS CONSISTENCY WITH LABORATORY

MEASUREMENTS AND GRANULAR-SCALE SIMULATIONS Before applying our model to field data, we validate it against laboratory measurements of the behavior of glacial till and DEM models. The

validation procedure relies on the effects of two non-dimensional parameters of the CNGF-PF model: _A_ scales the spatial extent of non-locality, and _b_ scales the weak rate dependence on

friction beyond yield. Natural glaciers systems show extremely variable strain rates of up to ~5 × 103 a−1. When studied over five orders of strain-rate magnitude (Fig. 1b), some tested

natural tills show slight rate weakening (Storglaciaren till, Two Rivers till, WIS till, Lower Cromer till), while others are slightly rate strengthening (Caesar till, Crowden till). Much

like the natural tills, our simulated till is effectively rate-independent over most of the range. At extreme shear-strain rates (Fig. 1b), higher values of _b_ provide larger frictional

resistance, leading to a slight hardening. Using published, rather than fitted, values of internal friction _μ_s and cohesion _C_, our model reproduces the Mohr-Coulomb behavior of tills

exactly34,35,36 (Fig. 1c). Laboratory constraints for the dimensionless non-locality parameter _A_ are not available, because we are not aware of any experiments that analyze the effect of

normal stress on the strain distribution in till. Instead, we compare the modeled strain distribution with discrete-element method results from51. By inserting relevant material parameters

for grain size, friction, stress, and shear velocity (DEM parameters in Supplementary Table 1), our model approximates the strain distribution well when _A_ = 0.5 (Fig. 1d), consistent with

models of deforming glass beads that used _A_ = 0.4837. Both models show that sediment transport is pressure dependent, with low effective normal stresses producing shallow deformation, and

high effective normal stresses deepening the deformation. Deep deformation leads to a higher sediment transport, because the entire sediment column above the shear zone is transported

downstream along with the ice movement. However, the DEM results required more than two months of computational time on a modern GPU, whereas the continuum model is completed in a fraction

of a second, albeit without details of individual particle kinematics and dynamical adjustment towards the critical state. We emphasize that a local-only granular model, such as

_μ_(_I_)55,56, does not include the effects of sediment texture (size, shape, and arrangement of grains) on shear-zone decay between actively flowing and stagnant parts of the bed. Comparing

Fig. 1d (NGF) with Supplementary Fig. 1 (_μ_(_I_)) demonstrates that the non-locality significantly contributes to shear strain distribution in a set of example shear tests, highlighting

the value of using a non-local rheology for the following analysis of subglacial deformation patterns. MELTWATER PULSES CAN LEAD TO DEEP SLIP IN SPEED-CONTROLLED SETTINGS To test the

hypothesis that meltwater input can alter the depth at which basal slip is concentrated, we impose daily sinusoidal variations in water pressure at the top of the model domain and simulate

pore-pressure diffusion and the resultant shear dynamics over seven days (Fig. 2a and Supplementary Fig. 2). The effective normal stress generally increases with depth due to increasing

weight of the overlying sediment. However, the time-variable input in meltwater at the ice-bed interface and its downward diffusion modulate the depth-dependence of deformation as well. Due

to diffusion, water pressure perturbations decay exponentially with depth, and travel with a phase shift (Fig. 2d inset). As a consequence, the distribution of water pressure can create

minima in effective normal stress at significant depth below the ice-bed interface, such that the effective stress profile locally reverses (Fig. 2d). Under speed-controlled conditions (Fig.

 2b, e), simulations show highly time-variable deformation patterns throughout the till. Granular failure and maximum shear deformation occur where the effective normal stress is at its

minimum, resulting in a plug-like motion of the sediment layer above the slip zone during reversal of the effective stress at depth. Deep deformation and plug-like till transport occurs

predominantly when the water pressure at the ice-bed interface is close to its minimum and rising. Under the same water-pressure forcing, the stress-controlled conditions (Fig. 2c, f)

produce a very different, dynamical pattern of deformation. Shear occurs almost exclusively in the uppermost part of the modeled till layer. The cyclic effective stress in combination with

the frictional properties of the till lead to stick-slip behavior, which is associated with dramatic variations in the shear speed (Fig. 2c). When water pressure at the top decreases and

effective stress increases, shear-strain rates decrease from the top and are maximal just below the ice-bed interface. When the effective stress at the top further increases, the shear

stress is insufficient to overcome even the minimal effective stress in the layer, and till deformation and transport stagnate. TILL FLUX IS CONTROLLED BY THE COUPLING AT THE ICE-TILL

INTERFACE In Fig. 3, we replot the simulations from Fig. 2 as time stacks to clarify the relationship between water pressure and stress, strain rate, and till flux. Under speed-controlled

conditions, the shear stress varies in an approximately linear manner as predicted for Mohr-Coulomb materials42, but with hysteresis at high effective normal stresses (Fig. 3a). Shear stress

is higher during deep shear because the lithostatic contribution increases effective normal stress and shear strength at depth. When driven by stress-controlled conditions, the simulated

water-sediment system shows stick-slip behavior with locally very high slip speeds and strong hysteresis (Fig. 3d). We emphasize that the specific values for the slip speed and till flux are

not realistic for a glacial setting. Far-field stresses such as lateral support from the margins57, which are not included in our model, are expected to restrain the high till shear speed,

and real ice-bed interfaces can transition from a stress-controlled to a speed-controlled configuration during slip. Under stress-controlled conditions, deformation occurs at shallow depth

with rapid slip when ice-bed interface when water pressures are at their highest magnitude (Figs. 2c, f and 3c). The trends in when and how much till transport occurs are therefore

drastically different for the two cases. The largest sediment transport under speed-controlled conditions occurs with transiently low water pressures and high effective normal-stresses at

the ice-bed interface (Fig. 3b). Instead, the majority of till transport under stress-controlled conditions occurs as shallow deformation during rapid slip events and high water pressures

(Fig. 3d). DEEP SLIP DEPENDS ON WATER-PRESSURE VARIATIONS AND TILL PERMEABILITY While the previous two sections shed light on the effect of meltwater pulses and the importance of the

boundary condition imposed at the till-ice interface, the occurrence of deep slip also depends sensitively on the hydraulic permeability of the till layer which can vary by orders of

magnitude. Here, we derive an analytical solution that can provide a quick order-of-magnitude estimate for the depth at which deep slip is expected to occur as a function of till

permeability and amplitude and frequency of the water pressure variations. The deepest deformation under speed-controlled conditions depend on the diffusion of pore-pressure perturbations

away from the ice-bed interface. The length-scale of pressure-perturbation decay due to diffusion is characterized by the skin depth _d_s [m]. Assuming that fluid and hydraulic skeleton

properties are constant and the layer is sufficiently thick: $${d}_{{\rm{s}}}=\sqrt{\frac{k}{(\alpha +{\beta }_{{\rm{f}}}\phi ){\eta }_{{\rm{f}}}\pi f}},$$ (1) where _k_ [m2] is the

hydraulic permeability, _α_ [Pa−1] is the grain-skeleton compressibility, _β_f [Pa−1] is the compressibility of water, _ϕ_ [-] is the porosity, _η_f [Pa s] is the dynamic viscosity of water,

and _f_ [s−1] is the frequency of the pore-pressure variations at the ice-bed interface. Figure 4a shows the skin depth for water at 0∘C under a range of permeabilities and water-pressure

forcing frequencies. Importantly, the deformation pattern depends sensitively on the distribution of effective stress and hence on the pressure-perturbation amplitude _A_f [m], which means

that the skin depth alone is insufficient to infer whether deep deformation occurs. We derive an analytical solution for diffusive pressure perturbation to find the largest depth beneath the

ice-bed interface where the effective stress is minimal over the course of a pressure-perturbation cycle (see Supplementary Note 2 for the full derivation). As the shear zone under

speed-controlled conditions follows the effective normal stress minimum, this depth corresponds to the deepest expected position of the shear zone midpoint, \(z^{\prime}\), during a cycle of

water-pressure forcing at the ice-bed interface: $$0=\sqrt{2}\sin \left(\frac{7\pi }{4}-\frac{z^{\prime} }{{d}_{{\rm{s}}}}\right)+\frac{({\rho }_{{\rm{s}}}-{\rho

}_{{\rm{f}}})G{d}_{{\rm{s}}}}{{A}_{{\rm{f}}}}\exp \left(\frac{z^{\prime} }{{d}_{{\rm{s}}}}\right),$$ (2) where _ρ_s and _ρ_f [kg m−3] is the till and water density, respectively, and _G_ [m

s−2] is the gravitational acceleration. The prediction of the analytical solution matches our simulations well (depth marked by dashed horizontal line in Fig. 2). We plot solutions to Eq.

(2) for various combinations of the water-pressure perturbation amplitude (_A_f), perturbation frequency (_f_), and permeability (_k_) in Fig. 4b and c. For a given pressure-perturbation

amplitude, deep deformation does not occur above a threshold value for the skin depth. Beneath this threshold, deformation quickly deepens to a substantial depth before gradually shallowing

at lower skin depth values. Our analysis hence suggests that deep deformation can occur in different tills. In high-permeability tills, deep deformation and till transport is facilitated by

rapid changes in water pressure, while transport of low-permeability tills are sensitive to longer, seasonal pressure variations. Larger water-pressure magnitudes facilitate deep deformation

at even higher till permeabilities and slower pressure perturbations. COMPARISON TO FIELD OBSERVATIONS Our model results demonstrate that deep slip in till occurs when remnant high water

pressures at depth overcome the effective lithostatic stress gradient. The depth of slip for deforming beds is hence dependent on several evolving parameters including ice thickness,

variability and magnitude in meltwater influx, and till properties. However, the key factor is the coupling at the ice-till interface or, in other words, the degree to which the slip speed

responds to in-situ changes in the interfacial shear stress. Interestingly, in natural systems, the degree of resistance provided by the interfacial shear stress varies widely from being an

almost negligible contribution to being the dominant term in the force balance57. The coupling could also change and, in fact, is likely to change over the course of a deglaciation or a

glacial cycle. The ice streams of the Siple Coast, West Antarctica, provide an interesting example in this context. While observations indicate that present till fluxes are small (<40

m3m−1a−158), large sedimentary grounding-zone wedges on the continental shelf appear to have formed rapidly, suggesting a significantly greater till flux (1.4 × 103 m3m−1a−1) during and

immediately after the last glacial maximum59. We conceptualize the contemporary Whillans Ice Stream at the Siple Coast as a stress-controlled setting, which is consistent with its current

stick-slip behavior54. Stress-controlled subglacial deformation results in shallow shear below the ice-bed interface (Figs. 1d and 2c). The shallow till deformation at the ice-till interface

produces relatively small till fluxes, which is consistent with modern observations58. During the last glacial maximum, however, the ice thickness in the Ross Sea was larger than today and

likely characterized by greater surface slopes. Both factors increase driving stress, suggesting that lateral stresses in the margin could have played a more important role in the force

balance of the ice stream than they do today, at least given comparable till properties underneath. Therefore, the ice-till interface during the last glacial maximum could have resembled

speed-controlled conditions more closely. A speed-controlled simulation produces shallow shear if the subglacial water pressure is steady (till parameters in Supplementary Table 1). Daily or

weekly variations in ice-bed interface water pressures are too frequent to create significant perturbations in the low-permeability till underneath Whillans Ice Stream, but variations of

approximately 50 kPa on the monthly, annual, or decadal time scale can transiently deepen shear deformation to 0.2, 0.6, and 1.3 m, respectively, greatly enhancing till transport. Such

longer-term variations, mainly driven from internal dynamics, have been observed both locally by in-situ borehole measurements60, and inferred over larger areas by remote sensing61, and are

to be expected in particular during ice advance and retreat. In our idealized analysis, we do not explicitly account for ice-bed interface physics of ploughing and regelation infiltration

that can influence till flux during shallow slip20,21,22. However, we demonstrate that hydraulic variability has the potential to greatly increase subglacial till flux through deep seated

deformation, which could contribute to rapid changes in sediment transport and the pace of landform development at the grounding zone. While we focus on depth-variability in deformation,

horizontal variations are likely to arise as well62, particularly if subglacial water transport is heterogeneously distributed in space. The interplay between water pressure fluctuations and

sediment mobilization together with a shift in the relative importance of basal strength could reconcile the conflicting observations of small till flux today with drastically larger fluxes

under past glacial configurations. Another interesting and observationally better constrained field site is Black Rapids Glacier, a contemporary mountain glacier in the central Alaska

Range. A transition in the coupling at the ice-till interface was observed in between field campaigns at Black Rapids Glacier that were only a few years apart. The till bed of Black Rapids

Glacier was probed by in-situ borehole measurements repeatedly9,10. During the earlier field campaign in 199710, basal hydrology and deformation did not significantly correlate with

ice-surface displacement, suggesting that the subglacial bed can be approximated by speed-controlled conditions. Assuming a diffusivity of 1.5 × 10−5 m2 s−1, water-pressure perturbations of

approximately 1 MPa, and a forcing period of 1 month10, we estimate the maximum deformation depth with Eq. (2) to be on the order of \(z^{\prime} =7.2\) m. This result is in broad agreement

with observations that ice slip resulted from till deformation at an undetermined depth of more than 2 m below the ice-bed interface10. Our model suggests that significant volumes of till

would be transported in this limit, because the entire till layer above the deep slip zone is mobilized. In contrast, later measurements at the same location on Black Rapids Glacier in 20029

showed that sliding occurred partially at the ice-till interface itself and partly at shallow depth within the till layer. The glacier geometry and flow remained largely unchanged between

the two field campaigns, but the recorded water-pressure variations were smaller in 2002. Our model framework reconciles these seemingly contradictory observations, because it clarifies the

role of varying pore-water pressure amplitude in shifting the depth of basal slip away from ice-till interface and deep into the till layer itself. Our analysis highlights the value of

continuous instrumentation of field sites9,10,47,60, because it suggests that the observed, large variability is an inherent property of the ice-meltwater-till system. As a consequence,

measurements performed at a single point in time do not always provide sufficient constraints to assess the evolution of basal slip and till transport over longer time scales. Similarly, our

results highlight the importance of not reducing the dynamics of the subglacial environment only to subglacial hydrology. While subglacial hydrology is important30, the effect it has on ice

speed and the depth of basal slip depends sensitively on the coupling at the ice-till interface. This insight could be relevant for understanding the distinct but variable response of

glaciers to seasonal water input53 and to climate forcing more generally. We emphasize that the motivation for providing a comparison between a highly idealized model and field observations

is to demonstrate the explanatory potential of the model we have derived. There is no doubt that any actual field setting is characterized by significantly more complexity than considered

here. Nonetheless, we argue that it is valuable to test how much of the observed variability can be reproduced within a relatively simple, unifying framework, where the complex coupling

between ice, till and water is not confounded by additional factors such as topography, ice-ocean interactions, and hydrological processes to only name a few. To conclude, we note that a

key, general outcome of our analysis is the understanding and recognition that contrasting field observations of basal behavior do not necessarily indicate different basal physics. Instead,

variability in till dynamics and flux could reflect the natural temporal and spatial variability in the effective stress conditions within the till due to changes in ice overburden and

meltwater percolation. Importantly, our modeling framework provides an opportunity to further refine these insights, because it is computationally cheap and adjustable to various grid

setups, making it conducive to integration with large-scale ice sheet models. METHODS MODEL FORMULATION Subglacial tills are saturated by meltwater and often have significant cohesion from

clay minerals. To generalize the existing non-local, granular fluidity (NGF) model by37 to subglacial till (original model detail listed in Supplementary Note 1), we allow pore pressure to

perturb the stress distribution in the sediment, and add the contribution of cohesion to shear strength. The extended model is named the cohesive NGF pore fluid (CNGF-PF) model. Typical

shear-strain magnitudes in subglacial tills are  >>116, so we neglect the elastic contribution to shear strain rate (\(\dot{\gamma }={\dot{\gamma }}^{{\rm{p}}}\) [s−1]). The transient

evolution of pore-fluid pressure (_p_f [Pa]) is modeled through Darcian pressure diffusion38,39: $$\frac{\partial {p}_{{\rm{f}}}}{\partial t}=\frac{1}{{\eta }_{{\rm{f}}}(\alpha +\phi {\beta

}_{{\rm{f}}})}\nabla \cdot (k\nabla {p}_{{\rm{f}}}).$$ (3) When comparing our model to published results of hydraulic diffusivity _D_ [m2 s−1], the right-hand side of Eq. (3) is _D_∇2_p_f.

In the granular phase, we use the effective normal stress \(\sigma ^{\prime} ={\sigma }_{{\rm{n}}}-{p}_{{\rm{f}}}\) [Pa] instead of the dry normal stress _σ_n. We further add a cohesion

contribution _C_ [Pa] to the shear strength in the cooperativity length, _ξ_, in37: $$\xi (\mu )=\frac{Ad}{\sqrt{| (\mu -C/\sigma ^{\prime} )-{\mu }_{{\rm{s}}}| }},$$ (4) and in the local

fluidity term, _g_local: $${g}_{{\rm{local}}}(\mu ,\sigma ^{\prime} )=\left\{\begin{array}{ll}\sqrt{{d}^{2}\sigma ^{\prime} /{\rho }_{{\rm{s}}}}((\mu -C/\sigma ^{\prime} )-{\mu

}_{{\rm{s}}})/(b\mu )&{\rm{if}}\ \mu -C/\sigma ^{\prime}\, > \, {\mu }_{{\rm{s}}}{\rm{,}}\ {\rm{and}}\\ 0\hfill &{\rm{if}}\ \mu -C/\sigma ^{\prime}\, \le\, {\mu

}_{{\rm{s}}}.\hfill\end{array}\right.$$ (5) The fluidity field is solved in the same manner as the original model37. SIMULATION SETUP We apply the model in a one-dimensional setup with

simple shear (Fig. 1a) of length _L__z_. The upper normal stress (i.e. the ice weight, _σ_n(_z_ = _L__z_)) is constant, and normal stress linearly increases with depth due to sediment

weight. In the stress-controlled experiments, the upper boundary (i.e. the ice-bed interface) applies a fixed shear stress _τ_ on the till. In speed-controlled experiments, the upper

boundary moves with a fixed shear velocity _v__x_(_z_ = _L__z_). For all simulations, the lower boundary condition for the granular phase is no slip (_v__x_(_L_ = 0) = 0). Effective normal

stress (\(\sigma ^{\prime} ={\sigma }_{{\rm{n}}}-{p}_{{\rm{f}}}\)) varies if the water pressure _p_f changes (Eq. (3)). For the water-pressure solver, the top pressure (_p_f(_z_ = _L__z_))

is either constant or varies through time. For the experiments with variable water pressure, we apply a water-pressure forcing amplitude of _A_f = 80 kPa that modulates effective normal

stress at the top around 100 kPa. At the start of each simulation, water pressure is set to follow the hydrostatic gradient at the lower boundary (_d__p_f/_d__z_(_z_ = 0) = _ρ_f_G_). Unless

noted, we use the value 0.94 for the dimensionless rate-dependence parameter _b_, which is empirically constrained from laboratory experiments on glass beads63. We solve the model components

iteratively as detailed in the Supplementary Note 1 with specific parameter values listed in Supplementary Table 1. A parameter sensitivity test is provided in Supplementary Note 3 and

Supplementary Fig. 3. DATA AVAILABILITY No datasets were generated or analyzed during the current study. CODE AVAILABILITY The grain-water model is written in C and is available under

free-software licensing at https://src.adamsgaard.dk/cngf-pf (permanently archived at doi:10.5281/zenodo.4106566). Run "man cngf-pf” after installing for usage information. The results

and figures in this paper can be reproduced by following the instructions in the experiment repository for this publication, available at https://src.adamsgaard.dk/cngf-pf-exp1 (permanently

archived at doi:10.5281/zenodo.4106575). REFERENCES * Church, J. A. et al. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of

the Intergovernmental Panel on Climate Change, chap. Sea level change, 1139–1216 (Cambridge University Press, 2013). * Vaughan, D. G. & Arthern, R. Why is it hard to predict the future

of ice sheets? _Science_ 315, 1503–1504 (2007). Article  CAS  Google Scholar  * Rignot, E., Jacobs, S., Mouginot, J. & Scheuchl, B. Ice-shelf melting around Antarctica. _Science_ 341,

266–270 (2013). Article  CAS  Google Scholar  * Pollard, D., DeConto, R. M. & Alley, R. B. Potential Antarctic Ice Sheet retreat driven by hydrofracturing and ice cliff failure. _Earth

Planet. Sci. Lett._ 412, 112–121 (2015). Article  CAS  Google Scholar  * Alley, R. B. et al. Oceanic forcing of ice-sheet retreat: West Antarctica and more. _Ann. Rev. Earth Planet. Sci._

43, 207–231 (2015). Article  CAS  Google Scholar  * Engelhardt, H. & Kamb, B. Basal sliding of ice stream B, West Antarctica. _J. Glaciol._ 44, 223–230 (1998). Article  Google Scholar  *

Engelhardt, H., Humphrey, N., Kamb, B. & Fahnestock, M. Physical conditions at the base of a fast moving Antarctic ice stream. _Science_ 248, 57–59 (1990). Article  CAS  Google Scholar

  * Hooke, R. L., Hanson, B., Iverson, N. R., Jansson, P. & Fischer, U. H. Rheology of till beneath Storglaciären, Sweden. _J. Glaciol._ 43, 172–179 (1997). Article  Google Scholar  *

Truffer, M. & Harrison, W. D. In situ measurements of till deformation and water pressure. _J. Glaciol._ 52, 175–182 (2006). Article  Google Scholar  * Truffer, M., Harrison, W. D. &

Echelmeyer, K. A. Glacier motion dominated by processes deep in underlying till. _J. Glaciol._ 46, 213–221 (2000). Article  Google Scholar  * Kjær, K. H. et al. Subglacial decoupling at the

sediment/bedrock interface: a new mechanism for rapid flowing ice. _Quat. Sci. Rev._ 25, 2704–2712 (2006). Article  Google Scholar  * Iverson, N. R., Hanson, B., Hooke, R. L. & Jansson,

P. Flow mechanism of glaciers on soft beds. _Science_ 267, 80–81 (1995). Article  CAS  Google Scholar  * Fischer, U. H. & Clarke, G. K. C. Stick-slip sliding behaviour at the base of a

glacier. _Ann. Glaciol._ 24, 390–396 (1997). Article  Google Scholar  * Boulton, G. S., Dobbie, K. E. & Zatsepin, S. Sediment deformation beneath glaciers and its coupling to the

subglacial hydraulic system. _Quatern. Int._ 86, 3–28 (2001). Article  Google Scholar  * Mair, D. et al. Hydrological controls on patterns of surface, internal and basal motion during three

"spring events”: Haut Glacier d’Arolla, Switzerland. _J. Glaciol._ 49, 555–567 (2003). Article  Google Scholar  * Iverson, N. R. Shear resistance and continuity of subglacial till:

hydrology rules. _J. Glaciol._ 56, 1104–1114 (2010). Article  Google Scholar  * Tulaczyk, S. M., Sherer, R. P. & Clark, C. D. A ploughing model for the origin of weak tills beneath ice

streams: a qualitative treatment. _Quatern. Int._ 86, 59–70 (2001). Article  Google Scholar  * Fischer, U. H. & Clarke, G. K. C. Review of subglacial hydro-mechanical coupling: Trapridge

glacier, Yukon Territory, Canada. _Quatern. Int._ 86, 29–43 (2001). Article  Google Scholar  * Iverson, N. R. et al. Effects of basal debris on glacier flow. _Science_ 301, 81–84 (2003).

Article  CAS  Google Scholar  * Iverson, N. R. & Hooyer, T. S. Estimating the sliding velocity of a Pleistocene ice sheet from plowing structures in the geologic record. _J. Geophys.

Res_. 109, F04006 (2004). Article  Google Scholar  * Thomason, J. F. & Iverson, N. R. A laboratory study of particle ploughing and pore-pressure feedback: a velocity-weakening mechanism

for soft glacier beds. _J. Glaciol._ 54, 169–181 (2008). Article  Google Scholar  * Zoet, L. K. & Iverson, N. R. A slip law for glaciers on deformable beds. _Science_ 368, 76–78 (2020).

Article  CAS  Google Scholar  * Iverson, N. R. et al. Soft-bed experiments beneath Engabreen, Norway: regelation infiltration, basal slip and bed deformation. _J. Glaciol._ 53, 323–340

(2007). Article  Google Scholar  * Hindmarsh, R. C. A. The stability of a viscous till sheet coupled with ice flow, considered at wavelengths less than the ice thickness. _J. Glaciol._ 44,

285–292 (1998). Article  Google Scholar  * Alley, R. B. Continuity comes first: recent progress in understanding subglacial deformation. _Geol. Soc. London_ 176, 171–179 (2000). Article 

Google Scholar  * Fowler, A. C. An instability mechanism for drumlin formation. _Geol. Soc. London_ 176, 307–319 (2000). Article  Google Scholar  * Schoof, C. Pressure-dependent viscosity

and interfacial instability in coupled ice–sediment flow. _J. Fluid Mech._ 570, 227–252 (2007). Article  Google Scholar  * Walder, J. S. & Fowler, A. Channelized subglacial drainage over

a deformable bed. _J. Glaciol_. 40, 3–15 (1994). Article  Google Scholar  * Kyrke-Smith, T. M. & Fowler, A. C. Subglacial swamps. _Proc. R. Soc. A_ 470, 20140340 (2014). Article  CAS 

Google Scholar  * Flowers, G. E. Modelling water flow under glaciers and ice sheets. _P. R. Soc. A_ 471, 20140907 (2015). Article  Google Scholar  * Alley, R. B., Anandakrishnan, S., Dupont,

T. K., Parizek, B. R. & Pollard, D. Effect of sedimentation on ice-sheet grounding-line stability. _Science_ 315, 1838–1841 (2007). Article  CAS  Google Scholar  * Larsen, N. K.,

Piotrowski, J. A. & Kronborg, C. A multiproxy study of a basal till: a time-transgressive accretion and deformation hypothesis. _J. Quaternary Sci._ 19, 9–21 (2004). Article  Google

Scholar  * Spagnolo, M. et al. Ice stream motion facilitated by a shallow-deforming and accreting bed. _Nat. Commun_. 7, 3–15 (2016). Article  CAS  Google Scholar  * Iverson, N. R., Hooyer,

T. S. & Baker, R. W. Ring-shear studies of till deformation: Coulomb-plastic behavior and distributed strain in glacier beds. _J. Glaciol._ 148, 634–642 (1998). Article  Google Scholar 

* Tulaczyk, S., Kamb, W. B. & Engelhardt, H. F. Basal mechanics of ice stream B, West Antarctica i. Till mechanics. _J. Geophys. Res._ 105, 463–481 (2000). Article  Google Scholar  *

Rathbun, A. P., Marone, C., Alley, R. B. & Anandakrishnan, S. Laboratory study of the frictional rheology of sheared till. _J. Geophys. Res._ 113, F02020 (2008). Article  Google Scholar

  * Henann, D. L. & Kamrin, K. A predictive, size-dependent continuum model for dense granular flows. _Proc. Nat. Acad. Sci. USA_ 110, 6730–6735 (2013). Article  CAS  Google Scholar  *

Goren, L., Aharonov, E., Sparks, D. & Toussaint, R. The mechanical coupling of fluid-filled granular material under shear. _Pure. Appl. Geophys._ 168, 2289–2323 (2011). Article  Google

Scholar  * Damsgaard, A. et al. A new methodology to simulate subglacial deformation of water-saturated granular material. _Cryosphere_ 9, 2183–2200 (2015). Article  Google Scholar  *

Damsgaard, A. et al. Ice flow dynamics forced by water pressure variations in subglacial granular beds. _Geophys. Res. Lett._ 43, 12165–12173 (2016). Article  Google Scholar  * Jaeger, H.

M., Nagel, S. R. & Behringer, R. P. Granular solids, liquids, and gases. _Rev. Mod. Phys._ 68, 1259–1273 (1996). Article  Google Scholar  * Schofield, A. N. & Wroth, P.Critical State

Soil Mechanics (McGraw-Hill London, 1968). * Nedderman, R. M. & Laohakul, C. The thickness of the shear zone of flowing granular materials. _Powder Technol._ 25, 91–100 (1980). Article

  CAS  Google Scholar  * Forterre, Y. & Pouliquen, O. Flows of dense granular media. _Ann. Rev. Fluid Mech._ 40, 1–24 (2008). Article  Google Scholar  * Kamrin, K. Quantitative

Rheological Model for Granular Materials: The Importance of Particle Size. In _Handbook of Materials Modeling_, 1–24 (Springer International Publishing, 2018). * Zhang, Q. & Kamrin, K.

Microscopic description of the granular fluidity field in nonlocal flow modeling. _Phys. Rev. Lett._ 118, 058001 (2017). Article  Google Scholar  * Hart, J. K. et al. Surface melt driven

summer diurnal and winter multi-day stick-slip motion and till sedimentology. _Nat. Commun._ 10, 1–11 (2019). Article  CAS  Google Scholar  * Moore, P. L. & Iverson, N. R. Slow episodic

shear of granular materials regulated by dilatant strengthening. _Geology_ 30, 843–846 (2002). Article  Google Scholar  * Andrews, L. C. et al. Direct observations of evolving subglacial

drainage beneath the Greenland Ice Sheet. _Nature_ 514, 80–83 (2014). Article  CAS  Google Scholar  * Iverson, N. R., Baker, R. W. & Hooyer, T. S. A ring-shear device for the study of

till deformation: tests on tills with contrasting clay contents. _Quat. Sci. Rev._ 16, 1057–1066 (1997). Article  Google Scholar  * Damsgaard, A. et al. Discrete element modeling of

subglacial sediment deformation. _J. Geophys. Res. Earth Surf._ 118, 2230–2242 (2013). Article  Google Scholar  * Damsgaard, A., Cabrales-Vargas, A., Suckale, J. & Goren, L. The coupled

dynamics of meltwater percolation and granular deformation in the sediment layer underlying parts of the big ice sheets. In _Poromechanics VI_ (Am. Soc. Civ. Eng., 2017). * Moon, T. et al.

Distinct patterns of seasonal Greenland glacier velocity. _Geophys. Res. Lett._ 41, 7209–7216 (2014). Article  Google Scholar  * Bindschadler, R. A., King, M. A., Alley, R. B.,

Anandakrishnan, S. & Padman, L. Tidally controlled stick-slip discharge of a West Antarctic ice stream. _Science_ 301, 1087–1089 (2003). Article  CAS  Google Scholar  * GDR-MiDi. On

dense granular flows. _Eur. Phys. J._ 14, 341–365 (2004). * da Cruz, F., Emam, S., Prochnow, M., Roux, J.-N. & Chevoir, F. Rheophysics of dense granular materials: discrete simulation of

plane shear flows. _Phys. Rev. E_ 72, 021309 (2005). * Raymond, C. F. Energy balance of ice streams. _J. Glaciol._ 46, 665–674 (2000). Article  Google Scholar  * Hodson, T. O. et al.

Physical processes in Subglacial Lake Whillans, West Antarctica: Inferences from sediment cores. _Earth Planet. Sc. Lett._ 444, 56–63 (2016). Article  CAS  Google Scholar  * Bart, P. J.,

Krogmeier, B. J., Bart, M. P. & Tulaczyk, S. The paradox of a long grounding during West Antarctic Ice Sheet retreat in Ross Sea. _Sci. Rep._ 7, 1–8 (2017). * Engelhardt, H. & Kamb,

B. Basal hydraulic system of a West Antarctic ice stream: constraints from borehole observations. _J. Glaciol._ 43, 207–230 (1997). Article  Google Scholar  * Fricker, H. A., Scambos, T.,

Bindschadler, R. & Padman, L. An active subglacial water system in West Antarctica mapped from space. _Science_ 315, 1544–1548 (2007). Article  CAS  Google Scholar  * Piotrowski, J. A.,

Larsen, N. K. & Junge, F. W. Reflections on soft subglacial beds as a mosaic of deforming and stable spots. _Quat. Sci. Rev._ 23, 993–1000 (2004). Article  Google Scholar  * Forterre, Y.

& Pouliquen, O. Long-surface-wave instability in dense granular flows. _J. Fluid Mech._ 486, 21–50 (2003). Article  Google Scholar  * Tika, T. E., Vaughan, P. R. & Lemos, L. J. L.

J. Fast shearing of pre-existing shear zones in soil. _Géotechnique_ 46, 197–233 (1996). Article  Google Scholar  Download references ACKNOWLEDGEMENTS This research was supported by the

National Science Foundation through the Office of Polar Programs awards PLR-1744758 and by the U. S. Army Research Laboratory under grant W911NF-12-R0012-04. AUTHOR INFORMATION AUTHORS AND

AFFILIATIONS * Department of Geophysics, Stanford University, 397 Panama Mall, Stanford, CA, 94305, USA Anders Damsgaard & Jenny Suckale * Department of Geoscience, Aarhus University,

Høegh-Guldbergs Gade 2, 8000, Aarhus C, Denmark Anders Damsgaard * Department of Earth and Environmental Sciences, Ben-Gurion University of the Negev, P.O.B. 653, Beer-Sheva, 84105, Israel

Liran Goren * Department of Civil and Environmental Engineering, Stanford University, 473 Via Ortega, Stanford, CA, 94305, USA Jenny Suckale * Institute for Computational and Mathematical

Engineering, Stanford University, 475 Via Ortega, Stanford, CA, 94305, USA Jenny Suckale Authors * Anders Damsgaard View author publications You can also search for this author inPubMed 

Google Scholar * Liran Goren View author publications You can also search for this author inPubMed Google Scholar * Jenny Suckale View author publications You can also search for this author

inPubMed Google Scholar CONTRIBUTIONS The authors are listed in sequence of their contribution. A.D. developed the numerical code, performed the simulations and produced the figures; J.S.

conceptualized the study; L.G. derived the analytical solution; All authors contributed to research design and to the text. CORRESPONDING AUTHOR Correspondence to Jenny Suckale. ETHICS

DECLARATIONS COMPETING INTERESTS All authors declare no competing interests. ADDITIONAL INFORMATION PEER REVIEW INFORMATION Primary handling editor: Joseph Aslin. PUBLISHER’S NOTE Springer

Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION PEER REVIEW FILE RIGHTS AND

PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any

medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The

images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not

included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly

from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Damsgaard, A.,

Goren, L. & Suckale, J. Water pressure fluctuations control variability in sediment flux and slip dynamics beneath glaciers and ice streams. _Commun Earth Environ_ 1, 66 (2020).

https://doi.org/10.1038/s43247-020-00074-7 Download citation * Received: 25 April 2020 * Accepted: 13 November 2020 * Published: 18 December 2020 * DOI:

https://doi.org/10.1038/s43247-020-00074-7 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative