ABSTRACT In recent years, spiking neural networks were introduced in science as the third generation of artificial neural networks leading to a tremendous energy saving on neuromorphic

processors. This sustainable effect is due to the sparse nature of signal processing in-between spiking neurons leading to much less scalar multiplications as in second-generation networks.

The spiking neuron’s efficiency is even more pronounced by their inherently recurrent nature being useful for recursive function approximations. We believe that there is a need for a general

regression framework for SNNs to explore the high potential of neuromorphic computations. However, besides many classification studies with SNNs in the literature, nonlinear neuromorphic

Legrendre Memory Units are introduced in the neuromorphic architecture. Path-dependencies and evolutions of signals can be tackled in this way. Furthermore, interfaces between real physical

and binary spiking values are necessary. Following this intention, a hybrid approach is introduced, exhibiting an autoencoding strategy between dense and spiking layers. However, to verify

the presented framework of nonlinear regression for a wide spectrum of scientific purposes, we see the need for obtaining realistic complex transient short-time signals by an extensive

experimental set-up. Hence, a measurement technique for benchmark experiments is proposed with high-frequency oscillations measured by capacitive and piezoelectric sensors resulting in wave

propagations and inelastic solid deformations to be predicted by the developed SNN regression analysis. Hence, the proposed nonlinear regression framework can be deployed to a wide range of

scientific and technical applications. SIMILAR CONTENT BEING VIEWED BY OTHERS DEEP LEARNING INCORPORATING BIOLOGICALLY INSPIRED NEURAL DYNAMICS AND IN-MEMORY COMPUTING Article 15 June 2020

FNS ALLOWS EFFICIENT EVENT-DRIVEN SPIKING NEURAL NETWORK SIMULATIONS BASED ON A NEURON MODEL SUPPORTING SPIKE LATENCY Article Open access 09 June 2021 A BIOMIMETIC NEURAL ENCODER FOR SPIKING

NEURAL NETWORK Article Open access 09 April 2021 INTRODUCTION The pioneering work of neuromorphic computing was described in1 following another strategy of chip architecture as in the case

of von-Neumann computer processors. Neuromorphic chips are regarded to be brain-inspired leading to a different signal processing as in the case of CPU/GPU chips. Due to their sparse nature,

spiking neurons outperform forward and backward passes through a neuromorphic network with much less energy than von-Neumann chips. Moreover, spiking neural networks (SNN) are inherently

recurrent and parallel2 leading to the possibility of performing mathematical operations simultaneously and recursively. SNNs are known as neural networks of the third generation to be

implemented on neuromorphic architecture resulting in low-power operations3 compared to traditional artificial neural networks (ANN) of the second generation. These ANNs of 2_n__d_

generations have been successfully explored for a wide range of scientific purposes such as uncertainty quantification4,5, fluid6,7,8,9 and solid mechanics10,11, biomechanics and

mechanobiology12 with applications in biomedicine13,14,15,16,17. Targeting especially nonlinear regression tasks, ANNs can be developed successfully from the mathematical point of view for

solving nonlinear differential equations with a physical application (e.g. material modeling)18,19,20,21,22,23,24,25,26,27. However, even though promising new possibilities for regression

tasks are offered by neuromorphic architectures, they were mostly applied to classification problems and hardly to function approximation28. ANNs of the second generation have been

successfully implemented in nonlinear regression but several computational bottlenecks arise as a result of their use, such as high memory access for model initialization, access latency,

and throughput29 leading to an increased demand for computational resources. These ANN attributes are due to the suboptimal nature of matrix multiplication depending on data communication

and memory. However, human brains perform classification tasks such as image recognition and natural language processing30,31 with significantly less energy31,32 and incorporating discrete

signals to communicate with each other. Neuromorphic chips being analog, digital, or mixed comprise small units mimicking the neurons in the brain such as Loihi33, SpiNNaker34, and

SynSense35. Information processing is only active when spikes appear otherwise the synaptic weights and memory remain inaccessible leading to the significant reduction in the consumption of

energy33,36,37. SNNs have been already deployed for tasks such as image processing38, image-recognition39, image segmentation40 and localization41, however, they find limited applications in

the field of nonlinear regression42,43. For the above-described reasons, we see the need for a non-linear regression framework for SNN architectures with fundamental formulations of signal

processing being applicable for a wide range of applications in computer science, Engineering, and Natural Science. Following this line of reasoning, we start with recurrent spiking

propagation with all hurdles discontinuous signals cause and yield basic formulation for function approximations. However, due to the vision of creating a most general mathematical

expression of implicit functional dependencies such as time and path dependency, additional memory access is provided by Legendre Memory Units (LMU)44 in a spiking variant. In comparison to

Long-Short-Term-Memory (LSTM) cells, the LMU principle exhibits the advantage of providing additional memory to the network without increasing the number of hidden neurons. One essential

part of SNN regression modeling is to develop an interface between physical real-valued signals and spike representations. For this reason, an autoencoding strategy is proposed, allowing the

first recurrent spiking layer to translate input signals to spike trains and vice versa at the output layer. In the present study, a framework is introduced to compute nonlinear regression

with SNNs to predict nonlinear path-dependent solid deformations and wave propagation phenomena based on short-time measurement signals. Furthermore, we extend the energy-efficient

communication of spiking neurons to a spiking variant of Legendre Memory Unit (LMU)44 to increase the memory capacity of the network. This leads to a framework to adapt the real-valued

mechanical signals to spikes and assess the performance for path-dependent nonlinear regression. The proposed LMU cell is independent of the number of neurons in the LMU layer, hence, the

required capacity to store nonlinear evolutions of path-dependent state variables is generated implicitly. The proposed SNNs when deployed on neuromorphic hardware lead to energy-efficient

computation and sustainable AI of physical problems. Motivated by this opportunity, we introduce a nonlinear regression framework for mechanical structural response. Further, the spiking

mechanism introduces brain-inspired regularisation that gouverns the learning abilities of the SNNs. The present approach is developed in a general way by proposing an autoencoding strategy

that is not restricted to a limited number of input neurons. If a neuromorphic processor e.g. such as SynSense Xylo-Av245,46,47 is used with a fixed number of input signals in the first

layer and a regression problem inhibits even more inputs, then the autoencoding behaves as a mapping function reducing the dimensionality of the input features that can be deployed on the

chip. Furthermore, from the mechanical point of view, as general as possible structural deformations are chosen which inhibit several properties during one deformation process such as

plasticity, strain-rate sensitivity, and short-time dynamics. The finally developed SNN topology will be trained by transient high-frequency signals belonging to short-time measurement

devices. Furthermore, the prediction capabilities of the network will be explored with additional data for validation. The signal history is obtained by capacitive and piezoelectric

measurement techniques allowing to record time- and path-dependent physical values for both electronic circuits and oscillating waves in solids48,49. RESULTS DATA PREPARATION AND PRINCIPLE

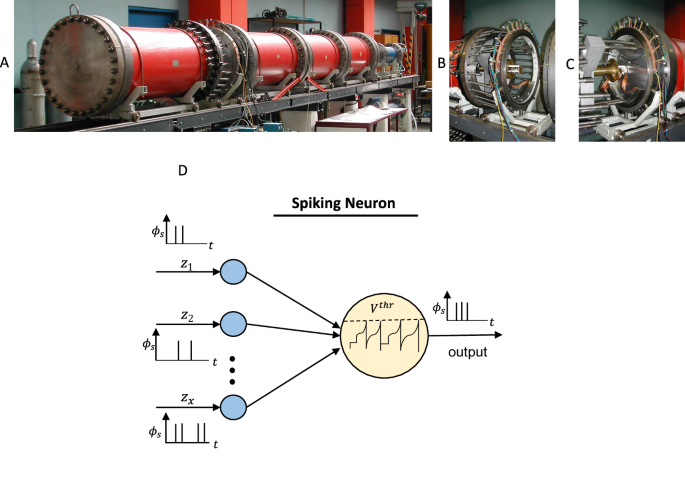
OF SIGNAL PROCESSING A compact summary of our study and its results is summarised in Figs. 1, 2 composed of an experimental set-up10 for data generation, the spike train principle, and a

comparison between recorded and calculated signals using second and third-generation neural networks. During a shock-wave propagation in the shock tube in Fig. 1A, a capacitive short-time

measurement technique (see Fig. 1B, C) records the deformation history of a thin plate while piezoelectric devices mounted next to this plate record the pressure evolution. The experiments

were carried out in10,48,49. In a further step, a crucial part of SNN regression starts, since these obtained real-valued physical signals have to undergo an encoding principle to be

transformed into binary signals. In the present study, an autoencoding strategy is developed which is discussed during the following presentations. However, all signals during non-linear

regression have to be composed out of spike strains as shown in Fig. 1D for a single neuron receiving spike signals of input variables _z__i_ and firing one spike train to a neighboring

neuron. In the neuron, a time-dependent evolution of the voltage is indicated by _t_, while _V__t__h__r_ denotes the threshold voltage. Each incoming spike causes a sudden step in the

neuron’s voltage. Once the threshold voltage is reached in the spiking neuron, the voltage drops to zero accompanied by an output of spike trains. The exact composition of spike trains and

their mathematical expression for regression analysis are discussed in the next subsections. The spikes themselves are denoted by Φ_s_ taking binary values. However, what turns out by this

illustration immediately is that the spiking neurons behave inherently time-dependent and that offers a great benefit for path-dependent regression analysis. Here, it is not necessary to

introduce recurrent neurons as it is done in the second-generation counterpart, but recursive processes are always included in the time evolution of spiking signal processing. We come back

to this fact in the mathematical development of the entire SNN. The evolution of pressure and deformation signals, measured during the shock wave duration representing non-harmonic transient

functions, are illustrated in Fig. 2. Furthermore, results obtained with trained networks (Fig. 2A) of the second and third kinds are shown, while the pressure, wave propagation speed, and

specimen’s properties are used as input quantities and the structural deflection as an output signal. In the legend, both cases ANN (second generation only) and hybrid prediction (third and

second generation) are shown for training and leading to good agreements with measurements. As precisely shown in the following neural network architectures, we introduce hybrid networks to

be composed of ANNs and SNNs combining advantages of both types of networks. The hybrid SNN/ANN approach in Fig. 2A computes better the oscillations at the end of the time interval than the

ANN does. The extrapolation capabilities are demonstrated in the validation study in Fig. 2B. Again, the results using the third-generation network turn out to be closer to the measurement.

Data-driven neural networks are known to exhibit a small range of extrapolation capabilities. However, in the present framework, we enhance the network’s prediction opportunities by making

use of the inherent path dependence of SNNs. Following this intention, not only single input pairs are passed through the network, but sequences composed of ordered pairs of values are

applied immediately at the input layer in Fig. 1D. This kind of data preparation (see Methods) including the physical path-dependency, is embedded into the inherently time-depending spiking

neurons, and, hence, allows it to outperform the prediction of path-dependent transient signals beyond the trained data. In other words, by making use of the time-dependent nature of SNNs,

the prediction capabilities of a regression framework can be improved compared to traditional ANNs. ENCODING STRATEGIES AND NONLINEAR REGRESSION FRAMEWORK The encoding principle plays a key

role in regression analysis with SNNs. Here, the need for a systematic transformation between real-valued and binary signals is more pronounced as in classification studies, where e.g. image

representations can directly be regarded as binary values diminishing the need for encoding strategies. Once a sufficient training result is established for second-generation networks, a

validation study can lead to sufficient correlations between measurement and predictions, see Fig. 2B. However, since the SNN works with sparse spike train signals, physical input values

have to be encoded towards binary quantities. Encoding strategies are reported in literature43,50 and play a crucial role in training SNNs, especially for regression tasks. In Fig. 3,

different principles are shown. For classification problems, rate-encoding can be adopted, accounting for the high intensity of pixels leading to the firing of spike trains. Alternatively,

the latency encoding and latency-coded decoding methods decide when a spike appears depending on the pixel’s intensity. In delta modulation, the spike firing depends on the positive gradient

of the input data. However, the present study intends to propose an encoding method that is appropriate for a broad spectrum of neuromorphic chips such as Loihi or SynSense Xylo and Speck.

For this reason and the aim of non-linear regression, a machine-learnable transformation of real physical values to spike representations is conducted by the first SNN layer, see Fig. 4.

Following this autoencoding principle, learnable parameters in the first layer are adapted for this transformation process accounting for path- and time-dependent signal evolutions. Due to

the fact that spiking neurons are inherently time-dependent, the propagation of spikes through the network has to run synchronously to incoming real-valued signals denoting the deformation

history of the considered structure. This is a constraint that occurs during a function approximation of dynamic solid deformations. The autoencoding strategy in Fig. 4 maps real values to

spike trains causing internal neuron voltage evolutions in the whole network. Here, we face a time- and path-dependent process with real physical times, which is typically in nonlinear

regression problems. For this reason, the time scale in spike trains must fit the time passed during a structural deformation process. Following this line of reasoning, one real physical

sequence is mapped to a binary sequence for the same time interval. However, in contrast to deep learning techniques of 2nd generation neurons, no activation functions such as e.g. sigmoid

are applied in the spiking neuron. Instead, the neuron’s membrane potential and, hence, its ability to send spike signals are covered by an ordinary differential equation. The most popular

one is the Leaky-Integrate-and-Fire model, which is applied in the present work as a first step to develop it further to a spiking variant of a Legrendre Memory Unit. This intention is

motivated by the need for a high amount of memory in the nonlinear regression of complex transient signals. Firstly, after adopting the autoencoding strategy for the input layer and the

first SNN layer (Fig. 4), we proceed with the sparse signal voltage processing to subsequent feed-forward layers. In a further step, the LMU is added for higher memory access. Assuming an

arbitrary number of hidden layers, the voltage representation in Figs. 1D, 4 can be developed further in component form for each hidden neuron. Starting with a voltage _V__t_ at a certain

time _t_, the output of a neuron _ℓ_ from an arbitrary hidden layer _d_ of an SNN at time _t_ can be written as $${V}_{\ell ,(d)}^{t}={\beta }_{\ell ,(d)}{V}_{\ell

,(d)}^{t-1}+\mathop{\sum}\limits_{j}{W}_{\ell j,(d)}{z}_{j,(d-1)}^{t}-{\phi }_{s}\left({V}_{\ell ,(d)}^{t-1}\right){V}_{\ell ,(d)}^{thr},$$ (1) with _ϕ__s_ representing the spike activation

when a voltage threshold \({V}_{\ell ,(d)}^{thr}\) is exceeded $${\phi }_{s}=\left\{\begin{array}{ll}1,\quad &{V}_{\ell ,(d)}^{t}\ge {V}_{\ell ,(d)}^{thr}\\ 0,\quad &{V}_{\ell

,(d)}^{t}\, < \,{V}_{\ell ,(d)}^{thr}.\end{array}\right.$$ (2) Here, the membrane potential of the neuron is expressed by \({V}_{\ell ,(d)}^{t}\), weights are stored in W(_d_),

_β__ℓ_,(_d_) stands for the membrane decay rate, and \({{{{\bf{z}}}}}_{d-1}^{t}\) is the output of the precedent hidden layer. Hence, the learnable parameters of the transformation are

$$\tilde{\theta }=\{{{{{\bf{W}}}}}_{(d)},{\beta }_{\ell ,(d)},{V}_{\ell ,(d)}^{thr}\}.$$ (3) Thus, the spiking neuron includes a membrane potential and once exceeding the threshold, an

activated signal of 1 is passed while the potential is reset, using the term \({\phi }_{s}({V}_{\ell ,(d)}^{t-1}){V}_{\ell ,(d)}^{thr}\), else an activated output of zero is passed to the

next layer. This principle of binary and sparse signal processing makes the SNNs so efficient concerning less energy consumption on neuromorphic chips. The memory and synaptic weights are

accessed only when a spike appears. On the contrary, 2nd generation networks use matrix multiplication and communicate through dense signals. Since the machine-learning process involves

backpropagation as well, the discontinuous nature of spikes has to be overcome. Following the method of surrogate gradients31,51,52 we prepare the SNN by an arcus tangent activation

surrogate proposed in42,51 for a backward pass with differentiable spike representations. SPIKING LEGENDRE MEMORY UNITS FOR NON-LINEAR REGRESSION The LMU approach as an alternative spike

activation compared to LIF enables us to separate the network’s architecture and the accessible memory from each other. This is an important attribute for the path-depending nonlinear

regression since the memory provides the necessary set of parameters, in which long and short-term events are stored. The advantage of memory access was described and proofed in works

of44,47. In Fig. 5, the result of the developed multilayered spiking variant of the Legendre Memory Unit (LMU)47 is shown, acting as unit cells inside the SNN architecture. With the

combination of sparse spiking signals and LMU cells, substituting activation functions of second-generation networks, nonlinear regression with time-dependent complex transient signals

becomes possible in the present study. However, for a better comparison, we also equip the second-generation counterpart with LMU. Alternatively, the spiking neurons to be enhanced by high

memory access for nonlinear regression can also be derived with LSTM cells. However, an alternative approach of spiking variants of LSTM units is not followed here, since their memory is

coupled to the number of hidden neurons. The memory of an LMU cell is not stored like in an LSTM cell53 and is, therefore, independent of the number of hidden neurons initialized in a layer

and is instead initialized through an ODE that approximates a linear transfer function for a continuous delay44, see Fig. 5. Since the memory capability is connected to the number of free

weights, the LMU approach cares for the available set of parameters and does not require an extension of the network’s architecture. This attribute enables the LMUs to perform

equivalently-sized LSTMs during long periods44. We make use in this approach of the dynamic computation of the LMU cell’s memory M_t_ by starting from the linear transfer function for the

continuous delay and approximating the memory by _n_ coupled ordinary differential equations (ODEs)44 expressed by $$\theta

\dot{{{{\bf{m}}}}}(t)={{{\bf{A}}}}{{{\bf{m}}}}(t)+{{{\bf{B}}}}{{{\bf{u}}}}(t),$$ (4) where M(_t_) ∈ R_n_ represents a state vector with _n_ dimensions, (A, B) represent ideal state-space

matrices derived from the Padé approximants as mentioned in studies44,54, and U(_t_) ∈ _R_ represents an input signal which is orthogonalized across a sliding time window of length _θ_.

These _n_ sets of equations are mapped to the memory of the cell at discrete time steps _t_ and are expressed by

$${{{{\bf{m}}}}}^{t}=\tilde{{{{\bf{A}}}}}{{{{\bf{m}}}}}^{t-1}+\tilde{{{{\bf{B}}}}}{{{{\bf{u}}}}}^{t},$$ (5) where \(\tilde{{{{\bf{A}}}}}\) and \(\tilde{{{{\bf{B}}}}}\) are discretized

matrices and are computed here using the zero-order hold (ZOH) method. The vector U_t_ writes to the memory in Eq. (5) and is computed by using the equation

$${{{{\bf{u}}}}}^{t}={{{{\bf{e}}}}}_{{{{\bf{x}}}}}{{{{\bf{x}}}}}^{t}+{{{{\bf{e}}}}}_{{{{\bf{h}}}}}{{{{\bf{h}}}}}^{t-1}+{{{{\bf{e}}}}}_{{{{\bf{m}}}}}{{{{\bf{m}}}}}^{t-1}.$$ (6) The

expressions EX, EH, EM are treated as parameters dynamically projecting relevant information in its memory cell, and X_t_ denotes the input fed into the model. In a final step, the memory is

passed to a recurrent hidden cell nonlinearly transforming the memory to finalize the output OT for the whole data sequence and the output for a time step _t_ with HT to be equal

$${{{{\bf{h}}}}}^{{{{\bf{t}}}}}=\tanh ({{{{\bf{W}}}}}^{{{{\bf{h}}}}}{{{{\bf{h}}}}}^{{{{\bf{t}}}}-{{{\bf{1}}}}}+{{{{\bf{W}}}}}^{{{{\bf{m}}}}}{{{{\bf{m}}}}}^{{{{\bf{t}}}}}+{{{\bf{b}}}})$$ (7)

and $${{{{\bf{o}}}}}^{{{{\bf{t}}}}}=\tanh ({{{{\bf{W}}}}}^{{{{\bf{h}}}}}{{{{\bf{h}}}}}^{{{{\bf{t}}}}-{{{\bf{1}}}}}+{{{{\bf{W}}}}}^{{{{\bf{m}}}}}{{{{\bf{m}}}}}^{{{{\bf{t}}}}}+{{{\bf{b}}}})$$

(8) with bias B. The spiking variant of the LMU cell (SLMU) can be computed by keeping the Eqs. (4), (5), and (6) unchanged and introducing the spikes in Eqs. (7) and (8) leading to

$${h}_{\ell ,(d)}^{t}=\mathop{\sum}\limits_{j}{W}_{\ell j,(d)}^{h}{h}_{j,(d)}^{t-1}+\mathop{\sum}\limits_{k}{W}_{\ell k,(d)}^{m}{m}_{k,(d)}^{t}+{b}_{\ell ,(d)}-{\phi }_{s}\left({h}_{\ell

,(d)}^{t-1}\right){V}_{\ell ,(d)}^{thr}$$ (9) with _j_, and _k_ representing the number of total units of neurons from the current layer and the memory. Also, _ϕ__s_ represents the spike

activation in the form $${\phi }_{s}=\left\{\begin{array}{ll}1,\quad &{h}_{\ell ,(d)}^{t}\ge {V}_{\ell ,(d)}^{thr}\\ 0,\quad &{h}_{\ell ,(d)}^{t}\, < \,{V}_{\ell

,(d)}^{thr}.\end{array}\right.$$ (10) Finally, a decoding strategy has to be introduced for re-transforming spiking signals to real physical values at the end of the forward pass, see Fig.

6A. Here, a recurrent variant of the spiking neural network (SRNN) is used to decode the binary spikes, with the potential to perform outputs in real values rather than the spikes42. A

recurrent principle is used here since it requires less energy than the LMU variant. This transformation process follows the expression for the voltage $${V}_{\ell ,(d)}^{t}={\beta }_{\ell

,(d)}{V}_{\ell ,(d)}^{t-1}+\mathop{\sum}\limits_{j}({W}_{\ell j,(d)}{z}_{j,d-1}^{t})+\mathop{\sum}\limits_{k}\left({U}_{\ell k,(d)}{\phi }_{s}\left({V}_{k,(d)}^{t-1}\right)\right)-{\phi

}_{s}\left({V}_{\ell ,(d)}^{t-1}\right){V}_{\ell ,(d)}^{thr}$$ (11) with an additional set of recurrent weights denoted by U(_d_) and where _j_ and _k_ denote the total number of units from

the previous layer and current layer, respectively. Other strategies for encoding and decoding between spikes and physical values can be found in55. In the present investigation, spiking and

non-spiking variants need the same number of transformations, however, to introduce robustness in the prediction of the non-spiking variant and avoid overfitting, a dropout operation56

specific to the non-spiking variant is introduced as shown in Fig. 6B. The spiking variant inhibits an inherent dropout operation to be discussed in the following subsections. SNN AND ANN

ARCHITECTURES WITH HYPERPARAMETERS In Fig. 6, the finally obtained third-generation neural network and its second-generation counterpart are presented. In Fig. 6A, the SNN together with

densely fully connected layers and input and output layers leading to a so-called hybrid model is shown. Sparse signal processing is indicated by dashed arrows while solid arrows denote

suddenly occurring spike transmissions. While the second generation neuron receives real-valued inputs and uses the weighted sum as a criterion for an output signal, the spiking neuron is

submitted to spike train signals leading to a time history of the voltage evolution and triggering the spike train output of the neuron as described in Eqs. (1), (2), (9), (10), (11) and in

Figs. 1D, 4. The input layer includes measured values denoted by neurons of the second generation. A number of three input values is illustrated. The real-valued signals are converted into

binary signals by an autoencoding strategy using the first SNN layer for transforming physical data into spike representations. During the propagation of signals and time sequences, solid

and dashed lines would always alternate depending on each spike train in between all spiking neurons. This fact gives already an impression of the remarkable energy efficiency compared to

the second-generation model in Fig. 6B. There, all dense neuronal connections are always active independently on the time leading to a much higher energy consumption. However, before the

data preparation and energy consumption are discussed in the following subsections, it can be concluded that the final architecture of the hybrid model is prepared with all the following

attributes. An input layer with measured pressure \({\left({p}^{n}\right)}^{t}\), a specimen’s property \({\left({s}^{n}\right)}^{t}\) denoting the ratio between Young’s Modulus and

diameter, and the shock wave velocity \({\left({v}^{n}\right)}^{t}\), see also28. The superscripts ()_n_ and ()_t_ stand for normalised values and time, respectively. The output layer

includes only the specimen’s deformation \({\left({d}^{n}\right)}^{t}\). The first SNN layer enables autoencoding, while the last SNN layer is used for decoding spikes to real-valued signals

by using a spiking recurrent neural network expressed by Eq. (11). In-between auto- and decoding areas, a variable number of hidden layers can be created. After encoding, a set of dense

layers can also be added if necessary e.g. for the training process. However, each dense connection needs more energy than the SNN communication, so this hybrid composition must be chosen

carefully concerning the intended sustainability. During the training of the described neural network models the number of SLMU layers, the number of hidden units in the SLMU layer, the

number of units of the SRNN layer, the number of memory units of the SLMU layer, the number of hidden dense layers, the number of dropout percentage, and the number of units of the dense

layers are determined and shown in Table 1. A Hyperband search algorithm57 for efficient exploration and investigation of suitable architectures as well as Adam optimizer’s learning rate

(_ζ_ = 0.001) and its exponential decay rates _β__e_1 = 0.9 and _β__e_2 = 0.999 were applied. As a comparison in Fig. 6B, the alternative second-generation neural network is presented,

working with dense connections, only. To account for regulation effects, a drop-out layer is used here, which is not necessary for the SNN counterpart due to the brain-inspired

regularisation in the present nonlinear regression as described below. NONLINEAR REGRESSION OF COMPLEX TRANSIENT SIGNALS In Figs. 7–9 the SSN model vs. the ANN counterpart are verified for

other loading histories and specimen properties. In Fig. 7 two examples are shown, in which both third and second-generation networks lead to good training results, while in Fig. 9 also

validation results are shown. The transient data in short-time scales is gained by an experimental set-up with an experimental procedure equivalent to the one in Fig. 1 but using different

specimens and pressure histories as it is visible in the diagrams. This ensures a mostly general approach in the present investigation. The set-up is decomposed in Fig. 8A–D into its details

for measuring solid deformations and pressures leading to the recording of deflection and pressure signals in Figs. 7, 9. In Fig. 9B, the prediction is tested with the trained networks of

Fig. 7B for steel, and a good agreement with the measurement is achieved. This observation continues in Fig. 10A, where four subsequent impulsive pressure loads are performed, causing

complex deflection histories of the specimen. However, both types of networks can outperform the signals with a deviation at the end. However, to investigate the extrapolation capability

after training of three loading steps, the fourth one is predicted by the SNN and ANN networks. In Fig. 10B, the green and indigo curves correspond to the response over the validation

sequences highlighting that the model has learned the nonlinear evolution and can be deployed for further extrapolation beyond the training data. Even though the external loadings during the

validation sequences are beyond the training data, the model behaves less sensitively towards sequence development. This indicates that with the proposed autoencoding strategy an SNN model

was developed, which is as accurate as the second-generation model. Due to the described network models with path dependency and high memory access, both networks have learned the underlying

nonlinear evolution of the output signals and perform, with a deviation, the oscillating behavior. Furthermore, another extrapolation capability of the networks is investigated in Fig. 10B

with data beyond the training range used in Fig. 9A. The subjected pressure is slightly different from the one in Fig. 9A but leading also to good agreements with the measurement. ACCURACY

AND BRAIN-INSPIRED REGULARISATION In Table 2, the accuracy of the calculated signal evolution compared to the measurements is presented taking RMSE values into account. In the first column,

T and V denote, if the neural network computing was used for training or validation, respectively. The accuracy of computing the measured signals is summarised in Table 2, where the RMSE

values indicate an acceptable correlation to the measurements. However, due to sparse binary communications between spiking neurons, in the present study, the training time is longer than

that of the second-generation counterpart. To find a compromise between training duration and energy need, the hybrid approach as shown in Fig. 6A is proposed, in which only the layers that

consume the most energy, in this case, the LMU, are converted into their spiking variant (SLMU) and combined with dense transformations to predict nonlinear behavior. Following this

strategy, a better convergence rate while training the hybrid SLMU model is obtained. Furthermore, validation experiments are performed and a stable response for these experiments highlights

that both models have not only memorized the data but have identified the trends of the physical evolution. One aspect can be in this case the dropout transformation and the spiking

mechanism deployed in the LMU and SLMU models. The observed effect of an inherent drop-out during regression with the SNN should be highlighted as well. In the SNN, a neuron is activated

only when the threshold potential (_V__t__h__r_) is exceeded, else it remains deactivated. Hence, during a forward pass only a certain amount of neurons fire the spike trains. A similar

behavior happens when a dropout56 layer is added after a second-generation layer, wherein a subset of neurons is set to zero with a certain probability. Consequently, we can conclude an

inherent brain-inspired regularization occurs in spiking neurons. ENERGY CONSUMPTION Even though the 2nd generation model performs similar results as the 3rd generation one, the neuromorphic

network leads to significantly lower energy consumption than the 2nd generation topology. To quantify these energy savings, a power profiling with different processors is carried out in

Tables 3, 4 representing the consumed energy during one forward pass. To trace the energy consumption throughout the networks, in Table 3, the energy values are shown for each layer

separately. Due to the hybrid network architecture, the comparison takes place between CPU, GPU, Loihi, Loihi (SLMU layers) + GPU (Dense layers), and Loihi (SLMU layers) + CPU (Dense

layers). The total energy denotes the one required to perform all synaptic operations and neuron updates. It should be mentioned that the energy cost for deploying the model on/off the

device is not included here. All energy values are determined with KerasSpiking33,58. Due to their sparse connections, the memory and neurons are accessed only when the threshold is

exceeded, initiating synaptic operations only for activated neurons. This effect has a dominant influence on the energy consumption of the network during signal processing on a Loihi chip,

see Tables 3, 4. The smallest energy consumption is obtained with a third-generation model on a Loihi chip. Each part of the framework does not save energy. Only those parts being deployed

on the neuromorphic chip having spiking transformation save energy. In Table 4, the reduction factor is shown for the energy needed by a conventional processor in relation to the

neuromorphic chip or a hybrid composition. A significant energy saving by the ratio of classical computing using CPU and GPU to the new approach with third-generation SNNs can be observed

due to reduction factors of 1176.33 and 35581.4 (see Table 4). The results are determined while comparing the energy of the spiking variant being deployed on the Loihi chip with the

non-spiking variant on the GPU and CPU. However, KerasSpiking assumes that the deployed NN model consists of only third-generation neurons. The energy values corresponding to the

second-generation dense layers do not represent the actual values for the proposed hybrid model. Since sustainable computing by SNNs is required in this study, the relation between spiking

and dense layers plays a crucial role in keeping overall energy saving for the entire network. A reliable set of values can be obtained by deploying only the SLMU layers on the Loihi chip

and the dense layers on GPU/CPU as shown in Tables 3 and 4. Hence, a total reduction factor of 21.2775 and 1663.878 per epoch can be expected in comparison to the second-generation

counterpart. DISCUSSION In the present study, a nonlinear regression framework for spiking neural networks on neuromorphic processors is proposed and its sustainability in the form of

significant energy saving is demonstrated. However, a crucial point for triggering the spiking neurons is the encoding between real physical and binary values, which was, here, introduced by

autoencoding with the first spiking layer. To keep the energy consumption during decoding as small as possible a recurrent spiking layer was introduced. Additional dense connections can be

introduced for improving convergence, however, then already gained energy savings could be reduced. Consequently, the developed hybrid neural network model accounts for several attributes

such as energy saving, reduced training loss due to a hybrid solution, and encoding strategies. Moreover, due to their inherently recurrent nature, the SNNs offer themselves for

path-dependent regression tasks, which must be implemented in second-generation networks more circumstantially by recurrent loops. Here, sequential data is used to account for the SNN’s

advantage of time dependency in function approximation. The SNNs are also appropriate to further enhance them by additional Legendre Memory Units (LMU) independently of the network

architecture. The LMU acts in the single neuron with additional memory, which is important for storing evolutive processes in path-dependent functions. To obtain complex transient signal

processing in hybrid neural networks, experimental data was used being recorded by short-time measurement techniques in shock tubes leading to wave propagation phenomena in solids. METHODS

DATA ACQUISITION In Fig. 11 the data acquisition for the data-driven neural network approach is described. The principle of a shock tube is shown in 11A consisting of a high-pressure chamber

(HPC) and a low-pressure chamber (LPC) separated by a membrane from each other. The membranes presented in part B of Fig. 11 can consist of Hostaphan or Aluminum depending on the desired

burst pressure. In the case of Hostaphan for pressures up to 15 bar a flange with an additional cross is inserted in the tube (see Fig. 11B) to avoid too early ruptures of the membranes.

Aluminum membranes (Fig. 11C) include a cross on their surfaces causing a controlled opening of the membrane with pressures up to 30 bar avoiding that parts of the membrane tear up and move

together with the shock wave. In the principle drawing (Fig. 11A) PCB 113A26 piezoelectric pressure sensors (PS) are located in flanges being able to measure fast pressure changes in rise

times of 1 _μ_s and are calibrated until 34.5 bar. Due to the conical shape of the tube between LPC and HPC, the pressure of the shock waves caused by the ruptured membrane is up to 7 bar in

the LPC. A solid plate specimen is clamped at the end of the LPC being subjected to a plane shock wave front reflected at the specimen and propagated back through the shock tube. In this

way, the pressure steps in the diagrams in Fig. 11D, E are caused. By varying the type of gas in the HPC different peak pressures and pressure evolutions, acting on the specimen, can be

obtained, see Fig. 11E. To measure inelastic deformations of specimens in the tube during the impulse duration, a capacitive sensor, developed in48,49 is located in front of the specimen’s

center. Control devices next to the sensor are used to calibrate the sensor and to conclude from voltage signals on displacement quantities. All measured data is recorded with 1MHz sampling

rate. To vary materials and geometry, the data of steel and copper specimens in an additional shock tube, shown in Fig. 8, is also used for data acquisition. Data collections of these

experiments can be found in10,48,49. DATA PREPARATION Here, data sequences instead of single pairs of data are prepared for training and validation. Following this procedure, it is made use

of the inherently time-dependent property of spiking neurons. This technique is beneficial for all these purposes where path-dependent input and output variables are incorporated. To prepare

the measured data for the neural network training, a sampling strategy with measurements that run over 15000 time steps is introduced. Generating a stack of experiments means analysing

sequences with 500 time steps, hence, the input and output vectors include sequences with 500 data points each. They are extracted by a windowing technique, sliding with 500 time-steps over

the measurements to collect the necessary training data. A stride of 500 steps is used during the training process to avoid any flow of redundant information. Following this strategy, a

total of 100 sequences were extracted. Furthermore, a set of experiments is used to demonstrate the proposed model’s ability to adapt to previously unseen data. Three input variables are

chosen for the neural networks, the pressure _p_ acting on the plate during the impulse period, the stiffness relation _s_ denoting the relation between Young’s Modulus and plate diameter,

and the shock wave velocity _v_. Hence, used notations for each sequence are ordered for the _m__t__h_ sequence by a superscript (_m_), the _i__t__h_ step in a sequence is denoted by

superscript _i_, an input sequence is represented as $${{{{\bf{x}}}}}^{(m)}=({[p,s,v]}^{1},{[p,s,v]}^{2},\ldots ,{[p,s,v]}^{i},\ldots {[p,s,v]}^{I})$$ (12) with a total number of _I_

sequences. The output sequence denotes the specimen’s midpoint displacement Y(_m_). Input and output sequences have to be scaled to avoid convergence issues during training, which is ensured

by a linear transformation following Min-Max standardization59 in the form $${\eta }^{std}=\frac{\eta -{\eta }_{min}}{{\eta }_{max}-{\eta }_{min}}$$ (13) $${\eta }^{n}=2\cdot {\eta

}^{std}-1.$$ (14) In Eq. (13), _η__m__a__x_ and _η__m__i__n_ stand for maximum and minimum values of each feature and Eq. (14) maps the features to be in the range of [ − 1, 1]. Thus, the

scaled ordered pair of input and output sequences are represented by \({[{{{{\bf{x}}}}}^{n},{{{{\bf{y}}}}}^{n}]}^{(m)}\). HARDWARE CAPABILITIES The inference corresponding to the amount of

energy consumed is computed through KerasSpiking V0.3. 1 where the Intel i7-4960X chip is used as the CPU, Nvidia GTX Titan Black as the GPU, and the Intel Loihi chip33 as the neuromorphic

hardware for processing the third-generation networks. DATA AVAILABILITY The data that support the findings of this study are available from the corresponding author upon reasonable request.

CHANGE HISTORY * _ 04 MARCH 2025 A Correction to this paper has been published: https://doi.org/10.1038/s44335-025-00019-3 _ REFERENCES * Mead, C. Neuromorphic electronic systems. _Proc.

IEEE_ 78, 1629–1636 (1990). Article  MATH  Google Scholar  * Schuman, C. D. et al. Opportunities for neuromorphic computing algorithms and applications. _Nature Computational Science_ 2

https://www.nature.com/articles/s43588-021-00184-y#citeas (2022). * Ma, D. et al. Darwin: A neuromorphic hardware co-processor based on spiking neural networks. _J. Syst. Archit._ 77, 43–51

(2017). Article  MATH  Google Scholar  * Papadopoulos, L., Bakalakos, S., Nikolopoulos, S., Kalogeris, I. & Papadopoulos, V. A computational framework for the indirect estimation of

interface thermal resistance of composite materials using xpinns. _Int. J. Heat. Mass Transf._ 200, 123420 (2023). Article  MATH  Google Scholar  * Olivier, A., Shields, M. D. &

Graham-Brady, L. Bayesian neural networks for uncertainty quantification in data-driven materials modeling. _Comput. Methods Appl. Mech. Eng._ 386, 114079 (2021). Article  ADS  MathSciNet 

MATH  Google Scholar  * Brenner, M. P., Eldredge, J. D. & Freund, J. B. Perspective on machine learning for advancing fluid mechanics. _Phys. Rev. Fluids_ 4, 100501 (2019). Article  ADS

  MATH  Google Scholar  * Brunton, S. L., Noack, B. R. & Koumoutsakos, P. Machine learning for fluid mechanics. _Annu. Rev. Fluid Mech._ 52, 477–508 (2020). Article  ADS  MathSciNet 

MATH  Google Scholar  * Kutz, J. N. Deep learning in fluid dynamics. _J. Fluid Mech._ 814, 1–4 (2017). Article  ADS  MATH  Google Scholar  * Raissi, M., Yazdani, A. & Karniadakis, G. E.

Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. _Science_ 367, 1026–1030 (2020). Article  ADS  MathSciNet  CAS  PubMed  PubMed Central  MATH  Google

Scholar  * Stoffel, M., Bamer, F. & Markert, B. Artificial neural networks and intelligent finite elements in non-linear structural mechanics. _Thin-Walled Struct._ 131, 102–106 (2018).

Article  MATH  Google Scholar  * Gorji, M. B., Mozaffar, M., Heidenreich, J. N., Cao, J. & Mohr, D. On the potential of recurrent neural networks for modeling path dependent plasticity.

_J. Mech. Phys. Solids_ 143, 103972 (2020). Article  MathSciNet  MATH  Google Scholar  * Gulakala, R., Markert, B. & Stoffel, M. Generative adversarial network-based data augmentation

for CNN-based detection of covid-19. _Scientific Reports_ 12 https://doi.org/10.1038/s41598-022-23692-x (2022). * Stoffel, M., Weichert, D. & Müller-Rath, R. Modeling of articular

cartilage replacement materials. _Arch. Mech._ 61, 69–87 (2009). MathSciNet  MATH  Google Scholar  * Stoffel, M. et al. Towards bioreactor development with physiological motion control and

its applications. _Med. Eng. Phys._ 39, 106–112 (2017). Article  PubMed  MATH  Google Scholar  * Gamez, C. et al. Bioreactor for mobilization of mesenchymal stem/stromal cells into scaffolds

under mechanical stimulation: Preliminary results. _PLoS One_ 15, e0227553 (2020). Article  CAS  PubMed  PubMed Central  Google Scholar  * Endres, M. et al. An ovine in vitro model for

chondrocyte-based scaffold-assisted cartilage grafts. _J. Orthop. Surg. Res._ 7, 1–14 (2012). Article  MATH  Google Scholar  * Nicolini, L. F. et al. Motion preservation surgery for

scoliosis with a vertebral body tethering system: a biomechanical study. _European Spine Journal_ 1–9 (2022). * Stoffel, M., Bamer, F. & Markert, B. Deep convolutional neural networks in

structural dynamics under consideration of viscoplastic material behaviour. _Mech. Res. Commun._ 108, 103565 (2020). Article  MATH  Google Scholar  * Wang, C., yan Xu, L. & sheng Fan,

J. A general deep learning framework for history-dependent response prediction based on ua-seq2seq model. _Comput. Methods Appl. Mech. Eng._ 372, 113357 (2020). Article  ADS  MathSciNet 

MATH  Google Scholar  * Fernández, M., Jamshidian, M., Böhlke, T., Kersting, K. & Weeger, O. Anisotropic hyperelastic constitutive models for finite deformations combining material

theory and data-driven approaches with application to cubic lattice metamaterials. _Comput. Mech._ 67, 653–657 (2021). Article  MathSciNet  MATH  Google Scholar  * Klein, D. K., Fernández,

M., Martin, R. J., Neff, P. & Weeger, O. Polyconvex anisotropic hyperelasticity with neural networks. _J. Mech. Phys. Solids_ 159, 104703 (2022). Article  MathSciNet  MATH  Google

Scholar  * Bastek, J.-H., Kumar, S., Telgen, B., Glaesener, R. N. & Kochmann, D. M. Inverting the structure–property map of truss metamaterials by deep learning. _Proc. Natl Acad. Sci._

119, e2111505119 (2022). Article  CAS  PubMed  MATH  Google Scholar  * Liang, M. et al. Interpretable ensemble-machine-learning models for predicting creep behavior of concrete. _Cem. Concr.

Compos._ 125, 104295 (2022). Article  CAS  MATH  Google Scholar  * Kirchdoerfer, T. & Ortiz, M. Data-driven computational mechanics. _Comput. Methods Appl. Mech. Eng._ 304, 81–101

(2016). Article  ADS  MathSciNet  MATH  Google Scholar  * González, D., Chinesta, F. & Cueto, E. Thermodynamically consistent data-driven computational mechanics. _Contin. Mech.

Thermodyn._ 31, 239–253 (2019). Article  ADS  MathSciNet  MATH  Google Scholar  * Ladevèze, P., Néron, D. & Gerbaud, P.-W. Data-driven computation for history-dependent materials.

_Comptes Rendus Mécanique_ 347, 831–844 (2019). Article  ADS  MATH  Google Scholar  * He, X., He, Q. & Chen, J.-S. Deep autoencoders for physics-constrained data-driven nonlinear

materials modeling. _Comput. Methods Appl. Mech. Eng._ 385, 114034 (2021). Article  ADS  MathSciNet  MATH  Google Scholar  * Tandale, S. B. & Stoffel, M. Spiking recurrent neural

networks for neuromorphic computing in nonlinear structural mechanics. _Comput. Methods Appl. Mech. Eng._ 412, 116095 (2023). Article  ADS  MathSciNet  MATH  Google Scholar  * Indiveri, G.

& Liu, S.-C. Memory and information processing in neuromorphic systems. _Proc. IEEE_ 103, 1379–1397 (2015). Article  CAS  MATH  Google Scholar  * Burr, G. W. et al. Neuromorphic

computing using non-volatile memory. _Adv. Phys.: X_ 2, 89–124 (2017). MATH  Google Scholar  * Perez-Nieves, N. & Goodman, D. F. M. Sparse spiking gradient descent

https://arxiv.org/abs/2105.08810 (2021). * Gerstner, W., Kistler, W. M., Naud, R. & Paninski, L. _Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition_ (Cambridge

University Press, Cambridge, 2014). * Davies, M. et al. Loihi: A neuromorphic manycore processor with on-chip learning. _IEEE Micro_ PP, 1–1 (2018). MATH  Google Scholar  * Furber, S. B.,

Galluppi, F., Temple, S. & Plana, L. A. The spinnaker project. _Proc. IEEE_ 102, 652–665 (2014). Article  Google Scholar  * Liu, Q. et al. Live demonstration: face recognition on an

ultra-low power event-driven convolutional neural network ASIC. In _Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops_, 0–0 (2019). * Rahimi

Azghadi, M. et al. Hardware implementation of deep network accelerators towards healthcare and biomedical applications. _IEEE Trans. Biomed. Circuits Syst._ PP, 1–1 (2020). MATH  Google

Scholar  * Ceolini, E. et al. Hand-gesture recognition based on emg and event-based camera sensor fusion: A benchmark in neuromorphic computing. _Front. Neurosci._ 14

https://www.frontiersin.org/articles/10.3389/fnins.2020.00637 (2020). * Fang, W. et al. Deep residual learning in spiking neural networks https://arxiv.org/abs/2102.04159 (2021). * Diehl, P.

& Cook, M. Unsupervised learning of digit recognition using spike-timing-dependent plasticity. _Frontiers in Computational Neuroscience_ 9

https://www.frontiersin.org/articles/10.3389/fncom.2015.00099 (2015). * Patel, K., Hunsberger, E., Batir, S. & Eliasmith, C. A spiking neural network for image segmentation

https://arxiv.org/abs/2106.08921 (2021). * Barchid, S., Mennesson, J., Eshraghian, J., Djéraba, C. & Bennamoun, M. Spiking neural networks for frame-based and event-based single object

localization https://arxiv.org/abs/2206.06506 (2022). * Henkes, A., Eshraghian, J. & Wessels, H. Spiking neural networks for nonlinear regression (2022). * Zhang, Q., Kahana, A.,

Karniadakis, G. E. & Stinis, P. Sms: Spiking marching scheme for efficient long time integration of differential equations https://arxiv.org/abs/2211.09928 (2022). * Voelker, A., Kajic,

I. & Eliasmith, C. Legendre memory units: Continuous-time representation in recurrent neural networks (2019). * Muir, D. R., Bauer, F. & Weidel, P. Rockpool documentaton

https://doi.org/10.5281/zenodo.3773845 (2019). * Tandale, S. B. & Stoffel, M. Physics-based self-learning spiking neural network enhanced time-integration scheme for computing

viscoplastic structural finite element response. _Computer Methods Appl. Mech. Eng._ 422, 116847 (2024). Article  ADS  MathSciNet  MATH  Google Scholar  * Tandale, S. B. & Stoffel, M.

Brain-inspired spiking neural networks in engineering mechanics: a new physics-based self-learning framework for sustainable finite element analysis. _Engineering with Computers_ (2024). *

Stoffel, M. An experimental method to validate viscoplastic constitutive equations in the dynamic response of plates. _Mech. Mater._ 37, 1210–1222 (2005). Article  MATH  Google Scholar  *

Stoffel, M. A measurement technique for shock wave-loaded structures and its applications. _Exp. Mech._ 46, 47–55 (2006). Article  MATH  Google Scholar  * Eshraghian, J., Wang, X. & Lu,

W. Memristor-based binarized spiking neural networks: Challenges and applications. _IEEE Nanotechnol. Mag._ 16, 2–11 (2022). Article  MATH  Google Scholar  * Fang, W. et al. Incorporating

learnable membrane time constant to enhance learning of spiking neural networks https://arxiv.org/abs/2007.05785 (2020). * Zenke, F. & Ganguli, S. Superspike: Supervised learning in

multilayer spiking neural networks. _Neural Comput._ 30, 1514–1541 (2018). Article  MathSciNet  PubMed  PubMed Central  MATH  Google Scholar  * Hochreiter, S. & Schmidhuber, J. Long

short-term memory. _Neural Comput._ 9, 1735–1780 (1997). Article  CAS  PubMed  MATH  Google Scholar  * Padé, H. Sur la représentation approchée d’une fonction par des fractions rationnelles.

_Annales scientifiques de. l’École Norm. Supérieure_ 9, 3–93 (1892). Article  MathSciNet  MATH  Google Scholar  * Eshraghian, J. K. et al. Training spiking neural networks using lessons

from deep learning https://arxiv.org/abs/2109.12894 (2021). * Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I. & Salakhutdinov, R. Dropout: A simple way to prevent neural

networks from overfitting. _J. Mach. Learn. Res._ 15, 1929–1958 (2014). MathSciNet  MATH  Google Scholar  * Li, L., Jamieson, K. G., DeSalvo, G., Rostamizadeh, A. & Talwalkar, A.

Efficient hyperparameter optimization and infinitely many armed bandits. _CoRR_ ABS/1603.06560 http://arxiv.org/abs/1603.06560 (2016). * Degnan, B., Marr, B. & Hasler, J. _IEEE

Transactions on Very Large Scale Integration (VLSI) Systems_. * Pedregosa, F. et al. Scikit-learn: Machine learning in python. _J. Mach. Learn. Res._ 12, 2825–2830 (2011). MathSciNet  MATH 

Google Scholar  Download references ACKNOWLEDGEMENTS We gratefully acknowledge the financial support provided by Deutsche Forschungsgemeinschaft (DFG: Grant No. STO 469/17-1). AUTHOR

INFORMATION AUTHORS AND AFFILIATIONS * Institute of General Mechanics, RWTH Aachen University, Eilfschornsteinstr. 18, D-52056, Aachen, Germany Marcus Stoffel & Saurabh Balkrishna

Tandale Authors * Marcus Stoffel View author publications You can also search for this author inPubMed Google Scholar * Saurabh Balkrishna Tandale View author publications You can also

search for this author inPubMed Google Scholar CONTRIBUTIONS M.S. wrote the main manuscript text and was responsible for Supervision, Resources, Project administration,Funding acquisition,

Conceptualization. S.B.T. participated in writing and was in charge of Visualization, Validation, Software, Resources, Methodology, Investigation, Formal analysis, Conceptualization. Both

authors prepared figures and reviewed the manuscript. CORRESPONDING AUTHOR Correspondence to Marcus Stoffel. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing

interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND

PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any

medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The

images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not

included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly

from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Stoffel, M.,

Tandale, S.B. Spiking neural networks for nonlinear regression of complex transient signals on sustainable neuromorphic processors. _npj Unconv. Comput._ 1, 2 (2024).

https://doi.org/10.1038/s44335-024-00002-4 Download citation * Received: 25 February 2024 * Accepted: 13 May 2024 * Published: 25 July 2024 * DOI: https://doi.org/10.1038/s44335-024-00002-4

SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to

clipboard Provided by the Springer Nature SharedIt content-sharing initiative