ABSTRACT We have measured the dynamical response of ZrO2 capacitors to applied triangular voltage waveforms with varying frequencies and amplitudes to determine the voltage and charge on the

devices as a function of time. We have fit our experimental results to a Landau–Khalatnikov dynamical equation with a sixth order Landau–Ginzburg–Devonshire polynomial to represent the

static charge-voltage behavior, and obtained coefficients of determination _R_2 > 0.99 for the fits. Analysis of the resulting quantitative model reveals an extremely small range of

negative differential capacitance <16 mV. The hysteresis loops in the dynamical charge-voltage curves are found to result primarily from energy loss during the ferroelectric transitions,

April 2022 INTRODUCTION Antiferroelectric materials, such as PbZrO3, exhibit pinched double hysteresis loops in their charge versus voltage curves1,2,3. The antiparallel dipoles align along

a single direction when an external bias is applied to an antiferroelectric capacitor, dramatically increasing the accumulated charge at the electrodes. When the bias is removed, the dipoles

lose their orientation, releasing the accumulated charge4. The structural transformation, i.e., dipole alignment, consumes energy, resulting in the hysteretic charge versus voltage curve.

Fluorite-structured ZrO2 and some HfxZr1-xO2 alloys represent another material system that manifests pinched double hysteresis loops5. Since their electrical response is similar, they have

often been assumed to be antiferroelectric. However, the fluorite-structured ground state of these oxides is a high-symmetry nonpolar tetragonal phase (P42/nmc) without antiparallel dipoles.

When an external bias is applied, the lattice loses its inversion symmetry and transforms into the ferroelectric orthorhombic phase (Pca21)6,7. Therefore, “field-induced ferroelectricity”

or “volatile ferroelectricity” best describe the pinched double hysteresis in these fluorite-structured oxides. ZrO2 and its derivatives are subjects of keen interest for their applications

in memory devices8,9,10,11, piezoelectric systems12, energy storage devices13,14 and potentially oscillators and signal amplifiers resulting from negative differential capacitance (NDC) in

the charge vs. voltage (_QV_) characteristic. However, a direct observation of NDC in ferroelectrics has been challenging because of the hysteresis in the dynamical _QV_ curves. Khan et al.

reported an increase in the charge on a Pb(Zr0.2Ti0.8)O3 (PZT) capacitor using a series resistor during which the indirectly measured voltage across the capacitor decreased15. Cheng et al

attributed the observation of imaginary impedance in a ZrO2 capacitor as an indicator of NDC16. Other researchers have interpreted the enhanced capacitance of a ferroelectric/dielectric

stack to have been caused by NDC of the ferroelectric17,18,19. There are also reports where researchers have designed material stacks and pulsed-voltage experiments in an attempt to probe

inside the hysteresis loops of a HfO2 and ZrO2 capacitor20,21. In addition to the experimental investigations, efforts have also been focused to accurately model ferroelectric

capacitors22,23,24,25,26. In this work, we investigated the _QV_ characteristics of ZrO2 capacitors using explicitly dynamical measurements and compact modeling of the experimental results.

We found that a simple static model based on a sixth-order polynomial Landau–Ginzburg–Devonshire (LGD) theory and dynamical response from Landau–Khalatnikov (LK) theory agreed extremely well

with our experimental measurements. For ZrO2, we found that any NDC was extremely small if not negligible, and that the hysteresis loops were caused by a dynamic (frequency-dependent)

resistance that accounted for the energy loss in the lattice degrees of freedom and possibly radiated energy during cycling of the capacitor. We computed and compared the reversible energy

stored on the capacitor during a charge-discharge cycle to the irreversible energy dissipated, and found they were similar. RESULTS ELECTRICAL CHARACTERIZATION OF ZRO2 CAPACITOR We first

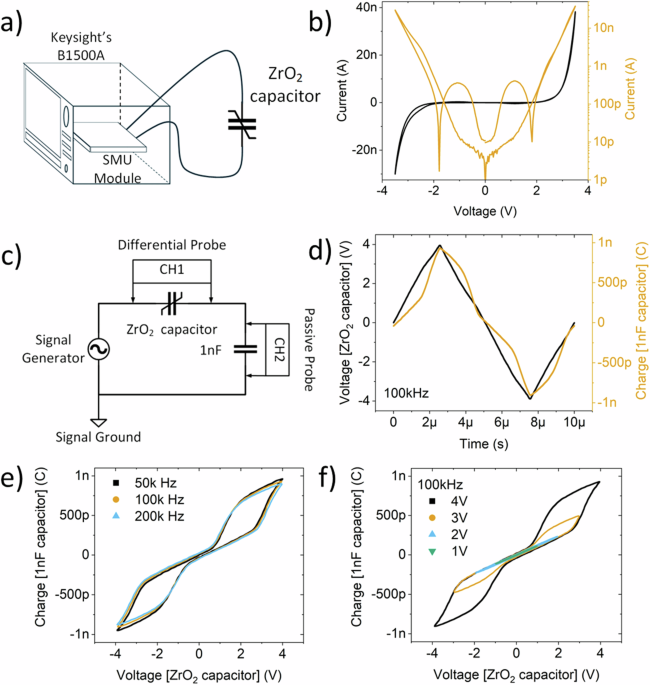
checked to see if there was a measurable tunneling current through the ZrO2 capacitor. Quasi-static current-voltage (_IV_) characteristics measured using the circuit of Fig. 1a are shown in

Fig. 1b. It is important to measure and model this leakage current, since it can contribute significantly to low-frequency dynamical measurements of the capacitive signal and induce a phase

shift between the voltage and charge that can interfere with the data analysis if not properly included in a model. In the dynamical measurement circuit schematic shown in Fig. 1c, the

voltage input was applied by the function generator as a triangular waveform, and the voltages across the ZrO2 and 1 nF linear capacitors were collected independently using an active

differential probe and a passive probe, respectively. The amplitude of the input voltage waveform was adjusted to ensure a maximum voltage drop of 4 V in either polarity across the ZrO2

capacitor. The voltage waveform across the linear capacitor was converted to charge by scaling it with the linear capacitance (_Q_ = _C_ _×_ _V_). The charge across the ZrO2 capacitor should

be identical to that measured for the linear capacitor, which is the Sawyer-Tower circuit used to measure the charge hysteresis in Rochelle salt27. The voltage and charge waveforms are

plotted against time in Fig. 1d. As shown in the figure, the voltage waveform across the ZrO2 capacitor is not triangular because of its non-linear nature. We emphasize the importance of

measuring the capacitance across a non-linear element using a circuit such as Fig. 1c. A strong nonlinearity may distort the signals measured by a capacitance meter, whereas the entire

circuit can be included in the analysis model of the signals measured in Fig. 1c to extract the behavior of the nonlinear element. To investigate the dynamical _QV_ characteristics of the

ZrO2 capacitor, input voltage frequencies of 50 kHz, 100 kHz, and 200 kHz were applied for 4 V triangular wave amplitude. The results are shown in Fig. 1e. The near independence of the

observed hysteresis on frequency is interesting and will be discussed later. As the frequency decreased, the saturation charge slightly increased and the coercive voltage slightly decreased,

yielding an apparent small rotation of the traces anti-clockwise about the origin, an effect attributed to local ferroelectric domains with different relaxation times28,29. The voltage

amplitude across the ZrO2 capacitor was then increased from 1 V to 4 V at 100 kHz, with the results shown in Fig. 1f. At lower amplitudes (1 V & 2 V), the ZrO2 capacitor exhibited linear

_QV_ characteristics without hysteresis. At larger amplitudes (3 V & 4 V), non-linearity emerged in the form of pinched double hysteresis loops, with a small apparent remnant charge at

zero voltage. The area of the hysteresis loops increased with voltage amplitude, indicating an increase of the amount of material undergoing the field-induced ferroelectric phase transition6

after a critical internal field has been attained. Such qualitative behavior in ZrO2 capacitors has been consistently reported in the literature and described using various models5,7,20.

COMPACT NONLINEAR MODEL OF ZRO2 CAPACITOR An accurate compact model is essential for emerging electronic devices, particularly for non-linear devices such as ZrO2 capacitors, to extract and

compare key parameters, simulate and analyze circuits, and design integrated circuits and systems. We tested several different models (including a memcapacitor model because of the

double-pinched hysteresis, described in the SI). By far the best agreement with our experimental results came from the venerable Landau–Ginzburg–Devonshire (LGD)30,31 theory for the static

(but not directly measurable) ferroelectric _QV_ characteristic, and the dynamical response with the Landau-Khalatnikov (LK) equation22,32. Since we are constructing a compact model, we use

the physically measurable quantities voltage _V_ and charge _Q_ rather than field and polarization, which is essentially averaging over edge effects, dead layers, domains and domain

boundaries of the ZrO2 capacitor. Using the LGD theory and truncating after \({q}^{6}\), the static free energy \({{\mathcal{F}}}_{q}\) of a ferroelectric sandwiched between two capacitor

plates can be modeled as $${{\mathcal{F}}}_{q}=\frac{1}{2}a{q}^{2}+\frac{1}{4}b{q}^{4}+\frac{1}{6}c{q}^{6}-q\cdot v$$ (1.0) where \(a\), \(b\), and \(c\) are scaled Landau parameters, and

\(v\) is the voltage across the terminals of the capacitor. The corresponding version of the LK equation is $${R}_{{dyn}}\cdot \frac{{dq}}{{dt}}=-\frac{d{{\mathcal{F}}}_{q}}{{dq}}$$ (2.0)

Thus, the resultant dynamic equation becomes $${R}_{{dyn}}\cdot \frac{{dq}}{{dt}}=-{aq}-b{q}^{3}-c{q}^{5}+v$$ (2.1) where \({R}_{{dyn}}\) is a frequency-dependent dynamical resistance of the

ferroelectric. Rearranging Eq. (2.1), we obtain $$v={aq}+b{q}^{3}+c{q}^{5}+{R}_{{dyn}}\cdot \frac{{dq}}{{dt}}$$ (2.2) which states that the voltage across the ZrO2 capacitor is divided

between the static ferroelectric (first three terms) and the dynamic series resistance (the last term). To include the experimentally observed tunnel current in the model, a non-linear

resistor was added in parallel to the series combination of the nonlinear capacitor and dynamical resistance. The experimental tunneling current (Fig. 1b) was fitted using an exponential

equation to model the nonlinear tunnel resistance: $${i}_{{tun}}=\frac{d{q}_{{tun}}}{{dt}}={i}_{0}\left(1-\exp \left(-{Bv}\right)\right)$$ (3.0) where \({i}_{0}\) and \(B\) are the fitting

parameters. Together, the nonlinear capacitor, the dynamic resistance and the tunnel resistance constitute the compact model for the physical ZrO2 device. Finally, the linear capacitor in

Fig. 1a was included to model the circuit as a whole (including the known characteristics of the probes did not affect the results for the ZrO2 device), which is shown in Fig. 2a. Applying

Kirchhoff’s current law at node N results in a pair of coupled nonlinear first-order ordinary differential equations (ODEs) that models the circuit:

$$\frac{d{q}_{{FE}}\left(t\right)}{{dt}}=\frac{1}{{R}_{{dyn}}}\left(-a{q}_{{FE}}-b{q}_{{FE}}^{3}-c{q}_{{FE}}^{5}+\left(v-\frac{{q}_{C}}{C}\right)\right)$$ (4.0)

$$\frac{d{q}_{C}}{{dt}}=\frac{d{q}_{{FE}}}{{dt}}+{i}_{0}\left(1-{exp} \left(-B\left(v-\frac{{q}_{C}}{C}\right)\right)\right)$$ (4.1) Here, \({q}_{{FE}}\) and \({q}_{C}\) are the charges on

the ZrO2 and the linear capacitors in series, respectively, and \(v\) is the source voltage. Because of the linear capacitor in series, the voltage across the ZrO2 capacitor becomes

\(v-{q}_{C}/C\). The parameters of the ODEs, specifically the scaled Landau parameters (\(a,b,c\)), and dynamical resistance (\({R}_{{dyn}}\)), were initially optimized manually through

trial-and-error. This involved comparing the solution (\({q}_{C}\)) of the ODEs in Eqs. (4.0) and (4.1) with the experimental data (in Fig. 1d). Equation (2.1) indicates that \({R}_{{dyn}}\)

needs to scale proportionally with frequency, as the current (\(d{q}_{{FE}}/{dt}\)) scales accordingly. This scaling condition ensures that the left-hand side term in Eq. (2.1)

(\({R}_{{dyn}}\cdot d{q}_{{FE}}/{dt}\)) is of the same order as the terms on the right-hand side (\(v,{aq},b{q}^{3},c{q}^{5}\)), which is what maintains the area of the hysteresis loops

nearly independent of applied AC voltage frequency. The manually optimized ODE parameters were further refined by using them as inputs to the Levenberg–Marquardt (LM) algorithm33,34,35,

which resulted in a model that agreed well with the experimental data as shown in Fig. 2b for the case of 100 kHz. The fitting results for 50 kHz and 200 kHz are available in the

Supplementary Information (see Supplementary Fig. 6). The set of optimized Landau parameters (\(a,b,c\)) remained highly consistent across the frequency spectrum (see Supplementary Table 1),

with coefficients of determination _R_2 > 0.99, as they are characteristic of the static energy of the capacitor. The circuit current, both experimental and model, was computed by

differentiating the charge–time data collected at 100 kHz, as shown in Fig. 2c, and then plotted against voltage. To mitigate noise in the experimental current data, the Savitzky–Golay

filter was applied to smoothen the raw data. The model succeeded in quantitatively predicting the experimental current measured across a series resistor. The results corresponding to 50 kHz

and 200 kHz and for measurements across a resistor are available in the supplementary information (see Supplementary Figs. 5 and 1). The tunneling charge overshadows the ferroelectric

characteristics in the _QV_ curves at low frequencies (see Fig. 1a, b). Additionally, input impedances from the instruments and parasitics interfere, making it essentially impossible to

obtain true quasi-static ferroelectric characteristics directly from experimental measurements. However, at higher frequencies and including the entire circuit in the model, we can determine

the Landau parameters to high accuracy by fitting the dynamical data and thus use them to construct the static model: $$V={aQ}+b{Q}^{3}+c{Q}^{5}$$ (5.0) This is plotted in Fig. 2d along

with the experimental and modeled dynamical curves obtained at 100 kHz, using the optimized parameters. A close examination of the two transition regions in the static curve revealed a

negative slope region less than 16 mV wide, which is smaller than the thermal voltage (25.85 mV) at room temperature (300 K). We thus see that the ~1.5 V width of the hysteresis in ZrO2 is

not determined by a large snap-back or ‘negative capacitance’ and instability in the static _QV_ curve, but rather is almost entirely the result of the dynamical resistance, which models the

energy dissipated in the ZrO2 as a result of the field-induced ferroelectric transition6,7 and possibly radiative loss. The model was analyzed in more detail to gain a deeper understand of

the ZrO2 capacitor. Firstly, the static (\({E}_{{stc}}\)) and differential (\({E}_{{dif}}\)) elastances (reciprocal of capacitance, to avoid physically unmeaningful divergences) were

calculated as: $${E}_{{stc}}\left(Q\right)=\frac{V}{Q}=a+b{Q}^{2}+c{Q}^{4}$$ (6.0) $${E}_{{dif}}\left(Q\right)=\frac{{dV}}{{dQ}}=a+3b{Q}^{2}+5c{Q}^{4}$$ (6.1) and plotted parametrically

against voltage (using Eq. (5) to convert from \(Q\) to \(V\), see Fig. 3a). Two distinctive points of inflection are evident in the plots of \({E}_{{stc}}\) and \({E}_{{dif}}\), where the

\({E}_{{stc}}\) curve bends inward before spreading outwards again, and the \({E}_{{dif}}\) curve transitions from positive to negative. These plots are the visual markers for the

field-induced ferroelectric transition. Contained in the inset of Fig. 3a is the Free Energy curve of the ZrO2 capacitor, plotted using Eq.(1.0) at zero voltage bias (\(v=0\)) and optimized

Landau parameters. The curve is remarkably featureless, with no local minima and only the single global minimum at \(Q=0\), representing the nonpolar and highly-symmetric tetragonal phase

(P42/nmc) ground state of ZrO26,7,36. DYNAMIC CHARACTERISTICS AND ENERGY OF ZRO2 CAPACITOR The applied voltage across the terminals of the ZrO2 capacitor is distributed between the two

principal elements of the model: the nonlinear capacitance and the dynamical resistance. It follows from Eq. (2.2) that \(v(q)\) and \(v({R}_{{dyn}})\) are the voltages across them, defined

as: $$v\left(q\right)={aq}+b{q}^{3}+c{q}^{5}$$ (7.0) $$v\left({R}_{{dyn}}\right)={R}_{{dyn}}\cdot \frac{{dq}}{{dt}}$$ (7.1) These voltage waveforms, for the case of 100 kHz, plotted against

time, can be found in Fig. 3b. The peaks in the \(v({R}_{{dyn}})\) waveform correspond to the ferroelectric switching in the ZrO2 capacitor. The ferroelectric characteristics of the ZrO2

capacitor were also obtained using a series resistor in place of the series capacitor in the circuit shown in Fig. 1c. Characterization results with the series resistor can be found in the

SI. The measured voltage waveform across the series resistor is quite similar to the \(v\left({R}_{{dyn}}\right)\) waveform, and thus reinforces the consistency of our measurements. The

\(v\left(q\right)\) waveform provides insight into the nonlinearity of the ZrO2 volatile ferroelectric capacitor. The plateaus in the \(v(q)\) waveform align with the peaks of the

\(v\left({R}_{{dyn}}\right)\) waveform, which again correlate to the ferroelectric switching. Utilizing these voltage waveforms, we calculated the stored (or reversible) and dissipated (or

irreversible) energies of the ZrO2 capacitor. Since energy can only be stored in the capacitance of the model, the reversible energy is defined using Eq. (7.0) as:

$${U}_{{rev}}\left(q\right)=\int v\left(q\right){dq}=\frac{1}{2}a{q}^{2}+\frac{1}{4}b{q}^{4}+\frac{1}{6}c{q}^{6}$$ (8.0) Optimized parameters were used to calculate

\({U}_{{rev}}\left(q\right)\). Due to the dynamical resistance in the model, energy was also dissipated. The irreversible energy loss is

$${U}_{{irv}}\left(t\right)={R}_{{dyn}}{\!\int}_{0}^{t}{\left(\frac{{dq}\left(t\right)}{{dt}}\right)}^{2}{dt}$$ (8.1) Both \({U}_{{rev}}\left(q\right)\) and \({U}_{{irv}}\left(t\right)\)

were plotted against time for one period of the applied voltage (see Fig. 3c). As the charge on the ZrO2 capacitor increases (or decreases), energy is stored (or returned to the circuit).

However, irreversible energy lost to thermal and radiative losses in the ZrO2 capacitor accumulate with time. The trend in irreversible energy loss shows a periodic sharp rise, which

coincides with the peaks observed in the \(v\left({R}_{{dyn}}\right)\) waveform, followed by a plateau. DISCUSSION This study elucidated the field-induced ferroelectric behavior of nonlinear

ZrO2 capacitors through comprehensive experimental measurements and modeling. We developed a compact dynamical model based on the Landau–Ginzburg–Devonshire and Landau–Khalatnikov theories

that agreed extremely well with experimental data, and enabled us to quantify the energy storage and dissipation mechanisms of the ZrO2 capacitor. The validation of the model against

experimental data provided valuable insights into the frequency-dependent dynamical resistance, nonlinear responses, and negative differential capacitance characteristics of ZrO2 capacitors,

the latter of which was found to be extremely small. Our findings not only deepen the understanding of field-induced ferroelectricity in ZrO2 capacitors but also pave the way for the

exploration of similar materials that may potentially be used to build oscillators and amplifiers. METHODS FABRICATION OF THE ZRO2 CAPACITORS The Zirconium Oxide (ZrO2) capacitors were

fabricated in a class 1000 cleanroom. A 100 mm Silicon wafer with 100 nm thermally grown silicon dioxide (SiO2) was chosen as the substrate. A 200 nm thin film of Tungsten (W) was deposited

as a blanket film onto the substrate for the bottom electrode using DC sputtering at 100 W power and 4 mtorr working pressure in an AJA Orion 8 Sputtering System. The wafer was then cut into

25 mm ×35 mm coupons. A 10 nm ZrO2 thin-film was deposited on top of the W electrode at 200 °C using a Cambridge NanoTech Savannah 100 Atomic Layer Deposition (ALD) system.

Tetrakis(dimethylamido)zirconium (TDMAZr or Zr[N(CH3)2]4) heated to 75 °C and water (H2O) at room temperature served as the Zr and Oxygen (O) precursors, respectively. Photolithography was

used to pattern the top electrodes as 50 µm × 50 µm pads, for which 100 nm of W and 50 nm of Platinum (Pt) was sputtered at 100 W and 4 mtorr, followed by lift-off. A second level of

photolithography was performed to selectively etch through regions of the ZrO2 to expose the buried bottom electrode. After patterning and developing the photoresist, ZrO2 was dry-etched

using Sulfur Hexaflouride (SF6), O2 and Argon (Ar). Subsequently, a 10 nm thin film of Titanium (Ti) and a 50 nm thin film of Pt were deposited using DC sputtering again. The thin film

layers were then lifted off to complete metallization and hence define bottom electrode contact pads. Ohmic contact to the bottom electrode was achieved and confirmed using quasi-static

linear DC current versus voltage (_IV_) characteristics and from the low measured resistance. The coupon was annealed at 600 °C for 1 min in nitrogen gas environment in a Rapid Thermal

Annealing system to crystallize the ZrO2 thin-film and complete the fabrication of the ZrO2 capacitors. The coupon containing the capacitors was diced and packaged in a dual in-line package

(DIP) using wire bonding directly onto the top contacts. This procedure yielded 10 out of 11 good devices as determined from the reproducibility of their measured electrical characteristics.

Several devices were subjected to high voltage inputs and long duration waveforms to characterize and recognize device degradation and failure. Other devices were also measured using probe

tips that yielded similar but less reproducible results. An appropriately sized sample was subjected to X-Ray Diffraction (XRD) analysis to determine the crystallographic structures of the

thin films that made up the ZrO2 capacitors. The XRD analysis was performed with a Rigaku Smartlab X-ray Diffractometer using Copper K-alpha radiation operated at 44 kV and 40 mA. The

measurements were acquired at an incidence angle of 1° and a step size of 0.01°, in the range from 20° to 110° (see Fig. 4a–d). ELECTRICAL CHARACTERIZATION Quasi-static DC _IV_

characteristics were measured using a Keysight B1500A Source Measurement Unit (SMU) at 83 mHz. Dynamic characteristics were obtained using a circuit consisting of a ZrO2 capacitor in series

with either a 1 nF linear capacitor or a 910 Ω resistor. A differential probe (Keysight N2750 Differential Active Probe) and a passive probe were used to simultaneously monitor the voltage

drops across the ZrO2 capacitor and the series circuit element (resistor or linear capacitor), respectively. Triangular voltage waveforms with different voltage amplitudes and frequencies

(1–200 kHz) were supplied as the input signal using a function generator (Keysight 33500B Trueform Waveform Generator). Since this circuit was mounted on a breadboard, necessary precautions

were taken to minimize ground loops and to have a unified grounding point. The chassis grounds of the function generator and the oscilloscope were connected using a thick, short, and good

electrical conductor. Data from this set-up was used to generate dynamic _QV_ characteristics. The voltages across the two elements being measured were collected in two channels of the

Keysight’s MSOX6004A Mixed Signal Oscilloscope. ODE SOLVER The Livermore Solver for Ordinary Differential Equations (LSODE/LSODA) was utilized in Python by employing the “integrate” function

from the SciPy Library to solve the non-linear first-order ordinary differential equations (ODEs) for the dynamical model37. Optimization of the ODE parameters involved a non-linear

least-squares fitting process, achieved through the “curve_fit” function of the SciPy Library. The Levenberg–Marquardt (LM) algorithm was the primary method used for the nonlinear

least-squares fitting, whereas the trust region reflective algorithm was used to constrain parameters and prevent unphysical solutions because the LM algorithm can yield unstable results

when parameter ranges are bounded33,34,35. DATA AVAILABILITY The data that support the findings of this study are available from the corresponding author upon reasonable request. REFERENCES

* Shirane, G., Sawaguchi, E. & Takagi, Y. Dielectric Properties of Lead Zirconate. _Phys. Rev._ 84, 476–481 (1951). Article  ADS  CAS  Google Scholar  * Sawaguchi, E. Ferroelectricity

versus Antiferroelectricity in the Solid Solutions of PbZrO3 and PbTiO3. _J. Phys. Soc. Jpn._ 8, 615–629 (1953). Article  ADS  CAS  Google Scholar  * Randall, C. A., Fan, Z., Reaney, I.,

Chen, L. & Trolier‐McKinstry, S. Antiferroelectrics: History, fundamentals, crystal chemistry, crystal structures, size effects, and applications. _J. Am. Ceram. Soc._ 104, 3775–3810

(2021). Article  CAS  Google Scholar  * Cross, L. E. Antiferroelectric-Ferroelectric Switching in a Simple “Kittel” Antiferroelectric. _J. Phys. Soc. Jpn._ 23, 77–82 (1967). Article  ADS 

CAS  Google Scholar  * Müller, J. et al. Ferroelectricity in Simple Binary ZrO2 and HfO2. _Nano Lett._ 12, 4318–4323 (2012). Article  ADS  PubMed  Google Scholar  * Lomenzo, P. D. et al.

Discovery of Nanoscale Electric Field‐Induced Phase Transitions in ZrO2. _Adv. Funct. Mater._ 33, 2303636 (2023). * Lomenzo, P. D. et al. Harnessing Phase Transitions in Antiferroelectric

ZrO2 Using the Size Effect. _Adv. Electron. Mater._ 8, 2100556 (2022). * Liu, Y. et al. Enhanced Ferroelectricity in Hf‐Based Ferroelectric Device with ZrO2 Regulating Layer. _Adv. Electron.

Mater._ 9, 2300208 (2023). * Liu, H. et al. ZrO2 Ferroelectric FET for Non-volatile Memory Application. _IEEE Electron Device Lett._ 40, 1419–1422 (2019). Article  ADS  CAS  Google Scholar

  * Park, J. Y. et al. Revival of Ferroelectric Memories Based on Emerging Fluorite‐Structured Ferroelectrics. _Adv. Mater._ 35, 2204904 (2023). * Xu, K. et al. Improved Ferroelectricity and

Tunneling Electroresistance by Inducing the ZrO 2 Intercalation Layer in La:HfO 2 Thin Films. _ACS Appl. Electron Mater._ 6, 1055–1062 (2024). Article  CAS  Google Scholar  * Starschich, S.

& Böttger, U. Doped ZrO2 for future lead free piezoelectric devices. _J. Appl. Phys._ 123, 044101 (2018). * Yang, K. et al. Energy conversion and storage using artificially induced

antiferroelectricity in HfO2/ZrO2 nanolaminates. _Compos B Eng._ 236, 109824 (2022). Article  CAS  Google Scholar  * Yi, S.-H., Lin, H.-C. & Chen, M.-J. Ultra-high energy storage density

and scale-up of antiferroelectric TiO 2 /ZrO 2 /TiO 2 stacks for supercapacitors. _J. Mater. Chem. A Mater._ 9, 9081–9091 (2021). Article  CAS  Google Scholar  * Khan, A. I. et al. Negative

capacitance in a ferroelectric capacitor. _Nat. Mater._ 14, 182–186 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Cheng, P.-H. et al. Negative capacitance from the inductance of

ferroelectric switching. _Commun. Phys._ 2, 32 (2019). Article  Google Scholar  * Gao, W. et al. Room-Temperature Negative Capacitance in a Ferroelectric–Dielectric Superlattice

Heterostructure. _Nano Lett._ 14, 5814–5819 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Islam Khan, A. et al. Experimental evidence of ferroelectric negative capacitance in

nanoscale heterostructures. _Appl. Phys. Lett._ 99, 113501 (2011). * Park, H. W. et al. Exploring the Physical Origin of the Negative Capacitance Effect in a

Metal–Ferroelectric–Metal–Dielectric Structure. _Adv. Funct. Mater._ 33, 2304754 (2023). * Hoffmann, M. et al. Antiferroelectric negative capacitance from a structural phase transition in

zirconia. _Nat. Commun._ 13, 1228 (2022). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Jo, S. et al. Negative differential capacitance in ultrathin ferroelectric hafnia.

_Nat. Electron_ 6, 390–397 (2023). Article  CAS  Google Scholar  * Sivasubramanian, S., Widom, A. & Srivastava, Y. Equivalent circuit and simulations for the Landau-Khalatnikov model of

ferroelectric hysteresis. _IEEE Trans. Ultrason Ferroelectr. Freq. Control_ 50, 950–957 (2003). Article  PubMed  Google Scholar  * Park, H. W., Roh, J., Lee, Y. Bin & Hwang, C. S.

Modeling of Negative Capacitance in Ferroelectric Thin Films. _Adv. Mater._ 31, 1805266 (2019). * Segatto, M., Rupil, F. & Esseni, D. Analytical Procedure for the Extraction of Material

Parameters in Antiferroelectric ZrO 2. _IEEE Trans. Electron Devices_ 70, 3037–3042 (2023). Article  ADS  CAS  Google Scholar  * Srivastava, N. & Weng, G. J. A theory of double

hysteresis for ferroelectric crystals. _J. Appl. Phys._ 99, 054103 (2006). * Andrawis, R. & Roy, K. Antiferroelectric Tunnel Junctions as Energy-Efficient Coupled Oscillators: Modeling,

Analysis, and Application to Solving Combinatorial Optimization Problems. _IEEE Trans. Electron Devices_ 67, 2974–2980 (2020). Article  ADS  CAS  Google Scholar  * Sawyer, C. B. & Tower,

C. H. Rochelle salt as a dielectric. _Phys. Rev._ 35, 269 (1930). Article  ADS  CAS  Google Scholar  * Zhu, Q. et al. Frequency dependence of antiferroelectricferroelectric phase transition

of PLZST ceramic. _J. Am. Ceram. Soc._ 105, 2634–2645 (2022). Article  MathSciNet  CAS  Google Scholar  * Chen, Z., Zhang, Y., Li, S., Lu, X.-M. & Cao, W. Frequency dependence of the

coercive field of 0.71Pb(Mg1/3Nb2/3)O3-0.29PbTiO3 single crystal from 0.01 Hz to 5 MHz. _Appl. Phys. Lett_. 110, 202904 (2017). * Devonshire, A. F. Theory of ferroelectrics. _Adv. Phys._ 3,

85–130 (1954). Article  ADS  Google Scholar  * Ginzburg, V. L. Phase Transitions in Ferroelectrics (Some Historical Remarks). _Ferroelectrics_ 267, 23–32 (2002). Article  ADS  CAS  Google

Scholar  * Ishibashi, Y. & Orihara, H. Theory of nonlinear response. _Ferroelectrics_ 156, 185–190 (1994). Article  ADS  Google Scholar  * Moré, J. J. The Levenberg-Marquardt algorithm:

Implementation and theory. 105–116 https://doi.org/10.1007/BFb0067700 (1978). * LEVENBERG, K. A Method For The Solution Of Certain Non-Linear Problems In Least Squares. _Q, Appl, Math._ 2,

164–168 (1944). Article  MathSciNet  Google Scholar  * Marquardt, D. W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. _J. Soc. Ind. Appl. Math._ 11, 431–441 (1963).

Article  MathSciNet  Google Scholar  * Reyes-Lillo, S. E., Garrity, K. F. & Rabe, K. M. Antiferroelectricity in thin-film ZrO2 from first principles. _Phys. Rev. B_ 90, 140103 (2014).

Article  ADS  Google Scholar  * Radhakrishnan, K. Description and use of LSODE, the Livermore Solver for Ordinary Differential Equations. https://ntrs.nasa.gov/citations/19940030753 (1993).

Download references ACKNOWLEDGEMENTS The authors thank the funding support by US Air Force Research Laboratory (FA8750-22-1-0501), Air Force Office of Scientific Research through the

Multidisciplinary University Research Initiative program under contract no. FA9550-19-1-0213, National Science Foundation under contract no. 2023752 and 2036359. R.K. appreciates the support

from AFOSR Young Investigator Research Program under contract no. FA9550-23-1-0201. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Electrical and Computer Engineering,

University of Massachusetts, Amherst, MA, 01003, USA Shiva Asapu, Qiangfei Xia & J. Joshua Yang * Department of Electrical and Computer Engineering, University of Southern California,

Los Angeles, CA, 90089, USA Taehwan Moon, Ruoyu Zhao, R. Stanley Williams & J. Joshua Yang * Materials and Manufacturing Directorate, Air Force Research Laboratory, Wright Patterson Air

Force Base, Dayton, OH, 45433, USA Krishnamurthy Mahalingam, Kurt G. Eyink & Sabyasachi Ganguli * Department of Polymer Science and Engineering, University of Massachusetts, Amherst, MA,

01003, USA James Nicolas Pagaduan & Reika Katsumata * Department of Electrical and Computer Engineering, Texas A&M University, College Station, TX, 77843, USA R. Stanley Williams

Authors * Shiva Asapu View author publications You can also search for this author inPubMed Google Scholar * Taehwan Moon View author publications You can also search for this author

inPubMed Google Scholar * Krishnamurthy Mahalingam View author publications You can also search for this author inPubMed Google Scholar * Kurt G. Eyink View author publications You can also

search for this author inPubMed Google Scholar * James Nicolas Pagaduan View author publications You can also search for this author inPubMed Google Scholar * Ruoyu Zhao View author

publications You can also search for this author inPubMed Google Scholar * Sabyasachi Ganguli View author publications You can also search for this author inPubMed Google Scholar * Reika

Katsumata View author publications You can also search for this author inPubMed Google Scholar * Qiangfei Xia View author publications You can also search for this author inPubMed Google

Scholar * R. Stanley Williams View author publications You can also search for this author inPubMed Google Scholar * J. Joshua Yang View author publications You can also search for this

author inPubMed Google Scholar CONTRIBUTIONS R.S.W., S.A. and J.J.Y. conceived the concept. R.S.W., J.J.Y., S.A. and T.M. designed the experiments. S.A. fabricated the devices, performed

electrical characterization, and wrote the code to solve the differential equations. J.N.P. carried out rapid thermal annealing. K.M. and K.J.E. performed GI-XRD characterization. S.A.,

T.M., R.S.W. and J.J.Y. prepared, reviewed and edited the manuscript with the help of inputs from R.Z., S.G., R.K. and Q.X. CORRESPONDING AUTHORS Correspondence to R. Stanley Williams or J.

Joshua Yang. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to

jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under

a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as

long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not

have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s

Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not

permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit

http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Asapu, S., Moon, T., Mahalingam, K. _et al._ Accurate compact nonlinear

dynamical model for a volatile ferroelectric ZrO2 capacitor. _npj Unconv. Comput._ 1, 7 (2024). https://doi.org/10.1038/s44335-024-00007-z Download citation * Received: 26 March 2024 *

Accepted: 12 August 2024 * Published: 02 September 2024 * DOI: https://doi.org/10.1038/s44335-024-00007-z SHARE THIS ARTICLE Anyone you share the following link with will be able to read

this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative