ABSTRACT An alternative measure of x-ray absorption spectroscopy (XAS) called inverse partial fluorescence yield (IPFY) has recently been developed that is both bulk sensitive and free of

saturation effects. Here we show that the angle dependence of IPFY can provide a measure directly proportional to the total x-ray absorption coefficient, µ(_E_). In contrast, fluorescence

yield (FY) and electron yield (EY) spectra are offset and/or distorted from µ(_E_) by an unknown and difficult to measure amount. Moreover, our measurement can determine µ(_E_) in absolute

units with no free parameters by scaling to µ(_E_) at the non-resonant emission energy. We demonstrate this technique with measurements on NiO and NdGaO3. Determining µ(_E_) across

CHARACTERIZATION OF JUST ONE ATOM USING SYNCHROTRON X-RAYS Article 31 May 2023 TUNABLE FREE-ELECTRON X-RAY RADIATION FROM VAN DER WAALS MATERIALS Article 14 September 2020 INTRODUCTION X-ray

absorption spectroscopy (XAS) is widely used in biology, the physical sciences and materials engineering as a powerful probe of spatial and electronic structure1,2,3,4. In XAS, the

byproducts of the absorption process, electron yield (EY) and fluorescence yield (FY), are commonly used as measures of the x-ray absorption5,6 since transmission experiments often require

impractically thin samples. The principle behind EY and conventional FY measurements (which measure the fluorescence from resonant emission processes and shall henceforth be simply referred

to as FY) is that the electron and fluorescence yields bear some proportionality to the absorption coefficient – the number of electrons or photons emitted from decaying atoms in a given

thickness of sample is proportional to the number atoms that are excited. However, the measured FY or EY spectra are not strictly proportional to the total absorption coefficient for several

reasons. First, the thickness of sample probed depends on the relative penetration depth (attenuation length) of the incident photons and the escape depth of the emitted electrons, in the

case of electron yield, or photons, in the case of fluorescence yield. As the attenuation length varies over an absorption edge, it is possible for the attenuation length to approach the

electron escape depth, leading to saturation effects in EY and distorting the measured spectra7. In the case of FY measurements of concentrated species, both the total x-ray absorption

coefficient and the absorption due to the edge of interest vary strongly, leading to distortions of the spectra referred to as saturation effects or as “self-absorption effects”8,9. Such FY

spectra can sometimes be corrected for self-absorption effects using the angle dependence of the FY8,9. However, this correction procedure can be unreliable since resonant x-ray emission

processes10 that are not accounted for in the self-absorption correction can have a significant influence on the energy dependence of the fluorescence yield11. Second, the magnitude of the

EY and FY both depend on the relative probability, ω_fl_ , that an excited atom will decay by emitting photons as opposed to electrons12. This relative probability differs from atom to atom

and edge to edge and is generally not known with great precision. Third, the emission is distributed over a range of electron and photon energies. A given detector will not detect all

electron or photon energies with equal efficiency. In the case of EY, magnetic or electrostatic fields will also influence the efficiency of detection in the system, which may vary between

experiments. In addition, the quantum efficiency of EY (the number of electrons emitted per incident photon) will also vary with photon energy3. The consequence of all these factors is that

the magnitude of the EY or FY signal will generally have a value that is not proportional to the total absorption coefficient but is rather offset or distorted by some often unknown or

difficult to calculate factors. Fortunately, for many applications of XAS, the key features in absorption spectra measured by EY or FY are retained and can still be interpreted to glean

important qualitative information about the electronic or spatial structure. However, in many instances, such as correcting for self-absorption effects, calculating resonant scattering

cross-sections or determining x-ray penetration depth, it is important to know the magnitude of the total absorption coefficient in absolute units. Moreover, knowing this could open the door

to using XAS as a quantitative tool for compositional analysis of materials. In principle, the magnitude and energy dependence of the total absorption coefficient contains information about

the composition of a material in addition to information about the electronic and spatial structure. As the photon energy is increased through an absorption edge, the absorption increases

in a step-wise fashion when core electrons are photo-excited with enough energy to enter the continuum of unoccupied states. The magnitude of the edge-step relative to the pre-edge can

provide a measure of material composition. The various atomic contributions can be determined using tabulated13 or calculated14 values of the absorption cross-section that are conveniently

and freely available online from the Center for X-ray Optics (CXRO) or the National Institute of Standards and Technology (NIST). With these inputs, the magnitude of the XAS, in particular

the edge-step, can be used as a robust quantitative measure of material composition. By fitting the available tabulated or calculated atomic absorption data to the pre- and post-edge of a

measured absorption spectrum, one can experimentally derive the stoichiometry of a material in a non-destructive manner. Since they do not measure the total absorption coefficient, FY and EY

are not well suited for this type of analysis. Transmission measurements, however, do provide a direct and quantitative measure of the absorption cross-section and such measurements are

routinely performed at hard and soft x-ray beamlines15. However, transmission spectra can be subject to “thickness effects” and should only be performed with sufficiently thin samples16,17.

Preparing samples with appropriate thickness may be challenging or impossible depending on the nature of the sample, particularly for soft x-rays where sample thicknesses less than 1 micron

are typically required. The recent development of inverse partial fluorescence yield allows us to overcome the aforementioned shortcomings of EY and FY18. Unlike EY and FY measurements, IPFY

is both bulk sensitive and free of saturation effects. In this paper, we demonstrate that the theory of IPFY can be extended and exploited to reliably obtain a measure proportional to the

total x-ray absorption coefficient, µ(_E_), with the proportionality constant being the total absorption coefficient at the non-resonant emission energy, µ(_E__f_ ). This result is confirmed

by excellent agreement with tabulated or calculated values of the measured IPFY of NiO and NdGaO3 single crystals. The ability to derive quantitative information from XAS with IPFY creates

new opportunities for chemical speciation and compositional analysis of materials. In addition, we demonstrate the applicability of IPFY to XAS measurements of strongly insulating samples.

In NdGaO3, neither EY or FY measurements provide reliable XAS spectra of the Nd _M_5,4 edges due to strong charging and saturation effects, respectively. In contrast, IPFY provides excellent

agreement with previously measured XAS on Nd metal. RESULTS INVERSE PARTIAL FLUORESCENCE YIELD IPFY operates on a different principle than EY or FY, effectively measuring the attenuation

length into a sample rather than the number of atoms that are excited and subsequently relax. With IPFY, an energy sensitive detector is used to monitor non-resonant x-ray emission as the

incident photon energy is scanned through an absorption edge. This non-resonant (normal) emission may be from a different element or core electron than that associated with the absorption

edge under investigation. As the attenuation length decreases through an absorption edge, the same number of atoms are excited (since all photons are absorbed for samples which are thick

relative to the x-ray penetration length), but fewer of these excitations will correspond to non-resonant transitions. Subsequently, the intensity of the non-resonant emission will dip as

the absorption coefficient peaks through an absorption edge. The intensity of the non-resonant emission will also depend on the absorption cross-section of the atom and core electron

corresponding to the non-resonant transition and on the attenuation length of the emitted photons. However, these factors are constant or vary weakly through an absorption edge, in the x-ray

absorption near edge structure (XANES). As a result, a straightforward inversion of the partial fluorescence yield (PFY) arising from a non-resonant emission process provides an accurate

measure of x-ray absorption cross-section in the XANES18. As discussed in Ref. 18, since it is non-resonant emission processes that contribute to this measure of PFY, saturation

(self-absorption) effects are avoided. Moreover, the large variation of the fluorescence decay rates observed across edge steps for resonant fluorescence processes11, as in conventional FY,

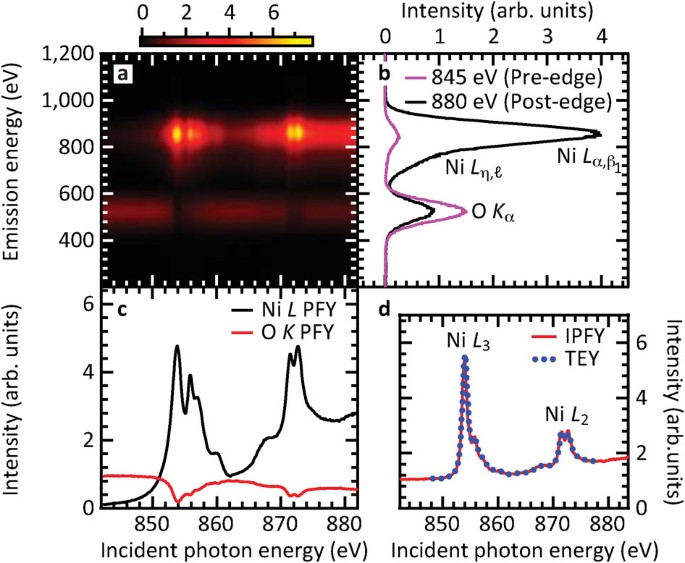
do not factor into the measurement of IPFY, simplifying the analysis and interpretation of IPFY relative to FY. The extraction of IPFY from the energy-resolved x-ray emission of NiO is

demonstrated in Fig. 1. The x-ray emission of NiO is measured as the incident photon energy, _E__i_ , is scanned through the Ni _L_ edge (Fig. 1a). The Ni _L_ absorption edge corresponds to

exciting a Ni 2_p_ electron into unoccupied 3_d_ states near the edge (and a continuum of states further above the edge), leaving behind a 2_p_ core hole. The emission spectra (Fig. 1b)

exhibit a peak at emission energy _E__f_ ∼ 840 eV that corresponds to resonant emission from Ni. This emission is due to the electrons making transitions to fill in the Ni 2_p_ core-hole

left behind by the Ni _L_ edge absorption process. The PFY from the Ni 2_p_ emission (Fig. 1c, black curve) suffers significantly from self-absorption effects and bears little resemblance to

the absorption coefficient. In addition to the Ni _L_ absorption, the x-ray absorption and emission also have contributions from non-resonant transitions of other core electrons of Ni

(3_s_, 3_p_) and from oxygen (the total linear absorption coefficient is the sum of these contributions, µ(_E__i_ ) = µ Ni(_E__i_ ) + µ O(_E__i_ ), where µ Ni(_E__i_ ) = µ Ni,2_p_(_E__i_ ) +

µ Ni,3_s_(_E__i_ ) + µ Ni,3_p_(_E__i_ )+ …)19. As shown in Fig. 1a and 1b there is a band of emission centred at 524 eV corresponding to the non-resonant emission of O 2_p_ valence

electrons decaying to fill in the O 1_s_ core hole (O _K_ emission). The PFY from the O _K_ emission (Fig. 1c, red curve) exhibits dips at the Ni _L_3,2 absorption edges. The inverse of this

spectrum, the IPFY = 1/PFYO_K_, is shown in Fig. 1d along with total electron yield (TEY) measurements of NiO from Ref. 20 that have been scaled and offset to match the IPFY. Similar to

previous work18 on La1.475Nd0.4Sr0.125CuO4, the agreement between IPFY and TEY is very good, highlighting the ability of IPFY to measure the energy dependence of the absorption coefficient

of Ni without the strong self-absorption effects experienced with PFY. GEOMETRY FACTOR OF IPFY IN THE XANES REGION It has been shown that the IPFY of thick, homogeneous materials is a

function of the total x-ray absorption coefficient µ(_E__i_ )18: where _A_ = 4π/η(_E__f_ )Ωω_Y_ (_E__f_ )µ_Y_ (_E__i_ ) and . Here α and β are the angles of incidence and emission,

respectively, as measured from the sample surface, η(_E__f_ ) is the quantum efficiency of the detector at the emission energy, Ω is the detector solid angle, µ_Y_ (_E__i_ ) is the

contribution to the total absorption coefficient from the excitation of core electron _Y_ (ex. O 1_s_) and ω_Y_ (_E__f_ ) is the probability of fluorescence at energy _E__f_ resulting from

electrons decaying to fill in the core hole left by _Y_. In Eq. (1), the constant _B_ is independent of _E__i_ and _A_ depends only weakly on _E__i_ over a narrow energy range (XANES) so it

can be treated approximately as constant18. This approximation fails over a large energy range, requiring one to account for the energy dependence of μ_Y_ (_E__i_ ) and the quantum

efficiency of the _I__0_ measurement, which we demonstrate later. However, in a narrow energy range, it follows that IPFY is proportional to μ(_E__i_ ) plus an offset proportional to _B_.

The crucial feature of Eq. (1) is that the size of the offset _B_ is determined by the geometrical factor sin α/sin β. This allows one to determine μ(_E__i_ )/μ(_E__f_ ) from experiments

with different measurement geometries. In Fig. 2, we demonstrate that the IPFY of NiO obeys the expected dependence on the sample geometry as detailed in Eq. (1). First, the Ni _L_3,2 PFY

spectra measured for various geometries (Fig. 2a) depict the strong angle-dependence of self-absorption effects in FY measurements. Notably, attempts to correct the PFY for self-absorption

effects using the angle dependence8,9 (not shown) do not yield the correct spectra. In contrast, the IPFY spectra measured with the same geometries (Fig. 2b) are undistorted and offset from

one another, in agreement with Eq. (1). The inset in Fig. 2b is a plot of the value of the IPFY spectra at a single value of the incident photon energy [_E__i_ = 845 eV (red circles)] as a

function of sin α/sin β for the given experimental geometries. As expected, this offset fits well to a straight line with an intercept equal to _Aμ_(845 eV) and a slope equal to _Aμ_(_E__f_

). Subtracting _Aμ_(_E__f_ ) sin α/sin β for each of the spectra, we find that they collapse onto a single curve (the slight variations in peak intensities are primarily due to magnetic

linear dichroism in NiO due to anti-ferromagnetic ordering of the Ni spins in the (111) plane21). The key point of this analysis is that the resulting spectra, derived entirely from

experiment, are directly proportional to the total absorption coefficient without any offsets. The proportionality to μ(_E__i_ ) is verified by comparing our measurement to tabulated13 and

calculated14 values of μ(_E__i_ ). The calculated and tabulated data capture the transitions from the core electron to the continuum, accurately reproducing the edge-step, but do not include

the multiplet physics associated with the 2_p_ to 3_d_ transition. We use the calculated value of the absorption coefficient at the O _K_ emission energy (μ(_E__f_ = 524eV) = 3.14×106 m−1

for NiO from Ref. 13) to normalize the subtracted offset and determine the proportionality constant _A_. Note that the O _K_ emission is due primarily to 2_p_ valence electrons decaying to

fill the 1_s_ core hole and is peaked at a photon energy below the absorption threshold. The data shown in Fig. 2c has been scaled using μ(_E__f_ ) (a non-arbitrary scaling factor) and is

shown along with the tabulated13 (green curve) and calculated14 (red squares) x-ray absorption coefficient. Using this single scaling parameter, we find that the measured spectra are in

excellent agreement with the tabulated coefficients in both the pre- and post-edge regions, capturing both the energy dependence and the edge-step. This demonstrates that IPFY provides a

measure directly proportional to the total absorption coefficient with the proportionality constant being μ(_E__f_ ). In contrast, quantitative analysis of EY or FY spectra requires scaling

and offsetting data to calculated values of the absorption coefficient above and below the edge, essentially fixing the edge-step3. This latter procedure requires prior knowledge of the

material composition and is subject to uncertainties in the tabulated or calculated values which are estimated at 5–20% between 500 and 1000 eV and even higher near absorption edges22.

Moreover, XAS measurements often still have significant structure above an absorption edge in the form of extended x-ray absorption fine structure (EXAFS) that is not accounted for in the

tabulated or calculated values, resulting in additional errors in normalizing data above an absorption edge. In contrast, with IPFY, we obtain the energy dependence of μ(_E__i_ ) directly

from measurement and can scale the data at a single point well below the absorption edge. The result of this normalization can be independently checked against the absorption above and below

the absorption edge in question and multiple angles can be measured to ensure self-consistency, resulting in a reliable and accurate normalization of the data. IPFY BEYOND THE XANES In the

NiO measurements shown above, the described offsetting procedure works well over the narrow energy range covered, giving a quantity approximately proportional to μ(_E__i_ ). However, over a

larger energy window, the energy dependence of μ_Y_ (_E__i_ ) can be significant. An example of this effect is shown in measurements of NdGaO3 over a wide energy range. In Fig. 3a, the IPFY

measured using the O _K_ emission of NdGaO3 is shown for three measurement geometries over an extended energy range covering the Nd _M_ edge. The spectra are not rigidly offset, instead

appearing to be subject to a sloping background in addition to an offset. This background is due to the energy dependence of μ O_K_(_E__i_ ) and also to the energy dependence of our

measurement of the incident photon flux, _I_0. In our measurement and many XAS measurements, _I_0 is measured using a Au grid with 85% transmission that is placed between the sample and the

last optical component. The total electron yield from the grid, _I_Grid, is used to measure the incident photon flux. This measurement, however, depends not only on _I_0, but also on the

quantum efficiency of the mesh, ν(_E__i_ ) (the number of electrons generated per incident photon), which in general will be energy dependent. As such, _I_Grid(_E__i_ ) = _I_0(_E__i_

)ν(_E__i_ ) and Eq. (1) should be modified to: where _D_ = _Aμ__Y_ (_E__i_ ). Fortunately, the energy dependence of both ν(_E__i_ ) and μ_Y_ (_E__i_ ) can be unambiguously eliminated from

the data by subtracting IPFY spectra measured with different measurement geometries and normalizing to the geometry (ν(_E__i_ ) generally also enters into EY and FY measurements, but is

typically not corrected for). From Eq. (2) it follows that where _j_ and _k_ correspond to different measurement geometries and _S_(_E__i_ ) is independent of the choice of _j_ and _k_. We

can now write which is simply rearranged to yield the total x-ray absorption coefficient: In Fig. 3, this subtraction is shown, giving _S_(_E__i_ ) that is a smooth function of energy. As

shown in Fig. 3c, dividing the spectra in Fig. 3a by _S_(_E__i_ ), provides spectra that are rigidly offset over a wide range in energy. Subtracting sin α/sin β from the spectra provides

µ(_E__i_ )/µ(_E__f_ ), collapsing the data onto a single curve, which is then scaled using a calculated value14 of µ(_E__f_ = 524 eV) as shown in Fig. 3d. When normalized in this way, the

spectra are in excellent quantitative agreement with the calculated absorption coefficient over a wide energy range above and below the Nd _M_5,4 absorption edge, as shown in Fig. 4. IPFY IN

STRONG INSULATORS Finally, we would like to emphasize the role of IPFY to study insulating samples that can be difficult or impossible to measure correctly using FY or EY. An example of

such a system is NdGaO3. This material is an insulator commonly used as a substrate for oxide film growth. EY measurements of the Nd _M_ edge in NdGaO3, shown in Fig. 5a, exemplify issues

one can encounter when measuring the EY of samples. Here the EY has an unphysical negative edge jump at the absorption edge. The unusual behaviour is attributed to a build-up in positive

charge near the surface of the sample that effectively reduces the number of emitted electrons. We were able to reduce the effect by recording the spectra by scanning the incident photon

energy in the negative direction (1020 eV to 980 eV) or measuring different spots on the sample, but ultimately these spectra are not reliable. PFY and TFY in this material are also

unreliable. The Nd edge PFY measurements, shown in Fig. 5b, are heavily distorted by self-absorption effects, similar to NiO. In contrast, the IPFY (Fig. 5c) provides the correct XAS

spectrum for Nd3+. This is evidenced by excellent agreement with XAS in pure Nd, which like NdGaO3 has Nd3+ character and is described well by atomic multiplet calculations23. In this case,

both EY and FY provide erroneous results and transmission measurements are not possible due to the thickness of the sample. As such, IPFY provides the only means to measure the correct XAS

spectrum. We anticipate IPFY to be widely applicable to similar cases. DISCUSSION Experimental studies that require accurate knowledge of optical constants or atomic scattering form factors,

such as in modelling of resonant reflectivity or x-ray scattering, stand to benefit substantially from angle dependent IPFY since it provides a measure of the total absorption coefficient.

In such studies, it is common to scale and offset XAS spectra above and below an absorption edge to tabulated atomic calculations or absorption data24. This procedure requires knowledge of

the composition of a material and requires measurements that extend sufficiently above absorption edges to avoid EXAFS resonances. It is not always possible to meet these requirements and in

such cases the determination of optical constants or atomic scattering form factors will necessarily be subject to systematic errors. In contrast, with angle dependent IPFY, µ(_E__i_ ) and

µ(_E__f_ ) can be determined with a simple fitting approach that does not depend on prior knowledge of material composition. Consequently, scaling the measured absorption to absolute units

using µ(_E__f_ ) enables the determination of atomic form factors with the appropriate edge-step even if sample composition is not previously known or if the XAS spectra do not extend

sufficiently above the EXAFS. As an accurate measure of µ(_E__i_ ), IPFY spectroscopy could become a powerful tool in non-destructive quantitative analysis of material composition, which can

be done separately or in conjunction with XANES or EXAFS measurements of electronic and spatial structure. Without prior knowledge of material composition, it is possible to fit µ(_E__i_

)/µ(_E__f_ ) to a sum of the tabulated atomic absorption coefficients in order to determine the relative weights of each atomic species in a sample. Furthermore, µ(_E__f_ ) can be determined

by the fitting routine as it too is the weighted sum of the atomic contributions. Thus, in a fully self-consistent way, it is possible to utilize IPFY spectra to estimate the composition of

an unknown sample. Even if a quantitative estimate is not needed, the magnitude of the pre-edge relative to the post-edge bears a distinct signature of the quantity of an element relative

to the other elements in the material. A simple comparison of the magnitude of the edge-step compared to calculations or to IPFY on similar materials can then be used as a clear measure of

sample composition. We believe this kind of non-destructive estimate of sample composition will be very useful to XAS practitioners as a simple means to verify the stoichiometry of a given

sample. Finally, we would like to comment on the applicability of IPFY to the hard x-ray regime. Thus far, IPFY has only been demonstrated using soft x-rays. However, we feel IPFY would

likely also be useful for XAS at hard x-ray energies. In order to measure IPFY in this case, one would require the appropriate selection of emission lines. While low energy emission lines

would exist, their excitation cross-section would be quite small and the presence of air and/or windows between the sample and the detector may make it impossible to detect these. However,

in compounds with multiple elements, one could in principle utilize non-resonant _K_ or _L_ emission lines (at intermediate to hard x-ray energies) to study the _K_ edge absorption of

another element. Hence, we believe that IPFY studies at hard x-ray energies are feasible and could be performed using a similar detection scheme as we have used at soft x-ray energies. In

conclusion, we have demonstrated a measure of the total x-ray absorption coefficient using angle dependent IPFY. Unlike in EY or conventional FY measurements, the offset in IPFY can be

subtracted unambiguously from experiments with varied geometry to provide data directly proportional to µ(_E__i_ ) and undistorted by saturation or self-absorption effects. By scaling to a

single value of µ(_E__f_ ), µ(_E_) is obtained in absolute units. We anticipate this technique to have wide applicability in many areas of science and engineering, potentially opening XAS up

to non-destructive, quantitative analysis of material composition. METHODS The XAS measurements were performed at the Canadian Light Source's 11-ID SGM beamline. All measurements were

made at room temperature. The drain current of the sample provided the electron yield. An energy-dispersive silicon drift detector (SDD) with an energy resolution of ∼120 eV was used to

collect the emission spectra as a function of incident photon energy. The SDD was fixed in position (25.8° below the plane and 42.5° from the beam axis) and the sample was rotated about the

vertical axis to vary α and β, the angles of incidence and emission, respectively. Dark counts on the detector were negligible. However, a small background in the 200–2000 eV region of the

NiO emission spectra was observed, likely due to a slight mis-calibration of the detector electronics. This background potentially introduced an error of up to 20% at the Ni _L_3 peak and 3%

in the post-edge. The single crystal of cubic NiO was polished to a surface roughness less than 0.03 µm. Its dimensions were 5×5 by 0.5 mm thick and it was oriented such that the 〈100〉

direction was perpendicular to the sample surface. The NdGaO3 single crystal was a 10×10 mm by 0.5 mm thick, polished substrate oriented with the 〈100〉 direction perpendicular to the sample

surface. CHANGE HISTORY * _ 06 MARCH 2013 A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has been fixed in the paper. _ REFERENCES

* Lee, P., Citrin, P., Eisenberger, P. & Kincaid, B. Extended X-ray absorption fine structure - its strengths and limitations as a structural tool. Rev. Mod. Phys 53, 769 (1981).

Article  CAS  ADS  Google Scholar  * Wende, H. Recent advances in x-ray absorption spectroscopy. Rep. Prog. Phys. 67, 2105–2181 (2004). Article  CAS  ADS  Google Scholar  * Stöhr, J. NEXAFS

Spectroscopy (Springer, New York, 1996). * deGroot, F. & Kotani, A. Core Level Spectroscopy of Solids (CRC Press, Boca Raton, FL, 2008). * Gudat, W. & Kunz, C. Close similarity

between photoelectric yield and photoabsorption spectra in the soft-x-ray range. Phys. Rev. Lett. 29, 169–172 (1972). Article  CAS  ADS  Google Scholar  * Jaklevic, J. et al. Fluorescence

detection of EXAFS: Sensitivity enhancement for dilute species and thin films. Solid State Commun. 23, 679–682 (1977). Article  CAS  ADS  Google Scholar  * Nakajima, R., Stöhr, J. &

Idzerda, Y. U. Electron-yield saturation effects in _L_-edge _x_-ray magnetic circular dichroism spectra of Fe, Co and Ni. Phys. Rev. B 59, 6421 (1999). Article  CAS  ADS  Google Scholar  *

Tröger, L. et al. Full correction of the self-absorption in soft-fluorescence extended x-rayabsorption fine structure. Phys. Rev. B 46, 3283–3289 (1992). Article  ADS  Google Scholar  *

Eisebitt, S., Böske, T., Rubensson, J.-E. & Eberhardt, W. Determination of absorption coefficients for concentrated samples by fluorescence detection. Phys. Rev. B 47, 14103–14109

(1993). Article  CAS  ADS  Google Scholar  * Kotani, A. & Shin, S. Resonant inelastic x-ray scattering spectra for electrons in solids. Rev. Mod. Phys. 73, 203–246 (2001). Article  CAS 

ADS  Google Scholar  * de Groot, F., Arrio, M., Sainctavit, P., Cartier, C. & Chen, C. Fluorescence yield detection: Why it does not measure the X-ray absorption cross section. Solid

State Communications 92, 991–995 (1994). Article  CAS  ADS  Google Scholar  * Hubbell, J. et al. A review, bibliography and tabulation of _K_, _L_ and higher atomic shell x-ray fluorescence

yields. J. Phys. Chem. Ref. Data 23, 339 (1994). Article  CAS  ADS  Google Scholar  * Henke, B., Gullikson, E. & Davis, J. X-ray interactions: photoabsorption, scattering, transmission

and reflection at _E_ = 50–30000 eV, _Z_ = 1–92. Atomic Data and Nuclear Data Tables 54, 181 (1993). Article  CAS  ADS  Google Scholar  * Chantler, C. Theoretical form factor, attenuation

and scattering tabulation for _Z_ = 1–92 from _E_ = 1–10 eV to _E_ = 0.4–1.0 MeV. J. Phys. Chem. Ref. Data 24, 71 (1995). Article  CAS  ADS  Google Scholar  * de Groot, F. M. F., de Smit,

E., van Schooneveld, M. M., Aramburo, L. R. & Weckhuysen, B. M. In-situ Scanning Transmission X-Ray Microscopy of Catalytic Solids and Related Nanomaterials. ChemPhysChem 11, 951–962

(2010). Article  CAS  Google Scholar  * Parratt, L. G., Hempstead, C. F. & Jossem, E. L. Thickness effect in absorption spectra near absorption edges. Phys. Rev 105, 1228–1232 (1957).

Article  CAS  ADS  Google Scholar  * Stern, E. A. & Kim, K. Thickness effect on the extended-x-ray-absorption-fine-structure amplitude. Physical Review B 23, 3781 (1981). Article  CAS 

ADS  Google Scholar  * Achkar, A. J. et al. Bulk sensitive x-ray absorption spectroscopy free of self-absorption effects. Phys. Rev. B 83, 081106 (2011). Article  ADS  Google Scholar  * Yeh,

J. & Lindau, I. Atomic subshell photoionization cross sections and asymmetry parameters: 1 ≤ _Z_ ≤ 103. At. Data Nucl. Data Tables 32, 1 (1985). Article  CAS  ADS  Google Scholar  *

Abbate, M. et al. Soft-x-ray-absorption studies of the location of extra charges induced by substitution in controlled-valence materials. Phys. Rev. B 44, 5419–5422 (1991). Article  CAS  ADS

  Google Scholar  * Stöhr, J., Padmore, H., Anders, S., Stammler, T. & Scheinfein, M. Principles of x-ray magnetic dichroism spectromicroscopy. Surf. Rev. Lett. 5, 1297 (1998). Article 

ADS  Google Scholar  * Chantler, C. Detailed tabulation of atomic form factors, photoelectric absorption and scattering cross section and mass attenuation coefficients in the vicinity of

absorption edges in the soft x-ray(_Z_ = 30–36, _Z_ = 60–89, _E_ = 0.1 keV–10 keV), addressing convergence issues of earlier work. J. Phys. Chem. Ref. Data 29, 597 (2000). Article  CAS  ADS

  Google Scholar  * Thole, B. T. et al. _3d_ x-ray-absorption lines and the 3_d_94_f__n_+1 multiplets of the lanthanides. Phys. Rev. B 32, 5107–5118 (1985). Article  CAS  ADS  Google Scholar

  * Stöhr, J. & Seigmann, H. Magnetism: From Fundamentals to Nanoscale Dynamics. (Springer-Verlag, Berlin-Heidelberg, 2006). Download references ACKNOWLEDGEMENTS This research is

supported by the Natural Sciences and Engineering Research Council of Canada and by the National Science Foundation through DMR-0847385 and the MRSEC program under DMR-0520404 (Cornell

Center for Materials Research). The research described in this paper was performed at the Canadian Light Source, which is supported by NSERC, NRC, CIHR and the University of Saskatchewan.

E.J.M. acknowledges NSERC for PGS support. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Physics and Astronomy, University of Waterloo, Waterloo, N2L 3G1, Canada A. J. Achkar 

& D. G. Hawthorn * Canadian Light Source, University of Saskatchewan, Saskatoon, Saskatchewan, S7N 0X4, Canada T. Z. Regier * Department of Physics, Laboratory of Atomic and Solid State

Physics, Cornell University, Ithaca, NY, 14853 E. J. Monkman & K. M. Shen * Kavli Institute at Cornell for Nanoscale Science, Cornell University, Ithaca, NY, 14853 K. M. Shen Authors *

A. J. Achkar View author publications You can also search for this author inPubMed Google Scholar * T. Z. Regier View author publications You can also search for this author inPubMed Google

Scholar * E. J. Monkman View author publications You can also search for this author inPubMed Google Scholar * K. M. Shen View author publications You can also search for this author

inPubMed Google Scholar * D. G. Hawthorn View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS A.J.A., D.G.H. and T.Z.R. conceived of and

performed the experiments. A.J.A. and D.G.H. performed the data analysis and wrote the manuscript. E.J.M. and K.M.S. assisted in experiments and data analysis. ETHICS DECLARATIONS COMPETING

INTERESTS The authors declare no competing financial interests. RIGHTS AND PERMISSIONS This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported

License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Achkar, A., Regier, T.,

Monkman, E. _et al._ Determination of total x-ray absorption coefficient using non-resonant x-ray emission. _Sci Rep_ 1, 182 (2011). https://doi.org/10.1038/srep00182 Download citation *

Received: 28 June 2011 * Accepted: 22 November 2011 * Published: 06 December 2011 * DOI: https://doi.org/10.1038/srep00182 SHARE THIS ARTICLE Anyone you share the following link with will be

able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing

initiative