ABSTRACT We have developed a microrheometer, based on optical tweezers, in which hydrodynamic coupling between the probe and fluid boundaries is dramatically reduced relative to existing

microrheometers. Rotational Brownian motion of a birefringent microsphere within an angular optical trap is observed by measuring the polarisation shifts of transmitted light. Data gathered

in this manner, in the strongly viscoelastic fluid Celluvisc, quantitatively agree with the results of conventional (bulk) rheometry. Our technique will significantly reduce the smallest

sample volumes which may be reliably probed, further extending the study of rare, difficult to obtain or highly nonhomogeneous fluids. SIMILAR CONTENT BEING VIEWED BY OTHERS OPTICAL TWEEZERS

flow and deformation, aims to characterise the manner in which fluids respond to applied stresses and/or strains. For soft materials this information is most commonly deduced by observing

the motion of one or more microscopic probes embedded in the medium1. Microrheology has been applied in the study of a variety of physical systems, including polymer networks2,3,4,5,6,7,

colloids2,8,9,10 and fluids with mesoscopic nonhomogeneities4,11. These systems, collectively known as complex fluids, are said to be viscoelastic, as their response to deformation may

exhibit characteristics of both elasticity and viscous dissipation. Complex fluids arise frequently in biology – examples include synovial fluid, tear films, lung surfactants and

cerebrospinal fluid – and changes in their rheology have been linked to the development and diagnosis of diseased states12,13,14. Microrheology is therefore a powerful emerging tool for

biophysics and medical diagnostics11,15. The frequency-dependent behaviour of a viscoelastic fluid is described by the complex shear modulus, _G_* (ω). The complex shear stress may be

expressed as σ (ω) = _G_* (ω)ε (ω), where ε is the complex shear strain16. One can show that _G_′ = Re{_G_*}, the storage modulus, describes the amount of recoverable mechanical energy

stored within the fluid. This is broadly similar to the interpretation of Young's modulus. Conversely, the loss modulus, _G_″ = Im{_G_*}, reflects the momentum-dependent contribution of

viscous damping. The extreme nonhomogeneities and small volumes encountered in the study of many biological fluids ensure that the determination of _G_* by conventional rheometry is

impractical. This necessitates the development of accurate microrheometers capable of reliably operating within ultra-small volume (~ pL) fluid samples. Such microrheometers must be

relatively insensitive to the effects of hydrodynamic coupling between the probe particle(s)10,17,18 and any fluid boundaries, potentially separated by only micrometres, as these

interactions lead to a position-dependent decrease in the apparent mobility of the probe19,20. Overcoming these hurdles will allow continued miniaturisation of rheometry in

lab-on-a-chip-style devices. The influences of this coupling on the centre-of-mass and angular mobilities (in a viscous fluid) are described by Faxén's corrections20. The modification

of the motion of a sphere near to a fluid boundary is specified as four coefficients; one each for the drag coefficients corresponding to rotations and translations parallel or perpendicular

to the boundary. To leading order, the translational corrections for a particle of radius _a_ scale as (_a_/_s_)1, whilst rotational corrections vary with (_a_/_s_)3, with _s_ being the

distance separating the probe's centre from the boundary20,21. As such, the rotational corrections do not become significant until _s_ ≈ _a_, allowing rotational microrheology to

operate in more tightly confined geometries, or more heterogeneous fluids, than its translational counterpart20,21. As we will show below, this statement holds even relatively far from a

boundary, despite the fact that rotational microrheology has a less favourable scaling of the uncertainty Δ_G_* with Δ_a_ than linear microrheology. Previously, single-particle rotational

optical microrheology has been restricted to measurements of viscosity19,22 or |_G_*|, rather than _G_′ and _G_″ individually. Herein we report the measurement of the full complex shear

modulus, by a single-particle rotational microrheometer, across a large frequency range. We achieve excellent quantitative agreement between conventional rheological data and those gathered

by monitoring the angular position fluctuations of a birefringent microsphere undergoing biased Brownian rotational motion in linearly polarised optical tweezers. RESULTS The experimental

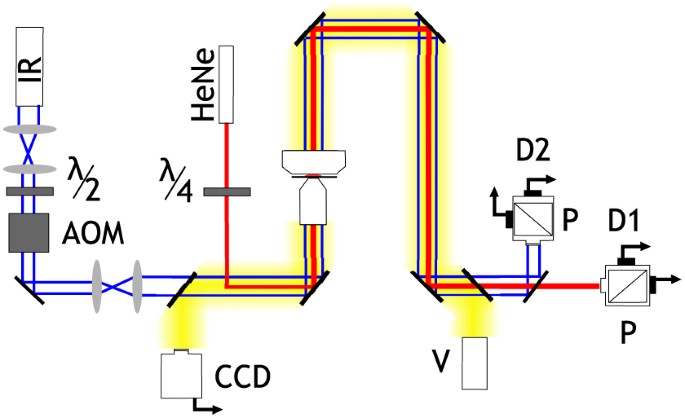
apparatus is shown in Fig. 1. Our microrheometer exploits two laser sources; one forms a three-dimensional optical trap in an inverted microscope (Olympus, 1.3 NA, 100× objective and matched

condenser lenses) whilst another monitors the angular position of the trapped probe particle. The beams are coaxial and share a common focal spot at the position of the trap. The single

optical trap is generated by highly-focused, linearly polarised infrared (IR) light (IPG Photonics YLR-5-1064-LP,CW, 1064 nm with stable output at 2.0 W). An acousto-optic modulator (AOM,

IntraAction DTD-274HA6, driven at 27 MHz) is aligned such that the first diffracted order is passed into the microscope, allowing fine control of the trapping power. Vaterite (CaCO3), our

chosen probe material, forms highly birefringent (Δ_n_ = 0.1) polycrystalline microspherulites23. Despite non-trivial internal structure, the spheres have a well-formed principal optic axis,

which allows the exchange of spin angular momentum with electromagnetic fields24. When held in linearly polarised optical tweezers these particles undergo biased diffusion about the stable

mechanical equilibrium position, with the optic axis in the transverse plane and the azimuthal angle ϕ0 determined by the polarisation vector of the trapping beam. Measurements of the

angular position are achieved _via_ polarisation tracking of a low-power (~ 3 mW at focal plane) HeNe laser beam (JDS Uniphase 1137P, CW, 632.8 nm) which is focused to a relatively broad

focal spot. This tracking technique is related to those employed by Wood _et al._ and Knöner _et al._25,26. Transmission through a vaterite microsphere deforms the initial circularly

polarised beam into an elliptically polarised state, in which the long axis of the polarisation ellipse runs parallel to the optic axis of the probe. The resulting difference in the power

carried by orthogonal (linearly polarised) beam components encodes ϕ. This information is recovered by passing the transmitted light through a polarising beam splitter cube and recording the

difference in power arriving at each output port. Assuming the photodiode voltage is linear in the optical power, the recorded voltage difference varies sinusoidally with twice the

azimuthal angle, Δ_V_ − 〈Δ_V_〉 ∝ sin 2ϕ, because of the probe's mirror symmetry about the optic axis. To recover absolute angles we observe the continuous rotation of the probe particle

under circularly polarised IR light: once the extreme values of Δ_V_ are known it is possible to map the data onto the interval [−1,1] and solve for ϕ as a function of Δ_V_. Each individual

probe is calibrated separately, requiring tens of seconds to one minute each, to ensure that variability of size and internal crystal structure23 within the population is properly accounted

for. Note that continuous rotations induce restructuring of polymer networks present in strongly viscoelastic fluids, altering their apparent rheology or pushing them into the nonlinear

regime1: this potential source of data contamination has been avoided by collecting passive measurements of Brownian motion before calibrating. The experimentalist concerned with small

samples of nonhomogeneous fluids will find this system holds several advantages over existing microrheometers. One of the simplest and most effective methods of measuring fluid properties is

by monitoring the rectilinear motions of an ensemble of suspended probe particles. The well-developed field of optical multi-probe microrheology makes extensive use of dynamic light

scattering (DLS)27 and diffusing wave spectroscopy (DWS)28, which generally extract data from the correlations of backscattered light. More specialised techniques, such as

localised-coherence-volume DLS (capable of measurements localised to a volume of ~ 100 μm cubed)29, are also in use. Additionally, the capacity for rapid multi-particle tracking afforded by

modern CCD cameras has found applications in microrheology1,30. Since the sample volume necessarily scales at least as rapidly as the number of probe particles (for any given technique) it

is not possible for any of these techniques to approach the spatial resolution (the minimum distance over which a difference in _G_* may be detected) achieved by a single-probe

microrheometer; they are ideally-suited to gathering large bodies of statistical data in near-homogeneous fluids. To increase the spatial resolution it is necessary to turn to few- and

single-particle microrheometers. Optical microrheometers based on translational motion of the probe particle(s) may monitor the Brownian motion of a trapped5,16 or untrapped31 probe, observe

relaxation into an optical potential6,16 or continuously modulate the trap position5,11, amongst other possible schemes. All of these measurements rely on rectilinear motion, so are limited

in spatial resolution by the strong dependence of the translational Faxén's corrections on the distance from a fluid boundary. Our rotational microrheometer increases the achievable

spatial resolution above those attained with the methods listed above through two mechanisms; firstly, the centre of the probe can be tightly constrained without degrading the

signal-to-noise ratio, unlike translational measurements; and secondly, the rotational Faxén's corrections are small even within a radius of a fluid boundary. Existing rotational

microrheometers may also be categorised as ensemble or single-particle devices. In the former category are magnetic rheometers, which probe _G_* by examining the net magnetisation of a fluid

interspersed with ferromagnetic probe beads – they are well-suited to measurement of low-frequency behaviour32,33, but are incapable of resolving _G_* at high frequencies (ω/2π > 1 kHz)

– and the rotational cousin of DLS, depolarised DLS34. In the latter category are single-particle rotational microrheometers. Many of these are faced with a trade-off between angular

sensitivity and ease of analysis; it is possible to optically track anisotropic and asymmetric objects, such as trapped wax micro disks3, but calculating their diffusive dynamics is highly

nontrivial; conversely, the symmetry of spheres makes them difficult to track but simpler to analyse. We have circumvented this issue by employing a spherical particle with an _optical_

anisotropy, allowing sensitive detection of its orientation with readily-available polarisers and photodetectors. Finally, this Brownian microrheometer is able to acquire data far more

rapidly than a similar instrument35 in which a birefringent sphere was sinusoidally driven with a well-defined frequency, because broad-band thermal forcing eliminates the necessity of

scanning over each frequency of interest serially. A combination of these techniques could allow one to rapidly identify interesting features in _G_* by thermal effects, then perform

high-resolution scans of those features with the active excitation method. We adopt a generalised Langevin equation to model the stochastic evolution of the azimuthal angle of a spherical

probe with moment of inertia _I_ and radius _a_3. Without loss of generality we choose ϕ0 = 0. The angular position evolves under the effects of a Hookean optical restoring torque with

effective stiffness χ, the zero-mean thermal torque τ_TH_ and the fluid's hydrodynamic contributions, here represented by the convolution of the angular velocity with the microscopic

memory function ζ (_t_)3. The existence of a linear optical restoring torque is confirmed by experiments, as clearly shown in Fig. 2. The distribution of occupied angular positions is in

accordance with a thermal ensemble within a harmonic potential. Therefore the angular trap stiffness may be confidently determined by way of the equipartition theorem. Note that this

calculation is independent of the fluid's rheological properties. Here brackets 〈···〉 indicate a measurement averaged over all _t_; experimentally, the measurement time must be

sufficiently long that the mean-squared displacement approaches a constant value. The normalised angular position autocorrelation function (NAPAF), defined by Eqn. (3), contains information

concerning the distribution of ϕ (_t_ + τ) conditioned on a measurement of ϕ (_t_). As such, it encapsulates the dynamical behaviour of the probe. By analogy with Preece _et al._16, we apply

the generalised Stokes-Einstein relation of Cheng and Mason3 to Eqn. (1) to find It is important to note that à is representative of the unilateral Fourier transform1 of _A_, defined as

Numerical evaluation of Eqn. (5) is performed using an approximation closely related to that of Evans _et al._36. This method treats the experimental data as a piecewise linear function,

interpolating between adjacent points. Times τ beyond the experimentally probed region are integrated over by extrapolating _A_ (τ) with an appropriate function. In order to choose said

function we note that, for a simple viscous fluid in the low Reynolds number (R) regime16, Eqn. (3) reduces to The majority of materials will respond in an essentially viscous manner if

deformed over timescales much greater than any characteristic relaxation times of their substructures, allowing us to apply Eqn. (6) as an approximation to the long-time behaviour of the

NAPAF measured in complex fluids. Given a uniformly-sampled set of _N_ points _A__j_ spaced by Δ_t_ in the domain τ ∈ [0, τ_N_], we extrapolate using to find The extrapolating function

introduces only a single fitting parameter, the effective decay constant αeff. Much of the theory presented above is predicated on the existence of low- flows. We confirm that we are probing

low- dynamics by comparing the experimentally determined NAPAF (water) with its corresponding theoretical form in this regime, Eqn. (6). As seen in Fig. 3, the agreement between these is

excellent. This indicates that Eqn. (4) may be simplified by neglecting the inertial terms (∝ _Iω_2)25. We benchmark our method against conventional techniques by examining four aqueous

dilutions of a common dry eye treatment, Celluvisc (Allergan). This fluid, a carboxymethylcellulose (CMC) sodium solution (10 mg mL−1), is designed to mimic the rheological properties of the

fluid film coating the cornea. CMC solutions are quite rheologically stable, with unpreserved samples aging over a number of weeks37. Microrheological measurements were conducted in

dilutions of 100, 50, 25 and 0 percent Celluvisc by weight, with trapping powers of approximately 20–60 mW. Rheological properties were found to be essentially independent of the trapping

power over this range, as noted in previous experiments22. Each measurement was carried out over three to five minutes. The bulk response of each fluid was probed with a parallel-plate

strain controlled rheometer (ARES, Rheometric Scientific). With time-temperature superposition at approximately 8, 25 and 40°C we were able to achieve measurements of _G_* across the range ω

∈ [1, 200] rad s−1 without entering the operating regime in which the inertia of the instrument significantly affects data. Although these frequencies are comparatively low, the region of

overlap with our tweezers-based method is sufficient for critical analysis. DISCUSSION In optimal conditions measurements of _G_* were repeatable and consistent. The largest sources of

uncertainty in the moduli stem from the low-frequency motion of the apparatus, which pollutes the NAPAF and an inability to precisely determine the probe radius. The former was able to be

partially mitigated by high-pass filtering the raw time-series prior to analysis (passing ω > 1 rad s−1). It may be possible to further suppress low-frequency noise by employing two

(mutually incoherent) trapping beams, allowing high (rectilinear) trap stiffnesses whilst maintaining a weak angular trap. The latter, which introduces a particle radius uncertainty,

contributes a goodly portion of the final experimental uncertainty in _G_*. With our estimated uncertainty of Δ_a_ ≈ 0.1_a_, the relative uncertainty in 1/_a_3 is ≈ 30%; this is smaller than

the systematic error associated with translational wall effects if the centre of the particle is within five radii of the boundary. This increases to _s_ ≈ 9_a_ if the uncertainty is

reduced to Δ_a_ ≈ 0.05_a_, illustrating that rotational microrheometers are capable of outperforming their translational counterparts even relatively far from a wall. We also note that if

the same probe particle is used to make comparative measurements, which are of immense interest to the biophysicist, the uncertainty in the radius does not affect the results. Data were

prepared for presentation by linearly interpolating each of _G_′ and _G_″ across four independent measurements, averaging these and selecting a logarithmically-spaced set of representative

points. We do not display _G_* (ω > 104 Hz) due to the presence of high-frequency artefacts caused by our finite sampling rate31,38. Fig. 4 and Fig. 5 compare our microrheological

measurements with conventional rheometry. The data compare favourably over the frequency range in which they overlap, spanning at least one decade. Slight deviations are evident in _G_′

measured in 25 percent solution, at frequencies exceeding 102 rad s−1. Although it is difficult to disentangle possible contributing factors, we believe that this difference may be due to

depletion interactions2 or the breakdown of the continuum approximation3. We note that the high-frequency behaviour of _G_″ is consistent with shear thinning, also observed in

methylcellulose solutions5. Our novel microrheological scheme has proven to reliably measure properties of complex fluids in small fluid samples. By analysing the rotational motion of a

single probe particle we have reduced the minimum volume of fluid required for a characterisation of its viscoelastic properties. Furthermore, our analysis relies on only a few key

assumptions, particularly those relevant to the generalised Stokes-Einstein relation1, so should be robust within the realms of their validity. This technique will allow more detailed

analysis of biological fluids, potentially for rapid and reliable diagnostics and will increase the range of (bio)physical studies able to be carried out inside living cells39,40 and in

chip-based devices. METHODS APPARATUS The arrangement of optical devices is depicted in Fig. 1. The IR laser (IPG Photonics YLR-5-1064-LP, CW, 1064 nm with stable output at 2.0 W, _P_ ≈ 10 

mW at the trap) is focused through an inverted high-NA microscope (Olympus, 1.3 NA, 100× objective and matched condenser lenses) to form the optical trap. A HeNe laser (JDS Uniphase 1137P,

CW, 632.8 nm, _P_ < 3 mW at focal plane) and plate are used for polarisation tracking. The AOMs (IntraAction DTD-274HA6, driven at 27 MHz with variable amplitude) allows the trapping

power to be controlled. FLUIDS Vaterite spheres were suspended in samples of Celluvisc (Allergan), a 10 g/L aqueous solution of CMC, after removal of the mother liquor through three repeated

cycles of centrifugation, re-suspension in ethanol and sonication. ANGLE CALIBRATION The transmitted HeNe light was passed through a polarising beam splitter cube and the resulting powers

of both perpendicular beams measured. The voltage difference generated (Δ_V_) relates sinusoidally to the azimuthal angle of the vaterite probe by Δ_V_ ∝ sin 2ϕ. Introducing a quarter wave

plate into the IR path causes the vaterite to spin. Recording the range of Δ_V_ allows an exact relationship between Δ_V_ and ϕ to be found. LARGE SCALE RHEOMETRY A parallel-plate strain

controlled rheometer (ARES, Rheometric Scientific) with sample temperatures of approximately 8, 25 and 40°C achieved measurements of _G_* across the frequency range 1–200 rad/s by standard

time-temperature superposition. REFERENCES * Squires, T. M. & Mason, T. G. Fluid mechanics of microrheology. Annual Review of Fluid Mechanics 21, 413–438 (2009). Google Scholar  *

Starrs, L. & Bartlett, P. Colloidal dynamics in polymer solutions: Optical two-point microrheology measurements. Faraday Discussions 123, 323–334 (2003). Article  ADS  CAS  Google

Scholar  * Cheng, Z. & Mason, T. G. Rotational diffusion microrheology. Physical Review Letters 90, 018304 (2003). Article  ADS  CAS  Google Scholar  * Mizuno, D., Head, D. A.,

Mackintosh, F. C. & Schmidt, C. F. Active and passive microrheology in equilibrium and nonequilibrium systems. Macromolecules 41, 7194–7202 (2008). Article  ADS  CAS  Google Scholar  *

Brau, R. R., Ferrer, J. M., Lee, H., Castro, C. E. & Tam, B. K. Passive and active microrheology with optical tweezers. Journal of Optics A 9, 102–112 (2007). Article  Google Scholar  *

Tassieri, M. et al. Measuring storage and loss moduli using optical tweezers: broadband microrheology. Physical Review E 81, 026308 (2010). Article  ADS  Google Scholar  * Gibson, G. M.,

Leach, J., Keen, S., Wright, A. J. & Padgett, M. J. Measuring the accuracy of particle position and force in optical tweezers using high-speed video microscopy. Optics Express 16,

405–412 (2008). Article  Google Scholar  * Otto, O. et al. High-speed video-based tracking of optically trapped colloids. Journal of Optics 13, 044011 (2011). Article  ADS  Google Scholar  *

Wilson, L. G., Harrison, A. W., Poon, W. C. K. & Puertas, A. M. Microrheology and the fluctuation theorem in dense colloids. EPL 93, 58007 (2011). Article  ADS  Google Scholar  * Wang,

G. M., Prabhakar, R., Gao, Y. X. & Sevick, E. M. Micro-rheology near fluid interfaces. Journal of Optics 13, 044009 (2011). Article  ADS  Google Scholar  * Wilson, L. G. & Poon, W.

C. K. Small-world rheology: an introduction to probe-based active microrheology. Physical Chemistry Chemical Physics 13, 10617–10630 (2011). Article  CAS  Google Scholar  * Thurston, G. B.

& Greiling, H. Viscoelastic properties of pathological synovial fluids for a wide range of oscillatory shear rates and frequencies. Rheologica Acta 17, 433–445 (1978). Article  Google

Scholar  * Rantamäki, A. H., Telenius, J., Koivuniemi, A., Vattulainen, I. & Holopainen, J. M. Lessons from the biophysics of interfaces: Lung surfactant and tear fluid. Progress in

Retinal and Eye Research 30, 204–215 (2011). Article  Google Scholar  * Kazakov, V. N. et al. Dilation rheology as medical diagnostics of human biological liquids. Colloids and Surfaces A:

Physicochemical and Engineering Aspects 391, 190–194 (2011). Article  CAS  Google Scholar  * Weihs, D., Mason, T. G. & Teitell, M. A. Bio-microrheology: A frontier in microrheology.

Biophysical Journal 91, 4296–4305 (2006). Article  ADS  CAS  Google Scholar  * Preece, D. et al. Optical tweezers: wideband microrheology. Journal of Optics 13, 044022 (2011). Article  ADS 

Google Scholar  * di Leonardo, R. et al. Eigenmodes of a hydrodynamically coupled micron-size multiple-particle ring. Physical Review E 76, 061402 (2007). Article  ADS  CAS  Google Scholar 

* Hough, L. A. & Ou-Yang, H. D. Correlated motions of two hydrodynamically coupled particles confined in separate quadratic potential wells. Physical Review E 65, 021906 (2002). Article

  ADS  CAS  Google Scholar  * Parkin, S. J., Knöner, G., Nieminen, T. A., Heckenberg, N. R. & Rubinsztein-Dunlop, H. Picoliter viscometry using optically rotated particles. Physical

Review E 76, 041507 (2007). Article  ADS  Google Scholar  * Leach, J. et al. Comparison of Faxén's correction for a microsphere translating or rotating near a surface. Physical Review E

79, 026301 (2009). Article  ADS  CAS  Google Scholar  * Berg-Sørensen, K. & Flyvbjerg, H. Power spectrum analysis for optical tweezers. Review of Scientific Instruments 75, 594–612

(2004). Article  ADS  Google Scholar  * Bishop, A. I., Nieminen, T. A., Heckenberg, N. R. & Rubinsztein-Dunlop, H. Optical microrheology using rotating laser-trapped particles. Physical

Review Letters 92, 14–17 (2004). Article  Google Scholar  * Vogel, R. et al. Synthesis and surface modification of birefringent vaterite microspheres. Langmuir 25, 11672–11679 (2009).

Article  CAS  Google Scholar  * Funk, M. et al. Constant power optical tweezers with controllable torque. Optics Letters 34, 139–141 (2009). Article  ADS  Google Scholar  * Wood, T. A.,

Roberts, G. S., Eaimkhong, S. & Bartlett, P. Characterization of microparticles with driven optical tweezers. Faraday Discussions 137, 319–333 (2008). Article  ADS  CAS  Google Scholar 

* Knöner, G., Parkin, S., Heckenberg, N. R. & Rubinsztein-Dunlop, H. Characterization of optically driven fluid stress fields with optical tweezers. Physical Review E 72, 031507 (2005).

Article  ADS  Google Scholar  * Dasgupta, B. R., Tee, S.-y., Crocker, J. C., Frisken, B. J. & Weitz, D. A. Microrheology of polyethylene oxide using diffusing wave spectroscopy and

single scattering. Physical Review E 65, 051505 (2002). Article  ADS  Google Scholar  * Weitz, D. A., Zhu, J. X., Durian, D. J., Gang, H. & Pine, D. J. Diffusing-wave spectroscopy: The

technique and some applications. Physica Scripta T49, 610–621 (1993). Article  ADS  Google Scholar  * Popescu, G., Dogariu, A. & Rajagopalan, R. Spatially resolved microrheology using

localized coherence volumes. Physical Review E 65, 041504 (2002). Article  ADS  CAS  Google Scholar  * Kurniawan, N. A., Lim, C. T. & Rajagopalan, R. Image correlation spectroscopy as a

tool for microrheology of soft materials. Soft Matter 6, 3499–3505 (2010). Article  ADS  CAS  Google Scholar  * Pesce, G., Rusciano, G. & Sasso, A. Blinking Optical Tweezers for

microrheology measurements of weak elasticity complex fluids. Optics Express 18, 2116–2126 (2010). Article  ADS  CAS  Google Scholar  * Besseris, G. J., Miller, I. F. & Yeates, D. B.

Rotational magnetic particle microrheometry: The Newtonian case. Journal of Rheology 43, 591–608 (1999). Article  ADS  CAS  Google Scholar  * Wilhelm, C., Browaeys, J., Ponton, A. &

Bacri, J.-C. Rotational magnetic particles microrheology: The Maxwellian case. Physical Review E 67, 011504 (2003). Article  ADS  CAS  Google Scholar  * Andablo-Reyes, E., Diaz-Leyva, P.

& Luis Arauz-Lara, J. Microrheology from rotational diffusion of colloidal particles. Physical Review Letters 94, 106001 (2005). Article  ADS  Google Scholar  * Funk, M., Parkin, S. J.,

Nieminen, T. A., Heckenberg, N. R. & Rubinsztein-Dunlop, H. Vaterite twist: microrheology with AOM controlled optical tweezers. Proceedings of SPIE 7227, 72270D (2009). Article  ADS 

Google Scholar  * Evans, R., Tassieri, M., Auhl, D. & Waigh, T. A. Direct conversion of rheological compliance measurements into storage and loss moduli. Physical Review E 80, 1–4

(2009). Google Scholar  * Naik, S. C., Lee, J. C. & Richardson, J. F. The rheology and aging characteristics of sodium carboxymethylcellulose solutions. The Canadian Journal of Chemical

Engineering 55, 90–92 (1977). Article  CAS  Google Scholar  * Fusco, S. et al. High frequency viscoelastic behaviour of low molecular weight hyaluronic acid water solutions. Biorheology 44,

403–418 (2007). CAS  PubMed  Google Scholar  * Sacconi, L., Tolić-Nørrelykke, I. M., Stringari, C., Antolini, R. & Pavone, F. S. Optical micromanipulations inside yeast cells. Applied

Optics 44, 2001–2007 (2005). Article  ADS  Google Scholar  * Oddershede, L., Flyvbjerg, H. & Berg-Sørensen, K. Single-molecule experiment with optical tweezers: improved analysis of the

diffusion of the λ-receptor in E. coli's outer membrane. Journal of Condensed Matter Physics 15, S1737 (2003). Article  ADS  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS

The authors gratefully acknowledge Mr Jim Johnson and Dr Jennifer Steen for supplying the viscoelastic materials examined in this work. We also thank Dr Alex Stilgoe for assistance with the

experimental apparatus and Dr Manlio Tassieri for useful conversations. This work was supported by an Australian Council Research Discovery Grant, DP110103015. AUTHOR INFORMATION AUTHORS AND

AFFILIATIONS * The University of Queensland, School of Mathematics and Physics, Brisbane, QLD, 4072, Australia James S. Bennett, Lachlan J. Gibson, Rory M. Kelly, Emmanuel Brousse, Bastian

Baudisch, Daryl Preece, Timo A. Nieminen, Norman R. Heckenberg & Halina Rubinsztein-Dunlop * The University of Queensland, School of Chemical Engineering, Brisbane, QLD, 4072, Australia

Timothy Nicholson Authors * James S. Bennett View author publications You can also search for this author inPubMed Google Scholar * Lachlan J. Gibson View author publications You can also

search for this author inPubMed Google Scholar * Rory M. Kelly View author publications You can also search for this author inPubMed Google Scholar * Emmanuel Brousse View author

publications You can also search for this author inPubMed Google Scholar * Bastian Baudisch View author publications You can also search for this author inPubMed Google Scholar * Daryl

Preece View author publications You can also search for this author inPubMed Google Scholar * Timo A. Nieminen View author publications You can also search for this author inPubMed Google

Scholar * Timothy Nicholson View author publications You can also search for this author inPubMed Google Scholar * Norman R. Heckenberg View author publications You can also search for this

author inPubMed Google Scholar * Halina Rubinsztein-Dunlop View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS J.S.B., L.J.G. and R.M.K.

performed data collection and analysis. E.B., B.B., J.S.B., D.P. and L.J.G. constructed the microrheometer. T.A.N. provided theoretical support. T.N. collected and analysed macrorheological

data. This manuscript was developed by J.S.B. in collaboration with L.J.G., D.P., T.A.N. and H.R.-D. The technique was conceived by T.A.N., N.R.H. and H.R.-D. ETHICS DECLARATIONS COMPETING

INTERESTS The authors declare no competing financial interests. RIGHTS AND PERMISSIONS This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.

To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Bennett, J., Gibson, L., Kelly, R. _et

al._ Spatially-resolved rotational microrheology with an optically-trapped sphere. _Sci Rep_ 3, 1759 (2013). https://doi.org/10.1038/srep01759 Download citation * Received: 08 January 2013 *

Accepted: 02 April 2013 * Published: 02 May 2013 * DOI: https://doi.org/10.1038/srep01759 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get

shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative