ABSTRACT In this study, the wetting behaviors of single droplet on a micro square-post patterned surface with different geometrical parameters are investigated theoretically and numerically.

A theoretical model is proposed for the prediction of wetting transition from the Cassie to Wenzel regimes. In addition, due to the limitation of theoretical method, a numerical simulation

is performed, which helps get a view of dynamic contact lines, detailed velocity fields, etc., even if the droplet size is comparable with the scale of the surface micro-structures. It is

found that the numerical results of the liquid drop behaviours on the square-post patterned surface are in good agreement with the predicted values by the theoretical model. SIMILAR CONTENT

surface wettability is an important subject of physics and can essentially influence a lot of cutting-edge topics in engineering such as textile1, micro/nano- fluidics2,3,4,5, film coating6

and tribology7. The effect of surface chemistry8,9,10,11,12,13 and topography14,15,16,17,18,19,20,21 on the wettability of surfaces has been intensively investigated over the past decades

and a remarkable progress has been achieved. It has been recognised that an appropriate modification on surface chemistry or structure can improve and help optimize surface wettability. The

chemical modification of surface alone can typically make water contact angles up to 120°; and to reach the extreme values of contact angles approaching approximately up to 180°, a

modification on surface structure has to be utilized22,23. Depending on the original chemical properties of surfaces, micro-roughness may make surfaces either more hydrophilic or more

hydrophobic. So far, the effects of surface roughness on wettability have been studied theoretically for several decades24,25,26,27. The pioneering work was carried out by Wenzel28 and

Cassie-Baxter29 who proposed Wenzel equation 27 and Cassie–Baxter equation29 on the basis of Young’s law30 to predict the wetting behaviors of a droplet. However, such equations are not

sufficient to thoroughly explain the mechanisms of wetting phenomena, although they are still necessary23. Numerical investigations have been carried out by several researchers based on

either molecular dynamics method31,32,33,34,35 or the lattice Boltzmann method36,37,38,39 to study the mechanism of wetting transitions. A comprehensive review on the progress in

understanding wetting transitions on rough surfaces have recently been completed by Bormashenko40. Very recent studies have focused on manipulating roughness to fabricate surfaces with

superhydrophobicity or superhydrophilicity. However, for the same roughness value, different surface geometries can exhibit completely different wetting behaviour. As typical surface

geometries, surfaces with pillars (post or spike) patterned have been extensively investigated theoretically and experimentally20,24,25,26,41,42,43,44,45. It is argued whether or not all

geometrical parameters of pillars, such as height, spacing and cross sections, individually play an important role in determining wetting behaviour. This indicates that it is far from enough

to only consider the value of surface roughness. To simulate the behaviours of two-phase droplets with relatively high density ratio, a lattice Boltzmann method (LBM) was developed for

studying both the static and dynamic behaviours of droplets on micro-roughness surfaces46. The method has already shown its capability in dealing with droplet behaviours on chemically

homogeneous and heterogeneous surfaces with large density ratio up to 1000. In general, the LBM has demonstrated a significant potential and broad applicability with many computational

advantages, which includes the parallelism of algorithm and the simplicity of programming47,48,49,50,51,52,53,54,55. In this study, the wetting phenomena of a droplet spreading on a micro

square-post patterned surface are analyzed theoretically and simulated numerically; the effects of surface geometrical parameters on the wetting properties are also discussed. RESULTS We

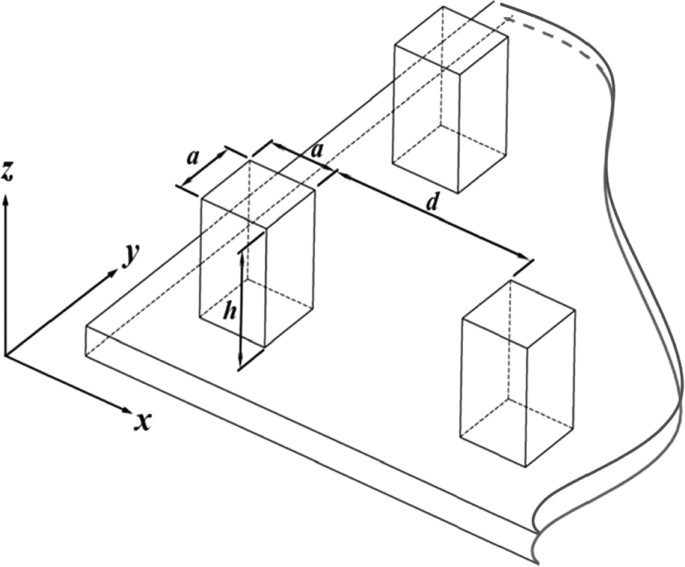
analyze the behaviours of a droplet on the substrate patterned by structured micro-square posts, as shown in Fig. 1; where _h, a_ and _d_ are the height, width and spacing of the posts,

respectively. The theoretical analysis is based on the assumption that the size of the micro posts is much smaller than that of the droplet. Thus, the wetting properties from a single unit

of the surface with periodical square-post pattern are studied. BACKGROUND Figure 2(a) shows the cross-section of the droplet on a flat partial wetting wall, when the relation of contact

angle θ_Y_ is governed by Young’s equation30 where, θ_Y_ is named as Young’s angle; γ_LG_, γ_SG_ and γ_SL_ are the surface tension forces of liquid-gas, solid-gas and solid-liquid,

respectively. Correspondingly, the equilibrium net surface energy, Ψ_Y_, can be given by56,57,58 where, _A_ and _A_′, respectively, denotes the area of solid-liquid and liquid-gas

interfaces. Similarly, as shown in Fig. 2(b), when the droplet in Cassie state (composite state), the contact angle, surface tension and the equilibrium net surface energy are related by

where, γ′_SL_ is the effective energy per unit area of solid-liquid interface, _A__CB_ the area of drop bottom projected on horizontal plane and _A_′_CB_ the area of the surface of drop

contacting with bulk gas phase. While, as shown in Fig. 2(c), for the droplet in Wenzel state the contact angle and the equilibrium net energy, respectively, can be valuated from the

following equations: It should be noted that, from microscopic point of view, as shown in Fig. 2(b,c), the drop bottom has many equilibrium states and each of them has a free energy

satisfying Eq. (2). Thus, Ψ_CB_ and Ψ_W_ can be written as, and where, _f_ is the fraction of the contact area referred to as the ratio of the total area of the liquid-solid interface

projected on the horizontal plane with respect to the total area of drop bottom projected on the plane; _r_ corresponds to the “roughness parameter”, also referred to as the roughness area

ratio of the actual surface with respect to the geometric surface. Combining Eq. (1), (3), (4) and (7) leads to a Cassie-Baxter’s equation 29. While, combining Eq. (1), (5), (6) and (8)

results in a Wenzel’s equation 28. Obviously, depending on the Young’s angle θ_Y_, micro-roughness may make surfaces either more hydrophilic or more hydrophobic. WENZEL’S ANGLE Let α = 

_d_/_a_ and β = _h_/_a_, the effects of surface geometrical parameters α and β on the wetting properties can be verified. When the droplet keeps in Wenzel state, according to Wenzel’s

equation, the apparent contact angle θ_W_ is given by where, the surface roughness parameter _r_ is given by It can be noted from Eq. (11) that the increase of parameter α, i.e. d/a, may

decrease Wenzel’s angle on a hydrophobic surface, but will increase the angle on a hydrophilic surface. While the increase of β, i.e. h/a, may make the hydrophilic surface to be more

hydrophilic and hydrophobic surface to be more hydrophobic. CASSIE-BAXTER’S ANGLE If the droplet is in Cassie state, the apparent contact angle θ_CB_ can be evaluated with Cassie and

Baxter’s equation as, where, the fraction of the contact area, _f_, is given by Eqs (13 and 14) indicate that, depending on the original chemical properties of surfaces, lager contact angles

can be obtained by increasing the value of α if the droplet remains in Cassie state. WETTING TRANSITION Form thermodynamic point of view, the droplet always tends to be in a lower energy

state. Thus, a threshold Young’s angle exists. Bico _et al_.59 has suggested a critical Young’s angle between Wenzel state and Cassie state, when Ψ_CB_ = Ψ_W_, For a flat surface, if the

contact angle θ_Y_ is larger than the critical Young’s angle θ_c_, the droplet will stay in a stable Cassie state. For θ_Y_ < θ_c_, on the other hand, the droplet will exist in Wenzel

state. However, it has been found that there is an energy barrier56 between the Cassie and Wenzel regimes, so that the droplet could exist in at a metastable wetting state, which may affect

the threshold contact angle θ_c_. As mentioned above, a droplet on the roughness surface could exist in a metastable wetting state that does not belong to the Cassie or the Wenzel regimes,

as shown in Fig. 3. Once an additional stimulus is applied, a complete transition can take place. It is noted that, from microscopic viewpoint, Eq. (2) is still available even under the

metastable equilibrium states, which allows us to predict the apparent contact angles when droplets are in metastable states. It is noted that the inter-post liquid-gas interface need to go

down a depth of _h_ to complete a transition from Cassie state to Wenzel state, as shown in Fig. 3. According to Eq. (2), an extreme free energy can be expressed as Thus, the energy barrier

from Cassie to Wenzel regimes can be evaluated as Note that Eq. (16) gives a critical contact angle as, If the drop has a free energy, , satisfying then it could stay in the metastable

Cassie state. Otherwise, the droplet either exists in stable Wenzel state or in stable Cassie state. Let , and to be the surface area of the metastable droplet, projected area of the

metastable droplet bottom and apparent contact angle respectively, then Substituting Eq. (2), (8) and (20) into the left part of in equation (19) gives While, substituting Eq. (2), (7), (8),

(16), (17) and (20) into right part of inequality (19), we have Assuming that the drop has constant volume, the original shape of the droplet is spherical with radius _r__s_ and that the

shape of equilibrium droplet after contacting with the surface is a spherical cap with radius _R, R__CB_ or _R__W_ as shown in Fig. 2, the values of _A__CB_, _A_′_CB_, _A__W_, _A_′_W_, , , ,

in the inequalities (21) and (22) can then be calculated as where Inequalities (21) and (22) are both implicit inequalities of and can be solved numerically using dichotomy algorithm.

Neglecting the changes of droplet surface area and projected area of droplet bottom during the transition progress, inequalities (21) and (22) can be simplified to an implicit equation as

where, and _r_′ is a virtual roughness parameter given by When θ_Y_ ≥ 90°, the solution of inequality (38) exists. Depending on the assumption that Eq. (3) is still available during the

wetting transition progress from Cassie to Wenzel state, i.e. , then the left part of inequality (38) gives a modified critical Young’s angle as For _a_ = 50 _μm, R_ = 1000 _μm_ and θ_Y_ = 

120°, Fig. 4 shows the comparison of θ′_W_ obtained by numerical solution of Eq. (22) and analytical solution of the left part of Eq. (38). The good agreement appears. This indicates that

the changes of droplet surface area and projected area of droplet bottom during the wetting transition process are negligible. Briefly, depending on the original chemical properties of

surfaces where θ_Y_ ≥ 90°, droplet could stay in a stable Cassie state if θ_CB_ < θ_W_; and if θ_W_ ≤ θ_CB_ ≤ θ′_W_, a transition from Cassie to Wenzel state can take place; else if θ_CB_

 > θ′_W_, the droplet can complete the transition to a stable Wenzel state. It should be pointed out that, although the present theoretical model is effective to predict the wetting

transition from the Cassie to Wenzel regimes, the kinetics of the energy barrier separating the Cassie and Wenzel wetting states should be much more complicated60. NUMERICAL SIMULATION As it

was mentioned before, the above theoretical analysis is limited to the conditions that the scale of surface micro-structures is much smaller than that of the droplet and is not able to

predict the dynamic contact angle. Therefore, a numerical simulation on wetting behaviour of a water droplet with a size comparable with the scale of square-posts on the surface is carried

out by extending the LBM46,61. As shown in Fig. 5, a spherical water drop with an initial velocity of 0.01 m/s falls down to the square-post patterned surface; the original radius of the

droplet is _r__s_ = 15 _μm_; the initial vertical distance from the droplet center to the top of post is 20 _μm_. Naturally, the densities of water and air are set at ρ_L_ = 1 × 103 _kgm_−3,

ρ_G_ = 1.204 _kgm_−3, the dynamic viscosities of them are μ_L_ = 1 × 10−3 _kgm_−1_s_−1, μ_G_ = 1.9 × 10−5 _kgm_−1_s_−1, liquid-gas surface tension is γ_LG_ = 7 × 10−2 _J_ ⋅ _m_−2 and the

gravitational acceleration _g_ = 9.8 _ms_−2. A cubic uniform grid is meshed and the grid independence certification is performed to select appropriate dimensional size of lattice spacing as

Δ_x_ = 1 _μm_. For _a_ = _d_ = _h_ = 5 _μm_ and θ_Y_ = 120°. The obtained numerical results will be compared with those of theoretical prediction. It should be pointed out that, with a

decrease of droplet size, the contribution of line tension free energy becomes increasingly important62,63,64,65. The effects of Line tension (i.e., the excess free energy of a

solid-liquid-vapour system per unit length of the contact line) may not be negligible for droplet with a smaller size comparable with the scale of surface micro-structures. Therefore, the

line tension effect needs to be checked in this case to ensure that the Cassie-Baxter equation (9) is still available. To take into account the line tension effects, a modified

Cassie-Baxter’s equation was proposed by Wong and Ho66 as where, τ is the line tension, _L_ is the length of three-phase contact line per unit area. For the square-post patterned surfaces,

as shown in Fig. 1, _L_ = 4_a_/(_a_ + _d_)2. In this particular case, _L_ = 1/_a_ = 2 × 105 _m_−1, γ_LG_ = 7 × 10−2 _J_ ⋅ _m_−2. According to the high resolution scanning microscopy

measurements67,68, contact line tensions are in the order of 10−11 to 10−10 _J_ ⋅ _m_−1. Thus, the third term on the right hand side of Eq. (42) should be on the order of 10−5 to 10−4, which

has limited effect on apparent contact angle. This means that, under the present condition, Cassie-Baxter’s equation (9) is available. However, when the droplet size approximates to be the

scale of the surface micro-structures, the error caused by the approximation of the fraction of the contact area _f_ with Eq. (14) becomes lager since the equation is obtained on the basis

of the assumption that the size of micro posts is much smaller than that of the droplet. To avoid this error, in the present comparison study, the parameter _f_ used in theoretical

prediction is set to be the same as that in LBM numerical simulation rather than the value given by Eq. (14). Figure 6 shows the dimensional shape of the droplet when _t_ = 2 × 10−3 _s_ and

_t_ = 1.75 × 10−2 _s_; and the development with time of three phase contact line and the corresponding velocity field are given in Fig. 7. It can be seen that, in spite of an initial

momentum, the droplet is still able to stay at a Cassie state; moreover, the movement can finally reaches an equilibrium state when _t_ ≈ 17.5 _ms_. The obtained equilibrium contact angle of

LBM simulation is 153.16°, for _f_ = 0.259; while the theoretical prediction using Cassie-Baxter’s equation for _f_ = 0.259 gives a slightly lower value of θ_CB_ = 150.52°. The

corresponding evolution of dynamic contact angle measured at the middle x-z cross section is shown in Fig. 8. It can be found clearly that there is an oscillation of apparent contact angle

with higher frequency at the initial stage of the evolution due to the impingement of the droplet on the solid wall. Also, there is still an oscillation of contact angle with smaller

amplitude caused by the interaction of droplet and the post corner of the solid surface. DISCUSSION To check the effects of surface roughness on wetting transition, equilibrium contact

angles of spherical water droplet with _r__s_ = 20 _μm_ on surfaces with the same values of width and spacing of the posts, _a_ and _d_, but different height of the posts, _h_, are examined.

The roughness parameters and chemical property used in the simulation are _a_ = _d_ = 5 _μm, h_ = 1, 2, 4 _μm_ and θ_Y_ = 120°. Initially, the droplet is set at a Cassie state with velocity

of zero as shown in Fig. 9. As shown in Fig. 10, when reaches the equilibrium state, the droplet on the surface with _h_ = 2 and 4 _μm_, respectively, is at Cassie state; while, the droplet

on the surface with _h_ = 1 _μm_ has been transferred to Wenzel state. To check the effects of energy barrier, a liquid drop of radius _r__s_ = 20 _μm_ on the surface with property of _a_ =

 _d_ = 5 _μm, h_ = 3 _μm_ and θ_Y_ = 120° is simulated (Fig. 11). The droplet initially at both Wenzel and Cassie states are considered. For the same surface property, different equilibrium

states are obtained due to the energy barrier. As shown in Fig. 12, the droplet initially at Wenzel or Cassie states can finally reach the equilibrium Wenzel and Cassie states, respectively.

To validate the proposed theoretical model of wetting transition, a comparison between the analytical and numerical results, as shown in Fig. 13, is performed under the condition that the

surface is square-post patterned with θ_Y_ = 120°, _a_ = _b_ = 5 _μm_ and _h_ increases form 0 to 5 _μm_. According to the proposed model in this paper, a critical value of _h_/_a_ = 0.38 is

obtained by calculating θ_CB_ = θ′_W_. It can be seen from the figure that the proposed wetting transition model can give more accurate critical value of _h_/_a_ than traditional model59

which calculates critical _h_/_a_ on the basis of the solution of θ_CB_ = θ_W_ because the energy barrier may decrease the critical value of _h_/_a_ for wetting transition. It should be

pointed out that the present theoretical perdition still uses Eqs (12 and 14) to calculate surface roughness parameter _r_ and the fraction of the contact area _f_. Thus, one of reasons

causing the differences in apparent contact angle between the numerical and theoretical results should be an approximation of _r_ and _f_ with Eqs (12 and 14) when the droplet size is

comparable with the scale of the surface micro-structures. For the cases in the present study, the differences in _r_ and _f_ between the theoretical and numerical results are up to 3.3% and

3.5%, respectively. In this study, the wettability of micro-roughness surfaces, especially of the square-post patterned surfaces is studied theoretically and numerically. A theoretical

model of wetting transition is proposed on the basis of the concept of net free energy and energy barrier. Furthermore, a numerical simulation using LBM is carried out successfully to show

surface wetting properties, droplet shapes evolution, dynamic contact angle and corresponding velocity fields. The comparison of the wetting behavior on the square-post patterned surface

shows that the predicted values by the proposed theoretical model are in good agreement with the numerical results. As current simulation is to validate the proposed theoretical model of

wetting transition, only the surfaces patterned by square posts with constant spacing and height are considered. It is known that each geometrical parameter of the posts such as the height,

width and spacing, etc., plays an important role in determining wetting behavior; and this will be considered in our future work. METHODS In the present study, a lattice Boltzmann method46

of Yan & Zu is extended to simulate the wetting behaviors of a droplet spreading on micro-roughness surfaces. In order to implement the wetting boundary condition on solid wall of a

liquid-gas system, the order parameter, ϕ, in LBM, derivative at the wall boundaries must be given to control the contact angle. The boundary treatment of two phase flow on flat partial

wetting surfaces can be given by46 where, N is the local normal direction of the wall pointing to the fluid, λ a coefficient of wetting potential and _k_ the surface tension coefficient.

However, for the square-post patterned surface, N does not exist at the intersection of two or three orthogonal planes. In the present study, it is artificially defined to have the same

angle to the two or three planes61. As shown in Fig. 14, at the top corners of the square posts like those with labels 1, N is defined as While, on the edges with label 2 At the bottom

corners of the posts with label 3, On the edges with labels 4 and 5, In a same way, the values of N at the other corners and edges of the surface can be defined. ADDITIONAL INFORMATION HOW

TO CITE THIS ARTICLE: Zu, Y.Q. and Yan, Y.Y. Single Droplet on Micro Square-Post Patterned Surfaces - Theoretical Model and Numerical Simulation. _Sci. Rep._ 6, 19281; doi: 10.1038/srep19281

(2016). REFERENCES * Cyranoski, D. Chinese plan pins big hopes on small science. Nature 414, 240–240 (2001). Article  CAS  ADS  PubMed  Google Scholar  * Pilnam, K., Seunghyun, B. &

Kahp, Y. S. Capillarity-driven fluidic alignment of single-walled carbon nanotubes in reversibly bonded nanochannels. Small 4, 92–95 (2008). Article  CAS  Google Scholar  * Joseph, P. et al.

Slippage of water past superhydrophobic carbon nanotube forests in microchannels. Phys. Rev. Lett. 97, 156104 (2006). Article  CAS  ADS  PubMed  Google Scholar  * Choi, C. H. & Kim, C.

J. Large slip of aqueous liquid flow over a nanoengineered superhydrophobic surface. Phys. Rev. Lett. 96, 066001 (2006). Article  ADS  CAS  PubMed  Google Scholar  * Cho, S. C. & Wang,

Y. Two-phase flow dynamics in a micro channel with heterogeneous surfaces. Int. J. Heat Mass Transfer 71, 349–360 (2014). Article  Google Scholar  * Veretennikov, I., Agarwal, A., Indeikina,

A. & Chang, H.-C. Unusual contact-line dynamics of thick films and drops. J. Colloid Interface Sci. 215, 425–440 (1999). Article  CAS  ADS  PubMed  Google Scholar  * Burton, Z. &

Bhushan, B. Hydrophobicity, adhesion and friction properties of nanopatterned polymers and scale dependence for micro- and nanoelectromechanical Systems. Nano Lett. 5, 1607–1613 (2005).

Article  CAS  ADS  PubMed  Google Scholar  * Li, M. et al. Electrochemical deposition of conductive superhydrophobic Zinc Oxide thin films. J. Phys. Chem. B 107, 9954–9957 (2003). Article 

CAS  Google Scholar  * Zhang, X. et al. Polyelectrolyte multilayer as matrix for eectrochemical deposition of gold clusters: Toward super-hydrophobic surface. J. Am. Chem. Soc. 126,

3064–3065 (2004). Article  CAS  PubMed  Google Scholar  * Ichimura, K., Oh, S.-K. & Nakagawa, M. Light-driven motion of liquids on a photoresponsive surface. Science 288, 1624–1626

(2000). Article  CAS  ADS  Google Scholar  * Lahann, J. et al. A reversibly switching surface. Science 299, 371–374 (2003). Article  CAS  ADS  PubMed  Google Scholar  * Crevoisier, G. d.,

Fabre, P., Corpart, J.-M. & Leibler, L. Switchable tackiness and wettability of a liquid crystalline polymer. Science 285, 1246–1249 (1999). Article  PubMed  Google Scholar  * Chen, H.

et al. Comparative analysis of the dynamic contact angles for two types of superhydrophobic layered double hydroxide film surfaces. Chem. Eng. Sci. 64, 2957–2962 (2009). Article  CAS  ADS 

Google Scholar  * Extrand, C. W. Model for contact angles and hysteresis on rough and ultraphobic surfaces. Langmuir 18, 7991–7999 (2002). Article  CAS  Google Scholar  * Guo, C. et al.

Large-area fabrication of a nanostructure-induced hydrophobic surface from a hydrophilic polymer. ChemPhysChem 5, 750–753 (2004). Article  CAS  PubMed  Google Scholar  * Park, C. I., Jeong,

H. E., Lee, S. H., Cho, H. S. & Suh, K. Y. Wetting transition and optimal design for microstructured surfaces with hydrophobic and hydrophilic materials. J. Colloid Interface Sci. 336,

298–303 (2009). Article  CAS  ADS  PubMed  Google Scholar  * Sommers, A. D. & Jacobi, A. M. Wetting phenomena on micro-grooved aluminum surfaces and modeling of the critical droplet

size. J. Colloid Interface Sci. 328, 402–411 (2008). Article  CAS  ADS  PubMed  Google Scholar  * Blondiaux, N., Scolan, E., Popa, A. M., Gavillet, J. & Pugin, R. Fabrication of

superhydrophobic surfaces with controlled topography and chemistry. Appl. Surf. Sci. 265, S46–S53 (2009). Article  CAS  Google Scholar  * Law, J. B. K., Ng, A. M. H., He, A. Y. & Low, H.

Y. Bioinspired ultrahigh water pinning nanostructures. Langmuir 30, 325–331 (2014). Article  CAS  PubMed  Google Scholar  * Bico, J., Tordeux, C. & Quéré, D. Rough wetting. Europhys.

Lett. 55, 214–220 (2001). Article  CAS  ADS  Google Scholar  * Bormashenko, E. Wetting transitions on biomimetic surfaces. Philos T R Soc A 368, 4695–4711 (2010). Article  CAS  ADS  Google

Scholar  * Blossey, R. Self-cleaning surfaces - virtual realities. Nat. Mater. 2, 301–306 (2003). Article  CAS  ADS  PubMed  Google Scholar  * Yan, Y. Y., Gao, N. & Barthlott, W.

Mimicking natural superhydrophobic surfaces and grasping the wetting process: A review on recent progress in preparing superhydrophobic surfaces. Adv. Colloid Interface Sci. 169, 80–105

(2011). Article  CAS  PubMed  Google Scholar  * Nakae, H., Yoshida, M. & Yokota, M. Effects of roughness pitch of surfaces on their wettability. J. Mater. Sci. 40, 2287–2293 (2005).

Article  CAS  ADS  Google Scholar  * Li, W. & Amirfazli, A. Microtextured superhydrophobic surfaces: A thermodynamic analysis. Adv. Colloid Interface Sci. 132, 51–68 (2007). Article  CAS

  PubMed  Google Scholar  * Zheng, Q. S., Yu, Y. & Zhao, Z. H. Effects of hydraulic pressure on the stability and transition of wetting modes of superhydrophobic surfaces. Langmuir 21,

12207–12212 (2005). Article  CAS  PubMed  Google Scholar  * Bormashenko, E. Young, Boruvka–Neumann, Wenzel and Cassie–Baxter equations as the transversality conditions for the variational

problem of wetting. Colloid Surface A 345, 163–165 (2009). Article  CAS  Google Scholar  * Wenzel, R. N. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem . 28, 988–994

(1936). Article  CAS  Google Scholar  * Cassie, A. B. D. & Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc . 40, 546– 551 (1944). Article  CAS  Google Scholar  * Young, T.

An essay on the cohesion of fluids. Phi. Trans. R. Soc. Lond . 95, 65–87 (1805). Article  ADS  Google Scholar  * Savoy, E. S. & Escobedo, F. A. Molecular simulations of wetting of a

rough surface by an oily fluid: Effect of topology, chemistry and droplet size on wetting transition rates. Langmuir 28, 3412–3419 (2012). Article  CAS  PubMed  Google Scholar  * Savoy, E.

S. & Escobedo, F. A. Simulation study of free-energy barriers in the wetting transition of an oily fluid on a rough surface with reentrant geometry. Langmuir 28, 16080–16090 (2012).

Article  CAS  PubMed  Google Scholar  * Giacomello, A., Meloni, S., Chinappi, M. & Casciola, C. M. Cassie-Baxter and Wenzel states on a nanostructured surface: phase diagram,

metastabilities and transition mechanism by atomistic free energy calculations. Langmuir 28, 10764–10772 (2012). Article  CAS  PubMed  Google Scholar  * Khan, S. & Singh, J. K. Wetting

transition of nanodroplets of water on textured surfaces: a molecular dynamics study. Mol Simulat 40, 458–468 (2014). Article  CAS  Google Scholar  * Koishi, T., Yasuoka, K., Fujikawa, S.,

Ebisuzaki, T. & Zeng, X. C. Coexistence and transition between Cassie and Wenzel state on pillared hydrophobic surface. Proc. Natl. Acad. Sci. USA . 106, 8435–8440 (2009). Article  CAS 

ADS  Google Scholar  * Kim, Y. H., Choi, W. & Lee, J. S. Water droplet properties on periodically structured superhydrophobic surfaces: a lattice Boltzmann approach to multiphase flows

with high water/air density ratio. Microfluidics and Nanofluidics 10, 173–185 (2011). Article  CAS  Google Scholar  * Dupuis, A. & Yeomans, J. M. Modeling droplets on superhydrophobic

surfaces: equilibrium states and transitions. Langmuir 21, 2624–2629 (2005). Article  CAS  PubMed  Google Scholar  * Shahraz, A., Borhan, A. & Fichthorn, K. A. Wetting on physically

patterned solid surfaces: the relevance of molecular-dynamics simulations to macroscopic systems. Langmuir 29, 11632–11639 (2013). Article  CAS  PubMed  Google Scholar  * Connington, K.

& Lee, T. Lattice Boltzmann simulations of forced wetting transitions of drops on superhydrophobic surfaces. J. Comput. Phys. 250, 601–615 (2013). Article  CAS  ADS  Google Scholar  *

Bormashenko, E. Progress in understanding wetting transitions on rough surfaces. Adv. Colloid Interface Sci. 283, 258–270 (2015). Google Scholar  * Öner, D. & McCarthy, T. J.

Ultrahydrophobic surfaces. Effects of topography length scales on wettability. Langmuir 16, 7777–7782 (2000). Article  CAS  Google Scholar  * Bico, J., Marzolin, C. & Quere, D. Pearl

drops. Europhys. Lett. 47, 220–226 (1999). Article  CAS  ADS  Google Scholar  * He, B., Patankar, N. A. & Lee, J. Multiple equilibrium droplet shapes and design criterion for rough

hydrophobic surfaces. Langmuir 19, 4999–5003 (2003). Article  CAS  Google Scholar  * Bormashenko, E. & Bormashenko, Y. Wetting of composite surfaces: when and why is the area far from

the triple line important? J Phys Chem C 117, 19552–19557 (2013). CAS  Google Scholar  * Kwon, H. M., Paxson, A. T., Varanasi, K. K. & Patankar, N. A. Rapid deceleration-driven wetting

transition during pendant drop deposition on superhydrophobic surfaces. Phys. Rev. Lett. 106 (2011). * Yan, Y. Y. & Zu, Y. Q. A lattice Boltzmann method for incompressible two-phase

flows on partial wetting surface with large density ratio. J. Comput. Phys. 227, 763–775 (2007). Article  CAS  ADS  MathSciNet  MATH  Google Scholar  * Chen, S. & Doolen, G. D. Lattice

Boltzmann method for fluid flows. Ann. Rev. Fluid Mech . 30, 329–364 (1998). Article  ADS  MathSciNet  MATH  Google Scholar  * Gunstensen, A. K., Rothman, D. H., Zaleski, S. & Zanetti,

G. Lattice Boltzmann model of immiscible fluids. Phys. Rev. A 43, 4320–4327 (1991). Article  CAS  ADS  PubMed  Google Scholar  * Shan, X. W. & Chen, H. D. Lattice Boltzmann model for

simulating flows with multiple phases and components. Phys. Rev. E 47, 1815–1819 (1993). Article  CAS  ADS  Google Scholar  * Swift, M. R., Osborn, W. R. & Yeomans, J. M. Lattice

Boltzmann simulation of nonideal fluids. Phys. Rev. Lett. 75, 830–833 (1995). Article  CAS  ADS  PubMed  Google Scholar  * Swift, M. R., Orlandini, E., Osborn, W. R. & Yeomans, J. M.

Lattice Boltzmann simulations of liquid-gas and binary fluid systems. Phys. Rev. E 54, 5041–5052 (1996). Article  CAS  ADS  Google Scholar  * He, X. Y., Chen, S. Y. & Zhang, R. Y. A

lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh-Taylor instability. J. Comput. Phys. 152, 642–663 (1999). Article  CAS  ADS 

MathSciNet  MATH  Google Scholar  * Zu, Y. Q. & He, S. Phase-field-based lattice Boltzmann model for incompressible binary fluid systems with density and viscosity contrasts. Phys. Rev.

E 87, 043301 (2013). Article  CAS  ADS  Google Scholar  * Li, Q., Luo, K. H., Gao, Y. J. & He, Y. L. Additional interfacial force in lattice Boltzmann models for incompressible

multiphase flows. Phys. Rev. E 85, 026704 (2012). Article  CAS  ADS  Google Scholar  * Fakhari, A. & Rahimian, M. H. Phase-field modeling by the method of lattice Boltzmann equations.

Phys. Rev. E 81, 036707 (2010). Article  ADS  CAS  MATH  Google Scholar  * Johnson, R. E. J. & Dettre, R. H. Contact angle hysteresis. I. Study of an idealized rough surface. Adv. Chem.

Ser . 43, 112–135 (1964). Article  CAS  Google Scholar  * Kim, D., Kim, J. & Hwang, W. Prediction of contact angle on a microline patterned surface. Surf. Sci . 600, L301–L304 (2006).

Article  CAS  ADS  Google Scholar  * Zu, Y. Q., Yan, Y. Y. & Li, J. Q. Wetting behaviours of a single droplet on biomimetic micro structured surfaces. J. Bionic Eng. 7, In Press (2010).

* Bico, J., Thiele, U. & Quere, D. Wetting of textured surfaces. Colloid Surface A 206, 41–46 (2002). Article  CAS  Google Scholar  * Whyman, G. & Bormashenko, E. Wetting transitions

on rough substrates: general considerations. J Adhes Sci Technol 26, 207–220 (2012). CAS  Google Scholar  * Zu, Y. Q. & Yan, Y. Y. Lattice Boltzmann method for modelling droplets on

chemically heterogeneous and microstructured surfaces with large liquid-gas density ratio. IMA J Appl Math 76, 743–760 (2011). Article  MathSciNet  Google Scholar  * Blecua, P., Lipowsky, R.

& Kierfeld, J. Line tension effects for liquid droplets on circular surface domains. Langmuir 22, 11041–11059 (2006). Article  CAS  PubMed  Google Scholar  * Bormashenko, E. General

equation describing wetting of rough surfaces. J. Colloid Interface Sci. 360, 317–319 (2011). Article  CAS  ADS  PubMed  Google Scholar  * Bormashenko, E. Progress in understanding wetting

transitions on rough surfaces. Adv. Colloid Interface Sci. 222, 92–103 (2015). Article  CAS  PubMed  Google Scholar  * Bormashenko, E. & Whyman, G. On the role of the line tension in the

stability of Cassie wetting. Langmuir 29, 5515–5519 (2013). Article  CAS  PubMed  Google Scholar  * Wong, T.-S. & Ho, C.-M. Dependence of macroscopic wetting on nanoscopic surface

textures. Langmuir 25, 12851–12854 (2009). Article  CAS  PubMed  PubMed Central  Google Scholar  * Pompe, T. & Herminghaus, S. Three-phase contact line energetics from nanoscale liquid

surface topographies. Phys. Rev. Lett. 85, 1930–1933 (2000). Article  CAS  ADS  PubMed  Google Scholar  * Checco, A., Guenoun, P. & Daillant, J. Nonlinear dependence of the contact angle

of nanodroplets on contact line curvature. Phys. Rev. Lett. 91, 186101 (2003). Article  ADS  CAS  PubMed  Google Scholar  Download references ACKNOWLEDGEMENTS This work is supported by

Shanghai Pujiang Program under grant 14PJ1401600, the Scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry and Fudan University Initiative

Scientific Research Program. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Mechanics and Engineering Science, Fudan University, Shanghai, 200433, P.R. China Y. Q. Zu * Faculty

of Engineering, University of Nottingham, University Park, Nottingham, NG7 2RD, UK Y. Y. Yan Authors * Y. Q. Zu View author publications You can also search for this author inPubMed Google

Scholar * Y. Y. Yan View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS Y.Q.Z. and Y.Y.Y. designed and managed the research work and improved

the manuscript. Y.Q.Z. wrote the main manuscript text and prepared figures 1–14. All authors reviewed the manuscript. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing

financial interests. RIGHTS AND PERMISSIONS This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article

are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to

obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS

ARTICLE CITE THIS ARTICLE Zu, Y., Yan, Y. Single Droplet on Micro Square-Post Patterned Surfaces – Theoretical Model and Numerical Simulation. _Sci Rep_ 6, 19281 (2016).

https://doi.org/10.1038/srep19281 Download citation * Received: 11 February 2015 * Accepted: 07 December 2015 * Published: 18 January 2016 * DOI: https://doi.org/10.1038/srep19281 SHARE THIS

ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard

Provided by the Springer Nature SharedIt content-sharing initiative