ABSTRACT We introduce and analyze a one-dimensional quantum walk with two time-independent rotations on the coin. We study the influence on the property of quantum walk due to the second

rotation on the coin. Based on the asymptotic solution in the long time limit, a ballistic behaviour of this walk is observed. This quantum walk retains the quadratic growth of the variance

if the combined operator of the coin rotations is unitary. That confirms no localization exhibits in this walk. This result can be extended to the walk with multiple time-independent

rotations on the coin. SIMILAR CONTENT BEING VIEWED BY OTHERS TWO COMPONENT QUANTUM WALK IN ONE-DIMENSIONAL LATTICE WITH HOPPING IMBALANCE Article Open access 11 November 2021 TIME AND

transport in biological systems10,11 and quantum simulations of physical system and important phenomena such as Anderson localization12,13,14,15,16,17,18,19, Bloch oscillation20,21,22,23 and

non-trivial topological structure24,25,26. We study one possible route to the localization effect for the QW on the line: the use of multiple-rotation on the coin in order to change

interference pattern between paths27. We find exact analytical expressions for the time-dependence of the first two moments and , show the behaviour of QWs with two time-independent

rotations on the coin and present that a ballistic behaviour instead of localization is observed. This result can be extended to the walk with multiple time-independent rotations on the

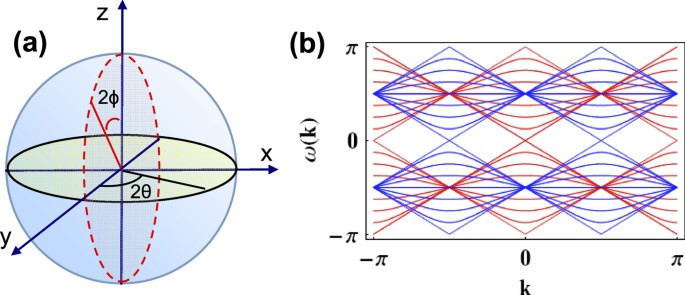
coin. RESULTS The unitary operator for single-step of this QW with two time-independent rotations on the coin is The two rotations on the coin shown in Fig. 1a where is the vector of Pauli

matrices. The rotations are followed by a conditional position shift operator where and are two orthogonal projectors on the Hilbert space of the coin spanned by , and are applied on the

walker’s position. One can identify the eigenvectors of _S_ and , with eigenvalues Here a discrete-time QW is considered as a stroboscopic realization of static effective Hamiltonian,

defined via the single-step evolution operator where is the time it takes to carry out one step and we set in the followings. The evolution operator for _N_ steps is given by . For the

general rotations in Eq. (2), the effective Hamiltonian can be written as where the quasi-energy (Fig. 1b) and the unit vector The inverse Fourier transformation is . The initial state of

the walker + coin system can be written as , where the original position state of the walker is . In the _k_ basis, the evolution operator becomes where is a unitary matrix with the matrix

elements At time _t_ (the time _t_ is proportional to the step number _N_), the walker + coin state evolves to The probability for the walker to reach a position _x_ at time _t_ is where ,

the group velocity of the walker . To determine if there is localization effect, we care more about the position variance and the dependence of the variance on time. Thus we restrict our

interest to the moments of the distribution With the formula of the delta function , the expression of the _m_th moment is rewritten as Similar to a Hadamard coined walk28, one can find the

eigenvectors of and corresponding eigenvalues . We can expand the initial coin state . With 29, we only keep the diagonal non-oscillatory terms and obtain For non-degenerate unitary matrix ,

except for the diagonal non-oscillatory terms, most of the terms are oscillatory, which average to zero in the long-time limit29. Similarly, the second moment is obtained From Eqs. (8) and

(11), we can see the spectrum of is non-degenerate. Even for degenerate one can modify Eqs. (17) and (18) to include appropriate cross terms, which does not change the dependence of the

position variance on time. Generically, in the long-time limit, for a unitary coin the first moment of the QW undergoes a linear drift and the variance grows quadratically with time. There

is a special case—the coined QW, i.e., , in which the eigenstates of are and , resulting in (for . Thus the variance of the coined QW does not depend on time. In the two rotations case, the

combination operation of two rotations on the coin shown in Eq. (11) is unitary. Thus for arbitrary choices of parameters θ and the position variance of the QW with two time-independent

rotations on the coin grows quadratically and the behaviour of the QW is ballistic. Therefore, a second coin rotation does not change the behaviour of QW from a ballistic spread to

localization. The asymptotic analysis of the behaviour of this QW with two time-independent coin rotations can be extended to more general QW with more time-independent rotations on the

coin. Once the combined operator of the multiple-rotation on the coin is unitary, the position variance grows quadratically with time and this QW shows ballistic behaviour. No localization

effect occurs. This walk is homogeneous in either spatial or temporal space. The coin rotations do not cause inhomogeneity in this walk which usually leads to interesting localization

effect. DISCUSSION In summary, we study the QW with two time-independent rotations on the coin through the analytical solutions for the time dependence of the position variance. The

asymptotic result can be extended to the walk with multiple time-independent rotations on the coin. As long as the combination of the multi-rotations is unitary, the variance grows

quadratically with time and the QW shows ballistic behaviour. No localization effect is observed in this QW. Although the fact that two topics—QWs and localization effect meet, is

fascinating and opens the door to rich theoretical and experimental investigation of quantum phenomena. Thus not only the investigation on simulating localization with QWs but also the study

on the limitations on localization in quantum walk are important and worthy of attention. Our research exactly gives insight into limitations on localization. ADDITIONAL INFORMATION HOW TO

CITE THIS ARTICLE: Xue, P. _et al._ A one-dimensional quantum walk with multiple-rotation on the coin. _Sci. Rep._ 6, 20095; doi: 10.1038/srep20095 (2016). REFERENCES * Kempe, J. Quantum

random walks: An introductory overview. Cont. Phys. 44, 307–327 (2003). Article  ADS  Google Scholar  * Ambainis, A. Quantum walks and their algorithmic applications. Int. J. Quant. Inf. 1,

507–518 (2003). Article  Google Scholar  * Childs, A. M. et al. Exponential algorithmic speedup by quantum walk. _Proc. ACM Symp. on Theory of Computing (STOC 2003)_ pp 59-68 (2003). *

Shenvi, N., Kempe, J. & Whaley, K. B. Quantum random-walk search algorithm. Phys. Rev. A 67, 052307 (2003). Article  ADS  CAS  Google Scholar  * Berry, S. D. & Wang, J. B.

Quantum-walk-based search and centrality. Phys. Rev. A 82, 042333 (2010). Article  ADS  CAS  Google Scholar  * Franco, C. & Di, McGettrick, M. & Busch, Th. Mimicking the probability

distribution of a two-dimensional Grover walk with a single-qubit coin. Phys. Rev. Lett. 106, 080502 (2011). Article  CAS  Google Scholar  * Childs, A. M. Universal computation by quantum

walk. Phys. Rev. Lett. 102, 180501 (2009). Article  MathSciNet  ADS  CAS  Google Scholar  * Childs, A. M., Gosset, D. & Webb, Z. Universal computation by multiparticle quantum walk.

Science 339, 791–794 (2013). Article  MathSciNet  ADS  CAS  Google Scholar  * Lovett, N. B., Cooper, S., Everitt, M., Trevers, M. & Kendon, V. Universal quantum computation using the

discrete-time quantum walk. Phys. Rev. A 81, 042330 (2010). Article  MathSciNet  ADS  CAS  Google Scholar  * Lloyd, S. Quantum coherence in biological systems. _J. Phys.: Conf. Series_302,

012037 (2011). Google Scholar  * Hoyer, S., Sarovar, M. & Whaley, K. B. Limits of quantum speedup in photosynthetic light harvesting. New J. Phys. 12, 065041 (2010). Article  ADS  CAS 

Google Scholar  * Anderson, P. W. Absence of diffusion in certain random lattices. Phys. Rev. 109, 1492 (1958). Article  ADS  CAS  Google Scholar  * Wójcik, A. et al. Trapping a particle of

a quantum walk on the line. Phys. Rev. A 85, 012329 (2012). Article  ADS  CAS  Google Scholar  * Konno, N. Localization of an inhomogeneous discrete-time quantum walk on the line. Quant.

Inf. Proc. 9, 405–418 (2010). Article  MathSciNet  CAS  Google Scholar  * Shikano, Y. & Katsura, H. Localization and fractality in inhomogeneous quantum walks with self-duality. Phys.

Rev. E 82, 031122 (2010). Article  MathSciNet  ADS  CAS  Google Scholar  * Zhang, R., Xue, P. & Twamley, J. One-dimensional quantum walks with single-point phase defects. Phys. Rev. A

89, 042317 (2014). Article  ADS  CAS  Google Scholar  * Schreiber, A. et al. Decoherence and disorder in quantum walks: from ballistic spread to localization. Phys. Rev. Lett. 106, 180403

(2011). Article  ADS  CAS  Google Scholar  * Crespi, A. et al. Localization properties of two-photon wave packets. Nat. Photonics 7, 322–328 (2013). Article  ADS  CAS  Google Scholar  * Xue,

P., Qin, H. & Tang, B. Trapping photons on the line: controllable dynamics of a quantum walk. Sci. Rep. 4, 4825 (2014). Article  ADS  Google Scholar  * Wójcik, A., Łuczak, T.,

Kurzyński, P., Grudka, A. & Bednarska, M. Quasiperiodic dynamics of a quantum walk on the line. Phys. Rev. Lett. 93, 180601 (2004). Article  ADS  CAS  Google Scholar  * Bañuls, M. C.,

Navarrete, C., Pérez, A., Roldán, E. & Soriano, J. C. Quantum walk with a time-dependent coin. Phys. Rev. A 73, 062304 (2006). Article  MathSciNet  ADS  CAS  Google Scholar  * Genske, M.

et al. Electric quantum walks with individual atoms. Phys. Rev. Lett. 110, 190601 (2013). Article  ADS  CAS  Google Scholar  * Xue, P., Qin, H., Tang, B. & Sanders, B. C. Observation of

quasiperiodic dynamics in a onedimensional quantum walk of single photons in space. New J. Phys. 16, 053009 (2014). Article  ADS  CAS  Google Scholar  * Kitagawa, T., Rudner, M. S., Berg,

E. & Demler, E. Exploring topological phases with quantum walks. Phys. Rev. A 82, 033429 (2010). Article  ADS  CAS  Google Scholar  * Asbóth, J. K. Symmetries, topological phases and

bound states in the one-dimensional quantum walk. Phys. Rev. B 86, 195414 (2012). Article  ADS  CAS  Google Scholar  * Kitagawa, T. et al. Observation of topologically protected bound states

in photonic quantum walks. Nat. Commun. 3, 882 (2012). Article  ADS  CAS  Google Scholar  * Xue, P. et al. Experimental quantum-walk revival with a time-dependent coin. Phys. Rev. Lett.

112, 120502 (2014). Article  CAS  Google Scholar  * Nayak, A. & Vishwanath, A. Quantum walk on the line. arXiv:quant-ph/0010117. * Brun, T. A., Carteret, H. A. & Ambainis, A. Quantum

to classical transition for random walks. Phys. Rev. Lett. 91, 130602 (2003). Article  ADS  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS This work has been supported by

National Natural Science Foundation of China, Grant Nos. 11174052 and 11474049 and the CAST Innovation fund. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Physics, Southeast

University, Nanjing, 211189, China Peng Xue, Rong Zhang, Hao Qin, Xiang Zhan, Zhihao Bian & Jian Li Authors * Peng Xue View author publications You can also search for this author

inPubMed Google Scholar * Rong Zhang View author publications You can also search for this author inPubMed Google Scholar * Hao Qin View author publications You can also search for this

author inPubMed Google Scholar * Xiang Zhan View author publications You can also search for this author inPubMed Google Scholar * Zhihao Bian View author publications You can also search

for this author inPubMed Google Scholar * Jian Li View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS P.X. developed the theory, supervised

R.Z., H.Q., X.Z., Z.B. and J.L. and wrote most of the paper. R.Z. and H.Q. wrote the code. X.Z. and Z.B. checked the numerical simulations. All authors reviewed the manuscript. ETHICS

DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests. RIGHTS AND PERMISSIONS This work is licensed under a Creative Commons Attribution 4.0 International

License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is

not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Xue, P., Zhang, R., Qin, H. _et al._ A one-dimensional quantum walk with

multiple-rotation on the coin. _Sci Rep_ 6, 20095 (2016). https://doi.org/10.1038/srep20095 Download citation * Received: 13 October 2015 * Accepted: 09 November 2015 * Published: 29 January

2016 * DOI: https://doi.org/10.1038/srep20095 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is

not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative