ABSTRACT We study the physical properties of double-cavity optomechanical system in which the mechanical resonator interacts with one of the coupled cavities and another cavity is used as an

auxiliary cavity. The model can be expected to achieve the strong optomechanical coupling strength and overcome the optomechanical cavity decay, simultaneously. Through the coherent

auxiliary cavity interferences, the steady-state squeezing of mechanical resonator can be generated in highly unresolved sideband regime. The validity of the scheme is assessed by numerical

simulation and theoretical analysis of the steady-state variance of the mechanical displacement quadrature. The scheme provides a platform for the mechanical squeezing beyond the resolved

INTERACTION WITH AN OPTOMECHANICAL CAVITY CONTAINING A QUANTUM WELL Article Open access 07 March 2022 INTRODUCTION The optomechanical system is a rapidly growing field in which researchers

study the interaction between the optical and mechanical degrees of freedom via radiation pressure, optical gradient, or photothermal forces. In optomechanical systems, quantum fluctuations

become the dominant mechanical driving force with strong radiation pressure, which leads to correlations between the mechanical motion and the quantum fluctuations of the cavity field1.

Originally, the goal of studying the optomechanical interaction is to detect gravitational wave2. As research continues, the optomechanical system has been developed to investigate quantum

coherence for quantum information processing3,4 and quantum-to-classical transition studying in macroscopic solid-state devices5,6. Many projects of cavity optomechanics systems have been

conceived and demonstrated experimentally, including red-sideband laser cooling in the resolved or unresolved sideband regime7,8,9,10,11,12,13,14,15, coherent-state transiting between the

cavity and mechanical resonator16,17, normal-mode splitting18,19, quantum network20, backaction-evading measurements21, entanglement between mechanical resonator and cavity field or

atom22,23,24,25,26, induced transparency27,28, macroscopic quantum superposition29, squeezing light30,31,32, and squeezing resonator33,34,35,36,37,38,39,40,41,42,43,44,45. In the above

applications, quantum squeezing is important for studying the macroscopic quantum effects and the precision metrology of weak forces. In the above schemes of squeezing, the theory of most

schemes is based on the nonlinear property. The history of squeezing is linked intimately to quantum-limited displacement sensing46, and many schemes have been proposed to generate squeezing

states in various systems47,48,49. The squeezing of light is proposed for the first time using atomic sodium as a nonlinear medium48. In recent years, researchers have found that the

optomechanical cavity, in which radiation pressure proportional to optical intensity changes the cavity length, could act as a low-noise Kerr nonlinear medium50 in form. So the

optomechanical cavity could be a better candidate to generate squeezing of the optical and mechanical modes. The squeezing of optical field is easy to be achieved in the optomechanical

systems, and has been reported experimentally31,51,52. Furthermore, many theoretical schemes have been proposed to generate mechanical squeezing in the optomechanical systems by using

different methods33,34,35,36,37,38,39,40,41,42,43,44. For example, in 2010, Nunnenkamp _et al_.41 proposed a scheme to generate mechanical squeezing via the quadratically nonlinear coupling

between optical cavity mode and the displacement of a mechanical resonator. In 2011, Liao _et al_.42 proposed a scheme to generate mechanical squeezing via periodically modulating the

driving field amplitude at a frequency matching the frequency shift of the resonator. In 2013, Kronwald _et al_.43 proposed a scheme to generate mechanical squeezing by driving the

optomechanical cavity with two controllable lasers with differing amplitudes in a dissipative mechanism. In 2015, Lü _et al_.44 proposed a scheme to generate steady-state mechanical

squeezing via utilizing the mechanical intrinsic nonlinearity. With the deepening of research, the squeezing of mechanical mode has finally been observed experimentally by Wollman _et

al_.53. In most theoretical schemes, the mechanical resonator squeezing must rely on the resolved sideband limit, requiring a cavity decay rate smaller than the mechanical resonator

frequency, which restricted the progress of the experiment. Traditionally and generally, the decay rate of cavity, which is a dissipative factor in optomechanical systems, is considered to

have negative effect on the performance of quantum manipulation and quantum information processing. The optomechanical coupling strength (with the cavity frequency _ω__c_, the mechanical

resonator mass _m_, and the mechanical resonator frequency _ω__m_) is inverse relation to the cavity length _L_. While the cavity quality factor _Q_ increases with increasing the cavity

volume _V_. Thus it is difficult to achieve small decay rate and strong optomechanical coupling strength simultaneously. Here we propose a method to generate steady-state mechanical

squeezing in a double-cavity optomechanical system with the highly dissipative cavity (_κ_1/_ω__m_ = 100). The scheme does not need to satisfy the conditions of the small cavity decay rate

and the strong optomechanical coupling strength simultaneously. The coherently driving on the cavity mode is a monochromatic laser source which can generate strong optomechanical coupling

between the mechanical and cavity modes. We show that, based on the mechanical nonlinearity and cavity cooling process in transformed frame, the steady-state mechanical squeezing can be

successfully and effectively generated in the highly unresolved sideband regime via the coherent auxiliary cavity interfering. The result indicate that the squeezing can reach 4.4 dB, beyond

the so-called 3 dB limit. Different from the hybrid atom-optomechanical systems9,23,37, the scheme does not have the challenge of putting a large number of atoms in the cavity. Unlike the

dissipative coupling mechanism32,43,49,54,55, our scheme utilizes the destructive interference coming from the coherent auxiliary cavity to resist the influence of cavity decay. The paper is

organized as follows: In Sec. II, we describe the model of a double-cavity optomechanical system and derive the linearized Hamiltonian and the effective coupling between the auxiliary

cavity and the mechanical resonator. In Sec. III, we engineer the mechanical squeezing and derive the analytical variance of the displacement quadrature of the mechanical resonator in the

steady-state. In Sec. IV, we study the relationship between the variance of mechanical mode and the system parameters and obtain the steady-state mechanical squeezing in the highly

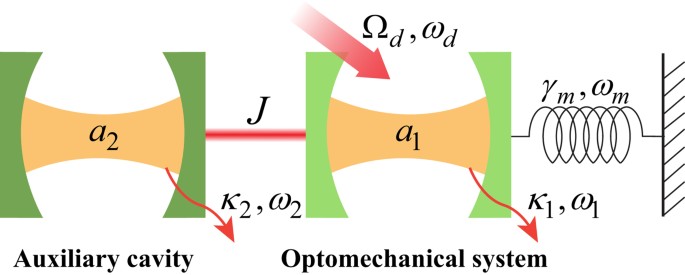
unresolved sideband regime by numerical simulations method. A conclusion is given in Sec. V. RESULTS BASIC MODEL We consider a double-cavity optomechanical system, which is composed of a

mechanical resonator and two coupled single-mode cavities, depicted in Fig. 1. The mechanical resonator couples to the first dissipative cavity which is driven by an external laser field,

forming the standard optomechanical subsystem. The second high _Q_ optical cavity is regarded as the auxiliary part, which couples to the first dissipative cavity with the coupling strength

_J_. The total Hamiltonian _H_ = _H_0 + _H_I + _H_pump, which describes the double-cavity optomechanical system, consists of three parts, which reads (_ħ_ = 1), respectively, The part _H_0

accounts for the free Hamiltonian of the two cavity modes (with frequency _ω_1, _ω_2 and decay rate _κ_1, _κ_2, respectively) and the mechanical resonator (with frequency _ω__m_ and damping

rate _γ__m_). Here is the bosonic annihilation (creation) operator of the first optical cavity mode, is the bosonic annihilation (creation) operator of the second optical cavity mode, and _b

(b_†) is the bosonic annihilation (creation) operator of the mechanical mode. The last term of _H_0 describes the Duffing nonlinearity56,57 of the mechanical resonator with amplitude _η_.

The intrinsic nonlinearity of the gigahertz mechanical resonator is usually very weak with nonlinear amplitude smaller than 10−15_ω__m_. We can obtain a strong nonlinearity through coupling

the mechanical mode to an auxiliary system58, such as the nonlinear amplitude of _η_ = 10−4_ω__m_ can be obtained when we couple the mechanical resonator to an external qubit44. The

resulting model is known as the Duffing oscillator and exhibits a bifurcation phenomenon as the strength of the mechanical driving is increased59. In our scheme, the bifurcation

phenomenon60,61 exists even in the joint influence of Duffing and optomechanical nonlinearities. While the driving power we need is far from reaching the bifurcation point, we will not

discuss the bifurcation detailedly in here. The part _H_I accounts for the interaction Hamiltonian consisting of the coupling interaction between two cavities and the optomechanical

interaction derived from the radiation pressures. Where _J_ represents the intercavity coupling strength between cavity mode _a_1 and _a_2, and _g_ is the single-photon optomechanical

coupling strength. The part _H_pump accounts for the external driving laser with frequency _ω__d_ used to coherently pump the cavity mode _a_1. The driving strength is related to the input

laser power _P_, frequency _ω__d_, and the decay rate of cavity 1 _κ_1. In the rotating frame defined by the transformation operator , the Hamiltonian of the system is given by where _δ_1 = 

_ω__d_ − _ω_1 and _δ_2 = _ω__d_ − _ω_2 are the detunings of the two cavity modes from the driving field, respectively. Considering the effect of the thermal environment, the quantum

Heisenberg-Langevin equations for the system are written as where the corresponding noise operators _a_1_in_, _a_2_in_, and _b__in_ satisfy the following correlations: here, is the mean

thermal excitation number of bath of the mechanical resonator at temperature _T, k__B_ is the Boltzmann constant. And under the assumption of Markovian baths, the noise operators _a_1_in_,

_a_2_in_, and _b__in_ have zero mean values. Since the system is driven by a classical laser field, in the case of strong driving field, we can treat the field operators as the sum of their

mean values and small quantum fluctuation. So we can apply a displacement transformation to linearize the equations, _a_1 → _α_1 + _a_1, _a_2 → _α_2 + _a_2, _b_ → _β_ + _b_, where _α_1,

_α_2, and _β_ are _c_ numbers denoting the mean values of the optical and mechanical modes. The mean values of the optical and mechanical modes satisfy the corresponding semiclassical

equations: The steady-state amplitudes of the optical and mechanical modes are relative to the driving power _P_, and the relationship can be derived by solving the above equations under the

condition of steady situation. One can see that when the driving power _P_ is in the microwatt range, the amplitudes of the cavity and mechanical modes satisfy the relationships: , as shown

in Fig. 2. And the amplitudes of the cavity and mechanical modes increase with increasing the driving power. At the point of the driving power _P_ = 0.53 mW, the result of and can be

obtained, respectively. Under the conditions of strong driving, the nonlinear terms are neglected. The quantum fluctuations satisfy the following linearized equations: with The linearized

Hamiltonian is given by When considering the system-reservoir interaction, which results in the dissipations of the system, the full dynamics of the system is described by the master

equation where is the standard Lindblad operators. _κ_1, _κ_2, and _γ__m_ are the decay rate of cavity mode _a_1, _a_2, and the damping rate of mechanical resonator, respectively. is the

average phonon number in thermal equilibrium. EFFECTIVE COUPLING BETWEEN THE AUXILIARY CAVITY AND THE MECHANICAL RESONATOR Since the decay rate of cavity 1 (_κ_1) is much larger than the

decay rate of cavity 2 (_κ_2) and the damping rate of mechanical resonator (_γ__m_), the cavity mode _a_1 can be eliminated adiabatically for the time scales longer than . The steady

solution of the first equation in Eq. (6) about cavity mode _a_1 can be written as Substituting Eq. (10) into the rear two equations of Eq. (6), we can obtain the effective coupling between

the cavity mode _a_2 and the mechanical mode _b_, which can be described by the following equations: where _A_2_in_ and _B__in_ denote the modified noise terms, the effective parameters of

the mechanical frequency, optomechanical coupling strength, detuning, decay rate, and coefficients of bilinear terms are given by Thus the effective Hamiltonian, describing the effective

coupling between the auxiliary cavity mode and the mechanical resonator, is written as and the master equation becomes The effective Hamiltonian describes the effective interaction between

the cavity 2 and the mechanical resonator. As we all know, if the Hamiltonian in the interaction picture has the form _b_2 + _b_†2, the corresponding evolution operator is a squeezed

operator. ENGINEERING THE MECHANICAL SQUEEZING Applying the unitary transformation _S_(_ζ_) = exp[_ζ_(_b_2 − _b_†2)/2], which is the single-mode squeezing operator with the squeezing

parameter to the total system. Then the transformed effective Hamiltonian becomes with where is the transformed effective mechanical frequency and _G_′ is the transformed effective

optomechanical coupling. The transformed Hamiltonian is a standard cavity cooling Hamiltonian and the best cooling in the transformed frame is at the optimal detuning . In the transformed

frame, the master equation, which is used for describing the system-reservoir interaction, can be obtained via applying the squeezing transformation _S_(_ζ_) to the master equation Eq. (14)

and the transformed density matrix _ρ__s_ = _S_†(_ζ_)_ρS_(_ζ_). The transformed master equation can achieve the cooling process, which can be seen from the Hamiltonian Eq. (16). Here, is the

transformed thermal phonon number. The steady-state density matrix _ρ_ (in the original frame) can be obtained by solving the master equation Eq. (14). Defining the displacement quadrature

_X_ = _b_ + _b_† for the mechanical mode, the steady-state variance of _X_ is given by 〈_δX_2〉 = 〈_X_2〉 − 〈_X_〉2, which can be derived in the transformed frame as where is the steady-state

phonon number coming from the cooling process in the transformed frame. When the best cooling in ideal situation is achieved by the cooling process, the steady-state variance of the

mechanical resonator displacement quadrature is 〈_δX_2〉 = _e_−2_ζ_. DISCUSSION In this section, we solve the original master equation Eq. (9) numerically to calculate the steady-state

variance of the mechanical displacement quadrature _X_. Firstly, we should provide the time evolution of variance 〈_δX_2〉 about the mechanical displacement quadrature, which is shown in Fig.

3. It indicate that the variance 〈_δX_2〉 gradually tends to be stable after a period of time. For simplicity, we have assumed that the system is initially prepared in its ground state and

the system parameters are chosen to be the same as in Fig. 2. The relationship between the steady-state variance and intercavity coupling strength is shown in Fig. 4. Before we study their

relationship, we should recalculate the steady-state amplitudes of the optical and mechanical modes |_α_1|, |_α_2|, and |_β_| with the different intercavity coupling strengths. We can find

that the steady-state mechanical squeezing can be achieved effectively when the intercavity coupling strength is appropriate, which reaches a balance between the enough large photons number

in cavity 1 and the coherent auxiliary cavity interferences. However, when we remove the coherent auxiliary cavity interferences (_J_ = 0), the mechanical steady-state squeezing can not be

obtained effectively under the present condition. The relationship between the steady-state variance and driving power is shown in Fig. 5. One can see from Fig. 5 that the steady-state

squeezing of the mechanical resonator changes observably with the laser driving power. We can obtain the steady-state mechanical squeezing effectively when the driving power is in milliwatts

level. At last, we consider the effect of the cavity 1 decay _κ_1. When calculate the relationship between the steady-state variance and cavity 1 decay, we consider a more variable _J_ as

shown in Fig. 6. The result show that the maximum value of squeezing can be reached with a appropriate _J_ when the cavity 1 decay is certain. In Fig. 6, the minimum value of the

steady-state variance is 0.36, corresponding to the 4.4 dB. In the above, we study the steady-state squeezing of the mechanical resonator in a double-cavity optomechanical system and

illustrate that the steady-state squeezing can be effectively generated in highly unresolved sideband regime with appropriate intercavity coupling strength and driving power. When the decay

rate of cavity is known, the maximum value of the squeezing parameter _ζ_ is achieved at the point of Δ_a_ = _κ_1/2, which can be easily seen from Eq. (12). The experimental studies of the

double-cavity optomechanical system with whispering-gallery microcavities have been reported62,63,64,65. Besides, in the latest experiment report66, the tunable nonlinearity of the

mechanical resonator has been greatly improved by exploring the anharmonicity in chemical bonding interactions. And our method, utilizing the coherent auxiliary cavity 2 to resist the

influence of decay coming from cavity 1, is also feasible with the cubic nonlinearity of mechanical resonator, which is easy to prove as refs 37, 44. We also notice anther approach beyond

the resolved sideband limit and demonstrated experimentally in optomechanical system67,68. Furthermore, the generated steady-state mechanical squeezing in the present scheme can be detected

based on the method proposed in refs 22, 44. As illustrated in refs 22, 44, for detecting the mechanical resonator, we consider another auxiliary cavity mode _a__s_ (another mode of the

cavity _a_1 or adding another cavity on the right) with resonant frequency _ω__s_, which is driven by a weak pump laser field of amplitude Ω_p_ and frequency _ω__p_. The presence of the

cavity _a__s_ will affect the mirror dynamics, which is no more exactly described by Eqs (6). The original Hamiltonian Eq. (2) should be added the new detection parts , where _δ__s_ = _ω__p_

 − _ω__s_ and _g__s_ is the strength of the single-photon optomechanical coupling. However, if the intracavity field is very weak under the weak driving field (the cavity mode steady-state

amplitude ), the cavity backaction on the mechanical mode can be neglected and the relevant dynamics is still well described by Eq. (6). Through homodyning detection of the output field of

another auxiliary cavity mode with an appropriate phase, we can obtain the information of the position and the momentum quadratures of the mechanical resonator. Effective detection of the

mechanical state requires that while , where _κ__s_ is decay rate of the another auxiliary cavity. The experimental detection technology of the output field has also been realized. In

conclusion, we have proposed a scheme for generating the steady-state squeezing of the mechanical resonator in a double-cavity optomechanical system via the mechanical nonlinearity and

cavity cooling process in transformed frame. The steady-state squeezing of the mechanical resonator can be obtained in the highly unresolve sideband regime through the coherent auxiliary

cavity interferences. Since the auxiliary cavity mode is not directly coupled to the mechanical resonator, it can be a high _Q_ optical cavity with big cavity volume _V_, while another

cavity coupling with the mechanical resonator can have a short cavity length _L_ to possess good mechanical properties. The effective coupling between the mechanical resonator and the

auxiliary cavity can be obtained by reducing the cavity mode adiabatically. We simulate the steady-state variance of the mechanical displacement quadrature numerically at a determinate laser

driving power and find that under an appropriate intercavity coupling strength the steady-state mechanical squeezing can be achieved effectively in highly unresolve sideband regime. Our

scheme opens up the possibility for application of cavity quantum optomechanics beyond the resolved sideband regime, solving the restricted experimental bounds at present. THE EFFECTIVE

INTERACTION BETWEEN THE AUXILIARY CAVITY AND THE MECHANICAL RESONATOR Here, we will introduce another way to derive the effective coupling between the auxiliary cavity and the mechanical

resonator. The quantum Langevin equations Eq. (6) can be formally integrated as Since the decay rate of cavity 1 _κ_1 is much larger than the decay rate of cavity 2 _κ_2 and the damping rate

of mechanical resonator _γ__m_, the dynamics of mode _b_ and _a_2 are only slightly affected by mode _a_1. We obtain the approximated expressions where and denote the nosie terms. By

Plugging Eq. (20) into the first equation of Eq. (19), we obtain where denote the noise term. Under the conditions of and , we obtain Neglecting the fast decaying term which contains

exp(−_κ_1_t_/2), and the above Eq. (22) is same form as Eq. (10). ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE: Wang, D.-Y. _et al_. Steady-state mechanical squeezing in a double-cavity

optomechanical system. _Sci. Rep._ 6, 38559; doi: 10.1038/srep38559 (2016). PUBLISHER'S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and

institutional affiliations. REFERENCES * Purdy, T. P., Peterson, R. W. & Regal, C. A. Observation of Radiation Pressure Shot Noise on a Macroscopic Object. Science 339, 801 (2013).

Article  ADS  CAS  PubMed  Google Scholar  * Barish, B. C. & Weiss, R. LIGO and the Detection of Gravitational Waves. Phys. Today 52, 44 (1999). Article  Google Scholar  * Marquardt, F.

& Girvin, S. M. Optomechanics. Physics 2, 40 (2009). Article  Google Scholar  * Blencowe, M. Quantum electromechanical systems. Phys. Rep. 395, 159 (2004). Article  ADS  Google Scholar 

* Kippenberg, T. J. & Vahala, K. J. Cavity Optomechanics: Back-Action at the Mesoscale. Science 321, 1172 (2008). Article  ADS  CAS  PubMed  Google Scholar  * Hu, X. & Nori, F.

Squeezed Phonon States: Modulating Quantum Fluctuations of Atomic Displacements. Phys. Rev. Lett. 76, 2294 (1996). Article  ADS  CAS  PubMed  Google Scholar  * Wilson-Rae, I., Nooshi, N.,

Zwerger, W. & Kippenberg, T. J. Theory of Ground State Cooling of a Mechanical Oscillator Using Dynamical Backaction. Phys. Rev. Lett. 99, 093901 (2007). Article  ADS  CAS  PubMed 

Google Scholar  * Liu, Y. C., Xiao, Y. F., Luan, X. S., Gong, Q. H. & Wong, C. W. Coupled cavities for motional ground-state cooling and strong optomechanical coupling. Phys. Rev. A 91,

033818 (2015). Article  ADS  CAS  Google Scholar  * Chen, X., Liu, Y. C., Peng, P., Zhi, Y. & Xiao, Y. F. Cooling of macroscopic mechanical resonators in hybrid atom-optomechanical

systems. Phys. Rev. A 92, 033841 (2015). Article  ADS  CAS  Google Scholar  * Guo, Y., Li, K., Nie, W. & Li, Y. Electromagnetically-induced-transparency-like ground-state cooling in a

double-cavity optomechanical system. Phys. Rev. A 90, 053841 (2014). Article  ADS  CAS  Google Scholar  * Marquardt, F., Chen, J. P., Clerk, A. A. & Girvin, S. M. Quantum Theory of

Cavity-Assisted Sideband Cooling of Mechanical Motion. Phys. Rev. Lett. 99, 093902 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Yin, Z. Q., Li, T. & Feng, M. Three-dimensional

cooling and detection of a nanosphere with a single cavity. Phys. Rev. A 83, 013816 (2011). Article  ADS  CAS  Google Scholar  * Clark, J. B., Lecocq, F., Simmonds, R. W., Aumentado, J.

& Teufel, J. D. Sideband Cooling Beyond the Quantum Limit with Squeezed Light. _arXiv:_ 1605.08795 (2016). * Asjad, M., Zippilli, S. & Vitali, D. Suppression of Stokes scattering and

improved optomechanical cooling with squeezed light. _arXiv:_ 1606.09007 (2016). * Zhang, W. Z., Cheng, J., Li, W. D. & Zhou, L. Optomechanical cooling in the non-Markovian regime.

Phys. Rev. A 93, 063853 (2016). Article  ADS  CAS  Google Scholar  * Tian, L. Cavity cooling of a mechanical resonator in the presence of a two-level-system defect. Phys. Rev. B 84, 035417

(2011). Article  ADS  CAS  Google Scholar  * Wang, Y. D. & Clerk, A. A. Using Interference for High Fidelity Quantum State Transfer in Optomechanics. Phys. Rev. Lett. 108, 153603 (2012).

Article  ADS  CAS  PubMed  Google Scholar  * Dobrindt, J. M. Wilson-Rae, I. & Kippenberg, T. J. Parametric Normal-Mode Splitting in Cavity Optomechanics. Phys. Rev. Lett. 101, 263602

(2008). Article  ADS  CAS  PubMed  Google Scholar  * Gröblacher, S., Hammerer, K. Vanner, M. R. & Aspelmeyer, M. Observation of strong coupling between a micromechanical resonator and an

optical cavity field. Nature (London) 460, 724 (2009). Article  ADS  CAS  Google Scholar  * Yin, Z. Q., Yang, W. L., Sun, L. & Duan, L. M. Quantum network of superconducting qubits

through an optomechanical interface. Phys. Rev. A 91, 012333 (2015). Article  ADS  CAS  Google Scholar  * Clerk, A. A., Marquardt, F. & Jacobs, K. Back-action evasion and squeezing of a

mechanical resonator using a cavity detector. New J. Phys. 10, 095010 (2008). Article  ADS  Google Scholar  * Vitali, D. et al. Optomechanical Entanglement between a Movable Mirror and a

Cavity Field. Phys. Rev. Lett. 98, 030405 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Genes, C., Vitali, D. & Tombesi, P. Emergence of atom-light-mirror entanglement inside an

optical cavity. Phys. Rev. A 77, 050307(R) (2008). Article  ADS  CAS  Google Scholar  * Bai, C. H., Wang, D. Y., Wang, H. F., Zhu, A. D. & Zhang, S. Robust entanglement between a movable

mirror and atomic ensemble and entanglement transfer in coupled optomechanical system. Sci. Rep. 6, 33404 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Nie, W. J.,

Lan, Y. H., Li, Y. & Zhu, S. Y. Generating large steady-state optomechanical entanglement by the action of Casimir force. Sci. China-Phys., Mech. Astron. 57, 2276 (2014). Article  ADS 

Google Scholar  * Asjad, M., Zippilli, S. & Vitali, D. Mechanical Einstein-Podolsky-Rosen entanglement beyond the resolved sideband regime with a finite-bandwidth squeezed reservoir.

Phys. Rev. A 93, 062307 (2016). Article  ADS  CAS  Google Scholar  * Wu, Q., Zhang, J. Q., Wu, J. H., Feng, M. & Zhang, Z. M. Tunable multi-channel inverse optomechanically induced

transparency and its applications. Opt. Express 23, 18534 (2015). Article  ADS  PubMed  Google Scholar  * Li, W. l., Jiang, Y. f., Li, C. & Song, H. S. Parity-time-symmetry enhanced

optomechanically-inducedtransparency. Sci. Rep. 6, 31095 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Liao, J. Q. & Tian, L. Macroscopic Quantum Superposition in

Cavity Optomechanics. Phys. Rev. Lett. 116, 163602 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Jähne, K. et al. Cavity-assisted squeezing of a mechanical oscillator. Phys. Rev. A

79, 063819 (2009). Article  ADS  CAS  Google Scholar  * Purdy, T. P., Yu, P. L., Peterson, R. W., Kampel, N. S. & Regal, C. A. Strong Optomechanical Squeezing of Light. Phys. Rev. X 3,

031012 (2013). Google Scholar  * kronwald, A., Marquardt, F. & Clerk, A. A. Dissipative optomechanical squeezing of light. New J. Phys. 16, 063058 (2014). Article  ADS  Google Scholar  *

Mari, A. & Eisert, J. Gently Modulating Optomechanical Systems. Phys. Rev. Lett. 103, 213603 (2009). Article  ADS  CAS  PubMed  Google Scholar  * Gu, W. J., Li, G. X. & Yang, Y. P.

Generation of squeezed states in a movable mirror via dissipative optomechanical coupling. Phys. Rev. A 88, 013835 (2013). Article  ADS  CAS  Google Scholar  * Tan, H. T., Li, G. X. &

Meystre, P. Dissipation-driven two-mode mechanical squeezed states in optomechanical systems. Phys. Rev. A 87, 033829 (2013). Article  ADS  CAS  Google Scholar  * Asjad, M. et al. Robust

stationary mechanical squeezing in a kicked quadratic optomechanical system. Phys. Rev. A 89, 023849 (2014). Article  ADS  CAS  Google Scholar  * Wang, D. Y., Bai, C. H., Wang, H. F., Zhu,

A. D. & Zhang, S. Steady-state mechanical squeezing in a hybrid atom-optomechanical system with a highly dissipative cavity. Sci. Rep. 6, 24421 (2016). Article  ADS  CAS  PubMed  PubMed

Central  Google Scholar  * Zhang, J., Liu, Y. X. & Nori, F. Cooling and squeezing the fluctuations of a nanomechanical beam by indirect quantum feedback control. Phys. Rev. A 79, 052102

(2009). Article  ADS  CAS  Google Scholar  * Blencowe, M. & Wybourne, M. Quantum squeezing of mechanical motion for micron-sized cantilevers. Phys. B (Amsterdam, Neth.) 280, 555 (2000).

Article  ADS  CAS  Google Scholar  * Rabl, P., Shnirman, A. & Zoller, P. Generation of squeezed states of nanomechanical resonators by reservoir engineering. Phys. Rev. B 70, 205304

(2004). Article  ADS  CAS  Google Scholar  * Nunnenkamp, A., Børkje, K., Harris, J. G. E. & Girvin, S. M. Cooling and squeezing via quadratic optomechanical coupling. Phys. Rev. A 82,

021806 (2010). Article  ADS  CAS  Google Scholar  * Liao, J. Q. & Law, C. K. Parametric generation of quadrature squeezing of mirrors in cavity optomechanics. Phys. Rev. A 83, 033820

(2011). Article  ADS  CAS  Google Scholar  * Kronwald, A. Marquardt, F. & Clerk, A. A. Arbitrarily large steady-state bosonic squeezing via dissipation. Phys. Rev. A 88, 063833 (2013).

Article  ADS  CAS  Google Scholar  * Lü, X. Y., Liao, J. Q., Tian, L. & Nori, F. Steady-state mechanical squeezing in an optomechanical system via Duffing nonlinearity. Phys. Rev. A 91,

013834 (2015). Article  ADS  CAS  Google Scholar  * Agarwal, G. S. & Huang, S. Strong mechanical squeezing and its detection. Phys. Rev. A 93, 043844 (2016). Article  ADS  CAS  Google

Scholar  * Braginsky, V. B. & Khalili, F. Y. Quantum Measurement (Cambridge University Press, Cambridge, England, 1992). * Wu, L. A., Kimble, H. J., Hall, J. L. & Wu, H. Generation

of Squeezed States by Parametric Down Conversion. Phys. Rev. Lett. 57, 2520 (1986). Article  ADS  CAS  PubMed  Google Scholar  * Slusher, R. E., Hollberg, L. W., Yurke, B., Mertz, J. C.

& Valley, J. F. Observation of Squeezed States Generated by Four-Wave Mixing in an Optical Cavity. Phys. Rev. Lett. 55, 2409 (1985). Article  ADS  CAS  PubMed  Google Scholar  * Ma, S.

L., Li, P. B., Fang, A. P., Gao, S. Y. & Li, F. L. Dissipation-assisted generation of steady-state single-mode squeezing of collective excitations in a solid-state spin ensemble. Phys.

Rev. A 88, 013837 (2013). Article  ADS  CAS  Google Scholar  * Mancini, S. & Tombesi, P. Quantum noise reduction by radiation pressure. Phys. Rev. A 49, 4055 (1994). Article  ADS  CAS 

PubMed  Google Scholar  * Safavi-Naeini, A. H. et al. Squeezed light from a silicon micromechanical resonator. Nature (London) 500, 185 (2013). Article  ADS  CAS  Google Scholar  * Brooks,

D. W. C. et al. Non-classical light generated by quantum-noise-driven cavity optomechanics. Nature (London) 488, 476 (2012). Article  ADS  CAS  Google Scholar  * Wollman, E. E. et al.

Quantum squeezing of motion in a mechanical resonator. Science 349, 952 (2015). Article  ADS  MathSciNet  CAS  PubMed  MATH  Google Scholar  * Su, S. L., Guo, Q., Wang, H. F. & Zhang, S.

Simplified scheme for entanglement preparation with Rydberg pumping via dissipation. Phys. Rev. A 92, 022328 (2015). Article  ADS  CAS  Google Scholar  * Su, S. L., Shao, X. Q., Wang, H. F.

& Zhang, S. Preparation of three-dimensional entanglement for distant atoms in coupled cavities via atomic spontaneous emission and cavity decay. Sci. Rep. 4, 7566 (2014). Article  CAS

  PubMed  PubMed Central  Google Scholar  * Aldridge, J. S. & Cleland, A. N. Noise-Enabled Precision Measurements of a Duffing Nanomechanical Resonator. Phys. Rev. Lett. 94, 156403

(2005). Article  ADS  CAS  PubMed  Google Scholar  * Katz, I., Retzker, A., Straub, R. & Lifshitz, R. Signatures for a Classical to Quantum Transition of a Driven Nonlinear

Nanomechanical Resonator. Phys. Rev. Lett. 99, 040404 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Jacobs, K. & Landahl, A. J. Engineering Giant Nonlinearities in Quantum

Nanosystems. Phys. Rev. Lett. 103, 067201 (2009). Article  ADS  CAS  PubMed  Google Scholar  * Bowen, W. P. & Miburn, G. J. Quantum Optomechanics (CRC Press, 2016). * Yan, D. et al.

Duality and bistability in an optomechanical cavity coupled to a Rydberg superatom. Phys. Rev. A 91, 023813 (2015). Article  ADS  CAS  Google Scholar  * Xiong, W., Jin, D. Y., Qiu, Y., Lam,

C. H. & You, J. Q. Cross-Kerr effect on an optomechanical system. Phys. Rev. A 93, 023844 (2016). Article  ADS  CAS  Google Scholar  * Jing, H. et al. PT-Symmetric Phonon Laser. Phys.

Rev. Lett. 113, 053604 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Peng, B. et al. Nonreciprocal light transmission in parity-time-symmetric whispering-gallery microcavities. Nat.

Phys. 10, 394 (2014). Article  CAS  Google Scholar  * Grudinin, I. S., Lee, H., Painter, O. & Vahala, K. J. Phonon Laser Action in a Tunable Two-Level System. Phys. Rev. Lett. 104,

083901 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Chang, L. et al. Parity-time symmetry and variable optical isolation in active-passive-coupled microresonators. Nat. Photon. 8,

524 (2014). Article  ADS  CAS  Google Scholar  * Huang, P. et al. Generating giant and tunable nonlinearity in a macroscopic mechanical resonator from a single chemical bond. Nat. Commun. 7,

11517 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Vanner, M. R. et al. Pulsed quantum optomechanics. Proc. Natl. Acad. Sci. USA 108, 16182 (2011). Article  ADS 

PubMed  PubMed Central  Google Scholar  * Vanner, M. R., Hofer, J., Cole, G. D. & Aspelmeyer, M. Cooling-by-measurement and mechanical state tomography via pulsed optomechanics. Nat.

Commun. 4, 2295 (2013). Article  ADS  CAS  PubMed  Google Scholar  Download references ACKNOWLEDGEMENTS This work was supported by the National Natural Science Foundation of China under

Grant Nos 11264042, 11465020, 61465013, 11564041, and the Project of Jilin Science and Technology Development for Leading Talent of Science and Technology Innovation in Middle and Young and

Team Project under Grant No. 20160519022JH. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Physics, College of Science, Yanbian University, Yanji, 133002, Jilin, China Dong-Yang

Wang, Cheng-Hua Bai, Hong-Fu Wang, Ai-Dong Zhu & Shou Zhang Authors * Dong-Yang Wang View author publications You can also search for this author inPubMed Google Scholar * Cheng-Hua Bai

View author publications You can also search for this author inPubMed Google Scholar * Hong-Fu Wang View author publications You can also search for this author inPubMed Google Scholar *

Ai-Dong Zhu View author publications You can also search for this author inPubMed Google Scholar * Shou Zhang View author publications You can also search for this author inPubMed Google

Scholar CONTRIBUTIONS D.Y.W. designed the scheme under the guidance of H.F.W., A.D.Z. and S.Z. D.Y.W. and C.H.B. carried out the theoretical analysis. All authors contributed to the

interpretation of the work and the writing of the manuscript. All authors reviewed the manuscript. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial

interests. RIGHTS AND PERMISSIONS This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included

in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain

permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS ARTICLE

CITE THIS ARTICLE Wang, DY., Bai, CH., Wang, HF. _et al._ Steady-state mechanical squeezing in a double-cavity optomechanical system. _Sci Rep_ 6, 38559 (2016).

https://doi.org/10.1038/srep38559 Download citation * Received: 05 August 2016 * Accepted: 10 November 2016 * Published: 05 December 2016 * DOI: https://doi.org/10.1038/srep38559 SHARE THIS

ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard

Provided by the Springer Nature SharedIt content-sharing initiative