ABSTRACT Dichroic polarizers and waveplates exploiting anisotropic materials have vast applications in displays and numerous optical components, such as filters, beamsplitters and isolators.

Artificial anisotropic media were recently suggested for the realization of negative refraction, cloaking, hyperlenses, and controlling luminescence. However, extending these applications

into the terahertz domain is hampered by a lack of natural anisotropic media, while artificial metamaterials offer a strong engineered anisotropic response. Here we demonstrate a terahertz

metamaterial with anisotropy tunable from positive to negative values. It is based on the Maltese-cross pattern, where anisotropy is induced by breaking the four-fold symmetry of the cross

BY OTHERS FUNCTIONAL THZ EMITTERS BASED ON PANCHARATNAM-BERRY PHASE NONLINEAR METASURFACES Article Open access 04 January 2021 NONVOLATILE CHIRALITY SWITCHING IN TERAHERTZ CHALCOGENIDE

METASURFACES Article Open access 30 September 2022 GIGANTIC TELLEGEN RESPONSES IN METAMATERIALS Article Open access 02 January 2025 INTRODUCTION Recently, in addition to traditional

applications in optical filters and polarization components, anisotropic media was suggested for the realization of various important novel ideas, including negative refraction1,2,

cloaking3,4, hyperlenses5,6, and controlling luminescence7,8. However, although asymmetries of crystalline lattices and their constiuent molecules often result in optical anisotropy of

natural materials, it is very difficult to find the required values of optical anisotropy for a prescribed wavelength, in particular in the far-infrared and terahertz parts of the spectrum.

On the contrary, metamaterials can be rationally designed to achieve optical anisotropy9,10,11,12,13,14,15,16,17,18,19 that can also be altered by changing the refractive index of the

surrounding medium20,21,22,23 or by emplying electrical or thermal effects in liquid crystals24,25. At the same time, substantial progress has been possible in developing metamaterials with

unit cells reconfigurable with micro-actuators26,27,28,29,30,31,32,33,34,35. Here we report the active control of anisotropy in the terahertz spectral region in a metamaterial array of

Maltese crosses driven by micro-actuators. By breaking the four-fold symmetry of the cross, we show that it is possible to tune linear birefringence and dichroism of the array between the

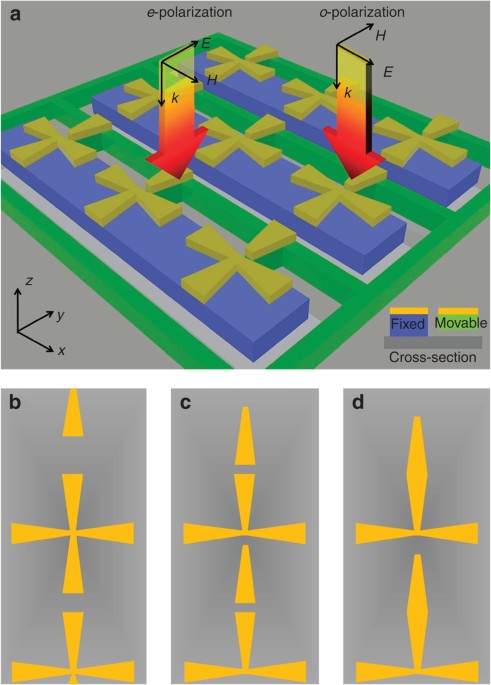
positive and negative values. RESULTS TUNABLE METAMATERIAL WITH MALTESE-CROSS-SHAPED UNIT CELLS The metamaterial presented here is a two-dimensional square-lattice array of Maltese crosses

with unit cell of 28 × 28 μm2 (Fig. 1a). It is designed to operate in the terahertz range of the spectrum and was characterized from 1 to 5 THz. The micro-actuator framework allowed for a

simultaneous reconfiguration of all unit cells in the array. This was achieved by manufacturing one of the trapezoid metal beams in each unit cell on a movable actuated silicon framework

(coloured green in Fig. 1). Three other beams of the Maltese cross are fixed to the substrate (blue in Fig. 1). The movable beam of the cross can be shifted away from the cross centre to a

distance _S_ up to half of its length. Figure 1b–d shows the unit cell for _S_=0, 2.5 and 5 μm, respectively. The metamaterial sample with an overall size of approximately 1 cm2 (400 × 400

unit cells) was fabricated on a silicon-on-insulator wafer as shown in Fig. 2a. Figure 2b shows a close-up view of the unit cells, which are formed by patterning a 0.5-μm thick evaporated

aluminium layer. The design parameters are shown in Supplementary Fig. S1. When the four metal trapezoid beams are arranged into the pattern of the Maltese cross that has a four-fold

symmetry axis, the metamaterial array exhibits no birefringence for normally incident radiation. On the contrary, when the four-fold symmetry of the design is broken by moving one of the

beams off-centre, the metamaterial retains a plane of symmetry and becomes birefringent for normally incident light. We define the extraordinary polarization (_e_-polarization) and ordinary

polarization (_o_-polarization) of this metamaterial with reference to the mirror symmetry axis of the pattern (Supplementary Fig. S1). The _e_-polarization is parallel to the line of

symmetry, whereas the _o_-polarization is perpendicular to it. EXPERIMENTAL RESULTS ON BIREFRINGENCE AND DICHROISM Optical anisotropy of the sample is completely characterized by its linear

birefringence, and dichroism can be derived from its polarization-sensitive transmission and phase retardation spectra. The transmission spectra were measured by using an optical

pump-terahertz probe (OPTP) system for different levels of asymmetry of the Maltese cross (Fig. 3). The experimental setup and data analysis approaches are discussed in the Methods and

Supplementary Figs S2–S6. These measurements show that indeed at zero displacement _S_, when the cross has a four-fold symmetry, the metamaterial shows no dichroism: the recorded absorption

spectra for both the _o_- and _e_- polarizations are nearly identical with the transmission peaks located at approximately 3.11 and 3.14 THz, respectively. Displacement of one of the beams

of the cross is signified by a strong modification of the transmission spectrum for the _e_-polarization, including the appearance of a new transmission peak >4 THz, whereas the

transmission spectrum for the _o_-polarization remains practically unchanged. The transmission peak moves from 3.11 to 2.73 THz, when the beam displacement changes from _S_=0 to 5 μm. See

more detail on variation of dichroism in Supplementary Figs S7–S9. Anisotropy of the metamaterial was also characterized by measuring the differential phase retardation Δ_Φ_=_Φ_e−_Φ_o and

transmitted power ratio _T_e/_T_o for _e_- and _o_-polarized waves as functions of _S_ (see Fig. 4). Large phase changes of the transmission are observed at the frequency regions highlighted

by grey colour as shown in Fig. 3a–f, where the transmission powers are bounced from the minimum to the maximum. Here the incident frequencies are fixed at 3.0 and 4.6 THz, which are the

transmission peak frequencies at _S_=2.5 μm. However, large tunability of optical anisotropy of both 3.0- and 4.6-THz incidence is observed either at 0 μm<_S_<1 μm or 4 μm<_S_<5 

μm, when the gap between the movable beam and the fixed part is significantly small as shown in Fig. 4. The optical anisotropy is changed abruptly, when the movable beam is disconnected from

the fixed ones. For _f_=3 THz, the phase difference is not sensitive to the shift distance _S_ in the range from 1 to 4 μm. At the same time, the anisotropy monotonically increased at the

high frequency of _f_=4.6 THz as shown in Fig. 4b. The anisotropy is more sensitive to the shift distance _S_ at 4.6 THz than that at 3.0 THz. The tuning of the anisotropy depends on the

variation of the dipole resonance mode of the Maltese cross, which is shown in Fig. 5. The transmission ratio variation (_T_e/_T_o) is approximately 1 and 1.2 for _f_=3 and 4.6 THz,

respectively. The effective refractive index of the Maltese-cross metamaterials is derived by fitting the measured transmission spectra with the Fresnel equations36. The differences between

the effective refractive indices of _o_- and _e_-polarized incidence are shown in Supplementary Fig. S9, which shows the same trend as the phase differences shown in Fig. 4. ORIGIN OF THE

TUNABLE OPTICAL ANISOTROPY The numerical analysis of the Maltese-cross structure without the substrate shows the dipole resonances of the surface current as shown in Fig. 5b–g, which result

in transmission dips in the spectra. For example, when S=2.5 μm, the dipole resonance at 5.94 and 9.85 THz (Fig. 5a) can be mapped to the two Fano resonance dips as shown in Fig. 3c. The

existence of the substrate has two effects. One is shifting the resonance dips to low frequencies, which is due to the permittivity difference between air and silicon substrate37. The other

effect is leading to Fano-type resonance profile, which is due to the coupling between the dipole resonance modes of the Maltese cross and the Fabry–Pérot mode of the substrate38. The

resonance frequency shifts shown in Fig. 3a are mainly due to the resonance features of the Maltese-cross design. Because the influence of the substrate does not change with the

reconfigurations of the cross, we can conclude that spectral changes observed with the movements of the beams are due to the changes in the dipole resonance of the cross pattern. When the

Maltese cross has a four-fold symmetry, the surface current is resonant between two opposite beams of the Maltese cross, which are parallel to the incident electric field, as shown in Fig.

4b. The other two beams have trivial effect on the dipole resonance. Therefore, the shifting of the Maltese-cross beam has trivial effects on the resonance modes when the movable beam is

perpendicular to the incident electric field (_o_-polarization). Considering the _e_-polarized incidence, however, the changing of the symmetry has vital effects on the dipole resonance

modes due to the structural change of the beams, where most of the induced surface currents are concentrated on. This explains the difference between _e-_ and _o_-polarized incidence of the

transmission spectra as a function of shift distance _S_, which is shown in Fig. 3. The tuning of the anisotropy can also be explained by the change of the resonance mode of the Maltese

cross when the movable beam is actuated. At low frequencies, the surface current cannot go to the movable beam, which is disconnected from the remaining parts of the Maltese cross. The

surface current is mainly concentrated at the fixed beam parallel to the incident electric field. This beam is weakly coupled to the two perpendicular beams. Therefore, the change of the

shift distance _S_ has small effects on the resonance mode of the Maltese cross, which explains the small variation of the optical anisotropy, when _S_ is in the range from 1 to 4 μm under

3.0-THz incidence (Fig. 4a). At high frequencies, the surface current is mainly concentrated at the movable beam and has a π phase difference from the incident electric field. Therefore, the

surface current resonance is mainly induced by the capacitance coupling between the fixed and movable beams of the Maltese cross. This capacitance is a strong function of the shift distance

_S_. Therefore, the resonance mode of the Maltese cross is a strong function of the shift distance _S_, which explains the rapid tuning of the anisotropy, when _S_ is in the range from 1 to

4 μm under 4.6-THz incidence (Fig. 4b). There is an abrupt resonance mode change at both low and high frequencies when the movable beam is being disconnected from the fixed parts, which

explains the abrupt anisotropy change observed either at 0 μm<_S_<1 μm or 4 μm<_S_<5 μm for both incident frequencies as shown in Fig. 4. INSERTION LOSS OF THE TUNABLE

METAMATERIAL The insertion loss of the tunable metamaterial consists of three parts, the ohmic loss due to the electron resonance within the metal structure, the reflection and the

scattering loss of the imperfect surface and edge. In the experiment, the total insertion loss can be measured by monitoring the output transmission versus the source. Figure 6a shows the

transmission and absorption spectra under the shift distance _S_=0.5 μm. Peak 1 and Peak 2 represent the transmission peaks, when the shift distance _S_ is in the range from 0 to 5 μm, at

low- and high-frequency region, respectively. The transmission peak and absorption peaks are staggered in the frequency domain, which is similar at different shift distance _S_. Therefore,

the ohmic loss is maintained under 12% at low-frequency region and 6% at high-frequency region. The ohmic losses of the transmission peaks under different shift distances _S_ are shown in

Supplementary Fig. S8. The transmission peaks in high-frequency region have lower ohmic absorption because of the rapid decaying of the absorption profile at high-frequency region. The

measured total insertion losses of the tunable metamaterial for Peak 1 and Peak 2 are shown in Fig. 6b. The symbols and lines show the experimental and numerical results, respectively. The

differences of the experimental and numerical results are approximately 1 dB, which is due to the misalignment, surface roughness and edge scattering of the tunable metamaterial. DISCUSSION

The breaking of the Maltese-cross symmetry results in the splitting of the two parallel Maltese-cross beams and, subsequently, two different resonators, which can be excited by the

_e_-polarized incidence. The breaking of the Maltese-cross symmetry splits and tunes the resonance modes of the _e_-polarized incidence but has minor effects on the _o_-polarized incidence

with the electric field perpendicular to the mirror symmetry axis, which is unaltered during the tuning. The Maltese-cross metamaterial is tuned between positive anisotropy, negative

anisotropy and isotropy states by actuators using microelectromechanical systems, which have promising applications such as waveplates, birefringent filters and light modulators. METHODS

FABRICATION PROCESSES The structures of the tunable metamaterial are fabricated on a silicon-on-insulator wafer by using the deep reactive ion etching processes39,40. Figure 2a shows the

overview of the micromachined tunable metamaterial imaged by using the scanning electron microscopy. Two identical micromachined comb drive actuators driven by the electrostatic force are

placed on both sides of the unit cell array. Each actuator provides bidirectional in-plane translation (along the _x_ direction) following the actuation relationship Δ_x_ = _AV_2, where Δ_x_

is the displacement, _V_ the actuation voltage and _A_=0.05 μm V−2 is the actuation coefficient. The displacement of the actuator can be monitored by using vertical microscopic system. The

actuation coefficient _A_ is derived by fitting the measured displacement–voltage curve. The actuation frequency can reach 10 kHz based on the dynamic measurement results of our previous

work40. Figure 2b shows a close-up view of the unit cells. The micro-ring unit cells are formed by patterning a 0.5-μm thick evaporated aluminium layer on the top of the structure layer. The

movable split rings are patterned on the central frame, which consists of many crossed narrow beams (2-μm width). The fixed split rings are patterned on the isolated anchors. Because each

anchor encloses a larger area of the underlying oxide layer than the frame, it needs much longer time to remove all the oxide under the anchor than that under the frame. Therefore, the

supporting frame is fully released and becomes freely movable, whereas the anchor remains fixed on the substrate by controlling the release time. EXPERIMENTAL SETUP Supplementary Figure S2

shows the experimental setup of the OPTP system used in the experiment. The terahertz probe pulse is generated by 35-fs pulses at centre wavelength of 800 nm with a repetition rate of 1 kHz

by using the air-plasma technique. The spectral range of the terahertz pulse is from 0.3 to 8 THz, which is detected by free-space electro-optical (EO) sampling with a 0.3-mm thick

<110> GaP crystal. The probe terahertz wave passes through the samples at normal incidence. The time domain terahertz signal is detected by the EO detector using a terahertz

time-domain spectroscopy (TDS) delay system. It should be pointed out that the pump-probe system of the OPTP, which is highlighted as a red dashed line, is not used during the experiment

because the Maltese-cross metamaterial is not tuned by laser pulses. Therefore, this OPTP system functions solely as a typical THz-TDS system in the experiment. The transmission spectra of

both amplitude and phase, as shown in Supplementary Figs S5 and S6, are derived by using the Fourier transform of the time domain signal from the EO detector and then normalized with the

source spectra. In Fig. 3, 20 equally spaced data points with the least mean-square error is chosen and compared with the simulation results. ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE:

Zhu, W. M. _et al_. Microelectromechanical Maltese-cross metamaterial with tunable terahertz anisotropy. _Nat. Commun._ 3:1274 doi: 10.1038/ncomms2285 (2012). REFERENCES * Brazhe R. A.

& Meftakhutdinov R. M. Negative optical refraction in crystals with strong birefringence. _Tech. Phys._ 52, 793–795 (2007). Article  CAS  Google Scholar  * Burkat T. M., Kostyuk G. K.

& Yakovlev E. B. Structural anisotropy and double refraction in porous glass plates. _Fizika i Khimiya Stekia_ 17, 781–790 (1991). CAS  Google Scholar  * Smolyaninov I. I., Smolyaninova

V. N., Kildishev A. V. & Shalaev V. M. Anisotropic metamaterials emulated by tapered waveguides: application to optical cloaking. _Phys. Rev. Lett._ 102, 213901 (2009). Article  ADS 

Google Scholar  * Zhang B. L., Luo Y., Liu X. G. & Barbastathis G. Macroscopic invisibility cloak for visible light. _Phys. Rev. Lett._ 106, 033901 (2011). Article  ADS  Google Scholar 

* Salandrino A. & Engheta N. Far-field subdiffraction optical microscopy using metamaterial crystals: theory and simulations. _Phys. Rev. B_ 74, 075103 (2006). Article  ADS  Google

Scholar  * Jacob Z., Alekseyev L. V. & Narimanov E. Optical hyperlens: Far-field imaging beyond the diffraction limit. _Opt. Express_ 14, 8247–8256 (2006). Article  ADS  Google Scholar 

* Tumkur T., Zhu G., Black P., Barnakov Y. A., Bonner C. E. & Noginov M. A. Control of spontaneous emission in a volume of functionalized hyperbolic metamaterial. _Appl. Phys. Lett._ 99,

151115 (2011). Article  ADS  Google Scholar  * Jacob Z., Kim J. Y., Naik G. V., Boltasseva A., Narimanov E. E. & Shalaev V. M. Engineering photonic density of states using

metamaterials. _Appl. Phys. B_ 100, 215–218 (2010). Article  CAS  ADS  Google Scholar  * Elser J., Wangberg R., Podolskiy V. A. & Narimanov E. E. Nanowire metamaterials with extreme

optical anisotropy. _Appl. Phys. Lett._ 89, 261102 (2006). Article  ADS  Google Scholar  * Singh R., Plum E., Zhang W. & Zheludev N. I. Highly tunable optical activity in planar achiral

terahertz metamaterials. _Opt. Express_ 18, 13425–13430 (2010). Article  CAS  ADS  Google Scholar  * Zhu W. M. et al. Polarization dependent state to polarization independent state change in

THz metamaterials. _Appl. Phys. Lett._ 99, 211102 (2011). Article  ADS  Google Scholar  * Sinchuk K. et al. Tunable negative group index in metamaterial structures with large form

birefringence. _Opt. Express_ 18, 463–472 (2010). Article  CAS  ADS  Google Scholar  * Anthony J. et al. Negative refraction in semiconductor metamaterials. _Nat. Mater._ 6, 946–950 (2007).

Article  Google Scholar  * Che M., Li Z. Y. & Liu R. J. Tunable optical anisotropy in three-dimensional photonic crystals. _Phys. Rev. A_ 76, 023809 (2007). Article  ADS  Google Scholar

  * Boardman A. D. et al. Active and tunable metamaterials. _Laser Photonics Rev._ 5, 287–307 (2011). Article  CAS  ADS  Google Scholar  * Wu K. D. & Wang G. P.

Transformation-optics-based nanopattern recognition. _J. Opt. Soc. Am. B_ 28, 2524–2528 (2011). Article  CAS  ADS  Google Scholar  * Lapine M., Jelinek L., Freire M. J. & Marques R.

Realistic metamaterial lenses: Limitations imposed by discrete structure. _Phys. Rev. B_ 82, 165124 (2010). Article  ADS  Google Scholar  * Strikwerda A. C., Fan K., Tao H., Pilon D. V.,

Zhang X. & Averitt R. D. Comparison of birefringent electric split-ring resonator and meanderline structures as quarter-wave plates at terahertz frequencies. _Opt. Express_ 17, 136–149

(2009). Article  CAS  ADS  Google Scholar  * Kanda N., Konishi K. & Kuwata-Gonokami M. Terahertz wave polarization rotation with double layered metal grating of complimentary chiral

patterns. _Opt. Express_ 15, 11117–11125 (2007). Article  CAS  ADS  Google Scholar  * Chen H. et al. Active terahertz metamaterial devices. _Nature_ 444, 597–600 (2006). Article  CAS  ADS 

Google Scholar  * Xiao S. et al. Tunable magnetic response of metamaterials. _App. Phys. Lett._ 95, 033115 (2009). Article  ADS  Google Scholar  * Zhang F. et al. Magnetically tunable left

handed metamaterials by liquid crystal orientation. _Opt. Express_ 17, 4360–4366 (2009). Article  CAS  ADS  Google Scholar  * Zhang S. et al. Photoinduced handedness switching in terahertz

chiral metamolecules. _Nat. Commun._ 3, 942 (2012). Article  Google Scholar  * Kahn F. J. Electric-field-induced orientational deformation of nematic liquid crystals: tunable birefringence.

_Appl. Phys. Lett._ 20, 199–201 (1972). Article  CAS  ADS  Google Scholar  * Busch K. & John S. Liquid-crystal photonic-band-gap materials: the tunable electromagnetic vacuum. _Phys.

Rev. Lett._ 83, 967–970 (1999). Article  CAS  ADS  Google Scholar  * Tao H., Strikwerda A. C., Fan K., Padilla W. J., Zhang X. & Averitt R. Reconfigurable terahertz metamaterials. _Phys.

Rev. Lett._ 103, 147401 (2009). Article  ADS  Google Scholar  * Bouyge D. et al. Split ring resonators (srrs) based on micro-electro-mechanical deflectable cantilever-type rings:

application to tunable stopband filters. _IEEE Microw. Wirel. Co_ 21, 243–245 (2011). Article  Google Scholar  * Gil I., Martin F., Rottenberg X. & De Raedt W. Tunable stop-band filter

at Q-band based on RF-MEMS metamaterials. _Electron. Lett._ 43, 1153–1154 (2007). Article  Google Scholar  * He X., Lv Z., Liu B. & Li Z. Tunable magnetic metamaterial based

multi-split-ring resonator (MSRR) using MEMS switch components. _Microsys. Tech._ 17, 1263–1269 (2011). Article  Google Scholar  * Ozbey B. & Aktas O. Continuously tunable terahertz

metamaterial employing magnetically actuated cantilevers. _Opt. Express_ 19, 5741–5752 (2011). Article  CAS  ADS  Google Scholar  * Perruisseau-Carrier J., Topalli K. & Akin T. Low-loss

Ku-band artificial transmission line with mems tuning capability. _IEEE Microw. Wirel. Co_ 19, 377–379 (2009). Article  Google Scholar  * Pryce I. M., Aydin K., Kelaita Y. A., Briggs R. M.

& Atwater H. A. Highly strained compliant optical metamaterials with large frequency tunability. _Nano Lett._ 10, 4222–4227 (2010). Article  CAS  ADS  Google Scholar  * Xun-jun H., Yue

W. & Tai-Long G. MEMS switches controlled multi-split ring resonator as a tunable metamaterial component. _Microsys. Tech._ 16, 1831–1837 (2010). Article  Google Scholar  * Zhu W. M. et

al. Switchable magnetic metamaterials using micromachining processes. _Adv. Mater._ 23, 1792–1796 (2011). Article  CAS  Google Scholar  * Fu Y. H. et al. A micromachined reconfigurable

metamaterial via reconfiguration of asymmetric split-ring resonators. _Adv. Fun. Mater._ 21, 3589–3594 (2011). Article  CAS  Google Scholar  * Driscoll T., Basov D. N., Padilla W. J., Mock

J. J. & Smith D. R. Electromagnetic characterization of planar metamaterials by oblique angle spectroscopic measurements. _Phys. Rev. B_ 75, 115114 (2007). Article  ADS  Google Scholar 

* Munk B. A. _Frequency Selective Surfaces: Theory and Design_ John Wiley & Sons (2000). * Mousavi S. H., Khanikaev A. B. & Shvets G. Optical properties of Fano-resonant metallic

metasurfaces on a substrate. _Phys. Rev. B_ 85, 155429 (2012). Article  ADS  Google Scholar  * Li J., Liu A. Q. & Zhang Q. X. Tolerance analysis for comb-drive actuator using DRIE

fabrication. _Sens. Actu. A_ 125, 494–503 (2006). Article  CAS  Google Scholar  * Zhang X. M., Zhao Q. W., Liu A. Q., Zhang J., Lau J. H., Kam C. H. Asymmetric tuning schemes of MEMS

dual-shutter VOA. _J. Lightwave Tech._ 26, 569–579 (208). Download references ACKNOWLEDGEMENTS This work was supported by the Science and Engineering Research Council (SERC) of Singapore

with project Metamaterials Programme: Nanoplasmonics (Grant No. SERC 092 154 0098), the MOE Singapore (Grant MOE2011-T3-1-005) and EPSRC (UK) Programme on Nanostructured Photonic

Metamaterials. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * School of Electrical and Electronic Engineering, Nanyang Technological University, Singapore, 639798, Singapore W.M. Zhu & 

A.Q. Liu * Institute of Microelectronics, 11 Science Park Road, Singapore 117685, Singapore, A.Q. Liu, G.Q. Lo & D.L. Kwong * School of Electrical and Electronic Engineering, ESIEE

Université Paris-Est, Paris, 93162, France T. Bourouina * Research Center for Applied Sciences, Academia Sinica, Taipei, 10617, Taiwan D.P. Tsai * Department of Physics, National Taiwan

University, Taipei, 10617, Taiwan D.P. Tsai * Institute of Materials Research and Engineering, 3 Research Link, Singapore 117602, Singapore, J.H. Teng & X.H. Zhang * Optoelectronics

Research Centre, Southampton, SO17 1BJ, United Kingdom N.I. Zheludev * Centre for Disruptive Photonic Technologies, Nanyang Technological University, Singapore, 639798, Singapore N.I.

Zheludev Authors * W.M. Zhu View author publications You can also search for this author inPubMed Google Scholar * A.Q. Liu View author publications You can also search for this author

inPubMed Google Scholar * T. Bourouina View author publications You can also search for this author inPubMed Google Scholar * D.P. Tsai View author publications You can also search for this

author inPubMed Google Scholar * J.H. Teng View author publications You can also search for this author inPubMed Google Scholar * X.H. Zhang View author publications You can also search for

this author inPubMed Google Scholar * G.Q. Lo View author publications You can also search for this author inPubMed Google Scholar * D.L. Kwong View author publications You can also search

for this author inPubMed Google Scholar * N.I. Zheludev View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS W.M.Z and A.Q.L. jointly conceived

the idea and prepared the manuscript. D.P.T. and T.B. assisted in the analysing and discussion of the results. J.H.T., X.H.Z., D.L. K. and G.Q.L. assisted in the experiment and fabrication.

A.Q.L. and N.I.Z. supervised and coordinated all the work. All authors commented on the manuscript. CORRESPONDING AUTHOR Correspondence to A.Q. Liu. ETHICS DECLARATIONS COMPETING INTERESTS

The authors declare no competing financial interests. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION Supplementary Figures S1-S9 (PDF 1373 kb) RIGHTS AND PERMISSIONS This work is

licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/ Reprints

and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Zhu, W., Liu, A., Bourouina, T. _et al._ Microelectromechanical Maltese-cross metamaterial with tunable terahertz anisotropy. _Nat

Commun_ 3, 1274 (2012). https://doi.org/10.1038/ncomms2285 Download citation * Received: 16 April 2012 * Accepted: 14 November 2012 * Published: 11 December 2012 * DOI:

https://doi.org/10.1038/ncomms2285 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently

available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative