ABSTRACT Our knowledge about the evolution of guarantee network in downturn period is limited due to the lack of comprehensive data of the whole credit system. Here we analyze the dynamic

Chinese guarantee network constructed from a comprehensive bank loan dataset that accounts for nearly 80% total loans in China, during 01/2007-03/2012. The results show that, first, during

the 2007-2008 global financial crisis, the guarantee network became smaller, less connected and more stable because of many bankruptcies; second, the stimulus program encouraged mutual

guarantee behaviors, resulting in highly reciprocal and fragile network structure; third, the following monetary policy adjustment enhanced the resilience of the guarantee network by

CONVERTIBLE BONDS IN FINANCIAL NETWORKS Article Open access 15 December 2023 SEISMIC SHOCKS AND FINANCIAL SYSTEMS: A TOPOLOGICAL PERSPECTIVE ON BORSA ISTANBUL AFTER THE EARTHQUAKE Article

Open access 26 November 2024 THE COMPLEX RELATIONSHIP BETWEEN CREDIT AND LIQUIDITY RISKS: A LINEAR AND NON-LINEAR ANALYSIS FOR THE BANKING SECTOR Article Open access 01 April 2024

INTRODUCTION A financial network represents a collection of entities (e.g., firms and banks), linked by mutually beneficial business relationships1,2. The guarantee relationship between two

firms represents the responsibility of a firm (guarantor) to assume the debt obligation of another firm (borrower) if the borrower failed to meet its legal obligation of a loan (default).

Based on the credit networks formed by the guarantee relationship, we can understand the systemic risk better by investigating the evolution of the credit system in downturn period. In

particular, it is critical to identify the risk of cascading failure in the guarantee network caused by the failure of one or a few entities, because such cascading failure could potentially

disrupt the connectivity and reliability of the whole credit system3,4. Since the guarantee relationship can be naturally represented as networks, applying network science methods to the

analysis of the cascading failures in financial networks has emerged as one of the most compelling and active research areas in economics and finance5. China has the biggest bank loan in the

world. The credit market is the core of China’s financial system, and the corresponding guarantee network might arguably be the largest credit networks in the world. With the outbreak of

2007–2008 global financial crisis, Chinese government implemented the stimulus program worth of RMB ¥4 trillion in 9 November 2008 to reduce the impact of the financial crisis on China’s

economy by investing hugely in infrastructure and social welfare by 2010. The credit condition was also loosen to encourage loan applications from firms6. This stimulus program, though

successfully sustained China’s economic growth and largely stabilized the world economy, has resulted in a surge in debt in China, and dramatic structural change of the credit system. There

were a huge amount of loans going to state-owned enterprises (SOEs), many of which could not meet the credit standard to obtain loans before the stimulus program7. These SOEs could meet the

loosened credit standard through guaranteeing each other8. Although many of these SOEs were saved by loans, economic studies suspected that the stimulus program could cause explosion of

credit debt and trigger future disruptions in the financial system because of huge loans to low-quality firms9,10,11. Decision makers also recognized such risk and took actions to regulate

the debt behavior. In March 2010, Chinese government announced the plan to improve macro-control regulations. Since then, the People’s Bank of China (PBoC, the central bank of China)

increased the reserve requirement ratio for five times in 2010 (from 15.5% to 18%). The major change of the monetary policy operations occurred on 20 October 2010, when PBoC raised the

interest rates for the first time since the financial crisis. These regulations and policy adjustment, to some extent, helped to reduce the impact of the negative consequence of the stimulus

program. Despite the qualitative critics and studies on the stimulus program, little is known about the changes of the guarantee networks and how these changes are linked to the risk of

cascading failures. A good understanding of the guarantee network’s dynamic structure under pressure could enhance the economic policy-making through identifying the potential systemic risks

such as the domino-like cascading failures. Facing the onset of financial crisis, it is of particular importance to examine the tradeoff between saving firms with government bailout and

maintaining a good resilience of the financial system. There is a critical need for data-driven quantitative studies of the guarantee network and its associated risk. However, how to

leverage real-world guarantee data to model such behaviors and the overall structure of the guarantee network remains a challenge. Network science presents a natural way to address the

challenge in modeling guarantee networks. Network science aims to discover the underlying patterns of interactions among elements in complex systems. It has been widely applied to modeling

structure and dynamics of real-world complex systems12. Recently, network science has been applied to finance research. Specifically, network science has been applied extensively to

analyzing the global banking system13, international financial network14, and interlocking boards of directors15,16,17. Please refer to the Related Work section in the Supplementary Note 1

for a detailed review. The guarantee interdependencies can be naturally represented as networks, in which each node represents a firm, and each (directed) edge represents the guarantee

relationship between the two corresponding firms. From such a guarantee network, we can capture the contagion path of obligations and failures. Using methods in network science to analyze

guarantee networks could fill the research gap in data-driven insights into how the topological structure of guarantee network is associated with economic policies and contagion risks, and

help decision makers identify the potential systemic risks caused by firms’ failures18. Existing research on guarantee networks mainly focused on the analytics of small sampled data with

only dozens or hundreds of firms. Although small-scale network analysis may lead to useful insights into the risk connection of individual client, it cannot tell big stories about the

stability of the whole credit market, not to mention the evolution of credit networks19,20,21,22. Large-scale empirical studies of the nationwide guarantee networks are needed to understand

the global topological properties of the guarantee system. By harnessing a comprehensive data provided by one of China’s major regulatory bodies ranging 01/2007–03/2012, we investigate the

structure and evolution of Chinese guarantee network to answer the following questions: What are the unique topological properties of the Chinese guarantee network? What is the influence of

2007–2008 global financial crisis, China’s stimulus program and the following monetary policy adjustment on the topological structure of Chinese guarantee network? Does the change of

topological structure of Chinese guarantee network influence the resilience of the system? To the best of our knowledge, this is the first attempt to quantitatively characterize the

evolution of the nationwide guarantee network. The empirical and simulation studies indicate that the financial crisis made the network more resilient, and conversely, the government bailout

degenerated network resilience. RESULTS STATIC TOPOLOGICAL AND FINANCIAL PROPERTIES In this section, we characterize the static topological and financial properties of the guarantee

network. Our dataset covers three important financial events: bankruptcy of New Century Financial Corporation in April 2007, bankruptcy of Lehman Brothers in September 2008, and

implementation of the Chinese economic stimulus program from December 2008 to December 2010. According to these extreme events, we divided the data range into three phases. Phase 1

(04/2007–11/2008) is the period of global financial crisis. Bankruptcy of New Century Financial Corp. on April 2007 could be considered as the beginning of subprime mortgage crisis. Lehman

Brothers Holdings Inc. filed for bankruptcy in September 2008 and global financial crisis reached the summit. Phase 2 (12/2008–12/2010) is the period when China implemented the four-trillion

stimulus program. Phase 3 (01/2011–03/2012) is the adjustment period after the stimulus program. We analyze the guarantee network in each month, and summarize the common properties for the

whole period, as well as the three phases. The topological properties of the guarantee network are presented in Supplementary Table 1. Despite the increasing size of the guarantee network,

there are a set of common topological properties throughout the whole period. First, the average in-/out-degree (<_d_>) is slightly lower than one, indicating that in general, firms

had a small number of guarantors, and did not provide guarantees to others frequently. Both in- and out-degrees exhibit a power-law distribution, with a slope (_λ_in and _λ_out) ranging from

3.23 to 3.30, and 2.30 to 2.76, respectively, indicating that the guarantee network are scale-free, a property that commonly exists in real-world networks. In such a scale-free network,

most firms have a small number of guarantee relationships, while a few hub firms provide/obtain guarantees to/from many others. A closer examination of the loan guarantee data reveals that

isolated mutual guarantee relationship (2–_node_(%)) is significantly more frequent than that would be expected for a random network generated (_p_-value = 0.002). Here, the random network

ensemble is generated by the commonly adopted Directed Configuration Model (DCM), which is configured by the in-degree and out-degree sequences of the network. Please refer to (Squartini and

Garlaschelli)23 for details. The financial properties show that these isolated mutual guarantee couples are at the bottom of the whole system with low assets and credit line and high

default rate, indicating that high-risk firms are more likely to obtain loans with the guarantee from firms that are also high-risk. We define two types of hubs: guarantor hubs and borrower

hubs. The guarantor hubs are those giving guarantees to others most frequently (top 1% out-degree). The borrower hubs are those obtaining guarantees from others most frequently (top 1%

in-degree). We find that the guarantor hubs are usually firms with large assets, liabilities, and credit line. About 15% of them are listed firms, (compared with 3.95 %, the listed ratio of

the whole network). On the other hand, the borrower hubs tend to have medium amount of asset and liability, but with high default rate and risk rating. The overlap of guarantor and borrower

hubs is rather small (around 15%) as compared with other real-world networks, echoing the aforementioned finding that guarantor hubs and borrower hubs have different characteristics. Second,

the largest weakly connected component (_WCC_) and the largest strongly connected component (_SCC_) stand for only 27.99% and 0.62% of all nodes in the network, respectively, indicating

that the network is more decentralized than most other complex networks such as social networks and biological networks. Within the largest _WCC_ and _SCC_, we observe the small-world effect

as indicated by the small average shortest path length in the largest WCC (10.10 ~ 10.54). In addition, the average clustering coefficient (_C (%)_) is also relatively large (0.97% ~

1.49%), indicating a strong transitivity effect (a friendʼs friend is also a friend) throughout the guarantee network (_p_-value < 0.001 as compared with the DCM null model23). The value

is also much higher than most of the real-world complex networks12. Such transitivity effect shows that the guarantee is a strong trust relationship. Third, we summarize the basic financial

characteristics in Supplementary Table 1. In general, the average leverage ratio, as measured by total liabilities divided by total assets, has been maintained at around 60%, which is higher

than the average leverage ratio for listed firms in the network (around 40%). The ratio of listed firms was relatively low (around 2%~5%). The ratio of listed firms decreased over time,

indicating more and more guarantees were obtained by non-listed firms. This echoes the above findings of large portion of isolated mutual guarantee relationships. We will discuss this in

detail in the following dynamic network analysis. DYNAMIC NETWORK ANALYSIS Analyzing the dynamics of the guarantee network could reveal the short- and long-term impact of economic conditions

and policies on the evolution of the credit system. We depict the topological properties and financial characteristics of the guarantee network for 63 months (01/2007–03/2012) that cover

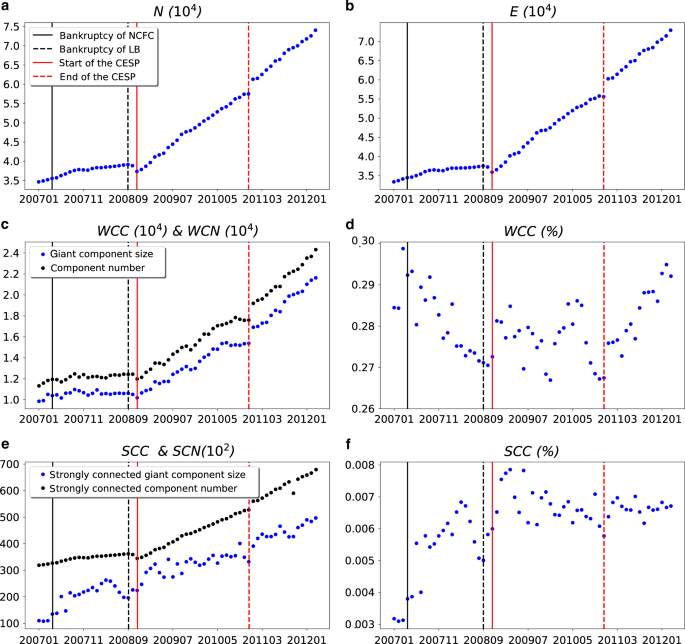
the global financial crisis and the implementation of the Chinese economic stimulus program. Figure 1 presents the evolution of the network scale. Figure 2 presents the dynamics of various

topological properties of the guarantee network. Figure 3 presents the dynamics of the financial properties of firms. In these figures, the vertical lines indicate bankruptcy of NCFC (New

Century Financial Co.) in April 2007, bankruptcy of LB (Lehman Brothers Inc.) in September 2008; start of the CESP (Chinese economic stimulus program) in December 2008, and end of the CESP

in December 2010. In general, the guarantee network exhibits different dynamic patterns in three phases. After the bankruptcy of New Century Financial Co., the network size increased slowly,

resulting in a less densely connected network. Then, the network size dropped after the bankruptcy of Lehman Brothers Inc. On the other hand, the average asset of the firms in the guarantee

network increased, indicating that the failed firms were with a relatively lower asset as compared with those did not fail. The implementation of the stimulus program immediately stopped

the decrease. Since then, the network had been increasing (almost linearly), even after the end of the stimulus program. The Pearson correlations between the growth of the amount of new

loans and the counts of nodes and edges are 0.56 (_p_-value < 0.001) and 0.58 (_p_-value < 0.001), respectively, indicating that the network size and amount of loan from banks are

positively associated. Similar pattern was also observed for the number of _WCC_, and the size of the largest _SCC_ and _WCC_. We observe clear turning points during Phase 2, when the

stimulus program was being implemented. More interestingly, the turning points for most topological properties were the same, but different for a few properties. In the following, we focus

on the description of these turning points, and the economic implications of them. The average degree, the exponents of the power-law in-degree distributions, reciprocity, ratio of fully

connected 3-node-subgraph, and average clustering coefficient were increasing rapidly after the initiation of the stimulus program (Fig. 2). These values suddenly dropped in the last quarter

of 2009, and quickly resumed the increasing trend until April 2010. Since then, all these values kept decreasing until the end of 2011 except a snap surge right after the end of the

stimulus program (December 2010). The exponent of the power-law out-degree distribution followed a similar pattern, expect that it did not drop significantly in April and May 2010. These

findings indicate that there were many new mutual guarantee relationships as a result of the stimulus program. This included both mutual guarantees between two firms (reciprocity), and among

three firms (ratio of fully connected 3-node-subgraph). Comparing the dynamics of the average assets and loans between the overall guarantee network and mutual guarantee network (Fig. 3),

we find that these newly mutual guarantee relationships were mainly formed by firms that were with low assets and loans (_p_-value < 0.001 in chi-square tests). A closer look at these

mutual guarantee firms reveals that around 70% of them were not part of the largest _WCC_, but in other smaller isolated components. After the initiation of the stimulus program, the

inclusion of these small firms caused the surges of loans and the loans to assets ratio (as shown in Fig. 3). This trend was turned over briefly in late 2009 because of the fine adjustments

of the People’s Bank of China. However, the trend resumed in 2010, until People’s Bank of China improved the macro-control regulations by increasing the reserve requirement ratio. Different

from the other properties, the average shortest path length in the largest _SCC_ and _WCC_ kept increasing after the initiation of the stimulus program until September 2010. This pattern is

similar to the size of the largest SCC and WCC. These findings indicated that the core of the guarantee network was not influenced significantly by the changes in regulations, until

September 2010, only one month before People’s Bank of China increased the interest rates. This echoes the above finding that mutual guarantee relationships were mostly in smaller isolated

components. In short, all turning points appeared in Figs. 2 and 3 are well-aligned with the changes of monetary policies and the practice of the stimulus program. At the beginning of the

stimulus program, the monetary policy was ultra-loose. People’s Bank of China took actions to tune the loose monetary policies in the second half of 2009. These fine tuning did not directly

change the monetary policy, but aimed to address the side-effect caused by the ultra-loose monetary policy by making it more targeted, flexible and forward-looking [goo.gl/Nq9yA5]. It was

perceived as a signal to change the monetary policy. In March 2010 (17 months since the initiation of stimulus program), the government announced the plan to improve macro-control

regulations in 2010. Since then, People’s Bank of China increased the required reserve ratio, and raised the interest rate. Our results indicate that these regulations and policy changes, to

some extent, helped to reduce the negative consequence of the stimulus program. To check the robustness of the findings above, we constructed weighted guarantee networks with the amount of

loans as the weight on edges, and did the same analyses. Please refer to the Supplementary Fig. 1 and discussions in the Supplementary Information for detailed discussions. INTERPRETING THE

NETWORK STRUCTURE USING ERGM The network analysis shows that the guarantee network experienced dramatic changes during financial crisis and the stimulus program. The burst of mutual

guarantees could be the main factor that influences the changes of the guarantee network. In this subsection, we used exponential random graph models (ERGM)24 to verify the significance of

the formation of mutual guarantee relationships. ERGM are a family of probabilistic models that identify the distribution over a specified set of graphs that maximizes the entropy subject to

the known constraints25,26. ERGM can effectively predict the edges as a function of these constraints, which usually represent the most important topological properties of the network

structure27. It has been applied to analyze various networks in finance and economy, such as28,29,30,23. Among all topological properties, network density and reciprocity are the defining

characteristics of the guarantee network, and other properties are with similar patterns driven by the values of these two properties. Network density is the most basic property that had

dramatic changes: first increasing because of many bankruptcies, and then decreasing because of many new loans and guarantees. Reciprocity is important because the stimulus program

encouraged low-quality firms to obtain loans by providing mutual guarantees to each other. In addition, we have found that the reciprocal edges are significantly more frequent than that

would be expected for a DCM null model (_p_-value < 0.001, z-score > 3000) throughout the entire time period. Therefore, we adopt the reciprocity model25, which considers the number of

edges and the number of reciprocal edges. The probability function of _G_ is as follows: $$P\left( G \right) = \frac{{e^{\beta _1D\left( G \right) + \beta _2R\left( G \right)}}}{Z},$$ (1)

where _D_(_G_) denotes the number of edges, and _R_(_G_) denotes the number of reciprocal edges. Z is the partition function defined by Eq. (10). Following the procedure in Methods section,

the coefficient of _D_(_G_) and _R_(_G_) are obtained (Fig. 4). On the other hand, the edge (representing both mutual and non-mutual guarantee relationship) is not significant. In addition,

_β_1 was negative and decreasing but _β_2 was positive and kept increasing after the initiation of the stimulus program until March 2012, except a drop at the end of the stimulus program.

These results indicate that firms were becoming increasingly likely to form mutual guarantee relationship. The ERGM analysis further demonstrates the significant role of mutual guarantee in

the formation of the guarantee network. SIMULATION ANALYSIS OF THE RESILIENCE OF GUARANTEE NETWORK Network analysis reveals that the stimulus program dramatically changed the topological

properties of the guarantee network, and resulted in a surge of mutual guarantee relationships. The following adjustments of monetary policies constrained the guarantee behaviors, thus

reverted the increasing trend of mutual guarantee relationships. Such mutual guarantee relationship, though helped low-quality SOEs obtain more loans to survive, could result in large-scale

cascading failures/defaults because of the risk and failures propagates via the guarantee relationships among firms. In this section, we examine the potential risk of cascading failures in

the guarantee network using a simulation model. We represent the assets and liabilities of a firm _i_ at time _t_ as _A__i__(t)_ and _L__i__(t)_, respectively. _G__ij__(t)_ denotes the

amount of loan guarantee firm _i_ provides for firm _j_ at time _t_. Following the literature, we adopt the Fermi distribution model to calculate the probability of default failure31,32.

Fermi distribution is a logistic function that has been successfully applied to modeling failures of firms and banks in economics and finance31,32. In our research, _P__i_(_t_) is a Fermi

logistic function that determines the probability that a firm defaults at time _t_: $$P_i\left( t \right) = \frac{1}{{1 + e^{ - k\left( {\frac{{L_i\left( t \right) + {\sum} {w_j\left( t

\right)G_{ij}\left( t \right)} }}{{A_i\left( t \right)}} - \delta } \right)}}},$$ (2) where _k_ represents the influence of external environment, _δ_ represents the mean value of the

leverage ratio (total liabilities/total assets), and _w__j_(_t_) represents whether firm _j_ has failed. The leverage ratio is determined by the current assets and liabilities of a firm, as

well as the assumed debt caused by the failure of the firms to which _i_ provides guarantee. Intuitively, the higher the leverage ratio a firm has, the more likely it would fail. The

simulation is based on the aforementioned dynamic guarantee network and the financial characteristics obtained from real-world data. We simulate the failures of firms caused by random

initial failures (random attack) in one month. In the simulation, _δ_ is the average leverage ratio of firms from real-world monthly guarantee network data. _k_ = 1.18, which is obtained by

learning from the real data. Specifically, we adopt Eq. (2) as a logistic regression to fit the real values of _P__i_(_t_). Specifically, if firm _i_ at time _t_ defaulted, _P__i_(_t_) = 1,

otherwise _P__i_(_t_) = 0. The values of other factors, including _A__i_(_t_), _L__i_(_t_),_G__ij_(_t_), and _δ_ of firm _i_, at time _t_ were provided by our dataset. \(\eta \in \left(

{0,1} \right)\) represents the initial default ratio. In particular, for each month, the simulation runs as follows_._ Initial failures: At the beginning of each simulation (_t_ = 1), a

small proportion (_η_ = 0.05) of firms were randomly selected as the initial failures (default). Their liabilities will be assumed by the adjacent firms in the network. Failure propagations:

At each time step _t_, we determine whether a firm _i_ fails or not at time _t_ based on Eq. (2). Finish: The simulation keeps running until there is no firm fails at

\(t_{\mathrm{finish}},t_{\mathrm{finish}} \ge 1\). We run the simulation for 10,000 times for each month, and take the average ratio of failed firms for each month (Fig. 5). We find that the

dynamic pattern of average ratio of failed firms is similar to the common pattern of topological properties (average degree, the exponent of the power-law in-degree distributions, average

reciprocity, average ratio of fully connected 3-node-subgraph, and average clustering coefficient). The correlation between the average ratio of failed firms and the average reciprocity is

very high (correlation coefficient = 0.83, _p_-value < 0.001). The turning points are the same (September 2009 and April 2010). This result indicates that the more prevalent mutual

guarantee relationships are, the more fragile the whole guarantee network is. Please also check the robustness check of the simulation analysis in the Supplementary Note 4. To summarize, the

stimulus program caused an elevated risk of cascading failure in the credit system. The fragility of the guarantee network was strongly influenced by the stimulus program and changes of

monetary policies. The follow-up adjustment reduced such risk, but the risk was still higher than it was before the financial crisis. Clearly, these findings do not coincide with our

traditional understanding of systemic crisis development. According to general assumption, the stability of financial network should become worse during financial crisis, and the government

bailout of stimulus program could reduce the systemic risk and restore the network stability. Nonetheless, the above findings lead us to opposite conclusions: the 2007–2008 financial crisis

resulted in more stable guarantee network, and the stimulus program decreased the stability of guarantee system. Such counterintuitive findings can be explained from the following

perspective of survivorship bias. In the real world, the external negative shock from financial crisis would knock out the low-quality enterprises and fragile linkages, resulting in a

smaller and less connected network. Those who were left behind are high-quality enterprises with robust guarantee relationships, leading to a more stable guarantee network. When it came to

the government’s rescue, with the injection of RMB ¥4 trillion into the credit market, the stimulus program saved substantial low-quality enterprises on the verge of bankruptcy. As a result,

the enterprises that survived by chance increased the network connectivity with more fragile links, thus lowering the stability of the credit guarantee network. In short, the behavior of

survivors within financial crisis and stimulus program played a crucial role in the network stability. DISCUSSION This research presents the first attempt to quantitatively characterize the

evolution of the entire Chinese guarantee system as a complex network. The empirical and simulation studies provide evidence that the financial crisis caused a large number of weak firms

unqualified to access bank loan, making the guarantee network smaller, and the loose monetary policy along with the stimulus program encouraged the mutual guarantee behavior between firms,

resulted in highly reciprocal and fragile network structure. The latter adjustment of the monetary policy reduced the ratio of mutual guarantee relationships, and enhanced the resilience of

the whole guarantee network. Our study contributes to the literature through proposing a complex network approach to analyzing the guarantee relationships between firms in a whole country.

The simulation model based on real-world guarantee network presents a novel network-based method to evaluate the fragility of the guarantee systems. The empirical and simulation results

provide data-driven insights of how the systemic risk, government bailout and following monetary policy adjustments influence the guarantee behaviors of firms, and the fragility of the

guarantee system. This study also sheds light on the data-driven research on using the network science methodologies to analyze real-world financial systems. The insights into the evolution

of the guarantee network have great potential to be applied to other finance and economic research, such as forecasting stock market returns33, credit allocation7 and international trade23.

In practice, this study indicates that although the mutual guarantee relationship could help low-quality firms obtain more loans, and reduce the risk of small-scale arbitrary risk events, it

could be the cause of large-scale cascading failures/defaults for the whole system. This research suggests that decision makers (e.g., government, central bank, and other authorities)

control the prevalence of mutual guarantee relationships through adjusting monetary policies. Importantly, much work about resilience of financial systems has focused on the theoretical

analysis due to the unavailability of confidential financial data. Therefore, the real conditions and evolution of financial systems have not yet been fully understood. Here, with the

nation-wide and real-world Chinese loan guarantee data, we show that the empirical results are opposite to the intuitions. Specifically, to take the effect of survivorship bias into

consideration, the guarantee network is much more stable during the period of financial crisis with the surviving and robust firms, however, the stability keeps on decreasing with the

implementation of stimulus program, for absorbing much more firms which should have been bankrupted without this government bailout. Our empirical findings would facilitate the study of

stability of real-world financial system and also enable better strategies to be developed for policy makers to perform financial bailout. The results of this study also pose an interesting

dilemma. Financial crisis has made the financial network healthier by obsoleting the weak firms, but with instantaneous huge economic consequence. The government bailout avoided the

instantaneous catastrophic loss at the expense of making the financial network fragile. In other words, government bailout could mitigate the current crisis by sacrificing the financial

stability in the future. The 2019-2020 novel coronavirus pandemic in fact tells a similar story. Risk management needs a consecutive endeavour that considers such trade-offs in a proactive

manner. The methods and results of this study provide such benchmark data, simulation platform, and baseline methods to facilitate decision makers in developing effective responses to

crisis. Although this study relies on the data of the Chinese guarantee network, the results and implications are still very beneficial from three perspectives. First, China is the second

largest economy in the world. The credit system is unique in many aspects (e.g., the significant role of indirect financing and bank credit in the credit system) as compared with those in

many developed countries, making it important to examine how the uniqueness of the Chinese credit system is associated with the unique challenge in running the financial system, especially

in crisis. Second, the credit guarantee relationship among Chinese firms are similar to those of other countries, as they are all following the standard procedure of commercial banks. Thus,

the guarantee network is general, as well as the network science methodologies. If we have equivalent data for another credit system, the methods are directly applicable by calibrating the

parameters of guarantee network and simulation model based on the new data. Many topological properties could be similar, such as the scale-free and small-world effects. In practice, it is

very difficult to obtain similar nationwide guarantee system data. In such case, we still can use the topological and financial properties of the Chinese guarantee network as a baseline, and

then calibrate the parameters to reflect our understanding of the guarantee system under consideration. For example, we may reduce the reciprocity to reflect the less prevalence of mutual

guarantee behaviors in a non-Chinese credit system. Third, we have been witnessing crises frequently, particularly the 2019–2020 novel coronavirus pandemic, which may trigger another

financial crisis in the near future. The results of this study provide needed data-driven insights into how the credit system may react and recover. Such insights are critical to the

decision making not only in China, but elsewhere as well. METHODS DATA In this research, we acquire a comprehensive nationwide dataset from one of the major regulatory bodies in China. The

data spans from January 2007 to March 2012, and contains the monthly information for all loans extended to the client firms, which have a credit line above 50 million RMBs. These loan

guarantee data are from all the 19 major banks of China, including the largest five state-owned commercial banks, twelve joint equity commercial banks, and two major policy banks

(Import-Export Banks of China and China Development Bank), which account for nearly 80% total loans in China. Totally, there are about 0.3 million guarantee relationships during

01/2007–03/2012, which covers around 0.1 million borrowing firms located in 30 province-level regions of China. More specifically, the data contains details regarding loan-level information

for each loan guarantee (borrower, provider, as well as amount of each loan guarantee, and the time of the guarantee relationship) and firm-level fundamentals (e.g., size, leverage, and

location). To the best of our knowledge, our data is by far the largest and the most comprehensive representation of the Chinese credit system. Particularly, our dataset covers two important

periods in the credit system: The 2007–2008 global financial crisis, and the implementation of the Chinese economic stimulus program from November 2008 to December 2010. Through harnessing

our data, these two rare natural experiments offer a good opportunity for us to investigate the change of guarantee network under extreme exogenous shocks. CONSTRUCTION AND ANALYSIS OF THE

GUARANTEE NETWORK To analyze the structure and dynamics of Chinese guarantee system, we constructed dynamic guarantee networks using the guarantee relationships between firms. Figure 6

illustrates the construction of the networks. Each node represents a firm, and each edge connecting two nodes represents the existence of guarantee relationship between the two corresponding

firms in a specific month. An edge goes from the guarantor to the borrower. This dynamic guarantee network consists of 63 monthly loan guarantee data, enabling us to analyze the evolution

and dynamics of the system over time. In this research, we adopted a set of commonly used topological metrics to characterize the structure and evolution of the guarantee network: NETWORK

CONNECTIVITY refers to how well nodes are connected with each other in the network. It is measured by three metrics, number of weakly or strongly connected components (_WCN_ or _SCN_), ratio

of the giant component (the largest weakly connected component, or largest _WCC (%)_), in the whole network, the ratio of the largest strongly connected component, or largest _SCC (%)_, in

the whole network, and the network density (Δ)34,35. In a weakly connected component (_WCC_), any node can reach another node through an undirected path. The giant component is the weakly

connected component with the largest number of nodes. Similarly, in a strong connected component (_SCC_), any node can reach another node through a directed path. Network density is the

ratio between the number of directed edge and the total number of possible directed edges, \({\mathrm{density}} = \frac{E}{{N(N - 1)}}\), where _E_ is the number of edges and _N_ is the

number of nodes in the network. Degree, <_d_>, refers to the number of edges adjacent to a node. In the guarantee network, edges are with directions, from guarantor to borrower. The

degree of a node indicates the extent to which it is connected within the system. In-degree measures the number of guarantors for the firm. Out-degree measures the number of borrowers that

received guarantee from the firm. In general, a higher value of average out/in-degree indicates more frequent guarantee relations among firms in the network. Scale-free property has been

observed in many real-world networks. In a scale-free network, degree distribution follows a power-law. Most nodes are only connected to a small number of edges, while there exist a few hub

nodes that are densely connected. To test the scale-free property of the guarantee network, we investigate both the in- and out-degree distributions, denoted by _p_in(_k_) and _p_out(_k_).

In a scale-free network, both _p_in(_k_) and _p_out(_k_) follow a power-law distribution. The frequency of nodes with degree of _k_ is proportional to _k_ to the power of _λ_,

\(p_{\mathrm{in}}\left( k \right)\sim k^{ - \lambda }\) and \(p_{out}\left( k \right)\sim k^{ - \lambda }\)36. Clustering coefficient, _C_(%), measures the extent to which a node’s neighbors

are also adjacent to each other. In real-world networks, nodes are likely to form such triads, resulting a higher average clustering coefficient of the networks. In social networks, it

refers to the tendency that friend of a friend is also a friend37,38. In the guarantee network, high clustering coefficient indicates that firms tend to form tightly guarantee clusters with

high frequency of guarantees among them. The reciprocity, _r(%)_ (dyad; mutual guarantee relationship between two firms) of a directed network is the ratio of the number of reciprocated

edges to the total number of edges. Here, node _A_ and node _B_ are reciprocated if an edge is connected from node _A_ to node _B_, and there is also an edge from node _B_ to node _A_. In

the guarantee network, it measures the ratio of mutual guarantee relationships to the total number of guarantee relationships in the network. Ratio of fully connected 3-node-subgraph,

3–_node_ (%) (triad; mutual guarantee relationship among three firms) of a directed network is the ratio of the number of edges forming a fully connected 3-node-subgraph to the total number

of edges in the graph. In the guarantee network, it measures the extent to which the three firms provide mutually guarantees to each other. Ratio of isolated 2-node reciprocal component,

2–_node_ (%), measures the prevalence of isolated 2-node mutual component in the network. It is calculated by dividing the number of isolated 2-node reciprocal component with the total

number of weakly components in the network. This measure quantifies the extent to which two firms formed mutual guarantee relationships without any interaction with other firms. We measure

the efficiency of the guarantee network in transferring the risk by calculating the average shortest path length, _l_, of the network. The average shortest path length is defined as the

average number of edges along the shortest path connecting all possible pairs of nodes. Real-world networks usually exhibit a relatively small average shortest path length, indicating the

small-world property39,40,41. Because the guarantee network has multiple connected components, we calculate the average shortest path length of the largest weakly connected component and the

largest strongly connected component. FINANCIAL PROPERTY We calculate a set of financial properties, including average assets and average loans of firms in the guarantee system, denoted by

_AA_ and _AL_, respectively. More specifically, the average assets _AA_ refers to average amount of assets of all firms in the guarantee system. A large value of _AA_ indicates that the

guarantee system is consisted of firms with high values. The average loans _AL_ refers to the average amount of loans of all firms in the guarantee system. A large value of _AL_ indicates

that the guarantee system is consisted of firms that owe a lot of debts to banks. We further calculate the average ratio of listed firms, _ARL_ (%), which is denoted \({\mathrm{ARL}} =

\frac{{\mathrm{number}\;\mathrm{of}\;\mathrm{listed}\;\mathrm{firm}}}{{\mathrm{number}\;\mathrm{of}\;\mathrm{all}\;\mathrm{firms}}}\). A large value of _ARL_ indicates that the guarantee

system has more firms whose stock trades on a stock exchange. EXPONENTIAL RANDOM GRAPH MODELS Given the structure of real network, first we need to choose a set of topological properties as

constraints, denoted as \(C_i^ \ast (i = 1,2,3 \ldots k)\), where _k_ is the total number of constraints23. We consider a set of networks \({\cal{G}}\), an ensemble of all networks of _n_

nodes without self-loops, whose expected value of constraints <_C__i_> over \({\cal{G}}\) is equal to that of the real guarantee network \(\left( {C_i^ \ast } \right)\). The

probability of a network \(G \in {\cal{G}}\) is denoted as _P_(_G_). It has been proved that we can obtain the value of _P_(_G_) under constraints \(C_i^ \ast\) by maximizing the Gibbs

entropy _S_, which is defined as follows, $$\begin{array}{*{20}{c}} {S = - \mathop {\sum }\limits_{G \in {\mathbf{{\cal{G}}}}} P\left( G \right)\ln P\left( G \right), } \end{array}$$ (3)

with the constraints $$\begin{array}{*{20}{c}} { < C_i > = \mathop {\sum }\limits_{G \in {\mathbf{{\cal{G}}}}} P\left( G \right)C_i\left( G \right) = C_i^ \ast , } \end{array}$$ (4)

and the normalization condition $$\begin{array}{*{20}{c}} {\mathop {\sum }\limits_{G \in {\mathbf{{\cal{G}}}}} P\left( G \right) = 1, } \end{array}$$ (5) where _C__i_(_G_) is the value of

_C__i_ in network _G_. Using the Lagrange multipliers, we can find that the maximum entropy is achieved for the distribution satisfying $$\begin{array}{*{20}{c}} {\frac{\partial }{{\partial

P\left( G \right)}}\left[ {S - \alpha \left( {1 - \mathop {\sum }\limits_{G \in {\mathbf{{\cal{G}}}}} P\left( G \right)} \right) - \mathop {\sum }\limits_i \beta _i( < C_i > - \mathop

{\sum }\limits_{G \in {\mathbf{{\cal{G}}}}} P\left( G \right)C_i\left( G \right))} \right] = 0. } \end{array}$$ (6) By solving Eq. (6), we obtain $$\begin{array}{*{20}{c}} { - \ln P\left( G

\right) - 1 + \alpha + \mathop {\sum }\limits_i \beta _i\;C_i\left( G \right) = 0. } \end{array}$$ (7) Or, equivalently, the probability of graph _G_ is obtained as follows

$$\begin{array}{*{20}{c}} {P\left( G \right) = \frac{{e^{H\left( G \right)}}}{Z}, } \end{array}$$ (8) with the graph Hamiltonian function $$\begin{array}{*{20}{c}} {H\left( G \right) =

\mathop {\sum }\limits_i \beta _i\;C_i\left( G \right), } \end{array}$$ (9) and the partition function $$\begin{array}{*{20}{c}} {Z = e^{1 - \alpha } = \mathop {\sum }\limits_{G \in

{\cal{G}}} e^{H\left( G \right)}.\ } \end{array}$$ (10) We define the topological structure of a network _G_ with an adjacency matrix A, whose entries _a__ij_ = 1 if node _i_ and node _j_

are connected, and _a__ij_ = 0 otherwise. In our study, we denote the real guarantee network by the particular matrix A*. In this study, we chose two constraints: edge number and reciprocal

edge number of guarantee network. Please refer to Results section for discussions of why these two properties are the defining features of the Chinese guarantee network. We assume that the

expected number of edges <_D_(_G_)> and the expected number of mutual edges <_R_(_G_)> of the real network are known. Then, the Hamiltonian of _G_ is $$\begin{array}{*{20}{c}}

{H\left( G \right) = \beta _1\;D\left( G \right) + \beta _2\;R\left( G \right), } \end{array}$$ (11) where \(D(G) = \sum \nolimits_{i < j} ( {a_{ij} + a_{ji}} )\) denotes the number of

edges, and \(R(G) = 2 \sum \nolimits_{i < j} a_{ij}a_{ji}\) denotes the number of reciprocal edges. Given fixed number of nodes, _R_(_G_) and _R_(_G_) essentially evaluate the density and

reciprocity of the network given the fixed number of nodes in the network, respectively. Taking (11) into (10), the partition function for the complete system is formulated as $$Z =

{\mathop {\sum }\limits_{\left\{ {a_{ij}} \right\}}} {\mathop {\sum }\limits_{\left\{ {a_{ji}} \right\}}} \exp \left( {{\mathop {\sum }\limits_{i < j}} [\beta _1\;(a_{ij} + a_{ji}) +

2\beta _2\;a_{ij}a_{ji}]} \right) \\ = {\mathop {\prod }\limits_{i < j}} {\mathop {\sum }\limits_{a_{ij} = 0,1}} {\mathop {\sum }\limits_{a_{ji} = 0,1}} e^{\beta _1(a_{ij} + a_{ji}) +

2\beta _2\;a_{ij}a_{ji}} \\ = {\mathop {\prod }\limits_{i < j}} \left[ {1 + 2e^{\beta _1} + e^{2(\beta _1 + \beta _2)}} \right] { = \left[ {1 + 2e^{\beta _1} + e^{2(\beta _1 + \beta _2)}}

\right]} ^{\left( {\begin{array}{*{20}{c}} n \\ 2 \end{array}} \right)}.$$ (12) Then, the free energy of network is $$\begin{array}{*{20}{c}} {F = \ln Z = \left( {\begin{array}{*{20}{c}} n

\\ 2 \end{array}} \right)\ln \left( {1 + 2e^{\beta _1} + e^{2(\beta _1 + \beta _2)}} \right). } \end{array}$$ (13) Finally, the expected values of edge and reciprocal edge are $${ <

D\left( G \right) > = \frac{{\partial F}}{{\partial \beta _1}} = n\left( {n - 1} \right)\frac{{e^{\beta _1} + e^{2(\beta _1 + \beta _2)}}}{{1 + 2e^{\beta _1} + e^{2(\beta _1 + \beta

_2)}}}, }$$ (14) $${ < R\left( G \right) > = \frac{{\partial F}}{{\partial \beta _2}} = n\left( {n - 1} \right)\frac{{e^{2(\beta _1 + \,\beta _2)}}}{{1 + 2e^{\beta _1} + e^{2(\beta _1

+ \,\beta _2)}}}. }$$ (15) We set the expected values of edge and mutual edge to be equal to the actual counts of edges and reciprocal edges, respectively. From Eqs. (14) and (15), we can

obtain the values of _β_1 and _β_2, which represents the log-odds of the probability of edges and the number of reciprocal edges, respectively. Then, the probability of edges and the

probability of reciprocal edges are the inverse-logits of _β_1 and _β_2, respectively. Thus, a large value of the coefficient indicates the high probability of forming the corresponding

topology (edge and reciprocal edge). Note that the coefficient can be negative, indicating the low prevalence of such topology in the real network. For more details of interpretations of

ERGM, please refer to23,25. REPORTING SUMMARY Further information on research design is available in the Nature Research Reporting Summary linked to this article. DATA AVAILABILITY The

dataset used in the paper is confidential and only available to reader on request. The source data underlying all figures, tables are provided as a Source Data file. CODE AVAILABILITY The

source codes have been made available on Github: [https://github.com/ElfLu/Chinese-credit-network-.git] REFERENCES * Systemic risk in banking ecosystems, Poledna, S. & Thurner, S.

Elimination of systemic risk in financial networks by means of a systemic risk transaction tax. _Quant. Financ._ 16, 1599–1613 (2016). Article  MathSciNet  Google Scholar  * Haldane, A. G.

& May, R. M. Systemic risk in banking ecosystems. _Nature_ 469, 351 (2011). Article  ADS  CAS  Google Scholar  * Lin, E. M., Sun, E. W. & Yu, M.-T. Systemic risk, financial markets,

and performance of financial institutions. _Ann. Oper. Res._ 262, 579–603 (2018). Article  MathSciNet  Google Scholar  * Glasserman, P. & Young, H. P. Contagion in financial networks.

_J. Economic Lit._ 54, 779–831 (2016). Article  Google Scholar  * Cimini, G., Squartini, T., Garlaschelli, D. & Gabrielli, A. Systemic risk analysis on reconstructed economic and

financial networks. _Sci. Rep._ 5, 15758 (2015). Article  ADS  CAS  Google Scholar  * Thakor, A. V. The financial crisis of 2007–2009: why did it happen and what did we learn? The Review of

Corporate Finance. _Studies_ 4, 155–205 (2015). Google Scholar  * Cong, L. W., Gao, H., Ponticelli, J. & Yang, X. Credit allocation under economic stimulus: evidence from China. _Rev.

Financial Stud._ 32, 3412–3460 (2019). Article  Google Scholar  * Pei, M. Are Chinese Banks Hiding “The Mother of All Debt Bombs”. The Diplomat 10 (2012). * Lin, J. Y. New structural

economics: a framework for rethinking development 1. _World Bank Res. Observer_ 26, 193–221 (2011). Article  Google Scholar  * Chen, Z. China’s dangerous debt. _Foreign Aff._ 94, 13 (2015).

Google Scholar  * Jiang, Y. Vulgarisation of Keynesianism in China’s response to the global financial crisis. _Rev. Int. Political Econ._ 22, 360–390 (2015). Article  CAS  Google Scholar  *

Newman, M. _Networks_. (Oxford university press, 2018). * Minoiu, C. & Reyes, J. A. A network analysis of global banking: 1978–2010. _J. Financial Stab._ 9, 168–184 (2013). Article 

Google Scholar  * Chinazzi, M., Fagiolo, G., Reyes, J. A. & Schiavo, S. Post-mortem examination of the international financial network. _J. Economic Dyn. Control_ 37, 1692–1713 (2013).

Article  MathSciNet  Google Scholar  * Conyon, M. J. & Muldoon, M. R. The Small World of Corporate Boards. _J. of Business Finance & Accounting_ 33, 1321–1343 (2006).  Article 

Google Scholar  * Davis, G. F., Yoo, M. & Baker, W. E. The small world of the American corporate elite, 1982-2001. _Strategic Organ._ 1, 301–326 (2003). Article  Google Scholar  *

Robins, G. & Alexander, M. Small worlds among interlocking directors: Network structure and distance in bipartite graphs. _Computational Math. Organ. Theory_ 10, 69–94 (2004). Article 

Google Scholar  * Jiangpo, P. The credit guarantee system of medium-and-small enterprises based on mutual guarantee. _J. Financial Res._ 2, 75–82 (2008). Google Scholar  * Niu, Z. &

Cheng, D. A hybrid approach for risk assessment of loan guarantee network. Preprint https://arxiv.org/abs/1702.04642 (2020). * Niu, Z. et al. Visual analytics for networked-guarantee loans

risk management. _IEEE Pacific Visualization Symposium._ 160–169 (2018). * Jian, M. & Xu, M. Determinants of the guarantee circles: the case of Chinese listed firms. _Pacific-Basin

Finance J._ 20, 78–100 (2012). Article  Google Scholar  * Leng, A., Xing, G. & Fan, W. Credit risk transfer in SME loan guarantee networks. _J. Syst. Sci. Complex._ 30, 1084–1096 (2017).

* Squartini, T. & Garlaschelli, D. Stationarity, non-stationarity and early warning signals in economic networks. _J. Complex Netw._ 3, 1–21 (2015). Article  MathSciNet  Google Scholar

  * Goodreau, S. M. Advances in exponential random graph (p*) models applied to a large social network. _Soc. Netw._ 29, 231–248 (2007). Article  Google Scholar  * Park, J. & Newman, M.

E. Statistical mechanics of networks. _Phys. Rev. E_ 70, 066117 (2004). Article  ADS  MathSciNet  Google Scholar  * Garlaschelli, D. & Loffredo, M. I. Multispecies grand-canonical models

for networks with reciprocity. _Phys. Rev. E_ 73, 015101 (2006). Article  ADS  MathSciNet  Google Scholar  * Robins, G., Pattison, P., Kalish, Y. & Lusher, D. An introduction to

exponential random graph (p*) models for social networks. _Soc. Netw._ 29, 173–191 (2007). Article  Google Scholar  * Engel, J., Pagano, A. & Scherer, M. Reconstructing the topology of

financial networks from degree distributions and reciprocity. _J. Multivar. Anal._ 172, 210–222 (2019). Article  MathSciNet  Google Scholar  * Brailly, J., Favre, G., Chatellet, J. &

Lazega, E. Embeddedness as a multilevel problem: a case study in economic sociology. _Soc. Netw._ 44, 319–333 (2016). Article  Google Scholar  * Mele, A. A structural model of dense network

formation. _Econometrica_ 85, 825–850 (2017). Article  MathSciNet  Google Scholar  * Palepu, K. G. Predicting takeover targets: a methodological and empirical analysis. _J. Account. Econ._

8, 3–35 (1986). Article  Google Scholar  * Ohlson, J. A. Financial ratios and the probabilistic prediction of bankruptcy. _J. Account. Res._ 18, 109–131 (1980). Article  MathSciNet  Google

Scholar  * Dai, Z. & Zhu, H. Forecasting stock market returns by combining sum-of-the-parts and ensemble empirical mode decomposition. _Appl. Econ._ 52, 2309–2323 (2019). * Clauset, A.,

Moore, C. & Newman, M. E. Hierarchical structure and the prediction of missing links in networks. _Nature_ 453, 98–101 (2008). Article  ADS  CAS  Google Scholar  * Palla, G., Derényi,

I., Farkas, I. & Vicsek, T. Uncovering the overlapping community structure of complex networks in nature and society. _Nature_ 435, 814–818 (2005). Article  ADS  CAS  Google Scholar  *

Newman, M. E. The structure and function of complex networks. _SIAM Rev._ 45, 167–256 (2003). Article  ADS  MathSciNet  Google Scholar  * Watts, D. J. & Strogatz, S. H. Collective

dynamics of ‘small-world’networks. _Nature_ 393, 440–442 (1998). Article  ADS  CAS  Google Scholar  * Scott, J. _Social Network Analysis_ (Sage, 2017). * Watts, D. J. & Strogatz, S. H.

Collective dynamics of’small-world’networks. _Nature_ 393, 440 (1998). Article  ADS  CAS  Google Scholar  * Barthélémy, M. & Amaral, L. A. N. Small-world networks: Evidence for a

crossover picture. _Phys. Rev. Lett._ 82, 3180 (1999). Article  ADS  Google Scholar  * Newman, M. E. & Watts, D. J. Renormalization group analysis of the small-world network model.

_Phys. Lett. A_ 263, 341–346 (1999). Article  ADS  MathSciNet  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS This work was supported by National Natural Science Foundation of

China Grants 71532013, 71850008, 71972164, and 71672163. AUTHOR INFORMATION Author notes * These authors contributed equally: Yingli Wang, Qingpeng Zhang, Xiaoguang Yang. AUTHORS AND

AFFILIATIONS * The Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, 100190, China Yingli Wang & Xiaoguang Yang * The University of Chinese Academy of

Sciences, Beijing, 100049, China Yingli Wang & Xiaoguang Yang * School of Data Science, City University of Hong Kong, Kowloon, 00001, Hong Kong, China Qingpeng Zhang Authors * Yingli

Wang View author publications You can also search for this author inPubMed Google Scholar * Qingpeng Zhang View author publications You can also search for this author inPubMed Google

Scholar * Xiaoguang Yang View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS The three authors are joint first authors. Y.W., Q.Z., and X.Y.

designed research; Y.W., and Q.Z. analyzed data and performed research; and Y.W., Q.Z., and X.Y. wrote the paper, and worked on the revision. CORRESPONDING AUTHORS Correspondence to Qingpeng

Zhang or Xiaoguang Yang. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PEER REVIEW INFORMATION _Nature Communications_ thanks

the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available. PUBLISHER’S NOTE Springer Nature remains neutral with regard to

jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION PEER REVIEW FILE REPORTING SUMMARY SOURCE DATA SOURCE DATA RIGHTS

AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in

any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The

images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not

included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly

from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Wang, Y., Zhang,

Q. & Yang, X. Evolution of the Chinese guarantee network under financial crisis and stimulus program. _Nat Commun_ 11, 2693 (2020). https://doi.org/10.1038/s41467-020-16535-8 Download

citation * Received: 25 October 2019 * Accepted: 11 May 2020 * Published: 01 June 2020 * DOI: https://doi.org/10.1038/s41467-020-16535-8 SHARE THIS ARTICLE Anyone you share the following

link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature

SharedIt content-sharing initiative