ABSTRACT Herein, we report a semiconductive, proton-conductive, microporous hydrogen-bonded organic framework (HOF) derived from phenylphosphonic acid and

5,10,15,20‐tetrakis[_p_‐phenylphosphonic acid] porphyrin (GTUB5). The structure of GTUB5 was characterized using single crystal X-ray diffraction. A narrow band gap of 1.56 eV was extracted

from a UV-Vis spectrum of pure GTUB5 crystals, in excellent agreement with the 1.65 eV band gap obtained from DFT calculations. The same band gap was also measured for GTUB5 in DMSO. The

proton conductivity of GTUB5 was measured to be 3.00 × 10−6 S cm−1 at 75 °C and 75% relative humidity. The surface area was estimated to be 422 m2 g−1 from grand canonical Monte Carlo

September 2024 A HIGHLY PROTON CONDUCTIVE PERFLUORINATED COVALENT TRIAZINE FRAMEWORK VIA LOW-TEMPERATURE SYNTHESIS Article Open access 08 December 2023 STRUCTURAL DETAILS OF CARBOXYLIC

ACID-BASED HYDROGEN-BONDED ORGANIC FRAMEWORKS (HOFS) Article Open access 12 October 2023 INTRODUCTION Metal-organic frameworks (MOFs) emerged as revolutionary microporous materials at the

beginning of the 21st century1,2,3. Owing to their well-ordered pores, which are surrounded by inorganic and organic components, MOFs have been used in a wide range of applications, such as

gas storage/separation4,5,6,7, catalysis8,9,10,11,12,13, magnetism14,15,16, electric conductivity17,18,19, proton conductivity20,21,22, and drug delivery23,24,25. In parallel to MOF

research, another closely related family of supramolecular architectures known as hydrogen-bonded organic frameworks (HOFs) has attracted immense interest in recent years26,27,28. In HOFs,

the linker connectivity is achieved via hydrogen-bonded networks rather than inorganic building units (IBUs)29,30,31,32,33. Hydrogen bonds provide simpler connectivity options compared to

the complex molecular, one-dimensional, two-dimensional, and three-dimensional IBUs of MOFs34. Therefore, the design and synthesis of stable hydrogen-bonded supramolecular networks can be

more easily achieved compared to that of MOFs. HOFs are also more convenient to recycle and are free of heavy metal ions, providing environmentally friendly solutions. The recent interest in

HOFs has resulted in several review articles35,36,37 summarizing their applications in CO2 capture38,39,40 and proton conductivity41,42. However, to date, no semiconducting HOFs have been

reported in the literature. Thermally stable and permanently microporous semiconducting HOFs could revolutionize the design of supercapacitors and electrodes due to their simpler chemistry

compared to MOFs. In this communication, we present the first example of a HOF (known as GTUB5, where TUB stands for Technische Universität Berlin and G for Gebze), synthesized using

phosphonic acid functional groups (R-PO3H2), which exhibits a low band gap, proton conductivity, and high thermal stability. The phosphonic acid functional group has two protons and one

oxygen from the P = O bond, which allow it to form multiple hydrogen bonds with other phosphonic acid groups and thereby stabilize the resulting HOF. Interestingly, the unique structure and

multiple metal-binding modes of the phosphonic acid functional group have led to some of the most thermally34,43,44,45,46 and chemically stable34,47,48,49 MOFs in the literature. The

phosphonic acid functional group contains two deprotonation modes with p_K_a values of 1.7 and 7.4, respectively31. Therefore, in order to synthesize our phosphonate HOF, we adopted a

crystallization method at pHs between 1.7 and 7.4 with mixed phosphonic acid linkers of phenylphosphonic acid (PPA) and 5,10,15,20‐tetrakis [_p_‐phenylphosphonic acid] porphyrin (H8-TPPA) to

ensure that at least one of the phosphonic acid moieties is not fully deprotonated. H8-TPPA exhibits a planar tetratopic geometry with a 90° angle between the phenylphosphonate

tethers49,50. Given these starting conditions and materials, it is expected that a mixed linker strategy involving H8-TPPA and PPA could produce two-dimensional HOFs with hexagonal void

channels. RESULTS DESIGN AND STRUCTURAL CHARACTERIZATION The H8-TPPA linker was synthesized according to our previously reported method involving a Pd-catalyzed Arbuzov reaction50, in order

to avoid the porphyrin core being occupied by Ni(II) after a Ni-catalyzed Arbuzov reaction49,50. The synthesized metal-free H8TPPA linker eliminated the possibility of metal–ligand

interactions that could have triggered the formation of MOFs. GTUB5 was synthesized following a conventional MOF crystallization method in scintillation vials in DMF/EtOH at a pH between 1.7

and 7.44 to ensure the presence of protonated phosphonic acid functional groups32. The synthesis of GTUB5 is quite facile, giving dark purple 1–2 mm long needle-shaped crystals in high

yield (see “Methods” section for synthesis details). The dark purple color of GTUB5 is an indication of its semiconductive nature. The structure of GTUB5 was characterized using single

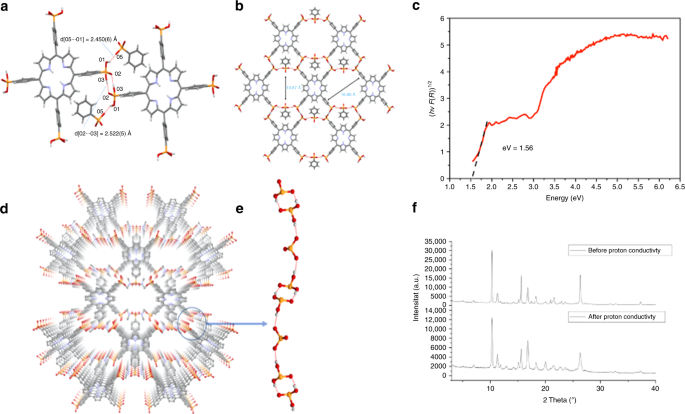
crystal X-ray diffraction. As seen in Fig. 1a, b, GTUB5 is composed of two-dimensional sheets of hydrogen-bonded H8-TPPA and PPA moieties. The structure contains two different

hydrogen-bonding patterns, which are observed between different H8-TPPA units and between H8-TPPA and PPA (see Fig. 1e). In the first pattern, the P = O bond from the H8-TPPA unit is

exclusively involved in creating the (almost linear) double hydrogen-bonding pattern between each unit. In the second pattern, the hydrogen bond forms between the second protonated hydroxyl

group of the H8-TPPA and the deprotonated PPA2−. The four DMF solvent molecules in the HOF structure act as a Lewis base acquiring the PPAs’ protons. The Brunauer–Emmett–Teller (BET) surface

area of GTUB5 was estimated to be 422 m2 g−1 from a simulated N2 adsorption isotherm at 77 K (see Supplementary Fig. 3) obtained using the grand canonical Monte Carlo method (see “Methods”

section for simulation details). BAND GAP MEASUREMENTS The band gap was estimated from a solid-state diffuse reflectance UV–Vis spectrum of the GTUB5 crystals (see Supplementary Fig. 8). As

seen in Fig. 1c, the Tauc plot derived from the spectrum yields a narrow band gap of 1.56 eV. The second jump at 2.88 eV corresponds to the Soret band of the porphyrin core at 430 nm. A

similar band gap was also obtained from a UV–Vis spectrum of a dissolved sample of GTUB5 in DMSO (see Supplementary Fig. 7), suggesting that the hydrogen-bonded supramolecular structure is

not disrupted in a polar aprotic solvent. From a cyclic voltammetry measurement on GTUB5 in DMSO (see Supplementary Fig. 9), the first oxidation and reduction potentials were measured to be

0.42 and −1.23 V, respectively, yielding a HOMO–LUMO gap of 1.65 eV, thereby supporting this hypothesis. DENSITY FUNCTIONAL THEORY (DFT) CALCULATIONS To gain insight into the semiconductive

nature of GTUB5, we performed DFT calculations. The details of the calculations, employing hybrid Gaussian plane-wave (GPW) and Slater-type orbital (STO) basis sets, can be found in the

“Methods” section. Figure 2 shows a periodic representation of the optimized geometry, which is in close agreement with the experimental crystal structure (see Supplementary Table 3 and

Supplementary Figs. 4–7). A single point calculation on the optimized structure yields a band gap of 1.65 eV, in very good agreement with the experimental result of 1.56 eV. As seen in Fig. 

2, the HOMO and LUMO are predominantly localized on some of the porphyrins within the supercell (in which, a single unit cell is delineated by the black rectangle), but not all of them; with

the LUMO localized on the same porphyrins as the HOMO. The fact that the HOMO and LUMO are aligned along the axis perpendicular to the plane of the page within the supercell suggests that

GTUB5 is only conductive along this direction. Focusing in on the portions of the structure that have significant HOMO and LUMO density, we see that the HOMO and LUMO are indeed localized on

the same porphyrin (see Fig. 3). Moreover, they are mostly confined to a subset of the carbons and nitrogens. The HOMO is composed of π orbitals mostly on _sp_2 hybridized carbons and

nitrogens, while the LUMO is composed of π* orbitals on some of the _sp_2 carbons and nitrogens. As shown in Table 1, ∼75% of the HOMO and LUMO orbital contributions are from the carbon and

nitrogen 2_p_ orbitals of the porphyrin. Table 1 also shows that a HOMO–LUMO transition would lead to an increase in the carbon 2_p__x_ orbital population, a slight decrease in the carbon

2_p__y_ population, and a slight increase in the carbon 2_p__z_ population; while the nitrogen 2_p__x_ and 2_p__z_ populations both decrease (the 2_p__y_ population remains negligible).

These results suggest that the semiconductive nature of GTUB5 is predominantly determined by π–π* transitions involving orbitals localized on some of the porphyrin carbons and nitrogens.

Inspection of the projected density of states (pDOS) confirms that the HOMO–LUMO gap is predominantly due to orbitals localized on carbons and nitrogens (see Fig. 4). THERMOGRAVIMETRIC

ANALYSIS The thermal decomposition of GTUB5 was investigated via a thermogravimetric analysis (TGA) of hand-picked crystals up to 900 °C. The TGA curve (see Supplementary Fig. 10) shows an

initial 2% loss between 50 and 100 °C, corresponding to the evaporation of the remaining MeOH on the crystal surface after the synthesis. The following 12% step until 250 °C corresponds to

the loss of dimethylammonium cations (calculated to be 12.9% based on the molecular formula). The remaining organic components of GTUB5 decompose in two steps at ca. 400 and 900 °C. The

second large weight loss at ca. 900 °C suggests the formation of phosphides above 400 °C52. PROTON CONDUCTIVITY Given the presence of –PO3H2 groups in its hydrogen-bonded framework, the

proton conductivity of GTUB5 was measured. Electrochemical impedance spectroscopy measurements were carried out at 75% and 90% relative humidity (%rh) and temperatures in the range of 25–75 

°C (see Supplementary Information and ref. 52 for setup details). At 75%rh, we see that the proton conductivity of GTUB5 increases from 8.29 × 10−7 to 3.00 × 10−6 S cm−1 as the temperature

is increased from 25 to 75 °C, while at 90%rh the conductivities are higher but the increase is more moderate (see Table 2 for full data set). The activation energies, i.e., sum of the

migration and defect formation energies, were extracted from the slopes of the Arrhenius plots (see Supplementary Fig. 15) to be _E_A = 0.26 eV and _E_A = 0.14 eV at 75 and 90 °C,

respectively. These low activation energies suggest that a Grotthuss mechanism with high proton mobility (and therefore low migration energy) and H-bridges to water molecules is the

predominant mechanism for proton conduction through the framework. As seen in Fig. 1f, the XRD pattern of the sample recorded before and after the proton conductivity experiments slightly

changes, indicating that the structure was slightly affected by the humidified atmosphere and the applied temperatures up to 75 °C during the measurements. Due to the large numbers of

phosphonate groups and hydrogen bonds in GTUB5, one might expect higher proton conductivities. However, in addition to the numbers of phosphonate groups and hydrogen bonds, one must also

(and more importantly) consider how rigidly the phosphonate groups are connected to the framework, i.e., how much they change their positions (through rotations and vibrations), and, in

turn, how strongly they interact with the water molecules. In a previous study, we found comparable proton conductivities (viz., 1.35 × 10−6 S cm−1 at 75% rh and 80 °C and 5.62 × 10−6 S cm−1

at 90% rh and 80 °C) for porous porphyrin-based metal tetraphosphonates of the CAU-29 type whose phosphonates sit similarly close to the network53. If, however, proton-conducting groups are

linked to the framework via flexible vibrating and rotating alkyl chains, like in SO3H-propylsilane modified Si-MCM-41, proton conductivities higher than 10−3 S cm−1 at 98% rh and 80 °C

could be achieved54. As quantum chemical calculations in that study confirmed, the proton conductivity is not only strongly dependent on the density of the proton-conducting groups per nm2,

but also on the length of the alkyl chain connecting the proton-conducting group with the rigid framework. In the cases of GTUB5 and CAU-29, no such flexible alkyl chains are present.

DISCUSSION Herein, we presented GTUB5, a two-dimensional, microporous phosphonic acid HOF (with a calculated surface area of 422 m2 g−1). Given its low band gap (as confirmed by

solid-state/solution measurements and DFT calculations), GTUB5 paves the way for the creation of new semiconductive microporous organic compounds. The use of hydrogen bonds in constructing a

framework comes with the advantages of simpler connectivity options and no toxic metal ions (which could possibly lead to environmentally friendly solutions for capacitors and batteries).

The hydrogen-bonded framework also renders GTUB5 proton-conductive (with proton conductivities on the order of 10−6 S cm−1). Owing to its structure, the phosphonic acid group can give rise

to structurally diverse frameworks, which could increase the number of potential HOF applications. GTUB5 has the same band gap of 1.65 eV in DMSO, suggesting that GTUB5 retains its

hydrogen-bonded network in polar aprotic solvents. Therefore, phosphonate HOFs have the potential to revolutionize the semiconductive materials industry with applications in printed

electronics, optoelectronics, photovoltaics, and electrodes in supercapacitors. Currently, we are focusing on different linker geometries and pH modulations to further optimize the pore

sizes and conductive behavior of phosphonate HOFs. METHODS SYNTHESIS All the reagents and solvents employed were commercially available and used as received without further purification. The

linker H8TPPA was synthesized according to our previously reported method50 (8.77 mg, 0.0088 mmol) and phenylphosphonic acid (PPA) (208 mg, 1.3 mmol) in a 1.6 mL mixture of DMF/EtOH or

DMF/MeOH (1.36:0.24, v/v) were added to a 5-mL glass vial. The reaction mixture was ultrasonically dissolved and then heated to 80 °C in an oven for 48 h. After cooling down to room

temperature, dark purple block crystals of GTUB5 formed, which were then isolated by filtration, washed with DMF and acetone, and finally air-dried. The yield of GTUB5 was 5 mg. SINGLE

CRYSTAL STRUCTURE SOLUTION Suitable single crystals of GTUB5 with appropriate dimensions (0.43 mm × 0.14 mm × 0.12 mm) were carefully chosen from the glass vial using a polarizing

microscope, coated with perfluoropolyether oil in order to eliminate the possibility of decomposition, and finally mounted to a thin glass fiber. Intensity data collection was performed with

a Bruker APEX II QUAZAR three-circle diffractometer equipped with the IμS Incoatec Microfocus Source with Mo-Kα radiation (_λ_ = 0.710723 Å) at room temperature (296 K). Indexing was

performed using APEX255. Data integration and reduction were carried out with SAINT56. Absorption correction was performed by multi-scan method implemented in SADABS57. The structure was

solved using SHELXT58 and then refined by full-matrix least-squares refinements on F2 using SHELXL59 in the Olex2 Software Package60. The positions of all H-atoms bonded to the carbon,

nitrogen, and oxygen atoms were geometrically optimized with the following HFIX instructions in SHELXL: HFIX 23 for the –CH2– moieties, HFIX 137 for the –CH3, HFIX 43 for the CH and NH

groups of the aromatic rings and porphyrin cores, and HFIX 147 for the –P–OH groups (H1a) of the phosphonic acid moieties. Another O-bound H atom (H3) was located from the difference

Fourier-map. Finally, their displacement parameters were set to isotropic thermal displacements parameters [_U_iso(H) = 1.2_U_eq for CH, NH, and CH2 groups and _U_iso(H) = 1.5_U_eq for OH

and CH3 groups]. In the chemical formula [(H8-TPPA)(PPA)2(DMA)4] of GTUB5, the H8-TPPA building block is not deprotonated, while the protons of the phenylphosphonic acid (PPA) groups are

acquired by the DMF solvent in the pores to form four dimethylammonium cations (DMA–[NH2(CH3)2]+) to balance the charge. SQUEEZE was used to remove the electron density caused by seriously

disordered solvent molecules in GTUB5. Along the _c_-axis, the 3D supramolecular network of GTUB5 produced a one-dimensional distinctive void space with a total potential solvent area

occupying 19.2% (785 Å3) of the unit cell volume (4081.7 Å3), obtained using the PLATON software package61. Analysis of solvent accessible voids in the structure was performed using CALC

SOLV in PLATON with a probe radius of 1.20 Å and grid spacing of 0.2 Å. Van der Waals (or ion) radii used in the analysis are 1.70 Å for C, 1.20 Å for H, 1.55 Å for N, 1.52 Å for O, and 1.80

 Å for P. Also, in this crystal structure, the rotationally disordered phosphonate part (–PO3) in PPA was refined as 0.77:0.23. Crystallographic data and refinement details of the data

collection for GTUB5 are given in Supplementary Table 4. Crystal structure validations and geometrical calculations were performed using PLATON61. The Mercury software package62 was used for

visualization of the cif files. GRAND CANONICAL MONTE CARLO (GCMC) SURFACE AREA CALCULATIONS The surface area of GTUB5 was calculated by force-field based atomistic simulations, which were

performed with the RASPA molecular simulation package63. For these simulations, the GTUB5 unit cell was replicated by 1 × 2 × 4 times in the _x_, _y_, and _z_ directions, respectively, and

the replicated framework atoms were fixed in their crystallographically determined positions. Lennard–Jones (LJ) and Coulomb potentials were employed to determine the non-bonded interaction

energies between atoms: $$V_{ij} = 4\varepsilon _{ij}\left[ {\left( {\frac{{\sigma _{ij}}}{{r_{ij}}}} \right)^{12} - \left( {\frac{{\sigma _{ij}}}{{r_{ij}}}} \right)^6} \right] +

\frac{{q_i\,q_j}}{{4\,\varepsilon _0\,r_{ij}}}$$ (1) where _r__ij_ is the distance between atoms _i_ and _j_, _ε__ij_ and _σ__ij_ are the LJ well depth and diameter, respectively, _q__i_ is

the partial charge of atom _i_, and _ε_0 is the dielectric constant. The LJ parameters between different types of sites were calculated using the Lorentz–Berthelot mixing rules, and the

Ewald summation method was employed to compute the electrostatic interactions. The LJ interactions were shifted to be 0 at a cutoff distance of 12.0 Å. For the real part of the Ewald

summation, the cutoff was also set to 12.0 Å. A N2 adsorption isotherm for GTUB5 was computed by performing GCMC simulations at 77 K and up to 0.4 bar. In the GC ensemble, the chemical

potential, volume, and temperature of the system are fixed; however, the number of molecules fluctuates. For all GCMC simulations, a 100,000 cycle initialization and a 100,000 cycle

production run were performed. Each cycle is _N_ steps, where _N_ is equal to the number of molecules in the system. Random insertions, deletions, translations, rotations, and reinsertions

of the N2 molecules were sampled with equal probability. The TraPPE force field was used to model the N2 molecules64, which was originally fit to reproduce the vapor–liquid coexistence curve

of N2. In this force field, the N2 molecule is rigid with the N–N bond length fixed at its experimental value of 1.10 Å. This model reproduces the experimental gas-phase quadrupole moment

of the N2 molecule by placing partial charges on nitrogen atoms and on a point located at the center of mass (COM) of the molecule. Supplementary Table 2 shows the LJ parameters and partial

charges for the N2 molecule. In GCMC simulations, one computes the absolute adsorption (_N_total); whereas, in adsorption experiments, the excess adsorption (_N_excess) is measured.

Therefore, the simulated excess adsorption of N2 was calculated using the following expression: $$N_{{\mathrm{total}}} = N_{{\mathrm{excess}}} + \,\rho _{{\mathrm{gas}}}V_{\mathrm{{{p}}}}$$

(2) where _ρ_gas is the bulk density of the gas at simulation conditions which were calculated using the Peng–Robinson equation of state and _V_p is the accessible pore volume. The BET

surface area of GTUB5 was obtained from the simulated N2 adsorption isotherm (see Supplementary Fig. 3) and estimated to be 422 m2 g−1. When applying the BET theory, we made sure that our

analysis satisfied the two consistency criteria as detailed by Walton and Snurr65. DENSITY FUNCTIONAL THEORY (DFT) CALCULATIONS The geometry optimization of GTUB5 was performed using DFT and

the conjugate gradient method66 within the Quickstep-CP2K program67,68, starting from the experimental crystal structure and with the lattice vectors set to their experimental values. Since

GTUB5 is a bulk material, periodic boundary conditions were applied to a reoriented 1 × 1 × 1 cell (_a_ = 25.452 Å, _b_ = 22.863 Å, _c_ = 7.1798 Å, _α_ = _γ_ = 90.0°, _β_ = 102.325°). The

Perdew–Burke–Ernzerhof (PBE)69 generalized gradient approximation (GGA) functional was used in conjunction with the Grimme D3 dispersion correction70 and BJ damping71. The Gaussian and plane

waves method70,72 was used, with the valence orbitals expanded in terms of molecularly optimized Gaussian basis sets of double-ζ plus polarization (MOLOPT-DZVP)73 quality and the core

electrons represented by norm-conserving Goedecker–Teter–Hutter pseudopotentials74,75. Γ-point sampling was used and the plane-wave cutoff in reciprocal space was set to 550 Ry, with a

Gaussian mapping of 60 Ry over five multi-grids. The self-consistent field was converged to 10−6 Ry with the FULL_ALL preconditioner using the orbital transformation method with a HOMO–LUMO

gap of 1.67 eV. Single point calculations were performed using CP2K to obtain the HOMO–LUMO iso-surface plots (Figs. 2 and 3), orbital populations (Table 1), and the HOMO–LUMO gap. Another

single point calculation was performed using the Slater-Type Orbital (STO) software ADF-BAND 2018.10476,77 to obtain the projected density of states (pDOS) (Fig. 4), band structure

(Supplementary Fig. 8), and the HOMO–LUMO gap. The periodic ADF-BAND calculations were performed using an all-electron double-ζ plus polarization (DZP) basis set, PBE-D3-BJ, and Γ-point

sampling for the 1 × 1 × 1 unit cell, with a good numerical quality. The HOMO–LUMO gaps obtained from CP2K and ADF-BAND were both 1.65 eV (thus, the HOMO–LUMO iso-surfaces and orbital

populations obtained from CP2K are expected to be the same as those from ADF-BAND). DATA AVAILABILITY All data is available in the main text and the Supplementary Information. The source

data for Table 1, Fig. 1c, Supplementary Figs. 2–4, 10, 13, 16, 17, and the CIF file are provided as a Source Data file. The X-ray crystallographic coordinates for the structure reported in

this study can be obtained free of charge from the Cambridge Crystallographic Data Centre (CCDC) [under the deposition number CCDC: 1963794 for GTUB5] via

www.ccdc.cam.ac.uk/data_request/cif. REFERENCES * Li, H., Eddaoudi, M., O’Keeffe, M. & Yaghi, O. M. Design and synthesis of an exceptionally stable and highly porous metal-organic

framework. _Nature_ 402, 276–279 (1999). Article  ADS  CAS  Google Scholar  * Schneemann, A. et al. Flexible metal-organic frameworks. _Chem. Soc. Rev._ 43, 6062–6069 (2014). Article  CAS 

PubMed  Google Scholar  * Férey, G., Mellot-Draznieks, C., Serre, C. & Millange, F. Crystallized frameworks with giant pores: are there limits to the possible?. _Acc. Chem. Res._ 38,

217–225 (2005). Article  PubMed  CAS  Google Scholar  * Mason, J. A., Veenstra, M. & Long, J. R. Evaluating metal-organic frameworks for natural gas storage. _Chem. Sci._ 5, 32–51

(2014). Article  CAS  Google Scholar  * Miller, S. R. et al. Structural transformations and adsorption of fuel-related gases of a structurally responsive nickel phosphonate metal-organic

framework, Ni-STA-12. _J. Am. Chem. Soc._ 130, 15967–15981 (2008). Article  CAS  PubMed  Google Scholar  * Liu, Y., O’Keeffe, M., Treacy, M. M. & Yaghi, O. M. The geometry of periodic

knots, polycatenanes and weaving from a chemical perspective: a library for reticular chemistry. _Chem. Soc. Rev._ 47, 4642–4664 (2018). Article  CAS  PubMed  Google Scholar  * Furukawa, H.,

Cordova, K. E., O’Keeffe, M. & Yaghi, O. M. The chemistry and applications of metal-organic frameworks. _Science_ 341, 1230444 (2013). Article  PubMed  CAS  Google Scholar  *

Dhakshinamoorthy, A., Li, Z. & Garcia, H. Catalysis and photocatalysis by metal organic frameworks. _Chem. Soc. Rev._ 47, 8134–8172 (2018). Article  CAS  PubMed  Google Scholar  * Yang,

D. & Gates, B. C. _ACS Catal._ 9, 1779 (2019). Article  CAS  Google Scholar  * Liu, M., Wu, J. & Hou, H. Metal-organic framework (MOF)-based materials as heterogeneous catalysts for

C–H bond activation. _Chem. Eur. J._ 25, 2935–2948 (2019). CAS  PubMed  Google Scholar  * Zhu, L., Liu, X.-Q., Jiang, H.-L. & Sun, L.-B. Metal-organic frameworks for heterogeneous basic

catalysis. _Chem. Rev._ 117, 8129–8176 (2017). Article  CAS  PubMed  Google Scholar  * Kang, Y.-S. et al. Metal-organic frameworks with catalytic centers: from synthesis to catalytic

application. _Coord. Chem. Rev._ 378, 262–280 (2019). Article  CAS  Google Scholar  * Chen, X. et al. Sixteen isostructural phosphonate metal-organic frameworks with controlled lewis acidity

and chemical stability for asymmetric catalysis. _Nat. Commun._ 8, 1–9 (2017). Article  ADS  CAS  Google Scholar  * Espallargas, G. M. & Coronado, E. Magnetic functionalities in MOFs:

from the framework to the pore. _Chem. Soc. Rev._ 47, 533–557 (2018). Article  Google Scholar  * Kurmoo, M. Magnetic metal-organic frameworks. _Chem. Soc. Rev._ 38, 1353–1379 (2009). Article

  CAS  PubMed  Google Scholar  * Stock, N. & Biswas, S. Syntheses of metal-organic frameworks (MOFs): routes to various MOF topologies, morphologies, and composites. _Chem. Rev._ 112,

933–969 (2012). Article  CAS  PubMed  Google Scholar  * Ko, M., Mendecki, L. & Mirica, K. A. Conductive two-dimensional metal-organic frameworks as multifunctional materials. _Chem.

Commun._ 54, 7873–7891 (2018). Article  CAS  Google Scholar  * Siemensmeyer, K. et al. Phosphonate metal-organic frameworks: a novel family of semiconductors. _Adv. Mater._

https://doi.org/10.1002/adma.202000474 (2020). Article  PubMed  Google Scholar  * Sun, L., Campbell, M. G. & Dincă, M. Electrically conductive porous metal-organic frameworks. _Angew.

Chem. Int. Ed._ 55, 3566–3579 (2016). Article  CAS  Google Scholar  * Taylor, J. M. et al. Facile proton conduction via ordered water molecules in a phosphonate metal-organic framework. _J.

Am. Chem. Soc._ 132, 14055–14057 (2010). Article  CAS  PubMed  Google Scholar  * Levenson, D. A. et al. Effects of secondary anions on proton conduction in a flexible cationic phosphonate

metal-organic framework. _Chem. Mater._ 32, 679–687 (2020). Article  CAS  Google Scholar  * Pili, S. et al. Proton conduction in a phosphonate-based metal-organic framework mediated by

intrinsic “free diffusion inside a sphere”. _J. Am. Chem. Soc._ 138, 6352–6355 (2016). Article  CAS  PubMed  PubMed Central  Google Scholar  * Cai, W. et al. Metal-organic framework-based

stimuli-responsive systems for drug delivery. _Adv. Sci._ 6, 1–20 (2019). ADS  Google Scholar  * Horcajada, P. et al. Metal-organic frameworks in biomedicine. _Chem. Rev._ 112, 1232–1268

(2012). Article  CAS  PubMed  Google Scholar  * Hartlieb, K. J. et al. Encapsulation of Ibuprofen in CD-MOF and related bioavailability studies. _Mol. Pharm._ 14, 1831–1839 (2017). Article 

CAS  PubMed  Google Scholar  * Huang, Q. et al. An exceptionally flexible hydrogen-bonded organic framework with large-scale void regulation and adaptive guest accommodation abilities. _Nat.

Commun._ 10, 1–8 (2019). Article  ADS  CAS  Google Scholar  * Yin, Q., Lü, J., Li, H.-F., Liu, T.-F. & Cao, R. Robust microporous porhyrin-based hydrogen-bonded organic framework for

highly selective separation of C2 hydrocarbons versus methane. _Cryst. Growth Des._ 19, 4157–4161 (2019). Article  CAS  Google Scholar  * Yoon, T.-U. et al. Efficient separation of C2

hydrocarbons in a permanently porous hydrogen-bonded organic framework. _Chem. Commun._ 54, 9360–9363 (2018). Article  CAS  Google Scholar  * Bao, S.-S., Shimizu, G. K. H. & Zheng, L.-M.

Proton conductive metal phosphonate frameworks. _Coord. Chem. Rev._ 378, 577–594 (2019). Article  CAS  Google Scholar  * Shearan, S. J. I. et al. New directions in metal phosphonate and

phosphinate chemistry. _Crystals_ 9, 270 (2019). Article  CAS  Google Scholar  * Sevrain, C. M., Berchel, M., Couthon, H. & Jaffrès, P.-A. Phosphonic acid: preparation and applications.

_Beilstein J. Org. Chem._ 13, 2186–2213 (2017). Article  CAS  PubMed  PubMed Central  Google Scholar  * Schoedel, A. et al. Structures of metal-organic frameworks with rod secondary building

units. _Chem. Rev._ 119, 12466–12535 (2016). Article  CAS  Google Scholar  * Ramaswamy, P., Wong, N. E. & Shimizu, G. K. H. MOFs as proton conductors—challenges and opportunities.

_Chem. Soc. Rev._ 43, 5913–5932 (2014). Article  CAS  PubMed  Google Scholar  * Tholen, P., Zorlu, Y., Beckmann, J. & Yücesan, G. Steps towards the next generation of stable and

functional MOFs. _Eur. J. Inorg. Chem._ 17, 1542–1554 (2020). Article  CAS  Google Scholar  * Lin, R.-B. et al. Multifunctional porous hydrogen-bonded organic framework materials. _Chem.

Soc. Rev._ 48, 1362–1389 (2019). Article  CAS  PubMed  Google Scholar  * Lou, J., Wang, J.-W., Zhang, J.-H., Lai, S. & Zhong, D.-C. Hydrogen-bonded organic frameworks: design, structures

and potential applications. _CrystEngComm_ 20, 5884–5898 (2018). Article  Google Scholar  * Hisaki, I., Xin, C., Takahashi, K. & Nakamura, T. Designing hydrogen-bonded organic

frameworks (HOFs) with permanent porosity. _Angew. Chem. Int. Ed._ 58, 11160–11170 (2019). Article  CAS  Google Scholar  * Wang, H. et al. A flexible microporous hydrogen-bonded organic

framework for gas sorption and separation. _J. Am. Chem. Soc._ 137, 9963–9970 (2015). Article  CAS  PubMed  Google Scholar  * Patil, R. S., Banerjee, D., Zhang, C., Thallapally, P. K. &

Atwood, J. L. Selective CO2 adsorption in a supramolecular organic framework. _Angew. Chem. Int. Ed._ 55, 4523–4526 (2016). Article  CAS  Google Scholar  * Luo, X.-Z. et al. A microporous

hydrogen-bonded organic framework: exceptional stability and highly selective adsorption of gas and liquid. _J. Am. Chem. Soc._ 135, 11684–11687 (2013). Article  CAS  PubMed  Google Scholar

  * Karmakar, A. et al. Hydrogen-bonded organic frameworks (HOFs): a new calss of porous crystalline proton-conducting materials. _Angew. Chem. Int. Ed._ 55, 10667–10671 (2016). Article  CAS

  Google Scholar  * Yang, W. et al. Microporous diaminotriazine-decorated porphyrin-based hydrogen-bonded organic framework: permanent porosity and proton conduction. _Cryst. Growth Des._

16, 5831–5835 (2016). Article  CAS  Google Scholar  * Yücesan, G., Zorlu, Y., Stricker, M. & Beckmann, J. Metal-organic solids derived from arylphosphonic acids. _Coord. Chem. Rev._ 369,

105–122 (2018). Article  CAS  Google Scholar  * Gagnon, K. J., Perry, H. P. & Clearfield, A. Conventional and unconventional metal-organic frameworks based on phosphonate ligands: MOFs

and UMOFs. _Chem. Rev._ 112, 1034–1054 (2012). Article  CAS  PubMed  Google Scholar  * Hermer, N. & Stock, N. The new triazine-based porous copper phosphonate [Cu3(PPT)(H2O)3]∙10H2O.

_Dalton Trans._ 44, 3720–3723 (2015). Article  CAS  PubMed  Google Scholar  * Zorlu, Y. et al. A cobalt arylphosphonate MOF—superior stability, sorption and magnetism. _Chem. Commun._ 55,

3053–3056 (2019). Article  CAS  Google Scholar  * Gao, C., Ai, J., Tian, H., Wub, D. & Sun, Z. An ultrastable zirconium-phosphonate framework as bifunctional catalyst for highly active

CO2 chemical transformation. _Chem. Commun._ 53, 1293–1296 (2017). Article  CAS  Google Scholar  * Zheng, T. et al. Overcoming the crystallization and designability issues in the ultrastable

zirconium phosphonate framework system. _Nat. Commun._ 8, 1–11 (2017). Article  ADS  CAS  Google Scholar  * Rhauderwiek, T. et al. Highly stable and porous porphyrin-based zirconiium and

hafnium phosphonates—electron crystallography as an important tool for structure elucidation. _Chem. Sci._ 9, 5467–5478 (2018). Article  CAS  PubMed  PubMed Central  Google Scholar  *

Maares, M. et al. Alkali phosphonate metal-organic frameworks. _Chem. Eur. J._ 25, 11214–11217 (2019). CAS  PubMed  Google Scholar  * Philipsen, P. H. T. et al. _BAND 2018.104, SCM,

Theoretical Chemistry_ (Vrije Universiteit, Amsterdam, The Netherlands, 2018). * Homburg, T. et al. Magnesium doped gallium phosphonates Ga1–x Mgx [H3+x (O3PCH2)3N] (x = 0, 0.20) and the

influence on proton conductivity. _Z. Anorg. Allg. Chem._ 644, 86–91 (2018). Article  CAS  Google Scholar  * Rhauderwiek, T. et al. Crystalline and permanently porous porphyrin-based metal

tetraphonates. _Chem. Comm._ 54, 389–392 (2018). Article  CAS  PubMed  Google Scholar  * Marschall, R. et al. Detailed simulation and characterization of highly proton conducting sulfonic

acid functionalized mesoporous materials under dry and humidified conditions. _J. Phys. Chem. C_ 113, 19218–19227 (2009). Article  CAS  Google Scholar  * APEX2, version 2014.11-0, Bruker

(Bruker AXS Inc., Madison, WI, 2014). * SAINT, version 8.34A, Bruker (Bruker AXS Inc., Madison, WI, 2013). * SADABS, version 2014/5, Bruker (Bruker AXS Inc., Madison, WI, 2014). * Sheldrick,

G. M. SHELXT—integrated space-group and crystal-structure determination. _Acta Crystallogr. A_ A71, 3–8 (2015). Article  MATH  CAS  Google Scholar  * Sheldrick, G. M. Crystal structure

refinement with SHELXL. _Acta Crystallogr. C_ C71, 3–8 (2015). Article  MATH  CAS  Google Scholar  * Dolomanov, O. V., Bourhis, L. J., Gildea, R. J., Howard, J. A. K. & Puschmann, H. _J.

Appl. Crystallogr._ 42, 336–338 (2009). Article  CAS  Google Scholar  * Spek, A. L. Structure validation in chemical crystallography. _Acta Crystallogr. D_ D65, 148–155 (2009). Article  CAS

  Google Scholar  * Macrae, C. F. et al. Mercury: visualization and analysis of crystal structures. _J. Appl. Crystallogr._ 39, 453–457 (2006). Article  CAS  Google Scholar  * Dubbeldam, D.,

Calero, S., Ellis, D. E. & Snurr, R. Q. RASPA: molecular simulation software for adsorption and diffusion in flexible nanoporous materials. _Mol. Simulat._ 42, 81–101 (2016). Article 

CAS  Google Scholar  * Potoff, J. J. & Siepmann, J. I. Vapor–liquid equilibria of mixtures containing alkanes, carbon dioxide, and nitrogen. _AIChE J._ 47, 1676–1682 (2001). Article  CAS

  Google Scholar  * Walton, K. S. & Snurr, R. Q. Applicability of the BET method for determining surface areas of microporous metal-organic frameworks. _J. Am. Chem. Soc._ 129, 8552–8556

(2007). Article  CAS  PubMed  Google Scholar  * Hestenes, M. R. & Stiefel, E. Methods of conjugate gradients for solving linear systems. _J. Res. Natl Bur. Stand._ 49, 409–436 (1952).

Article  MathSciNet  MATH  Google Scholar  * VandeVondele, J. et al. Quickstep: fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. _Comput.

Phys. Commun._ 167, 103–128 (2005). Article  ADS  CAS  Google Scholar  * Hutter, J., Iannuzzi, M., Schiffmann, F. & Vandevondele, J. CP2K: atomistic simulations of condensed matter

systems. _WIRES Comput. Mol. Sci._ 4, 15–25 (2014). Article  CAS  Google Scholar  * Perdew, J., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. _Phys. Rev.

Lett._ 77, 3865–3868 (1996). Article  ADS  CAS  PubMed  Google Scholar  * Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density

functional dispersion correction (DFT-D) for the 94 elements H-Pu. _J. Chem. Phys._ 132, 154104-1–154104–19 (2010). Article  ADS  CAS  Google Scholar  * Grimme, S., Ehrlich, S. &

Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. _J. Comput. Chem._ 32, 1456–1465 (2011). Article  CAS  PubMed  Google Scholar  * Lippert, G.,

Hutter, J. & Parrinello, M. A hybrid Gaussian and plane wave density functional scheme. _Mol. Phys._ 92, 477–488 (1997). Article  ADS  CAS  Google Scholar  * VandeVondele, J. &

Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. _J. Chem. Phys._ 127, 114105-1–114105-9 (2007). Article  ADS  CAS  Google Scholar 

* Goedecker, S. & Teter, M. Separable dual-space Gaussian pseudopotentials. _Phys. Rev. B_ 54, 1703–1710 (1996). Article  ADS  CAS  Google Scholar  * Hartwigsen, C., Goedecker, S. &

Hutter, J. Relativistic separable dual-space gaussian pseudopotentials from H to Rn. _Phys. Rev. B_ 58, 3641–3662 (1998). Article  ADS  CAS  Google Scholar  * Philipsen, P. H. T. et al.

_BAND 2018.104, SCM, Theoretical Chemistry_ (Vrije Universiteit, Amsterdam, The Netherlands, 2018). * te Velde, G. et al. Chemistry with ADF. _J. Comput. Chem._ 22, 931–967 (2001). Article 

Google Scholar  Download references ACKNOWLEDGEMENTS The authors thank Dr. Pradip Pachfule from TU-Berlin for his help in measuring the solid state UV–Vis spectrum of GTUB5. Gündoğ Yücesan

would like to thank the DFG for funding his work with grant number DFG YU 267/2-1 and DAAD for supporting Prof. Dr. Bünyemin Çoşut’s visit to his lab at TU-Berlin. We acknowledge support by

the German Research Foundation and the Open Access Publication Fund of TU Berlin. Gabriel Hanna acknowledges support from the Natural Sciences and Engineering Research Council of Canada

(NSERC). The DFT calculations were enabled by support provided by WestGrid (www.westgrid.ca) and Compute Canada (www.computecanada.ca). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS *

Technische Universität Berlin, Gustav-Meyer-Allee 25, 13355, Berlin, Germany Patrik Tholen & Gündoğ Yücesan * University of Alberta, 116 St. and 85 Ave., Edmonton, AB, T6G 2R3, Canada

Craig A. Peeples & Gabriel Hanna * Carl von Ossietzky Universität Oldenburg, Carl-von-Ossietzky Str. 9-11, 26129, Oldenburg, Germany Raoul Schaper & Michael Wark * Gebze Technical

University, Kimya Bölümü, 41400, Gebze-Kocaeli, Turkey Ceyda Bayraktar, Mehmet Menaf Ayhan, Bünyemin Çoşut & Yunus Zorlu * University College London, Torrington Place, London, WC1E 7JE,

UK Turan Selman Erkal & A. Ozgur Yazaydin * Universität Bremen, Leobener Str. 7, 28359, Bremen, Germany Jens Beckmann Authors * Patrik Tholen View author publications You can also search

for this author inPubMed Google Scholar * Craig A. Peeples View author publications You can also search for this author inPubMed Google Scholar * Raoul Schaper View author publications You

can also search for this author inPubMed Google Scholar * Ceyda Bayraktar View author publications You can also search for this author inPubMed Google Scholar * Turan Selman Erkal View

author publications You can also search for this author inPubMed Google Scholar * Mehmet Menaf Ayhan View author publications You can also search for this author inPubMed Google Scholar *

Bünyemin Çoşut View author publications You can also search for this author inPubMed Google Scholar * Jens Beckmann View author publications You can also search for this author inPubMed 

Google Scholar * A. Ozgur Yazaydin View author publications You can also search for this author inPubMed Google Scholar * Michael Wark View author publications You can also search for this

author inPubMed Google Scholar * Gabriel Hanna View author publications You can also search for this author inPubMed Google Scholar * Yunus Zorlu View author publications You can also search

for this author inPubMed Google Scholar * Gündoğ Yücesan View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS G.Y. created the hypothesis,

supervised the project, wrote the manuscript and co-wrote/revised the non-computational parts of the manuscript. P.T. resynthesized the compound, determined the experimental band gap,

contributed to the crystal structure refinement, prepared the crystallographic figures, organized the proton conductivity work, and contributed to the text. C.A.P. performed the DFT

calculations, generated the corresponding figures/tables, and wrote the initial draft of the corresponding parts of the manuscript. R.S. performed the proton conductivity and powder XRD

experiments, and contributed to the text. T.S.E. performed the Monte Carlo simulations. C.B. and M.A. synthesized the linker. B.Ç. generated the Tauc Plot figures, performed, cyclic

voltammetry and obtained UV–Vis in DMSO and contributed to the text in corresponding section. A.O.Y. supervised the Monte Carlo simulations and wrote the corresponding text. J.B. critically

read the text and contributed to the manuscript. M.W. supervised the proton conductivity work and wrote the corresponding section. G.H. supervised the DFT calculations, co-wrote the

corresponding parts of the manuscript, performed extensive critical revisions of the entire manuscript, and edited the entire manuscript. Y.Z. optimized the crystallization, supervised the

crystal refinement, supervised the synthesis of the linker, and generated the text/tables corresponding to the crystallographic refinement and synthesis. CORRESPONDING AUTHORS Correspondence

to Yunus Zorlu or Gündoğ Yücesan. ETHICS DECLARATIONS COMPETING INTERESTS Gündoğ Yücesan has a patent pending for some of the presented results. The other authors declare no competing

interests. ADDITIONAL INFORMATION PEER REVIEW INFORMATION _Nature Communications_ thanks Jon Zubieta and the other, anonymous, reviewer(s) for their contribution to the peer review of this

work. PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY

INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution

and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if

changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the

material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to

obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS

ARTICLE Tholen, P., Peeples, C.A., Schaper, R. _et al._ Semiconductive microporous hydrogen-bonded organophosphonic acid frameworks. _Nat Commun_ 11, 3180 (2020).

https://doi.org/10.1038/s41467-020-16977-0 Download citation * Received: 12 March 2020 * Accepted: 04 June 2020 * Published: 23 June 2020 * DOI: https://doi.org/10.1038/s41467-020-16977-0

SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to

clipboard Provided by the Springer Nature SharedIt content-sharing initiative