ABSTRACT High-entropy alloys are random alloys with five or more components, often near equi-composition, that often exhibit excellent mechanical properties. Guiding the design of new

materials across the wide composition space requires an ability to compute necessary underlying material parameters via ab initio methods. Here, density functional theory is used to compute

the elemental misfit volumes, alloy lattice constant, elastic constants, and stable stacking fault energy in the fcc noble metal RhIrPdPtNiCu. These properties are then used in a recent

theory for the temperature and strain-rate dependent yield strength. The parameter-free prediction of 583 MPa is in excellent agreement with the measured value of 527 MPa. This quantitative

SHORT-RANGE ORDER, AND PHASE STABILITY OF THE AL_X_CRFECONI HIGH-ENTROPY ALLOY: INSIGHTS FROM A PERTURBATIVE, DFT-BASED ANALYSIS Article Open access 28 November 2024 ANOMALOUS SIZE EFFECT ON

YIELD STRENGTH ENABLED BY COMPOSITIONAL HETEROGENEITY IN HIGH-ENTROPY ALLOY NANOPARTICLES Article Open access 19 May 2022 STRENGTH CAN BE CONTROLLED BY EDGE DISLOCATIONS IN REFRACTORY

HIGH-ENTROPY ALLOYS Article Open access 16 September 2021 INTRODUCTION High-entropy alloys (HEAs), also called multiple principal element alloys, nominally consist of five or more elements

at near-equal compositions in a single crystalline phase.1 Many HEAs possess high yield strengths, ultimate strengths, and/or ductility, making them a broad new class of candidates for

structural applications.2,3,4 As a result, new materials are emerging rapidly. In the noble metal family, Sohn et al.5 reported a single-fcc-phase RhIrPdPtNiCu system with compressive yield

strength _σ__y_ = 527 MPa, ultimate strength of 1839 MPa, and strain to failure of 32.4%, the latter two properties rivaling the strongest and toughest steels.6 However, HEAs must not only

match currently available structural alloys but exceed them in one or more properties. Since there is no physical restriction to near-equi-composition random alloys, the available

composition space for multi-property optimization is vast. Searching through that space can be greatly facilitated by theory and modeling for both property prediction and phase stability.

Accurate predictions require both accurate theories and the chemically accurate inputs to those models, and the latter leads to the application of first-principles methods. Strength and

ductility depend on the motion and interaction of dislocations through the random alloy. First-principles modeling of dislocations in pure elemental metals alone is challenging. Studying the

required properties/behaviors of dislocations in complex HEAs is even more formidable. Thus, theories are needed to predict the desired properties based on computationally accessible

material inputs. The first property of interest is the initial yield strength. This is the stress at which pre-existing dislocations can first start to move through the crystalline lattice

and generate the on-going plastic strain at the macroscopic imposed strain-rate and temperature. A general theory has been developed to predict the temperature and strain-rate dependent

yield strength in random fcc alloys.7,8 The theory envisions the HEA as an “effective-medium matrix”, and each elemental atom in the alloy acts as a solute in the effective matrix. With an

additional assumption that the solute/dislocation interaction energies are governed by elasticity, the model then requires only the average material properties of the alloy matrix and the

properties of the elemental solutes in that average matrix. Here, we use first-principles density functional theory (DFT) to compute all the necessary alloy properties that enter the theory,

for the 6-component RhIrPdPtNiCu alloy studied recently. We present a new and general method to compute the required solute misfit volumes in the multicomponent random alloys, which then

enables parameter-free and experiment-free prediction of the yield strength. Good agreement with experiment is achieved, establishing the overall methodology as a framework for

computationally guided design of new fcc HEAs. RESULTS THEORY OF YIELD STRENGTH IN MULTICOMPONENT RANDOM ALLOYS We consider a general fcc alloy containing _N_elem types of alloying elements

at concentrations {_c__n_} (with \(\mathop {\sum}\nolimits_{n = 1}^{N_{{\mathrm{elem}}}} {\kern 1pt} c_n = 1\)), with all alloying elements distributed randomly on the fcc lattice sites.

There is thus a probability _c__n_ that any given lattice site will be occupied by a type-_n_ atom. The strengthening of the random alloy arises through solute/dislocation interactions. The

interaction of the dislocation with the random fluctuations in the local solute concentrations induces the dislocation to become wavy over some characteristic wavelength 4_ζ__c_ and

amplitude _w__c_ that minimize the total energy of the system. The wavy dislocation is then locally trapped in low-energy regions. Dislocation motion, and plastic strain, thus occurs by

stress-assisted thermal activation across the adjacent high-energy regions along the dislocation glide plane and into the next low-energy regions. The theory computes the fundamental

zero-stress energy barrier Δ_E__b_ and zero-temperature flow stress _τ__y_0 from which the yield stress at finite temperature _T_ and finite strain-rate \(\dot \epsilon\) are obtained. The

theory is well described in the recent literature8 and has been validated against molecular dynamics simulations in model alloys using semi-empirical interatomic potentials.7 To make the

theory computationally accessible, it has been simplified through the use of elasticity theory.7 In this limit, the solute/dislocation interaction energy of a type-_n_ solute in the alloy is

modeled as −_p_(_x_, _y_)Δ_V__n_ where _p_(_x_, _y_) is the elastic pressure field at solute position (_x_, _y_) due to a dislocation centered at the origin and Δ_V__n_ is the average

misfit volume of the type-_n_ solute in the alloy. With this simplification, the theory becomes analytic for fcc alloys. Specifically, the zero-stress activation barrier Δ_E__b_ and the

zero-temperature shear yield stress _τ__y_0 (stress at which the energy barrier is zero) are $${\mathrm{\Delta }}E_b = 2.5785\left[ {\frac{{\mathrm{\Gamma }}}{{b^2}}}

\right]^{\frac{1}{3}}b^3P^{\frac{2}{3}}\delta ^{\frac{2}{3}},\\ \tau _{y0} = 0.04865\left[ {\frac{{\mathrm{\Gamma }}}{{b^2}}} \right]^{ - \frac{1}{3}}P^{\frac{4}{3}}\delta ^{\frac{4}{3}},$$

(1) where _b_ is the dislocation Burgers vector, and $$\delta = \sqrt {2\mathop {\sum}\limits_n c_n{\mathrm{\Delta }}V_n^2{\mathrm{/}}(9b^6)}$$ (2) is the well-known _δ_-parameter that

describes the collective effect of the misfit volumes of all the elements in the alloy. In addition, $$\begin{array}{l}{\mathrm{\Gamma }} = \alpha \mu _{110/111}b^2,\\ \mu _{110/111} =

(C_{11} - C_{12} + C_{44}){\mathrm{/}}3\end{array}$$ (3) are the dislocation line tension and shear modulus for fcc slip on the {111} plane in the 〈110〉 direction expressed in terms of the

standard cubic elastic constants, respectively. The dimensionless line tension parameter _α_ = 1/8 is accurate for several fcc metals. The last quantity in Eq. (1) is an elastic coefficient

_P_ = _P_(_C__ij_) associated with the anisotropic dislocation pressure field. For fcc metals, _P_ can be written in terms of appropriate averaged isotropic elastic constants _μ_ave and

_ν_ave as $$P\left( {C_{11},C_{12},C_{44}} \right) = \mu ^{{\mathrm{ave}}}\frac{{1 + \nu ^{{\mathrm{ave}}}}}{{1 - \nu ^{{\mathrm{ave}}}}}.$$ (4) Previous applications of the model used

experimentally measured isotropic elastic constants of the alloy, _μ_expt and _ν_expt.7,9,10 A forthcoming full anisotropic analysis will demonstrate that the use of the Voigt-averaged

elastic constants $$\mu ^V = \left( {C_{11} - C_{12} + 3C_{44}} \right){\mathrm{/}}5,\\ \nu ^V = \frac{{3B - 2\mu ^V}}{{2(3B + \mu ^V)}},\\ B = \left( {C_{11} + 2C_{12}}

\right){\mathrm{/}}3,$$ (5) where _B_ is the bulk modulus agrees with the full anisotropic model to within ~3% over a wide range of elastic anisotropy. We will thus use the Voigt-averaged

values. The resulting strength versus temperature _T_ and strain-rate \(\dot \epsilon\) is $$\tau _y(T,\dot \epsilon ) = \tau _{y0}(T)\left[ {1 - \left( {\frac{{k_BT}}{{{\mathrm{\Delta

}}E_b(T)}}ln\frac{{\dot \epsilon _0}}{{\dot \epsilon }}} \right)^{\frac{2}{3}}} \right]{\mathrm{,}}$$ (6) where \(\dot \epsilon _0\) = 104 s−1 is a reference strain-rate determined by the

dislocation density and other factors. The properties entering _τ__y_0(_T_) and Δ_E__b_(_T_) should in principle be computed at the temperature of interest, especially the elastic constants.

We discuss this further in Section “Yield strength prediction.” Experiments are typically performed in uniaxial tension on random untextured polycrystalline specimens. The measured uniaxial

yield stress is related to the shear yield stress as _σ__y_ = _Mτ__y_ where _M_ = 3.06 is the Taylor factor for random fcc polycrystals. Dislocations in fcc metals dissociate into two

partial dislocations separated by a stacking fault. The two partials are separated by a distance _d_ and each partial dislocation also spreads across a few atoms with the spreading

characterized by a Gaussian function with standard deviation _σ_. This complex dislocation structure should thus influence the strengthening, since the solutes interact with the actual

dislocation structure. Full analysis of the elastic theory as a function of _d_ reveals that the strength is nearly _independent_ of _d_ for _d_ ≳ 6.5_b_. The spreading parameter _σ_ has

been examined in several atomistic simulations using interatomic potentials and the typical values are 1.5 ≤ _σ_/_b_ ≤ 2.0. The analytic model above (Eq. (1)) with the numerical coefficients

given corresponds to a sufficiently large partial separation _d_ ≳ 6.5_b_ and _σ_/_b_ = 1.5. The use of these values has yielded very good predictions in comparison with experiments.7,9,10

From the above summary, we see that the required inputs to the analytic theory are the fcc lattice constant (_a_0 with \(b = a_0{\mathrm{/}}\sqrt 2\)), the elastic constants (_C_11, _C_12,

_C_44), and the solute misfit volumes (Δ_V__n_) at the alloy composition {_c__n_}. The partial separation must also be _d_ ≳ 6.5_b_, which can be well-estimated in anisotropic elasticity as

_d_ = _K_/_γ_ssf where _γ_ssf is the stable stacking fault energy of the alloy and _K_ is an anisotropic elastic parameter computed exactly in terms of dislocation character, elastic

constants, and Burgers vector.11,12,13,14,15 All of the above quantities can be computed by first-principles using the methods described in Section “DFT methodology”, leading to yield

strength predictions given in Section “Yield strength prediction.” MISFIT VOLUMES We consider, in general, an alloy containing _N_elem types of alloying elements at concentrations {_c__n_}.

The average misfit volume of a type-_n_ atom in the random alloy can be conceptually defined as $${\mathrm{\Delta }}V_n = \mathop {\sum}\limits_m {\kern 1pt} c_m\left\langle {{\mathrm{\Delta

}}V^{n/m}} \right\rangle ,$$ (7) where 〈Δ_V__n_/_m_〉 is the volume change caused by replacing one type-_m_ atom with type-_n_ atom and with the brackets indicating averaging over many

different such replacements where the atom of interest has different surrounding atomic environments.16 Performing this actual procedure is computationally costly and unnecessary, but the

definition remains useful. Operationally, we consider a macroscopic sample with _N_tot atoms and total volume \(V_0^{{\mathrm{tot}}}\) at the alloy composition. We then add Δ_N__n_ type-_n_

atoms by replacing Δ_N__m_ = −Δ_N__n__c__m_/(1 − _c__n_) type-_m_ atoms for all _m_ ≠ _n_ at randomly chosen type-_m_ atom sites in the sample. The volume of the new random alloy is

\(V^{{\mathrm{tot}}} = V_0^{{\mathrm{tot}}} + \mathop {\sum}\nolimits_m \left( { - {\mathrm{\Delta }}N_m} \right)\left\langle {{\mathrm{\Delta }}V^{n/m}} \right\rangle\). The average atomic

volume _V_ = _V_tot/_N_tot can then be expressed as $$V = V_0 + {\mathrm{\Delta }}V_nx_{\mathrm{s}},\\ {\mathrm{with}}\,x_s = \frac{{{\mathrm{\Delta }}N_n}}{{N^{{\mathrm{tot}}}(1 - c_n)}}.$$

(8) After adding the additional type-_n_ atoms, the changes of the elemental compositions are (1 − _c__n_)_x__s_ for the type-_n_ atom and −_c__m__x__s_ for all the other element types _m_ 

≠ _n_. The new alloy can thus be considered as a pseudo-binary alloy with a formula \({\mathrm{[type - }}n\,{\mathrm{atom]}}_{x_s}\left[ {{\mathrm{matrix}}\left\{ {c_n} \right\}} \right]_{1

- x_s}\), where the matrix is the original alloy and the “solutes” are the extra type-_n_ atoms introduced into the effective matrix. Similarly, Δ_N__n_ type-_n_ atoms can be removed

(Δ_N__n_ < 0) with other atom types added as Δ_N__m_ = −Δ_N__n__c__m_/(1 − _c__n_) for all _m_ ≠ _n_. The total volume is then \(V^{{\mathrm{tot}}} = V_0^{{\mathrm{tot}}} + \mathop

{\sum}\nolimits_m {\kern 1pt} {\mathrm{\Delta }}N_m\left\langle {{\mathrm{\Delta }}V^{m/n}} \right\rangle\), with 〈Δ_V__m_/_n_〉 = −〈Δ_V__n_/_m_〉. This procedure leads again to Eq. (8), but

with _x__s_ being negative. Therefore, measuring the sample volume at different values of \(\left| {x_s} \right| \ll 1\) for all solute types enables the determination of the desired misfit

volumes Δ_V__n_ for all solutes in the alloy at the composition of interest. To compute the average atomic volumes _V_(_x__s_) of the various pseudo-binary random alloys, and the lattice

constant and elastic constants at the central composition, there are various methods, such as cluster expansion (CE) method,17 small set of ordered structures (SSOS) method,18 similar local

atomic environment (SLAE) method,19 etc. To date, the two most widely used methods are the special quasi-random structures (SQS)20 and the coherent potential approximation (CPA).21 The

supercell method combined with the concept of SQS has the very important advantage that explicit local lattice distortions within the SQS supercell are possible. On the other hand, the CPA

method can mimic the perfect chemical disorder within one primitive cell. In this work, we need to compute the atomic volumes, lattice constants, and elastic constants precisely, where the

local lattice distortion should be explicitly considered. Previous literature has shown that the local lattice relaxation has a significant effect on the alloy properties, e.g., formation

energy.22 We also wish to assess accuracy of the computed quantities, which can be accomplished using multiple realizations and sizes of the SQS cells. The SQS method is strongly preferred

for these reasons, and is used here. Application of the above strategy to the equi-composition 6-component (ABCDEF) alloy such as RhIrPdPtNiCu alloy is achieved as follows. We start with a

supercell \(\left( {{\mathrm{ABCDEF}}} \right)_{N_0}\) (total number of atoms _N_tot = 6_N_0). We then add 5_N_1 atoms of type A and remove other atom types equally, leading to the

pseudo-binary composition \({\mathrm{A}}_{6N_1}\left( {{\mathrm{ABCDEF}}} \right)_{N_0 - N_1}\) with _x__s_ = 6_N_1/_N_tot. Similarly, removing 5_N_1 atoms of type A and adding the other

elements equally leads to the pseudo-binary composition \({\mathrm{A}}_{ - 6N_1}\left( {{\mathrm{ABCDEF}}} \right)_{N_0 + N_1}\) and _x__s_ = −6_N_1/_N_tot. This is repeated for each

individual atom type (B, C, …) in the alloy. In fact, there is no actual need to use the same supercell when adding/removing atoms; this is just the clearest way to understand the process.

Then, the pseudo-binary formula becomes of particularly high value. In practice, only the quantities 6_N_1 and _N_0 − _N_1 (or −6_N_1, _N_0 + _N_1) need to be integers. For example, in Table

1, the _x__s_ = −3.1 at.% case is achieved using _N_1 = 2/3 and _N_0 = 64/3, corresponding to −6_N_1 = −4, _N_0 + _N_1 = 22 with _N_tot = 128. The pseudo-binary concept thus leads to

considerable flexibility in the choice of supercell size for each individual composition. The choice of the supercell composition formulas is flexible but a few guidelines are helpful.

First, _N_tot should be neither too large nor too small. A large value is computationally costly while a small value might be insufficient for achieving an SQS of high quality. According to

the literature, good representations of chemical disorder can usually be achieved using approximately several tens of atoms.22 Second, |_x__s_| should be neither too large nor too small. If

too large, the volume change might exceed the domain of linear changes around the central composition. If too small, the uncertainty due to the configurational randomness will greatly

increase the uncertainty in the deduced misfit volumes. The supercells and formula units used here are shown in Table 1, and satisfy 100 < _N_tot < 150 and 0.03 < |_x__s_| < 

0.06. For each composition, the SQSs are generated _independently_ using the atat code.23 For the 6-element alloys here, SQS generation at the necessary supercell sizes of 100 ~ 150 atoms is

computationally intensive.18 Fortunately, the resulting structures can be used multiple times by switching the atom types. In addition, these SQSs can immediately provide candidate SQSs for

other alloys having fewer components with compositions in multiples of 1/6, such as A2BCDE, A4B2, etc. For a given 6-component SQS, there are many different possible SQS structures for

alloys with fewer components. The best SQS from among the possibilities is easily determined by evaluating the SQS quality, e.g., the SQS error using available error estimates.24 The present

SQSs can therefore be easily used for studying new alloys without any further time-consuming searches for new SQSs. For this reason, we provide the exact SQSs used here

(https://doi.org/10.24435/materialscloud:2018.0019/v1). With the SQS construction as described above, the equilibrium atomic volumes are computed by minimizing the total energy versus volume

with full relaxation of all ions and supercell shape. We perform calculations for multiple samples at the same and/or various _x__s_ to improve the overall accuracy of the final misfit

volumes. From the entire set of DFT-computed equilibrium atomic volumes, we then perform a linear regression with one constraint \(\mathop {\sum}\nolimits_n {\kern 1pt} c_n{\mathrm{\Delta

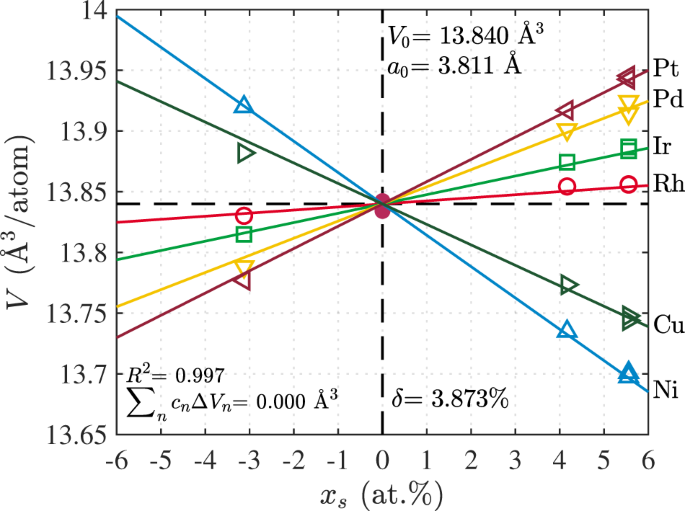
}}V_n = 0\) to obtain the misfit volumes Δ_V__n_ for all solutes and the atomic volume _V_0 at the desired composition {_c__n_}. Figure 1 shows the computed atomic volumes versus

compositions _x__s_ for all alloys studied here around the RhIrPdPtNiCu composition. We obtain the lattice constant and misfit volumes shown in Table 2. Importantly, from the totality of the

data computed, we can compute the 95% confidence intervals for the lattice constant (±0.00017 Å) and misfit volumes (±0.093 Å3), respectively. The misfit quantity _δ_ in the theory for

yield strength is then computed as _δ_ = 3.873%, as shown in Fig. 1 and summarized in Table 2, with 95% confidence interval within ±0.2%. ELASTIC CONSTANTS The elastic constants of the alloy

are computed starting from the equilibrium states of the two SQS structures of the random RhIrPdPtNiCu alloy containing 108 and 144 atoms, respectively. These systems have small initial

(Pulay) stresses \(\sigma _i^0\) (_i_ = 1...6) using the Reuss contracted notation. We use the well-established stress method.25 Six linearly independent strain tensors are applied (non-zero

components = 0.002) and the corresponding stress tensors are computed in DFT. The elastic constants are then computed from \(\sigma _i - \sigma _i^0 = C_{ij}\epsilon _j\). In one

least-squares fitting, we calculate all 21 _C__ij_ components of _C__ij_,108 and _C__ij_,144 (in GPa). The elastic constants expressed in the standard 6 × 6 Voigt matrix notation for the two

different SQS cells are $$\left[ {\begin{array}{*{20}{c}} {286} & {176} & {176} & { - 4} & { - 2} & { - 3} \\ {} & {296} & {182} & { - 4} & 1 & { -

3} \\ {} & {} & {297} & { - 5} & 0 & { - 2} \\ {} & {} & {} & {111} & { - 2} & { - 2} \\ {} & {{\mathrm{Sym}}} & {} & {} & {113} &

{ - 2} \\ {} & {} & {} & {} & {} & {113} \end{array}} \right],\left[ {\begin{array}{*{20}{c}} {284} & {172} & {171} & { - 1} & { - 3} & { - 2} \\ {}

& {288} & {176} & { - 1} & 0 & { - 1} \\ {} & {} & {286} & 0 & { - 2} & { - 1} \\ {} & {} & {} & {111} & { - 1} & 0 \\ {} &

{{\mathrm{Sym}}} & {} & {} & {110} & { - 2} \\ {} & {} & {} & {} & {} & {112} \end{array}} \right].$$ The fcc-symmetry is broken in these small cells of

random alloys. To obtain the fcc constants _C__ij_, we take the averages of all the fcc-symmetry-equivalent components over both structures. The remaining _C__ij_ components are set to zero

(the averages being negligible). The resulting values are _C_11 = 289 GPa, _C_12 = 176 GPa, and _C_44 = 112 GPa. Since each elastic constant is an average over six values, we can compute the

95% confidence interval, which results in ~±2% of the mean value. The bulk modulus _B_ = (_C_11 + 2_C_12)/3 = 214 GPa obtained from the averaging is very close to the values of _B_ computed

from the energy versus volume for the two structures (215 and 214 GPa, respectively). This alloy is moderately anisotropic, with Zener anisotropy index _A_ = 2_C_44/(_C_11 − _C_12) = 1.98.

The Voigt-averaged elastic constants that enter the strength theory are _μ__V_ = 90 GPa and _ν__V_ = 0.316. For this value of _A_, the full anisotropic value of _P_ in Eq. (1) is only ~0.5%

smaller than the isotropic approximation using these Voigt averages. The shear modulus used in the line tension is computed as _μ_110/111 = 75 GPa. Note that the _measured_ shear modulus of

the polycrystalline material is expected to be closer to the Voigt-Reuss-Hill average _μ_VRH = 85 GPa.26 This value does not enter the strength theory and indicates the typical error that

might be expected when using an experimentally measured shear modulus. All of the various elastic constants (anisotropic and associated isotropic average) for RhIrPdPtNiCu are shown in Table

3. STABLE STACKING FAULT ENERGY AND PARTIAL SEPARATION The stable stacking fault energy _γ_ssf is computed using the ANNNI model. In this model, _γ_ssf is related to the difference between

hcp and fcc cohesive energies of the alloy as \(\gamma _{{\mathrm{ssf}}} = 2\left( {E_0^{{\mathrm{hcp}}} - E_0^{{\mathrm{fcc}}}} \right){\mathrm{/}}A_0^{{\mathrm{fcc}}}\), where

\(E_0^{{\mathrm{hcp}}}\) and \(E_0^{{\mathrm{fcc}}}\) are the atomic energy for the fully relaxed hcp and fcc structures, respectively. \(A_0^{{\mathrm{fcc}}}\) is the fcc atomic area on the

stacking fault plane. Direct computation of _γ_ssf in random alloys is deemed likely to have large fluctuations since it is a planar defect energy computed from two bulk energies of

3-dimensional random structures.27 Furthermore, application of the analytic strengthening theory requires only that _γ_ssf be sufficient to ensure sufficiently large partial dislocation

separation _d_. Benchmark DFT computations of _γ_ssf for the individual elemental metals using the direct tilted-cell method28 and ANNNI model show differences (which can be positive or

negative) within ±20 mJ/m2. The differences arise, in part, from the two fcc/hcp interfacial energies that are not considered in the ANNNI model.29 We can thus anticipate that application of

the ANNNI model to the 6-component alloy will have a similar level of uncertainty. The formation energy of the fcc HEA phase is obtained from the previous DFT calcuations. For all fcc

samples, we have the equilibrium energies. Performing a linear regression to the DFT energy data, analogous to what was done for the equilibrium atomic volumes in Fig. 1, gives the formation

energy of fcc RhIrPdPtNiCu as \(E_0^{{\mathrm{fcc}}} = 34\) meV/atom, relative to the compositional average of the pure metal atomic energies in the fcc phase. The positive formation energy

indicates that the single-phase RhIrPdPtNiCu HEA is either entropically stabilized or metastable. This result is in contrast to a negative formation energy roughly estimated from an

empirical literature model.5 To calculate \(E_0^{{\mathrm{hcp}}}\), we use the process employed for fcc at the composition of interest. We create the hcp SQSs for the HEA

(https://doi.org/10.24435/materialscloud:2018.0019/v1), and perform DFT calculations to obtain the ground state energy on the compositions surrounding the central composition to improve the

accuracy, and then perform linear regression to the DFT energy data for hcp structures. The resulting formation energy of RhIrPdPtNiCu in hcp phase is \(E_0^{{\mathrm{hcp}}} = 61\) meV/atom

relative to the same compositional average of the pure metal atomic energies in the fcc phase. With \(A_0^{{\mathrm{fcc}}} = (\sqrt 3 {\mathrm{/}}4)a_0^2\), the ANNNI model yields a stable

stacking fault energy _γ_ssf = 138 mJ/m2 for RhIrPdPtNiCu. The uncertainty in _γ_ssf is determined from the 95% confidence intervals of \(E_0^{{\mathrm{fcc}}}\) and \(E_0^{{\mathrm{hcp}}}\),

which are ±1 and ±2 meV, respectively. Therefore, the uncertainty in the DFT result itself for _γ_ssf is about ±15 mJ/m2. Combined with the intrinsic error/uncertainty of the ANNNI model, a

conservative estimate of the uncertainty in the stable stacking fault energy is ~±35 mJ/m2. Finally, using the computed anisotropic elastic constants and lattice constant, the elastic

parameter is _K_ = 0.180 eV/Å and the estimated partial separation is then _d_ = _K_/_γ_ssf = 7.8_b_. Considering the uncertainty in _γ_ssf, the corresponding partial separation ranges from

6.2_b_ to 10.4_b_. This estimation is an upper bound of the uncertainty since the value ±20 mJ/m2 is probably higher than the true value in the HEA. The analysis thus generally satisfies the

requirement _d_ ≳ 6.5_b_ for applying the analytic solute strengthening model above. YIELD STRENGTH PREDICTION With all of the necessary material properties computed via DFT as described in

the previous section, the yield strength of the alloy can be predicted. The experiments were performed at _T_ = 300 K and strain-rate \(\dot \epsilon\) = 10−4 s−1. As shown in Table 3, the

predicted strength using only the DFT-computed inputs is _σ__y_ = 583 MPa. The uncertainty in this prediction due to the uncertainties in DFT-computed materials parameters is small. Using

the 95% confidence intervals of the lattice constant, misfit volumes, and elastic constants, the 95% confidence interval for the strength prediction is ~±10% of the above mean value. This

uncertainty is due to the configurational randomness in the computations, at the SQSs qualities that we achieve. The average prediction of 583 MPa is in very good agreement with the single

experimental value of 527 MPa. While there is only one experimental data point, the yield strength of well-characterized alloys usually has small scatter. As analyzed in previous work using

approximate methods,10 this as-cast alloy has two different phases but these phases have very similar lattice constants and estimated strengths. The above experimental value is thus likely

close to the “true value” of a single-phase homogenous alloy. There are a few other aspects that could affect the strength prediction here. First, the DFT-calculated elastic constants must

have some (unknown) error, as demonstrated by the deviations between DFT and experiment for the elemental metals. Here, we might expect that the Perdew-Burke-Ernzerhof (PBE) DFT predictions

of the elastic moduli _C__ij_ of the HEA are slightly lower than the (unknown) true experimental values due to the underestimate of the moduli of elemental Pd and Pt, as discussed in Section

“DFT methodology.” Second, the experiments are at room temperature and so the room-temperature elastic constants should be used in the predictions. Room-temperature calculations are

possible but computationally onerous, and so here we make reasonable estimates based on the elemental values. In experiments, the elastic constants _C__ij_ of the pure metals all decrease,

but by less than 10% from _T_ = 0 K to _T_ = 300 K. Therefore, the yield strength predictions made using the _T_ = 0 K elastic constants are likely <10% too high. Thus, use of the

(unknown) _T_ = 300 K elastic constants would bring the predictions closer to the experimental value. For purposes of efficient identification of trends for alloy design, we advocate the use

of the easily computed _T_ = 0 K elastic constants, with temperature effects at room temperature estimated from a concentration-weighted average of the elemental elastic constants. Third,

the lattice constant _a_0 and the _δ_-parameter are also temperature-dependent. Applying Vegard’s law (defined below) using the temperature-dependent lattice constants of the pure metals to

estimate both the alloy volume and solute misfit volumes at finite temperature, we find that the overall _δ_-parameter decreases by <2% with increasing temperature. The thermal expansion

effects can thus be safely neglected. Although there are uncertainties in the DFT-computed properties and the temperature dependencies, there are no adjustable/fitted parameters in the

model. Overall, we thus consider the predictions to be robust and the agreement indicative of the applicability of the theory. DISCUSSION The present methodology can be expanded to scan over

a wide range of the composition space so as to predict optimized composition(s) with the highest yield strength(s). Suppose we have a database of the atomic volumes over a set of

equi-spaced compositions spanning the entire configurational space. Then one could fit the entire set to some overall function of the compositions, i.e., _V_({_c__n_}). The misfit volume of

type-_n_ atom at composition {_c__n_} could be computed by taking the derivative respect to _x__s_ in the direction of {(1 − _c__n_) for _n_, −_c__m_ for _m_ ≠ _n_}, i.e., $${\mathrm{\Delta

}}V_n = \frac{{V\left( {\left\{ {c_n + \left( {1 - c_n} \right)x_s{\mathrm{,}}c_m - c_mx_s} \right\}} \right) - V\left( {\left\{ {c_n} \right\}} \right)}}{{x_s}},$$ (9) with _x__s_ → 0.

Here, the challenging task is the computation of the data set. In order to have a quantitative estimate of the size of the database, we assume that the well-spaced compositions consist of

elemental concentrations spanning from 0 to 100% by the step of 10%. For senary alloys studied here, the database needs 3003 different compositions for SQS sizes of ~100 atoms; this is not

computationally feasible at present. However, for quaternary and ternary alloys, such a database requires 286 and 66 compositions, respectively, and so could be achieved computationally. In

any case, the computation of the data set remains demanding but the methodology for the misfit volumes remains useful and will become more feasible as computational power increases. Given

the combinatoric challenge of performing DFT over the huge composition space of a many-component alloy, it is very useful to consider other more-approximate but more-efficient approaches.

One such approach is by assuming Vegard’s law and assuming a simple rule-of-mixtures for elastic constants.10 Then only the lattice constants and elastic constants of the elemental metals

are needed in the crystal structure of the HEA. These quantities are computationally trivial to obtain if all the elements are metastable in the HEA crystal structure. Vegard’s law uses the

atomic volumes \(V_0^{(n)}\) of the individual elements and predicts the atomic volume of the alloy as \(V_0^{{\mathrm{Vegard}}} = \mathop {\sum}\nolimits_n {\kern 1pt} c_nV_0^{(n)}\). The

misfit volumes follow as \({\mathrm{\Delta }}V_n^{{\mathrm{Vegard}}} = V_0^{(n)} - V_0^{{\mathrm{Vegard}}}\). The rule-of-mixtures (ROM) estimate for the elastic constants is simply

\(C_{ij}^{{\mathrm{ROM}}} = \mathop {\sum}\nolimits_n {\kern 1pt} c_nC_{ij}^{(n)}\) and yields a rule-of-mixtures Voigt average for the required _μ_ and _ν_. With DFT results computed

explicitly here for fcc RhIrPdPtNiCu, we can assess the accuracy of such a simple model since all the elements are stable in the fcc structure. Using the DFT-computed atomic volumes for the

constituents of the RhIrPdPtNiCu, Vegard’s law yields _δ_ = 4.193%. This is ~8% larger than the direct DFT result of _δ_ = 3.873% on the actual random alloy, as compared in Table 2.

Similarly, using the DFT values for the elastic constants of the elements, the alloy ROM values are \(C_{11}^{{\mathrm{ROM}}} = 326\) GPa, \(C_{12}^{{\mathrm{ROM}}} = 177\) GPa and

\(C_{44}^{{\mathrm{ROM}}} = 131\) GPa. Two of these values are ~15% larger than the DFT-computed alloy values (Table 3). The resulting Voigt estimate _μ__V_ is then ~20% larger (108 GPa vs.

90 GPa). With the approximate estimates for both _δ_ and _μ__V_ being larger than the true DFT-computed properties for the alloy, the predicted strength using the approximate model is 775 

MPa, which is rather larger than the full prediction. The approximate approach above is thus of limited value for _quantitative_ prediction in this family of alloys. However, the approximate

approach may be too high mainly due to the moduli estimates, and the moduli estimates may be systematically high for other composition in the configurational space. This can be further

validated with the calculations at other {_c__n_}. The approximate approach may be useful only for rapid _relative_ assessment of the relative strengths of alloy compositions. But even such

a relative assessment can then point to a limited set of promising new alloy compositions that could be studied _quantitatively_ using the computationally intensive but chemically accurate

DFT calculations proposed in this work. In summary, we have presented a general approach to DFT-level computations of the properties necessary to make strength predictions in HEAs and other

random alloys using a recent analytic theory. The theory requires solute misfit volumes, alloy lattice constant, elastic constants, and stable stacking fault energy, all of which are

accessible within current DFT capabilities. The DFT computational methodology for misfit volumes in multicomponent random alloys is new and general. Executing the methodology on the fcc

RhIrPdPtNiCu HEA, we obtain parameter-free predictions of the yield strength with no experimental inputs and find very good agreement with the experimental strength. We are also able to

assess uncertainties in the approach and to assess concepts for highly efficient scanning of the huge composition space of HEAs. This work thus connects alloy composition to yield strength,

establishing a general first-principles methodology for the computationally guided design of high-strength alloys. METHODS DFT METHODOLOGY All first-principles calculations are performed

using DFT as implemented in the vasp code30 within the generalized gradient approximation (GGA) and using the PBE XC functional.31 The core electrons are replaced by the projector augmented

wave (PAW) pseudopotentials.32 The valence-electron eigenstates are expanded using a spin-polarized plane wave basis set with a cutoff energy 550 eV. A first-order Methfessel-Paxton method33

with smearing parameter 0.2 eV is used. In reciprocal space, a Γ-centered Monkhorst-Pack34 _k_-mesh is used with line density consistent across all geometries. The interval between the

neighboring _k_-points along each reciprocal lattice vector B_j_ is 0.02 Å−1 (in vasp, A_i_ · B_j_ = _δ__ij_). This _k_-mesh density leads to, for example, 14 × 14 × 14 for Ni and Cu in the

fcc cubic unit cell, and 13 × 13 × 13 for the other four elements. Ionic forces are relaxed to less than 1 meV/Å, corresponding to a stress tolerance of ~0.01 GPa in vasp. Benchmark

calculations of the lattice constant, elastic constants, and stable stacking fault energy for the pure metal elements are in very good agreement with previous DFT literature.35,36,37 In the

benchmark results for the elements, the PBE functional predicts the bulk moduli for Rh, Ir, Ni, and Cu within ±5% of experiment values but underestimates the bulk moduli of Pd and Pt by ~13%

(169 GPa vs. 195 GPa for Pd, 249 GPa vs. 288 GPa for Pt; see ref. 35 (Table S25.3) and ref. 38). Results using the PBEsol functional39 improve the results for Pd and Pt relative to

experiments but increase the differences between DFT and experiments for the other four elements in the alloy. These trends are already known in the literature. For this study, we use PBE so

as to capture the better agreement with experiment for four of the six alloying elements studied here. DATA AVAILABILITY The data that support the findings of this study are available from

the corresponding authors upon reasonable request. The SQSs used in this work are provided in (https://doi.org/10.24435/materialscloud:2018.0019/v1). REFERENCES * Miracle, D. B. &

Senkov, O. N. A critical review of high entropy alloys and related concepts. _Acta Mater._ 122, 448–511 (2017). Article  CAS  Google Scholar  * Gludovatz, B. et al. A fracture-resistant

high-entropy alloy for cryogenic applications. _Science_ 345, 1153–1158 (2014). Article  CAS  Google Scholar  * Miao, J. et al. The evolution of the deformation substructure in a Ni-Co-Cr

equiatomic solid solution alloy. _Acta Mater._ 132, 35–48 (2017). Article  CAS  Google Scholar  * Li, Z. & Raabe, D. Strong and ductile non-equiatomic high-entropy alloys: Design,

processing, microstructure, and mechanical properties. _JOM_ 69, 2099–2106 (2017). Article  CAS  Google Scholar  * Sohn, S. et al. Noble metal high entropy alloys. _Scr. Mater._ 126, 29–32

(2017). Article  CAS  Google Scholar  * Kimura, Y., Inoue, T., Yin, F. & Tsuzaki, K. Inverse temperature dependence of toughness in an ultrafine grain-structure steel. _Science_ 320,

1057–1060 (2008). Article  CAS  Google Scholar  * Varvenne, C., Luque, A. & Curtin, W. A. Theory of strengthening in fcc high entropy alloys. _Acta Mater._ 118, 164–176 (2016). Article 

CAS  Google Scholar  * Varvenne, C., Leyson, G. P. M., Ghazisaeidi, M. & Curtin, W. A. Solute strengthening in random alloys. _Acta Mater._ 124, 660–683 (2017). Article  CAS  Google

Scholar  * Varvenne, C. & Curtin, W. A. Strengthening of high entropy alloys by dilute solute additions: CoCrFeNiAlx and CoCrFeNiMnAlx alloys. _Scr. Mater._ 138, 92–95 (2017). Article 

CAS  Google Scholar  * Varvenne, C. & Curtin, W. A. Predicting yield strengths of noble metal high entropy alloys. _Scr. Mater._ 142, 92–95 (2018). Article  CAS  Google Scholar  * Wu,

Z., Yin, B. & Curtin, W. A. Energetics of dislocation transformations in hcp metals. _Acta Mater._ 119, 203–217 (2016). Article  CAS  Google Scholar  * Anderson, P. M., Hirth, J. P.

& Lothe, J. _Theory of dislocations_ (Cambridge University Press,

https://www.cambridge.org/ch/academic/subjects/engineering/materials-science/theory-dislocations-3rdedition?format=HB&isbn=9780521864367, 2017). * Ting, T. C. T. _Anisotropic elasticity:

Theory and applications_ (Oxford University Press,

https://global.oup.com/academic/product/anisotropic-elasticity-9780195074475?q=Anisotropic%20Elasticity:%20Theory%20and%20Applications&lang=en&cc=ch, 1996). * Stroh, A. N.

Dislocations and cracks in anisotropic elasticity. _Philos. Mag._ 3, 625–646 (1958). Article  CAS  Google Scholar  * Bacon, D., Barnett, D. & Scattergood, R. Anisotropic continuum theory

of lattice defects. _Prog. Mater. Sci._ 23, 51–262 (1980). Article  Google Scholar  * Varvenne, C., Luque, A., Nöhring, W. G. & Curtin, W. A. Average-atom interatomic potential for

random alloys. _Phys. Rev. B_ 93, 104201 (2016). Article  Google Scholar  * Sanchez, J. M., Ducastelle, F. & Gratias, D. Generalized cluster description of multicomponent systems. _Phys.

A Stat. Mech. its Appl._ 128, 334–350 (1984). Article  Google Scholar  * Jiang, C. & Uberuaga, B. P. Efficient Ab initio modeling of random multicomponent alloys. _Phys. Rev. Lett._

116, 105501 (2016). Article  Google Scholar  * Song, H. et al. Local lattice distortion in high-entropy alloys. _Phys. Rev. Mater._ 1, 023404 (2017). Article  Google Scholar  * Zunger, A.,

Wei, S. -H., Ferreira, L. G. & Bernard, J. E. Special quasirandom structures. _Phys. Rev. Lett._ 65, 353–356 (1990). Article  CAS  Google Scholar  * Vitos, L., Abrikosov, I. A. &

Johansson, B. Anisotropic lattice distortions in random alloys from first-principles theory. _Phys. Rev. Lett._ 87, 156401 (2001). Article  CAS  Google Scholar  * Ikeda, Y., Grabowski, B.

& Körmann, F. Ab initio phase stabilities and mechanical properties of multicomponent alloys: A comprehensive review for high entropy alloys and compositionally complex alloys. _Mater.

Charact._ 147, 464–511 (2019). Article  CAS  Google Scholar  * Van De Walle, A. et al. Efficient stochastic generation of special quasirandom structures. _Calphad Comput. Coupling Phase

Diagr. Thermochem._ 42, 13–18 (2013). Article  Google Scholar  * Von Pezold, J., Dick, A., Friák, M. & Neugebauer, J. Generation and performance of special quasirandom structures for

studying the elastic properties of random alloys: Application to Al-Ti. _Phys. Rev. B_ 81, 094203 (2010). Article  Google Scholar  * Le Page, Y. & Saxe, P. Symmetry-general least-squares

extraction of elastic data for strained materials from ab initio calculations of stress. _Phys. Rev. B_ 65, 104104 (2002). Article  Google Scholar  * Hill, R. The elastic behaviour of a

crystalline aggregate. _Proc. Phys. Soc. Sect. A_ 65, 349–354 (1952). Article  Google Scholar  * Zhao, S., Stocks, G. M. & Zhang, Y. Stacking fault energies of face-centered cubic

concentrated solid solution alloys. _Acta Mater._ 134, 334–345 (2017). Article  CAS  Google Scholar  * Yin, B., Wu, Z. & Curtin, W. A. Comprehensive first-principles study of stable

stacking faults in hcp metals. _Acta Mater._ 123, 223–234 (2017). Article  CAS  Google Scholar  * Li, R. et al. Stacking fault energy of face-centered cubic metals: Thermodynamic and ab

initio approaches. _J. Phys. Condens. Matter_ 28, 395001 (2016). Article  Google Scholar  * Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy

calculations using a plane-wave basis set. _Phys. Rev. B_ 54, 11169–11186 (1996). Article  CAS  Google Scholar  * Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient

approximation made simple. _Phys. Rev. Lett._ 77, 3865–3868 (1996). Article  CAS  Google Scholar  * Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector

augmented-wave method. _Phys. Rev. B_ 59, 1758–1775 (1999). Article  CAS  Google Scholar  * Methfessel, M. & Paxton, A. T. High-precision sampling for Brillouin-zone integration in

metals. _Phys. Rev. B_ 40, 3616–3621 (1989). Article  CAS  Google Scholar  * Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. _Phys. Rev. B_ 13, 5188–5192

(1976). Article  Google Scholar  * Lejaeghere, K. et al. Reproducibility in density functional theory calculations of solids. _Science_ 351, aad3000 (2016). Article  Google Scholar  * Shang,

S. L. et al. First-principles calculations of pure elements: Equations of state and elastic stiffness constants. _Comput. Mater. Sci._ 48, 813–826 (2010). Article  CAS  Google Scholar  *

Wu, X. Z., Wang, R., Wang, S. F. & Wei, Q. Y. Ab initio calculations of generalized-stacking-fault energy surfaces and surface energies for FCC metals. _Appl. Surf. Sci._ 256, 6345–6349

(2010). Article  CAS  Google Scholar  * Simmons, G. & Wang, H. _Single Crystal Elastic Constants and Calculated Aggregate Properties: A Handbook_ (The M.I.T. Press,

https://mitpress.mit.edu/books/single-crystal-elastic-constants-and-calculated-aggregate-properties-secondedition, 1971). * Perdew, J. P. et al. Restoring the density-gradient expansion for

exchange in solids and surfaces. _Phys. Rev. Lett._ 100, 136406 (2008). Article  Google Scholar  Download references ACKNOWLEDGEMENTS This research was supported by the NCCR MARVEL, funded

by the Swiss National Science Foundation. We also acknowledge support of high-performance computing provided by Scientific IT and Application Support (SCITAS) at EPFL. AUTHOR INFORMATION

AUTHORS AND AFFILIATIONS * Laboratory for Multiscale Mechanics Modeling (LAMMM) and National Centre for Computational Design and Discovery of Novel Materials (NCCR MARVEL), École

Polytechnique Fédérale de Lausanne, 1015, Lausanne, Switzerland Binglun Yin & William A. Curtin Authors * Binglun Yin View author publications You can also search for this author

inPubMed Google Scholar * William A. Curtin View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS The initial project idea was from W.A.C., B.Y.

and W.A.C. devised the methodology for the DFT computation of misfit volumes in multicomponent random alloys. B.Y. performed all the calculations. B.Y. and W.A.C. analyzed the results and

wrote the manuscript. CORRESPONDING AUTHOR Correspondence to Binglun Yin. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION

PUBLISHER’S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is

licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give

appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in

this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative

Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a

copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Yin, B., Curtin, W.A. First-principles-based prediction

of yield strength in the RhIrPdPtNiCu high-entropy alloy. _npj Comput Mater_ 5, 14 (2019). https://doi.org/10.1038/s41524-019-0151-x Download citation * Received: 17 August 2018 * Accepted:

10 January 2019 * Published: 05 February 2019 * DOI: https://doi.org/10.1038/s41524-019-0151-x SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content:

Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative