ABSTRACT Materials datasets usually contain many redundant (highly similar) materials due to the tinkering approach historically used in material design. This redundancy skews the

performance evaluation of machine learning (ML) models when using random splitting, leading to overestimated predictive performance and poor performance on out-of-distribution samples. This

issue is well-known in bioinformatics for protein function prediction, where tools like CD-HIT are used to reduce redundancy by ensuring sequence similarity among samples greater than a

given threshold. In this paper, we survey the overestimated ML performance in materials science for material property prediction and propose MD-HIT, a redundancy reduction algorithm for

SIMILAR CONTENT BEING VIEWED BY OTHERS MATERIALS PROPERTY PREDICTION FOR LIMITED DATASETS ENABLED BY FEATURE SELECTION AND JOINT LEARNING WITH MODNET Article Open access 03 June 2021 MLMD: A

PROGRAMMING-FREE AI PLATFORM TO PREDICT AND DESIGN MATERIALS Article Open access 21 March 2024 UNVEILING THE COMPLEX STRUCTURE-PROPERTY CORRELATION OF DEFECTS IN 2D MATERIALS BASED ON HIGH

THROUGHPUT DATASETS Article Open access 01 February 2023 INTRODUCTION Density functional theory (DFT) level accuracy of material property prediction1 and >0.95 _R_2 for thermal

conductivity prediction2 with less than a hundred training samples have been routinely reported recently by an increasing list of machine learning algorithms in the material informatics

community. In3, an AI model was shown to be able to predict formation energy of a hold-out test set containing 137 entries from their structure and composition with a mean absolute error

(MAE) of 0.064 eV/atom which significantly outperformed DFT computations for the same task (discrepancies of >0.076 eV/atom). In another related work in Nature Communication by the same

group4, an MAE of 0.07 eV/atom was achieved for composition-based formation energy prediction using deep transfer learning, which is comparable to the MAE of DFT computation. Pasini et al.5

reported that their multitasking neural networks can estimate the material properties (total energy, charge density, and magnetic moment) for a specific configuration hundreds of times

faster than first-principles DFT calculations while achieving comparable accuracy. In6, the authors claimed their graph neural network (GNN) models can predict the formation energies, band

gaps, and elastic moduli of crystals with better than DFT accuracy over a much larger data set. In7, Farb et al. showed numerical evidence that ML model predictions deviate from DFT less

than DFT deviates from the experiments for all nine properties that they evaluated over the QM9 molecule dataset. They also claimed the out-of-sample prediction errors with respect to hybrid

DFT reference were on par with, or close to, chemical accuracy. In8, Tian et al. reported that current ML models can achieve accurate property-prediction (formation energy, band gap, bulk

and shear moduli) using composition alone without using structure information, especially for compounds close to the thermodynamic convex hull. However, this good performance may be

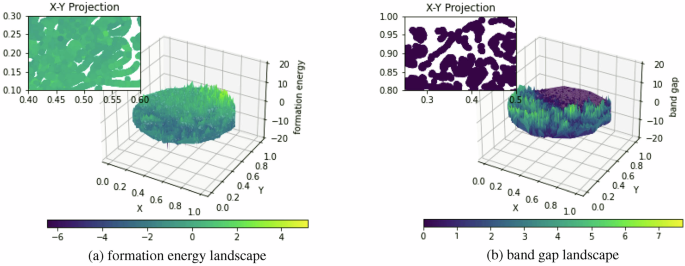
partially due to the over-represented redundancy in their test samples obtained with 6:2:2 random selection from Matminer datasets without redundancy control. To illustrate this point, Fig.

1 shows the formation energy and band gap landscape over the Materials Project (MP)9 composition space, which is generated by mapping the MatScholar features of all MP unique compositions to

the 2D space using t-SNE10 and then plotting the surface. We additionally denote the X-Y projection alongside the corresponding property colors subfigure positioned in the upper left

corner, showing detailed property ranges in some specific areas. Both figures show that there exists a large number of local areas with smooth or similar property values. Random splitting of

samples in those areas into training and test sets may lead to information leakage and over-estimation of the prediction performance. Despite these encouraging successes, the DFT accuracy

reports of these ML models for material property prediction should be cautiously interpreted as they are all average performance evaluated over mostly randomly held-out samples that come

from unexpectedly highly redundant datasets. Materials databases such as Materials Project and Open Quantum Materials Database (OQMD)11,12 are characterized by the existence of many

redundant (highly similar) materials due to the tinkering approach historically used in material design13,14,15. For example, the Materials Project database has many perovskite cubic

structure materials similar to SrTiO3. This sample redundancy within the dataset causes the random splitting of machine learning model evaluation to fail, leading ML models to achieve

over-estimated predictive performance which is misleading for the materials science community. This issue is well known in the area of ecology16 and bioinformatics for protein function

prediction, in which a redundancy reduction procedure (CD-HIT17) is required to reduce the sample redundancy by ensuring no pair of samples has a sequence similarity greater than a given

threshold e.g., 95% sequence identity. In a recent work in 2023, it was also shown that an excellent benchmark score may not imply good generalization performance18. The overestimation of ML

performance for materials has been investigated in a few studies. In19, Meredig et al. examined the extrapolation performance of ML methods for material discovery. They found that

traditional ML metrics, even with cross-validation (CV), overestimate model performance for material discovery and introduce the leave-one-(material) cluster-out cross-validation (LOCO CV)

to objectively evaluate the extrapolation performance of ML models. They especially highlighted that material scientists often intend to extrapolate with trained ML models, rather than

interpolate, to discover new functional materials. Additionally, the sampling in materials training data is typically highly non-uniform. Thus, the high interpolation performance of ML

models trained with datasets with high sample redundancy (e.g., due to doping) does not indicate their strong capability to discover new materials or out-of-distribution (OOD) samples. They

showed that current ML models have much higher difficulty in generalizing from the training clusters to distinct test clusters. They suggested the use of uncertainty quantification (UQ) on

top of ML models to evaluate and explore candidates in new regions of design space. Stanev et al.20 also discussed this generalization issue across different superconductor families. In21,

Xiong et al. proposed K-fold forward cross-validation (FCV) as a new way for evaluating exploration performance in material property prediction by first sorting the samples by their property

values before CV splitting. They showed that current ML models’ prediction performance was actually very low as shown by their proposed FCV evaluation method and the proposed exploratory

prediction accuracy. A similar study for thermal conductivity prediction22 also showed that when ML models are trained with low property values, they are usually not good at predicting

samples with high property values, indicating a weak extrapolation capability. A recent large-scale benchmark study of OOD performances by Omee et al.23 of structure-based graph neural

network models (GNN) for diverse materials properties showed that most of state-of-the-art GNN models tended to have significantly degraded property prediction performance. All these studies

show the need for the material property model developers to focus more on extrapolative prediction performance rather than average interpolation performance over test samples with high

similarity to training samples due to dataset redundancy. The redundancy issue of material datasets has also been studied recently from the point of view of training efficient ML models or

achieving sample efficiency. Magar and Farimani24 proposed an adaptive sampling strategy to generate/sample informative samples for training machine learning models with the lowest amounts

of data. They assumed that informative samples for a model are those with the highest K MAEs (e.g., 250 MAEs) in the test set, which are added to the initial 1000 training set iteratively.

Another selection approach is to add samples similar to data points of the train set having the maximum MAE during training. They showed that their sampling algorithms can create smaller

training sets that obtain better performance than the baseline CGCNN(Crystal Graph Convolutional Neural Networks) model trained with all training samples. This approach can be used with

active learning to build high-performance ML models in a data-efficient way. In a more recent work13, Li et al. studied the redundancy in large material datasets and found that a significant

degree of redundancy across multiple large datasets is present for various material properties and that up to 95% of data can be removed from ML model training with little impact on

prediction performance for test sets sampled randomly from the same distribution dataset. They further showed that the redundant data is due to over-represented material types and does not

help improve the low performance on out-of-distribution samples. They proposed a pruning algorithm similar to24 which first splits the training set into A and B, then trains a ML model on A,

and evaluates the prediction errors on samples in B. After that, the test samples with low MAEs are pruned and the remaining samples are merged and split into A and B again, and so on. Both

approaches rely on the iterative training of ML models and are specific to a given material property. They also proposed an uncertainty quantification-based active learning method to

generate sample-efficient training sets for model training. While these works recognize the possibility to build data-efficient training sets, they did not mention how redundancy has led to

the overestimated ML model performance commonly seen in the literature. Moreover, all approaches for building informative training sets are material property specific, making it difficult to

generate a single non-redundant benchmark dataset for benchmarking material property prediction algorithms for all material properties. Another limitation of these methods is that they show

different similarity thresholds when applied to different datasets, which makes the resulting non-redundant datasets have different minimum distances among the samples. Since material

property prediction research is now pivoting toward developing ML models with high accuracy that are generalizable and transferable between different materials (including those of different

families), a healthy evaluation of ML algorithms is needed to recognize the limitations of existing ML models and to invent new models for material property prediction. Within this context,

reducing the dataset redundancy of both training and test sets can avoid the overestimation of ML model performance, ameliorate the training bias towards samples in crowded areas, and push

the model developers to focus on improving extrapolation performance instead of only interpolation performance. Our work aims to address two major limitations of the latest data redundancy

study on material property prediction13: (1) their redundancy removal procedure is specific to a given material property of interest, and they showed that such redundancy removal may

deteriorate the prediction performance, but not too much. However, in materials property prediction problems, having too many training samples is usually not our major concern. Instead, it

is the out-of-distribution performance of the materials property prediction model that is most interesting to material researchers. However, their work does not show how redundancy removal

may affect the OOD prediction performance; (2) the ’OOD’ samples of their study are not defined rigorously as they are just ’new materials included in a more recent version of the database’.

However, such new samples in a new Materials Project version do not guarantee they are OOD samples that are significantly different from the training set. In this paper, we discuss the

importance of redundancy control in the training and test set selection to achieve objective performance evaluation, especially for extrapolative predictions. Neglecting this aspect has led

to many overestimated ML performances as reported in the literature for both composition-based and structure-based material property prediction. We conduct experiments to demonstrate that

the overestimated ML models often fail for samples that are distant from training samples, indicationg a lack of extrapolation performance. To address this issue, we developed two

redundancy-reducing algorithms (MD-HIT-composition and MD-HIT-structure) with open-sourced code for reducing the dataset redundancy of both composition datasets and structure datasets. These

algorithms utilize composition- and structure-based distance metrics to add samples that are above a defined distance threshold. After this data redundancy control, the dataset can be

randomly split into training, validation, and test sets to achieve objective performance evaluation. We show that with this dataset redundancy control, the predicted performance tends to

reflect their true prediction capability more accurately. RESULTS MD-HIT-COMPOSITION ALGORITHM FOR REDUNDANCY REDUCTION OF COMPOSITION DATASETS The early version of the CD-HIT algorithm17 of

bioinformatics was originally developed to handle large-scale sequence datasets efficiently. It employs a clustering approach to group similar sequences together based on a defined sequence

identity threshold. Within each cluster, only one representative sequence, called the “centroid,” is retained, while the rest of the highly similar sequences are considered duplicates and

removed. However, the clustering approach is still inefficient in dealing with datasets containing hundreds of thousands of sequences. The next generation of CD-HIT further improved the

efficiency by using a greedy algorithm25. Our MD-HIT-composition and MD-HIT-structure redundancy reduction algorithms are designed based on this idea, utilizing greedy incremental

algorithms. In our case, MD-HIT starts the selection process with a seed material (default to _H_2_O_) and then sorts the remaining materials by the number of atoms instead of the formula

lengths. Subsequently, it classifies each material as redundant or representative, depending on its similarity to the existing representatives already selected into the cluster. Composition

similarities are estimated using the ElMD (The Element Movers Distance)26 package, which offers the option to choose linear, chemically derived, and machine-learned similarity measures. By

default, we utilized the Mendeleev similarity and the MatScholar similarity27 for our non-redundant composition dataset generation. Mendeleev similarity measures the similarity between

chemical compositions by comparing the properties of their constituent elements, such as atomic radius and electronegativity, based on the principles used by Dmitri Mendeleev in organizing

the periodic table. The MatScholar distance function is defined as the Euclidean distance between two MatScholar feature vectors27 for a given pair of material compositions. This distance

function is essentially a literature-based word embedding for materials that capture the underlying structure of the periodic table and structure-property relationships in materials. The

Matminer (Materials Data Mining) package28 provides several other material composition descriptors that can also be employed. In this study, our focus was on the ElMD package and the

MatScholar feature-based distance function for redundancy control of composition datasets for material property prediction. The complete composition similarity metrics can be found in Table

1. MD-HIT-STRUCTURE ALGORITHM FOR REDUNDANCY REDUCTION OF STRUCTURE DATASETS MD-HIT-structure algorithm uses the same greedy adding approach as the MD-HIT-composition, except that it uses a

structure-based distance metric. However, due to the varying number of atoms in different crystals, comparing the similarity of two given structures is non-trivial and challenging, given

that most structure descriptors tend to have different dimensions for structures with different numbers of atoms. In this study, we chose two structure distances for redundancy reduction.

One is the distance metric based on XRD (X-ray diffraction) features calculated from crystal structures. We utilized a Gaussian smoothing operation to first smooth the calculated XRD with

the Pymatgen XRDCalculator module29 and then sampled 900 points evenly distributed between 0 and 90 degrees, which leads to XRD features with a fixed 900-dimension. We also selected the OFM

(OrbitalFieldMatrix) feature to calculate the distances of two structures. This kind of feature has also been used in ref. 24 to select informative samples for ML model training. It is a set

of descriptors that encode the electronic structure of a material. These features, which have fixed dimensions (1024), provide information about the distribution of electrons in different

atomic orbitals within a crystal structure and a comprehensive representation of the electronic structure and bonding characteristics of materials. Similar to the MD-HIT-composition, the

MD-HIT-structure algorithm also starts the selection process with a seed material (default to _H_2_O_) which is put in the non-redundant set. It then sorts the remaining materials in the

candidate set by the number of atoms instead of the formula lengths, and classifies them one-by-one as redundant or representative materials based on their similarities (we use Euclidean

distance of XRD features or OFM features) to the existing representatives already selected into the non-redundant set. Redundant samples are discarded, while non-redundant ones are added to

the non-redundant set until the candidate set is empty. DATASETS GENERATION We downloaded 125,619 cif files with material structures from the Materials Project database, which includes

89,354 materials with unique compositions. In cases where compositions corresponded to multiple polymorphs, we adopted average material property values by default, with the exception of

formation energy property, for which we used the minimum value. Additionally, we excluded mp-101974 (_H__e__S__i__O_2) due to issues with calculating Matscholar features. After eliminating

formulas with over 50 atoms, we obtained a non-duplicate composition dataset with 86,741 samples and then used different similarity (distance) thresholds to generate non-redundant datasets.

For Mendeleev similarity, we used distance thresholds of 0.5, 0.8, 1, 1.5, 2, 2.5, and 3 to generate seven non-redundant datasets (Mendeleev-nr). The dataset sizes range from 86,740 to 3177.

Similarly, we generated eight Matscholar non-redundant datasets (Matscholar-nr) with percentages of the total range from 50.82% to 2.33%. We also applied the MD-HIT-structure algorithm to

all 125,619 structures and used different thresholds to generate seven XRD non-redundant datasets and eight OFM non-redundant datasets. After removal of redundancy based on varying degrees

of sample identity using MD-HIT algorithms, we obtained all non-redundant datasets, and the details are shown in Table 2. To visually understand the effect of redundancy removal on datasets,

Fig. 2 shows the material distribution t-SNE maps of the whole dataset and two non-redundant datasets. For each dataset, we calculated the MatScholar composition features for all samples.

Then, we used t-SNE dimension reduction algorithm to map the features to a two-dimensional space. Figure 2a shows the distribution of the whole dataset, which is filled with crowded samples

with high redundancy. Figure 2b shows the less redundant dataset Matscholar-nr generated with the threshold of 0.1. It contains only 50.82% of the samples. Figure 2c shows the Mendeleev-nr

non-redundant dataset with only 4930 samples, which has only 5.68% of the samples of the whole dataset while still covering the entire map with much lower redundancy. The non-redundant

datasets thus allow us to test the true generalization capability when trained and tested on them. COMPOSITION BASED MATERIAL PROPERTY PREDICTION WITH REDUNDANCY CONTROL To investigate the

impact of redundancy control on the performance of ML models for predicting material properties, we conducted experiments using datasets filtered by Mendeleev and Matscholar distances. We

evaluated two state-of-the-art composition-based property prediction algorithms, Roost and CrabNet (See Methods section), on non-redundant datasets derived from the MP composition dataset

with 86,740 samples using different distance thresholds. The datasets were randomly divided into training, validation, and test sets with an 8:1:1 ratio. Figures 3 and 4 compare the

performances of Roost and CrabNet for formation energy and band gap prediction on datasets of varying sizes, filtered by Mendeleev distance thresholds of 0, 0.5, 0.8, 1, 1.5, 2, 2.5 and 3

and Matscholar distance thresholds of 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, and 0.4. Please note that we have chosen to report the results from a single random split for each dataset in

Figs. 3 and 4. This decision was made due to the large number of experiments conducted and our verification that the standard deviations of performances across multiple repeat experiments

are small relative to the mean values. This approach allows for a clear presentation of results while maintaining statistical reliability. For formation energy prediction (Figs. 3a and 4a),

both models exhibit a deteriorating trend with increasing thresholds (i.e., lower data redundancy), as evidenced by decreasing _R_2 and increasing MAE scores. Matscholar distance yields

higher correlations between prediction performance and thresholds compared to Mendeleev distance, indicating that it generates more evenly distributed non-redundant datasets. For band gap

prediction (Figs. 3b and 4b), the _R_2 scores of both models are gradually decreasing with increasing thresholds. However, the MAE scores show a general uptrend with abrupt jumps at certain

points, possibly due to outliers in the band gap datasets, highlighting the challenges in band gap prediction. The inconsistent trends in MAE and _R_2 for band gap prediction using

Matscholar distance (Fig. 4b) may be attributed to the large percentage of zero band gap samples. Overall, removing dataset redundancy allows for more realistic performance evaluations of ML

models in real-world applications, where query materials often differ training samples. Experiments reveal that samples within dense areas tend to have lower prediction errors (Fig. 9).

Without reducing redundancy, a significant portion of test samples may be located in areas crowded with similar training samples, leading to low prediction errors and over-estimated

performance. This occurs because the model may overly rely on information from redundant samples during training while disregarding more diverse samples. STRUCTURE BASED MATERIAL PROPERTY

PREDICTION WITH REDUNDANCY CONTROL To investigate the impact of redundancy control on structure-based material datasets, we utilized the Materials Project database of 123,108 crystal

structures with their formation energy per atom and band gaps. We employed the XRD and OFM features of crystal structures to define the similarity between pairs of structures, which was used

to control the structure redundancy using the minimum XRD/OFM distance thresholds between any pair of samples. For XRD-based non-redundant datasets (XRD-nr), we used thresholds of 0.5, 0.6,

0.8, and 0.9. We evaluated the material property prediction performances of two state-of-the-art graph neural network algorithms, ALIGNN30 and DeeperGATGNN31 (See Methods section), on these

datasets. For formation energy prediction (Fig. 5a), XRD-distance provides effective control of data redundancy, as evidenced by the gradual increase in MAEs and decrease in _R_2 scores for

both algorithms with increasing XRD thresholds. For band gap prediction (Fig. 5b), the effect of dataset redundancy on the performance of both algorithms is more complex. While the _R_2

scores decrease with increasing thresholds, the MAE of ALIGNN for thresholds 0.8 and 0.9 are lower than for the threshold of 0.6, despite lower _R_2 scores. This discrepancy suggests higher

nonlinearity and the influence of outlier band gap values in the prediction problem, a phenomenon also observed in the composition-base results (Figs. 3 and 4). We further evaluated the

impact of OFM-controlled data redundancy on the algorithms’ performance (Fig. 6). Both algorithms showed high consistency in formation energy prediction (Fig. 6a), with _R_2 scores decreaing

and MAE scores increasing with increasing thresholds, indicating that OFM distance is an effective redundacy control method for crystal structure datasets. However, for band gap prediction

(Fig. 6b), while the _R_2 scores decrease with increasing thresholds as expected, the MAE scores also decrease, which is counter-intuitive. Analysis of the test sets revealed that the MD-HIT

algorithm accidentally selected a higher percentages of near-zero band gap samples (<0.01 eV) for higher thresholds, making the prediction task easier. In particular, while the whole

redundant dataset contains only 48.64% near-zero band gap samples, our MD-HIT algorithm selected 64.09%, 67.81%, 84.52%, and 92.43% near-zero band gap samples for thresholds 0.15, 0 2, 0.45,

and 0.7, respectively. This data bias explains the unexpected decrease in MAEs scores. To further elucidate the data bias, we constructed scatter plots depicting the band gaps predicted by

DeeperGATGNN across the entire dataset and two non-redundant datasets, as illustrated in Fig. 7. The analysis reveals a striking predominance (92.43%) of near-zero samples in the

non-redundant dataset with a threshold of 0.7. Choosing a different seed structure other than SrTiO3, which has a band gap close to zero, may reduce this bias. These findings highlight the

importance of monitoring data bias, which can easily lead to overestimated ML model performance in material property prediction. PERFORMANCE COMPARISONS BETWEEN ID AND OOD SETS Our

experiments have demonstrated that redundant material datasets often lead to overestimated high performance for material prediction, as reported in the current literature. When we reduce the

dataset redundancy, the ML performances significantly decreases. Previous work has also shown that removing redundant samples enables the training of efficient ML models with reduced

data13, which can achieve comparable in-distribution (ID) prediction performance while eliminating up to 95% of samples. In this study, we aim to showcase the additional potential benefit of

redundancy removal: enhancing the ML performance for out-of-distribution (OOD) samples. We first selected 1000 OOD test samples to create the MatscholarOOD test set, based on the densities

calculated using Matscholar features of compositions from the entire MP dataset (86,740 samples) for formation energy prediction. The remaining samples were then used to prepare the training

sets. We selected a non-redundant training set (_non-rdfe_) from the MP dataset with a threshold of 0.1, resulting in approximately 40,000 samples. A redundant training set (_rdfe_) of

equal size was then randomly selected from the entire dataset, excluding the OOD samples. The Roost model trained on non-rdfe is referred to as Roost_n__r_ and the Roost model trained on

rdfe is referred to as Roost_r__e__d_. However, our experimental results in previous sections do not demonstrate whether ML models trained with non-redundant sets can achieve performance

improvements for OOD test sets. We found that models trained with non-redundant training samples exhibit lower performance for the randomly split leave-out test set, which is reasonable as

the reduction of redundancy between the training set and the test set makes it more challenging for the models to predict test samples. In this section, we aim to illustrate the effect of

reducing dataset redundancy on ML performance for OOD samples. However, our Roost model trained with the naively created non-redundant training set based on the Matscholar feature space

achieves an MAE of 0.1322 eV, which is worse than that of the Roost model trained with the redundant training set (MAE: 0.1224 eV). Upon close examination, we discovered that the sparse

samples in the MatscholarOOD test set are not necessarily located in the sparse areas of the embedding space for the deep learning models such as Roost, CrabNet, and DeeperGATGNN, indicating

that these OOD samples are not true OOD samples. This finding also explains the fact that our Roost trained with non-redundant set has an MAE of 0.1322 eV when evaluated on the

MatscholarOOD test set, while it achieves a higher MAE of 0.1728 eV on the random-split test set. To compare the true OOD performance of models trained on non-redundant and redundant

dataset, we prepared another OOD test set named EmbeddingOOD. First, we used a pretrained Roost model as an encoder to obtain the latent representations for all samples in the entire dataset

(86,740 samples). We then calculated the pairwise distances of all samples using their latent representations and selected 1000 OOD samples that are furthest away on average from their

three nearest neighbors, forming our EmbeddingOOD test set. We then compared the performance of Roost models on the random-split test sets (split from nonrdfe and rdfe in a 9:1 ratio) and

this EmbeddingOOD test set. It should be noted that we removed all OOD samples from the original nonrdfe and rdfe datasets. Figure 8 shows the performance of two Roost models on two test

sets (ID and OOD sets). The MAE of the Roost_r__e__d_ increases from 0.1278 eV on the random-split test set to 0.4089 eV for the EmbeddingOOD test set, while _R_2 significantly decreases

from 0.9168 to 0.5318 (Fig. 8c, d), indicating that our EmbeddingODD samples pose a significant challenge for our Roost_r__e__d_ model. In contrast, for Roost_n__r_, its MAE increased from

0.1994 eV to 0.3679 eV, and _R_2 reduced from 0.8544 to 0.6998 (Fig. 8a, b). However, we find that the Roost_n__r_ significantly outperforms Roost_r__e__d_ model, with 10.03% improvement in

MAE and a 31.6% improvement in _R_2 for the OOD test set. This result demonstrates that removing redundant data can steer an ML model away from focusing on crowded samples, ensuring

equitable attention to all other samples, and consequently improving OOD prediction performance. Moreover, to demeonstrate that the prediction errors tend to be lower in areas of high sample

density, we created parity plot showing the correlation between MAEs of the Roost models and sample density. The Roost models were trained with both redundant and non-redundant training

sets. We first sorted all test samples in the random-split or OOD test sets according to their densities, calculated using their latent representations. The sorted samples were then split

into 50 bins, and the average MAE was calculated for each bin, resulting in 50 (density & MAE) data points for each test set, as shown in Fig. 9. Fitted curves for the 50 data points of

the random-split and OOD sets were added to the scatter plots in Fig. 9a, b. The fitted curves in both Fig. 9a, b show a trend of decreasing MAEs as sample density increases. However, the

MAEs for OOD samples have much higher variance compared to those of the random-split test samples. Furthermore, for the Roost model trained with the non-redundant dataset (Fig. 9b), the two

fitted curves are closer to each other than those for the predictions by the Roost_r__e__d_ in Fig. 9a. This indicates that the ML model trained on the non-redundant dataset has more

consistent performance across the random-split and the OOD test sets. Another interesting question arises as to why the deep learning models (Roost, CrabNet, and DeeperGATGNN) trained with

the non-redundant dataset perform worse than those trained with the redundant dataset when testing the MatscholarOOD test set. In contrast, Random Forest models behave oppositely: the

RF_n__r_ model achieves better performance than RF_r__e__d_ model for the MatscholarOOD test set. A possible explanation is that deep learning models project raw composition or structural

inputs into a high-level latent representation space, which differs from the Matscholar feature space used to build the MatscholarOOD test set. This difference makes our MatscholarOOD

samples not sparse in the latent space used for decision-making by the deep learning models, explaining why deep learning models trained with redundant samples work better than trained with

non-redundant samples. In contrast, RF models lack representation learning capability and use the Matscholar feature space directly as their decision space. This charecteristic allows the

RF_n__r_, trained with non-redundant training set, to work better than the _R__F__r__e__d_ model for the true Matscholar OOD set. To further explore the performance of ML models on OOD

samples selected using Matscholar features, we train two RF models, RF_n__r_ and RF_r__e__d_, on the non-rdfe and rdfe datasets, respectively. We then selected the 1000 OOD samples that are

furthest away on average from their corresponding three nearest neighbors according to their Matscholar features. The performance of RF models was tested on both the random-split test sets

and the OOD test set. As shown in Fig. 10c, d, for the RF model trained with the redundant rdfe dataset (RF_r__e__d_), there is a significant performance difference between the random-split

test set and the OOD test set. The MAE increases from 0.4014 eV to 0.7562 eV, while _R_2 significantly decreases from 0.7094 to 0.0527. In contrast, for RF_n__r_, the MAE increases from

0.4330 eV to 0.6427 eV, and _R_2 is reduced from 0.6382 to 0.2668 (Fig. 10a, b). Although the performance of RF_n__r_ on the OOD test set is worse than on random-split test set, it is still

much better than the 0.0527 _R_2 value of the RF_r__e__d_ model. This indicates that removing data redundancy can improve OOD prediction performance for RF models. Another interesting

question is how to determine the threshold for redundancy control. Instead of having a commonly agreed value as used in the CD-HIT code by the bioinformatics community, we can use the

standard validation method for hyper-parameter tuning to find the optimal threshold value. DISCUSSION Large material databases such as the Materials Project usually contain a high degree of

redundancy, which causes biased ML models and overestimated performance evaluations due to the redundancy between randomly selected test samples and the remaining training samples. The

claimed DFT accuracy averaged over all data samples from the literature deviates from the common needs of material scientists who usually want to discover new materials that are different

from known training samples, which makes it important to evaluate and report the extrapolation rather than interpolation material property prediction performance and performance comparison

across different datasets should be interpreted within the context of data redundancy levels. Here we propose and develop two material dataset redundancy-reducing algorithms based on a

greedy algorithm inspired by the peer bioinformatics CD-HIT algorithm. We use two composition distance metrics and two structure distance metrics as the thresholds to control the sample

redundancy of our composition and structure datasets. Our benchmark results over two composition-based and two structure-based material property prediction models over two material

properties (formation energy and band gap) showed that the prediction performance of current ML models all tend to degrade due to the removal of redundant samples, leading to the measurement

of more realistic prediction performance of current ML material property models in practice. The more different the query samples, the more difficult it is to predict them accurately by

current machine learning models that focus on interpolation. The out-of-distribution prediction problem is now under active research in the machine learning community which focuses on OOD

generalization performance32,33 including works that use domain adaptation to improve OOD prediction performance for composition-based property prediction34. More investigation is needed to

check the exact relationships between dataset redundancy and machine learning model generalization performance. The availability of our easy-to-use open-source code of MD-HIT-composition and

MD-HIT-structure makes it easy for researchers to conduct objective evaluations and report realistic performances of their ML models for material property prediction. It should also be

noted that the current multi-threaded implementation of our MD-HIT algorithms is still slow and more improvements are highly desirable. METHODS COMPOSITION-BASED MATERIAL PROPERTY PREDICTION

ALGORITHMS We evaluated two state-of-the-art composition-based material property prediction algorithms including Roost35 and Crabnet36 to study the impact of dataset redundancy on their

performance. The Roost algorithm is a DL model specifically designed for material property prediction based on material composition. It utilizes a graph neural network framework to learn

relationships between material compositions and their corresponding properties. CrabNet is a transformer self-attention-based model for composition-only material property prediction. It

matches or exceeds current best-practice methods on nearly all of 28 total benchmark datasets. STRUCTURE-BASED MATERIAL PROPERTY PREDICTION ALGORITHMS We evaluated two state-of-the-art

structure-based material property prediction algorithms including ALIGNN (Atomistic Line Graph Neural Network)30 and DeeperGATGNN (a global attention-based GNN with differentiable group

normalization and residual connection)31 to compare the impact of dataset redundancy on their performance. The ALIGNN model addresses a major limitation of the majority of current GNN models

used for atomistic predictions, which only rely on atomic distances while overlooking the bond angles. Actually bond angles play a crucial role in distinguishing various atomic structures

and small deviations in bond angles can significantly impact several material properties. ALIGNN is a GNN architecture that conducts message passing on both the interatomic bond graph and

its corresponding line graph specifically designed for bond angles. It has achieved state-of-art performances in most benchmark problems of the matbench37. The DeeperGATGNN model is a global

attention-based graph neural network that uses differentiable group normalization and residual connection to achieve high-performance deep graph neural networks without performance

degradation. It has achieved superior results as shown in a set of material property predictions. EVALUATION CRITERIA We use the following performance metrics for evaluating dataset

redundancy’s impact on model performance, including Mean Absolute Error (MAE) and R-squared (_R_2). $$MAE=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}\left\vert

{y}_{i}-{\hat{y}}_{i}\right\vert$$ (1) $${R}^{2}=1-\frac{\mathop{\sum }\nolimits_{i = 1}^{n}{({y}_{i}-{\hat{y}}_{i})}^{2}}{\mathop{\sum }\nolimits_{i = 1}^{n}{({y}_{i}-\bar{y})}^{2}}$$ (2)

Where _y__i_ represents the observed or true values, \({\hat{y}}_{i}\) represents the predicted values, and \(\bar{y}\) represents the mean of the observed values. The summation symbol ∑ is

used to calculate the sum of values, and _n_ represents the number of data points in the dataset. DATA AVAILABILITY The non-redundant datasets can be freely accessed at

https://github.com/usccolumbia/MD-HIT. CODE AVAILABILITY The source code can be freely accessed at https://github.com/usccolumbia/MD-HIT. REFERENCES * Xie, T. & Grossman, J. C. Crystal

graph convolutional neural networks for an accurate and interpretable prediction of material properties. _Phys. Rev. Lett._ 120, 145301 (2018). Article  CAS  PubMed  Google Scholar  * Chen,

L., Tran, H., Batra, R., Kim, C. & Ramprasad, R. Machine learning models for the lattice thermal conductivity prediction of inorganic materials. _Comput. Mater. Sci._ 170, 109155 (2019).

Article  CAS  Google Scholar  * Jha, D., Gupta, V., Liao, W.-k, Choudhary, A. & Agrawal, A. Moving closer to experimental level materials property prediction using ai. _Sci. Rep._ 12,

1–9 (2022). Article  Google Scholar  * Jha, D. et al. Enhancing materials property prediction by leveraging computational and experimental data using deep transfer learning. _Nat. Commun._

10, 5316 (2019). Article  CAS  PubMed  PubMed Central  Google Scholar  * Pasini, M. L. et al. Fast and stable deep-learning predictions of material properties for solid solution alloys. _J.

Phys.: Condens. Matter_ 33, 084005 (2020). Google Scholar  * Chen, C., Ye, W., Zuo, Y., Zheng, C. & Ong, S. P. Graph networks as a universal machine learning framework for molecules and

crystals. _Chem. Mater._ 31, 3564–3572 (2019). Article  CAS  Google Scholar  * Faber, F. A. et al. Prediction errors of molecular machine learning models lower than hybrid dft error. _J.

Chem. theory Comput._ 13, 5255–5264 (2017). Article  CAS  PubMed  Google Scholar  * Tian, S. I. P., Walsh, A., Ren, Z., Li, Q. & Buonassisi, T. What information is necessary and

sufficient to predict materials properties using machine learning?_arXiv preprint arXiv:2206.04968_ (2022). * Jain, A. et al. Commentary: The materials project: A materials genome approach

to accelerating materials innovation. _APL Mater._ 1 (2013). * Van der Maaten, L. & Hinton, G. Visualizing data using t-sne. _J. Mach. Learn. Res._ 9 (2008). * Saal, J. E., Kirklin, S.,

Aykol, M., Meredig, B. & Wolverton, C. Materials design and discovery with high-throughput density functional theory: the open quantum materials database (oqmd). _Jom_ 65, 1501–1509

(2013). Article  CAS  Google Scholar  * Kirklin, S. et al. The open quantum materials database (oqmd): assessing the accuracy of dft formation energies. _npj Comput. Mater._ 1, 1–15 (2015).

Article  Google Scholar  * Li, K. et al. Exploiting redundancy in large materials datasets for efficient machine learning with less data. _Nat. Commun._ 14, 7283 (2023). Article  CAS  PubMed

  PubMed Central  Google Scholar  * Trabelsi, Z. et al. Superconductivity phenomenon: Fundamentals and theories. In _Superconducting Materials: Fundamentals, Synthesis and Applications_,

1–27 (Springer, 2022). * Zunger, A. & Malyi, O. I. Understanding doping of quantum materials. _Chem. Rev._ 121, 3031–3060 (2021). Article  CAS  PubMed  Google Scholar  * Roberts, D. R.

et al. Cross-validation strategies for data with temporal, spatial, hierarchical, or phylogenetic structure. _Ecography_ 40, 913–929 (2017). Article  Google Scholar  * Li, W. & Godzik,

A. Cd-hit: a fast program for clustering and comparing large sets of protein or nucleotide sequences. _Bioinformatics_ 22, 1658–1659 (2006). Article  CAS  PubMed  Google Scholar  * Li, K.,

DeCost, B., Choudhary, K., Greenwood, M. & Hattrick-Simpers, J. A critical examination of robustness and generalizability of machine learning prediction of materials properties. _npj

Comput. Mater._ 9, 55 (2023). Article  CAS  Google Scholar  * Meredig, B. et al. Can machine learning identify the next high-temperature superconductor? examining extrapolation performance

for materials discovery. _Mol. Syst. Des. Eng._ 3, 819–825 (2018). Article  CAS  Google Scholar  * Stanev, V. et al. Machine learning modeling of superconducting critical temperature. _npj

Comput. Mater._ 4, 29 (2018). Article  Google Scholar  * Xiong, Z. et al. Evaluating explorative prediction power of machine learning algorithms for materials discovery using k-fold forward

cross-validation. _Comput. Mater. Sci._ 171, 109203 (2020). Article  CAS  Google Scholar  * Loftis, C., Yuan, K., Zhao, Y., Hu, M. & Hu, J. Lattice thermal conductivity prediction using

symbolic regression and machine learning. _J. Phys. Chem. A_ 125, 435–450 (2020). Article  PubMed  Google Scholar  * Omee, S. S., Fu, N., Dong, R., Hu, M. & Hu, J. Structure-based

out-of-distribution (OOD) materials property prediction: a benchmark study. _Npj Comput. Mater._ 10, 144 (2024). Article  Google Scholar  * Magar, R. & Farimani, A. B. Learning from

mistakes: Sampling strategies to efficiently train machine learning models for material property prediction. _Comput. Mater. Sci._ 224, 112167 (2023). Article  CAS  Google Scholar  * Fu, L.,

Niu, B., Zhu, Z., Wu, S. & Li, W. Cd-hit: accelerated for clustering the next-generation sequencing data. _Bioinformatics_ 28, 3150–3152 (2012). Article  CAS  PubMed  PubMed Central 

Google Scholar  * Hargreaves, C. J., Dyer, M. S., Gaultois, M. W., Kurlin, V. A. & Rosseinsky, M. J. The earth mover’s distance as a metric for the space of inorganic compositions.

_Chem. Mater._ 32, 10610–10620 (2020). Article  CAS  Google Scholar  * Tshitoyan, V. et al. Unsupervised word embeddings capture latent knowledge from materials science literature. _Nature_

571, 95–98 (2019). Article  CAS  PubMed  Google Scholar  * Ward, L. et al. Matminer: An open source toolkit for materials data mining. _Comput. Mater. Sci._ 152, 60–69 (2018). Article 

Google Scholar  * De Graef, M. & McHenry, M. E.Structure of materials: an introduction to crystallography, diffraction and symmetry (Cambridge University Press, 2012). * Choudhary, K.

& DeCost, B. Atomistic line graph neural network for improved materials property predictions. _npj Comput. Mater._ 7, 185 (2021). Article  Google Scholar  * Omee, S. S. et al. Scalable

deeper graph neural networks for high-performance materials property prediction. _Patterns_ 3, 100491 (2022). Article  PubMed  PubMed Central  Google Scholar  * Arjovsky, M. Out of

distribution generalization in machine learning. Ph.D. thesis, New York University (2020). * Krueger, D. et al. Out-of-distribution generalization via risk extrapolation (rex). In

_International Conference on Machine Learning_, 5815–5826 (PMLR, 2021). * Hu, J., Liu, D., Fu, N. & Dong, R. Realistic material property prediction using domain adaptation based machine

learning. _Digital Discov._ 3, 300–312 (2024). Article  CAS  Google Scholar  * Goodall, R. E. & Lee, A. A. Predicting materials properties without crystal structure: Deep representation

learning from stoichiometry. _Nat. Commun._ 11, 6280 (2020). Article  CAS  PubMed  PubMed Central  Google Scholar  * Wang, A. Y.-T., Kauwe, S. K., Murdock, R. J. & Sparks, T. D.

Compositionally restricted attention-based network for materials property predictions. _Npj Comput. Mater._ 7, 77 (2021). Article  Google Scholar  * Dunn, A., Wang, Q., Ganose, A., Dopp, D.

& Jain, A. Benchmarking materials property prediction methods: the matbench test set and automatminer reference algorithm. _npj Comput. Mater._ 6, 138 (2020). Article  Google Scholar 

Download references ACKNOWLEDGEMENTS The research reported in this work was supported in part by National Science Foundation under the grant number 2311202. The views, perspectives, and

content do not necessarily represent the official views of the NSF. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * College of Big Data and Statistics, Guizhou University of Finance and

Economics, Guiyang, China Qin Li * Department of Computer SCience and Engineering, University of South Carolina, Columbia, SC, USA Nihang Fu, Sadman Sadeed Omee & Jianjun Hu Authors *

Qin Li View author publications You can also search for this author inPubMed Google Scholar * Nihang Fu View author publications You can also search for this author inPubMed Google Scholar *

Sadman Sadeed Omee View author publications You can also search for this author inPubMed Google Scholar * Jianjun Hu View author publications You can also search for this author inPubMed 

Google Scholar CONTRIBUTIONS Conceptualization, J.H.; methodology, Q.L., N.F., J.H., S.O.; software, Q.L., N.F., J.H., and S.O.; resources, J.H.; writing–original draft preparation, J.H.,

Q.L, N.F., and S.O.; writing–review and editing, J.H. and N.F.; visualization, N.F., J.H., and S.O.; supervision, J.H.; funding acquisition, J.H. CORRESPONDING AUTHOR Correspondence to

Jianjun Hu. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to

jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International

License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source,

provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons

licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Li, Q., Fu, N., Omee, S.S. _et al._ MD-HIT: Machine learning for material property

prediction with dataset redundancy control. _npj Comput Mater_ 10, 245 (2024). https://doi.org/10.1038/s41524-024-01426-z Download citation * Received: 22 April 2024 * Accepted: 23 September

2024 * Published: 18 October 2024 * DOI: https://doi.org/10.1038/s41524-024-01426-z SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get

shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative