ABSTRACT Topological photonics has emerged as a route to robust optical circuitry protected against disorder1,2 and now includes demonstrations such as topologically protected lasing3,4,5

and single-photon transport6. Recently, nonlinear optical topological structures have attracted special theoretical interest7,8,9,10,11, as they enable tuning of topological properties by a

change in the light intensity7,12 and can break optical reciprocity13,14,15 to realize full topological protection. However, so far, non-reciprocal topological states have only been realized

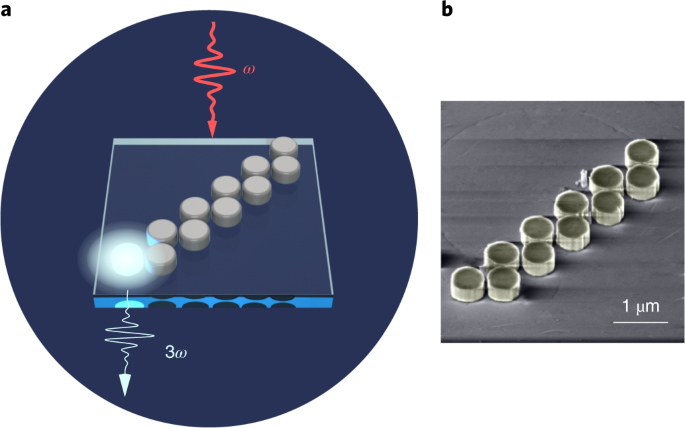
using magneto-optical materials and macroscopic set-ups with external magnets4,16, which is not feasible for nanoscale integration. Here we report the observation of a third-harmonic signal

robust against various perturbations and structural defects. Moreover, we show that the interplay between topology, bi-anisotropy and nonlinearity makes parametric photon generation tunable

and non-reciprocal. Our study brings nonlinear topological photonics concepts to the realm of nanoscience. Access through your institution Buy or subscribe This is a preview of subscription

content, access via your institution ACCESS OPTIONS Access through your institution Access Nature and 54 other Nature Portfolio journals Get Nature+, our best-value online-access

subscription $32.99 / 30 days cancel any time Learn more Subscribe to this journal Receive 12 print issues and online access $259.00 per year only $21.58 per issue Learn more Buy this

article * Purchase on SpringerLink * Instant access to full article PDF Buy now Prices may be subject to local taxes which are calculated during checkout ADDITIONAL ACCESS OPTIONS: * Log in

* Learn about institutional subscriptions * Read our FAQs * Contact customer support SIMILAR CONTENT BEING VIEWED BY OTHERS NON-HERMITIAN TOPOLOGICAL PHASE TRANSITIONS CONTROLLED BY

NONLINEARITY Article 23 October 2023 ADIABATIC TOPOLOGICAL PHOTONIC INTERFACES Article Open access 02 August 2023 MAGNETICALLY CONTROLLABLE MULTIMODE INTERFERENCE IN TOPOLOGICAL PHOTONIC

CRYSTALS Article Open access 14 May 2024 DATA AVAILABILITY The data that support the plots within this paper and other findings of this study are available from the corresponding author upon

reasonable request. REFERENCES * Lu, L., Joannopoulos, J. D. & Soljačić, M. Topological states in photonic systems. _Nat. Phys._ 12, 626–629 (2016). Article  CAS  Google Scholar  *

Khanikaev, A. B. & Shvets, G. Two-dimensional topological photonics. _Nat. Photon._ 11, 763–773 (2017). Article  CAS  Google Scholar  * St-Jean, P. et al. Lasing in topological edge

states of a one-dimensional lattice. _Nat. Photon._ 11, 651–656 (2017). Article  CAS  Google Scholar  * Bahari, B. et al. Nonreciprocal lasing in topological cavities of arbitrary

geometries. _Science_ 358, 636–640 (2017). Article  CAS  Google Scholar  * Bandres, M. A. et al. Topological insulator laser: experiments. _Science_ 359, eaar4005 (2018). Article  Google

Scholar  * Barik, S. et al. A topological quantum optics interface. _Science_ 359, 666 (2018). Article  CAS  Google Scholar  * Hadad, Y., Khanikaev, A. B. & Alù, A. Self-induced

topological transitions and edge states supported by nonlinear staggered potentials. _Phys. Rev. B_ 93, 155112 (2016). Article  Google Scholar  * Solnyshkov, D. D., Nalitov, A. V. &

Malpuech, G. Kibble–Zurek mechanism in topologically nontrivial zigzag chains of polariton micropillars. _Phys. Rev. Lett._ 116, 046402 (2016). Article  CAS  Google Scholar  * Leykam, D.

& Chong, Y. D. Edge solitons in nonlinear-photonic topological insulators. _Phys. Rev. Lett._ 117, 143901 (2016). Article  Google Scholar  * Bardyn, C.-E., Karzig, T., Refael, G. &

Liew, T. C. H. Chiral Bogoliubov excitations in nonlinear bosonic systems. _Phys. Rev. B_ 93, 020502 (2016). Article  Google Scholar  * Kartashov, Y. V. & Skryabin, D. V. Bistable

topological insulator with exciton-polaritons. _Phys. Rev. Lett._ 119, 253904 (2017). Article  Google Scholar  * Zhou, X., Wang, Y., Leykam, D. & Chong, Y. D. Optical isolation with

nonlinear topological photonics. _New J. Phys._ 19, 095002 (2017). Article  Google Scholar  * Fan, L. et al. An all-silicon passive optical diode. _Science_ 335, 447–450 (2011). Article 

Google Scholar  * Li, E., Eggleton, B. J., Fang, K. & Fan, S. Photonic Aharonov–Bohm effect in photon–phonon interactions. _Nat. Commun._ 5, E3225 (2014). Article  Google Scholar  * Shi,

Y., Yu, Z. & Fan, S. Limitations of nonlinear optical isolators due to dynamic reciprocity. _Nat. Photon._ 9, 388–392 (2015). Article  CAS  Google Scholar  * Wang, Z., Chong, Y.,

Joannopoulos, J. D. & Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. _Nature_ 461, 772–775 (2009). Article  CAS  Google Scholar  *

Rechtsman, M. C. et al. Photonic Floquet topological insulators. _Nature_ 496, 196–200 (2013). Article  CAS  Google Scholar  * Hafezi, M., Mittal, S., Fan, J., Migdall, A. & Taylor, J.

Imaging topological edge states in silicon photonics. _Nat. Photon._ 7, 1001–1005 (2013). Article  CAS  Google Scholar  * Blanco-Redondo, A. et al. Topological optical waveguiding in silicon

and the transition between topological and trivial defect states. _Phys. Rev. Lett._ 116, 163901 (2016). Article  Google Scholar  * Poddubny, A., Miroshnichenko, A., Slobozhanyuk, A. &

Kivshar, Y. Topological Majorana states in zigzag chains of plasmonic nanoparticles. _ACS Photonics_ 1, 101 (2014). Article  CAS  Google Scholar  * Sinev, I. S. et al. Mapping plasmonic

topological states at the nanoscale. _Nanoscale_ 7, 11904 (2015). Article  CAS  Google Scholar  * Kruk, S. et al. Edge states and topological phase transitions in chains of dielectric

nanoparticles. _Small_ 13, 1603190 (2017). * Smirnova, D. & Kivshar, Y. S. Multipolar nonlinear nanophotonics. _Optica_ 3, 1241–1255 (2016). Article  CAS  Google Scholar  * Slobozhanyuk,

A. P., Poddubny, A. N., Miroshnichenko, A. E., Belov, P. A. & Kivshar, Y. S. Subwavelength topological edge states in optically resonant dielectric structures. _Phys. Rev. Lett._ 114,

123901 (2015). Article  Google Scholar  * Hadad, Y., Soric, J. C., Khanikaev, A. B. & Alù, A. Self-induced topological protection in nonlinear circuit arrays. _Nat. Electron._ 1, 178–182

(2018). Article  Google Scholar  * Shen, S.-Q. _Topological Insulators. Dirac Equation in Condensed Matters_ (Springer, Heidelberg, 2013). * Rose, A., Huang, D. & Smith, D. R. Nonlinear

interference and unidirectional wave mixing in metamaterials. _Phys. Rev. Lett._ 110, 063901 (2013). Article  Google Scholar  * Poutrina, E. & Urbas, A. Multipolar interference for

non-reciprocal nonlinear generation. _Sci. Rep._ 6, 25113 (2016). Article  CAS  Google Scholar  * Alaee, R. et al. All-dielectric reciprocal bianisotropic nanoparticles. _Phys. Rev. B_ 92,

245130 (2015). Article  Google Scholar  * Slobozhanyuk, A. et al. Three-dimensional all-dielectric photonic topological insulator. _Nat. Photon._ 11, 130–136 (2016). Article  Google Scholar

  * O’Brien, K. et al. Predicting nonlinear properties of metamaterials from the linear response. _Nat. Mater._ 14, 379–383 (2015). Article  Google Scholar  * Kujala, S., Canfield, B. K.,

Kauranen, M., Svirko, Y. & Turunen, J. Multipole interference in the second-harmonic optical radiation from gold nanoparticles. _Phys. Rev. Lett._ 98, 167403 (2007). Article  Google

Scholar  * Lu, L. et al. Experimental observation of Weyl points. _Science_ 349, 622 (2015). Article  CAS  Google Scholar  * Wang, L. et al. Nonlinear wavefront control with all-dielectric

metasurfaces. _Nano Lett._ 18, 3978–3984 (2018). Download references ACKNOWLEDGEMENTS The authors acknowledge financial support from the Australian Research Council and the Strategic Fund of

the Australian National University. A part of this research was conducted at the Center for Nanophase Materials Sciences, which is a DOE Office of Science User Facility. Numerical

calculations were supported in part by the Ministry of Education and Science of the Russian Federation (Zadanie no. 3.2465.2017/4.6) and the Russian Foundation for Basic Research (grant no.

18-02-00381). A.P. and A.Sl. acknowledge partial support from the Russian Foundation for Basic Research (grant no. 18-32-20065). Y.K. thanks H. Atwater, B. Kanté, D. Leykam and E. Poutrina

for discussions. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Nonlinear Physics Centre, Australian National University, Canberra, Australian Capital Territory, Australia Sergey Kruk, 

Alexander Poddubny, Daria Smirnova, Lei Wang & Yuri Kivshar * ITMO University, St Petersburg, Russia Alexander Poddubny, Alexey Slobozhanyuk & Yuri Kivshar * Ioffe Institute, St

Petersburg, Russia Alexander Poddubny * Institute of Applied Physics, Russian Academy of Science, Nizhny Novgorod, Russia Daria Smirnova * Lomonosov Moscow State University, Moscow, Russia

Alexander Shorokhov * Center for Nanophase Materials Sciences, Oak Ridge National Laboratory, Oak Ridge, TN, USA Ivan Kravchenko * Laser Physics Centre, Australian National University,

Canberra, Australian Capital Territory, Australia Barry Luther-Davies Authors * Sergey Kruk View author publications You can also search for this author inPubMed Google Scholar * Alexander

Poddubny View author publications You can also search for this author inPubMed Google Scholar * Daria Smirnova View author publications You can also search for this author inPubMed Google

Scholar * Lei Wang View author publications You can also search for this author inPubMed Google Scholar * Alexey Slobozhanyuk View author publications You can also search for this author

inPubMed Google Scholar * Alexander Shorokhov View author publications You can also search for this author inPubMed Google Scholar * Ivan Kravchenko View author publications You can also

search for this author inPubMed Google Scholar * Barry Luther-Davies View author publications You can also search for this author inPubMed Google Scholar * Yuri Kivshar View author

publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS S.K., A.Sl. and Y.K. conceived the idea. S.K., A.Sh. and B.L.-D. performed the experimental

measurements. A.P. and D.S. developed the discrete dipole theoretical model. D.S., L.W. and A.Sl. performed numerical calculations. I.K. and S.K. fabricated the samples. Y.K. supervised the

project. All authors contributed to the discussion of results and manuscript preparation. CORRESPONDING AUTHOR Correspondence to Yuri Kivshar. ETHICS DECLARATIONS COMPETING INTERESTS The

authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION Supplementary Notes 1–6; supplementary figures 1–12 RIGHTS AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE

THIS ARTICLE Kruk, S., Poddubny, A., Smirnova, D. _et al._ Nonlinear light generation in topological nanostructures. _Nature Nanotech_ 14, 126–130 (2019).

https://doi.org/10.1038/s41565-018-0324-7 Download citation * Received: 10 April 2018 * Accepted: 10 November 2018 * Published: 17 December 2018 * Issue Date: February 2019 * DOI:

https://doi.org/10.1038/s41565-018-0324-7 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative