ABSTRACT Removing influential nodes or shortcuts in a network restrains epidemic or information diffusion, but this method destroys the connectivity of the network and changes the

topological structure. As an alternative, an additional field can be imposed in the network to affect node behaviors and slow down diffusion dynamics. However, little research has been

performed systematically to analyze and compare these methods. This paper investigates epidemic dynamics and proposes the following four methods to restrain the diffusion process: blocking

nodes, blocking edges, distracting node attention, and propagating opposite information. We compare differences in the actions of these methods, and investigate their joint effects. Through

whereas distracting node attention only takes effect for the information with a small rate. Meanwhile, the effects of these two methods mainly depend on their action time. From the joint

effects, we can select the optimal method for different situations. SIMILAR CONTENT BEING VIEWED BY OTHERS GENERAL PROTOCOL FOR PREDICTING OUTBREAKS OF INFECTIOUS DISEASES IN SOCIAL NETWORKS

Article Open access 12 March 2024 IDENTIFYING INFLUENTIAL SPREADERS IN COMPLEX NETWORKS FOR DISEASE SPREAD AND CONTROL Article Open access 01 April 2022 HETEROGENEOUS UPDATE PROCESSES SHAPE

INFORMATION CASCADES IN SOCIAL NETWORKS Article Open access 22 April 2025 INTRODUCTION There is currently considerable research on modeling and analyzing dissemination dynamics. Diffusion

models capture the features of microscopic interactions, and determine the rules of node behaviors1, 2. Approaches from statistical physics, applied probability, graph theory and other

methodologies are applied to determine the spreading threshold, relaxation time and other characteristics3,4,5. Early studies investigated the propagation of epidemic diseases over an entire

population. Epidemic models include the susceptible - infected (SI) model6, 7, the susceptible- infected - susceptible (SIS) model8, and the susceptible - infected - refractory (SIR)

model9,10,11. In the SIR model, the cessation of diffusion behaviors is caused by spontaneous node immunization. The rumor model describes the diffusion process of rumors among people, and

nodes stop propagating when they contact other spreaders or refractory nodes12,13,14. These models and their revised versions are also used to characterize information diffusion15, 16. The

forgetting mechanism was introduced to the rumor model, which describes the diffusion process in a real network called LiveJournal. The results demonstrated that when the average network

degree is sufficiently large, the influence of a rumor reaches saturation17. Information diffusion in online social networks was explored, and reposting behaviors were considered among node

interactions18. Meanwhile, the addition of a behavioral classification mode into an existing epidemic framework revealed the impact of available information on the population19. In addition

to these methods, an evolutionary game theoretic framework was also used to model diffusion dynamics, and heterogeneous actions and socio-economic interactions among nodes were elaborated in

the model20. The availability of diffusion models was validated over real networks, and the topological structure of the underlying network seriously affected the dynamic process. An

experiment was conducted to study the effect of network structure on behavior diffusion, demonstrating that behaviors spread farther and faster across clustered-lattice networks than across

random networks21. For information diffusion in a network of microblogs, scale-free degree distribution achieves optimal diffusion dynamics22. When social-physical networks are conjoined,

information diffusion is further accelerated based on the SIR model23. For harmful epidemics or information, it is valuable to determine strategies that can effectively prevent diffusion.

Many studies concentrate on detecting influential nodes24 or community bridges in a network and then remove them to prevent information diffusion25. Both node isolation and quarantine were

included in epidemic dynamics according to self-compliance with the medical requests26. In the context of disease spreading, coreness constitutes a better topological descriptor to identify

influential spreaders27. However, for rumor dynamics, coreness does not determine the spreading capabilities of nodes, but it can be used to prevent the diffusion of a rumor to a system-wide

scale28. Analogously, weak ties in online social networks have a similar effect, and they might be of use in the control of information diffusion29. In ref. 30, an efficient network

immunization strategy was put forward, and the network was partitioned into clusters with an approximately equal size. This graph-based strategy requires fewer immunization doses. Moreover,

critical blocks were defined as sets of nodes that evenly partition the entire network at a small cost31. Critical blocks play a key role during the diffusion process. These strategies

require global knowledge of the network. When network knowledge is not available, the immunization of random acquaintances of random nodes is efficient for networks of any broad-degree

distribution32. In many studies, the method of removing nodes is adopted to restrain the diffusion, but network connectivity is also reduced by this method. In addition to changing the

topological structure of the network, one can select an alternative method to achieve the same goal, such as imposing a field into the system to affect node behaviors. These methods have

rarely been investigated and systematically compared. The joint effects of integration of these methods are worth further exploration. Furthermore, the effects of these methods are different

for information with different spreading capabilities and for different action time. It is unclear how to find a practical and economical method to effectively prevent diffusion in

different situations. For instance, if the information is checked in the initial stage or after the early stage of the diffusion, which method is suitable to restrain it? In this paper, we

present four methods to restrain information diffusion in static networks. These methods can be divided into two categories: altering the network structure, and imposing an addition field.

We compare the outcomes of these methods via analysis and numerical simulations. The results show that these methods have different control capacities for diffusion, and they change the

final diffusion scale and spreading threshold to different degrees. We also investigate coactions and dependence on attributes of target information, and provide an appropriate method for

different situations. The rest of this paper is structured as follows. Section 2 briefly reviews the traditional SIR model to describe information diffusion, and provides relative notations

of macroscopic states. Section 3 proposes four restraining methods, and analysis is conducted. Section 4 presents numerical simulations and discussions about these methods. Concluding

remarks are presented in Section 5. EPIDEMIC MODEL The SIR model33 was originally used to describe the diffusion of epidemic diseases. The model23 and its modified versions17, 18 were also

applied in information diffusion. In terms of epidemic models, nodes spread information to their neighbors, and information diffusion is characterized by a stochastic process. Nodes may be

in one of the following three possible epidemic states: the susceptible state, the infected state and the refractory state. The susceptible state means that nodes are unaware of the

information. When nodes are affected by neighbor’s information, they become a spreader and enter the infected state. Nodes in the refractory state lose interest in the information and will

never be infected again. The model is governed by the following rules33. * (a) When a susceptible node meets an infected node, the susceptible node is infected with probability _λ_. * (b)

Each time, infected nodes become refractory with probability _δ_. At the beginning of the dynamics, a node is infected, acting as the initial spreader, whereas all the other nodes are

susceptible. The diffusion process continues until all infected nodes become refractory. As the underlying network may be heterogeneous, nodes with different degrees should be investigated

separately. In this paper, the underlying network is a static network. It is assumed that node degrees follow distribution _P_(_k_). The probability _P_(_k_′|_k_) represents degree

correlations among nodes. The overall densities of nodes at degree _k_ in the susceptible, infected and refractory states are defined as _ρ_ _s_ (_k_, _t_), _ρ_ _i_ (_k_, _t_), and _ρ_ _r_

(_k_, _t_), respectively. The transition of these densities is listed as follows. $$\begin{array}{c}\frac{\partial {\rho }_{s}(k,t)}{\partial t}=-{\lambda }k{\rho }_{s}(k,t)\sum _{k^{\prime}

=0}^{+\infty }P(k^{\prime} |k){\rho }_{i}(k^{\prime} ,t)\\ \frac{\partial {\rho }_{i}(k,t)}{\partial t}={\lambda }k{\rho }_{s}(k,t)\sum _{k^{\prime} =0}^{+\infty }P(k^{\prime} |k){\rho

}_{i}(k^{\prime} ,t)-\delta {\rho }_{i}(k,t)\\ \frac{\partial {\rho }_{r}(k,t)}{\partial t}=\delta {\rho }_{i}(k,t)\end{array}$$ (1) In uncorrelated networks, the degree-degree correlations

can be written as $$P(k^{\prime} |k)=k^{\prime} P(k^{\prime} )/\bar{k}$$ (2) where \(\bar{k}\) indicates the average degree of the network. Then, from Eq. (1), one obtains the spreading

threshold of the model below which information cannot propagate in the network. $$\lambda > \frac{\bar{k}}{\overline{{k}^{2}}}\delta $$ (3) METHODS BLOCK DIFFUSION AT IMPORTANT NODES We

can block certain important nodes from participating in the diffusion. If a node is blocked, it will never be infected by neighboring spreaders, and information cannot traverse it. If we

block influential nodes that play a significant role in the diffusion, we may prevent the information from spreading beyond a local region or reduce the diffusion scale. We block some

influential nodes before the diffusion process. The influence of nodes may be reflected by their status in the topological structure. The indicators to describe node influence are listed as

follows. * (1) Node degree Nodes with a large degree spread information to more neighbors. If they are blocked, the chance that susceptible nodes contact the information is reduced. With

this method, nodes are sorted according to their degrees, and a proportion _γ_ of nodes at the top of the list will be blocked. Now, we consider a special case in which an uncorrelated

scale-free network mediates the diffusion. In a scale-free network, it is satisfied that \(\overline{{k}^{2}}={\bar{k}}^{2}\,\mathrm{log}(N)/4\). If _γ_ is very small, the degree

distribution is not altered by the method of blocking nodes. Thus, we obtain the spreading threshold $$\lambda > \frac{\bar{k}}{{\bar{k}}^{2}\,\mathrm{log}(N)/4}\delta =\frac{4\delta

}{\bar{k}\,\mathrm{log}(N)}\propto \frac{1}{\bar{k}}$$ (4) when nodes with a large degree are blocked, these nodes become unreachable. The underlying network is changed, and the average

network degree decreases. Therefore, this method increases the spreading threshold, and it becomes more difficult for information to propagate at a large scale. * (2) Betweenness Betweenness

of nodes represents the proportion of the shortest paths across a node. Nodes with large betweenness act as bridges that connect different communities. Through these nodes, information

propagates to more indirect nodes. If we block nodes with large betweeness, shortcuts in the network are cut off, and information may be limited to a local region. We sort nodes by their

betweenness, and block a proportion _γ_ of nodes with the largest betweenness. * (3) Clustering coefficient Clustering coefficients represent aggregation levels among nodes, and are

calculated by counting the number of connected triangles between a node and its neighbors. For nodes with a large clustering coefficient, large connectivity exists among their neighbors. For

this method, a proportion _γ_ of nodes with the top clustering coefficients are blocked. * (4) _k_-core index The _k_-core index indicates the status of a node according to its location in

the network. When a node has a large _k_-core index, it is close to the center of the network. If we block nodes with a large _k_-core index, information may be trapped at the margin of the

network. Information cannot reach hub nodes, and does not have a wide impact. For this method, we block a proportion _γ_ of nodes with the largest _k_-core index. BLOCK DIFFUSION AT

IMPORTANT EDGES We can cut off important edges, instead of blocking nodes. After deleting some edges, the connectivity of the network may be broken. Dynamics are slowed down and the

diffusion extent is limited. For this method, a proportion _γ_ of edges are removed from the network. Compared with nodes, the number of edges is much larger. Therefore, the value of _γ_ in

this method should be larger. * (1) Strong tie The tie strength between two neighboring nodes represents the heterogeneity between their neighborhoods. When nodes from two ends of an edge

have more common neighbors, the edge has a large tie strength, and vice versa. It should be investigated whether cutting off the connection of two nodes with a large or small overlap in

neighborhood more efficiently restrains information diffusion. We sort all edges by tie strength, and remove a proportion _γ_ of edges at the top of the list. * (2) Weak tie For this method,

we cut off a proportion _γ_ of edges with the smallest tie strength. * (3) Betweenness We sort edges according to their betweenness and remove a proportion _γ_ of edges at the top of the

list. DISTRACT ATTENTION OF NODES Nodes have limited activity, and they do not concentrate on the diffusion of all information. When they contact more than one piece of information, they

will choose the information that is of most interest, and consider diffusion actions. Thus, one can create another piece of information to distract node attention and restrain diffusion of

the target information. In the SIR model, the spreading probability of information _l_ 1 is defined as _λ_. We introduce information _l_ 2 with spreading probability _λ_ 2, and _l_ 2 meets

the public interest. We assume that information _l_ 2 is injected to the network at time _T_. When _t_ < _T_, only information _l_ 1 propagates in the system. When _t_ > _T_, both

pieces of information _l_ 1 and _l_ 2 simultaneously propagate. We define the densities of susceptible, infected and refractory nodes for information _l_ 1 as _ρ_ 1,_s_ (_k_, _t_), _ρ_ 1,_i_

(_k_, _t_) and _ρ_ 1,_r_ (_k_, _t_), respectively. Similarly, the densities for _l_ 2 are given by _ρ_ 2,_s_ (_k_, _t_), _ρ_ 2,_i_ (_k_, _t_), and _ρ_ 2,_r_ (_k_, _t_). Susceptible nodes

may be infected by neighboring spreaders. In the mean-field approximation, a susceptible node at degree _k_ connects to an infected node for _l_ 1 at degree _k_′ with probability

\(P({i}_{1},k^{\prime} |{s}_{1},k)\approx {\rho }_{1,i}(k^{\prime} ,t)\). With the simultaneous diffusion of the information, the dynamics are governed by the following rules. The

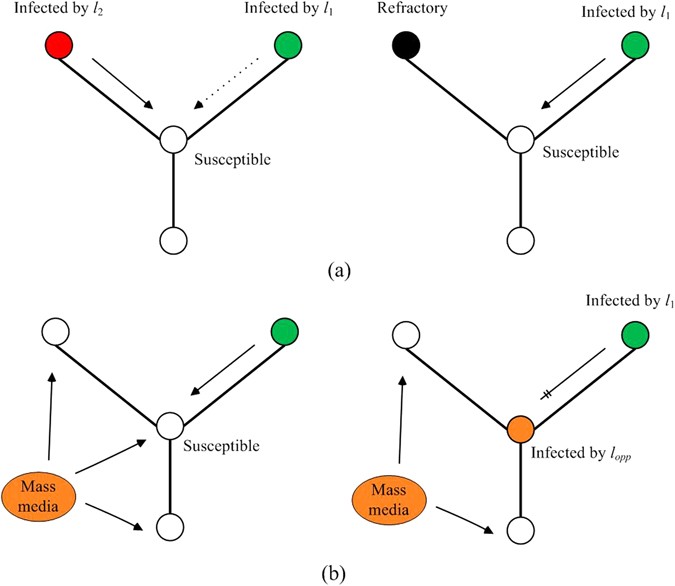
illustration for the diffusion of both pieces of information can be seen in Fig. 1a. * (a) When a susceptible node with degree _k_ for information _l_ 2 contacts an infected neighbor of _l_

2, the node may be infected by _l_ 2. Considering the influence of network topology, the probability of being infected by _k_ neighboring spreaders during each time is defined as _P_(_i_ 2,

_k_). Analogously to ref. 9, _P_(_i_ 2, _k_) is obtained by $$P({i}_{2},k)=1-\mathop{\mathrm{lim}}\limits_{{\rm{\Delta }}t\to 0}{(1-{\lambda }_{2}{\rm{\Delta }}t)}^{k/{\rm{\Delta

}}t}=1-{e}^{-{\lambda }_{2}k}$$ (5) where _λ_ 2 is the spreading rate for _l_ 2. Here, we only consider discrete time steps, and the probability at each time is approached by

\(P({i}_{2},k)={\lambda }_{2}k\). For the susceptible node, the average density of neighboring spreaders for _l_ 2 is written as $$\rho ({i}_{2}|{s}_{2},k)=\sum _{k^{\prime} }P(k^{\prime}

|k){\rho }_{2,i}(k^{\prime} ,t)$$ (6) Therefore, a susceptible node with degree _k_ may be infected by _l_ 2 at time _t_ with probability $${P}_{{s}_{2}\to {i}_{2}}(k,t)=P({i}_{2},k)\rho

({i}_{2}|{s}_{2},k)={\lambda }_{2}k\sum _{k^{\prime} }P(k^{\prime} |k){\rho }_{2,i}(k^{\prime} ,t)$$ (7) * (b) When a susceptible node with degree _k_ for information _l_ 1 contacts an

infected node of _l_ 1, the node may be infected by _l_ 1. If the susceptible node does not receive information _l_ 2, the probability of being infected by _k_ neighboring spreaders is

_P_(_i_ 1, _k_) = _λk_; otherwise, the probability of being infected by _l_ 1 is 0. For the susceptible node, the average density of neighboring spreaders for _l_ 1 that are non-spreaders

for _l_ 2 is written as $$\rho ({i}_{1},{\rm{not}}\,{i}_{2}|{s}_{1},k)=\sum _{k^{\prime} }P(k^{\prime} |k){\rho }_{1,i}(k^{\prime} ,t)(1-{\rho }_{2,i}(k^{\prime} ,t))$$ (8) Therefore, a

susceptible node with degree _k_ may be infected by _l_ 1 at time _t_ with probability $${P}_{{s}_{1}\to {i}_{1}}(k,t)=P({i}_{1},k)\rho ({i}_{1},\,{\rm{not}}{i}_{2}|{s}_{1},k)=\lambda k\sum

_{k^{\prime} }P(k^{\prime} |k){\rho }_{1,i}(k^{\prime} ,t)(1-{\rho }_{2,i}(k^{\prime} ,t))$$ (9) * (c) Each time, spreaders of information _l_ 1 and _l_ 2 become refractory with probability

_δ_. Overall, in the diffusion process, information _l_ 2 that is injected at time _T_ starts spreading over the network during the transient phase of information _l_ 1, and it exerts an

inhibitory effect on _l_ 1 after _T_. When a node simultaneously contacts information _l_ 1 and _l_ 2, _l_ 2 is preferentially adopted. Therefore, the probability that a susceptible node is

infected by spreaders for _l_ 2 is the same as that in the SIR model; therefore, the transition of densities for _l_ 2 agrees with Eq. (1). Now, we study the diffusion of information _l_ 1.

We obtain the transition of _ρ_ 1,_s_ (_k_, _t_), _ρ_ 1,_i_ (_k_, _t_), and _ρ_ 1,_r_ (_k_, _t_) from the model. $$\begin{array}{c}\frac{\partial {\rho }_{1,s}(k,t)}{\partial t}=-\lambda

k{\rho }_{1,s}(k,t)\sum _{k^{\prime} }P(k^{\prime} |k){\rho }_{1,i}(k^{\prime} ,t)(1-{\rho }_{2,i}(k^{\prime} ,t))\\ \frac{\partial {\rho }_{1,i}(k,t)}{\partial t}=\lambda k{\rho

}_{1,s}(k,t)\sum _{{k}^{\text{'}}}P(k^{\prime} |k){\rho }_{1,i}(k^{\prime} ,t)(1-{\rho }_{2,i}(k^{\prime} ,t))-\delta {\rho }_{1,i}(k,t)\\ \frac{\partial {\rho }_{1,r}(k,t)}{\partial

t}=\delta {\rho }_{1,i}(k,t)\end{array}$$ (10) When _t_ < _T_, it holds true that _ρ_ 2,_i_ (_k_′, _t_) = 0, and the diffusion of _l_ 1 is the same as the SIR model. If _T_ > 0, the

spreading threshold for information _l_ 1 remains unchanged under the action of _l_ 2. Then, we consider the special case _T_ = 0, i.e., information starts to propagate at the beginning of

the dynamics. We integrate the first equation of Eq. (10) from time 0 to time _t_, and obtain $${\rho }_{1,s}(k,t)={\rho }_{1,s}(k,0){e}^{-\lambda k\varphi (t)}$$ (11) where _ρ_ 1,_s_ (_k_,

0) is the initial density of susceptible nodes for information _l_ 1, and it yields _ρ_ 1,_s_ (_k_, 0) ≈ 1. The auxiliary function _ϕ_(_t_) is expressed as $$\begin{array}{rcl}\varphi (t)

& = & \sum _{{k}^{\text{'}}}P(k^{\prime} |k){\int }_{0}^{t}{\rho }_{1,i}(k^{\prime} ,t^{\prime} )(1-{\rho }_{2,i}(k^{\prime} ,t^{\prime} ))dt^{\prime} \\ & = &

\frac{1}{\bar{k}}\sum _{k^{\prime} }k^{\prime} P(k^{\prime} ){\int }_{0}^{t}{\rho }_{1,i}(k^{\prime} ,t^{\prime} )(1-{\rho }_{2,i}(k^{\prime} ,t^{\prime} ))dt^{\prime} \end{array}$$ (12)

Multiplying both sides of the second equation of Eq. (10) by \(kP(k)/\bar{k}\), and summing over different _k_, we have the following expression. $$\begin{array}{c}\frac{1}{\bar{k}}\sum

_{k}kP(k)\frac{\partial {\rho }_{1,i}(k,t)}{\partial t}=\,\frac{\lambda }{\bar{k}}\sum _{k}{k}^{2}P(k){\rho }_{1,s}(k,t)\sum _{{k}^{\text{'}}}\frac{k^{\prime} P(k^{\prime}

)}{\bar{k}}{\rho }_{1,i}(k^{\prime} ,t)(1-{\rho }_{2,i}(k^{\prime} ,t))-\frac{\delta }{\bar{k}}\sum _{k=0}^{+\infty }kP(k){\rho }_{1,i}(k,t)\\ \phantom{\rule{5em}{0ex}}\qquad \quad

\,\,\,=\,\frac{\lambda }{\bar{k}}\sum _{k}{k}^{2}P(k){\rho }_{1,s}(k,t)\frac{d\varphi (t)}{dt}-\frac{\delta }{\bar{k}}\sum _{k=0}^{+\infty }kP(k){\rho }_{1,i}(k,t)\end{array}$$ (13) We

integrate Eq. (13) by _t_, and obtain $$\frac{1}{\bar{k}}\sum _{k}kP(k){\rho }_{1,i}(k,t)=\frac{\lambda }{\bar{k}}\sum _{k}{k}^{2}P(k){\int }_{0}^{t}{e}^{-\lambda k\varphi (t^{\prime}

)}\frac{d\varphi (t^{\prime} )}{dt^{\prime} }dt^{\prime} -\frac{\delta }{\bar{k}}\sum _{k=0}^{+\infty }kP(k){\int }_{0}^{t}{\rho }_{1,i}(k,t^{\prime} )dt^{\prime} $$ (14) Noting that when

_t_ → +∞, _ρ_ 1,_i_ (_k_, _t_) = 0, after some elementary manipulations, Eq. (14) becomes $$0=\frac{1}{\bar{k}}\sum _{k}kP(k)(1-{e}^{-\lambda k\varphi (\infty )})-\frac{\delta }{\bar{k}}\sum

_{k=0}^{+\infty }kP(k){\int }_{0}^{+\infty }{\rho }_{1,i}(k,t^{\prime} )dt^{\prime} $$ (15) We focus on the second part of the right side of Eq. (15). When information _l_ 2 can propagate

in the network, i.e., \({\lambda }_{2} > \bar{k}\delta /\bar{{k}^{2}}\), it holds true that 1 − _ρ_ 2,_i_ (_k_,_ t_) < 1. Therefore, we have $$\varphi (\infty )=\frac{1}{\bar{k}}\sum

_{{k}^{\text{'}}}k^{\prime} P(k^{\prime} ){\int }_{0}^{+\infty }{\rho }_{1,i}(k^{\prime} ,t^{\prime} )(1-{\rho }_{2,i}(k^{\prime} ,t^{\prime} ))dt^{\prime} < \frac{1}{\bar{k}}\sum

_{k^{\prime} }k^{\prime} P(k^{\prime} ){\int }_{0}^{+\infty }{\rho }_{1,i}(k^{\prime} ,t^{\prime} )dt^{\prime} $$ (16) We assume that $$\frac{1}{\bar{k}}\sum _{k^{\prime} }k^{\prime}

P(k^{\prime} ){\int }_{0}^{+\infty }{\rho }_{1,i}(k^{\prime} ,t^{\prime} )dt^{\prime} =\beta \varphi (\infty )$$ (17) where _β_ is a constant with _β_ > 1. Around the threshold, _ϕ_(∞) is

small, so _e_ −_λkϕ_(∞) → 1. Inserting Eq. (17) into Eq. (15) and making the Taylor expansion of_ e_ −_λkϕ_(∞),we obtain $$0=\frac{1}{\bar{k}}\sum _{k}(\lambda {k}^{2}P(k)\varphi (\infty

)-{\lambda }^{2}{k}^{3}P(k){\varphi }^{2}(\infty ))+o({\varphi }^{2}(\infty ))-\beta \delta \varphi (\infty )$$ (18) We calculate _ϕ_(∞) from Eq. (18) $$\varphi (\infty )=\frac{\lambda

\overline{{k}^{2}}/\bar{k}-\beta \delta }{{\lambda }^{2}\overline{{k}^{3}}/\bar{k}}$$ (19) When information _l_ 1 can propagate, it should hold true that _ϕ_(∞) > 0. Therefore, we obtain

the spreading threshold for _l_ 1 $$\lambda > \frac{\beta \delta \bar{k}}{\overline{{k}^{2}}}$$ (20) As _β_ > 1, the spreading threshold increases. Therefore, when _T_ = 0, the method

of distracting node attention changes both the spreading threshold and diffusion extent. PROPAGATE OPPOSITE INFORMATION BY MASS MEDIA We can utilize mass media to propagate information _l_

_opp_ that has the opposite content with current information _l_ 1, and to restrain the diffusion of _l_ 1. For instance, website administrators may clarify the truth to restrain rumor

diffusion in online networks. The authorities create positive information and propagate it. The information is often located in conspicuous places of the website, such that it can easily be

seen by all users. When users read information that originates from mass media, they are likely to accept the information. If they are convinced by the truth, they will no longer be infected

by the rumor. Assume that the opposite information _l_ _opp_ is injected to the network at time _T_, and nodes are infected by it with probability _λ_ _opp_ . The model evolves following

the rules below. Figure 1b illustrates the dynamic diffusion. * (a) A susceptible node with degree _k_ may be infected by _l_ 1 at time _t_ with probability $${P}_{{s}_{1}\to

{i}_{1}}(k,t)=\lambda k\sum _{k^{\prime} }P(k^{\prime} |k){\rho }_{1,i}(k^{\prime} ,t)$$ (21) * (b) Each time, infected nodes of _l_ 1 become refractory with probability _δ_. * (c)

Information _l_ _opp_ is injected to the network at time _T_. It infects all susceptible nodes with probability _λ_ _opp_ . In that case, if a node was previously in the susceptible state,

it will never be infected by _l_ 1. The density of susceptible nodes for _l_ 1 decreases by the inhibitory action of _l_ _opp_ . We obtain the transition of densities in different states for

information _l_ 1 when _t_ > _T_. $$\begin{array}{c}\frac{\partial {\rho }_{1,s}(k,t)}{\partial t}=-\lambda k{\rho }_{1,s}(k,t)\sum _{k^{\prime} =0}^{+\infty }P(k^{\prime} |k){\rho

}_{1,i}(k^{\prime} ,t)-{\lambda }_{opp}{\rho }_{1,s}(k,t)\\ \frac{\partial {\rho }_{1,i}(k,t)}{\partial t}=\lambda k{\rho }_{1,s}(k,t)\sum _{k^{\prime} =0}^{+\infty }P(k^{\prime} |k){\rho

}_{1,i}(k^{\prime} ,t)-\delta {\rho }_{1,i}(k,t)\\ \frac{\partial {\rho }_{1,r}(k,t)}{\partial t}=\delta {\rho }_{1,i}(k,t)\end{array}$$ (22) Obviously, the diffusion process is divided into

two stages, i.e., _t_ < _T_ and _t_ > _T_. For _t_ < _T_, the evolution is the same as the traditional SIR model. Now we consider the case _t_ > _T_. After time _T_, it holds

true that \({\rho }_{1,s}(k,T)+{\rho }_{1,i}(k,T)+{\rho }_{1,r}(k,T)\ne 1\). If _T_ is large, it is easy to infer from the second equation of Eq. (22) that the spreading threshold is not

changed by mass media. If _T_ is small, the influence of mass media cannot be neglected. The system is governed by two dynamics: the diffusion of information _l_ 1 and its opposite edition

_l_ _opp_ . These two pieces of information have different time scales of diffusion. Compared with information _l_ 1, the dynamics of _l_ _opp_ are much faster because it is published by

mass media and can simultaneously act on all nodes. Therefore, when _T_ is sufficiently small, in the early stage of the diffusion process for _l_ 1, the initial condition is \({\rho

}_{1,i}(k,t)\approx 0\) at _t_ = _T_ + Δ_t_, but the initial density of susceptible nodes _ρ_ 1,_s_ (_k_,_t_) does not approach 1. Therefore, the spreading threshold for _l_ 1 increases. We

conclude that for small _T_, this method not only affects the threshold for the diffusion of _l_ 1, but it also changes the diffusion extent. RESULTS We conducted Monte-Carlo simulations to

investigate the effects of the aforementioned four methods. Initially, a node is selected at random, and it is set in the infected state, whereas all the other nodes are susceptible. The

system size is defined as _N_. Simulations are synchronously performed. At each time step, all infected nodes contact their neighbors, and persuade them to participate in diffusion. Then,

infected nodes may simultaneously become refractory. As these restraining methods have different scales and action mechanisms, we cannot depict the results together in the same parameter

space. However, we can compare the effects of these methods on the spreading threshold, relaxation speed and other properties as well as determine the optimal restraining method in different

situations. It should be noted that the methods of removing nodes and edges increase the cost, because the network connectivity is destroyed. Barabasi-Albert scale-free networks and a real

social network are used as interaction topology. The average degree of scale-free networks is \(\bar{k}=4\). The social network was collected from the Sina micro-blog (www.weibo.com), which

is one of the most popular online social networks in China. The network contains 5906 nodes. The average degree is \(\bar{k}=4.5008\), and the average clustering coefficient is 0.0772.

First, we separately studied the effects of the four restraining methods, and then we compared their mechanisms together. BLOCK NODES Figure 2 shows the time evolution for the density of

refractory nodes with the method of blocking different nodes in a scale-free network. The method of blocking nodes with large degrees takes effect most evidently, whereas blocking nodes with

large cluster coefficients seems ineffective for preventing information diffusion. Increasing the proportion of nodes that are blocked clearly decreases the number of refractory nodes,

reducing the impact of the information. However, even when _γ_ = 0.05, information still succeeds in propagating in the network, as a result of high connectivity in the network. When _γ_ = 

0.05, very few nodes are infected from the method of blocking nodes with large degrees. The effect of betweenness is larger than the _k_-core, especially when _γ_ increases. The method

restrains information diffusion from the beginning of the evolutionary process until the system stabilizes. To further understand the essential mechanism of the method, we observed the

impact of the method of blocking different nodes on network connectivity. When nodes are blocked according to their betweenness, the average degree of the network drops to 3.1016 for _γ_ = 

0.01 and 2.1856 for _γ_ = 0.05. When the method regarding clustering coefficients is used, the average degree is 3.9552 for _γ_ = 0.01 and 3.1680 for _γ_ = 0.05. Obviously, blocking nodes at

large betweenness increases the loss of network connectivity. With more extensive damage to network connectivity, information can be seriously limited. Figure 3 shows the evolution in the

real network. The results are analogous to those in a scale-free network. The effect of the degree-dependent method almost approaches the betweenness-dependent method, especially when _γ_ = 

0.05. However, the difference between the effect of _k_-core and betweenness is enlarged in the real network. Dramatically, the final density of refractory nodes remains nearly unchanged

under the action of the method regarding clustering coefficients, when the proportion of blocked nodes increases. We observed that the average clustering coefficient in the real network is

much larger than that in a scale-free network. Comparing Fig. 3 with Fig. 2, the extent of information diffusion drops in the real network, as a result of a more heterogeneous degree

distribution. We normalized the distribution to [0, 1] and quantize it with equal intervals. Next, we calculated the Gini coefficient of the distribution34. The Gini coefficient of node

degrees in a scale-free network is 0.9645, whereas that in the real network is 0.9825. If some nodes in the shortcuts are blocked, the network may be divided into several unconnected

communities, such that information diffusion is trapped in a single community. For _γ_ = 0.05, if nodes with large degrees or betweenness are blocked, information cannot propagate in the

real network. We investigated the impact of the method on the spreading threshold, as shown in Fig. 4. As the effect of the betweenness-dependent method is close to that of the

degree-dependent method, the result is not shown here when blocking nodes with large betweenness. Obviously, blocking nodes changes the threshold of _λ_, which agrees with analytical

results. By increasing the restraining proportion _γ_, the spreading threshold is enlarged especially for the degree-dependent method, and some nodes are always blocked from the information

even when _λ_ = 1. With the method regarding _k_-core and clustering coefficients, when _γ_ is small, the threshold is almost 0, implying that it is easy for information to propagate in the

real network. In the right plot, when _γ_ is increased, a small threshold is observed for the core-dependent method, but the threshold remains 0 when blocking nodes with large clustering

coefficients. Therefore, the method regarding clustering coefficients hardly affects the threshold for information diffusion. BLOCK EDGES Figure 5 illustrates the effect of blocking

diffusion at different edges in a scale-free network. From this figure, the method of blocking weak ties achieves a better performance in all situations than blocking strong ties, meaning

that weak ties act as bridges to connect isolated groups together and deleting weak ties can trap information in local regions. However, blocking these edges cannot completely prevent

information diffusion. Even if the proportion of these edges that are blocked is 0.4, more than 17% of nodes are affected by the information. The method of blocking edges with large

betweenness takes effect depending on the proportion _γ_. When _γ_ is small, blocking edges with large betweenness cannot obviously prevent the occurrence of refractory nodes; however, for

large _γ_, betweenness becomes the most effective feature. Because there are many shortcuts in the scale-free network, information can still propagate at a large scale through remaining

shortcuts unless sufficient edges are removed. As shown in Fig. 6, because there is large heterogeneity in the edge distribution of the real network, more nodes can be prevented from

information in the network than in a scale-free network except for the method of blocking strong ties. This result is similar to that shown in Fig. 3. Betweenness remains an important

feature for restraining diffusion, despite _γ_. We also observed that the method of blocking edges has little effect on the spreading threshold, except for the case of a small spreading

threshold from the weak tie-dependent method with large _γ_. DISTRACT THE ATTENTION OF NODES We introduced information _l_ 2 that is more attractive to all nodes, and subsequently studied

its restraining action on the diffusion of _l_ 1. Figure 7 shows the time evolution of infected nodes for two pieces of information. _l_ 2 is injected into the network at the beginning,

i.e., _T_ = 0, and therefore, _l_ 1 is influenced as soon as it propagates. When the spreading probability of information _l_ 2 is small, the evolutionary trend of the density of infected

nodes for _l_ 1 is similar to _l_ 2, implying that the restraining action is generated all along with the diffusion of _l_ 1. The densities of infected nodes for _l_ 1 and _l_ 2 increase at

first, and then peak at almost the same time. Finally, all infected nodes for _l_ 1 and _l_ 2 quickly become extinct. The maximal density for _l_ 1 is not far from that for _l_ 2, meaning

the impact is not significant. When _λ_ 2 is large, the peak for _l_ 2 is greatly enhanced. It is dramatic that the density of infected nodes for _l_ 1 has two peaks. When the density of

spreaders for _l_ 2 drops to a low level, more infected nodes for _l_ 1 occur and their density increases. Therefore, the restraining action plays a role in the initial phase of diffusion.

When information _l_ 2 stops propagating, the diffusion of _l_ 1 is recovered. However, the maximal density for _l_ 1 declines severely, implying that a strong restraining effect has

occurred. In addition, the method of distracting node attention accelerates the diffusion process. Within less than 30 time steps, all infected nodes become refractory, leading to a short

relaxation time of the system. Figure 8 shows the final density of refractory nodes for information _l_ 1 under different actions of _l_ 2. When information _l_ 2 propagates at the

beginning, the spreading threshold of _l_ 1 is changed. For _T_ = 0, larger spreading probability _λ_ 2 increases the threshold of _l_ 1, and decreases the final density of refractory nodes.

However, if the diffusion of information _l_ 2 is delayed, the threshold of _l_ 1 remains nearly unchanged, coinciding with the analysis. Therefore, the spreading threshold is sensitive to

the action time of this method. Especially, when _T_ = 20, more nodes become refractory even with large _λ_ 2. Unlike Fig. 4, the final density for _l_ 1 approximately increases linearly

with _λ_ beyond the threshold, and it will reach a large value even if the spreading capacity of _l_ 2 is strong. Because a large proportion of nodes may be infected during the diffusion

process, the method cannot efficiently prevent the diffusion of information that has large spreading probability. PROPAGATE OPPOSITE INFORMATION BY MASS MEDIA Figure 9 demonstrates the

restraining result for the method of propagating opposite information by mass media. Compared with the method of distracting node attention, this method has a more distinct effect.

Increasing the spreading probability of opposite information _λ_ _opp_ , the diffusion of _l_ 1 is restrained and the final density of refractory nodes decreases especially when _T_ is

smaller. The final density decreases for _λ_ _opp_  < 0.8, but it gradually stabilizes for _λ_ _opp_  > 0.8. Therefore, it is not economical to promote the spreading probability for

mass media beyond 0.8. When _T_ = 5, the threshold for _l_ 1 is changed with _λ_ _opp_ , which agrees with the analysis. However, when _T_ > 10, the threshold becomes independent of _λ_

_opp_ , and the decrease for the density of refractory nodes is not marked as _λ_ _opp_ increases. Compared with the spreading probability of opposite information, the time when it is

injected plays a far more important role in restraining _l_ 1. Even if the spreading probability _λ_ of _l_ 1 is increased, _l_ 1 can be effectively restrained by mass media on the condition

that mass media work as early as possible. The effect is different from the method of distracting node attention. COMPARISON AND COMBINATION From the left plot of Fig. 3 and right plot of

Fig. 6, the method of blocking nodes with large betweenness for _γ_ = 0.01 has a similar restraining effect to that of blocking edges with large betweenness for _γ_ = 0.4. By blocking edges

for _γ_ = 0.4, 80.41% nodes in the network are involved with these removed edges; however, by blocking nodes, the proportion of involved nodes is 1%. On the one hand, more effort should be

made to restrain the diffusion by the method of blocking edges, and the method of blocking nodes is more effective. On the other hand, when nodes are blocked, all the edges that link to

these nodes are invalid, destroying the network connectivity. After blocking nodes with large betweenness, the average degree of the network is 2.4840, whereas after blocking edge, the

average degree is 2.7005. Therefore, the method of blocking nodes causes a larger loss of network connectivity. With respect to injecting another piece of information, the method of

distracting node attention can be regarded as an internal field, and propagating opposite information refers to an external field. These two methods exert an obvious effect in the early

stage of diffusion. Especially for distracting node attention, only when _T_ is approximately 0, the spreading threshold is changed, and the final density of refractory nodes decreases. The

method of propagating opposite information is more effective because it is induced by mass media. We integrated multiple methods to restrain information diffusion and investigated the

coherent action of these methods. Figure 10 illustrates the joint effect of methods of distracting node attention and propagating opposite information by mass media. Here, we considered that

the target information has large spreading probability _λ_, and studied whether the methods are sufficient to restrain it. In Fig. 10, mass media considerably reduce the final diffusion

extent of the information. Although the method of distracting node attention makes the final refractory density decrease, the target information is not effectively limited. The coherent

effect of the two methods is mainly determined by mass media. Contours of the curved surface are nearly parallel to the axis of _λ_ 2, implying that increasing _λ_ _opp_ has a great

advantage over _λ_ 2. Therefore, for information with large spreading probability, a better approach to restrain diffusion is to propagate opposite information by mass media, although more

cost may be required. We investigated the combination of blocking nodes with large degrees and propagating opposite information. Here, we considered that the target information is detected

late after the early stage, and investigated whether these remedial measures are effective when they do not work early. To achieve the same baseline, we did not block nodes at the beginning;

instead, we blocked them at _t_ = _T_. From Fig. 11, both methods reduce the final density of refractory nodes. The contours of the curved surface are not parallel to the coordinate axis;

instead, they correlate with both _γ_ and _λ_ _opp_ , demonstrating the joint effect of the two methods. Large _γ_ restrains the diffusion, and large _λ_ _opp_ further lessens the refractory

nodes. Moreover, blocking nodes has a stronger influence and the diffusion extent has a dramatic drop with this method, but propagating opposite information cannot limit the diffusion at a

low level. Therefore, if the method is not adopted in a timely manner, the only effective choice is to block nodes at large degrees. CONCLUSIONS To restrain information diffusion, we may

remove nodes and community bridges to break network connectivity and trap information in local regions. Substantial effort should be made to block many elements in a large-scale network.

Meanwhile, we can also impose a field to the network, and affect interactions among nodes. The field may work from the outside or inside of the network. In this paper, we presented four

methods of restraining information diffusion. These methods belong to two categories: changing the network structure and changing node behavior. Based on the epidemic model, we analyzed the

spreading threshold of the target information with the mean-field approach, and investigated the effects on the final diffuse extent with different conditions. The results indicate that the

methods restrain information diffusion and change the spreading threshold in defined conditions. Blocking nodes with large degrees or betweenness effectively prevents diffusion, and the

method may even completely limit information to local regions. Blocking edges with large betweenness has a distinct effect in the real network. The method of blocking nodes is more efficient

and economical than blocking edges. Distracting node attention restrains the diffusion only when the method is adopted at the beginning, and it is only available for information with small

spreading capabilities. The effect of propagating opposite information is more determined by the action time than the action intensity. Different situations require the selection of optimal

methods that lead to a compromise between effectiveness and cost. For information with small spreading probability, distracting node attention can restrain diffusion. However, for

information with large spreading probability, the better approach is to propagate opposite information. If the remedial measure works after the early stage of information diffusion, the only

effective method is to block nodes with large degrees or betweenness. In the present work, we assume that the imposed field has the same influence on each node. However, nodes may have

different behaviors under identical measures. In the future, we will investigate how node behaviors are affected in detail and study the influence of heterogeneous spreading capabilities.

REFERENCES * Castellano, C., Fortunato, S. & Loreto, V. Statistical physics of social dynamics. _Rev. Mod. Phys._ 81, 591 (2009). Article  ADS  Google Scholar  * Albert, R. &

Barabasi, A. L. Statistical mechanics of complex networks. _Rev. Mod. Phys._ 74, 47 (2002). Article  ADS  MathSciNet  MATH  Google Scholar  * Barthelemy, M., Barrat, A., Pastor-Satorras, R.

& Vespignani, A. Velocity and hierarchical spread of epidemic outbreaks in scale-free networks. _Phys. Rev. Lett._ 92, 178701 (2004). Article  ADS  PubMed  Google Scholar  * Genois, M.,

Vestergaard, C. L., Cattuto, C. & Barrat, A. Compensating for population sampling in simulations of epidemic spread on temporal contact networks. _Nat. Commun._ 6, 8860 (2015). Article 

ADS  CAS  PubMed  PubMed Central  Google Scholar  * Rocha, L. E. C. & Masuda, N. Individual-based approach to epidemic processes on arbitrary dynamic contact networks. _Sci. Rep._ 6,

31456 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Fuhrman, K. M., Lauko, I. G. & Pinter, G. A. Asymptotic behavior of an SI epidemic model with pulse removal.

_Math. Comput. Model._ 40, 371 (2004). Article  MathSciNet  MATH  Google Scholar  * Liu, B., Duan, Y. & Luan, Shi Dynamics of an SI epidemic model with external effects in a polluted

environment. _Nonlinear Anal.-Real._ 13, 27 (2012). Article  MathSciNet  MATH  Google Scholar  * Parshani, R., Carmi, S. & Havlin, S. Epidemic threshold for the

susceptible-infectious-susceptible model on random networks. _Phys. Rev. Lett._ 104, 258701 (2010). Article  ADS  PubMed  Google Scholar  * Newman, M. E. J. Spread of epidemic disease on

networks. _Phys. Rev. E_ 66, 016128 (2002). Article  ADS  MathSciNet  CAS  Google Scholar  * Silva, R. D. & Fernandes, H. A. A study of the influence of the mobility on the phase

transitions of the synchronous SIR model. _J. Stat. Mech._ 2015, P06011 (2015). Article  MathSciNet  Google Scholar  * Wang, Y., Cao, J. D., Alofi, A., AL-Mazrooei, A. & Elaiw, A.

Revisiting node-based sir models in complex networks with degree correlations. _Physica A_ 437, 75 (2015). Article  ADS  Google Scholar  * Moreno, Y., Nekovee, M. & Pacheco, A. F.

Dynamics of rumor spreading in complex networks. _Phys. Rev. E_ 69, 066130 (2004). Article  ADS  Google Scholar  * Trpevski, D., Tang, W. K. S. & Kocarev, L. Model for rumor spreading

over networks. _Phys. Rev. E_ 81, 056102 (2010). Article  ADS  Google Scholar  * Zanette, D. H. Dynamics of rumor propagation on small-world networks. _Phys. Rev. E_ 65, 041908 (2002).

Article  ADS  Google Scholar  * Li, W. _et al_. How multiple social networks affect user awareness: The information diffusion process in multiplex networks. _Phys. Rev. E_ 92, 042810 (2015).

Article  ADS  Google Scholar  * Wang, Q. Y., Lin, Z., Jin, Y. H., Cheng, S. D. & Yang, T. ESIS: Emotion-based spreader-ignorant-stifler model for information diffusion. _Knowl.-Based

Syst._ 81, 46 (2015). Article  Google Scholar  * Zhao, L. J. _et al_. SIHR rumor spreading model in social networks. _Physica A_ 390, 2619 (2011). Article  ADS  Google Scholar  * Xiong, F.,

Liu, Y., Zhang, Z. J., Zhu, J. & Zhang, Y. An information diffusion model based on retweeting mechanism for online social media. _Phys. Lett. A_ 376, 2103 (2012). Article  ADS  CAS 

Google Scholar  * Mishra, B. K., Haldar, K. & Sinha, D. N. Impact of information based classification on network epidemics. _Sci. Rep._ 6, 28289 (2016). Article  ADS  CAS  PubMed  PubMed

Central  Google Scholar  * Jiang, C., Chen, Y. & Liu, K. J. Evolutionary dynamics of information diffusion over social networks. _IEEE T. Signal Proces._ 62, 4573 (2014). Article  ADS 

MathSciNet  Google Scholar  * Centola, D. The spread of behavior in an online social network experiment. _Science_ 329, 1194 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Li, Y.,

Qian, M. J., Jin, D. P., Hui, P. & Vasilakos, A. V. Revealing the efficiency of information diffusion in online social networks of microblog. _Inform. Sci._ 293, 383 (2015). Article 

Google Scholar  * Yagan, O., Qian, D. J., Zhang, J. S. & Cochran, D. Conjoining speeds up information diffusion in overlaying social-physical networks. _IEEE J. Sel. Area Comm._ 31, 1038

(2013). Article  Google Scholar  * Aral, S. & Walker, D. Identifying influential and susceptible members of social networks. _Science_ 337, 337 (2012). Article  ADS  MathSciNet  CAS 

PubMed  MATH  Google Scholar  * Holme, P. & Liljeros, F. Birth and death of links control disease spreading in empirical contact networks. _Sci. Rep._ 4, 4999 (2014). Article  ADS  CAS 

PubMed  PubMed Central  Google Scholar  * Crokidakis, N. & Queiros, S. M. D. Probing into the effectiveness of self-isolation policies in epidemic control. _J. Stat. Mech._ 2012, P06003

(2012). Google Scholar  * Kitsak, M. _et al_. Identification of influential spreaders in complex networks. _Nat. Phys._ 6, 888 (2010). Article  CAS  Google Scholar  * Borge-Holthoefer, J.

& Moreno, Y. Absence of influential spreaders in rumor dynamics. _Phys. Rev. E_ 85, 026116 (2012). Article  ADS  Google Scholar  * Zhao, J. C., Wu, J. J. & Xu, K. Weak ties: subtle

role of information diffusion in online social networks. _Phys. Rev. E_ 82, 016105 (2010). Article  ADS  Google Scholar  * Chen, Y. P., Paul, G., Havlin, S., Liljeros, F. & Stanley, H.

E. Finding a better immunization strategy. _Phys. Rev. Lett._ 101, 058701 (2008). Article  ADS  PubMed  Google Scholar  * Zhang, E. N., Wang, G. R., Gao, K. N. & Yu, G. Finding critical

blocks of information diffusion in social networks. _World Wide Web_ 18, 731 (2015). Article  Google Scholar  * Cohen, R., Havlin, S. & ben-Avraham, D. Efficient immunization strategies

for computer networks and populations. _Phys. Rev. Lett._ 91, 247901 (2003). Article  ADS  PubMed  Google Scholar  * Moreno, Y., Pastor-Satorras, R. & Vespignani, A. Epidemic outbreaks

in complex heterogeneous networks. _Eur. Phys. J. B_ 26, 521 (2002). ADS  CAS  Google Scholar  * Dagum, C. The generation and distribution of income, the Lorenz curve and the Gini ratio.

_Econ. Appl._ 33, 327 (1980). Google Scholar  Download references ACKNOWLEDGEMENTS This work has been supported by the National Natural Science Foundation of China under Grant 61401015, the

Fundamental Research Funds for the Central Universities under Grant 2017JBM013 the Talent Fund of Beijing Jiaotong University under Grant 2015RC013. AUTHOR INFORMATION AUTHORS AND

AFFILIATIONS * School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing, 100044, China Fei Xiong & Zhao-Yi Li * Key Laboratory of Communication and

Information Systems (Beijing Jiaotong University), Beijing Municipal Commission of Education, Beijing, 100044, China Fei Xiong & Zhao-Yi Li Authors * Fei Xiong View author publications

You can also search for this author inPubMed Google Scholar * Zhao-Yi Li View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS F.X. designed the

research and wrote the paper, F.X. and Z.Y.L. performed the numerical simulations and analyzed the results. CORRESPONDING AUTHOR Correspondence to Fei Xiong. ETHICS DECLARATIONS COMPETING

INTERESTS The authors declare that they have no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in

published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use,

sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative

Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated

otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds

the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and

permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Xiong, F., Li, ZY. Effective Methods of Restraining Diffusion in Terms of Epidemic Dynamics. _Sci Rep_ 7, 6013 (2017).

https://doi.org/10.1038/s41598-017-06171-6 Download citation * Received: 22 December 2016 * Accepted: 09 June 2017 * Published: 20 July 2017 * DOI: https://doi.org/10.1038/s41598-017-06171-6

SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy

to clipboard Provided by the Springer Nature SharedIt content-sharing initiative