ABSTRACT Cells orchestrate the action of various molecules toward organizing their chromosomes. Using a coarse-grained computational model, we study the compaction of bacterial chromosomes

by the cross-linking protein H-NS and cellular crowders. In this work, H-NS, modeled as a mobile “binder,” can bind to a chromosome-like polymer with a characteristic binding energy. The

simulation results reported here clarify the relative role of biomolecular crowding and H-NS in condensing a bacterial chromosome in a quantitative manner. In particular, they shed light on

the nature and degree of crowder and H-NS synergetics: while the presence of crowders enhances H-NS binding to a chromosome-like polymer, the presence of H-NS makes crowding effects more

POLYMER PHYSICS INDICATES CHROMATIN FOLDING VARIABILITY ACROSS SINGLE-CELLS RESULTS FROM STATE DEGENERACY IN PHASE SEPARATION Article Open access 03 July 2020 NONLINEAR MECHANICS OF HUMAN

MITOTIC CHROMOSOMES Article Open access 04 May 2022 INTRODUCTION Chromosomes in cells are tightly packed but maintain a high level of organization1,2,3. What holds them in organized

structures, as required for their biological functions (e.g. transcription or replication, ...)? Indeed, chromosome organization is a challenging task every cell faces and relies on the

action of various molecules and the physical effects they bring about1,2,3. In the case of bacterial chromosomes, a number of studies clarify the roles of nucleoid associated proteins (NAPs)

such as HU and H-NS4,5,6,7. They bend, cross-link, loop, or supercoil the chromosomal DNA. Also, the significance of biomolecular crowding has been highlighted2,8,9,10,11,12,13,14,15. In a

crowded cellular space8,16,17, chain molecules such as chromosomes can be entropically collapsed and phase-separated from the surrounding crowders2,8,9,10,11,12,13,14,15. As shown at the

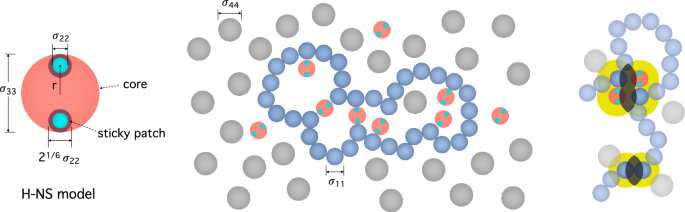
bottom right in Fig. 1, chain segments experience entropic (depletion) attractions induced by crowding effects18. Each monomer can be viewed as being surrounded with a ‘depletion layer’

(shown in yellow) inside which the center of crowders are excluded18. Overlapping of depletion layers increases the space available to crowders. As a result, association of monomers is

favored by the entropy of crowders. This is the origin of depletion forces. While relying heavily on this non-specific (entropic) mechanism, bacterial chromosome organization should be

controlled in such a way that it works in concert with other processes, such as transcription, chromosome segregation, and cell growth2,3,19. Furthermore, a number of recent studies point to

the synergetic effects brought about by crowders and the protein H-NS20,21. H-NS alone has a relatively-minor effect on chromosome compaction, similarly to what other chromosome-associating

proteins do14, but its effect can be magnified in the presence of crowders. H-NS is one of about 12 NAPs best known for _E. coli_. It is abundantly present at \(\sim 20000\) copies per

genome equivalent or at the concentration of \(\sim 20\upmu \text{M}\)4,5,6. It forms a dimer and binds preferentially curved (otherwise non-specifically) DNA, which is characteristic of

promoters; it is a transcriptional repressor4,6. Also, it condenses bacterial DNA by cross-linking two sites on DNA, which are possibly distant along the DNA4,6,7,22,23. Together with other

NAPs, H-NS is responsible for small-scale (\(\le 1 \, \text{kb}\)) DNA compaction4,7. Along this line of the discussion on H-NS and crowder synergetics above, it is worth mentioning that

depletion interactions are size-dependent2,9,12,15. First, the effect of crowders on chain compaction is marginal when the crowders are bigger in size than monomers12,15. The typical size of

cellular crowders (\(\approx 5 \, \text{nm}\)) is larger than the thickness of DNA (\(\approx 2 \, \text{nm}\)). Nevertheless, crowding is known to be the main player in condensing

bacterial chromosomes11,14. Indeed, recent studies show that the binding of molecules to an otherwise homogeneous polymer can make more effective chain compaction by crowding effects, as is

particularly the case for bacterial chromosome compaction9. This aligns well with the aforementioned H-NS and crowder synergetics20,21. Despite much effort, a clear physical picture of the

interplay between H-NS and crowders is still elusive. To explain the aforementioned synergetics, a mean-field type approach was employed, in which the binding of H-NS to DNA was viewed as

thickening the DNA20. In a computational approach24, H-NS was adequately modeled as a mobile binder but crowders were not included. In the absence of crowders, the cross-linking activity of

H-NS can be mimicked by sparse bridging attractions between designated monomers dispersed along the chain backbone25. A better understanding of the interplay between cross-linking and

crowding effects would necessitate a more systematic consideration of the interplay under controlled conditions without suppressing important details such as crowders, the association of

H-NS with DNA, and the interactions between H-NS and crowders. Here, using coarse-grained molecular dynamics simulations based on polymer physics, we study the compaction of bacterial

chromosomes by H-NS and crowders. Indeed, much of the recent progress in understanding chromosome organization is owed to polymer models of chromosomes2,9,10,11,13,24,25,26,27,28. In this

work, we build on recent modeling efforts2,9,10,13,24. To this end, we consider a ring polymer interacting with mobile binders in a crowded space. Each binder, modeled as a dimer with two

binding sites, can bridge two segments of the polymer, which are possibly distant along the backbone; as detailed below, for this, we follow the modeling strategy proposed in Ref.24. Its

effect mimics the action of H-NS on bacterial chromosomes. The simulation results reported here clarify the relative significance of biomolecular crowding and H-NS in chromosome compaction

in a quantitative manner. In particular, they offer a clear picture of crowder and H-NS synergetics beyond recent efforts20,21. The general picture emerging from our work can be summarized

as follows. While the presence of crowders enhances H-NS binding to a chromosome-like polymer by increasing the cross-linking tendency of H-NS, the presence of H-NS makes crowding effects

more efficient. This interdependence suggests two-way synergetics between H-NS and crowders in chromosome compaction. Furthermore, our results suggest that crowding effects can promote

clustering of bound H-NS and clarify the conditions under which H-NS forms clusters. For a sufficiently large (biologically relevant) concentration of H-NS (\(\gtrsim 20 \, \upmu

\text{M}\)), H-NS clusters with the cluster size increasing with the volume fraction of crowders. Our finding of H-NS clustering is reminiscent of oligomerization of H-NS4,6. However, it was

shown that H-NS dimers can cluster even in the absence of crowders, driven by a bridging-induced attraction between the dimers24: when H-NS dimers bridge two parallel DNA strands and form a

cluster, the bending energy of DNA and the entropic penalty for DNA looping can be minimized. Nevertheless, our finding based on crowding effects points to the possibility that crowding

effects can enhance the oligomerization of H-NS proteins. COMPUTATIONAL MODELING MOLECULAR DYNAMICS SIMULATIONS Our simulations are aimed at modeling bacterial DNA organization by crowders

and the cross-linking protein H-NS. As illustrated in Fig. 1, the DNA is modeled as a string of spherical monomers and crowders as simple spheres as in other studies9,10,23,24,25. As in

Ref.24, H-NS is modeled as a sphere with circular “sticky” patches on the south and north poles of the sphere, as shown on the left in Fig. 1. It is only the sticky patch that can be

nonspecifically attached to the DNA (see below for details). In our simulations, all spheres (DNA, H-NS, and crowders) interact with each other through a truncated-shifted Lennard-Jones (LJ)

potential29, given by $$\begin{aligned} U(r)=\left\{ \begin{array}{ll} U_{\text {LJ}}(r) - U_{\text {LJ}}(r_{\text {c}}) &{} \text{ for }\ r<r_{\text {c}}\\ 0 &{} \text{

otherwise } \end{array}\right. , \end{aligned}$$ (1) where \(U_{\text {LJ}}(r)\) is the conventional LJ potential: $$\begin{aligned} U_{\text {LJ}}(r)=4\epsilon _{ij}\left[ \left(

\frac{\sigma _{ij}}{r}\right) ^{12}-\left( \frac{\sigma _{ij}}{r}\right) ^{6}\right] . \end{aligned}$$ (2) Here, _r_ is the center-to-center distance between two spheres and \(r_c\) is a

cutoff distance. The parameter \(\epsilon _{ij}\) determines the strength of the short-range interactions between two spheres labeled as _i_ and _j_; the energy unit is set to \(\epsilon

=1.0 \,k_{\text {B}}T\), where \(k_{\text {B}}\) is the Boltzmann constant and _T_ is the absolute temperature. The parameter \(\sigma _{ij}\) represents the range of the LJ potential. The

subscripts \(i, j = 1, 2, 3, 4\) refer to DNA monomers, H-NS patches, H-NS core, and crowders, respectively. For instance, \(\sigma _{11} \equiv \sigma\) is the monomer size chosen to be

length units; \(\sigma _{22}\) is the H-NS patch size; \(\sigma _{33}\) is the H-NS core size; and \(\sigma _{44}\equiv \sigma _c\) is the crowder size; \(\sigma _{12}\) specifies the range

of the interaction between a DNA monomer and a H-NS patch in Eq. (2). Other interaction parameters can be interpreted similarly. DNA monomers are strung together into a chain via the finite

extensible nonlinear elastic (FENE) potential between two consecutive monomers, $$\begin{aligned} U_{\text {FENE}}(r)=-\frac{1}{2}k_{0} \left( r_{0}\right) ^{2} \ln \ \left[ 1-\left(

\frac{r}{r_{0}}\right) ^{2}\right] .\end{aligned}$$ (3) The spring constant is set to \(k_0 = 30 \epsilon / \sigma ^2\) and the range of the potential to \(r_0=1.5 \sigma\)30,31. These

choices are to prevent the crossing of monomers. H-NS is modeled as a complex (triplex) consisting of a core sphere of diameter \(\sigma\) and two small patchy spheres of diameter

\(0.178\sigma\), as noted above. In essence, we follow the modeling strategy in Ref. 24. The two patches are embedded into the core sphere and placed near its north and south poles as shown

on the left in Fig. 1; their center is \(0.4\sigma\) away from the center of the core sphere. This configuration is to avoid multiple contacts between a sticky patch and monomers24. To this

end, we use the potential energy given by $$\begin{aligned} U_\text {H-NS}(r)=K(r-r_0)^2+k_b(\theta -\pi )^2 \, \end{aligned}$$ (4) where _r_ is the center-to-center distance between the

core sphere and one of the patches, as shown in Fig. 1 (see the H-NS model on the left). Here \(K=120 \epsilon / \sigma ^2\), \(r_0=0.4\sigma\) and \(k_b=50 \epsilon\); \(\theta\) is the

angle between two vectors drawn from the center of the core to the two patch spheres. When the patch spheres are on the opposite sides, \(\theta =\pi\) as in the H-NS configuration in Fig. 

1. In order to explore the phase space, the equation of motion for monomers is integrated using the velocity-Verlet algorithm with a time step \(0.005\tau\). The system is kept at a constant

temperature, \(T = 1.0 \epsilon /k_{\text {B}}\), via a Langevin thermostat with a damping time, \(\tau = \sigma \sqrt{m/\epsilon }\), where _m_ is the DNA monomer mass. The choices of _m_

is not important in our work because they do not affect equilibrium quantities. For our simulations, we used the simulation package LAMMPS32. We first performed \(10^8\) integration steps

(\(=5\times 10^5 \, \tau\)) in order for the system to equilibrate. After equilibration, we ran additionally \(10^9\) integration steps (\(=5\times 10^6 \, \tau\)) and collected data every

\(5\times 10^3\) time steps (\(=25 \, \tau\)). CHOOSING THE SIMULATION PARAMETERS In our simulations, we chose the parameters as follows. First, we primarily use \(N=200\) and \(\sigma

_{44}=\sigma _c=2 \sigma\) (except in Fig. 2). As a result, the interaction range between a monomer and a crowder becomes \(\sigma _{14}=1.5 \sigma\). We also consider a longer chain

\(N=2000\) with \(\sigma _{44}=\sigma _c = 4\sigma\) and \(\sigma _{14}= 2.5\sigma\). Recall that the subscripts \(i, j = 1, 2, 3, 4\) refer to DNA, H-NS patches, H-NS core, and crowders,

respectively. In all cases, \(\sigma _{33}=\sigma\) and thus \(\sigma _{13}=\sigma\); unless otherwise stated, all lengths are given in units of the monomer size \(\sigma _{11}\equiv

\sigma\). In this work, the interactions between all pairs except between a sticky patch-sphere and a monomer are chosen to be purely repulsive (i.e. hard-sphere like) with a short-range

cutoff distance \(r_{ij}^c = \sigma _{ij} \times 2^{1/6}\). Two patches belonging to different H-NS molecules interact with each other when their center-to-center distance is within

\(r_{22}^c=0.2 \sigma\): \(\sigma _{22} = 0.2/2^{1/6} \sigma \simeq 0.178\sigma\). If the interaction between each patch (small sphere in cyan on the left in Fig. 1) and a monomer were

purely repulsive with the cutoff distance \(r_{12}^c=0.6 \sigma\), \(\sigma _{12}\) would be chosen to be \(\sigma _{12} = r_{12}^c/2^{1/6}= 0.6/2^{1/6} \sigma \simeq 0.535\sigma\). Based on

this, we choose \(r_{12}^c = \sigma _{12} \times 2^{1/6}+ 0.085\sigma =0.685\sigma\) so that the interaction is attractive in the range \(0.6< r < r_{12}^c\approx 0.685\). The

simulation parameters specifying the interaction _U_(_r_) in Eq. (1) are listed in Table 1. For \(N=2000\), we set \(\sigma _{14}=2.5\sigma\), \(\sigma _{34}=2.5\sigma\), and \(\sigma

_{44}=4.0\sigma\) (the corresponding cutoff distances are \(r_{14}^c = 2.5\sigma \times 2^{1/6}\), \(r_{34}^c = 2.5\sigma \times 2^{1/6}\), and \(r_{44}^c = 4.0\sigma \times 2^{1/6}\),

respectively), but other parameter values remain the same as those chosen for \(N=200\). We set the strength of interaction between the H-NS patch and a monomer to \(\epsilon _{12} = 29.0

\epsilon\). With this choice, the interaction energy _U_(_r_) in Eq. (1) evaluated at \(r=r_\text{min} \approx 0.6\) becomes \(U(r_\text{min}) \approx -8.65\) in units of \(\epsilon

=k_{{\text{B}}}T\), where \(r_\text{min}\) is the distance at which the potential energy reaches its minimum. At this value, about a third of H-NS binds to DNA in the absence of crowders as

evidenced later (see red line on the left in Fig. 3). The potential energy (\(-8.65 \, k_{{\text{B}}}T\)) resulting from our choice of \(\epsilon _{12}\) is close to the binding free energy

of H-NS to DNA at \(20^\circ \text{C}\): \(-21.09 \,{\mathrm{kJ/mol}} \simeq -8.51 \, k_{{\text{B}}}T\)33. The strength of interaction between all other pairs is set to \(\epsilon _{ij} =

\epsilon\). Each DNA monomer coarse-grains and represents about 7.35 hydrated B-DNA basepairs (bp). A natural choice for the monomer size is thus \(\sigma =\sigma _{11}=2.5 \, \text

{nm}\)2,24. The diameter of both DNA and H-NS is \(2.5 \, \text {nm}\); the size of a crowding particle is then \(\sigma _c = 2\sigma =5.0 \, \text {nm}\)2. All the particles are confined

within a cubic box of side \(50\sigma = 125 \, \text {nm}\) for \(N=200\) and \(110\sigma \simeq 270 \, \text {nm}\) for \(N=2000\), respectively. As a result, the concentration of monomers

in the cube is approximately \(170\, \mu \text {M}\). The periodic boundary conditions are imposed on each side. The volume fraction of crowding particles is in the range: \(0\le \phi _c

\lesssim 0.4\). The volume fraction of H-NS varies from 0 to \(25.5 \, \upmu \text{M}\). RESULTS In our studies, both the volume fraction of crowders, \(\phi _c\), and the number of H-NS,

\(N_\text{HNS}\), are key parameters. Following the simulation procedure described in Sect. "Computational modeling", we have first calculated chain size as a function of \(\phi

_c\) for various choices of \(N_\text{HNS}\) and plotted the results in Fig. 2. Primarily, we have chosen \(N=200\) and \(N_\text {HNS}=0, 4, 8, 12, 16, 20, 30\), which correspond to H-NS

concentrations \([\text {H-NS}] =0, 3.4, 6.8, 10.2, 13.6, 17.0, 25.5 \, \mu \text {M}\), respectively. The entire system is confined inside a cube of volume \(125\!\times \! 125\! \times \!

125\,\text {nm}^3\), as discussed in Sect. "Computational modeling". In this work, \([\cdots ]\) denotes a molar concentration. Displayed in Fig. 2 is the reduced chain size as a

function of \(\phi _c\): \(R_g/R_{g0}\), where \(R_g\) is the radius of gyration and \(R_{g0}=R_g(\phi _c=0,[\text {H-NS}]=0)\). In all cases shown, the reduced polymer size decreases as

\(\phi\) increases; it decreases more rapidly for larger \([\text {H-NS}]\). For given \(\phi _c\), it is smaller for larger \([\text {H-NS}]\). When \([\text {H-NS}]=25.5 \, \mu \text

{M}\), for example, DNA is compacted by about \(13 \%\) (\(R_g/R_{g0} \approx 0.87\)) and \(46\%\) (\(R_g/R_{g0} \approx 0.54\)) for \(\phi _c=0\) and 0.32, respectively. Also shown in Fig. 

2 are curves that represent a much longer chain: \(N=2000\) confined in a cube (\(270\!\times \! 270\! \times \! 270\,\text {nm}^3\)). For this, we have chosen \([\text {H-NS}]=0, 25.5 \,

\mu \text {M}\). When \([\text {H-NS}]=25.5 \, \upmu \text{M}\) and \(\phi _c=0.32\), the polymer is condensed more effectively in reference to the corresponding short chain case:

\(R_g/R_{g0} \approx 0.34\). This trend persists even when \([\text {H-NS}]=0\); compare the solid curve with filled circles with the dashed curve with open circles. This points to the

significance of chain length in chain compaction by biomolecular crowding. Nevertheless, the general trend observed with a shorter chain remains applicable to a longer chain, which is

computationally more demanding. For the remainder of this work, we will only consider the short-chain case \(N=200\). As noted above, the chain size decreases more rapidly with \(\phi _c\),

when \([\text {H-NS}]\) is larger. This points to the synergy between crowders and H-NS. It appears to be consistent with the recent observation that H-NS enhances bacterial chromosome

compaction by crowding effects20,21. As it turns out, H-NS not only enhances the depletion force between chain segments by enlarging the chain thickness, as assumed in Ref. 20, it also binds

more tightly to a chromosome-like polymer for larger \(\phi _c\), as if the presence of crowders increases the binding affinity of H-NS, as shown below. This interdependence is also

implicated in crowder and H-NS synergetics. We have examined further how the effects of H-NS and crowders are interrelated. Figure 3 shows the fraction of bound H-NS molecules to a ring

polymer, denoted as \(\theta\); if all H-NS molecules are bound in a “hypothetical” situation, \(\theta =1\). As shown in the graph on the left in Fig. 3, \(\theta\) increases with

increasing \([\text {H-NS}]\); it is expected to get saturated as \([\text {H-NS}]\rightarrow \infty\). In this graph, different colors represent various choices of \(\phi _c\). For given

\([\text {H-NS}]\), \(\theta\) is larger for larger \(\phi _c\), as if the presence of crowers enhances the binding affinity of H-NS for the polymer. This observation suggests that chain

collapse induced by crowding promotes H-NS binding possibly by enhancing their propensity for cross-linking, as evidenced below. It proves useful to decompose H-NS binding into the two

binding modes: single-site or dangling and two-site binding; in the latter case, both the two binding sites of a H-NS dimer are occupied. In earlier studies22,23, two-site binding was

further classified into _cis_ and _trans_. If a H-NS dimer binds two distant genomic sites (e.g. more than two monomers or beads apart), it is in _trans_; otherwise, it is in _cis_. Cis

binding requires bending of a H-NS dimer into a ‘U’ shape, which is suppressed in our modeling as in Ref.24. One can argue on physics grounds that this complication will not limit the

physical picture presented in Fig. 2: cross-linking or bridging two adjacent monomers will not contribute toward chain compaction much more effectively than dangling. See below for

additional discussions. In this work, two-site binding and cross-linking can be used interchangeably. In the graph on the right in Fig. 3, the two binding modes, i.e. dangling and

cross-linking are represented by different curves: solid lines with diamonds (cross-linking) and circles (dangling). The curves were obtained with a representative value of \([\text

{H-NS}]=25.5 \, \mu \text {M}\). As \(\phi _c\) increases, the fraction of cross-linking H-NS increases rather rapidly but the fraction of dangling H-NS decreases slowly. But the sum of the

two, represented by the top curve, increases with \(\phi _c\). The dependence of H-NS binding displayed in this graph shows how the presence of crowders enhances the binding of H-NS in

cross-linking mode: crowding brings close otherwise distant monomers, making easier their cross-linking by H-NS. We note from Fig. 3 that the presence of crowders enhances the binding of

H-NS to a bacterial chromosome. Can H-NS binding in turn enhance chain compaction? Earlier studies suggest that this is indeed the case20,21: H-NS enhances the ability of crowders to

collapse bacterial chromosomes. This was interpreted in terms of bound H-NS enlarging the polymer thickness20. While this mean-field approach serves its purpose, a more complete

understanding would necessitate a systematic analysis of the effects of H-NS and crowders on chain compaction under controlled conditions. In the graph on the left in Fig. 4, two sets of

curves are compared: the curves obtained with \(\epsilon _{34} =1\) (dashed lines with symbols) and \(\epsilon _{34}=0\) (solid lines); the curves in various colors represent different

choices of \([\text {H-NS}]\). Here, \(\epsilon _{34}\) is the strength of the LJ potential between H-NS and crowders; recall that \(R_g\) is the radius of gyration and \(R_{g0}\) is its

unperturbed value in the absence of both crowders and H-NS. When \(\epsilon _{34}=0\), H-NS is permeable to crowders: it can penetrate them. As a result, H-NS does not feel any steric

hindrance caused by the surrounding crowders; two H-NS molecules will not experience any depletion force. The difference between the solid and dashed curves arises solely from the depletion

force between H-NS molecules (solid curves) and can be viewed as a quantitative measure of the synergy between H-NS and crowders. This difference is more pronounced for large \([\text

{H-NS}]\) and increases with increasing \(\phi _c\). The results in Fig. 3 capture the enhancement of H-NS binding by crowding. To examine its consequence on H-NS and crowder synergetics, in

the graph on the right in Fig. 4, we have included a grey dashed curve with filled squares. For this, we chose \(\epsilon _{34} =1\) as for the dashed line with diamonds from the left graph

and anchored 10 H-NS molecules to randomly-chosen sites on the polymer; the curve was averaged over 10 independent choices of binding sites. The number of anchored H-NS chosen represents

the case \([\text {H-NS}]=25.5 \, \upmu \text{M}\) in the absence of crowders (\(\phi _c=0\)). As shown in Fig. 3, when \(\phi _c=0\), \(\theta\) approaches 0.3, as \([\text {H-NS}]\)

increases; \(\theta \approx 0.33\) if \([\text{HNS}]=25.5 \, \upmu \text{M}\). We thus set the number of anchored H-NS molecules to the total number of bound H-NS: \(0.33 \times 30 \approx

10\) (recall 30 H-NS molecules in a cube of volume \(125\!\times \! 125\! \times \! 125\,\text {nm}^3\) corresponds to \([\text{HNS}]=25.5 \, \upmu \text{M}\)). By fixing the number of bound

H-NS at this value, the enhancement of H-NS binding induced by crowding effects as seen in Fig. 4 is turned off. The resulting curve in grey obtained with the parameters used is close to

the solid curve in magenta obtained with \(\epsilon _{34}=0\). Ignoring crowding-enhanced H-NS binding has as significant effects on chain compaction as ignoring H-NS-enhanced depletion

forces between monomers. As discussed earlier, our model does not distinguish between the two binding modes: _cis_ and _trans_. H-NS dimers in _cis_ mode would not contribute to chain

compaction as efficiently as those in _trans_ mode. In the absence of crowders, their effect on chain compaction is expected to be minimal, similarly to the effect of dangling H-NS. In the

presence of crowders, H-NS dimers enhance chain compaction by crowders irrespectively of their binding mode. The degree of enhancement is expected to be insensitive to their binding mode,

since the depletion free energy gain depends solely on the degree of overlapping between depletion layers for a given value of \(\phi _c\), as shown on the right in Fig. 1. As a result, the

essence of our finding in Fig. 4 will not reflect sensitively the coarse-grained nature of H-NS binding in this work. A general picture emerging from Figs. 3 and 4 is that the synergetics

between H-NS and crowders in condensing bacterial chromosomes is two-way one: H-NS binding enhances the depletion forces between chain segments20,21; the presence of crowders enhances the

binding of H-NS to the chromosome, which in turn makes even stronger the depletion forces. Even when H-NS and crowders separately do not have a significant impact on chain compaction, the

simultaneous presence of the two condenses a chromosome-like polymer appreciably better than what we would expect from the sum of the two individual effects. To be specific, consider the

case \([\text {H-NS}]=25.5 \, \upmu \text{M}\) and \(\phi _c=0.32\), and relate it to the corresponding H-NS-only or crowder-only case. The following inequality holds: \(46\% \, \text

{compaction (both)} > 23\% \, \text {compaction}\), which is a sum of \(13\% \, \text {(H-NS only)}\) and \(10\% \, \text {(crowder only)}\). This exemplifies the degree of H-NS and

crowder synergetics in a quantitative manner. We have also considered the clustering of H-NS driven by depletion forces. Figures 5 and 6 summarize the results for H-NS clustering: the

cluster-size distribution (on the left) and the average cluster size (on the right). When the center-to-center distance between the two neighboring H-NS cores is within \(3\sigma\), they are

viewed as forming a cluster. Here, we do not differentiate between different clustering configurations, e.g. a linear array of three H-NS particles and three H-NS forming a triangle; both

clusters have the same size, i.e. 3. The graph on the left in Fig. 5 shows the cluster-size distribution as a function of the cluster size. When \(\phi _c\) is in the range \(0\le \phi _c

\le 0.20\), the cluster-size distribution has a single peak around 2 or reaches its maximum at 1. In contrast, for \(\phi _c> 0.2\), it has double peaks with the second peak located at a

much larger value of the cluster size, signalling the formation of a large cluster of H-NS particles. The snapshot shows such a cluster for \(\phi _c= 0.32\); for simplicity, only H-NS is

included. The graph on the right in Fig. 5 displays the average cluster size, obtained with \([\text {H-NS}]=25.5 \, \upmu \text{M}\). It increases with increasing \(\phi _c\), as expected

from the graph on the left. The left and right snapshots included in this graph correspond to \(\phi _c=0\) and \(\phi _c=0.32\), respectively. The enlarged view captures several H-NS

clusters, including the big one in the lower middle. For visual clarity, in all the snapshots in both graphs, the crowders are hidden and the patches are sticking out of the core. Shown in

Fig. 6 is the cluster-size distribution for various values of \([\text {H-NS}]\) (on the left) and the average cluster size as a function of \([\text {H-NS}]\) (on the right); the volume

fraction of crowders is held fixed at \(\phi _c=0.32\). As shown on the left in Fig. 6, the cluster-size distribution is single-peaked at 1 except for \([\text {H-NS}] =25.5 \, \upmu

\text{M}\); when \([\text {H-NS}] =25.5 \, \upmu \text{M}\), however, it develops a second peak at a large value of the cluster size (\(\approx 24\)). The graph on the right in Fig. 6

suggests that the average cluster size, obtained with \(\phi _c=0.32\), increases with increasing \([\text {H-NS}]\), as expected from the graph on the left. The snapshots included in this

graph correspond to \([\text {H-NS}] =3.4 \, \upmu \text{M}\) (left inset) and \(25.5 \, \upmu \text{M}\) (right inset). H-NS clustering suggested in Figs. 5 and 6 is analogous to

oligomerization of H-NS4,6. However, the former is not conclusive for the latter, since our simplified model leaves out potentially relevant biological details such as possible biomolecular

interactions between H-NS proteins and chain stiffness. Nevertheless, they point to the possibility that crowding effects can be involved in the oligomerization of H-NS proteins; they also

complement the finding that bridging-induced attraction drives H-NS clustering24. DISCUSSIONS Polymer physics has proven to be useful for advancing our understanding of chromosome

organization and its impact on their biological functions2,9,10,11,13,24,25,26,27,28. Our work expands its repertory by including the effects of the cross-linking protein H-NS in addition to

those of biomolecular crowders. The computational model employed in this work clarifies the cooperative nature of their effects on chromosome compaction. In our simulations, H-NS is modeled

as a triplex consisting of a core sphere and two small patch spheres, which are diagonally positioned inside the core. The patch spheres can bind to a (chromosome-like) ring polymer with

characteristic binding energy. In this work, H-NS binding is further classified into two binding modes: dangling and cross-linking (or trans). Because of the way it is modeled, H-NS does not

show a _cis_ configuration, in which the two binding sites of a H-NS dimer bind simultaneously to DNA sites nearby (e.g. within a few monomers)22,23. _Cis_ binding requires bending of a

H-NS dimer into a ‘U’ shape and is not realized in our modeling. In the absence of crowders, however, H-NS dimers in _cis_ binding does not contribute to DNA compaction. In a crowded medium,

they can enhance DNA compaction by crowding effects, similarly to what we expect from dangling H-NS dimers. As a result, the addition of _cis_ binding in our consideration will not change

the general picture of DNA compaction by H-NS and crowders. Along the line of what is discussed above, it is worth mentioning that H-NS binding and its impact on DNA, carrying a negative

charge, depend on the presence of \(\text{Mg}^{2+}\)4,34,35: at a low concentration of \(\text{Mg}^{2+}\) (\(< 2 \, \text{mM}\)), H-NS coats DNA without looping it; at a high

concentration (\(> 5 \, \text{mM}\)), it can bridge the DNA and thus contribute to DNA compaction. \(\text{Mg}^{2+}\) can reduce the repulsion between the backbone charges on DNA or even

turn the repulsion into attraction36. As a result, the presence of \(\text{Mg}^{2+}\) enhances the propensity of H-NS to cross-link DNA and thus that of clustering. This effect can be taken

into account at least implicitly by adjusting the simulation parameters such as \(\epsilon _{ij}\) and \(r^c_{ij}\). The model used in this work clearly captures the synergy between H-NS and

crowders in condensing the polymer beyond the recent effort, in which the effect of H-NS binding is viewed as thickening the chromosome20. The results presented in this work suggest a

two-way synergetics between H-NS and crowders: if the presence of crowders enhances H-NS binding to a chromosome-like polymer by increasing their propensity for chain cross-linking, the

presence of H-NS makes crowding effects more efficient by locally enlarging chain segments, analogous to what was observed with a heterogeneous polymer in a crowded medium9. Besides H-NS and

other NAPs (e.g. HU and IHF), RNA polymerases are known to be key players in organizing bacterial chromosomes2,37,38. It has been shown that the binding of RNA polymerases to _E. coli_

chromosomes especially under fast grow conditions induces clustering of transcription-active units2. Recent computer simulations support this picture9. Both H-NS and RNS polymerases enhance

chromosome compaction by crowding effects. In a more general perspective, depletion forces induced by biomolecular crowding are size-dependent2,12,13,18. They are stronger between bigger

objects (e.g. H-NS bound sites on a chromosome). It is worth appreciating the clear difference between H-NS and RNA polymerases (or some other chromosome-associated proteins that do not

induce cross-linking). H-NS not only enhances depletion forces between chromosome segments but also cross-links two sites on a chromosome. The results reported here tend to illustrate the

dual or multiple roles of biomolecules. Beyond their biological specificity, they are physical entities, exerting excluded volume interactions or causing steric hindrance to other molecules,

as is the case for H-NS. Similar analysis of other chromosome-associated proteins is desired for a fuller picture. In this work, we have focused our effort on examining the equilibrium

behavior of chromosome compaction by H-NS and crowders. Accordingly, the results for H-NS binding in Fig. 3 left out the dynamical aspects of H-NS binding/unbinding and cross-linking. In

light of studies on ‘facilitated’ (concentration-accelerated) dissociation of chromosome-associated proteins (e.g. Fis)39,40, it will be useful to extend our equilibrium effort toward

modeling association/dissociation and cross-linking dynamics of H-NS in a crowded medium. Finally, we would like to add that biomolecular crowding can influence other biological processes

such as protein folding/aggregation, gene regulation, and cell growth2,41,42,43. We hope that our work will inspire more investigation into the intriguing roles of crowders in biological

processes. DATA AVAILABILITY The datasets used and analysed during the current study are available from the corresponding authors on reasonable request. CODE AVAILABILITY The codes used to

generate the datasets in this work are available at the following link: https://github.com/yjung-github/H-NS-crowder. REFERENCES * Bonev, B. & Cavalli, G. Organization and function of

the 3D genome. _Nat. Rev. Genet._ 17, 661–678 (2016). Article  CAS  PubMed  Google Scholar  * Marenduzzo, D., Micheletti, C. & Cook, P. R. Entropy-driven genome organization. _Biophys.

J._ 90, 3712–3721 (2006). Article  CAS  PubMed  PubMed Central  ADS  Google Scholar  * Badrinarayanan, A., Le, T. B. K. & Laub, M. T. Bacterial chromosome organization and segregation.

_Annu. Rev. Cell Dev. Biol._ 31, 171–199 (2015). Article  CAS  PubMed  PubMed Central  Google Scholar  * Verma, S. C., Qian, Z. & Adhya, S. L. Architecture of the Escherichia coli

nucleoid. _PLoS Genet._ 15, e1008456 (2019). Article  PubMed  PubMed Central  Google Scholar  * Friedrich, K., Gualerzi, C. O., Lammi, M., Losso, M. A. & Pon, C. L. Proteins from the

prokaryotic nucleoid. Interaction of nucleic acids with the 15 kDa Escherichia coli histone-like protein H-NS. _FEBS Lett._ 229, 197–202 (1988). Article  CAS  PubMed  Google Scholar  *

Dorman, C. J. H-NS: A universal regulator for a dynamic genome. _Nat. Rev. Microbiol._ 2, 391–400 (2004). Article  CAS  PubMed  Google Scholar  * Stavans, J. & Oppenheim, A. DNA-protein

interactions and bacterial chromosome architecture. _Phys. Biol._ 3, R1–R10 (2006). Article  CAS  PubMed  ADS  Google Scholar  * Jun, S. Chromosome, cell cycle, and entropy. _Biophys. J._

108, 785–786 (2015). Article  CAS  PubMed  PubMed Central  ADS  Google Scholar  * Jung, Y. & Ha, B.-Y. Collapse transition of a heterogeneous polymer in a crowded medium. _J. Chem.

Phys._ 155, 054902 (2021). Article  CAS  PubMed  ADS  Google Scholar  * Ha, B.-Y. & Jung, Y. Polymers under confinement: Single polymers, how they interact, and as model chromosomes.

_Soft Matter_ 11, 2333–2352 (2015). Article  CAS  PubMed  ADS  Google Scholar  * Pelletier, J. _et al._ Physical manipulation of the Escherichia coli chromosome reveals its soft nature.

_Proc. Natl. Acad. Sci. U.S.A._ 109, E2649–E2656 (2012). Article  CAS  PubMed  PubMed Central  Google Scholar  * Jeon, C., Jung, Y. & Ha, B.-Y. Effects of molecular crowding and

confinement on the spatial organization of a biopolymer. _Soft Matter_ 12, 9436–9450 (2016). Article  CAS  PubMed  ADS  Google Scholar  * Jeon, C., Hyeon, C., Jung, Y. & Ha, B.-Y. How

are molecular crowding and the spatial organization of a biopolymer interrelated. _Soft Matter_ 12, 9786–9796 (2016). Article  CAS  PubMed  ADS  Google Scholar  * de Vries, R. DNA

condensation in bacteria: Interplay between macromolecular crowding and nucleoid proteins. _Biochimie_ 92, 1715–1721 (2010). Article  PubMed  Google Scholar  * Kang, H., Pincus, P. A.,

Hyeon, C. & Thirumalai, D. Effects of macromolecular crowding on the collapse of biopolymers. _Phys. Rev. Lett._ 114, 068303 (2015). Article  PubMed  ADS  Google Scholar  * Ellis, R. J.

Macromolecular crowding: Obvious but underappreciated. _Trends Biochem. Sci._ 26, 597–604 (2001). Article  CAS  PubMed  Google Scholar  * Zhou, H.-X. Influence of crowded cellular

environments on protein folding, binding, and oligomerization: Biological consequences and potentials of atomistic modeling. _FEBS Lett._ 587, 1053–1061 (2013). Article  CAS  PubMed  PubMed

Central  Google Scholar  * Asakura, S. & Oosawa, F. On interaction between two bodies immersed in a solution of macromolecules. _J. Chem. Phys._ 22, 1255–1256 (1954). Article  CAS  ADS 

Google Scholar  * Jun, S. & Wright, A. Entropy as the driver of chromosome segregation. _Nat. Rev. Microbiol._ 8, 600–607 (2010). Article  CAS  PubMed  PubMed Central  Google Scholar  *

Wegner, A. S. _et al._ Compaction of isolated Escherichia coli nucleoids: Polymer and H-NS protein synergetics. _J. Struct. Biol._ 194, 129–137 (2016). Article  CAS  PubMed  Google Scholar 

* Cristofalo, T. M. _et al._ Cooperative effects on the compaction of DNA fragments by the nucleoid protein H-NS and the crowding agent PEG probed by magnetic tweezers. _Biochim. Biophys.

Acta (BBA) Gen. Subj._ 1864, 129725 (2020). Article  CAS  Google Scholar  * Wiggins, P. A., Dame, R. T., Noom, M. C. & Wuite, G. J. Protein-mediated molecular bridging: A key mechanism

in biopolymer organization. _Biophys. J._ 97, 1997–2003 (2009). Article  CAS  PubMed  PubMed Central  ADS  Google Scholar  * Joyeux, M. & Vreede, J. A model of H-NS mediated compaction

of bacterial DNA. _Biophys. J._ 104, 1615–1622 (2013). Article  CAS  PubMed  PubMed Central  ADS  Google Scholar  * Brackley, C. A., Taylor, S., Papantonis, A., Cook, P. R. & Marenduzzo,

D. Nonspecific bridging-induced attraction drives clustering of DNA-biding proteins and genome organization. _Proc. Natl. Acad. Sci. U.S.A._ 110, E3605–E3611 (2013). Article  CAS  PubMed 

PubMed Central  ADS  Google Scholar  * Scolari, V. F. & Lagomarsino, M. C. Combined collapse by bridging and self-adhesion in a prototypical polymer model inspired by the bacterial

nucleoid. _Soft Matter_ 11, 1677 (2015). Article  CAS  PubMed  ADS  Google Scholar  * Guido, T. & Giorgetti, L. _Modeling the 3D Conformation of Genomes_ (CRC Press, 2019). Google

Scholar  * Shi, G., Liu, L., Hyeon, C. & Thirumalai, D. Interphase human chromosome exhibits out of equilibrium glassy dynamics. _Nat. Commun._ 9, 3161 (2018). Article  PubMed  PubMed

Central  ADS  Google Scholar  * Cook, P. R. & Marenduzzo, D. Entropic organization of interphase chromosomes. _J. Cell Biol._ 186, 825–834 (2009). Article  CAS  PubMed  PubMed Central 

Google Scholar  * Frenkel, D. & Smit, B. _Understanding Molecular Simulation_ (Academic Press, 2002). Google Scholar  * Kremer, K. & Grest, G. S. Dynamics of entangled linear polymer

melts–A molecular-dynamics simulation. _J. Chem. Phys._ 92, 5057–5086 (1990). Article  CAS  ADS  Google Scholar  * Grest, G. S. & Kremer, K. Molecular dynamics simulation for polymers

in the presence of a heat bath. _Phys. Rev. A_ 33, 3628–3631 (1986). Article  CAS  ADS  Google Scholar  * Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. _J.

Comput. Phys._ 117, 1–19 (1995). Article  CAS  ADS  Google Scholar  * Ono, S. _et al._ H-NS is a part of a thermally controlled mechanism for bacterial gene regulation. _Biochem. J._ 391,

203–213 (2005). Article  CAS  PubMed  PubMed Central  Google Scholar  * Liu, Y., Chen, H., Kenney, L. J. & Yan, J. A divalent switch drives H-NS/DNA-binding conformations between

stiffening and bridging modes. _Genes Dev._ 24, 339–344 (2010). Article  CAS  PubMed  PubMed Central  Google Scholar  * van der Valk, R. A. _et al._ Mechanism of environmentally driven

conformational changes that modulate H-NS DNA-bridging activity. _eLife_ 6, e27369 (2017). Article  PubMed  PubMed Central  Google Scholar  * Gelbart, W. M., Bruinsma, R. F., Pincus, P. A.

& Parsegian, V. A. DNA-inspired electrostatics. _Phys. Today_ 53, 38–44 (2000). Article  CAS  Google Scholar  * Jin, D. J., Cagliero, C. & Zhou, Y. N. Role of RNA polymerase and

transcription in the organization of the bacterial nucleoid. _Chem. Rev._ 113, 8662–8682 (2013). Article  CAS  PubMed  Google Scholar  * Jin, D. J. & Cabrera, J. E. Coupling the

distribution of RNA polymerase to global gene regulation and the dynamic structure of the bacterial nucleoid in Escherichia coli. _J. Struct. Biol._ 156, 284–291 (2006). Article  CAS  PubMed

  Google Scholar  * Tsai, M. Y., Zhang, B., Zheng, W. & Wolynes, P. G. Molecular mechanism of facilitated dissociation of Fis protein from DNA. _J. Am. Chem. Soc._ 138, 13497–13500

(2016). Article  CAS  PubMed  PubMed Central  Google Scholar  * Kamar, R. I. _et al._ Facilitated dissociation of transcription factors from single DNA binding sites. _Proc. Natl. Acad.

Sci._ 114, E3251–E3257 (2017). Article  CAS  PubMed  PubMed Central  Google Scholar  * Contessoto, V. G., Ferreira, P. H. B., Chahine, J., Leite, V. B. P. & Oliveira, R. J. Small neutral

crowding solute effects on protein folding thermodynamic stability and kinetics. _J. Phys. Chem. B_ 125, 11673–86 (2021). Article  CAS  PubMed  Google Scholar  * Zegarra, F. C. _et al._

Crowding-induced elongated conformation of urea-unfolded Apoazurin: Investigating the role of crowder shape in silico. _J. Phys. Chem. B_ 123, 3607–17 (2019). Article  CAS  PubMed  PubMed

Central  Google Scholar  * Zimmerman, S. B. & Minton, A. P. Macromolecular crowding: Biochemical, biophysical, and physiological consequences. _Annu. Rev. Biophys. Biomol. Struct._ 22,

27–65 (1993). Article  CAS  PubMed  Google Scholar  Download references ACKNOWLEDGEMENTS This work was supported by NSERC (Canada) (B-YH) and the National Research Foundation grant (NRF-

2021R1F1A1064098; YJ) and the National Supercomputing Center (KSC-2022-CRE-0464). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Supercomputing Center, Korea Institute of Science and

Technology Information, Daejeon, 34141, South Korea Youngkyun Jung * Department of Physics and Astronomy, University of Waterloo, Waterloo, ON, N2L 3G1, Canada Amir Sadeghi & Bae-Yeun Ha

Authors * Youngkyun Jung View author publications You can also search for this author inPubMed Google Scholar * Amir Sadeghi View author publications You can also search for this author

inPubMed Google Scholar * Bae-Yeun Ha View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS B.-Y.H. and Y.J. conceived the project; Y.J.

performed the simulations in collaboration with A.S.; B.-Y.H. primarily wrote the manuscript and all authors contributed to writing by reviewing and commenting on the manuscript.

CORRESPONDING AUTHORS Correspondence to Youngkyun Jung or Bae-Yeun Ha. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION

PUBLISHER'S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article

is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give

appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in

this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative

Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a

copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Jung, Y., Sadeghi, A. & Ha, BY. Modeling the

compaction of bacterial chromosomes by biomolecular crowding and the cross-linking protein H-NS. _Sci Rep_ 14, 139 (2024). https://doi.org/10.1038/s41598-023-50355-2 Download citation *

Received: 27 September 2023 * Accepted: 19 December 2023 * Published: 02 January 2024 * DOI: https://doi.org/10.1038/s41598-023-50355-2 SHARE THIS ARTICLE Anyone you share the following link

with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt

content-sharing initiative