ABSTRACT Maternal investment influences the survival and reproduction of both mothers and their progeny and plays a crucial role in understanding individuals’ life-history and population

ecology. To reveal the complex mechanisms associated with reproduction and investment, it is necessary to examine variations in maternal investment across species. Comparisons across species

call for a standardised method to quantify maternal investment, which remained to be developed. This paper addresses this limitation by introducing the maternal investment metric – _MI_ – 

for mammalian species, established through the allometric scaling of the litter mass at weaning age by the adult mass and investment duration (i.e. gestation + lactation duration) of a

confirms that _Eutheria_ have a higher maternal investment than _Metatheria_. We discuss how further research could use the maternal investment metric as a valuable tool to understand

variation in reproductive strategies. SIMILAR CONTENT BEING VIEWED BY OTHERS NEONATAL ANTIPREDATOR TACTICS SHAPE FEMALE MOVEMENT PATTERNS IN LARGE HERBIVORES Article 04 December 2024

MATERNAL RISK-MANAGEMENT ELUCIDATES THE EVOLUTION OF REPRODUCTIVE ADAPTATIONS IN SHARKS BY MEANS OF NATURAL SELECTION Article Open access 29 August 2024 NEW ESTIMATES INDICATE THAT MALES ARE

NOT LARGER THAN FEMALES IN MOST MAMMAL SPECIES Article Open access 12 March 2024 INTRODUCTION In mammals, maternal investment, i.e. the allocation of resources to meet the basic needs of

offspring during the pre- and post-natal development, holds a significant influence over the survival and reproduction of mothers and their progeny1. The concept of maternal investment has

thus played a pivotal role in the development of life-history theory2 and population ecology3. Understanding the intricate relationships associated with reproduction and maternal investment

is essential for comprehending how an animal can achieve adequate fitness within a specific niche4. Maternal investment is shaped by genetically influenced factors connected to life-history

traits such as metabolic rate, body mass, and longevity, which all scale with each other due to their relationship with body size5,6. In addition, mothers adjust their investment depending

on circumstances, such as their condition7, access to resources8 and experience9,10, as well as environmental cues11. To gain a comprehensive understanding of these reproduction strategies,

it is essential to examine the variations in maternal investment across species that are not simply due to allometry, i.e. due to differences ultimately resulting from variation in body

size. Previous studies have tried to compare investment strategies using proxies such as calorimetry, basal metabolic rate, growth rate, and gestation or lactation

duration12,13,14,15,16,17,18. Moreover, experiments within single species (typically insects) have been conducted to understand specific mechanisms8,19. However, these approaches have been

limited by the scarcity of data and the absence of a standardised methodology capable of comparing a large number of species based on the available information. Consequently, conducting

large-scale studies to unravel the complexities of investment strategies has remained unfeasible. In an effort to overcome this lack, we build on the scaling laws governing life-history

traits to propose a metric of maternal investment comparable across mammalian species. Stemming from the allometric concept pioneered by D’Arcy Thompson and Julian Huxley, these scaling laws

indicate that biological traits change as a function of an organism’s body size20,21. This idea has undergone thorough examination in the realm of mammalian biology, showing consistent

patterns across diverse species. Guided by this principle, we introduce the maternal investment metric which we define in terms of the nutritional investment of the mother in her offspring.

This innovative tool should facilitate comprehensive comparisons of maternal investment strategies across mammalian species. By utilising empirical data on weaning mass, litter size, adult

mass, and investment duration (i.e. gestation + lactation duration) from a comprehensive database encompassing hundreds of mammalian species, we studied the robustness of this metric to

alternative regression methods used to fit allometric relationships and to alternative proxies used to quantify the body mass of individuals in a species. We also used the database to study

the extent to which taxonomy influences maternal investment once allometry is accounted for. The chief aim of this paper is to establish a standardised method for comparing and enhancing our

understanding of investment strategies among different species of mammal. We designed a tool to comprehensively analyse the maternal investment patterns across species, in order to

understand what influences reproductive success and to provide insights for future investigations into reproductive strategies and their consequences. RESULTS A METRIC TO QUANTIFY MATERNAL

INVESTMENT PREDICTOR FOR MATERNAL INVESTMENT Maternal investment in mammals starts with the development of a fertilised oocyte and culminates with a weaned individual. Therefore, the mass at

weaning reflects maternal investment until that point. Since litter weaning mass encompasses the entire litter’s mass (i.e. the cumulative body mass measured at weaning age across all

offspring from a given litter at weaning age) and thus represents the complete investment by the mother, we considered this variable as the most appropriate predictor to use for the

characterisation of offspring mass. To identify whether the litter mass at weaning is correlated with the adult mass and could therefore be allometrically scaled, we measured a linear

Pearson correlation between the (log10) adult mass and (log10) litter weaning mass. This analysis revealed a strong correlation between the litter weaning mass and adult mass (r = 0.967, _N_

 = 1041, _p_ < 0.001). We therefore went on to allometrically scale the litter weaning mass with adult mass. SENSITIVITY OF THE ALLOMETRIC RELATIONSHIP TO THE FITTING METHOD There is a

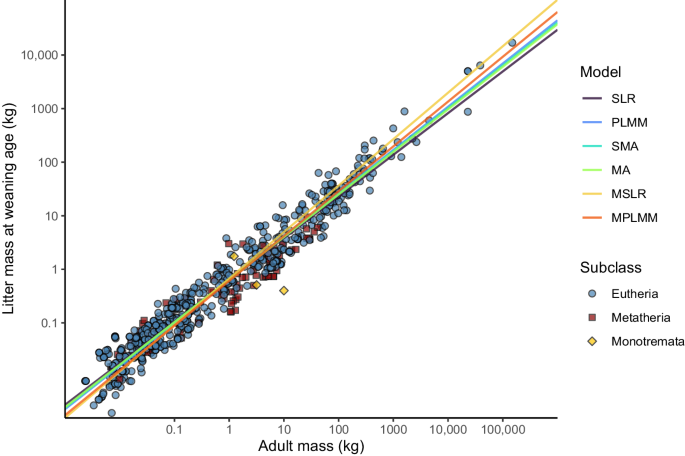
long-standing debate about how to best fit allometric relationships22,23,24. We thus relied on six alternative regression models to estimate the litter mass at weaning. Specifically, we used

a simple linear regression (SLR), a linear (heteroscedastic) mixed-effects model accounting for phylogenetic inertia (PLMM), a standardised major axis regression (SMA), a major axis

regression (MA), a multiple linear regression model representing an extension of the model SLR (MSLR), and a multiple linear regression representing an extension of the model PLMM (MPLMM).

On top of the effect of the adult mass on the litter mass at weaning considered in the bivariate models (SLR, PLMM, SMA and MA), the MSLR and MPLMM models also account for a possible effect

of investment duration. The rationale behind these multiple linear regression models (i.e. MSLR and MPLMM) is to account for the possibility that an extended maternal investment in offspring

could result in greater offspring growth. This possibility is not a priori obvious since the effect of the investment duration may already be accounted for in the simpler models, via the

adult mass predictor, due to the allometric relationship between body mass and the pace of life. The rationale behind the models PLMM and MPLMM is that, for a given adult mass, the litter

mass at weaning may differ between taxa due to the influence of factors correlated with phylogeny such as the genetic make-up of individuals or their ecology. Therefore, accounting for the

phylogenetic distances between species while fitting the allometric relationship decreases the impact of variation in the density of observations along the mammalian phylogenetic tree on

estimates produced by regression methods. We fitted the linear regressions on a single subset of our data (_N_ = 738) that, for each species, contained information about the litter mass at

weaning, the adult body mass, the investment duration and phylogenetic position25. The estimates of the allometric relationship obtained for the different regression methods are depicted in

Fig. 1 and summarised in Table 1. Using the six fitted models, the expected litter mass at weaning for a given species can be predicted based on the adult mass, and in case of the multiple

linear regression models, based on the adult mass and investment duration, for that species. By comparing the actual litter mass at weaning to the predicted litter mass at weaning, a metric

can be produced to allow for the objective comparison of maternal investment between species. We propose the following maternal investment metrics based on the ratio between these

quantities: \({\it{{MI}}}={\log}_{10}\frac{{observed\; litter\; mass\; at\; weaning}}{{litter\; mass\; at\; weaning\; predicted\; by\; allometry}}\), where _MI_ is the maternal investment (a

unitless number since [kg]\(\times\)[kg]−1 = [1]). The six maternal investment metrics stemming from our six linear regression models are presented in Table 2. The _MI_ metrics directly

correspond to the residuals associated with the regression lines shown in Fig. 1. For bivariate models using only a single predictor (adult mass), a species characterised by _MI_ value of 0

is thus a species that does not deviate from the regression line for the allometric relationship between the litter mass at weaning, the adult mass, and in case of MSLR and MPLMM the

investment duration. More generally, an _MI_ value of 0 corresponds to a species for which the litter mass at weaning equates to what is expected for an average species with the same adult

mass and (if applicable) the same investment duration. A species with a positive or negative _MI_ value thus corresponds to a species for which the litter mass at weaning is respectively

higher or lower than predicted from a given regression model. Computing the _MI_ for all 738 species for which the default adult mass, the investment duration, and the position of any given

species within the phylogenetic tree were known resulted in species-level predictions relatively consistent across the six regression methods. Models not accounting for phylogenetic inertia

resulted in _MI_ estimates similar between each other (all r > 0.92, Quade test: F3,2211 = 0.642, _p_ = 0.59). However, the fit of the phylogenetic linear mixed models (i.e. models PLMM

and MPLMM) revealed a strong phylogenetic signal in the data that is not captured by the allometric relationships. Indeed, both phylogenetic linear mixed models fitted the data significantly

better than their non-phylogenetic counterparts (PLMM vs SLR: Likelihood Ratio Test (LRT) = 933, df = 3, _p_ < 0.001; MPLMM vs MSLR: LRT = 827, df = 3, _p_ < 0.001). In the model

MPLMM, the confidence interval for effect of investment duration (as represented by the scaling coefficient of the allometric relationship between investment duration and the litter mass at

weaning) was significantly negative (Table 1). This does not imply that a longer investment duration means a lower maternal investment. In fact, if investment duration becomes the sole

predictor in the model, the effect is clearly positive (scaling d = 1.82; CI95% = 1.60, 2.04; _N_ = 738). The negative effect of the log10 investment duration in the model MPLMM instead

implies that the longer mothers invest in their offspring the less the litter mass at weaning increases with adult mass. Together, the adult mass and the investment duration therefore

predicted maternal investment significantly better, leading to a more meaningful denominator for the _MI_ value. For these reasons, we chose to perform all subsequent steps of our analysis

using the model MPLMM, which captures both the effect of the phylogeny and that of the investment duration. SENSITIVITY OF THE ALLOMETRIC RELATIONSHIP TO ADULT MASS DEFINITION The first

series of models was based on the default adult mass (i.e. computed by the database provider – Amniote26 – as “the body mass of an adult individual in grams”, not taking sex into account).

Since, in mammals, the maternal investment should be related to the body mass of the female specifically, we used a subset of the data for which estimates of adult mass were available for

both sexes (_N_ = 105) and refitted the model MPLMM separately for the two proxies for adult mass (Fig. 2). The predicted maternal investment metrics remained relatively similar for the same

species irrespective of the type of adult mass proxy used (exact Wilcoxon-Pratt signed-rank test, z = 1.66, _p_ = 0.0970). The difference between the maternal investment metric computed

using the default adult mass and the maternal investment metric computed using the female adult mass differed by more than 0.1 for only 15.2% of the species (Fig. 3). A difference of 0.1 in

maternal investment accounts for ca. 0.40 SD in the variation in the _MI_ metrics. These results demonstrate that the choice of the adult mass proxy had little influence upon inferences on

maternal investment across a wide range of mammals. This finding justifies our decision to analyse default adult mass rather than female adult mass, as it allows us to benefit from a much

larger sample size. TAXONOMIC PATTERNS OF MATERNAL INVESTMENT Since the fit of the phylogenetic linear mixed models (PLMM and MPLMM) revealed a strong phylogenetic signal that is not

captured by the allometric relationship, we now turn to the study of how the taxonomy impacts the maternal investment metric. EFFECT OF MAMMALIAN SUBCLASSES ON MATERNAL INVESTMENT Using the

introduced maternal investment metric (_MI_MPLMM), we compared the maternal investment across the three mammalian subclasses using the same 738 species that we used for the comparison of

fitting methods (Fig. 4). This resulted in a mean ± SD maternal investment of 0.0483 ± 0.242 for _Eutheria_ (_N_ = 654), −0.0708 ± 0.313 for _Metatheria_ (_N_ = 81) and −0.356 ± 0.697 for

_Monotremata_ (_N_ = 3). A Kruskal-Wallis test revealed a significant difference in maternal investment between subclasses (Kruskal–Wallis test: χ2 = 16.2, df = 2, _p_ < 0.001). A

post-hoc comparison showed that the maternal investment of _Eutheria_ was significantly higher compared to that of _Metatheria_ (asymptotic Wilcoxon–Mann–Whitney test; z = 3.87, _p_ < 

0.001). The low sample size for _Monotremata_ precludes meaningful pairwise comparison with this group. The three species of this subclass included in our analysis widely differed in

maternal investment estimate. While the Platypus (_Ornithorhynchus anatinus_) was associated with a relatively high _MI_MPLMM value, one species of echidna (the Western long-beaked echidna –

_Zaglossus bruijnii_) presented the smallest maternal investment value of all 738 species analysed. Refitting the model MPLMM so as to account for the mammalian subclass shows that the

scaling coefficients of the allometric relationships significantly differed between _Eutheria_ and _Metatheria_ (LRT of interaction “subclass”:“log10 default adult mass” = 7.22, df = 1, _p_ 

= 0.023; LRT of interaction “subclass”:“log10 investment duration” = 7.50, df = 1, _p_ = 0.014). Consequently, we refitted the model MPLMM independently in _Eutheria_ and _Metatheria_ to

obtain parameters required to establish subclass-species _MI_ formulas. For _Eutheria_, we obtained a scaling coefficient for the default adult mass of 0.848 (CI95% = 0.818, 0.865) and a

scaling coefficient for the investment duration of −0.190 (CI95% = −0.217, −0.0373). For _Metatheria_, we obtained a scaling coefficient for the default adult mass of 0.778 (CI95% = 0.686,

0.845) and a scaling coefficient for the investment duration of −0.0806 (CI95% = -0.404, 0.279). Omitting the investment duration, and thus refitting the model PLMM, yielded a scaling

coefficient for the default adult mass of 0.820 (CI95% = 0.802, 0.840) for _Eutheria_ and 0.748 (CI95% = 0.703, 0.811) for _Metatheria_. EFFECT OF MAMMALIAN ORDERS ON MATERNAL INVESTMENT

Using the maternal investment metrics (_MI_MPLMM) computed separately for the 632 _Eutherian_ species and for the 67 _Metatherian_ species, we compared the maternal investment across

mammalian orders within these mammalian subclasses (Fig. 5). The data used here correspond to the subset for which all required information was available for more than 15 species per order.

Maternal investment metrics significantly differed between orders within _Eutheria_ (Kruskal–Wallis test: χ2 = 196, df = 6, _p_ < 0.0001) and within _Metatheria_ (exact

Wilcoxon–Mann–Whitney test: z = 5.48, _p_ < 0.001). Within _Eutheria_, _Eulipotyphla_ (_N_ = 58) had the highest average _MI_ value (0.183 ± 0.152) and _Primates_ (_N_ = 83) the lowest

one (−0.318 ± 0.191). Yet, considerable variation was present within orders. For example, variation in _MI_ seems particularly large in _Carnivora_ (−0.134 ± 0.258; _N_ = 85). Refitting the

model MPLMM so as to account for the mammalian orders shows that the scaling coefficient of the allometric relationship between the default adult mass and the litter mass at weaning tended

to significantly differ between mammalian orders within both subclasses (LRT of interaction “order”:“log10 default adult mass”: _Eutheria_ = 21.6, df = 6, _p_ = 0.0571; _Metatheria_ = 16.6,

df = 1, _p_ = 0.036). The results were however less clear for the allometric relationship between the investment duration and the litter mass at weaning (LRT of interaction “order”:“log10

investment duration”: _Eutheria_ = 12.5, df = 6, _p_ = 0.134; _Metatheria_ = 1.61, df = 1, _p_ = 0.314). ILLUSTRATION OF THE MATERNAL INVESTMENT METRIC USING 20 REPRESENTATIVE MAMMALIAN

SPECIES To illustrate the variation in maternal investment between mammals, we calculated maternal investment (_MI_MPLMM) for 20 indicator species belonging to three different subclasses and

13 different taxonomic orders (Table 3, Fig. 6). Since our goal here is to compare species scattered within the entire mammalian tree, we computed all _MI_MPLMM values based on a single fit

of the model MPLMM (for the resulting _MI_ formula, see row MPLMM in Table 2). We selected these species subjectively so as to strike a good balance between retaining well-known species,

including species with various characteristics, and encompassing a priori a relatively large range of maternal investment. For example, for _Eutheria_ our sample includes what we thought may

result in substantially different _MI_ values. On the one hand, we selected the tailless tenrec (_Tenrec ecaudatus_) which has a litter size of up to 32 pups, the largest of all

_Eutheria_27 and which also produces relatively large offspring. On the other hand, we included the greater short-nosed fruit bat, a species in which mothers give birth to a singleton twice

a year28. For most _Eutheria_, the duration of the gestation and lactation period is roughly equal29, whilst the lactation duration in the greater short-nosed fruit bat only takes a third of

the gestation duration (42 and 120 days, respectively30). Our indicator species also include several _Metatheria_ and _Monotremata_ that we expected to fall within the lower end of the

distribution of our metric. DISCUSSION How much energy, material and information organisms allocate to their offspring is extremely diverse and influenced by many factors31,32. Understanding

variation in these investment strategies is a challenging task and many questions about the ecology and evolution of maternal investment remain unanswered (e.g. What factors influence

maternal investment? How does maternal investment affect long-term fitness? How does maternal investment interact with other forms of parental care?). This lack of knowledge stems in part

from the lack of a standardised approach that would allow for an effective comparison of maternal investment across species. In this study, we addressed this methodological gap by

introducing a novel metric, allowing a large-scale comparison using existing data: the maternal investment metric, or _MI_ for short. To quantify maternal investment, we chose to rely on the

weaning mass of offspring produced – an integrative measure of investment encompassing both gestation and lactation33,34. Rather than directly using the litter mass at weaning however, we

rescaled this quantity so as to remove most of the influence stemming from differences in body mass and investment duration between species. A well-known methodological parallel to the _MI_

metric is thus the encephalization quotient, which has also been estimated as an allometric residual in numerous studies to provide a proxy for intelligence35. The measurement of _MI_

implies to fit allometric relationships influencing the litter mass at weaning. Determining the best method to fit such relationships has been subject of debate22,24,36,37,38. We thus

applied and compared a large set of possible methods. As we detected a strong phylogenetic signal in the data, we favoured the use of a phylogenetically-controlled model. Although investment

duration scales with adult mass5,6 and has been shown in some taxa to be consistent with the metabolic theory of ecology39, the effect of investment duration appeared not to be completely

absorbed by the effect of the adult mass. These results explain why we chose a phylogenetically-controlled model that accounts for both adult mass and investment duration, rather than opting

for a more traditional bivariate model that would only consider the former predictor. While we favoured the most complex method (a heteroscedastic linear mixed-effects model accounting for

phylogenetic inertia, which we labelled MPLMM), predictions did not differ substantially across the different methods. Therefore, simple regression methods remain acceptable to compute _MI_

across mammals. In particular, the four simple methods we considered (i.e. SLR, MA, SMA and MSLR) led here to very similar results. To our knowledge, we are the first to fit an allometric

relationship using a particular heteroscedastic phylogenetic linear mixed model that includes random effects both in the modelling of the main response and of the residual variance, and

therefore belongs to the class of double hierarchical generalised linear models40. This model (i.e. MPLMM) addresses at once multiple statistical challenges related to fitting allometric

relationships. Being a multiple linear regression, the model fits the influence of quantitative predictors using straight lines, which is appropriate to estimate the scaling coefficients of

the allometric relationships. Being a mixed model, MPLMM allowed us to model how much the random effects – used to describe how different species depart from a global intercept – covary as a

function of the phylogenetic distance between species. Being a heteroscedastic model, the selected model did account for the fact that a standard multiple linear regression would violate

the homoscedasticity assumption as the residual variance increases with the (log10) adult mass. Being a hierarchical model, we were able to consider as well that the residual variance also

depends on the species identity through a random term. Accounting for all these specificities does exert some impact on the inferred allometric relationships and should thus lead to more

reliable _MI_ values. To provide meaningful _MI_ values, several specifications have to be considered beyond the choice of the statistical model used to predict the litter mass at weaning.

First of all, one needs to consider which proxies of body mass to include in the data. Ideally one would consider adult mass data coming from females only since females do most of the

parental investment in mammals. Unfortunately, sex-specific data are scarce for many organisms and yet ignoring the sex may sound problematic given that for 19% of mammals the sexual size

dimorphism is thought to be noticeably male-biased, and for 7% of them it is female-biased41. Fortunately, our results show that relying on the default adult mass as a predictor for litter

mass at weaning, a piece of information that is more available in the literature, does not seem to be particularly limiting in practice. This is true at least when a phylogenetic linear

mixed model is used. Indeed, we found that the use of default adult mass to compute _MI_ did not lead to a marked difference from the use of the females’ adult mass despite the

overrepresentation of species with high sexual size dimorphism within the sample of 105 species used for the comparison (e.g. 6 species of _Pinnipedia_42 and 44 species of

_Cercopithecidae_43). A possible explanation is that the ratio of the body mass of males to females remains relatively constant among closely related species within our subset. In this

condition, the fitted allometric relationships should yield similar slopes irrespective of whether a default adult mass or a female adult mass is used as a predictor. This is because, in the

linear model, the shift in intercept compensates for the effect of the shift in predictor values on the predicted values, resulting in predictions fairly unaffected by the choice of the

adult mass proxy. Such a choice may become a more serious limitation if the metric is used for research within closely related species for which the degree of size dimorphism varies from

species to species. In such a case, we strongly recommend spending effort to gather data on female adult mass and fit the allometric relationships using these data. Irrespective of the proxy

used for body mass, the quality of such data is important for trusting the metric. Indeed, the _MI_ values as any allometric residuals, while valuable for understanding the relationships

between biological variables22, demand careful consideration due to their susceptibility to reflect both biological signal and measurement errors. Hence, an unusually high or low _MI_ value

for a given species needs to be carefully examined, as it might be the result of such errors in the data rather than the indication of an interesting biological phenomena. Datasets on a

large number of species are becoming increasingly more available but the quality of such data is not always optimal. For example, after noticing an extreme _MI_ value for the walrus, we

found out that the female adult mass of the walrus (_Odobenus rosmarus_), was incorrectly described to be 6.4 g, whereas the actual mass is on average 900 kg44. The differences in _MI_

values obtained for the two alternative proxies of body mass dramatically decreased once we discarded a number of data entry inconsistencies in the Amniote database. Beyond obvious mistakes

of this kind, which are relatively easy to handle automatically (see Methods), another limitation of such databases is that they tend to be based on captive populations for which data

collection on life-history traits is easier. Yet, management and circumstances in captivity can affect certain parameters related to reproductive success45. The body mass of adult animals is

often higher in captivity compared to the wild as demonstrated by the chimpanzee (_Pan troglodytes_)46, Iberian lynx (_Lynx pardinus_)47, elephant (_Elephantidae_)48, and vervet monkey

(_Chlorocebus aethiops sabaeus_)49. The mass of the offspring is often higher in zoos as well50. As the maternal investment metric uses a ratio between body masses, the effect of higher

masses in captivity is partially corrected, but data from wild-roaming populations would remain better for the study of evolutionary adaptations. Litter size might be affected by captive

management as well; however, depending on the species and the institution, this influence can be both positive or negative (e.g. refs. 45,51). Other sampling biases may also be present in

large-scale datasets. In particular, since most data is collected in captivity or for popular study species, a taxonomic bias towards larger species exists52. To decrease the potential

effect of taxonomic biases, one possibility is to consider a sample that is taxonomically quite diverse. For example, we relied here on a sample of 23 different mammalian orders including

≥5% of the species for 22 out of the 27 recognised mammalian orders. That being said, we recommend that the fit should ideally not include species from taxa that are too distant from the

focal group of species one is interested in. This is because our results show that the parameters for the allometric relationships used to compute _MI_ may vary across taxa. This variation

of the allometry across taxa should not however justify fitting the underlying statistical model for the different groups separately. Indeed, _MI_ values stemming from different fits of the

same allometric relationship(s) are not comparable to each other. A comparison would introduce biases comparable to those introduced by performing conditional predictions (see Methods for

details). Whenever sample size allows it, we therefore recommend fitting a single model using only data containing representatives of the groups that must be compared. For example, to

compare the maternal investment between different orders, a single fit of the allometric relationships to the species of the different orders should be used for the scaling of the metric.

Similarly, to compare maternal investment between for instance rodents, the metric should be scaled on a dataset including all the rodents to be compared. How _MI_ behaves for intraspecific

comparison remains to be determined, but in that case the same advice follows: a single model should be fitted on many individuals of the target species. Even with a great statistical model

and a great dataset in hand, one should not forget that _MI_ suffers from the general limitation of most metrics: _MI_ is only an approximation of a complex phenomenon. The proposed metric

captures the direct allocation of energy to the offspring, quantified as body mass gain, but it does not include actual maternal investment that does not impact the litter mass at weaning or

the investment duration. This includes several forms of parental care and protection. For example, we predicted a low _MI_ value for the leopard (_Panthera pardus_), which correctly

reflects that the investment duration through lactation is short in this species. However, this fails to capture that mothers do continue to invest in their offspring by hunting with and for

them for many months after weaning53. Our metric also fails to capture the impact of pre-weaning loss. Such loss of offspring might again impact maternal investment. This latter limitation

may not be severe however since the use of a correction for pre-weaning loss in previous research did not result in significant differences in the production rate of _Eutheria_ and

_Metatheria_29. Another potential caveat of our metric is that the effect of paternal investment is not explicitly considered. Although paternal investment in mammalian species is limited,

the energetic costs and opportunity costs of male care might affect reproductive strategies54. As long as male care corresponds to an alternative energetic contribution to the offspring, the

metric we used can successfully capture variation in paternal investment when it leads to a decrease in lactation duration. Indeed, all else being equal, in species for which paternal

investment is higher, the _MI_ value is thus lower, reflecting energy being saved for the mother. We cannot exclude however that in some species, parental care provided by both sexes is not

alternative but acts synergistically. In such a case, paternal investment would positively impact the litter mass at weaning which would lead to _MI_ values that overestimate the specific

contribution of the mother. Fortunately, this issue should be limited in mammals since the weaning mass, and therefore the direct nutritional investment in the offspring, has been shown to

remain the same overall irrespective of the amount of paternal care55. With all the aforementioned caveats in mind, the proposed metric retains its use for many possible applications. Here

we employed it to compare the maternal investment of the three mammalian subclasses. Although it is well established that _Eutheria_ invest more energy in their offspring during gestation

compared to _Metatheria_56, comparisons of the total energy expenditure on reproduction are rare across the two mammalian subclasses. Our results confirmed unambiguously that many _Eutheria_

do invest more energy than _Metatheria_. Importantly, our maternal investment metric remains adequate for comparing these two subclasses because it considers the litter mass at weaning and

not at birth or hatching. Indeed, the importance of the two major investment periods, the gestation and lactation periods, differs substantially between the three mammalian subclasses.

_Monotremata_ and _Metatheria_ both produce very small offspring and have a relatively short gestation and long lactation, resulting in the birth of highly altricial offspring29,57 relying

mainly on the lactation58,59. _Eutheria_ on the other hand have a developmental state that can vary between altricial and precocial60 and have an equally long gestation and lactation period.

In contrast to our results, one study has argued that the total energy expenditure was higher in _Metatheria_ than in _Eutheria_61. We want to point out however that this previous study was

only based on a comparison between one _Metatherian_ and two _Eutherian_ species. Given the large interspecies variation62 in _MI_ within a subclass revealed by our study, comparisons

should not be based on a small number of species if one wants to draw conclusions at such a high taxonomic level. Similarly, another study reported that no significant differences in

maternal investment could be demonstrated between _Metatheria_ and _Eutheria_ of the same mass63. Given that our sample is more taxonomically diverse and around seven times larger than the

one previously used, we are confident that the signal present in our data is real. Nonetheless, albeit large, our study encompasses a still small proportion of the total number of extant

_Eutheria_ (_N_ ~ 6164) and _Metatheria_ (_N_ ~ 230) species64,65 and we encourage others to collect or assemble a larger dataset and reassess differences in _MI_ metrics between taxonomic

groups. Our study also suggests that the mean maternal investment of _Monotremata_ may be lower than the mean investment of _Eutheria_ and _Metatheria_, although we could not test such a

difference due to the lack of data on _Monotremata_ (_N_ = 3). This mammalian subclass consists of only two additional species of echidna (_Tachyglossidae_) which were not present in our

sample. Given the similar reproductive biology between several echidna species, the chances of a similar maternal investment are however high66, which would confirm a lower maternal

investment for _Monotremata_ compared to _Eutheria_ and _Metatheria_. This would be in line with the expectations for non-mammalian oviparous species investing less in their offspring

compared to viviparous species67,68,69 (see also ref. 70), but this would not explain why we estimated an _MI_ value for the platypus (_Ornithorhynchus anatinus_) much higher than the two

species of echidnas, and even higher than many _Eutheria_ and _Metatheria_. The argument of oviparity being associated with lower maternal investment does not however account for lactation

which occurs in _Monotremata_ – the only oviparous mammals. Upon an exploration of the literature to better understand our findings, we discovered that the uptake of milk by the offspring is

much higher in platypuses than in echidnas. Whereas a young short-beaked echidna requires a milk intake of 10–12% of its body mass every three to five days, the platypus requires a much

higher milk intake of 10–20% of its body mass every single day71. The total intake of solids per kilogram of body mass, and thus maternal investment in milk production, is therefore higher

in the platypus72. This remains true even after considering that the total concentration of solids (e.g. lipids, protein, and carbohydrates) and the investment duration are somewhat lower in

platypuses compared to short-beaked echidnas. This difference in milk production could therefore explain why _MI_ values differ between the two families of _Monotremata_ and why the _MI_

value of the platypus remains high relative to many species from other mammalian subclasses. We also compared maternal investment for twenty well known species present in the Amniote

database. Although we did not have clear predictions about how high maternal investment may be for every single species, our results confirmed specific predictions. In particular, our metric

shows that the tailless tenrec presents the highest maternal investment among the 738 species in agreement with being the mammal with the highest known litter size. The greater short-nosed

fruit bat – a species for which the reproductive characteristics made us predict a particularly low maternal investment – also appeared to be the species with the lowest _MI_ value within

the 15 selected _Eutheria_. Additionally, the highest ranking _Metatherian_ only reached the tenth position in decreasing order of _MI_ values. Applying the maternal investment metric

methodology, it should be possible to use our _MI_ metric for animal classes other than mammals. It may even be useful to study reproductive strategies in plants. Indeed, Hendriks and

Mulder73 showed that total offspring mass per reproductive event and the adult mass scale with each other in both animals and plants. In addition, Brown et al.74 showed that the individual

biomass production (i.e. the investment in reproduction and/or growth in ratio to the biomass of the investor per year) scales with the mass of the organism for plants, zooplankton, fish,

birds, and insects. Comparing different classes of animals should be handled with care due to different reproductive strategies (such as no/limited post-partum/hatching parental care in most

reptiles75 or extensive parental care of both males and females in most birds76). Additionally, large gaps in life-history data are present in non-mammalian species77. Some adjustment would

also have to be made for computing the _MI_ metric. An equivalent value for litter mass at weaning for non-mammalian species would have to be determined, such as clutch mass in birds and

reptiles78. Additionally, an equivalent for the investment duration would have to be defined, or it would have to be dropped (i.e. the maternal investment metric would have to be based on

the model PLMM rather than MPLMM). Further research might make it possible to include more aspects of maternal investment in the metric and expand the opportunities of this approach to

quantify maternal investment. Importantly, a dataset containing direct estimates of maternal investment (e.g. calorimetric maternal investment data) for multiple species would be required to

further optimise and validate the _MI_ metric. Despite some of the difficulties aforementioned, collecting data on body mass on a large number of species is generally easier compared to

acquiring physiological data more directly reflecting maternal investment. The ease of data collection makes the established metric highly practical and applicable across a wide range of

versatile scenarios. By introducing a novel approach to quantify maternal investment, this research strives to advance our understanding of the intricate relationships associated with

reproduction, offering a foundation for further exploration in the field of maternal investment and its impact on the fitness and dynamics of animal populations. It is a promising tool to

further improve our understanding of maternal investment and, in a larger context, of the evolution of reproductive strategies. METHODS DATA COLLECTION All life-history data were derived

from the Amniote database26. Only data on mammalian species for which the default adult mass, weaning mass, and litter size were available (_N_ = 1053) were used. Default adult masses,

exceeding the highest or the lowest sex specific adult mass with more than 15% were excluded. The same was applied to weaning masses exceeding the default adult mass with more than 15%. An

obvious error in walrus and sea otter data was corrected with data derived from the Encyclopedia of Marine Mammals44 and Walker’s Mammals of the World79. This resulted in a subset of 1041

species. To conduct phylogenetically-controlled analyses, we derived data from the Mammal tree25. A subset was generated based on species present in both the phylogenetic tree and Amniote

database. Additionally, for the comparison of the six regression methods (SLR, PLMM, SMA, MA, MSLR, MPLMM), species for which the gestation duration (excluding embryonic diapause) and

lactation duration were not available, were dropped, resulting in a subset of 738 species. The data from the Amniote database were mainly collected from captive animals. Unfortunately

details on the source of the default adult mass were not provided in the Amniote database. A subset (_N_ = 105) of species for which female adult masses were reported was created to

determine the effect of sex on the predicted litter mass at weaning and consequently on the maternal investment metric. STATISTICS AND REPRODUCIBILITY All analyses were conducted using R

version 4.3.180. We provide all the R code used to produce the results and the illustrations of this paper via a repository hosted on GitHub (https://github.com/courtiol/mammalianMI). To fit

the allometric relationships, we fitted six different regression models: 1) SLR, 2) PLMM, 3) SMA, 4) MA, 5) MSLR, and 6) MPLMM. We used the R packages smatr version 3.4.881 to fit the

models SMA and MA and we used spaMM version 4.4.16 & 4.4.23.182 to fit all the other models. The SLR, SMA and MA models all correspond to a simple bivariate linear regression of the

form: \({y}_{i}=a+b\times {x}_{i}+{\epsilon }_{i}\), where in our case \({y}_{i}\) is the log10 of the litter mass at weaning for the species \(i\), \(a\) is the intercept of the linear

regression, \(b\) is the slope of the linear regression, \({x}_{i}\) is the log10 adult mass, and \({\epsilon }_{i}\) is the residual for species \(i\). The exact form of \({\epsilon

}_{i}\), and how \(a\) and \(b\) are estimated, differ between the simple linear regression (SLR), the standardised major axis regression (SMA), and the major axis regression (MA). The

differences between these three methods lies in what errors the residuals are encompassing. In SLR, the residuals only capture errors in the _y_-axis, while SMA and MA are two closely

related methods accounting for errors in both axes. These differences have been detailed extensively in the literature (see e.g. Warton et al.24 for a presentation in the context of

allometry) and debates about when to use one method or the other have been going on for decades22,23,24. Irrespective of these technical differences, all three regressions yield the

following allometric relationship: \({{y{{\hbox{'}}}}}_{i}={a{{\hbox{'}}}}\times {{x{{\hbox{'}}}}}_{i}^{b}\), where \({{y{{\hbox{'}}}}}_{i}\) is the litter mass at

weaning for the species \(i\) (without log-transformation), \(a\)’ equates \({10}^{a}\) (with \(a,\) as defined above, the intercept of the linear regression), \({{x{{\hbox{'}}}}}_{i}\)

is the adult mass (without log-transformation), and \(b\) is the scaling coefficient of the allometric relationship and thus equates the slope of the underlying linear regression. The MSLR

method is a simple extension of the SLR method that enabled us to consider the influence of a second predictor: the investment duration. The corresponding equations are thus

\({y}_{i}=a+b\times {x}_{i}+c\times {z}_{i}+{\epsilon }_{i}\) and \({{y{{\hbox{'}}}}}_{i}={a{{\hbox{'}}}}\times {{x{{\hbox{'}}}}}_{i}^{b}\times

{{z{{\hbox{'}}}}}_{i}^{c}\), where \({z}_{i}\) is the log10 of the investment duration, \({{z{{\hbox{'}}}}}_{i}\) the investment duration in its original scale (i.e. days) and

\(c\) is both the slope associated with the log10 investment duration in the linear regression and the (partial) scaling coefficient of the allometric relationship between investment

duration and the litter mass at weaning. The meaning of the other parameters does not change from the original SLR model, except that \(b\) becomes a partial scaling coefficient of the

allometric relationship between the adult mass and the litter mass at weaning. The PLMM and the MPLMM are more complex. They correspond to linear mixed-effects models, often referred as

mixed-models or LMM for short. In these models, the regression equations become \({y}_{i}=a+b\times {x}_{i}+{r}_{i}+{\epsilon }_{i}\) and \({y}_{i}=a+b\times {x}_{i}+c\times

{z}_{i}+{r}_{i}+{\epsilon }_{i}\) where \({r}_{i}\) is a random effect term which contributes to the departure of each species from the intercept \(a\). This random term has mean 0, a

variance \(\lambda\) and a covariance that is a function of the phylogenetic distance between species. We used the Pagel’s correlation function83,84, as implemented by the function

corPagel() from the R package ape version 5.7.185. We initialised the correlation matrix produced by corPagel() using the R package nlme version 3.1.16486 and provided it to the function

fitme() used to fit the model in spaMM using the argument corrMatrix. Since we noticed heteroscedasticity in the errors of these mixed-model fits, we defined a specific residual model for

the models PLMM and MPLMM. As in the models SLR and MSLR, the residuals are normally distributed and defined as \({\epsilon }_{i}=N(0,\phi )\); but while\(\,\phi\) – the variance of a

Gaussian distribution of the error – is a constant value in these simpler models, for the models PLMM and MPLMM,\(\,\phi\) is itself a variable described by a statistical model to be fitted.

Specifically, we have defined \(\log (\phi )=d+e\times {\alpha }_{i}+{s}_{i}\), where \(d\) is the intercept of the residual dispersion model, \(e\) its slope, \({\alpha }_{i}\) the log10

adult body mass of the species \(i\) and \({s}_{i}\) is a random gaussian term which contributes to the departure of each species from the intercept \(d\). This random term has mean 0, a

variance \(\gamma\), but this time we considered a null covariance between the realisations of the random effects and thus did not consider the effect of the phylogenetic distance for the

residual dispersion model. The models PLMM and MPLMM are thus models with two components. The first component, called mean model, models the log10 litter mass at weaning based on the log10

adult mass, the log10 investment duration (in the case of the MPLMM), the species identity and the phylogenetic distance of that species to the other species. The second component, called

the residual dispersion model, is the model for the (log) variance of residual error of the first component, based on the log10 adult mass and the species identity. In spaMM, the function

fitme() allows to fit jointly all the parameters indicated above (i.e.\(\,a,b,c,\lambda ,d,e,\gamma\)) and the models PLMM and MPLMM thus correspond to so-called double hierarchical

generalised linear model40. There is one parameter that cannot be fitted by a single call to fitme() without further programming: the correlation parameter of the function corPagel() which

is usually referred to as Pagel’s lambda (here denoted Λ). To estimate this parameter, we thus built a wrapper around the function fitme(), returning the log likelihood of the fit for fixed

Λ, and maximised the likelihood, using this wrapper as objective function, using the function optimise() from R. Note however that fitme() can directly fit the model including corPagel()

correlation structure with fixed Λ. For all six regression models, we computed confidence intervals using the generic function confint() which calls a specific underlying function for each

case. For the model PLMM and MPLMM, we computed the confidence intervals for all parameters but Λ by parametric bootstrap using 1000 bootstrap replicates. We computed the confidence interval

for Λ using log-likelihood profiling. We compared the models SLR, PLMM and MPLMM using a likelihood ratio test for which the distribution of the test statistic under the null hypothesis was

also estimated using parametric bootstrap using 1000 bootstrap replicates. For this, we used the function anova() from spaMM. When manipulating mixed models for predicting values (in our

case the predicted litter mass at weaning, which is used to obtain _MI_ values), two alternative types of predictions can be computed: so-called conditional predictions which include the

realisation of the random effects, and marginal predictions which consider the expected values of random effects independently of their values predicted by the fit of the model to the data.

This expected value is zero in our case. The marginal predictions here reflect only the allometric relationship, while the conditional predictions include random effect values which are

driven by differences in ecology and genetics that are correlated along the phylogeny. Residuals from such conditional predictions would therefore remove these ecological and genetic 

effects. On the contrary, residuals from the marginal predictions include them as components of the _MI_ we aim to measure. These marginal species-level predictions do account for the

phylogeny in the sense that the allometry relationships established for all species depend on the phylogenetic correlations (this is because fixed effects depends on random effects and vice

versa), and species-level predictions remain influenced by the specificities of the species that correlate with the phylogeny. Beyond the fit of statistical models, we also relied on a few

traditional statistical parametric and non parametric tests. Specifically, we relied on Pearson correlations using the functions cor() and cor.test() to assess potential correlation between

different variables. We used Quade tests to compare predicted _MI_ values obtained for the different species across alternative regression methods using the function quade.test() readily

available in R. We used the Wilcoxon-Pratt signed-rank test, which directly corresponds to a Quade test for comparison of two conditions only, to test whether using two alternative proxies

for adult body mass had a noticeable effect in predicted _MI_ values. This time, since we used a smaller dataset, we used the version of this test provided by the R package coin version

1.4.387 named wilcoxsign_test(), which we set so as to provide an exact computation of the p-value. For comparisons between groups made of different species, we similarly used the

Kruskal-Wallis test implemented in the function kruskal.test() available in R and the Wilcoxon-Mann-Whitney test provided by the function wilcox_test() from the R package coin. For creating

the figures, we used the R packages ggplot 2 version 3.4.488, ggdist version 3.3.189 which provides the geometries used to represent distributions in Figs. 4 and 5, and patchwork version

1.2.090 which we used to assemble sub-figures togethers. We also used the package rphylopic version 1.3.091 to handle the silhouettes of animals in Fig. 6. For reshaping datasets, we finally

used the R package tidyr version 1.3.192. REPORTING SUMMARY Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article. DATA

AVAILABILITY The life history data and R code that support the findings of this study are available in an open access GitHub repository: https://github.com/courtiol/mammalianMI. REFERENCES *

Bugental, D. B. Maternal Investment. In _Encyclopedia of Evolutionary Psychological Science_ 1–3 (Springer International Publishing, 2016). * Trivers, Robert L. Parental investment and

sexual selection. In _Sexual Selection and the Descent of Man_ 1871–1971 (Aldine, 1972). * Macdonald, K. R., Rotella, J. J., Garrott, R. A. & Link, W. A. Sources of variation in maternal

allocation in a long‐lived mammal. _J. Anim. Ecol._ 89, 1927–1940 (2020). Article  PubMed  PubMed Central  Google Scholar  * Edward, D. A. & Chapman, T. Mechanisms underlying

reproductive trade-offs: costs of reproduction. In _Mechanisms of Life History Evolution_ 137–152 (Oxford University Press, 2011). . * Speakman, J. R. Body size, energy metabolism and

lifespan. _J. Exp. Biol._ 208, 1717–1730 (2005). Article  PubMed  Google Scholar  * West, G. B., Woodruff, W. H. & Brown, J. H. Allometric scaling of metabolic rate from molecules and

mitochondria to cells and mammals. _Proc. Natl Acad. Sci._ 99, 2473–2478 (2002). Article  PubMed  PubMed Central  Google Scholar  * Koskela, E., Mappes, T., Niskanen, T. & Rutkowska, J.

Maternal investment in relation to sex ratio and offspring number in a small mammal - a case for Trivers and Willard theory? _J. Anim. Ecol._ 78, 1007–1014 (2009). Article  PubMed  PubMed

Central  Google Scholar  * Kim, J.-y Influence of resource level on maternal investment in a leaf-cutter bee (_Hymenoptera: Megachilidae_). _Behav. Ecol._ 10, 552–556 (1999). Article  Google

Scholar  * Broussard, D. R., Dobson, F. S. & Murie, J. O. Previous experience and reproductive investment of female Columbian ground squirrels. _J. Mammal._ 89, 145–152 (2008). Article

  Google Scholar  * Snyder, R. J., Perdue, B. M., Zhang, Z., Maple, T. L. & Charlton, B. D. Giant panda maternal care: a test of the experience constraint hypothesis. _Sci. Rep._ 6,

27509 (2016). Article  CAS  PubMed  PubMed Central  Google Scholar  * Barbosa, M. et al. Maternal response to environmental unpredictability. _Ecol. Evol._ 5, 4567–4577 (2015). Article 

PubMed  PubMed Central  Google Scholar  * Capellini, I., Venditti, C. & Barton, R. A. Placentation and maternal investment in mammals. _Am. Nat._ 177, 86–98 (2011). Article  PubMed 

Google Scholar  * Mauget, C., Mauget, R. & Sempéré, A. Energy expenditure in European roe deer fawns during the suckling period and its relationship with maternal reproductive cost.

_Can. J. Zool._ 77, 389–396 (1999). Article  Google Scholar  * McNab, B. K. The energetics of reproduction in endotherms and its implication for their conservation. _Integr. Comp. Biol._ 46,

1159–1168 (2006). Article  PubMed  Google Scholar  * Schubert, K. A. et al. Maternal energy allocation to offspring increases with environmental quality in house mice. _Am. Nat._ 173,

831–840 (2009). Article  PubMed  Google Scholar  * Viblanc, V. A., Saraux, C., Murie, J. O. & Dobson, F. S. Kin effects on energy allocation in group‐living ground squirrels. _J. Anim.

Ecol._ 85, 1361–1369 (2016). Article  PubMed  Google Scholar  * Weiss, M. N. et al. Costly lifetime maternal investment in killer whales. _Curr. Biol._ 33, 744–748 (2023). Article  CAS 

PubMed  Google Scholar  * Zeveloff, S. I. & Boyce, M. S. Maternal investment in mammals. _Nature_ 321, 537–538 (1986). Article  CAS  PubMed  Google Scholar  * Hargrove, J. W., Muzari, M.

O. & English, S. How maternal investment varies with environmental factors and the age and physiological state of wild tsetse _Glossina pallidipes_ and _Glossina morsitans morsitans_.

_R. Soc. Open Sci._ 5, 171739 (2018). Article  PubMed  PubMed Central  Google Scholar  * Huxley, J. S. _Problems of Relative Growth_ (Johns Hopkins University Press, 1932). * Thomson, J. A.

On Growth and Form. _Nature_ 100, 21–22 (1917). Article  Google Scholar  * Hansen, T. F. & Bartoszek, K. Interpreting the evolutionary regression: the interplay between observational and

biological errors in phylogenetic comparative studies. _Syst. Biol._ 61, 413–425 (2012). Article  PubMed  Google Scholar  * Riska, B. Regression models in evolutionary allometry. _Am. Nat._

138, 283–299 (1991). Article  Google Scholar  * Warton, D. I., Wright, I. J., Falster, D. S. & Westoby, M. Bivariate line‐fitting methods for allometry. _Biol. Rev._ 81, 259–291 (2006).

Article  PubMed  Google Scholar  * Upham, N. S., Esselstyn, J. A. & Jetz, W. Inferring the mammal tree: species-level sets of phylogenies for questions in ecology, evolution, and

conservation. _PLOS Biol._ 17, e3000494 (2019). Article  CAS  PubMed  PubMed Central  Google Scholar  * Myhrvold, N. P. et al. An amniote life‐history database to perform comparative

analyses with birds, mammals, and reptiles. _Ecology_ 96, 3109–3109 (2015). Article  Google Scholar  * Nicoll, M. E. & Racey, P. A. Follicular development, ovulation, fertilization and

fetal development in tenrecs (_Tenrec ecaudatus_). _Reproduction_ 74, 47–55 (1985). Article  CAS  Google Scholar  * Meenakumari, K. J. & Krishna, A. Delayed embryonic development in the

Indian short-nosed fruit bat, _Cynopterus sphinx_. _Zoology_ 108, 131–140 (2005). Article  PubMed  Google Scholar  * Hamilton, M. J., Davidson, A. D., Sibly, R. M. & Brown, J. H.

Universal scaling of production rates across mammalian lineages. _Proc. R. Soc. B Biol. Sci._ 278, 560–566 (2011). Article  Google Scholar  * Tacutu, R. et al. Human Ageing Genomic

Resources: integrated databases and tools for the biology and genetics of ageing. _Nucleic Acids Res._ 41, 1027–1033 (2012). Article  Google Scholar  * Behringer, R. R., Eakin, G. S. &

Renfree, M. B. Mammalian diversity: gametes, embryos and reproduction. _Reprod. Fertil. Dev._ 18, 99 (2006). Article  PubMed  Google Scholar  * Powell, L. E., Barton, R. A. & Street, S.

E. Maternal investment, life histories and the evolution of brain structure in primates. _Proc. R. Soc. B Biol. Sci._ 286, 20191608 (2019). Article  Google Scholar  * Kovacs, K. M. &

Lavigne, D. M. Maternal investment and neonatal growth in phocid seals. _J. Anim. Ecol._ 55, 1035 (1986). Article  Google Scholar  * Reiss, M. J. The intraspecific relationship of parental

investment to female body weight. _Funct. Ecol._ 1, 105 (1987). Article  Google Scholar  * Jerison, H. J. The theory of encephalisation. _Ann. N. Y. Acad. Sci._ 299, 146–160 (1977). Article

  CAS  PubMed  Google Scholar  * Kilmer, J. T. & Rodríguez, R. L. Ordinary least squares regression is indicated for studies of allometry. _J. Evol. Biol._ 30, 4–12 (2017). Article  CAS

  PubMed  Google Scholar  * Martin, R. D., Genoud, M. & Hemelrijk, C. K. Problems of allometric scaling analysis: examples from mammalian reproductive biology. _J. Exp. Biol._ 208,

1731–1747 (2005). Article  PubMed  Google Scholar  * Smith, R. J. Use and misuse of the reduced major axis for line‐fitting. _Am. J. Phys. Anthropol._ 140, 476–486 (2009). Article  PubMed 

Google Scholar  * Dubman, E., Collard, M., Mooers & A, Ø. Evidence that gestation duration and lactation duration are coupled traits in primates. _Biol. Lett._ 8, 998–1001 (2012).

Article  PubMed  PubMed Central  Google Scholar  * Lee, Y., Nelder, J. A. & Pawitan, Y. _Generalized Linear Models With Random Effects: Unified Analysis Via H-Likelihood_ (CRC Press,

Taylor & Fancis Group, 2021). * Jones, M. E. & Sheard, C. The macroevolutionary dynamics of mammalian sexual size dimorphism. _Proc. R. Soc. B Biol. Sci._ 290, 20231211 (2023).

Article  Google Scholar  * Cullen, T. M., Fraser, D., Rybczynski, N. & Schröder-Adams, C. Early evolution of sexual dimorphism and polygyny in _Pinnipedia_. _Evolution_ 68, 1469–1484

(2014). Article  PubMed  Google Scholar  * Dixson, A. F. _Primate Sexuality: Comparative Studies of the Prosimians, Monkeys, Apes, and Humans_ (Oxford University Press, 2012). * Lydersen, C.

Walrus. in _Encyclopedia of Marine Mammals_ 1045–1048 (Elsevier, 2018). * Farquharson, K. A., Hogg, C. J. & Grueber, C. E. A meta-analysis of birth-origin effects on reproduction in

diverse captive environments. _Nat. Commun._ 9, 1055 (2018). Article  PubMed  PubMed Central  Google Scholar  * Curry, B. A. et al. Body mass and growth rates in captive chimpanzees (_Pan

troglodytes_) cared for in African wildlife sanctuaries, zoological institutions, and research facilities. _Zoo. Biol._ 42, 98–106 (2023). Article  PubMed  Google Scholar  * Reeves, J.,

Smith, C., Dierenfeld, E. S. & Whitehouse-Tedd, K. Captivity-induced metabolic programming in an endangered felid: implications for species conservation. _Sci. Rep._ 10, 3630 (2020).

Article  CAS  PubMed  PubMed Central  Google Scholar  * Morfeld, K. A., Meehan, C. L., Hogan, J. N. & Brown, J. L. Assessment of body condition in African (_Loxodonta africana_) and

Asian (_Elephas maximus_) elephants in North American zoos and management practices associated with high body condition scores. _PLOS One_ 11, e0155146 (2016). Article  PubMed  PubMed

Central  Google Scholar  * Turner, T. R., Cramer, J. D., Nisbett, A. & Gray, J. P. A comparison of adult body size between captive and wild vervet monkeys (_Chlorocebus aethiops

sabaeus_) on the island of St. Kitts. _Primates_ 57, 211–220 (2016). Article  PubMed  PubMed Central  Google Scholar  * Lim, J. N., Senior, A. M. & Nakagawa, S. Heterogeneity in

individual quality and reproductive trade-offs within species. _Evolution_ 68, 2307–2318 (2014). Google Scholar  * Keeley, T. et al. Seasonality and breeding success of captive and wild

Tasmanian devils (Sarcophilus harrisii). _Theriogenology_ 95, 33–41 (2017). Article  CAS  PubMed  Google Scholar  * Santos et al. Drivers of taxonomic bias in conservation research: a global

analysis of terrestrial mammals. _Anim. Conserv._ 23, 679–688 (2020). Article  Google Scholar  * Balme, G. A., Robinson, H. S., Pitman, R. T. & Hunter, L. T. B. Flexibility in the

duration of parental care: female leopards prioritise cub survival over reproductive output. _J. Anim. Ecol._ 86, 1224–1234 (2017). Article  PubMed  Google Scholar  * Etienne, L., Rousset,

F., Godelle, B. & Courtiol, A. How choosy should I be? The relative searching time predicts evolution of choosiness under direct sexual selection. _Proc. R. Soc. B Biol. Sci._ 281,

20140190 (2014). Article  Google Scholar  * West, H. E. R. & Capellini, I. Male care and life history traits in mammals. _Nat. Commun._ 7, 11854 (2016). Article  CAS  PubMed  PubMed

Central  Google Scholar  * Smith, K. K. & Keyte, A. L. Adaptations of the marsupial newborn: birth as an extreme environment. _Anat. Rec._ 303, 235–249 (2020). Article  Google Scholar  *

Stannard, H. J., Miller, R. D. & Old, J. M. Marsupial and monotreme milk-a review of its nutrient and immune properties. _PeerJ_ 8, 9335 (2020). Article  Google Scholar  * Capuco, A. V.

& Akers, R. M. The origin and evolution of lactation. _J. Biol._ 8, 37 (2009). Article  PubMed  PubMed Central  Google Scholar  * Guernsey, M. W., Chuong, E. B., Cornelis, G., Renfree,

M. B. & Baker, J. C. Molecular conservation of marsupial and eutherian placentation and lactation. _eLife_ 6, e27450 (2017). Article  PubMed  PubMed Central  Google Scholar  * Ferner,

K., Schultz, J. A. & Zeller, U. Comparative anatomy of neonates of the three major mammalian groups (monotremes, marsupials, placentals) and implications for the ancestral mammalian

neonate morphotype. _J. Anat._ 231, 798–822 (2017). Article  PubMed  PubMed Central  Google Scholar  * Thompson, S. D. & Nicoll, M. E. Basal metabolic rate and energetics of reproduction

in therian mammals. _Nature_ 321, 690–693 (1986). Article  CAS  PubMed  Google Scholar  * Weir, B. J. & Rowlands, I. W. Reproductive strategies of mammals. _Annu. Rev. Ecol. Syst._ 4,

139–163 (1973). Article  Google Scholar  * Hayssen, V., Lacy, R. C. & Parker, P. J. Metatherian reproduction: transitional or transcending? _Am. Nat._ 126, 617–632 (1985). Article 

Google Scholar  * Burgin, C. J., Colella, J. P., Kahn, P. L. & Upham, N. S. How many species of mammals are there? _J. Mammal._ 99, 1–14 (2018). Article  Google Scholar  * Norris, D. O.

& Carr, J. A. The Endocrinology of Mammalian Reproduction. In _Vertebrate Endocrinology_ 315–369 (Elsevier, 2021). * Berkovitz, B. & Shellis, P. Monotremata and Marsupialia. In _The

Teeth of Mammalian Vertebrates_ 57–74 (Elsevier, 2018). * Orrell, K. S. & Kunz, T. H. Energy Costs of Reproduction. In _Reference Module in Earth Systems and Environmental Sciences_

(Elsevier, 2016). * Whittington, C. M. et al. Understanding the evolution of viviparity using intraspecific variation in reproductive mode and transitional forms of pregnancy. _Biol. Rev._

97, 1179–1192 (2022). Article  PubMed  Google Scholar  * Zhang, L., Guo, K., Zhang, G.-Z., Lin, L.-H. & Ji, X. Evolutionary transitions in body plan and reproductive mode alter

maintenance metabolism in squamates. _BMC Evol. Biol._ 18, 45 (2018). Article  PubMed  PubMed Central  Google Scholar  * Recknagel, H. & Elmer, K. R. Differential reproductive investment

in co-occurring oviparous and viviparous common lizards (_Zootoca vivipara_) and implications for life-history trade-offs with viviparity. _Oecologia_ 190, 85–98 (2019). Article  PubMed 

PubMed Central  Google Scholar  * Holz, P. Monotremata (Echidna, Platypus). in _Fowler’s Zoo and Wild Animal Medicine, Volume_ _8_ 247–255 (Elsevier, 2015). * Grijfiths, M., Green, B., Mc

Leckie, R., Messer, M. & Newgrain, K. Constituents of Platypus and Echidna Milk, with Particular Reference to the Fatty Acid Complement of the Triglycerides. _Aust. J. Biol. Sci._ 37,

323 (1984). Article  Google Scholar  * Hendriks, A. J. & Mulder, C. Scaling of offspring number and mass to plant and animal size: model and meta-analysis. _Oecologia_ 155, 705–716

(2008). Article  PubMed  PubMed Central  Google Scholar  * Brown, J. H., Gillooly, J. F., Allen, A. P., Savage, V. M. & West, G. B. Toward a metabolic theory of ecology. _Ecology_ 85,

1771–1789 (2004). Article  Google Scholar  * While, G. M., Uller, T. & Wapstra, E. Family conflict and the evolution of sociality in reptiles. _Behav. Ecol._ 20, 245–250 (2009). Article

  Google Scholar  * Mota-Rojas, D. et al. Parental behavior and newborn attachment in birds: life history traits and endocrine responses. _Front. Psychol._ 14, 1183554 (2023). Article 

PubMed  PubMed Central  Google Scholar  * Titley, M. A., Snaddon, J. L. & Turner, E. C. Scientific research on animal biodiversity is systematically biased towards vertebrates and

temperate regions. _PLoS One_ 12, 0189577 (2017). Article  Google Scholar  * Werner, J. & Griebeler, E. M. New insights into non-avian dinosaur reproduction and their evolutionary and

ecological implications: linking fossil evidence to allometries of extant close relatives. _PLoS ONE_ 8, 72862 (2013). Article  Google Scholar  * Jones, J. K. Walker’s Mammals of the World.

_J. Mammal._ 65, 171–171 (1984). Article  Google Scholar  * R Computing Team. _R: A language and environment for statistical computing_ (R Computing Team, 2022). * Warton, D. I., Duursma, R.

A., Falster, D. S. & Taskinen, S. smatr 3– an R package for estimation and inference about allometric lines. _Methods Ecol. Evol._ 3, 257–259 (2012). Article  Google Scholar  * Rousset,

F. & Ferdy, J.-B. Testing environmental and genetic effects in the presence of spatial autocorrelation. _Ecography_ 37, 781–790 (2014). Article  Google Scholar  * Pagel, M. Inferring

the historical patterns of biological evolution. _Nature_ 401, 877–884 (1999). Article  CAS  PubMed  Google Scholar  * Freckleton, R. P., Harvey, P. H. & Pagel, M. Phylogenetic analysis

and comparative data: a test and review of evidence. _Am. Nat._ 160, 712–726 (2002). Article  CAS  PubMed  Google Scholar  * Paradis, E. & Schliep, K. ape 5.0: an environment for modern

phylogenetics and evolutionary analyses in R. _Bioinformatics_ 35, 526–528 (2019). Article  CAS  PubMed  Google Scholar  * Pinheiro, J. & Bates, D. _Mixed-Effects Models in S and S-PLUS_

(Springer-Verlag, 2000). * Hothorn, T., Hornik, K., Wiel, M. A. V. D. & Zeileis, A. Implementing a class of permutation tests: the coin package. _J. Stat. Softw_. 28, 1–23 (2008). *

Wickham, H. _ggplot2: Elegant Graphics for Data Analysis_. (Springer, 2009). * Kay, M. ggdist: visualizations of distributions and uncertainty in the grammar of graphics. _IEEE Trans. Vis.

Comput. Graph_. 30, 414–424 (2023) . * Pedersen, T. patchwork: the composer of plots. R package version 1.2.0, https://github.com/thomasp85/patchwork (2024). * Gearty, W. & Jones, L. A.

rphylopic: an R package for fetching, transforming, and visualising PhyloPic silhouettes. _Methods Ecol. Evol._ 14, 2700–2708 (2023). * Wickham, H., Vaughan, D. & Girlich, M. tidyr: tidy

messy data. R package version 1.3.1, https://github.com/tidyverse/tidyr (2024). Download references ACKNOWLEDGEMENTS We thank Leonie Walter and Olivia Judson for commenting on the

manuscript. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Internal Medicine, Reproduction and Population Medicine, Faculty of Veterinary Medicine, Ghent University,

Salisburylaan 133, 9820, Merelbeke, Belgium Tim E.R.G. Huijsmans, Ann Van Soom & Katrien Smits * Department of Evolutionary Genetics, Leibniz Institute for Zoo & Wildlife Research,

Alfred-Kowalke-Str. 17, 10315, Berlin, Germany Alexandre Courtiol * Institute of Evolutionary Science of Montpellier, University of Montpellier, CNRS, IRD, campus Triolet, 34095, Montpellier

cedex 05, France François Rousset * Department of Reproduction Biology, Leibniz Institute for Zoo & Wildlife Research, Alfred-Kowalke-Str. 17, 10315, Berlin, Germany Jella Wauters *

Laboratory of Integrative Metabolomics, Department of Translational Physiology, Infectiology and Public Health, Faculty of Veterinary Medicine, Ghent University, Salisburylaan 133, 9820,

Merelbeke, Belgium Jella Wauters * Department of Reproduction Management, Leibniz Institute for Zoo & Wildlife Research, Alfred-Kowalke-Str. 17, 10315, Berlin, Germany Thomas B.

Hildebrandt * Freie Universität Berlin, Kaiserswerther Str. 16-18, 14195, Berlin, Germany Thomas B. Hildebrandt Authors * Tim E.R.G. Huijsmans View author publications You can also search

for this author inPubMed Google Scholar * Alexandre Courtiol View author publications You can also search for this author inPubMed Google Scholar * Ann Van Soom View author publications You

can also search for this author inPubMed Google Scholar * Katrien Smits View author publications You can also search for this author inPubMed Google Scholar * François Rousset View author

publications You can also search for this author inPubMed Google Scholar * Jella Wauters View author publications You can also search for this author inPubMed Google Scholar * Thomas B.

Hildebrandt View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS The authors confirm contribution to the paper as follows: Conceptualisation,

T.E.R.G.H., A.C. and T.B.H.; statistical analyses, A.C., T.E.R.G.H., and F.R.; writing—original draft preparation, T.E.R.G.H., A.C.; writing—review and editing, A.v.S., K.S., J.W., F.R. and

T.B.H; visualisation, T.E.R.G.H. and A.C. CORRESPONDING AUTHOR Correspondence to Tim E.R.G. Huijsmans. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests.

PEER REVIEW PEER REVIEW INFORMATION _Communications Biology_ thanks Owen Jones and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling

Editors: Katie Davis and Luke R. Grinham. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. SUPPLEMENTARY INFORMATION REPORTING SUMMARY RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which

permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to

the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless

indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or

exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints

and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Huijsmans, T.E., Courtiol, A., Van Soom, A. _et al._ Quantifying maternal investment in mammals using allometry. _Commun Biol_ 7, 475

(2024). https://doi.org/10.1038/s42003-024-06165-x Download citation * Received: 18 October 2023 * Accepted: 09 April 2024 * Published: 18 April 2024 * DOI:

https://doi.org/10.1038/s42003-024-06165-x SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative