ABSTRACT High-entropy alloys (HEAs) composed of multiple-principal elements with (nearly) equimolar ratio establish a new conceptual framework for alloy design and hold a promise for

extensive applications in industry, akin to the controlled expansion alloys (CEAs), such as Invar alloys. Spontaneously, one question emerges - would it be possible to synthesize a novel

class of alloys combining the virtues of both CEAs and HEAs? Here, we report the pressure-induced magnetovolume effect in the body-centered-cubic CoCrFeAl HEA coupled with magnetic phase

transitions from ferromagnetic to paramagnetic, and to non-magnetic states, originating from the successive collapses of local magnetic moments of Co and Fe. The observed magnetovolume

ALLOY SHOWING GIGAPASCAL SUPERELASTIC STRESS AND NEARLY TEMPERATURE-INDEPENDENT MODULUS Article Open access 31 January 2025 LATTICE DISTORTION ENABLING ENHANCED STRENGTH AND PLASTICITY IN

HIGH ENTROPY INTERMETALLIC ALLOY Article Open access 08 August 2024 NEGATIVE MIXING ENTHALPY SOLID SOLUTIONS DELIVER HIGH STRENGTH AND DUCTILITY Article 03 January 2024 INTRODUCTION

Discoveries of new materials with excellent properties promoted the advancements of civilization. Metals and their alloys, in particular, have been the dominating enabling sources for

thousands of years. However, in order to develop new alloys, an ever-repeating strategy—mixing one principal metallic element with the addition of minor property-tuning elements—has been

applied since the Bronze Age. In the perspective of positioning in the compositional phase diagram, conventional alloys have been confined to the vicinities of their uni-elemental corners

until 2004, when Yeh et al.1 and Cantor et al.2 proposed a novel approach to design alloys composed of multiple-principal elements in a (nearly) equimolar ratio. This novel class of alloys

has been coined as high-entropy alloys (HEAs), stressing the high-configuration-entropy effect, originally believed to represent the reason why HEAs crystallize into a chemically disordered

simple structure (bcc, fcc, and hcp) rather than forming intermetallic compounds1. This revolutionary concept advances material scientists to the center—hitherto a no man’s land—of the

compositional phase diagram. The newly developed HEAs display superior properties compared to the conventional alloys, including an exceptional mechanical performance at cryogenic3 and high

temperatures4, excellent strength5, and high resistance to corrosion6. Also reported are their intriguing electronic7, magnetic8, superconducting9, and catalytic10 properties. Consequently,

HEAs attract intense and increasing attention because of immense potential applications11,12,13. Nonetheless, the immaturity in the synthesis process and a lack of fundamental understanding

of properties hinders HEAs from finding their way from laboratory to market, calling for further investigations. Controlled expansion alloys (CEAs) are widely used when the thermal expansion

of designed engineered structures needs to be critically considered. Among the CEAs, Invar alloys represent the most common ones. Invar alloys were discovered by Guillaume in 189714, and

were characterized by anomalously small thermal expansion in a certain temperature range, i.e., Invar effect, which has various industrial applications. However, the underlying mechanism of

the Invar effect still represents a longstanding controversy15,16,17,18,19. In an attempt to explain the effect, Weiss proposed the 2γ model where the unusual thermal expansion originating

from the anharmonicity of the lattice vibration was compensated by the volume collapse of Fe atoms during the high spin to low-spin transition15. Later, Van Schilfgaarde et al.16 considered

that the usual thermal expansion was counteracted by a gradual volume decrease during the continuous transformation of the direction of magnetic moment—from the parallel to the non-collinear

configuration. Nevertheless, both the 2γ and the non-collinear models attribute the Invar effect to the mutual dependence on magnetism and volume, the so-called magnetovolume effect.

Bearing the prominent properties of Invar alloys and HEAs in mind, an interesting question arises—is it possible to synthesize materials, which possess combined merits of both classes of

these extraordinary alloys? In the present study, by employing the techniques of in situ high-pressure X-ray diffraction (XRD) and ab initio calculation, we report the observation of the

magnetovolume effect in CoCrFeAl HEA. Upon hydrostatic compression, CoCrFeAl undergoes a magnetic moment collapse—from ferromagnetic (FM), to paramagnetic (PM), and to non-magnetic (NM)

state—while retaining the bcc crystal structure throughout the entire experimental pressure range up to 61 GPa. Decompressing the NM state results in a direct transformation into the FM

state. The volume collapse during the PM to NM phase transition is large enough to counteract the effect of anharmonicity of lattice vibrations, thus leading to a very small coefficient of

thermal expansion (CTE). The magnetovolume effect in CoCrFeAl HEA turns out to be sensitive to the degree of non-hydrostaticity, and the magnetic phase transition pathways differ during the

compression and decompression cycles. The results of this study show that the newly-emerged HEAs exhibit intriguing and potentially useful properties worth to be investigated further. They

also reveal the future possibility of designing promising Invar high-entropy alloys (IHEAs), which combine outstanding properties of Invar alloy and HEAs. RESULTS STABILITY OF THE BCC

STRUCTURE The composition of the synthesized sample was analyzed by energy-dispersive X-ray fluorescence spectroscopy (EDS) method, and the results indicated the average composition is

Co0.249Cr0.228Fe0.240Al0.282 (Supplementary Fig. 1), close to the nominal composition. For simplicity, we use nominal composition CoCrFeAl in the following discussion. Combining the diamond

anvil cell (DAC) and synchrotron-based XRD techniques, the crystal-structure evolution of the CoCrFeAl HEA at high pressures was investigated up to 61 GPa using different pressure

transmitting media (PTM, Ne, and NaCl). More information is provided in the Methods section. At ambient pressure, the CoCrFeAl HEA crystallizes in the single bcc phase. This bcc CoCrFeAl HEA

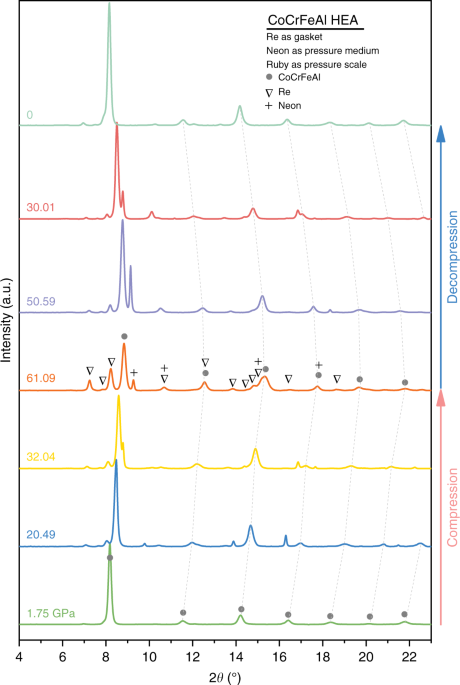
remains stable up to 61 GPa during the complete cycles of compression and decompression, regardless of the type of PTM used (Figs. 1 and 2 and Supplementary Fig. 2). The typical XRD

patterns at selected pressures in the hydrostatic run are shown in Fig. 1. All the diffraction peaks from the bcc CoCrFeAl HEA shift towards higher 2_θ_ angles with increasing pressure, as

expected from the pressure-induced volume reduction. Neither peak disappearance nor new peak growths were observed, except for the reflections from the Re gasket and Ne PTM. The ab initio

calculation (Supplementary Fig. 3) predicts that the bcc CoCrFeAl is thermodynamically stable over the fcc and hcp structures up to 60 GPa at 300 K, consistent with the present experimental

results. ANOMALOUS COMPRESSIVE BEHAVIOR Although the bcc lattice of CoCrFeAl has been found stable in three independent runs up to 61 GPa, its pressure (_P_)–volume (_V_) data points show

subtle kinks (Fig. 2), especially at 41–50 GPa during the hydrostatic decompression. The existence of these kinks makes it impossible to fit the _P_–_V_ data using one single equation of

state (EOS) and indicates potential magnetic or electronic phase transitions of bcc CoCrFeAl at high pressures. To illustrate these kinks, the local bulk modulus (_K_=−_V_(d_P_/d_V_)) is

calculated using the following procedure20: Every five adjacent experimental _P_–_V_ data points were fitted linearly to get the slope (d_P_/d_V_) of the central point, and consequently the

local bulk modulus. The calculated local bulk modulus as a function of pressure is displayed in Fig. 3a. Pronounced kinks stand out at ~12, ~21, ~24, and ~32 GPa. In addition, the anomalous

diffraction peak width (full-width at half-maximum, FWHM) of the strongest (110) peak as a function of pressure (Fig. 3b) supports the existence of phase transitions. In high-pressure XRD

experiments, the FWHM variation is mainly contributed by the micro-strain of the sample21, especially for the present disordered and distorted HEAs sample. The observed peak width anomaly

reflects the micro-strain evolution of CoCrFeAl upon compression, originating from the competition between the pressure-induced volume reduction and the free volume release during the

potential phase transitions. MAGNETIC PHASE TRANSITION Previous investigations on iron-based alloys (FeAl alloy) indicate that chemically disordered alloys that exhibit larger volumes favor

the FM state22. For the bcc CoCrFeAl HEA with the largest chemical disorder, the addition of the large Al atom enlarges the free volume of Fe atoms. Moreover, a very recent theoretical

calculation predicts that, upon the Al content increases, the CoCrFeNi-based HEA transforms from the PM state (fcc CoCrFeNi) to the FM state (bcc CoCrFeNiAl) at room temperature23.

Consequently, for the bcc CoCrFeAl HEA that possesses both high Al content and large chemical disorder, the FM state at room temperature is expected. Magnetic susceptibility measurements

demonstrate that CoCrFeAl adopts a FM state at the ambient condition with the Curie temperature of ~470 K (Fig. 4). The performed theoretical calculations reveal a consistent result—the FM

state represents the most stable state with the Curie temperature of ~500 K (Supplementary Figs. 3 and 4). For the sake of providing further insights into the FM properties of CoCrFeAl, the

magnetic moment (Fig. 5a), electronic density of states (spin-polarized DOS, Fig. 6), and exchange interaction between alloy components (see Methods for detail, Supplementary Fig. 5) are

also calculated. The ferromagnetism of CoCrFeAl mainly originates from the FM interactions of the nearest-neighbor Fe–Fe, Fe–Co, and Co–Co pairs (Supplementary Fig. 5). Al makes a negligible

contribution to the magnetism of bcc CoCrFeAl, while the magnetic state of Cr is anti-FM and thus strongly destabilizes the FM order. Although the local magnetic moment of Cr is altered by

the neighboring atoms24, and the addition of Al may suppress the anti-FM order of Cr by altering its DOS near the Fermi level25, the antiparallel Cr moments turn out to be primarily

responsible for the small Curie temperature of the alloy compared to that of pure Fe and Co. The theoretical calculations are solely ab initio, without any experimental inputs. To

investigate the underlying mechanism of the compressive anomaly, the energy difference between the FM, PM, and NM states of bcc CoCrFeAl have been calculated. The results indicate that their

energy differences decrease with increasing pressure (Supplementary Fig. 3a). Furthermore, the Curie temperature of the FM CoCrFeAl decreases with pressure and falls below room temperature

at high pressure (∼250 K at 60 GPa, Supplementary Fig. 4). Thus the FM to PM magnetic state phase transition is expected in CoCrFeAl at high pressure and room temperature according to the

theoretical results. Upon further increase in pressure, the local magnetic moments of all the component atoms collapse to zero at ~60 GPa, i.e., the CoCrFeAl transforms to an NM state at

higher pressures. This pressure-induced sequence of FM–PM–NM magnetic state transitions provides a viable explanation for the observed compressive anomaly in the present study. The

isothermal EOS at 300 K of FM, PM, and NM phases of CoCrFeAl up to 60 GPa were calculated and are illustrated in Fig. 2. At corresponding pressures, the FM state occupies the largest average

atomic volume while the NM state has the smallest one. Roughly, the experimental hydrostatic compression _P_–_V_ data points agree with the calculated FM EOS at low pressure, the PM EOS at

moderate pressure, and the NM EOS at high pressure (Fig. 2). In order to determine the equilibrium volume (_V_0) and isothermal bulk modulus (_K_0) at ambient pressure, experimental data

points were fitted with the Vinet EOS26. In the pressure range of 0–10 GPa, the _P_–_V_ data are well reproduced using _V_0 = 12.062 Å3 per atom, _K_0 = 144.62 GPa with its pressure

derivative fixed at _K_′0 = 4. Considering uncertainties, this experimental bulk modulus agrees reasonably well with the estimated values of 153.75 GPa using the additivity law27. In the

pressure range of 50–61 GPa (the pure NM state), we obtain _V_0 = 11.727 Å3 per atom, _K_0 = 190.09 GPa with _K_′0 fixed at 4. These results demonstrate that the NM state has a smaller

equilibrium volume. In the pressure range 0–43 GPa during decompression, the CoCrFeAl HEA adopts a pure FM state (as discussed below). The fitted EOS parameters are _V_0 = 12.019 Å3 per

atom, _K_0 = 179.12 GPa, and _K_′0 = 4.26, consistent with the calculated EOS of the FM phase at 300 K (_V_0 = 12.047 Å3 per atom, _K_0 = 167.10 GPa, and _K_′0 = 4.52). These EOS parameters

are listed in Table 1. According to the above discussions, we suggest that CoCrFeAl undergoes a sequence of magnetic state phase transitions from FM state, to PM state, and to NM state under

hydrostatic compression. However, upon the hydrostatic decompression, CoCrFeAl transfers from the NM state to FM state directly, omitting the PM state according to the isothermal EOS data

(Fig. 2). Under non-hydrostatic compression, CoCrFeAl transforms from FM to PM state, without entering the NM state up to 55 GPa. During the following decompression, CoCrFeAl transforms back

to the FM state below 42 GPa, signifying that the degree of non-hydrostaticity has a significant effect on the magnetic state transition of CoCrFeAl. The magnetic state transformation

sequence under the non-hydrostatic condition is also confirmed by the experiment using NaCl as the PTM (Supplementary Fig. 2). The transition sequence of CoCrFeAl, along with magnetic

moments calculated for the case of hydrostatic compression, is summarized in Fig. 5. The pressure dependence of the local bulk modulus (Fig. 3a) and the diffraction peak width (Fig. 3b),

both show that the magnetic state transition of CoCrFeAl HEA during the hydrostatic compression includes several steps. The onset pressures of the transition, visually read from Fig. 3a, b,

are roughly consistent with each other. However, according to the procedure used to calculate the local bulk modus, four other adjacent data points affect the local bulk modulus at specific

pressure, thus the phase transition pressure read from Fig. 3a lags behind the real transition pressure. Consequently, in the ensuing discussion, we use the onset pressures of the phase

transition from Fig. 3b, which may reflect the phase transition instantly. Interpreting the experimental observations with the help of ab initio calculations, we suggest that, under

hydrostatic compression up to 61 GPa (Fig. 3a, b), the bcc CoCrFeAl HEA undergoes the following magnetic transitions in three stages: In the pressure range 0–16 GPa, CoCrFeAl gradually

transforms from the initial FM to PM state. From 0 to ~10 GPa, the alloy remains in the FM state. Both the local bulk modulus and FWHM of the (110) diffraction peak increase monotonically

with increasing pressure. The pressure-induced micro-strain accounts for the diffraction peak width increase. From ~10 to ~16 GPa, the local bulk modulus decreases slightly to begin with,

then increases again with increasing pressure, while the FWHM of the (110) diffraction peak remains constant. Such a pressure-induced lattice softening has also been reported in Fe–Ni17 and

Cd_1−x_Mn_x_GeAs228 Invar alloys, originating from their magnetic structure relaxation16. Furthermore, the previous study29 indicates that the Fe–Fe interatomic distance _d_i controls the

magnetic coupling between Fe atoms with the critical value of 2.45 Å: for _d_i < 2.45 Å, the magnetic moments favor antiparallel coupling, whereas for _d__i_ > 2.45 Å the preferred

coupling is parallel. According to the present _P_–_V_ data, the nearest-neighbor distance in bcc CoCrFeAl reaches 2.45 Å at around 10 GPa, from where the material gradually transforms from

the FM to the PM state. At this stage, the population of the PM state increases at the expense of the FM state. Because the PM state has a smaller volume (Fig. 2), both the pressure effect

and magnetic transition account for the volume decrease. The free volume release from the FM to PM state transition compensates the pressure-induced micro-strain in the sample, thus the

diffraction peak width of the sample remains almost constant in this range. According to the DOS calculation, the most pronounced change across this FM to PM phase transition is that the

partial density of states of Co becomes highly symmetric (Fig. 6). The high-spin (HS) to the low-spin (LS) transition causes a major magnetic moment decrease by 70% at 10 GPa, from 1.22_µ_B

for HS to 0.37_µ_B for LS at 10 GPa (Fig. 5a). With further increases in pressure, the magnetic moment of Co vanishes at around 18 GPa. By comparison, the magnetic moment of Fe decreases by

only 12% (from 2.00_µ_B to 1.76_µ_B at 10 GPa). Accordingly, the magnetovolume effect of CoCrFeAl in this range accompanies the HS to LS transition of Co, not Fe as proposed by the 2γ

model15. In the second stage, spanning pressure range 16–31 GPa, a gradual transformation from the PM to the NM state takes place. From ~16 to ~23 GPa, the local bulk modulus decreases

slowly with increasing pressure. However, the FWHM of the (110) diffraction peak increases steeply as a function of pressure. At this stage, the sample remains in the PM state. The pressure

effect solely accounts for the volume decrease of the sample, and as the micro-strain in the sample increase quickly, so does the diffraction peak width. From ~23 to ~31 GPa, the local bulk

modulus increases slowly with increasing pressure. In this pressure range, the FWHM of the (110) diffraction peak decreases drastically. Both the pressure effect and magnetic transition

account for the volume decrease during this range. However, the micro-strain released by the magnetic transition is larger than that induced by the compression effect, which is why the peak

width decreases overall. At this stage, the sample transforms from the PM to NM state. This transition is accompanied with a magnetic moment collapse of Fe (Fig. 5a) and contributes to the

magnetovolume anomaly of CoCrFeAl in this pressure range. Finally, in the pressure range 31–61 GPa, the alloy remains in the NM state. Both the local bulk modulus and FWHM of the (110)

diffraction peak increase monotonically with increasing pressure. The material is in the pure NM state. Only the pressure effect accounts for the volume decrease of the sample, and as the

micro-strain in the sample increases again, so does the diffraction peak width. The observed FM–PM and PM–NM transitions are of the first order because of the associated volume reduction

(Fig. 2). However, as it takes 6 and 8 GPa, respectively, to be completed, both transitions are sluggish. A similar sluggishness has been reported in the fcc to hcp transitions of CoCrFeMnNi

HEA30,31 and CoCrFeNi32. Tracy et al.31 considered that the sluggish nature of transition in CoCrFeMnNi HEA originated from the rising energy barrier associated with stacking fault

formation upon pressure increase, akin to the fcc to hcp phase transition of Ar. On the other hand, Zhang et al.32 argued that a pressure-induced kinetic inhibition of the atomic motion

caused the sluggish phase transition of CoCrFeAl at high pressure. However, in the present case of CoCrFeAl, no crystal lattice reconstruction is involved in the course of transition. We

speculate that the sluggish nature of phase transition, not only structural phase transition, but also magnetic and/or electronic phase transitions, is a general phenomenon in HEAs and may

arise from inherent properties of HEAs, for example, the local energy fluctuations originating from the intrinsic chemical disorder in HEAs33. ANOMALOUS CTE AT HIGH TEMPERATURES The ensuing

question is how the volume collapse during the magnetic phase transition influences the CTE of CoCrFeAl HEA. To address this point, we measured the temperature dependence of the linear CTE

up to 820 K (Fig. 7). The CTE of CoCrFeAl exhibits two deviations from a regular behavior: (1) from 430 to 720 K, the CTE remains almost a constant. We consider this anomaly arises from the

FM–PM phase transition—the anharmonic lattice expansion is offset partly by the volume collapse during the FM–PM phase transition (Fig. 7). The upper temperature agrees reasonably well with

the measured Curie temperature of CoCrFeAl (Fig. 4). (2) From 720 to 770 K, the CTE decreases with increasing temperature, reaching almost zero at around 770 K. Meanwhile, the sample length

stays practically constant in the range 760–775 K (Fig. 7). This is reminiscent of an Invar effect. We interpret the second anomaly to originate from the PM–NM phase transition, in which the

lattice expansion is counterbalanced entirely by the volume collapse during the magnetic transition. These results agree with the calculated equilibrium volume collapses during magnetic

phase transitions at ambient pressure (Table 1). The FM–PM volume collapse is Δ_V_1 = _V_FM − _V_PM = 0.056 Å3, while the PM–NM volume collapse is Δ_V_2 = _V_PM − _V_NM = 0.352 Å3 which is

about 6.3 times higher than Δ_V_1. HYSTERESIS DURING THE DECOMPRESSION AND NON-HYDROSTATIC EFFECT The decompression behavior of CoCrFeAl is reversible in the high-pressure range (42–61 GPa),

while it does not follow the same behavior as during compression in the lower pressure range (Fig. 2). In the low-pressure range of 0–42 GPa, the average atomic volume of the sample is

larger during decompression than that during compression. The reason is that during compression and decompression, the sample possesses a different FM/PM ratio at the same pressures—where a

higher FM/PM ratio results in a larger volume. However, the volume difference decreases with decreasing pressure and almost vanishes at ambient pressure, indicating the sample returns fully

to the FM state at ambient pressure. In the pressure range of 0–42 GPa, the _P_–_V_ data during decompression can be well fitted by the Vinet EOS26, with _V_0 = 12.019 Å3 per atom, _K_0 = 

179.12 GPa, and its pressure derivative _K_′0 = 4.26. The compression/decompression equilibrium volumes _V_0 are mutually consistent. However, the isothermal bulk modulus _K_0 and its

pressure derivative are larger during decompression than their corresponding values obtained during compression. As shown in Fig. 2, the average atomic volume of CoCrFeAl under

non-hydrostatic compression is larger than that under hydrostatic compression. However, when decompressed to pressures below 42 GPa, the average atomic volumes determined from both

hydrostatic and non-hydrostatic runs are mutually consistent. The pressure dependencies of the FWHM of the (110) diffraction peak under hydrostatic and non-hydrostatic compressions differ

(Fig. 3b and Supplementary Fig. 6). These results can be understood by considering that different pathways are followed in the phase transitions, as shown in Fig. 5. In the hydrostatic run,

the followed phase transition sequence reads FM–PM–NM, while upon decompression the NM state transforms directly into the FM state. On the other hand, in the non-hydrostatic run, the NM

state is absent up to 55 GPa. These results indicate that not only the degree of hydrostaticity but also the compression/decompression history affects the pathways of the magnetic state

transitions in CoCrFeAl HEA. The pressure hysteresis during compression and decompression implies that the PM and/or NM phases are metastable34. The phase transition pathways which involve

metastable phases are substantially affected by the degree of hydrostaticity, the compression and decompression history, as well as rate, and sample condition (single crystal/powder,

impurities) (see ref. 35 and references therein). DISCUSSION The magnetovolume effect is discovered in CoCrFeAl HEA by in situ high-pressure XRD techniques with the assistance of ab initio

calculations. The calculations reveal that the experimentally observed phase transitions are of magnetic origin and result from the collapse of local magnetic moments of Co and Fe. The large

volume decrease during the PM to NM transition results in a dramatically reduced CTE at high temperature, evoking an Invar-like behavior, though only in a very narrow temperature range.

Moreover, the FM to PM and the PM to NM phase transition temperatures can be pressure-tuned to the ambient temperature, suggesting a potential way of tuning the temperature range of the

magnetovolume anomaly, and conceivably of the Invar effect. This work also reveals the possibility of designing and synthesizing extraordinary IHEAs in the future. METHODS SYNCHROTRON XRD

The CoCrFeAl HEAs with a nominal molar ratio were prepared by the arc melting method in a high purity argon atmosphere. The chemical composition and the homogeneity of the synthesized sample

were examined by the EDS analysis (see Supplementary Fig. 1). Small fragments of CoCrFeAl were produced by scraping the synthesized bulk materials with a fine rasp, then a tiny piece of

appropriate size (∼30 µm) was selected, and loaded into the sample chamber of DAC. Three runs of in situ high-pressure XRD experiments were carried out under hydrostatic and non-hydrostatic

conditions, respectively. In the hydrostatic run, diamond anvils with 200 μm culet size were mounted on the symmetric cells to generate high pressure. The Re gasket with an initial thickness

of 250 μm was indented to 30 μm, and a sample chamber with a diameter of 80 μm was drilled in the center of the pre-indented hole. The sample with a typical size of ~30 μm was loaded into

the sample chamber, along with tiny ruby balls serving as pressure gauge36 and neon as a PTM. The in situ high-pressure angle-dispersive XRD experiments were carried out at the Extreme

Conditions Beamline (ECB) P02.2 (ref. 37), PETRA III, Hamburg, Germany. The pressure in the sample chamber was varied using the membrane control system, and monitored by the online ruby

system. The incident X-rays were monochromatized to 42.68 keV corresponding to a wavelength of 0.2905 Å. The beam was focused to a size of 1.25 μm (vertical) × 2.44 μm (horizontal) (FWHM) by

Kirkpatrick–Baez mirrors. Two-dimensional diffraction images were collected using the fast area XRD 1621 (Perkin Elmer) 2D detector (2048 × 2048 pixels, 200 µm × 200 µm pixel size) with a

typical exposure time of 30 s. The distance from the sample to the detector and the detector’s geometric parameters were calibrated by the CeO2 standard (674b from the National Institute of

Standards). Two independent non-hydrostatic runs were also performed in order to evaluate the effect of non-hydrostaticity. The DACs and the sample assemblies were similar to the hydrostatic

run, although T301 stainless steel gaskets and different PTMs (neon and NaCl) were used. In the neon run, the sample chamber collapsed after the gas loading, causing the sample to bridge

the anvils. The sample was thus compressed non-hydrostatically despite the presence of a soft PTM neon. These two runs of experiments were performed at the Advanced Photon Source of Argonne

National Laboratory, beamline 13BM-C, GSECARS38. The incident X-ray beam was monochromatized to 28.57 keV (wavelength of 0.4340 Å) and focused to a spot size of 18 μm (vertical) × 12 μm

(horizontal) (FWHM). The diffraction patterns were collected by the MAR165 CCD detector (2048 × 2048 pixels, 79 µm × 79 µm pixel size). The distance from the sample to the detector and the

detector’s geometric parameters were calibrated by the NIST 660a LaB6 standard. The EOS of neon and NaCl39 were used as pressure scales respectively in these two runs. All the measurements

were conducted at room temperature. The two-dimensional diffraction patterns were integrated by Dioptas40 in order to obtain the 2_θ_–intensity curves for a further analysis. The software

Fityk41 was used to fit and resolve the overlapped diffraction peaks by applying the Voigt-profile peak function. The parameters of the EOS of CoCrFeAl in different states were determined by

the EosFit7-GUI software42. CALCULATION The present ab initio calculations were based on density functional theory43 implemented in the framework of the exact muffin-tin orbitals

formalism44,45. The single-electron equations were solved within the scalar-relativistic approximation and soft-core scheme. The exchange-correlation effects were treated within the

generalized gradient approximation46. The chemical and magnetic disorders were taken into account using the coherent potential approximation47,48,49. The PM state was simulated by the

disordered local moment model50. The Monte-Carlo simulations were based on the effective Heisenberg-like Hamiltonian, \(H = - \mathop {\sum}\nolimits_{{{i}},{{j}}}

{J_{{{ij}}}{\mathbf{m}}_{{i}} \cdot {\mathbf{m}}_{{j}}}\), where _J__ij_ represents the strength of the magnetic exchange interaction between atomic sites _i_ and _j_ with magnetic moments

M_i_ and M_j_. Further technical details can be found in the previous work23,51. MAGNETIC SUSCEPTIBILITY MEASUREMENTS The magnetic susceptibility of the sample was measured as a function of

temperature, with an AGICO MFK1-FA Kappabridge equipped with a CS4 furnace. Temperature-dependent susceptibility measurements were made at room temperature up to 296 °C with average heating

and cooling rates of 8.6 °C/min. The sample was exposed to an argon gas flow, providing an inert sample environment. An AC field with 200 A/m field strength and 976 Hz frequency was used for

the measurements. EDS ANALYSIS EDS analyses were performed using a PANalytical Epsilon 3 XL ED-XRF spectrometer, equipped with a 50 kV Ag-anode X-ray tube, six filters, a helium purge

facility, and a high-resolution silicon drift detector. The system was calibrated using a number of international and national certified reference materials. The analysis was done in an air

atmosphere and the sample was exposed to X-ray for 600 s. The sample was transferred into a P1 cup assembled with a high transmission Prolene supporting foil. The sample was measured 10

times at 10 different spots on the sample consecutively. COEFFICIENT OF THERMAL EXPANSION MEASUREMENT A Linseis-L 75/230 type dilatometer was applied to study the thermal dilatation behavior

and to determine the transition temperature. The dilatometer measurement was carried out in air applying a heating rate of 10 K/min. The initial length of the cylindrical sample was _l__0_ 

= 5.220 mm. The obtained data are presented in Fig. 7. The value of the physical coefficient of expansion was calculated with the relation: _α_ = (1/_l__t_)(d(_l__t_ − _l_0)/d_t_), where

_l_0 and _l__t_ are the sample length at initial and high temperatures, and _t_ is the temperature. DATA AVAILABILITY The data that support the findings of this study are available from the

corresponding authors upon a reasonable request. REFERENCES * Yeh, J.-W. et al. Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes.

_Adv. Eng. Mater._ 6, 299–303 (2004). Article  Google Scholar  * Cantor, B., Chang, I. T. H., Knight, P. & Vincent, A. J. B. Microstructural development in equiatomic multicomponent

alloys. _Mater. Sci. Eng. A_ 375–377, 213–218 (2004). Article  Google Scholar  * Gludovatz, B. et al. A fracture-resistant high-entropy alloy for cryogenic applications. _Science_ 345,

1153–1158 (2014). Article  ADS  Google Scholar  * Zou, Y., Ma, H. & Spolenak, R. Ultrastrong ductile and stable high-entropy alloys at small scales. _Nat. Commun._ 6, 7748 (2015).

Article  ADS  Google Scholar  * Youssef, K. M., Zaddach, A. J., Niu, C., Irving, D. L. & Koch, C. C. A novel low-density, high-hardness, high-entropy alloy with close-packed single-phase

nanocrystalline structures. _Mater. Res. Lett._ 3, 95–99 (2015). Article  Google Scholar  * Lee, C. P., Chen, Y. Y., Hsu, C. Y., Yeh, J. W. & Shih, H. C. The effect of boron on the

corrosion resistance of the high entropy alloys Al0.5CoCrCuFeNiB_x_. _J. Electrochem. Soc._ 154, C424–C430 (2007). Article  Google Scholar  * Guo, J. et al. Robust zero resistance in a

superconducting high-entropy alloy at pressures up to 190 GPa. _Proc. Natl Acad. Sci._ 114, 13144–13147 (2017). Article  ADS  Google Scholar  * Zhang, Y., Zuo, T., Cheng, Y. & Liaw, P.

K. High-entropy alloys with high saturation magnetization, electrical resistivity, and malleability. _Sci. Rep._ 3, 1455 (2013). Article  ADS  Google Scholar  * Koželj, P. et al. Discovery

of a superconducting high-entropy alloy. _Phys. Rev. Lett._ 113, 107001 (2014). Article  ADS  Google Scholar  * Yao, Y. et al. Carbothermal shock synthesis of high-entropy-alloy

nanoparticles. _Science_ 359, 1489–1494 (2018). Article  ADS  Google Scholar  * Zhang, Y. et al. Microstructures and properties of high-entropy alloys. _Prog. Mater. Sci._ 61, 1–93 (2014).

Article  Google Scholar  * Ye, Y. F., Wang, Q., Lu, J., Liu, C. T. & Yang, Y. High-entropy alloy: challenges and prospects. _Mater. Today_ 19, 349–362 (2016). Article  Google Scholar  *

Miracle, D. B. & Senkov, O. N. A critical review of high entropy alloys and related concepts. _Acta Mater._ 122, 448–511 (2017). Article  Google Scholar  * Guillaume, C. E. Recherches

sur les aciers au nickle. Dilatations aux températures élevées; résistance électrique. _C. R. Acad. Sci._ 125, 235–238 (1897). Google Scholar  * Weiss, R. J. The origin of the ‘Invar'

effect. _Proc. Phys. Soc._ 82, 281–288 (1963). Article  ADS  Google Scholar  * Van Schilfgaarde, M., Abrikosov, I. A. & Johansson, B. Origin of the Invar effect in iron-nickel alloys.

_Nature_ 400, 46–49 (1999). Article  ADS  Google Scholar  * Dubrovisky, L. et al. Pressure-induced Invar effect in Fe-Ni alloys. _Phys. Rev. Lett._ 86, 4851–4854 (2001). Article  ADS  Google

Scholar  * Rueff, J. P. et al. Magnetism of Invar alloys under high pressure examined by inelastic x-ray scattering. _Phys. Rev. B_ 63, 132409 (2001). Article  ADS  Google Scholar  *

Decremps, F. & Nataf, L. Abrupt discontinuity of the bulk modulus pressure dependence in Fe64Ni36. _Phys. Rev. Lett._ 92, 157204 (2004). Article  ADS  Google Scholar  * Zeng, Q. S. et

al. Anomalous compression behavior in lanthanum/cerium-based metallic glass under high pressure. _Proc. Natl Acad. Sci._ 104, 13565–13568 (2007). Article  ADS  Google Scholar  * Singh, A. K.

X-ray diffraction from solids under nonhydrostatic compression-some recent studies. _J. Phys. Chem. Solids_ 65, 1589–1596 (2004). Article  ADS  Google Scholar  * Nogués, J. et al. Volume

expansion contribution to the magnetism of atomically disordered intermetallic alloys. _Phys. Rev. B_ 74, 024407 (2006). Article  ADS  Google Scholar  * Huang, S. et al. Mechanism of

magnetic transition in FeCrCoNi-based high entropy alloys. _Mater. Des._ 103, 71–74 (2016). Article  Google Scholar  * Niu, C., LaRosa, C. R., Miao, J., Mills, M. J. & Ghazisaeidi, M.

Magnetically-driven phase transformation strengthening in high entropy alloys. _Nat. Commun._ 9, 1363 (2018). Article  ADS  Google Scholar  * Zuo, T. et al. Tailoring magnetic behavior of

CoFeMnNiX (X = Al, Cr, Ga, and Sn) high entropy alloys by metal doping. _Acta Mater._ 130, 10–18 (2017). Article  ADS  Google Scholar  * Poirier, J.-P. _Introduction to the Physics of the

Earth’s Interior_ (Cambridge University Press, Cambridge, 2000). Book  Google Scholar  * Fakirov, S. On the application of the “rule of mixture” to microhardness of complex polymer systems

containing a soft component and/or phase. _J. Mater. Sci._ 42, 1131–1148 (2007). Article  ADS  Google Scholar  * Mollaev, A. Y. et al. Anomalies of magnetic properties and magnetovolume

effect in Cd_1-x_Mn_x_GeAs2 at hydrostatic pressure. _Appl. Phys. Lett._ 100, 202403 (2012). Article  ADS  Google Scholar  * Gorria, P. et al. Crystal structure, magnetocaloric effect and

magnetovolume anomalies in nanostructured Pr2Fe17. _Acta Mater._ 57, 1724–1733 (2009). Article  Google Scholar  * Zhang, F. et al. Polymorphism in a high-entropy alloy. _Nat. Commun._ 8,

15687 (2017). Article  ADS  Google Scholar  * Tracy, C. M. et al. High pressure synthesis of a hexagonal close-packed phase of the high-entropy alloy CrMnFeCoNi. _Nat. Commun._ 8, 15634

(2017). Article  ADS  Google Scholar  * Zhang, F. X. et al. Pressure-induced fcc to hcp phase transition in Ni-based high entropy solid solution alloys. _Appl. Phys. Lett._ 110, 011902

(2017). Article  ADS  Google Scholar  * Tsai, K. Y., Tsai, M. H. & Yeh, J. W. Sluggish diffusion in Co–Cr–Fe–Mn–Ni high-entropy alloys. _Acta Mater._ 61, 4887–4897 (2013). Article 

Google Scholar  * Martin, N. et al. Magnetovolume effect, macroscopic hysteresis and moment collapse in the paramagnetic state of cubic MnGe under high pressure. _Phys. Rev. B_ 93, 214404

(2016). Article  ADS  Google Scholar  * Machon, D., Meersman, F., Wilding, M. C., Wilson, M. & McMillan, P. F. Pressure-induced amorphization and polyamorphism: inorganic and biochemical

systems. _Prog. Mater. Sci._ 61, 216–282 (2014). Article  Google Scholar  * Dewaele, A., Torrent, M., Loubeyre, P. & Mezouar, M. Compression curves of transition metals in the Mbar

range: experiments and projector augmented-wave calculations. _Phys. Rev. B_ 78, 104102 (2008). Article  ADS  Google Scholar  * Liermann, H.-P. et al. The extreme conditions beamline P02.2

and the extreme conditions science infrastructure at PETRA III. _J. Synchrotron Radiat._ 22, 908–924 (2015). Article  Google Scholar  * Zhang, D. et al. High pressure single crystal

diffraction at PX^2. _J. Vis. Exp._ 119, e54660 (2017). Google Scholar  * Fei, Y. et al. Toward an internally consistent pressure scale. _Proc. Natl Acad. Sci._ 104, 9182–9186 (2007).

Article  ADS  Google Scholar  * Prescher, C. & Prakapenka, V. B. DIOPTAS: a program for reduction of two-dimensional X-ray diffraction data and data exploration. _High Press. Res._ 35,

223–230 (2015). Article  ADS  Google Scholar  * Wojdyr, M. Fityk: a general-purpose peak fitting program. _J. Appl. Crystallogr._ 43, 1126–1128 (2010). Article  Google Scholar  *

Gonzalez-Platas, J., Alvaro, M., Nestola, F. & Angel, R. EosFit7-GUI: a new graphical user interface for equation of state calculations, analyses and teaching. _J. Appl. Cryst._ 49,

1377–1382 (2016). Article  Google Scholar  * Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. _Phys. Rev._ 136, B864–B871 (1964). Article  ADS  MathSciNet  Google Scholar  * Vitos,

L. _Computational Quantum Mechanics for Materials Engineers_ (Springer, London, 2007). * Vitos, L. Total-energy method based on the exact muffin-tin orbitals theory. _Phys. Rev. B_ 64,

014107 (2001). Article  ADS  Google Scholar  * Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. _Phys. Rev. Lett._ 77, 3865–3868 (1996). Article 

ADS  Google Scholar  * Soven, P. Coherent-potential model of substitutional disordered alloys. _Phys. Rev._ 156, 809–813 (1967). Article  ADS  Google Scholar  * Gyorffy, B. L.

Coherent-potential approximation for a nonoverlapping-muffin-tin-potential model of random substitutional alloys. _Phys. Rev. B_ 5, 2382–2384 (1972). Article  ADS  Google Scholar  * Vitos,

L., Abrikosov, I. A. & Johansson, B. Anisotropic lattice distortions in random alloys from first-principles theory. _Phys. Rev. Lett._ 87, 156401 (2001). Article  ADS  Google Scholar  *

Gyorffy, B. L., Pindor, A. J., Staunton, J., Stocks, G. M. & Winter, H. A first-principles theory of ferromagnetic phase transitions in metals. _J. Phys. F Met. Phys._ 15, 1337–1386

(1985). Article  ADS  Google Scholar  * Skubic, B., Hellsvik, J., Nordström, L. & Eriksson, O. A method for atomistic spin dynamics simulations: implementation and examples. _J. Phys.

Condens. Matter_ 20, 315203 (2008). Article  Google Scholar  Download references ACKNOWLEDGEMENTS This research was supported by Uppsala University and by the National Natural Science

Foundation of China (No. 11504354). S.H. and L.V. acknowledge the Swedish Research Council (VR), the Swedish Foundationfor Strategic Research (SSF), and the Swedish Energy Agency. L.V. and

L.K.V. acknowledge the Hungarian Scientific Research Fund (OTKA 128229). The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at

Linköping. Parts of this research were carried out at the light source PETRA III at DESY, a member of the Helmholtz Association (HGF). Parts of studies were performed at GSECARS (The

University of Chicago, Sector 13), Advanced Photon Source (APS), Argonne National Laboratory. GSECARS is supported by the National Science Foundation—Earth Sciences (EAR-1634415) and

Department of Energy-GeoSciences (DE-FG02–94ER14466). Use of the COMPRES-GSECARS gas loading system was supported by COMPRES under NSF Cooperative Agreement EAR-1606856 and by GSECARS

through NSF grant EAR-1634415 and DOE grant DE-FG02–94ER14466. The PX2 program is supported by COMPRES under NSF Cooperative Agreement EAR-1661511. This research used resources of the

Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No.

DE-AC02–06CH11357. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Earth Sciences, Uppsala University, 75236, Uppsala, Sweden Lei Liu, Bjarne S. G. Almqvist & Peter Lazor *

Applied Materials Physics, Department of Materials Science and Engineering, Royal Institute of Technology, 10044, Stockholm, Sweden Shuo Huang & Levente Vitos * Department of Physics and

Astronomy, Division of Materials Theory, Uppsala University, 75120, Uppsala, Sweden Levente Vitos * Institute for Solid State Physics and Optics, Wigner Research Centre for Physics,

Budapest, H-1525, Hungary Levente Vitos * Department of Physics and Astronomy, Division of Molecular and Condensed Matter Physics, Uppsala University, 75120, Uppsala, Sweden Minjie Dong 

& Jan-Erik Rubensson * Photon Science, DESY, PETRA III, 22607, Hamburg, Germany Elena Bykova * Partnership for Extreme Crystallography, University of Hawaii at Manoa, Honolulu, HI,

96822, USA Dongzhou Zhang * Department of Engineering Sciences, Uppsala University, 75121, Uppsala, Sweden Sergey Ivanov * Department of Inorganic Materials, Karpov’s Institute of Physical

Chemistry, Vorontsovo pole, Moscow, Russia, 105046 Sergey Ivanov * Department of Materials Sciences, Transilvania University, 500036, Brasov, Romania Bela Varga * Wigner Research Center for

Physics of Hung. Acad. Sciences, PO Box 49, Budapest, 1525, Hungary Lajos K. Varga Authors * Lei Liu View author publications You can also search for this author inPubMed Google Scholar *

Shuo Huang View author publications You can also search for this author inPubMed Google Scholar * Levente Vitos View author publications You can also search for this author inPubMed Google

Scholar * Minjie Dong View author publications You can also search for this author inPubMed Google Scholar * Elena Bykova View author publications You can also search for this author

inPubMed Google Scholar * Dongzhou Zhang View author publications You can also search for this author inPubMed Google Scholar * Bjarne S. G. Almqvist View author publications You can also

search for this author inPubMed Google Scholar * Sergey Ivanov View author publications You can also search for this author inPubMed Google Scholar * Jan-Erik Rubensson View author

publications You can also search for this author inPubMed Google Scholar * Bela Varga View author publications You can also search for this author inPubMed Google Scholar * Lajos K. Varga

View author publications You can also search for this author inPubMed Google Scholar * Peter Lazor View author publications You can also search for this author inPubMed Google Scholar

CONTRIBUTIONS L.L. and P.L. conceived the project. L.L., P.L., M.D., E.B. and D.Z. performed the synchrotron XRD measurements with help from J.-E.R., S.H. and L.V. carried out the

theoretical calculation. B.S.G.A. and L.L. conducted the magnetic measurement. S.I. characterized the sample. B.V. and L.K.V. measured the CTE of the sample. L.L., P.L., S.H. and L.V.

analyzed the data and drafted the manuscript. All authors contributed to the discussions and comments on the final manuscript. CORRESPONDING AUTHORS Correspondence to Lei Liu or Peter Lazor.

ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE: Springer Nature remains neutral with regard to jurisdictional

claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative

Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the

original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in

the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended

use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Liu, L., Huang, S., Vitos, L. _et al._ Pressure-induced magnetovolume effect in

CoCrFeAl high-entropy alloy. _Commun Phys_ 2, 42 (2019). https://doi.org/10.1038/s42005-019-0141-9 Download citation * Received: 04 July 2018 * Accepted: 11 March 2019 * Published: 02 May

2019 * DOI: https://doi.org/10.1038/s42005-019-0141-9 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable

link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative