ABSTRACT As is well established, the symmetry breaking by isotope substitution in the water molecule results in localisation of the vibrations along one of the two bonds in the ground state.

In this study we find that this localisation may be broken in excited electronic states. Contrary to the ground state, the stretching vibrations of HDO are delocalised in the bound

core-excited state in spite of the mass difference between hydrogen and deuterium. The reason for this effect can be traced to the narrow “canyon-like” shape of the potential of the state

along the symmetric stretching mode, which dominates over the localisation mass-difference effect. In contrast, the localisation of nuclear motion to one of the HDO bonds is preserved in the

instantaneously, to a single vibrational eigenstate. SIMILAR CONTENT BEING VIEWED BY OTHERS MEASUREMENT OF COHERENT VIBRATIONAL DYNAMICS WITH X-RAY TRANSIENT ABSORPTION SPECTROSCOPY

SIMULTANEOUSLY AT THE CARBON K- AND CHLORINE L2,3- EDGES Article Open access 13 September 2024 UNDERSTANDING X-RAY ABSORPTION IN LIQUID WATER USING TRIPLE EXCITATIONS IN MULTILEVEL COUPLED

CLUSTER THEORY Article Open access 26 April 2024 VIBRATIONAL COUPLINGS AND ENERGY TRANSFER PATHWAYS OF WATER’S BENDING MODE Article Open access 25 November 2020 INTRODUCTION The phenomena of

localisation and delocalisation become increasingly important in studies related to migration of vibrational excitations in solid matter and liquids. Philip Anderson discovered that the

addition of a critical amount of disorder to a periodic system results in the interference of multiply scattered electrons, which can cause their wave functions to localise while the

electrons come to an effective standstill state1. Recently it was recognised that vibrational modes2 and surface plasmons3 of disordered systems are not universally localised according to

Andersons mechanism and have properties both of localisation and delocalisation. Special attention has been paid to the confinement of optical phonons in novel kinds of heterostructures and

isotopic superlattices4. The localisation of vibrational modes is of crucial importance also in molecules, especially from the point of view of migration of vibrational excitations in large

systems or in liquids5. The interest in vibrational mode localisation is stimulated by studies of bond-selective vibrationally mediated photochemistry6,7,8,9. The isotopomer of the water

molecule, HDO, plays a central role in such studies10,11,12,13,14. In infra-red (IR) spectroscopy the diluted isotope substitution of water, HDO, has been widely used as a unique probe of

local hydrogen bond environments and of reorientational motion and hydrogen bond dynamics using pump-probe IR and multidimensional correlation techniques15,16,17. The symmetric character of

the ordinary water molecule is reflected by its vibrational wave functions, with the two O-H bonds vibrating coherently forming the symmetric and antisymmetric stretching modes delocalised

on both O-H bonds, leading to the properties observed previously in resonant inelastic X-ray Raman scattering (RIXS)18,19 and IR studies20,21,22,23. However, as soon as this symmetry is

broken, as in HDO where one hydrogen atom is substituted by deuterium, the coherence of the O-H and O-D stretching vibrations is destroyed and the vibrational motion in the ground electronic

state becomes localised to one of the bonds. Even though this localisation holds true for the ground state vibrations in HDO and is well established by numerous experiments10,11,12,13,14,

it does not represent a strict physical principle. We show in this article that even though the ground state vibrations of HDO are fully localised to the bonds, the vibrations become

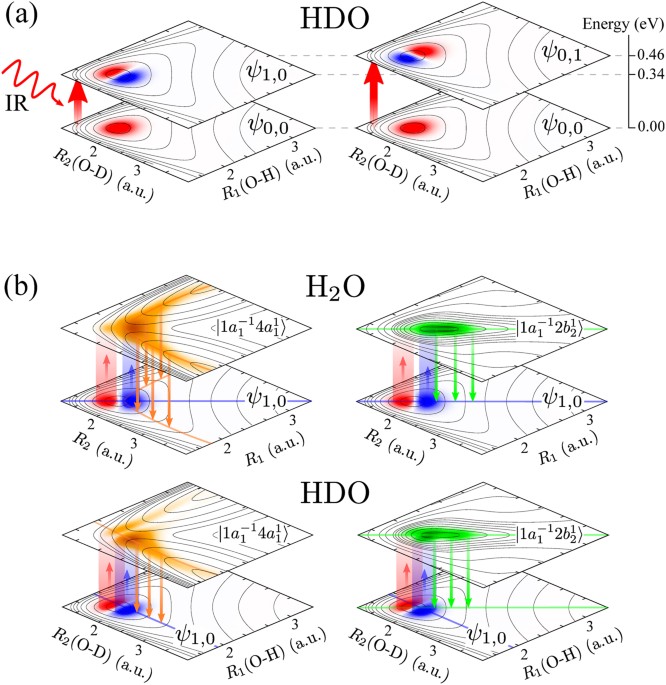
delocalised in certain core-excited states (Fig. 1). The reason for this unexpected delocalisation of vibrations in the asymmetric isotopomer HDO can be found in the competition between the

symmetric shape of the potential energy surface (PES) and the asymmetric kinetic energy operator, which allows for a coexistence of localised and delocalised nuclear motions in the same

molecule. We show that the mode delocalisation in an excited electronic state, exemplified by the HDO molecule, can be controlled by using an IR pump-RIXS probe technique24,25. Employing a

pump IR pulse one can selectively populate a particular localised vibrational level of the ground electronic state, for example the _ψ_1,0 state localised in the O-D bond, Fig. 1a. Then a

probe X-ray photon promotes the system into a core-excited state, where the nuclear motion may be localised along the selected O-D bond in the case of the dissociative state (left panel of

Fig. 1b) and delocalised in the case of the bound state (right panel in Fig. 1b). Subsequent decay back into the ground electronic state will populate vibrations localised either only on the

selected O-D bond or on both O-D and O-H bonds, depending on the degree of delocalisation in the core-excited state. The final population of the ground state vibrational modes, which are

localised on different bonds, gives direct information about the degree of delocalisation in the core-excited state. One should notice that in the H2O molecule the delocalised character of

the ground state vibrational wave functions is preserved in the vibrational functions of the investigated core-excited states (Fig. 1b). RESULTS AND DISCUSSION MECHANISM OF DELOCALISATION OF

VIBRATIONAL EXCITATIONS IN ASYMMETRIC MOLECULES The HDO molecule is an asymmetric isotopomer of H2O with the symmetry reduced from C2_v_ to C_s_. In spite of the fact that the electronic

structure of HDO is equivalent to H2O, the nuclear dynamics along the O-H and O-D bonds is asymmetric due to the mass difference () which introduces an asymmetry in the nuclear Hamiltonian

of the stretching motion via the kinetic energy operator _K_ (see Methods). The localisation or delocalisation of the vibrations in HDO thus depends on the competition between the symmetric

potential (_U__i_(_R_1, _R_2) = _U__i_(_R_2, _R_1)) and the asymmetric kinetic energy operator _K_ responsible for the dynamics, where _R_1 and _R_2 are the lengths of the O-H and O-D bonds.

While the symmetric potential, being the same for H2O and HDO, forces symmetry preservation and maintains the vibrations delocalised on both bonds of the HDO molecule, the role of the

asymmetric kinetic energy operator is qualitatively different: The mass difference (_m__H_ ≠ _m__D_) results in a localisation of the vibration on one bond. It is here instructive to look at

the spatial shape of the nuclear wave functions, which directly indicates if the vibration is localised on one bond or it is delocalised over the both bonds (see Fig. 2 and Supplementary

Fig. S1). The vibrationally (IR) excited _ψ_1,0 and _ψ_0,1 wave functions of the ground state HDO are strongly localised along either the O-D bond or the O-H bond, whereas in H2O the

corresponding wave functions are delocalised. This motivates us to assign the vibrational states of HDO in the electronic ground state using the quantum numbers _n__D_ and _n__H_ of the

vibrational states localised to the O-D and O-H bonds, respectively. In contrast, the vibrational states of the symmetric H2O molecule are fully delocalised in all electronic states. We use

for this molecule the quantum numbers _n__s_ and _n__a_ of coupled symmetric and asymmetric stretching normal modes, respectively. In the HDO molecule, the difference between the ground and

core-excited state wave functions is remarkable (see Fig. 2 and Supplementary Fig. S1). In spite of the strong asymmetry of HDO, the few lowest stretching vibrations in the core-excited

state are almost fully delocalised, very similar to the symmetric H2O molecule. The main reason for this effect is that the narrow “canyon-like” PES of the bound core-excited state is

aligned along the symmetric stretching coordinate between the bonds (Fig. 1), which traps the O-H and O-D vibrations, thereby, overcoming the localisation trend imposed by the asymmetric

kinetic energy operator (see Methods Eq. (17)). Due to the delocalisation of the vibrations in the core-excited state, we use for this state the same assignment of vibrations as in H2O. To

avoid confusion, we mark the vibrational states of the core-excited state by the label (_c_). For further clarity, the notations used for ground and core-excited vibrational states can be

summarised as follows Using perturbation theory we can now quantify the degree of the localisation of the vibrational states in HDO by means of the kinetic energy operator of H2O and the

asymmetric perturbation _δK_, related to the mass difference of H and D Here _μ_1 = _m__H__m__O_/(_m__H_ + _m__O_) and _μ_2 = _m__D__m__O_/(_m__D_ + _m__O_) are the reduced masses. The _ab

initio_ vibrational wave functions shown in Fig. 2 provide direct information about the localisation or delocalisation of the stretching vibrations. In order to explain the physical

mechanism of localisation/delocalisation and the shape of the wave functions, shown in Fig. 2, let us consider a simple two-level model which catches the essence of the investigated effect.

Apparently, to get the localisation we should mix the symmetric and antisymmetric wave functions. For HDO these can be constructed from the symmetric and antisymmetric wave functions of H2O

(Fig. 2), which are mixed by the perturbation _δK_ where . The degree of localisation is defined by the dimensionless parameter Apparently, the spacing between vibrational levels is directly

related to the shape of the potential. In the ground state H2O, the symmetric and antisymmetric vibrationally excited modes are almost degenerate,  eV (see eigenvalues in Fig. 2), which

makes the parameter |_ζ_| large. This explains the perfect localisation of vibrational states (2) in the ground state HDO, (, , ) as seen in Fig. 2. These wave functions correspond to the

HDO stretching vibrations localised on either the O-D bond or the O-H bond. The picture drastically changes for the core-excited state where the PES shape resembles the narrow “canyon” along

the symmetric stretching coordinate (Fig. 1). In this case, the spacing between the and states of H2O is large ( eV (see eigenvalues in Fig. 2 and Supplementary Fig. S1), and hence, the

parameter _ζ_ is small. Contrary to the ground state, the vibrational wave functions of the asymmetric HDO molecule are delocalised, almost identically to the symmetric H2O wave functions. A

natural method to study localisation/delocalisation of vibrational excitations in the core-excited state of HDO is the pump-probe RIXS technique, in which an IR laser is used to pump the

system to a vibrational level localised along either the O-H bond or the O-D bond. In order to find “experimental” evidence of the delocalisation of stretching vibrations in the core-excited

state, the vibrationally excited HDO molecule is probed by RIXS starting from different initial vibrational states: _ψ_0,0 (delocalised), _ψ_1,0 (localised along the O-D bond) and _ψ_0,1

(localised along O-H bond) (see Fig. 2). As we show below, the X-ray scattering back into the ground electronic state provides direct means to quantify the degree of delocalisation of the

vibrational excitation in the core-excited state. In the present study, we focus on quasi-elastic RIXS channels, namely, the scattering via the two lowest core-excited states back into the

ground electronic state. As we have shown recently26,27, the main spectral features of the RIXS spectrum in this case originate from the two stretching vibrational modes, which are strongly

coupled. Following this result, we neglect the bending normal mode excitation in our simulations, while treating explicitly the coupled nuclear dynamics in the stretching modes (Fig. 1)

using the strict 2D Hamiltonian (see Methods Eq. (17)) in a time-dependent representation of the Kramer’s-Heisenberg formalism (see Supplementary Material for details). The RIXS processes is

sensitive to the nuclear dynamics in the core-excited state, defined by the nuclear wave packet where _ν_0 = (_n__s_, _n__a_) (_ν_0 = (_n__D_, _n__H_)) is the initial vibrational level of

the electronic ground state of H2O (HDO) with energy . The RIXS cross section is computed as28,29 Here, _ω (ω_′) and E (E') are the frequency and polarisation vector of incoming

(outgoing) photon; is the energy between the PES minima of the ground and core-excited states; , _D__c_0 = (E · D_c_0), D_c_0 is the absorption transition dipole moment; Γ and Γ_f_ are the

core-hole and final state lifetime broadening, respectively; _h_0 end _h__c_ are defined in Methods Eq. (17). RIXS AT RESONANCE To show the strong sensitivity of the studied effect to the

core-excited state character, we first analyse RIXS via the dissociative core-excited state, where the fragmentation of HDO along the O-H and O-D bonds is strongly asymmetric. Conventional

RIXS starts from the lowest vibrational state _ψ_0,0 which is delocalised (see Fig. 3, upper panel). This delocalisation is preserved in the core-excited state, as one can see from the

spatial distribution of the integral wave packet |Ψ(∞)〉 (5), except for an asymmetry between the O-H and O-D dissociation channels. The O-H branch of |Ψ(∞)|2 is more pronounced than the O-D

branch due to slower dissociation of the twice as heavy deuterium atom. The delocalisation is reflected in the RIXS spectrum (Fig. 3, upper panel), which is defined by the overlap between

the core-excited wave packet |Ψ(∞)〉 and the final vibrational wave function26 (Supplementary Eq. (S1)). Due to this fact, the final vibrational states _ψ_1,0 and _ψ_0,1 (Fig. 3, left) have

almost the same intensities in the RIXS spectrum (peaks _ε_1,0 and _ε_0,1 in Fig. 3, respectively). The reason for the slightly weaker intensity of the _ψ_1,0 (O-D) resonance is the above

mentioned slower dissociation of deuterated O-D bond in relation to the O-H bond. The picture changes qualitatively when the RIXS starts from the excited vibrational state _ψ_1,0 (_ψ_0,1),

localised on the O-D (O-H) bond (Fig. 2), resulting in a clear bond selectivity of the RIXS (Fig. 3, mid and bottom panels). Indeed, when the RIXS starts from _ψ_1,0 (Fig. 3, mid panel), the

intensity of the O-D peak (_ε_1,0) is much larger than the intensity of the _ε_0,1 resonance. This phenomenon is qualitatively illustrated by the scheme on the left hand-side of Fig. 3 (see

also Fig. 1). The complementary scenario was observed for RIXS starting from _ψ_0,1 (Fig. 3, lower panel). In this case, the _ε_0,1 RIXS resonance, which corresponds to O-H bond, has the

strongest intensity. RIXS AT THE RESONANCE The bound PES exhibits a “canyon-like” shape along the symmetric stretching coordinate _R_1 = _R_2 (Fig. 1). Even though the ground state wave

functions of HDO are completely localised, the core-excited wave functions are very similar to the H2O molecule (Fig. 2), as discussed above. In order to have a complete picture of the

localisation in the IR-pumped RIXS via the resonance, we consider for each initial vibrational state four different incoming photon frequencies tuned in resonance with the , , and

core-excited vibrational states of HDO (Fig. 2 and Supplementary Fig. S2). The resonant condition is described by the detuning from the excitation energy of the lowest core-excited

vibrational level as Let us consider the conventional RIXS from the lowest vibrational state _ψ_0,0 (Fig. 4). The delocalisation of the vibrational state _ψ_0,0 is preserved in the

core-excited state (similar to the case) and the core-excited wave packet is distributed over the both bonds _R_2(_D_ − _O_) and _R_1(_O_ − _H_) for all considered detuning values (Fig. 4,

right-hand side). One can clearly see this delocalisation in the RIXS spectra (left panels in Fig. 4), which have comparable intensities of the final vibrational states _ψ_1,0 and _ψ_0,1

localised on O-D and O-H bonds, respectively (peaks _ε_1,0 and _ε_0,1 in Fig. 4). Thus, when a delocalised core-excited wave packet is created, the selectivity of the final state vibrations

localised on the O-H or O-D bonds is lost. The dependence of the relative intensity of the _ε_1,0 and _ε_0,1 peaks on detuning stems from the change of the core-excited wave packet shape

with excitation energy (see Supplementary Notes 3). Let us now focus on the RIXS from one of the localised initial vibrational state _ψ_1,0 (Fig. 2). Contrary to the case of the core-excited

state, a delocalised core-excited wave packet is now formed for detuning Ω = 0.000 and 0.152 eV (Fig. 5, right-hand side), due to the “canyon-like” shape of the PES along the symmetric

stretching coordinate (see Fig. 1). The tight confinement of the nuclear motion in this PES forces the H and D atoms to oscillate coherently along the symmetric stretching coordinate, like

in the H2O molecule, in spite of the large mass difference between the H and D atoms. This effect is clearly reflected in the RIXS spectrum, as the intensities of the peaks _ε_1,0 and _ε_0,1

are comparable for low positive detuning energies (Fig. 5, Ω = 0.152, 0.301 eV) and no bond selectivity is observed. The same behaviour is observed for RIXS initiated from the excited

vibrational state _ψ_0,1 localised on the O-H bond (Fig. 6). As one can see from the topmost panel of Figs 5 and 6 (Ω = −1.00 eV), the core-excited wave packet is fully localised along the

bond, exactly as the vibrational wave function initial to the RIXS process. The case of Ω = 0.0, which shows smaller intensity of OH peak, corresponds to a transition state between the fully

localised (Ω = −1.0 eV) and almost fully delocalised (Ω = 0.152 eV) cases. This phenomenon is related to the scattering duration and the collapse of the wave function, which will be

described in the following section. The delocalisation of the core-excited wave packet on the PES is broken for higher excitation energy (Ω ≥ 0.301 eV), as one can see from Figs 5 and 6.

This happens due to the anharmonicity of the the PES which makes the spacing between levels smaller as we reach higher vibrational excitations. When the spacing between the vibrational

levels becomes comparable or smaller than the core-hole lifetime broadening (Γ = 0.08 eV), the core-excited wave packet becomes a mixture of several core-excited vibrational states. This

coherent superposition of the core-excited states leads to a loss of delocalisation of the vibrational wave function, and thus retains localisation of the ground state nuclear dynamics along

the bonds. Analysing the RIXS spectrum at Ω = 0.301 eV (Figs 5 and 6), one can see that core-excited wave packet shows a localisation tendency, but that it is still insufficient to drive

the bond selectivity of the final states in RIXS so that the _ψ_1,0 and _ψ_0,1 peaks have comparable intensities. The localisation of the core-excited wave packet is more pronounced for

higher excitation energy Ω = 0.721 eV, manifested as a strong asymmetry of the RIXS intensities _ε_1,0 and _ε_0,1 (see Figs 5 and 6). DYNAMICS OF WAVE FUNCTION COLLAPSE Different

orientations of the initial vibrational state _ψ_1,0 localised along the OD bond with respect to the eigenstate of _h__c_ delocalised between the OH and OD bonds (Fig. 1) give an interesting

opportunity to visualise the gradual rotation of _ψ_1,0 in the direction of the valley in the 2_b_2 core-excited state potential in the course of X-ray absorption or RIXS measurements. Such

a rotation has direct relation to the cornerstone quantum mechanical problem - the collapse of the wave function. Indeed, one of the most debated postulates of quantum mechanics is the

collapse of a quantum system from a coherent superposition of several quantum states to a single one at the moment of a measurement. The wave function collapse, often regarded as a sudden

and indeterministic process during a measurement, is related to von Neumann’s projection postulate, and remains one of most controversial magenta aspects of quantum physics30,31. Let us

remind the expression for the absorption cross section of continuous wave (CW) light in the vicinity of the resonance with the _ν__c_ vibrational level of a core-excited state with the

energy , selected by the resonant condition: The initial _ν_0 vibrational level of the ground electronic state is not an eigenstate of the core-excited Hamiltonian, and can thus be written

as a coherent superposition of vibrational states _ν__c_ of the core-excited state According to (7), the absorption probability is defined by the projection of the initial wave packet (8) on

a single eigenstate of the core-excited state. This leads to an erroneous conclusion that there is a sudden collapse from the coherent superposition (8) to a single state. However, Eq. (7)

assumes that the duration of the measurement is much longer than the lifetime of the core-excited state 1/Γ, defined mainly by the Auger decay duration in our case. To describe properly the

wave function collapse, one has to take into account the finite time of the measurement32. The HDO system, investigated above, is a good example to demonstrate the gradual Schrödinger

evolution of the quantum system to a single “collapsed” state during the process of measurement. To describe the dynamics of the wave function collapse, one has to include in the formalism

the interaction of the quantum system with the spectral recording device. Let us consider the dynamics of the absorption of low intense X-ray light propagating along the _z_ axis. Here

E(_t_) = E _E_(_t_) and _k_ = _ω_/_c_. The X-ray field, resonant to the transition frequency, creates a coherent superposition of the ground |_ϕ_0〉 and core-excited |_ϕ__c_〉 electronic

states (see Supplementary Notes 1,2) and the polarisation . The evolution of the nuclear wave packet _χ__c_(_R, t_) in the core-excited state is non-unitary and obeys the Schrödinger

equation with the damping where , D_c_0 = 〈_ϕ_0|D|_ϕ__c_〉 is the electronic transition dipole moment, is the Rabi frequency. The light-induced polarisation changes the intensity of the

field, described by the wave equation within the slowly varying amplitude approximation as (see Supplementary Eq. (S9)) This equation makes the direct link between the absorption coefficient

at the time _t_ and the field-dependent wave packet |Φ(_t_)〉 Let us consider a rectangular pulse with the duration _T_. In this case the wave packet gradually converges to the wave packet

|Φ(∞)〉 (5) for the CW X-ray field, when the interaction time _t_ → ∞ (_T_ = ∞). Here Θ(_T_ − _t_) is the step function. Considering an increasing pulse duration _T_, one can observe the

rotation of the nuclear wave packet (Fig. 7), which is nothing else than the gradual evolution of the initial state to the eigenstate state of the nuclear Hamiltonian of core-excited state.

In the present case, the initial |_ψ_1,0〉 wave function, aligned along the O-D bond, transforms into the eigenstate of the core-excited state nuclear Hamiltonian (“collapsed state”), aligned

along the valley of the core-excited potential. Thus, the wave packet |Φ(_t_)〉 approaches the collapsed state evolutionary, according to the Shrödinger equation with the damping Γ, see Eq.

(10). There is an alternative way to observe the dynamics of the wave function collapse using the stationary RIXS measurement with CW X rays. Indeed, the wave packet in the core-excited

state (5) can be written in the following form (see Supplementary Notes) where . The complex time _τ_ has the physical meaning of a scattering duration33, defined by two characteristic time

values. The first one is the lifetime of the core-excited state 1/Γ, which is responsible for its irreversible decay. The second one 1/|Ω|, originating from the detuning Ω, can be associated

with a dephasing time because the contributions to the integral in Eq. (14) interfere destructively owing to the phase difference Ω(_t_2 − _t_1). The destructive interference quenches the

contributions at times _t_ > _τ__s_ Now we are able to see the gradual evolution of the wave packet |Ψ(∞)〉 from _τ__s_ ≈ 0 (large detuning) to the region of large _τ__s_ = 1/Γ = 8.23 fs

at strict resonance (Fig. 8a). The advantage of this technique is that we can visualise the Schrödinger evolution using the RIXS spectra, as it is depicted on Fig. 8a by the relative

intensity of the O-H peak Here, _σ_O_H_ and _σ_O_D_ denote the _ε_0,1 and _ε_1,0 peak intensities, respectively, in the RIXS spectra with initial vibrational state _ψ_1,0 (Fig. 5). When the

scattering duration is short (large |Ω|), the shape of the wave packet |Ψ(∞)〉 is close to the initial wave function _ψ_1,0 localised on the O-D bond and only the resonance related to the O-D

stretching is observed in the RIXS spectrum (Fig. 5, top panel). When the scattering duration is sufficiently long (small Ω), the wave packet |Ψ(∞)〉 has time to align along the valley of

the PES, so its shape becomes similar to the core-excited state eigenstate . One can see that the evolution of the wave packet |Ψ(∞)〉 in the scattering duration time (Fig. 8a) is rather

similar to the evolution of the wave packet |Φ(_t_)〉 (Fig. 7). The comparison between the time evolution of the wave packet |Ψ(∞)〉 and the relative intensity of the O-H resonance (Fig. 8a)

demonstrates the possibility to observe the dynamics of the wave function collapse by changing the scattering duration, controlled by the detuning in the RIXS experiment (Fig. 8b). We note,

that our simulations do not include the close-lying core-excited state (0.8 eV above the state)26. Due to this circumstance, we exclude in Fig. 8 the region Ω > 0.2 eV, where interference

between the and RIXS channels becomes important. CONCLUSION In the present work we have demonstrated how a gradual collapse, or localisation, of nuclear wave functions of a triatomic

system, HDO, can be regulated by frequency detuning of X-ray scattering experiment. This is shown by a theoretical analysis of quasi-elastic IR-pump X-ray-probe RIXS spectra of the HDO

molecule selectively excited to a few localised vibrational levels in the ground electronic state. The localisation/delocalisation problem in the core-excited states was studied by the

time-dependent wave-packet propagation method. It is shown that the localisation of the ground vibrational state is preserved in the course of the core-excitation in the dissociative state,

while in the case of the bound core-excited state the nuclear wave packet is trapped in the valley of the PES aligned between the O-H and O-D bonds and localisation is broken. In this state,

the narrow “canyon-like” symmetric potential overcomes the “localising” role of the kinetic energy operator, and the nuclear wave packet is confined along the valley of the potential. We

show that the degree of the delocalisation in the state decreases when the probe X-ray photon is tuned in resonance with higher vibrational levels of the core-excited state (Ω ≥ 0.300 eV).

The studied isotopomer HDO is thus found to be a good showcase system to examine the gradual evolution of the nuclear wave function to a single eigenstate of the nuclear Hamiltonian in a

core-excited state, thus featuring a gradual rather than instantaneous collapse. We described two schemes of possible experimental observation of the collapse phenomena – using short X-ray

free-electron laser pulses of controlled duration and by controlling the detuning from the resonance using a CW X-ray synchrotron source. The possibility of using the pump-probe RIXS

technique to dynamically control the degree of delocalisation of vibrations, here demonstrated for HDO, can also be applied to other asymmetric triatomic systems. METHODS The PESs of the

ground and and core-excited states were computed with the MOLCAS 8.0 package34 using the scalar-relativistic restricted-active-space self-consistent-field (RASSCF) method35 followed by

second-order perturbation theory (RASPT2) method36, with the ANO-RCC37 basis set. Details of the RASPT2 calculations can be found in our previous study of H2O26. All wave packet simulations

were performed employing the eSPec program38 using nuclear Hamiltonian written in the valence coordinate representation39. Here, the label _i_ = 0, _c_ denotes the ground and core-excited

electronic states, respectively, _R_1 and _R_2 are the lengths of the O-H and O-D bonds, the bond angle _θ_ is here assumed constant in our model and equal to the equilibrium geometry of H2O

_θ_ = 104.21° 26,27, is the potential energy with respect to the bottom of the potential energy surface _E__i_(_R_1, _R_2). ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE: Ignatova, N. _et

al_. Gradual collapse of nuclear wave functions regulated by frequency tuned X-ray scattering. _Sci. Rep._ 7, 43891; doi: 10.1038/srep43891 (2017). PUBLISHER'S NOTE: Springer Nature

remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. REFERENCES * Anderson, P. W. Local moments and localised states. _Rev. Mod. Phys._ 50,

191–201 (1978). Article  CAS  ADS  Google Scholar  * Levitov, L. S. Delocalisation of vibrational modes caused by electric dipole interaction. _Phys. Rev. Lett._ 64, 547–550 (1990). Article

  CAS  ADS  MathSciNet  Google Scholar  * Stockman, M. I., Faleev, S. V. & Bergman, D. J. Localisation versus delocalisation of surface plasmons in nanosystems: Can one state have both

characteristics? _Phys. Rev. Lett._ 87, 167401 (2001). Article  CAS  ADS  Google Scholar  * Plekahnov, V. G. Isotope low-dimensional structures. _Elementary excitations and applications_

p.29 (Springer, Heidelberg, 2012). * Ramasesha, K., De Marco, L., Mandal, A. & Tokmakoff, A. Water vibrations have strongly mixed intra- and intermolecular character. _Nature Chemistry_

5, 935–940 (2013). Article  CAS  ADS  Google Scholar  * Crim, F. F. Bond-Selected Chemistry: Vibrational State Control of Photodissociation and Bimolecular Reaction. _J. Phys. Chem._ 100,

12725–12734 (1996). Article  CAS  Google Scholar  * Zare, R. N. Laser Control of Chemical Reactions. _Science_ 279, 1875–1879 (1998). Article  CAS  ADS  Google Scholar  * Komeda, T., Kim,

Y., Kawai, M., Persson, B. N. J. & Ueba, H. Lateral hopping of molecules induced by excitation of internal vibration mode. _Science_ 295, 2055–2058 (2002). Article  CAS  ADS  Google

Scholar  * Pascual, J. I., Lorente, N., Song, Z., Conrad, H. & Rust, H.-P. Selectivity in vibrationally mediated single-molecule chemistry. _Nature_ 423, 525–528 (2003). Article  CAS 

ADS  Google Scholar  * Metz, R. B., Thoemke, J. D., Pfeiffer, J. M. & Crim, F. F. Selectively breaking either bond in the bimolecular reaction of HOD with hydrogen atoms. _J. Chem.

Phys._ 99, 1744–1751 (1993). Article  CAS  ADS  Google Scholar  * Sinha, A., Hsiao, M. C. & Crim, F. F. Bond-selected bimolecular chemistry: H + HOD (4_v_ _OH_ ) → OD + H2 . _J. Chem.

Phys._ 92, 6333–6335 (1990). Article  CAS  ADS  Google Scholar  * Bronikowski, M. J., Simpson, W. R., Girard, B. & Zare R. N. Bond-specific chemistry: OD:OH product ratios for the

reactions H + HOD(100) and H + HOD(001). _J. Chem. Phys._ 95, 8647–8648 (1991). Article  CAS  ADS  Google Scholar  * Pfeiffer, J. M., Woods III, E., Metz, R. B. & Crim, F. F. Probing the

new bond in the vibrationally controlled bimolecular reaction of O with HOD(4_v_ _OH_ ). _J. Chem. Phys._ 113, 7982–7987 (2000). Article  CAS  ADS  Google Scholar  * Song, H. & Guo, H.

Mode specificity in bond selective reactions F + HOD → HF + OD and DF + OH. _J. Chem. Phys._ 142, 174309 (2015). Article  ADS  Google Scholar  * Nibbering, E., Fidder, H. & Pines E.

ULTRAFAST CHEMISTRY: Using Time-Resolved Vibrational Spectroscopy for Interrogation of Structural Dynamics. _Annu. Rev. Phys. Chem_ 56, 337–67 (2005). Article  CAS  ADS  Google Scholar  *

Asbury, J., Steinel, T., Stromberg, C., Gaffney, K., Piletic, I. & Fayer, M. Hydrogen bond breaking probed with multidimensional stimulated vibrational echo correlation spectroscopy. _J.

Chem. Phys._ 119, 12981–13005 (2003). Article  CAS  ADS  Google Scholar  * Perakis, F. et al. Vibrational Spectroscopy and Dynamics of Water. _Chemical Reviews_ 116 (13), 7590–7607 (2016).

Article  CAS  Google Scholar  * Harada, Y. et al. Selective Probing of the OH or OD Stretch Vibration in Liquid Water Using Resonant Inelastic Soft-X-Ray Scattering. _Phys. Rev. Lett._ 111,

193001 (2013). Article  ADS  Google Scholar  * Pietzsch, A. et al. Snapshots of the Fluctuating Hydrogen Bond Network in Liquid Water on the Sub-Femtosecond Timescale with Vibrational

Resonant Inelastic x-ray Scattering. _Phys. Rev. Lett._ 114, 088302 (2015). Article  CAS  ADS  Google Scholar  * Coheur, P.-F. et al. New water vapor line parameters in the 26000–13000 cm−1

region. _J. Quant. Spectrosc. Radiat. Transfer_ 74, 493–510 (2002). Article  CAS  Google Scholar  * Carleer, M. et al. The near infrared, visible, and near ultraviolet overtone spectrum of

water. _J. Chem. Phys._ 111, 2444–2450 (1999). Article  CAS  ADS  Google Scholar  * Kassi, S., Macko, P., Naumenko, O. & Campargue, A. The absorption spectrum of water near 750 nm by

CW-CRDS: contribution to the search of water dimer absorption. _Phys. Chem. Chem. Phys._ 7, 2460–2467 (2005). Article  CAS  Google Scholar  * Naus, H. et al. Cavity-ring-down spectroscopy on

water vapour in the range 555–604 nm. _J. Mol. Spectrosc._ 205, 117–121 (2001). Article  CAS  ADS  Google Scholar  * Ignatova, N. et al. IR-pump - X-ray-probe spectroscopy of vibrationally

excited molecules, submitted. * Guimarães, F. F. et al. Infrared-x-ray pump-probe spectroscopy of the NO molecule. _Phys. Rev. A_ 72, 012714 (2005). Article  ADS  Google Scholar  * Couto, R.

C. et al. Selective gating to vibrational modes through resonant X-ray scattering. _Nature Communications_ 8, 14165 (2017). Article  CAS  ADS  Google Scholar  * Cruz, V. V. et al. Advanced

study of water molecule using frequency control of nuclear dynamics in resonant X-ray scattering, submitted. * Gel’mukhanov, F. & Ågren, H. Resonant X-ray Raman scattering. _Phys. Rep._

312, 87–330 (1999). Article  ADS  Google Scholar  * Sałek, P., Gel’mukhanov, F. & Ågren, H. Wave-packet dynamics of resonant x-ray Raman scattering: Excitation near the Cl L _II,III_

edge of HCl. _Phys. Rev. A_ 59, 1147–1159 (1999). Article  ADS  Google Scholar  * Bell, J. S. Against ‘measurement’. In _Sixty-two years of uncertainty: historical philosophical and physics

enquiries into the foundations of quantum mechanics_ (ed. Miller, A. I. ) pp. 17–33 (Springer, Berlin, 1979). * Schlosshauer, M. Decoherence, the measurement problem, and interpretations of

quantum mechanics. _Rev. Mod. Phys._ 76, 1267–1305 (2004). Article  ADS  Google Scholar  * Murch, K. W., Weber, S. J., Macklin, C. & Siddiqi, I. Observing single quantum trajectories of

a superconducting quantum bit. _Nature_ 502, 211–214 (2013). Article  CAS  ADS  Google Scholar  * Gel’mukhanov, F., Sałek, P., Privalov, T. & Ågren, H. Duration of X-ray Raman

scattering. _Phys. Rev. A_ 59, 380–389 (1999). Article  ADS  Google Scholar  * Aquilante, F. et al. Molcas 8: New Capabilities for Multiconfigurational Quantum Chemical Calculations across

the Periodic Table. _J. Comput. Chem._ 37, 506–541 (2016). Article  CAS  Google Scholar  * Olsen, J., Jørgensen, P. & Simons, J. Passing the one-billion limit in full

configuration-interaction (FCI) calculations. _Chem. Phys. Lett._ 169, 463–472 (1990). Article  CAS  ADS  Google Scholar  * Malmqvist, P.-Å., Pierloot, K., Shahi, A. R. M., Cramer, C. J.

& Gagliardi, L. The restricted active space followed by second-order perturbation theory method: theory and application to the study of CuO2 and Cu2O2 systems. _J. Chem. Phys._ 128,

204109 (2008). Article  ADS  Google Scholar  * Roos, B. O., Lindh, R., Malmqvist, P.-Å., Veryazov, V. & Widmark, P. O. Main group atoms and dimers studied with a new relativistic ANO

basis set. _J. Phys. Chem. A_ 108, 2851–2858 (2004). Article  CAS  Google Scholar  * Felicíssimo, V. C., Guimarães, F. F., Gel’mukhanov, F., Cesar, A. & Ågren, H. The principles of

infrared-X-ray pump-probe spectroscopy. Applications on proton transfer in core-ionized water dimers. _J. Chem. Phys._ 122, 094319 (2005). Article  ADS  Google Scholar  * Jensen, P.

Hamiltonians for the internal dynamics of triatomic molecules. _J. Chem. Soc., Faraday Trans. 2: Molecular and Chemical Physics_ 84, 1315–1339 (1988). Article  CAS  Google Scholar  Download

references ACKNOWLEDGEMENTS This work was supported by the Swedish Research Council (VR), Russian Science Foundation (Grant No. 16-12-10109), Carl Tryggers foundation, and the Knut and Alice

Wallenberg foundation (Grant No. 2013.0020). NI and AZ acknowledge Russian President’s scholarship, R.C.C and V.V.C. acknowledge the Conselho Nacional de Desenvolvimento Científico e

Tecnológico (CNPq - Brazil), MO acknowledges funding from the Helmholtz Virtual Institute VI419 “Dynamic Pathways in Multidimensional Landscapes”. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS

* Theoretical Chemistry and Biology, Royal Institute of Technology, Stockholm, S-10691, Sweden Nina Ignatova, Vinícius V. Cruz, Rafael C. Couto, Andrey Zimin, Hans Ågren, Victor Kimberg 

& Faris Gel’mukhanov * Institute of Nanotechnology, Spectroscopy and Quantum Chemistry, Siberian Federal University, Krasnoyarsk, 660041, Russia Nina Ignatova, Andrey Zimin, Sergey

Polyutov, Victor Kimberg & Faris Gel’mukhanov * Instituto de Química, Universidade Federal de Goiás, Campus Samambaia, CP 131 CEP, Goiânia-GO, 74001-970, Brazil Rafael C. Couto & 

Freddy F. Guimarães * Department of Physics, Stockholm University, AlbaNova University Center, Stockholm, 10691, Sweden Emelie Ertan & Michael Odelius Authors * Nina Ignatova View author

publications You can also search for this author inPubMed Google Scholar * Vinícius V. Cruz View author publications You can also search for this author inPubMed Google Scholar * Rafael C.

Couto View author publications You can also search for this author inPubMed Google Scholar * Emelie Ertan View author publications You can also search for this author inPubMed Google Scholar

* Andrey Zimin View author publications You can also search for this author inPubMed Google Scholar * Freddy F. Guimarães View author publications You can also search for this author

inPubMed Google Scholar * Sergey Polyutov View author publications You can also search for this author inPubMed Google Scholar * Hans Ågren View author publications You can also search for

this author inPubMed Google Scholar * Victor Kimberg View author publications You can also search for this author inPubMed Google Scholar * Michael Odelius View author publications You can

also search for this author inPubMed Google Scholar * Faris Gel’mukhanov View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS N.I. performed all

nuclear dynamics simulations, prepared the text of manuscript and figures; R.C.C., V.V.C. and A.Z. participated in the results discussion and prepared the text of manuscript; V.V.C. and

F.F.G. developed the software and participated in the theoretical analysis and results discussion; E.E. and M.O. did all electronic structure calculations; V.K., S.P., H.Å., F.G. took main

responsibility for the theoretical modelling and the writing of the paper, in which all authors contributed. All authors reviewed the manuscript. CORRESPONDING AUTHOR Correspondence to

Victor Kimberg. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION (PDF 1669 KB) RIGHTS AND

PERMISSIONS This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s

Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the

license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE

Ignatova, N., Cruz, V., Couto, R. _et al._ Gradual collapse of nuclear wave functions regulated by frequency tuned X-ray scattering. _Sci Rep_ 7, 43891 (2017).

https://doi.org/10.1038/srep43891 Download citation * Received: 18 November 2016 * Accepted: 30 January 2017 * Published: 07 March 2017 * DOI: https://doi.org/10.1038/srep43891 SHARE THIS

ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard

Provided by the Springer Nature SharedIt content-sharing initiative