ABSTRACT The scalability and efficiency of numerical methods on parallel computer architectures is of prime importance as we march towards exascale computing. Classical methods like finite

difference schemes and finite volume methods have inherent roadblocks in their mathematical construction to achieve good scalability. These methods are popularly used to solve the

Navier-Stokes equations for fluid flow simulations. The discontinuous Galerkin family of methods for solving continuum partial differential equations has shown promise in realizing parallel

efficiency and scalability when approaching petascale computations. In this paper an explicit modal discontinuous Galerkin (DG) method utilizing Implicit Large Eddy Simulation (ILES) is

of Re = 1600, which had a normalized RMS error of 3.43 × 10−4 in the dissipation rate for a 603 element mesh. The scalability and performance study of the method was then conducted for a

Reynolds number of 1600 for polynomials orders from _P_ = 2 to _P_ = 6. The highest order polynomial that was tested (_P_ = 6) was found to have the most efficient scalability using both the

MPI and OpenMP implementations. SIMILAR CONTENT BEING VIEWED BY OTHERS AN EFFICIENT PARALLELIZATION TECHNIQUE FOR THE COUPLED PROBLEMS OF FLUID, GAS AND PLASMA MECHANICS IN THE GRID

ENVIRONMENT Article Open access 13 March 2025 A DYNAMIC BLOCK ACTIVATION FRAMEWORK FOR CONTINUUM MODELS Article 17 March 2025 A HIGH-EFFICIENCY DISCRETIZED IMMERSED BOUNDARY METHOD FOR

MOVING BOUNDARIES IN INCOMPRESSIBLE FLOWS Article Open access 30 January 2023 INTRODUCTION Advances in modern computer hardware have enabled numerical computations to reach progressively

larger scales. To handle the challenging and costly simulations, parallel computations have become widespread in both research and production Computational Fluid Dynamics (CFD) and other

Computer-Aided Engineering (CAE) codes. To keep up with the demand for increasingly larger and more complex numerical models, the scalability and efficiency of a parallel implementation for

a numerical discretization is an important factor. One way to improve the parallel efficiency of CFD software is to optimize the underlying code. Examples of these types of optimizations are

the improvement of loop-level parallelism, serial efficiency of the code1, reducing the number of cache misses and optimizing the achievable memory bandwidth2. Another possible path to

improve the parallel efficiency is to consider the numerical method implemented in the software. One promising direction is the application of high-order methods for massively parallel CFD.

In the CFD community, high-order methods are considered to be those which are third order and higher3. Low-order schemes are widely used in CFD, but there are applications for which they are

considered insufficient, including turbulence, aeroacoustics, boundary layer flows, vortical flows, shock-boundary layer interactions and others4. For these types of flows, low-order

methods require extremely small discretization scale lengths to accurately resolve the unsteady vortices over relevant length and time scales. This has led to a large amount of research in

high-order methods aimed at solving physics problems which are not well suited to low-order methods. Outside of this “physics” argument for use of high-order methods, there is the issue of

parallel scalability. Since higher order polynomial approximations require more calculations to be carried out per element, it is expected that the scheme will exhibit a higher efficiency

when higher order polynomials are used. The parallel algorithm requires a finite setup and communication time, which decreases its efficiency below the ideal linear speed-up. This overhead

time depends on the scale of the parallel simulation, i.e. the number of parallel tasks or threads used. Since the higher order polynomials spend a longer time calculating the solution on a

per degree of freedom basis, it is expected that the overhead time would be more negligible in comparison. The objective of this paper is to demonstrate a scalable, parallel, high-order

description of modal Discontinuous Galerkin (DG) elements for supersonic, turbulent boundary layer flows using Runge-Kutta explicit time marching. The spatial discretization scheme

considered in the DG method can be made high-order by increasing the approximation order _P_ of the interpolating polynomial. Polynomial approximations ranging from _P_ = 2 to _P_ = 6 are

compared for a canonical problem of isotropic turbulence to study their parallel efficiency. In addition, the computational cost required to reach the same error as a lower-order polynomial

is considered. This is an important metric to obtain the full picture of the computational cost of the different polynomial orders. Other authors have proposed using operation count instead

of runtime comparisons, and found that for implicit solvers, high-order methods were more efficient than low-order ones5. Parallel scalability is important, but only if the underlying serial

computational cost is not prohibitively expensive to the point where the benefit gained from a better scalability is lost. In addition to the isotropic turbulence, the method was also

validated on a zero-pressure gradient supersonic Mach 2.25 turbulent boundary layer flow over a flat plate. This paper is organized as follows. The next section describes the governing

equations used in the study. Then an overview of the numerical method, including the DG spatial discretization, the numerical fluxes and the time integration is given. The ensuing section

provides the background and results for the isotropic turbulence (Taylor-Green vortex) test case. Following that the results of the parallel scalability studies and performance comparisons

of different polynomial orders are presented. Then, the turbulent boundary layer flow solution for a supersonic flow over a flat plate is documented. Finally the conclusions from these

studies are summarized. GOVERNING EQUATIONS To understand the fluid mechanics, one must appreciate the partial differential equations which govern fluid flow. This section describes these

governing equations as well as other equations involved in this study. COMPRESSIBLE NAVIER-STOKES EQUATIONS For a compressible Newtonian fluid, the multi-dimensional N-S equations in

normalized conservative form can be written as $$\frac{\partial {\boldsymbol{\rho }}}{\partial {\boldsymbol{t}}}+\nabla \cdot ({\boldsymbol{\rho }}v)=0$$ (1) $$\frac{{\rm{\partial

}}({\boldsymbol{\rho }}v)}{{\rm{\partial }}{\boldsymbol{t}}}+{\rm{\nabla }}\cdot ({\boldsymbol{\rho }}v{{\boldsymbol{v}}}^{{\boldsymbol{\top }}}+p{\bf{I}}-\bar{{\boldsymbol{\tau }}})=0$$ (2)

$$\frac{\partial ({\boldsymbol{\rho }}E)}{\partial {\boldsymbol{t}}}+\nabla \cdot [({\boldsymbol{\rho }}E+p){\boldsymbol{v}}-k\nabla T-{\boldsymbol{v}}\cdot \bar{{\boldsymbol{\tau }}}]=0$$

(3) $$\bar{{\boldsymbol{\tau }}}=[\begin{array}{ccc}{\tau }_{xx} & {\tau }_{xy} & {\tau }_{xz}\\ {\tau }_{yx} & {\tau }_{yy} & {\tau }_{yz}\\ {\tau }_{zx} & {\tau }_{zy}

& {\tau }_{zz}\end{array}];{\tau }_{ij}=\mu (\frac{{\rm{\partial }}{v}_{i}}{{\rm{\partial }}{x}_{j}}+\frac{{\rm{\partial }}{v}_{j}}{{\rm{\partial

}}{x}_{i}}-\frac{2}{3}\frac{{\rm{\partial }}{v}_{k}}{{\rm{\partial }}{x}_{k}}{\delta }_{ij});i,j,k=x,y,z$$ (4) $$p=(\gamma -1)[\rho E-\frac{1}{2}\rho {|{\bf{v}}|}^{2}];T=\frac{p}{\rho

R};R=\frac{1}{\gamma {M}^{2}};k=\frac{\mu {c}_{p}}{{\rm{\Pr }}}$$ (5) Here \(\bar{{\boldsymbol{\tau }}}\) denotes the viscous stress tensor which is given by Eq. (4). The term _μ_ in the

viscous stresses is the dynamic viscosity of the fluid and Sutherland’s law is used to define it. The term _k_ denotes the thermal conductivity of the fluid with _T_ being its temperature.

This term comes from the Fourier’s Law of heat conduction. The thermal conductivity is obtained using the dynamic viscosity _μ_, Prandtl number (Pr) and specific heat (_c__p_) of the fluid

given by Eq. (5). The velocity vector is denoted by V, which includes the three components, _u_, _v_ and _w_ in streamwise (_x_), wall normal (_y_) and spanwise (_z_) directions,

respectively. NUMERICAL METHOD DG finite element was first presented by Reed and Hill6 to solve the neutron transport equations. Due to its inherent advantage of solving linear equation

systems on an element-by-element basis, it has become one of the most promising computational technique to solve large equation systems with high parallel efficiency, even allowing the

numerical formulation to approach an “embarrassingly parallel problem”. However, the next challenge was to solve the nonlinear systems of equations such as the hyperbolic conservation laws,

which are prominent in most physical systems. For this, an explicit version of this method was devised7 which employed the use of Runge – Kutta time discretization with a Total Variation

Diminishing in the Means (TVDM) and Total Variation Bounded (TVB) slope limiter. This method was called the RKDG method. This was extended to high order RKDG methods8 which showed _P_ + 1

order of convergence for _P_ order space discretization. The development of DG methods for nonlinear hyperbolic systems occurred rapidly over the past two decades. The improvement of the

computer architecture (for example, the advent of petascale computing machines) combined with the need to solve both hyperbolic and elliptic problems led to the extension of this method to

convection-diffusion type problems. The first study of this form of equations was conducted on hydrodynamic models for semiconductor device simulations9,10. This was further studied for

compressible Navier Stokes equations11 to achieve higher order of accuracy. It involved the simple breakdown of the second order equation into two first order equations with _U_ and _dU_ as

independent variables and then solving the system using the original RKDG method. This method also known as the first Bassi – Rebay (BR1) method11 was further extended to achieve higher

stability. This incorporated the explicit evaluation of the term _dU_ without making it a new variable. This is also known as the second Bassi – Rebay (BR2) method12. There are numerous

other methods13 to tackle these type of equation systems and can also be generalized as the Local Discontinuous Galerkin (LDG) methods14. It should also be noted that different methods have

been implemented on the DG framework. Some of these methods include Spectral DG method and _hp_ – adaptive methods. The first DG spectral method was conducted for elliptic problems15 and

linear hyperbolic problems16. It was further studied for advection diffusion problems, compressible flow and complex geometries17,18,19. Implementation of adaptive methods in DG is straight

forward. This is because there is no inter – element continuity requirement, which allows for simple changes of the element order based on the gradient. Lower orders are achieved by making

the higher order terms zero. This method has been applied to both hyperbolic conservation laws20 and convection diffusion problems21,22. The entire DG framework was implemented in an

in-house code called the Multiscale Ionized Gas (MIG) flow code. This is a FORTRAN 90 modular code, which can be used to solve various problems like plasma drift diffusion equations23,

hypersonic non-equilibrium flow24, magnetohydrodynamic equations25, and subsonic turbulent flow control26. The framework is parallelized via the message passing interface (MPI), which

enables it to perform computations on multiple nodes on conventional supercomputing clusters. The sections ahead, will describe the space and time discretization for the Discontinuous

Galerkin finite element framework, convergence study, implementation of slope limiters, and parallelization of the code. DISCONTINUOUS GALERKIN SPACE DISCRETIZATION To understand the

discretization process for convection – diffusion problems, a generic scalar equation is chosen which can be extended to any equation system. This is given by $$\frac{\partial U}{\partial

t}+\nabla \cdot {\mathop{F}\limits^{\rightharpoonup }}^{inv}(U)-\nabla \cdot {\mathop{F}\limits^{\rightharpoonup }}^{v}(U,\nabla U)=0$$ (6)

$$U({\boldsymbol{x}},0)={U}_{0}({\boldsymbol{x}})$$ (7) Where _U_ denotes the conserved scalar variable, _F__inv_ and _F__v_ denote the inviscid and viscous fluxes respectively and _X_ ∈ 

_Ω_, which is the multidimensional domain. All the boundaries are considered periodic in this section. For an element, the approximate solution _U__h_ (_X_, _t_) is represented by Eq. (8).

$${U}_{h}(x,t)=\mathop{\sum }\limits_{l=0}^{p}{U}_{K}^{l}(t){\phi }_{l}(x)$$ (8) Where subscript _K_ denotes the element, \({U}_{K}^{l}\) denotes the modal degrees of freedom of that

element, _φ__l_ denotes the basis function. Legendre polynomials are chosen as the local basis functions because of their property of L2 – orthogonality, which leads to a diagonal mass

matrix and is beneficial when performing explicit calculations. The list of basis functions for a transformed coordinate system of \(x,y,z\in [-1,1]\) is provided in Table 1. To obtain the

weak form of the equation, the variable _U_ is replaced by _U__h_ and Eq. (6) is multiplied with the basis function _φ__l_. After integration by parts, Eq. (9) is obtained.

$$\begin{array}{c}\frac{d}{dt}{\int }_{K}{U}_{h}\phi (x)\,dx-{\int }_{K}{\mathop{F}\limits^{\rightharpoonup }}^{inv}\cdot \nabla \phi (x)dx+\sum _{e\in \Gamma }{\int

}_{e}{\mathop{F}\limits^{\rightharpoonup }}^{inv}\cdot {\mathop{n}\limits^{\rightharpoonup }}_{e,K}\phi (x)d\Gamma \\ +{\int }_{K}{\mathop{F}\limits^{\rightharpoonup }}^{v}\cdot \nabla \phi

(x)dx-\sum _{e\in \Gamma }{\int }_{e}{\mathop{F}\limits^{\rightharpoonup }}^{v}\cdot {\mathop{n}\limits^{\rightharpoonup }}_{e,K}\phi (x)d\Gamma =0\end{array}$$ (9) In Eq. (9), _n__e_,_K_

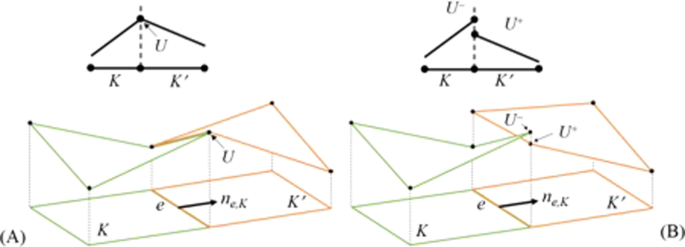
denotes the outward unit normal for the edge _e_ (it can be a face or an edge) of element _K_. Figure 1 shows a representation of these elements. The element boundary space is denoted by Γ.

For the terms in summation, where fluxes are to be evaluated at the element interfaces, the solution _U__h_ is discontinuous and cannot be uniquely defined. Thus, the terms must be replaced

by a locally Lipschitz, consistent, monotone flux to maintain the stability and convergence properties of the scheme with higher order of accuracy8. In Eq. (9),

\({\mathop{F}\limits^{\rightharpoonup }}^{v}\) is a function of both _U_ and ∇_U_, which implies that either ∇_U_ needs to be evaluated as a new variable or treated explicitly. Detailed

descriptions of the numerical integration, fluxes and terms are provided in the next two sections. NUMERICAL INTEGRATION All the integrals can be written in discrete form using Gauss –

Legendre quadrature rules. $${\int }_{K}f(x)dx=jac{\int }_{-1}^{1}f(x^{\prime} )dx^{\prime} =jac\mathop{\sum }\limits_{n=1}^{N}{w}_{n}\,f({x^{\prime} }_{n})dx^{\prime} $$ (10) In Eq. (10)

_jac_ is obtained when transforming from global coordinate system to local coordinate system. Also for all the integrals shown, the basis functions vary with space, while the degrees of

freedom vary in time as shown in Eq. (8). Since the basis functions are already in transformed space \({x^{\prime} }_{n}\) are the Gauss – Legendre points provided in Table 2. One should

note that for multidimensional integration the single summation becomes multiple summations with quadrature points \({x^{\prime} }_{n}\) and weights _w__n_ being obtained via tensor product

of one-dimensional weights and points. INVISCID FLUXES As mentioned earlier, the discontinuity at the element interfaces requires the use of numerical fluxes. There are wide variety of

numerical fluxes which satisfy the locally Lipschitz, monotone and consistent criteria27. However, the present work uses either Godunov flux or Local Lax-Friedrichs flux28. The later, also

known as ENO-LLF, provides better shock capturing with improved accuracy. Although it is more diffusive than the Roe flux and the Godunov flux, its impact on the solution is insignificant

for higher order approximations27. After replacing the inviscid flux in Eq. (9) with the numerical flux \({h}_{e,K}^{inv}\), the first summation term can be written as $$\sum _{e\in \Gamma

}{\int }_{e}{\mathop{F}\limits^{\rightharpoonup }}^{inv}\cdot {\mathop{n}\limits^{\rightharpoonup }}_{e,K}\phi (x)d\Gamma =\sum _{e\in \Gamma }{\int

}_{e}{h}_{e,K}^{inv}({U}_{h}^{-},{U}_{h}^{+})\phi (x)d\Gamma $$ (11) The + and − states of the solution refer to the outside and inside solution along edge _e_ as depicted in Fig. 1. The

Godunov flux is given by $${h}_{e,K}^{inv}({U}^{-},{U}^{+})=\{\begin{array}{c}{{\rm{\min }}}_{{U}^{-}\le U\le {U}^{+}}{F}^{inv}(U),\,{\rm{if}}\,{U}^{-}\le {U}^{+}\\ {{\rm{\max

}}}_{{U}^{+}\le U\le {U}^{-}}{F}^{inv}(U),\,{\rm{otherwise}}\end{array}\}$$ (12) Eq. (12) can be interpreted as, if the neighbouring solution _U_+ is larger than the inside solution _U_−

then choose the minimum flux \(({\rm{\min }}\,[{F}^{inv}({U}^{+}),\,{F}^{inv}({U}^{-})])\) otherwise choose the maximum of the two. The Lax – Friedrichs flux is given by

$${h}_{e,K}^{inv}({U}_{h}^{+},{U}_{h}^{-})=\frac{1}{2}[{\mathop{F}\limits^{\rightharpoonup }}^{inv}({U}_{h}^{-})\cdot {\mathop{n}\limits^{\rightharpoonup

}}_{e,K}+{\mathop{F}\limits^{\rightharpoonup }}^{inv}({U}_{h}^{+})\cdot {\mathop{n}\limits^{\rightharpoonup }}_{e,K}-{\alpha }_{e,K}({U}_{h}^{+}-{U}_{h}^{-})]$$ (13) In Eq. (13) _α__e_,_K_

is obtained by evaluating the largest absolute eigenvalue of the jacobian matrices for the outside and inside elements. $$\begin{array}{c}{\alpha }_{e,K}=\,{\rm{\max

}}[\{abs({{\boldsymbol{\lambda }}}^{+})\},\{abs({{\boldsymbol{\lambda }}}^{-})\}]\\ {{\boldsymbol{\lambda }}}^{+}=eigenvalue\{\frac{\partial F({\bar{U}}^{+})}{\partial U}\cdot {n}_{e,K}\}\\

{{\boldsymbol{\lambda }}}^{-}=eigenvalue\{\frac{\partial F({\bar{U}}^{-})}{\partial U}\cdot {n}_{e,K}\}\end{array}$$ (14) For Euler equations or Navier-Stokes equations the eigenvalues are

_u_ + _a_, _u_ − _a_ and _u_, where _a_ is the speed of sound. In Eq. (14), \(\bar{U}\) is the mean solution of the inside or outside element depending on the _λ_ being evaluated. VISCOUS

FLUXES The viscous terms in Eq. (9) can be modelled in numerous ways. Some of the common methods are LDG14, Bassi – Rebay (BR1 and BR2)11,12, Interior Penalty (IP)29, Baumann – Oden21 etc.

type methods. A detailed comparison and insight on these methods can be found in Arnold _et al_.13. However, for brevity only the LDG, BR1 and BR2 schemes are described here. The viscous

fluxes include ∇_U_ as an unknown which must be evaluated either a priori or along with the equation system. To evaluate ∇_U_, Eq. (6) is first changed to Eq. (15) and Eq. (16).

$$\frac{\partial U}{\partial t}+\nabla \cdot {\mathop{F}\limits^{\rightharpoonup }}^{inv}(U)-\nabla \cdot {\mathop{F}\limits^{\rightharpoonup }}^{v}(U,\theta )=0$$ (15) $$\theta =\nabla U$$

(16) The same procedure as mentioned before is followed and finally equations like Eq. (9) are obtained. $$\begin{array}{c}\frac{d}{dt}{\int }_{K}{U}_{h}\phi (x)dx-{\int

}_{K}{\mathop{F}\limits^{\rightharpoonup }}^{inv}({U}_{h})\cdot \nabla \phi (x)dx+\sum _{e\in \Gamma }{\int }_{e}{\mathop{F}\limits^{\rightharpoonup }}^{inv}({U}_{h})\cdot

{\mathop{n}\limits^{\rightharpoonup }}_{e,K}\phi (x)d\Gamma \\ \,+{\int }_{K}{\mathop{F}\limits^{\rightharpoonup }}^{v}({U}_{h},{\theta }_{h})\cdot \nabla \phi (x)dx-\sum _{e\in \Gamma

}{\int }_{e}{\mathop{F}\limits^{\rightharpoonup }}^{v}({U}_{h},{\theta }_{h})\cdot {\mathop{n}\limits^{\rightharpoonup }}_{e,K}\phi (x)d\Gamma =0\end{array}$$ (17) $${\int }_{K}{\theta

}_{h}\phi (x)dx+{\int }_{K}{U}_{h}\nabla \phi (x)dx-\sum _{e\in \Gamma }{\int }_{e}{U}_{h}{\mathop{n}\limits^{\rightharpoonup }}_{e,K}\phi (x)d\Gamma =0$$ (18) It should be noted that in Eq.

(17) and Eq. (18) _θ__h_ denotes the approximate solution of the auxiliary variable _θ_ as in the definition given in Eq. (8). As discussed earlier, the discontinuous interface requires the

fluxes in the summation terms to be evaluated using a locally Lipschitz, consistent and monotone flux. Therefore the last terms in Eq. (17) and Eq. (18) are represented as Eq. (19) and Eq.

(20). $$\sum _{e\in \Gamma }\,{\int }_{e}{\mathop{F}\limits^{\rightharpoonup }}^{v}({U}_{h},{\theta }_{h})\cdot {\mathop{n}\limits^{\rightharpoonup }}_{e,K}\phi (x)d\Gamma =\sum _{e\in

\Gamma }{\int }_{e}{h}_{e,K}^{v}({U}_{h}^{+},{U}_{h}^{-},{\theta }_{h}^{+},{\theta }_{h}^{-})\cdot {\mathop{n}\limits^{\rightharpoonup }}_{e,K}\phi (x)d\Gamma $$ (19) $$\sum _{e\in \Gamma

}{\int }_{e}{U}_{h}{\mathop{n}\limits^{\rightharpoonup }}_{e,K}\phi (x)\,d\Gamma =\sum _{e\in \Gamma }{\int }_{e}{h}_{e,K}^{\theta }({U}_{h}^{+},{U}_{h}^{-},{\theta }_{h}^{+},{\theta

}_{h}^{-}){\mathop{n}\limits^{\rightharpoonup }}_{e,K}\phi (x)d\Gamma $$ (20) The choice of numerical fluxes \({h}_{e,K}^{v}\) and \({h}_{e,K}^{\theta }\) gives rise to different methods.

LOCAL DISCONTINUOUS GALERKIN METHOD The viscous numerical fluxes for this method can be written as $$\begin{array}{c}h({U}_{h}^{+},{U}_{h}^{-},{\theta }_{h}^{+},{\theta

}_{h}^{-})=\frac{1}{2}[{\mathop{F}\limits^{\rightharpoonup }}^{v}({U}_{h}^{+},{\theta }_{h}^{+})+{\mathop{F}\limits^{\rightharpoonup }}^{v}({U}_{h}^{-},{\theta

}_{h}^{-})+{\boldsymbol{C}}({{\boldsymbol{U}}}^{+}-{{\boldsymbol{U}}}^{-})]\\ {\boldsymbol{C}}=[\begin{array}{cc}{c}_{11} & {c}_{12}\\ -{c}_{12} &

0\end{array}],{\boldsymbol{U}}=\{U,\theta \}\end{array}$$ (21) Using Eq. (21) and since \({\mathop{F}\limits^{\rightharpoonup }}^{v}\) for Eq. (16) is _U_, obtain the expressions for

\({h}_{e,K}^{v}\) and \({h}_{e,K}^{\theta }\) are $$\begin{array}{c}{h}_{e,K}^{v}({U}_{h}^{+},{U}_{h}^{-},{\theta }_{h}^{+},{\theta }_{h}^{-})=\frac{1}{2}[{\mathop{F}\limits^{\rightharpoonup

}}^{v}({U}_{h}^{+},{\theta }_{h}^{+})+{\mathop{F}\limits^{\rightharpoonup }}^{v}({U}_{h}^{-},{\theta }_{h}^{-})]+{c}_{11}({U}_{h}^{+}-{U}_{h}^{-})+{c}_{12}({\theta }_{h}^{+}-{\theta

}_{h}^{-})\\ {h}_{e,K}^{\theta }({U}_{h}^{+},{U}_{h}^{-},{\theta }_{h}^{+},{\theta }_{h}^{-})=\frac{1}{2}({U}_{h}^{+}+{U}_{h}^{-})-{c}_{12}({U}_{h}^{+}-{U}_{h}^{-})\end{array}$$ (22) A

detailed discussion about the choice of constants _c_11 and _c_12, as well as the extension to multidimensional problems have been described by Cockburn and Shu14. BASSI – REBAY METHOD I The

numerical fluxes \({h}_{e,K}^{v}\) and \({h}_{e,K}^{\theta }\) are obtained by averaging the fluxes at the edge of the element and its neighbor. This is provided in Eq. (23) and Eq. (24)

$${h}_{e,K}^{v}({U}_{h}^{+},{U}_{h}^{-},{\theta }_{h}^{+},{\theta }_{h}^{-})=\frac{1}{2}[{\mathop{F}\limits^{\rightharpoonup }}^{v}({U}_{h}^{+},{\theta

}_{h}^{+})+{\mathop{F}\limits^{\rightharpoonup }}^{v}({U}_{h}^{-},{\theta }_{h}^{-})]$$ (23) $${h}_{e,K}^{\theta }({U}_{h}^{+},{U}_{h}^{-},{\theta }_{h}^{+},{\theta

}_{h}^{-})=\frac{1}{2}[{U}_{h}^{+}+{U}_{h}^{-}]$$ (24) The above method describes the BR1 scheme. However due to the method’s deficiencies, such as non – optimal accuracy for purely elliptic

problems, spread stencil and increase in the number of degrees of freedom per element (specially for implicit algorithm)12, lead to the implementation of BR2 scheme. BASSI – REBAY METHOD II

This scheme uses the property that, the evaluation of a solution gradient inside the element is trivial and can be obtained using the gradients of the basis functions. However, for _P_ = 0

elements and at interface discontinuities it is not trivial. To obtain ∇_U_ without adding an extra equation a correction term _R_ is added. This is known as the lift operator. After few

mathematical manipulations12 Eq. (18) can be rewritten as Eq. (25). $${\int }_{K}{\theta }_{h}\phi (x)dx={\int }_{K}\phi (x)\nabla {U}_{h}dx+\sum _{e\in \Gamma }{\int

}_{e}\frac{1}{2}({U}_{h}^{+}+{U}_{h}^{-}){\mathop{n}\limits^{\rightharpoonup }}_{e,K}\phi (x)d\Gamma $$ (25) Thus, we can write _θ__h_ = ∇_U__h_ + _R__h_, where _R__h_ is defined like Eq.

(8) and can be obtained using Eq. (26). $${\int }_{K}{R}_{h}\phi (x)dx=\sum _{e\in \Gamma }{\int }_{e}\frac{1}{2}({U}_{h}^{+}+{U}_{h}^{-}){\mathop{n}\limits^{\rightharpoonup }}_{e,K}\phi

(x)d\Gamma $$ (26) Using the global lifting operator leads to a non-compact stencil which can be avoided by using local lift operators _r__h_. This is defined by $${\int }_{K}{r}_{h}\phi

\,(x)dx={\int }_{e}\frac{1}{2}({U}_{h}^{+}+{U}_{h}^{-}){\mathop{n}\limits^{\rightharpoonup }}_{e,K}\phi (x)d\Gamma ,\,{R}_{h}=\sum _{e\in K}{r}_{h}$$ (27) When performing volume integrals,

global lift operators are used and for element boundary integrals, local lift operators are used. Using this scheme leads to a reduction in the number of degrees of freedom. The information

from immediate neighbors is only required producing a compact stencil. This minimization of information needed from the local region means that the method spends most of its time computing

local integrals, and the communication workload is far smaller than the computational workload. A scenario then arises where most of the calculations in each individual element are

independent and thus almost “embarrassingly parallel” making them amenable to exploit maximum parallel efficiencies. TEMPORAL DISCRETIZATION The choice of time integration depends on the

problem in hand. For transient accuracy, high order time accurate schemes need to be implemented. Problems involving acoustic wave propagation fall in this category. This section will

describe some of the common time integration methods implemented and their advantages and disadvantages. EXPLICIT TIME INTEGRATION To solve the nonlinear hyperbolic conservation laws in a DG

framework an explicit implementation of the method was introduced30. This overcame the issue of solving nonlinear problems on an element by element basis. However, an explicit method is

restricted by the CFL condition. To improve the stability of the scheme a TVDM slope limiter was implemented31. However, this method was only first order accurate in time and the slope

limiter affected the smooth regions of the solution reducing the spatial accuracy. This was finally overcome by using the RKDG method and a modified slope limiter which was second order in

time and maintained the accuracy of the scheme in smooth regions7. This made the scheme stable for CFL ≤ 1/3. To show the explicit time integration Eq. (9) is written in a modified form

given by Eq. (29). $$\frac{d}{dt}{\int }_{K}{U}_{h}(x,{t}^{n})\phi (x)dx={L}_{h}[{U}_{h}(x,{t}^{n})]$$ $$\frac{d}{dt}{\int }_{K}{U}_{K}^{l}({t}^{n}){\phi }_{l}(x){\phi

}_{l}^{T}(x)dx={L}_{h}[{U}_{h}(x,{t}^{n})]$$ $$\frac{d}{dt}[{U}_{K}^{l}({t}^{n})]{\int }_{K}{\phi }_{l}(x){\phi

}_{l}^{T}(x)dx=\frac{d}{dt}[{U}_{K}^{l}({t}^{n})][M]={L}_{h}[{U}_{h}(x,{t}^{n})]$$ (28) $$\frac{d}{dt}[{U}_{K}^{l}({t}^{n})]={L}_{h}[{U}_{h}(x,{t}^{n})]{[M]}^{-1}$$ (29) The mass matrix

[_M_], is diagonal for the present choice of basis functions. For the simple Euler explicit case, Eq. (29) can be written as Eq. (30) which yields first order accuracy in time.

$$[{U}_{K}^{l}({t}^{n+1})-{U}_{K}^{l}({t}^{n})]=(\Delta t){L}_{h}[{U}_{h}(x,{t}^{n})]{[M]}^{-1}$$ (30) Using the second order RKDG method the solution can be more time accurate. This is

described in Eq. (31) $$[{U}_{K}^{l}({t}^{m})]=[{U}_{K}^{l}({t}^{n})]\,+(\Delta t){L}_{h}[{U}_{h}(x,{t}^{n})]{[M]}^{-1}$$ $$[{U}_{K}^{l}({t}^{m+1})]=[{U}_{K}^{l}({t}^{m})]\,+(\Delta

t){L}_{h}[{U}_{h}(x,{t}^{m})]{[M]}^{-1}$$ $$[{U}_{K}^{l}({t}^{n+1})]=\frac{1}{2}([{U}_{K}^{l}({t}^{m+1})+{U}_{K}^{l}({t}^{n})])$$ (31) The RKDG method has been proven to give CFL ≤ 1/3 for

_P_ = 1 and CFL ≤ 1/5 for _P_ = 2 case7. Although RKDG scheme has high parallelizability, being an explicit scheme it has CFL restrictions. IMPLICIT TIME INTEGRATION Since the problems

studied are nonlinear in nature, the Newton’s method is employed to solve for the equation system. The goal here is to find a value iteratively, which would be closest to the actual

solution. Thus, Eq. (29) is written as Eq. (32) for iteration _q_ $$f({U}_{K}^{l}({t}^{n,q}))=\frac{d}{dt}[{U}_{K}^{l}({t}^{n,q})]-{L}_{h}[{U}_{h}(x,{t}^{n,q})]{[M]}^{-1}\approx 0$$ (32) To

get the next time step solution Eq. (32) is discretized in time using the Euler Implicit algorithm to obtain Eq. (33).

$$f({U}_{K}^{l}({t}^{n+1,q}),{U}_{K}^{l}({t}^{n+1,q-1}))=[{U}_{K}^{l}({t}^{n+1,q})-{U}_{K}^{l}({t}^{n+1,q-1})]-\Delta t{L}_{h}[{U}_{h}(x,{t}^{n+1,q})]{[M]}^{-1}$$ (33) Therefore, for _q_ ≥ 

1, Newton’s method can be applied to Eq. (33). It should be noted that when _q_ = 1 in Eq. (33), \({U}_{K}^{l}({t}^{n+1,q-1})={U}_{K}^{l}({t}^{n})\). $$[\frac{\partial

\{f({U}_{K}^{l}({t}^{n+1,q}),{U}_{K}^{l}({t}^{n,q}))\}}{\partial

{U}_{K}^{l}({t}^{n+1,q})}][{U}_{K}^{l}({t}^{n+1,q+1})-{U}_{K}^{l}({t}^{n+1,q})]=-\,f({U}_{K}^{l}({t}^{n+1,q+1}),{U}_{K}^{l}({t}^{n+1,q}))$$ (34) TEST CASES TAYLOR GREEN VORTEX BACKGROUND

This is one of the canonical problems studied for hydrodynamic turbulence. This has been extensively studied in literature to derive empirical and analytical relations in turbulent flow

physics. Early in depth numerical investigation of this problem was done by Orszag32 and Brachet _et al_.33,34. This problem was also studied by Comte-Bellot and Corrsin35 experimentally as

a grid turbulence problem. These studies have become the benchmark for turbulent code validation. Since then, different numerical methods36,37,38,39 have been used to improve or validate

these studies. Results for different Reynolds number, mesh and spatial order of accuracy are compared and investigated. The domain size \(\,\Omega =(2\pi \times 2\pi \times 2\pi )\) with

periodic boundaries on all faces. The initial conditions for this problem are $${u}_{0}=\,\sin (x)\,\cos (y)\,\cos (z),\,{v}_{0}=\,\sin (y)\,\cos (x)\,\cos (z),\,{w}_{0}=0,$$

$${p}_{0}=100+\frac{1}{16}(\cos (2x)+\,\cos (2y))(\cos (2z)+2),{\rho }_{0}=1\,$$ (35) This problem is solved using RKDG method, which involves RK2 time marching and LDG scheme for viscous

flux. Two types of inviscid fluxes are tested, namely Godunov flux and LLF flux. The mesh is uniform in all directions and the DOFs for an _N_3 mesh corresponds to \({N}^{3}\times

{(P+1)}^{3}\). Although the cases can be run at different time step Δ_t_, the solutions are obtained using Δ_t_ = 2.5 × 10−4, to have similar time diffusion. The time step is kept low since

the Godunov flux requires more restrictive time stepping than the LLF flux. The simulations are run till _t_ = 10. Three main parameters are used to study this case. These include the

integrated kinetic energy _E__k_, kinetic energy dissipation rate _ε_ and integrated enstrophy _ζ_. These parameters are given in Eq. (36). For incompressible flows _ε_ and _ζ_ can be

related using the relation given in Eq. (37). It should be noted that evaluation of _ε_ (_ζ_) requires additional degrees of freedom to reach the correct _ε_ levels when compared to _ε_

(_E__k_). $${E}_{k}=\frac{1}{{\rho }_{0}\Omega }{\int }_{\Omega }\rho \frac{{\bf{v}}\cdot {\bf{v}}}{2}d\Omega \,;\,\varepsilon ({E}_{k})=-\,\frac{\partial {E}_{k}}{\partial t};\,\zeta

=\frac{1}{{\rho }_{0}\Omega }{\int }_{\Omega }\rho \frac{{\boldsymbol{\omega }}\cdot {\boldsymbol{\omega }}}{2}d\Omega \,$$ (36) $$\varepsilon (\zeta )=\frac{2\zeta }{{\rm{Re}}}$$ (37)

EFFECT OF REYNOLDS NUMBER To study the effect of Reynolds number (Re), the inviscid flux is kept as Godunov flux and a 603 (1803 degrees of freedom) mesh size is used. The third order

accurate (_P_ = 2) spatial accuracy is chosen. The Reynolds numbers tested are 100, 200, 400, 800 and 1600. The normalized Root Mean Square (RMS) error of \(\varepsilon ({E}_{k})\) in

comparison with DNS data is given in Table 3. The norm error is evaluated using Eq. (38). The timestep is 10−3 sec and data is printed at every 250 steps within the 10 sec interval (_N_ = 

40) for all cases considered for Eq. (38). Except Re = 1600 all the other Reynolds number have results that are comparative to DNS results34. The profile of kinetic energy dissipation rate

_ε_ (_E__k_) is shown in Fig. 2. The dissipation rate is captured accurately by MIG DG ILES. However, in the next section it will be seen that using LLF inviscid flux has slightly more error

than the Godunov flux due to its higher dissipation. $${\rm{Norm}}\,{\rm{RMS}}\,{\rm{Error}}=\sqrt{\frac{{\sum }_{i=1}^{N}{({\varepsilon }_{i}-{\varepsilon }_{{\rm{DNS}}})}^{2}}{N}}$$ (38)

EFFECT OF INVISCID NUMERICAL FLUX To study the effect of numerical fluxes, the Godunov flux and LLF flux are tested for a 603 with _P_ = 2 (1803 DOF), 453 with _P_ = 3 (1803 DOF) and 363

with _P_ = 4 (1803 DOF) mesh sizes. It should be noted that the total DOF is calculated by _N_3 × (_P_ + 1)3. The Reynolds number for the cases here is kept at Re = 1600. The normalized RMS 

error of _ε_ (_E__k_) in comparison with DNS data36 is given in Table 4. The dissipation rate has higher errors when the LLF scheme is used. The greater diffusive nature of LLF flux was also

observed by Beck _et al_.40 when comparing with the Roe scheme. However, the differences are very low as the errors are two orders of magnitude lower than the variable value. It should be

noted that although Godunov flux is more accurate due to its least dissipative nature, it creates larger oscillations which can result in backscatter and also requires a lower time step.

Therefore, although LLF has higher numerical dispersion, it is preferable to be used with slightly higher degrees of freedom. For this problem using around 1.4 times the number of DOF in

each direction matches the solutions for both the fluxes at _P_ = 2. For higher orders, the differences in dissipation rate due to fluxes become negligible. This can be observed in Fig. 3

which depicts the similarity in solutions for the two fluxes at different degrees of freedom for a _P_ = 2 and _P_ = 4 case. EFFECT OF SPATIAL ORDER OF ACCURACY To study the effect of

spatial order of accuracy LLF flux is chosen as the inviscid numerical flux. The problem is studied using orders _P_ = 2, _P_ = 3 and _P_ = 4. The Reynolds number for the cases here is kept

at Re = 1600. All the parameters mentioned in Eq. (36) and Eq. (37) are depicted in Fig. 4. Both _ε_ (_ζ_) and _ε_ (_E__k_) are compared to highlight the differences between ILES results and

DNS results36 as well as to show that, capturing gradients in ILES requires more degrees of freedom. The DNS results are obtained using 13-point DRP scheme with 5123 grid. The solutions

obtained using _P_ = 2 have the largest error for the same DOF. This is a known property which is utilized in turbulent flow simulations using higher order methods. However, as shown in the

previous paragraph, the differences between the fluxes are negligible. To see if the solution converges, higher DOFs were compared to the DNS solution. This is depicted in Fig. 5. Although

_ε_ (_E__k_) has converged to the DNS solution, _ε_ (_ζ_) has not converged yet. This behavior was also observed by DeBonis36 who performed a comparison between 4th, 8th and 12th order

central finite difference schemes with a 13-point DRP scheme (DNS). Similar behavior has been found for DNS41 solutions using DG methods. ENERGY SPECTRUM The kinetic energy spectrum for all

the cases is plotted at _t_ = 10 in Fig. 6. All the curves follow the standard turbulent spectrum of −5/3 slope. The differences between the spectrums for different order polynomials

depicted in Fig. 6(A) are negligible. Note, the effect of flux is not significant on the energy spectrum. FLOW STRUCTURES The instantaneous iso-surface of _Q_ – criterion (positive second

scalar invariant of ∇_u_) colored with velocity magnitude is depicted in Fig. 7. The equation defining _Q_ – criterion is provided in Eq. (39). The data corresponds to the simulation with

_P_ = 3 (DOF = 3203). The coherent structures keep breaking down into smaller structures as the time progresses and finally around _t_ = 9 the flow becomes fully turbulent.

$$Q=\frac{1}{2}[{|\Omega |}^{2}-{|{\bf{S}}|}^{2}];\,\Omega =\frac{1}{2}[\nabla {\bf{v}}-{(\nabla {\bf{v}})}^{T}];\,{\bf{S}}=\frac{1}{2}[\nabla {\bf{v}}+{(\nabla {\bf{v}})}^{T}]$$ (39)

PARALLEL ALGORITHMS To parallelize the MIG code, open MPI was used and the code was tested at the University of Florida high performance computing center. All the tests were run on servers

with Intel E5-2698 v3 processors with the capability to achieve HPL R_max_ of 7.381 × 105 GFlops. The domain was decomposed lexicographically with equal elements in each processor. The

solution time for N-S equations was studied for processor counts of 1, 8, 16, 32, 64, 128, 256 and 512. The parallel performance is studied by solving the time explicit N-S equations for the

Taylor Green vortex isotropic turbulence problem. Two cases were tested with total number of elements, 323 (DOF = 5570560) and 643 (DOF = 44545480). A small number of elements was chosen to

result in a partitioning scheme with significant communication time with respect to the calculations performed. The problem is run for 100 time steps to average out the total time duration

and the all the tests are repeated three times. Figure 8(A) shows that the speedup on a log-log plot is similar for both 323 and 643 cases up to 512 processors. The power data fit to 323

case shows a speedup slope of 0.94 while for 643 it shows 0.95. Based on the data fit the parallel speedup (speedup/ideal) efficiency ranges from 99% for 8 processors to 63% for 512

processors. In Fig. 8(B) the speedup is plotted on a linear scale and the 323 case starts to plateau due to increase in communication time between processors while the 643 case maintains a

linear slope. The processors show different performances for different runs since each case is not run on the same server, which gives a deviation in speedup of up to 5%. The initial higher

speedup for the 323 case compared to the 643 case is within this tolerance limit. Further improvements can be made by using non – blocking instead of blocking MPI send and receive commands.

Also optimizing the domain decomposition can lower communication time. The convergence study is shown in Fig. 9 compares the convergence rates for different orders of polynomials. As evident

from the plots, the higher order methods show the higher convergence rates in agreement with theory. A similar scaling study was performed on the Stampede2 machine at the Texas Advanced

Computing Center. The study was performed on the new Intel Knights Landing architecture. This new hardware promises much better performance through improved memory bandwidth and larger cache

memory per computational core. The Knights Landing processor from intel consists of 36 active tiles each consisting of 2 processing computational cores, hence having a maximum total of 72

processing cores per compute node (Fig. 10). The cores are connected to each other via a two dimensional on-die ring type interconnect which can deliver an aggregate data bandwidth in excess

of 700 gigabytes per second. Each tile containing 2 processing cores shares a 1-megabyte level 2 cache and each compute core has its individual L1 instruction and data caches of 32

kilobytes respectively. Additionally, each core has two vector processing units (VPUs) which allows for very fast floating-point arithmetic operations in parallel. The local nature of the

discontinuous Galerkin method makes it a prime candidate for peak performance on such a vectorized architecture. The fundamental idea behind the Galerkin method is the repeated interpolation

and integral computations within each discretized element. As higher orders of the approximation polynomials are employed the amount of computations being performed on the data increases

exponentially. This ideally suits the kind of architecture possessed by the Knights Landing processor which relies on bringing in chunks of data from higher level, slow memory like

conventional RAM (Random Access Memory) to large caches less frequently and then working on them for longer periods of time. Figures 11 and 12 show the scaling of different orders of

polynomials with numerical accuracy via MPI and OpenMP implementations of the MIG code. It is quite evident from the initial results that the higher order polynomial solutions show the best

promise of parallel scaling. The MPI scaling showed the most dramatic difference between the higher order polynomials. For 100 MPI tasks, the parallel efficiency was 56.6% for _P_ = 2, 79.5%

for _P_ = 4 and 89.0% for _P_ = 6. At 400 MPI tasks, the efficiency fell to 55.7% for _P_ = 2 and 77.4% for _P_ = 4. The OpenMP scaling showed much less of a difference between the three

polynomial orders. The code was run for as many as 64 OpenMP threads on the Knights Landing processor. The highest order tested (_P_ = 6) was marginally more efficient, with the biggest

difference occurring as the number of threads was increased. For 64 threads, the efficiencies were 90.6%, 92.0% and 92.5% for _P_ = 2, 4, and 6, respectively. Overall, the OpenMP efficiency

was greater than the MPI efficiency for equivalent number of threads and tasks. As described earlier, improvements to the MPI implementation and domain decomposition method can improve the

efficiency of the MPI scaling. For scientific or an engineering problems one is interested in the eventual computational cost for a pre-specified level of acceptable error in the

simulations. The combination of a better error convergence rate and superior scaling for higher order methods leads to the evaluation that for reasonably large numerical problem the

computational cost for a specific level of numerical error will be the lowest for higher order methods. MACH 2.25 TURBULENT BOUNDARY LAYER FLOW The scheme described in the Numerical Method

was used to simulate the zero pressure gradient developing turbulent boundary layer at Mach 2.25. This case serves as a good stepping stone for high speed turbulent flow simulations with

higher freestream Mach numbers. The primary challenge in simulating high speed turbulent boundary layers is tied to the large temperature gradient that develops across the boundary layer

caused by the increased influence of viscous dissipation (Spina _et al_. 1994). The freestream conditions and the corresponding range of the momentum thickness-based Reynolds number

\({{\rm{Re}}}_{\theta }={u}_{\infty }\theta /{\nu }_{\infty }\) (based on the freestream viscosity as opposed to the wall viscosity) for the present case are listed in Table 5. In order to

transition the flow to turbulence, the flow is tripped using the method of Schlatter and Örlü (2012) through bypass transition. The tripping body force is in the wall-normal direction, and

it is given by $${f}_{y}=\exp [{[(x-{x}_{0})/{\ell }_{x}]}^{2}-{[y/{\ell }_{y}]}^{2}]g(z,t)$$ (40) The forcing function g(z,t) in Eq. (12) fluctuates as a function of time, and it also

contains a random coefficient which varies in the spanwise direction. The full form of the forcing function is given in Schlatter and Örlü (2012). The computational domain consists of

\({N}_{x}\times {N}_{y}\times {N}_{z}=900\times 64\times 64\) finite elements. Within each element, a modal basis function representation is employed. Quadratic Legendre basis functions (p =

 2) with third-order spatial accuracy are used to interpolate the solution. The grid in the direction normal to the wall is stretched, with the smallest grid spacing (based on the inner wall

units) of Δy+ = 0.5 at the wall. In the spanwise and streamwise directions, the grid is uniform. The boundary conditions for the computational domain are as follows. The laminar boundary

layer solution is used as an inflow boundary condition for the simulation. At the wall, the adiabatic and no-slip boundary conditions are prescribed. In the spanwise direction, symmetric

boundary conditions are enforced. In the streamwise direction, a fringe region is added at the outlet to eliminate reflections from the outlet boundary. This concept has been successfully

used in simulations of turbulent boundary layers in the past, _e.g_. Spalart and Watmuff42. INSTANTANEOUS FLOW FIELD The features of the instantaneous flow are studied in Fig. 13, which

gives the plot of the Q criterion iso-surfaces at the value of Q = 3. The iso-surfaces are colored by the magnitude of the streamwise velocity for a momentum thickness Reynolds number Re_θ_

in the range of 400-1350. The plane below the iso-surfaces represents the flat plate. The flow is tripped and the initial coherent structures quickly break down into a fully turbulent flow.

Asymmetric one-legged hairpin vortices can be observed along with the more typical structures. The flow in Fig. 13 is plotted after both the initial transients disappeared and the mean flow

calculations were carried out, corresponding roughly to three flow-through times (the fluid convecting three times over the streamwise length of the plate). Figure 14 shows the instantaneous

normalized density, normalized streamwise velocity and temperature fields for the flow after two flow-through times. The slice location of the xy-plane corresponds to the center of the

domain in the spanwise direction (z = 1.5 mm and k = 32). The height of the domain in the wall normal direction was found to be sufficient to avoid the reflections from the top boundary

destroying the rest of the solution. A large-scale structure angle of about 45 degrees has been observed for this problem, along with a shallower 10 degree angle for structures closer to the

wall. These angles can also roughly be seen in Fig. 14, despite the lesser level of resolution in this study in comparison with that of Poggie43. The ratio of the freestream temperature to

the wall temperature matches the expected value that can be obtained from a similarity solution of a compressible laminar boundary layer with the adiabatic wall boundary condition. The

growth of the boundary layer is shown in Fig. 14(b) by plotting the boundary layer thickness. Figure 15 shows the fluctuations of the normalized density, normalized streamwise velocity and

temperature fields. The xy-plane slice location is identical to that in Fig. 14. The fluctuations are plotted to offer additional visualization of the turbulent flow field. The high

intensity fluctuations in the boundary layer show packets of fluid which are hotter and lighter than the freestream fluid and which are pushed upward as the boundary layer grows. In Fig. 16,

the flow structures along a wall normal plane are visualized by plotting the velocity contours at the j = 15 plane (y ≈ 6 × 10−2 mm). The vortices are seen to produce low speed streaks

which spread out as the flow becomes fully turbulent. The figure also shows that the fluid in the boundary layer is drawn upward away from the wall. The normalized density profile is plotted

along various spanwise planes and shows the growth of the flow structures as the thickness of the boundary layer increases. MEAN FLOW FIELD Figure 17 shows the skin friction coefficient

plotted against the momentum thickness Reynolds number in the range of Re_θ_ = 700–1200. This range is chosen because the flow has already become fully turbulent. The skin friction decreases

with increasing momentum thickness Reynolds number. Figure 18 plots the mean velocity profiles for the turbulent boundary layer, scaled in both the inner and outer coordinates. For the

inner wall coordinates, the mean velocity is plotted in the van Driest-transformed form26. The transformed velocity is given by $${u}_{VD}^{+}={\int }_{0}^{{u}^{+}}{(\frac{\bar{\rho

}}{{\bar{\rho }}_{w}})}^{1/2}d{u}^{+}$$ (41) The transformed velocity is plotted at downstream locations of Re_θ_ = 800–1100. The streamwise velocity profiles are seen to collapse reasonably

well to the law of the wall in the viscous sublayer (indicated by a solid line in Fig. 18) and the buffer layer (dashed and dotted line in Fig. 18) for this particular case. Figures 19 and

20 give the Reynolds stresses scaled by the wall shear stress. The transformed Reynolds stress is plotted using the inner coordinates in Fig. 19 and the outer coordinates in Fig. 20. The

transformed Reynolds stress is calculated as $${R}_{ij}^{+}=\frac{\bar{\rho }\overline{{u}_{i}^{^{\prime} }{u}_{j}^{^{\prime} }}}{{\tau }_{w}}=\frac{\bar{\rho }\overline{{u}_{i}^{^{\prime}

}{u}_{j}^{^{\prime} }}}{{\bar{\rho }}_{w}{u}_{\tau }^{2}}$$ (42) The Reynolds stresses are plotted at the downstream location of Re_θ_ = 1000, which is not in close proximity to the outflow

boundary but still sufficiently far from the flow tripping region. At this location, the peak value of the normal Reynolds stress occurs at approximately y+ = 11 (y/δ = 0.06). The wall

normal and spanwise components of the Reynolds stress are smaller in comparison, and their peak values occur further away from the wall. After reaching their peak values, all the stresses

decay with increasing y/δ sufficiently far away from the wall. The Reynolds stresses indicate that the majority of the turbulence is produced in the region of y+ = 10–100, fairly close to

the wall. CONCLUSIONS A scalable, parallel, high-fidelity DG formulation was demonstrated for the test case of isotropic turbulent flow for a Taylor-Green vortex problem for Reynolds numbers

ranging between 100–1600. The solutions for the DG ILES method were found to match up well with DNS results up to the Reynolds number of 1600, for which a higher resolution is necessary.

Tests using the Godunov and LLF numerical fluxes showed negligible differences in the dissipation rates for polynomial orders beyond _P_ = 2. The kinetic energy dissipation rate was found to

converge to the DNS solution when a higher number of DOFs was used. A Reynolds number of 1600 was then used to study the performance of different polynomial orders from _P_ = 2 to _P_ = 6

with regard to computational cost and scalability in parallel. The DG method demonstrated the advantages of the higher-order polynomials for parallel implementation. Namely, the higher-order

polynomials showcased superior scalability and performance to achieve a given level of error over the range that was tested. The studies showed that increasing the order of the

interpolating polynomial increased the parallel efficiency using both the MPI and OpenMP parallel implementations. The improvement in parallel efficiency was larger for the MPI

implementation than for the OpenMP implementation. The MPI implementation showed improvements of 20–30% in parallel efficiency between _P_ = 2 and _P_ = 6 depending on the number of tasks.

The difference between _P_ = 2 and _P_ = 6 for the OpenMP implementation was as small as 2%. It is not conclusive from this study whether this behaviour continues into higher order

polynomials or if the efficiency saturates. The same parallel framework was used to compute simulations of the development of a supersonic turbulent boundary layer at Mach 2.25. These

computations employed nearly 33 million spatial degrees of freedom with the solution domain being approximated with quadratic Legendre polynomials. Numerical investigations into the physics

such as the variation of the skin friction coefficient with the Reynolds number and characteristics of the Reynolds stress in the boundary layer are presented. These computations provide

confidence in the capabilities of the numerical framework to perform more investigations to provide deeper physical insights in such phenomena in future work. The parallel scalability and

efficiency of this framework suggests that such large studies can now be attainable in reasonable amount of time. The focus of future studies is exploring polynomial orders beyond _P_ = 6 to

determine the diminishing returns on scaling when continuing to increase the polynomial order. In addition, domain decomposition will be performed by minimizing the surface area over which

separate MPI tasks are required to communicate with each other. These changes should improve the scaling of the MPI implementation, which is not as optimized as the OpenMP scaling at the

present time. DATA AVAILABILITY The data for the presented results is available and will be posted on a public link at APRG website. CHANGE HISTORY * _ 21 JANUARY 2020 An amendment to this

paper has been published and can be accessed via a link at the top of the paper. _ REFERENCES * Behr, M., Pressel, D. M. & Sturek, W. B. Comments on CFD code performance on scalable

architectures. _Comput. Methods Appl. Mech. Engrg_. 263–277 (2000). * Gropp, W. D., Kaushik, D. K., Keyes, D. E. & Smith, B. F. High-performance parallel implicit CFD. _Parallel

Computing_, 337–362 (2001). * Wang, Z. _et al_. High-order CFD methods: current status and perspective. _International Journal for Numerical Methods in Fluids_, 811–845 (2013). Article  ADS

  MathSciNet  Google Scholar  * Deng, X., Mao, M., Tu, G., Zhang, H. & Zhang, Y. High-Order and High Accurate CFD Methods and Their Applications for Complex Grid Problems. _Commun.

Comput. Phys_. 1081–1102 (2012). * Huerta, A., Angeloski, A., Roca, X. & Peraire, J. Efficiency of high-order elements for continuous and discontinuous Galerkin methods. _International

Journal for Numerical Methods in Engineering_, 529–560 (2013). * Reed, W. H., & Hill, T. R. _Triangular mesh methods for the Neutron Transport equation_. Los Alamos, NM: LA-UR-73-479

(1973). * Cockburn, B. & Shu, C. W. The Runge-Kutta local projection P1 - discontinuous Galerkin method for scalar conservation laws. _ESAIM: Mathematical Modelling and Numerical

Analysis_ 25(3), 337–361 (1991). Article  MATH  Google Scholar  * Cockburn, B. & Shu, C. W. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation

laws. II. General framework. _Mathematics of Computation_ 52(186), 411–435 (1989). MathSciNet  MATH  Google Scholar  * Chen, Z. & Cockburn, B. Analysis of a finite element method for

the drift-diffusion semiconductor device equations. _Numerische Mathematik_ 71(1), 1–28 (1995). Article  MathSciNet  MATH  Google Scholar  * Chen, Z. A Finite element method for the quantum

hydrodynamic model for semiconductor devices. _Computers & Mathematics with Applications_ 31(7), 17–26 (1996). Article  MathSciNet  MATH  Google Scholar  * Bassi, F. & Rebay, S. A

high-order accurate discontinuous finite element method for numerical solution of the compressible Navier-Stokes equations. _Journal of Computational Physics_ 131(2), 267–279 (1997). Article

  ADS  MathSciNet  MATH  Google Scholar  * Bassi, F., Crivellini, A., Rebay, S. & Savini, M. Discontinuous Galerkin solution of the Reynolds-averaged Navier-Stokes and k–ω turbulence

model equations. _Computer and Fluids_ 34(4), 507–540 (2005). Article  MATH  Google Scholar  * Arnold, D. N., Brezzi, F., Cockburn, B. & Marini, L. D. Unified analysis of discontinuous

Galerkin methods for elliptic problems. _SIAM Journal on Numerical Analysis_ 39(5), 1749–1779 (2002). Article  MathSciNet  MATH  Google Scholar  * Cockburn, B. & Shu, C. W. The local

discontinuous Galerkin method for time-dependent convection-diffusion systems. _SIAM Journal on Numerical Analysis_ 35(6), 2440–2463 (1998). Article  MathSciNet  MATH  Google Scholar  *

Funaro, D. A multidomain spectral approximation of elliptic equations. _Numerical Methods for Partial Differential Equations_ 2(3), 187–205 (1986). Article  MathSciNet  MATH  Google Scholar

  * Funaro, D. & Gottlieb, D. Convergence results for pseudospectral approximations of hyperbolic systems by a penalty-type boundary treatment. _Mathematics of Computation_ 57(196),

585–596 (1991). Article  ADS  MathSciNet  MATH  Google Scholar  * Hesthaven, J. S. & Gottlieb, D. A stable penalty method for the compressible Navier–Stokes equations: I. Open boundary

conditions. _SIAM Journal on Scientific Computing_ 17(3), 579–612 (1996). Article  MathSciNet  MATH  Google Scholar  * Hesthaven, J. S. A Stable Penalty Method for the Compressible

Navier–Stokes Equations: II. One-Dimensional Domain Decomposition Schemes. _SIAM Journal on Scientific Computing_ 18(3), 658–685 (1997). Article  MathSciNet  MATH  Google Scholar  *

Hesthaven, J. S. A Stable Penalty Method for the Compressible Navier–Stokes Equations: III. Multidimensional Domain Decomposition Schemes. _SIAM Journal on Scientific Computing_ 20(1), 62–93

(1998). Article  MathSciNet  MATH  Google Scholar  * Bey, K. S., Oden, T. J. & Patra, A. A parallel hp-adaptive discontinuous Galerkin method for hyperbolic conservation laws. _Applied

Numerical Mathematics_ 20(4), 321–336 (1996). Article  MathSciNet  MATH  Google Scholar  * Baumann, C. E. & Oden, T. J. A discontinuous hp finite element method for convection—diffusion

problems. _Computer Methods in Applied Mechanics and Engineering_ 175(3–4), 311–341 (1999). Article  ADS  MathSciNet  MATH  Google Scholar  * Houston, P., Schwab, C. & Suli, E.

Discontinuous hp-finite element methods for advection-diffusion-reaction problems. _SIAM Journal on Numerical Analysis_ 39(6), 2133–2163 (2002). Article  MathSciNet  MATH  Google Scholar  *

Roy, S. & Gaitonde, D. Radio Frequency induced ionized collisional flow model for application at atmospheric pressures. _Journal of Applied Physics_ 96(5), 2476–2481 (2004). Article  ADS

  CAS  Google Scholar  * Bhatia, A., Roy, S. & Gosse, R. Effect of dielectric barrier discharge plasma actuators on non-equilibrium hypersonic flows. _Journal of Applied Physics_

116(16), 164904 (2014). Article  ADS  CAS  Google Scholar  * Das Gupta, A. & Roy, S. Discontinuous Galerkin Method for Solving Magnetohydrodynamic Equations. _53rd AIAA Aerospace

Sciences Meeting_. Kissimmee, Florida: AIAA (2015). * Das Gupta, A. & Roy, S. Three-dimensional plasma actuation for faster transition to turbulence. _J. Phys. D: Appl. Phys._ 50, 425201

(2017). Article  CAS  Google Scholar  * Cockburn, B. Discontinuous Galerkin Methods for Convection-Diffusion Problems. In T. J. Barth, & H. Deconinck (Eds), _High-Order Methods for

Computational Physics_ (pp. 69–224). Springer (2001). * Shu, C. W. & Osher, S. Efficient Implementation of Essentially Non-Oscillatory Shock-Capturing Schemes II. _Journal of

Computational Physics_ 83(1), 32–78 (1989). Article  ADS  MathSciNet  MATH  Google Scholar  * Douglas, J. Jr. & Dupont, T. Interior Penalty Procedures for Elliptic and Parabolic Galerkin

Methods. _Computing Methods in Applied Sciences. Lecture Notes in Phys_ 58, 207–216 (1976). Article  ADS  MathSciNet  Google Scholar  * Chavent, G. & Salzano, G. A finite element method

for the 1D water flooding problem with gravity. _Journal of Computational Physics_ 45(3), 307–344 (1982). Article  ADS  MathSciNet  MATH  Google Scholar  * Chavent, G. & Cockburn, B.

The local projection P0 P1 discontinuous-Galerkin finite element method for scalar conservation laws. _ESAIM: Mathematical Modelling and Numerical Analysis_ 23(4), 565–592 (1989). Article 

MATH  Google Scholar  * Orszag, S. A. Numerical simulation of the Taylor-Green vortex. In R. Glowinski, & J. L. Lions, _Computing Methods in Applied Sciences and Engineering Part 2.

Lecture Notes in Computer Science_ (Vol. 11, pp. 50–64). (Berlin, Heidelberg: Springer, 1974). * Brachet, M. E. Direct simulation of three-dimensional turbulence in the Taylor—Green vortex.

_Fluid dynamics research_ 8(1–4), 1–8 (1991). Article  ADS  Google Scholar  * Brachet, M. E. _et al_. Small-scale structure of the Taylor–Green vortex. _Journal of Fluid Mechanics_ 130,

411–452 (1983). Article  ADS  MATH  Google Scholar  * Comte-Bellot, G. & Corrsin, S. Simple Eulerian time correlation of full-and narrow-band velocity signals in grid-generated,

‘isotropic’ turbulence. _Journal of Fluid Mechanics_ 48(2), 273–337 (1971). Article  ADS  Google Scholar  * DeBonis, J. Solutions of the Taylor-Green vortex problem using high-resolution

explicit finite difference methods. _51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition_. Grapewine, Texas (2013). * Fureby, C. & Grinstein,

F. F. Large eddy simulation of high-Reynolds-number free and wall-bounded flows. _Journal of Computational Physics_ 181(1), 68–97 (2002). Article  ADS  MathSciNet  MATH  Google Scholar  *

Gassner, G. J. & Beck, A. D. On the accuracy of high-order discretizations for underresolved turbulence simulations. _Theoretical and Computational Fluid Dynamics_ 27(3–4), 221–237

(2013). Article  ADS  Google Scholar  * Hickel, S., Adams, N. A. & Domaradzki, J. A. An adaptive local deconvolution method for implicit LES. _Journal of Computational Physics_ 213(1),

413–436 (2006). Article  ADS  MathSciNet  MATH  Google Scholar  * Beck, A. D., Gassner, G. J. & Munz, C. D. On the effect of flux functions in discontinuous Galerkin simulations of

underresolved turbulence. In M. Azaïez, H. El Fekih, & J. Hesthaven, _Spectral and High Order Methods for Partial Differential Equations - ICOSAHOM 2012. Lecture Notes in Computational

Science and Engineering_ (Vol. 95, pp. 145–155). Springer, Cham (2014). * Chapelier, J. B., De La Llave Plata, M., Renac, F. & Lamballais, E. Evaluation of a high-order discontinuous

Galerkin method for the DNS of turbulent flows. _Computers & Fluids_ 95, 210–226 (2014). Article  MathSciNet  MATH  Google Scholar  * Spalart, P. R. & Watmuff, J. H. Experimental and

numerical study of a turbulent boundary layer with pressure gradients. _Journal of Fluid Mechanics_ 249, 337–371 (1993). Article  ADS  CAS  Google Scholar  * Poggie, J. Compressible

Turbulent Boundary Layer Simulations: Resolution Effects and Turbulence Modeling. AIAA Paper 2015–1983 (2015). Download references ACKNOWLEDGEMENTS This work used the Extreme Science and

Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. TH and SR acknowledge the support of this work by the AFRL

Computational Sciences Center and the DoD HPCMP’s User Productivity Enhancement, Technology Transfer, and Training (PETTT) Program (Contract No: GS04T09DBC0017 through Engility Corporation).

AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * SurfPlasma Inc, Gainesville, FL, 32601, USA Tomas Houba & Subrata Roy * Applied Physics Research Group, Department of Mechanical and

Aerospace Engineering, University of Florida, Gainesville, FL, 32601, USA Arnob Dasgupta & Subrata Roy * Department of Mechanical Engineering, Indian Institute of Technology Bombay,

Mumbai, 400076, India Shivasubramanian Gopalakrishnan * Vanilla Peak Ct, Vail, AZ, 85641, USA Ryan Gosse Authors * Tomas Houba View author publications You can also search for this author

inPubMed Google Scholar * Arnob Dasgupta View author publications You can also search for this author inPubMed Google Scholar * Shivasubramanian Gopalakrishnan View author publications You

can also search for this author inPubMed Google Scholar * Ryan Gosse View author publications You can also search for this author inPubMed Google Scholar * Subrata Roy View author

publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS R.G. and S.R. conceived the research; T.H. and A.D. implemented the formulation and performed the

numerical experiments; T.H., A.D. and S.G. made the figures; T.H., A.D.G., S.G. and S.R. analyzed the data and wrote the paper; R.G. and S.R. supervised the project. CORRESPONDING AUTHOR

Correspondence to Subrata Roy. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral

with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0

International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the

source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative

Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Houba, T., Dasgupta, A., Gopalakrishnan, S. _et al._ Supersonic turbulent flow

simulation using a scalable parallel modal discontinuous Galerkin numerical method. _Sci Rep_ 9, 14442 (2019). https://doi.org/10.1038/s41598-019-50546-w Download citation * Received: 25

March 2019 * Accepted: 10 September 2019 * Published: 08 October 2019 * DOI: https://doi.org/10.1038/s41598-019-50546-w SHARE THIS ARTICLE Anyone you share the following link with will be

able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing

initiative