ABSTRACT Population structure and spatial heterogeneity are integral components of evolutionary dynamics, in general, and of evolution of cooperation, in particular. Structure can promote

the emergence of cooperation in some populations and suppress it in others. Here, we provide results for weak selection to favor cooperation on regular graphs for any configuration, meaning

any arrangement of cooperators and defectors. Our results extend previous work on fixation probabilities of rare mutants. We find that for any configuration cooperation is never favored for

birth-death (BD) updating. In contrast, for death-birth (DB) updating, we derive a simple, computationally tractable formula for weak selection to favor cooperation when starting from any

that appear in evolutionary trajectories. They also inform the strategic design of initial states in social networks to maximally promote cooperation. We also derive general results that

characterize the interaction of any two strategies, not only cooperation and defection. SIMILAR CONTENT BEING VIEWED BY OTHERS STRATEGY EVOLUTION ON DYNAMIC NETWORKS Article 11 September

2023 TEMPORAL ASSORTMENT OF COOPERATORS IN THE SPATIAL PRISONER’S DILEMMA Article Open access 12 November 2021 GRAPH-STRUCTURED POPULATIONS ELUCIDATE THE ROLE OF DELETERIOUS MUTATIONS IN

LONG-TERM EVOLUTION Article Open access 10 March 2025 INTRODUCTION Mechanisms favoring the emergence of cooperation in social dilemmas have become central focuses of evolutionary game theory

in recent years1,2,3. The dilemma of cooperation, which is characterized by conflicts of interest between individuals and groups, poses a significant challenge to models of evolution since

many of these models predict that cooperation cannot persist in the presence of exploitation by defectors4,5. Yet cooperation is widely observed in nature, and the spatial assortment that

results from population structure is one element that can promote its emergence. In fact, spatial structure is among the most salient determinants of the evolutionary dynamics of a

population6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28. In social dilemmas, population structure can allow for the emergence of localized cooperative clusters that would

normally be outcompeted by defectors in well-mixed populations5,29. However, whether population structure promotes or suppresses cooperation depends on a number of factors such as the update

rule, the type of social dilemma, and the spatial details of the structure (which determine the extent of local competition see refs 28 and 30). For example, cooperation need not be favored

in prisoner’s dilemma interactions under all update rules31,32,33,34. As a consequence, population structure should be considered in the context of the game and the underlying update rule.

In the donation game, a cooperator (_C_) pays a cost, _c_, to provide the opponent with a benefit, _b_, and a defector (_D_) pays no cost and provides no benefit35. Provided _b_ > _c_ 

> 0, this game represents a prisoner’s dilemma since then the unique Nash equilibrium is mutual defection, but both players would prefer the payoff from mutual cooperation36. In addition

to representing one of the most important social dilemmas, the donation game also admits a simple way in which to quantify the efficiency of cooperation: the benefit-to-cost ratio, _b_/_c_.

As this ratio gets larger, the act of cooperation has a more profound effect on the opponent relative to the cost paid by the cooperator. As we shall see, for any configuration of

cooperators and defectors, this ratio is a vital indicator of the evolutionary performance of cooperation. Evolutionary graph theory is a framework for studying evolution in structured

populations30,32,33,37,38,39,40,41,42,43,44,45,46,47. In a graph-structured population, the players reside on the vertices and the edges indicate who is a neighbor of whom. In fact, there

are two types of neighborhoods: (i) those that generate payoffs (“interaction neighborhoods”) and (ii) those that are relevant for evolutionary updating (“dispersal neighborhoods”). Thus, an

evolutionary graph is actually a pair of graphs consisting of an interaction graph and a dispersal graph46,48,49,50. As in many other studies, we assume that the interaction and dispersal

graphs are the same. Other extensions of evolutionary graph theory involve dynamic graphs, which allow the population structure to change during evolutionary updating51,52,53,54. Our focus

is on static, regular graphs of degree _k_, meaning the population size, _N_, is fixed and each player has exactly _k_ neighbors. We study two prominent update rules: birth-death (BD) and

death-birth (DB). In both processes, players are arranged on a graph and accumulate payoffs by interacting with all of their neighbors. This payoff, _π_, is then converted to fitness, _f_,

via _f_ = 1 + _wπ_, where _w_ ≥ 0 is the intensity of selection5. For BD updating5,55, a player is chosen with probability proportional to fitness for reproduction; the offspring of this

player then replaces a random neighbor (who dies). For DB updating32, a player is chosen uniformly at random for death; a neighbor of this player then reproduces (with probability

proportional to fitness) and the offspring fills the vacancy. For each of these processes, we assume that _w_ is small, which means selection is weak. Weak selection is often a biologically

meaningful assumption since an individual might possess many traits (strategies), and each trait makes only a small contribution to fitness5,56,57,58,59,60,61. The effects of selection on

fixation probability have been studied chiefly for states with just a single cooperator since, if the mutation rate is small, the process will reach a monomorphic state prior to the

appearance of another cooperator through mutation62,63. Although small mutation rates are often reasonable from a biological standpoint64,65,66,67, there are several reasons to study

arbitrary cooperator configurations. Even when starting from a state with a single cooperator, an evolutionary process typically transitions subsequently through states with many

cooperators. From a mathematical standpoint, it is therefore natural to ask how selection affects the fixation probability of cooperators from each possible transient state that might arise

in an evolutionary trajectory. Furthermore, many-mutant states could arise through migration68,69,70,71 or environmental mutagenic agents72,73, which, even when rare, might result in several

cooperators entering the population at once. In the case of social networks, cooperators could arise through design rather than mutation or exploration; if cooperators can be strategically

planted within the population, then one can ask how to do so in order to maximize the chances that cooperators take over. Therefore, the effects of selection on arbitrary numbers and

configurations of cooperators and defectors play an important role in the evolutionary dynamics of cooperation. When starting from a configuration with _n_ cooperators and _N_ − _n_

defectors, weak selection is said to favor the evolution of cooperation (on a regular graph) if the probability that cooperators fixate exceeds _n_/_N_ if _w_ is sufficiently small but

positive. This comparison is based on the fact that the fixation probability of _n_ cooperators for neutral drift (_w_ = 0) is _n_/_N_. Ohtsuki _et al_.32 show that, on large regular graphs

of degree _k_, selection favors the fixation of a single, randomly-placed cooperator under DB updating as long as Taylor _et al_.46 show that for finite bi-transitive graphs of size _N_ and

degree _k_, the condition for selection to favor the fixation of a single cooperator is Bi-transitive graphs constitute a subset of regular graphs. In another refinement of the ‘_b_/_c_ >

 _k_’ result, Chen39 shows that, for any _n_ with 0 < _n_ < _N_, selection favors cooperation when starting from a random configuration of _n_ cooperators and _N_ − _n_ defectors on a

regular graph of size _N_ and degree _k_ if and only if Eq. (2) holds. This ratio, which characterizes when selection increases the fixation probability of cooperators, is independent of the

location of the mutants, despite the fact that the probability of fixation itself depends on the location74. As the population size, _N_, gets large, the critical benefit-to-cost ratio of

Eq. (2) approaches _k_, which recovers the result of Ohtsuki _et al_.32. Our goal here is to move beyond Eq. (2) and give an explicit, computationally feasible critical benefit-to-cost ratio

for any configuration of cooperators and defectors on any regular graph. Given the profusion of possible ways to structure a population of a fixed size, it quickly becomes difficult to

determine when a population structure favors the evolution of cooperation. Here, we provide a solution to this problem for BD and DB updating on regular graphs. We show that, for any

configuration of cooperators and defectors, (i) cooperation is never favored for BD updating, and (ii) for DB updating, there exists a simple, explicit critical benefit-to-cost ratio that

characterizes when selection favors the emergence of cooperation. Moreover, if _N_ is the population size and _k_ is the degree of the graph, then the complexity of calculating this ratio is

_O_(_k_2_N_), and, in particular, linear in _N_. Thus, while the calculations of fixation probabilities in structured populations are famously intractable75,76,77, the determination of

whether or not selection increases the probability of fixation, for weak selection, is markedly simpler. In addition to providing a computationally feasible way of determining whether

selection favors cooperation on a particular graph, our results highlight the importance of the initial configuration for the emergence of cooperation. Depending on the graph, adding

additional cooperators to the initial condition can either suppress or promote the evolution of cooperation. A careful choice of configuration of cooperators and defectors can minimize the

critical benefit-to-cost ratio for selection to favor cooperation. If cooperation is not favored by selection in such a strategically chosen initial state, then it cannot be favored under

any other initial configuration. In this sense, there exists a configuration that is most conducive to the evolution of cooperation, which is not apparent from looking at single-cooperator

configurations or random configurations with _n_ cooperators since these initial configurations need not minimize the critical benefit-to-cost ratio. RESULTS CRITICAL BENEFIT-TO-COST RATIOS

Let _ξ_ be a configuration of cooperators and defectors on a fixed regular graph of size _N_ and degree _k_, and let C denote the configuration consisting solely of cooperators. For the

donation game, the probability that cooperators take over the population when starting from state _ξ_ may be viewed as a function of the selection intensity, _ρ__ξ_,C(_w_). We consider here

the following question: when does weak selection increase the probability that cooperators fixate? In other words, when is _ρ__ξ_,C(_w_) > _ρ__ξ_,C(0) for sufficiently small _w_ > 0?

Note that if there are _n_ cooperators in state _ξ_, then _ρ__ξ_,C(0) = _n_/_N_, so this condition is equivalent to _ρ__ξ_,C(_w_) > _n_/_N_ for small _w_ > 0. To answer this question,

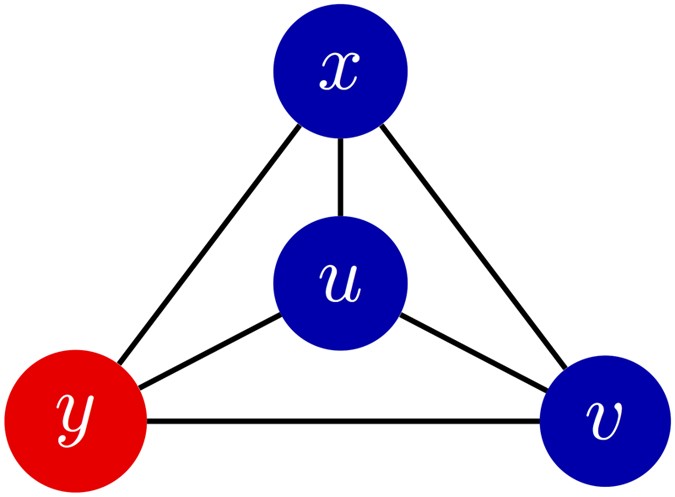
we first need to introduce some notation. If _x_ is a vertex of the graph and _ξ_ is a configuration, then let _f_1(_x, ξ_) and _f_0(_x, ξ_) be the frequencies of cooperators and defectors,

respectively, among the neighbors of the player at vertex _x_. Similarly, let _f_10(_x, ξ_) be the fraction of paths of length two, starting at _x_, that consist of a cooperator followed by

a defector. From these quantities, let which are obtained by averaging these ‘local frequencies’ over all of the players in the population. From these local frequencies, which are

straightforward to calculate (see Fig. 1), we obtain our main result: for small _w_ > 0, _ρ__ξ_,C(_w_) > _ρ__ξ_,C(0) if and only if the benefit-to-cost ratio exceeds the critical value

whenever the denominator is positive (and ∞ otherwise). Since the calculations of , , and are _O_(_kN_) and the calculation of is _O_(_k_2_N_), it follows that the complexity of finding the

critical benefit-to-cost ratio is _O_(_k_2_N_), so it is feasible to calculate even when the population is large. Note also that if is the state obtained by swapping cooperators and

defectors in _ξ_, then both _ξ_ and have the same critical benefit-to-cost ratio. We discuss these ‘conjugate’ states further in our treatment of structure coefficients. When _ξ_ has just a

single cooperator, the ratio of Eq. (7) reduces to that of Eq. (2), which, in particular, does not depend on the location of the cooperator. This property is notable because the fixation

probability itself usually does depend on the location of the cooperator, even on regular graphs74. We show in Methods that one recovers from Eq. (7) the result of Chen39 that Eq. (2) gives

the critical benefit-to-cost ratio for a randomly-chosen configuration with a fixed number of cooperators. For fixed _k_ ≥ 2, the critical benefit-to-cost ratio in Eq. (7) converges

uniformly to _k_ as _N_ → ∞ (see Methods). Therefore, on sufficiently large graphs, the critical ratio is approximated by _k_ for any configuration, regardless of the number of cooperators.

As a result, on large graphs there is less of a distinction between the various transient (non-monomorphic) states in terms of whether or not selection favors the fixation of cooperators. On

smaller graphs, these transient states can behave quite differently from one another. This effect is particularly pronounced on very small social networks in which cooperators can be

strategically planted in the population to ensure that cooperators are favored by selection. STRATEGIC PLACEMENT OF COOPERATORS IN (SMALL) SOCIAL NETWORKS Among the more interesting

consequences of Eq. (7) are its implications for the success of cooperators as a function of the initial configuration. Recall that Eq. (2) gives the critical benefit-to-cost ratio for both

(i) configurations with a single cooperator and (ii) random configurations with a fixed number of cooperators. When cooperators and defectors are configured randomly, this critical ratio is

independent of the number of cooperators, which suggests that the effects of selection cannot be improved by increasing the initial abundance of cooperators. Equation (7), on the other hand,

shows that the initial configuration of cooperators, including their abundance, does affect how selection acts on the population. First of all, there are graphs for which the critical

benefit-to-cost ratio is infinite for configurations with a single cooperator but finite for some configurations with multiple cooperators (see Fig. 2(a)). In contrast, there are graphs for

which this ratio is finite for configurations with a single cooperator but infinite for some states with multiple cooperators (see Fig. 2(b)). Therefore, despite the fact that the critical

ratio for a single mutant is the same as the critical ratio for a random configuration with any fixed number of mutants, the critical ratio does (in general) depend on the number of mutants

present in the configuration. We say that a configuration has isolated cooperators (resp. defectors) if the minimum distance between any two cooperators (resp. defectors) is at least three

steps. Let _N_0 denote the maximum number of isolated strategies that a configuration can carry. (Examples of configurations with isolated cooperators on a graph with _N_0 = 3 are given in

Fig. 3). If a strategy (cooperate or defect) appears only once in a configuration, then that strategy is clearly isolated, so _N_0 ≥ 1. We show in Methods that if _N_ > 2_k_, then

cooperation can be favored for a mixed initial condition with _n_ cooperators whenever 1 ≤ _n_ ≤ _N_0 + 1 or 1 ≤ _N_ − _n_ ≤ _N_0 + 1, and, moreover, these bounds on _n_ are sharp. Stated

differently, under these conditions any configuration with _n_ cooperators has a finite critical benefit-to-cost ratio. Furthermore, if _N_0 ≥ 2, then, for any _n_ with 2 ≤ _n_ ≤ _N_0, there

exists a configuration with _n_ cooperators whose critical ratio is strictly less than the ratio for a single cooperator (Eq. (2)). Such a configuration necessarily has no isolated

strategies since the minimum critical ratio among configurations with an isolated strategy is attained by any state with just a single cooperator. The strategic placement of cooperators and

defectors can therefore produce a critical benefit-to-cost ratio that is less than the ratio for a single cooperator among defectors. In fact, starting from a configuration with just one

cooperator, one can reduce this critical ratio by placing a second cooperator adjacent to the first cooperator (see Methods). If _b_/_c_ lies below Eq. (2) and above Eq. (7), then a

strategically chosen configuration can ensure that the fixation of cooperation is favored by selection even if it is disfavored for any single-cooperator state. This behavior is particularly

pronounced on small social networks, where the critical ratios take on a significant range of values (see Fig. 3), and less apparent on large networks, where the critical ratios are much

closer to the degree of the graph, _k_. Fortunately, on small networks it is easier to directly search for configurations that have small critical benefit-to-cost ratios via Eq. (7).

STRUCTURE COEFFICIENTS Consider now a generic 2 × 2 game whose payoff matrix is The donation game is a special case of this game with _A_ indicating a cooperator and _B_ indicating a

defector. If A denotes the monomorphic state consisting of only _A_-players and if _ξ_ is a configuration of _A_- and _B_-players, then a natural generalization of the question we asked for

the donation game is the following: when is _ρ__ξ_,A(_w_) > _ρ__ξ_,A(0) for sufficiently small _w_ > 0? That is, when does (weak) selection favor the fixation of _A_ when starting from

state _ξ_? For technical reasons, this question is more difficult to answer when the payoff matrix is Eq. (8) instead of that of the donation game. There is, however, an alternative way of

generalizing the critical benefit-to-cost ratio to Eq. (8). When considering the evolutionary success of strategy _A_ based on configurations with only one mutant, another standard measure

is whether the fixation probability of a single _A_-mutant in a _B_-population exceeds that of a single _B_-mutant in an _A_-population [see ref. 34, Eq. 2]. That is, one compares the

fixation probability of _A_ to the fixation probability of _B_ after swapping _A_ and _B_ in the initial state. This interchange of strategies may be defined for any initial state: formally,

if _ξ_ is a configuration of _A_-players and _B_-players, the conjugate of _ξ_, written , is the state obtained by swapping _A_ and _B_ in _ξ_. In other words, the _A_-players in _ξ_ are

the _B_-players in . A natural generalization of this criterion to arbitrary configurations involves comparing the fixation probability of _A_ in _ξ_ to the fixation probability of _B_ in .

Let A and B be the monomorphic states consisting of all _A_-players and all _B_-players, respectively. In this context, our main result is that for all sufficiently small _w_ > 0 if and

only if where, for DB updating, In Methods, we give an explicit formula for the structure coefficient, _σ__ξ_, for BD updating as well. Just as it is for the critical benefit-to-cost ratio

of Eq. (7), the complexity of calculating _σ__ξ_ is _O_(_k_2_N_). In fact, the relationship between and _σ__ξ_ is remarkably straightforward: which, for DB updating, generalizes a result of

Tarnita _et al_.34 to arbitrary configurations. Note that the critical benefit-to-cost ratio increases as _σ__ξ_ decreases. Moreover, unlike the critical benefit-to-cost ratio, _σ__ξ_ is

always finite. Interestingly, both and _σ__ξ_ are invariant under conjugation, meaning they are the same for as they are for _ξ_. For the donation game, Eq. (9) is equivalent to . Of course,

Eq. (9) applies to a broader class of games as well and represents a simple way to compare the success of a strategy (_A_) relative to its alternative (_B_) when selection is weak. In this

sense, Eq. (9) may be thought of as a generalization of the critical benefit-to-cost rule to arbitrary 2 × 2 games. DISCUSSION Selection always opposes the emergence of cooperation for BD

updating, regardless of the configuration of cooperators and defectors (see Methods). This result is consistent with previous studies showing that cooperation cannot be favored under random

configurations32,33,78,79, and it specifies further that cooperation cannot be favored under any configuration. For general 2 × 2 games given by Eq. (8), we show in Methods that one can also

find a simple formula for _σ__ξ_ in the selection condition of Eq. (9) that can be easily calculated for a given graph. Remarkably, for DB updating, both the critical benefit-to-cost ratio

and _σ__ξ_ depend on only local properties of the configuration, which makes these quantities straightforward to calculate. Furthermore, the complexity of calculating both of these

quantities is _O_(_k_2_N_), where _N_ is the size of the population and _k_ is the degree of the graph, so they are computationally feasible even on large graphs. Therefore, our results

provide a tractable way of determining whether or not selection favors cooperation for any configuration. Finding an optimal configuration, which is one that minimizes the critical

benefit-to-cost ratio, seems to be a difficult nonlinear optimization problem. The critical ratio is easily computed for any given configuration, but a graph of size _N_ has 2_N_ possible

configurations, which makes a brute-force search unfeasible for all but small _N_. Our results qualitatively show that both the abundance and the configuration of cooperators can strongly

influence the effects of selection. We leave as an open problem whether it is possible to find a polynomial-time algorithm that produces an optimal configuration on any regular graph.

However, since Eq. (7) is extremely easy to compute for a given configuration, and since small graphs generally exhibit broader variations of critical ratios than do larger graphs (since

uniformly as _N_ → ∞), it is typically feasible to find a state that is more conducive to cooperation than a random configuration. Our analysis of arbitrary configurations uncovers two

important features of the process with DB updating: (i) there exist graphs that suppress the spread of cooperation when starting from a single mutant but promote the spread of cooperation

when starting from configurations with multiple mutants (Fig. 2(a)), and (ii) there exist graphs that promote the spread of cooperation when starting from a single mutant but suppress the

spread of cooperation when starting from configurations with many mutants (Fig. 2(b)). The proper initial configuration is thus a crucial determinant of the evolutionary dynamics, and our

results help to engineer initial conditions that promote the emergence of cooperation on social networks. More importantly, these results provide deeper mathematical insights into the

complicated problem of how selection affects the outcome of an evolutionary process at each point along an evolutionary trajectory. METHODS NOTATION AND GENERAL SETUP In what follows, the

population structure is given by a simple, connected, _k_-regular graph, _G_ = (_V, E_), where _V_ denotes the vertex set of _G_ and _E_ denotes the edge set. For _x, y_ ∈ _V_, we write

_x_~_y_ to indicate that _x_ and _y_ are neighbors, i.e. (_x, y_) ∈ _E_. Throughout the paper, we assume that #_V_ = _N_ is finite and _k_ ≥ 2. The payoff matrix for a generic game with

strategies _A_ and _B_ is A configuration on _G_, denoted _ξ_, is a function from _V_ to {0, 1}. If _ξ_(_x_) = 1, then the player at vertex _x_ is using _A_; otherwise, this player is using

_B_. A special case of Eq. (12) is the donation game, When we are considering the donation game, _ξ_(_x_) = 1 indicates a cooperator at vertex _x_ and _ξ_(_x_) = 0 indicates a defector at

vertex _x_. For any such configuration, _ξ_, the conjugate configuration, , is defined as for _x_ ∈ _V_. In other words, if _ξ_(_x_) = 1 and if _ξ_(_x_) = 0. For any configuration, _ξ_, on a

_k_-regular graph, _G_, and for _x_ ∈ _V_ and _i, j_ ∈ {0, 1}, let For any function, _f_(_x, ξ_), let be the arithmetic average of _f_ with respect to the vertices of _G_. (Fig. 1 in the

main text gives an example of how these quantities are calculated). The arithmetic averages of the functions formed from these local frequencies admit simple probabilistic interpretations:

If a random walk is performed on the graph at a starting point chosen uniformly-at-random, then (resp. ) is the probability that the player at the first step is a cooperator (resp. a

defector), and is the probability that the player at the first step is a cooperator and the player at the second step is a defector. If two independent random walks are performed at the same

starting point, then is the probability of finding a cooperator at step one in the first random walk and a defector at step one in the second random walk. If one chooses an enumeration of

the vertices and represents _G_ by an adjacency matrix, Γ, and _ξ_ as a column vector, then which gives a simple, alternative way to calculate each of and . Let _w_ ≥ 0 be a sufficiently

small selection intensity. The effective payoff of an _i_-player at vertex _x_ in configuration _ξ_, denoted , for the game whose payoffs are given by the generic matrix of Eq. (12), is

defined via The basic measure we use here to define the evolutionary success of a strategy is fixation probability. If _X_ is a strategy (either in {_A, B_} or in {_C, D_}), let X denote the

monomorphic configuration in which every player uses _X_. For any configuration, _ξ_, and a fixed game, we write _ρ__ξ_,X(_w_) to denote the probability that strategy _X_ fixates in the

population given an initial configuration, _ξ_, and selection intensity, _w_. In the following sections, we consider DB and BD updating under weak selection (_w_ ≪ 1). DB UPDATING Under DB

updating, a player is first selected for death uniformly-at-random from the population. The neighbors of this player then compete to reproduce, with probability proportional to fitness

(effective payoff), and the offspring of the reproducing player fills the vacancy. We assume that the strategy of the offspring is inherited from the parent. Therefore, if the player at

vertex _x_ dies when the state of the population is _ξ_, then the probability that this vacancy is filled by an _i_-player is This DB update rule defines a rate-_N_ pure-jump Markov chain,

where _N_ is the size of the population. When _w_ = 0, this process reduces to the voter model such that, at each update time, a random individual adopts the strategy of a random neighbor;

see ref. 80. CRITICAL BENEFIT-TO-COST RATIOS Recall that our goal is to determine when, for any configuration, _ξ, ρ__ξ_,C(_w_) > _ρ__ξ_,C(0) for all sufficiently small _w_ > 0. We

first need some technical lemmas: LEMMA 1. For any configuration, _ξ_, we have the following first-order expansion as _w_ → 0+: _Proof_. By Theorem 3.8 in ref. 39, we have whenever _w_ is

sufficiently small, where By the definition of , Eq. (21), we have so Eq. (22) follows at once from Eq. (23), which completes the proof.□ REMARK 1. The approach of studying fixation

probabilities via first-order expansions, as in Eq. (23), also appears in refs 81, 82, 83. The proof of Eq. (23) in ref. 39, which is valid under mild assumptions on the game dynamics, was

obtained independently and is a particular consequence of a series-like expansion for fixation probabilities. In addition to the identification of the first-order coefficients in selection

strength, _w_, in Eq. (23), the proof of this series-like expansion obtains a bound for the _O_(_w_2) error terms that is explicit in selection strength and the rate to reach monomorphic

configurations of the underlying game dynamics. Therefore, one can deduce an explicit range of selection strengths such that the comparison of fixation probabilities requires only the sign

of . We refer the reader to ref. 60 for a further discussion of selection strengths and their consequences for the comparison of fixation probabilities. In order to compute the voter-model

integrals in Eq. (22), we now turn to coalescing random walks on graphs. Suppose that {_B__x_}_x_∈_V_ is a system of rate-1 coalescing random walks on _G_, where, for each _x_ ∈ _V, B__x_

starts at _x_. These interacting random walks move independently of one another until they meet, and thereafter they move together. The duality between the voter model and these random walks

is given by for each _S_ ⊆ _V, t_ > 0, and strategy configuration, _ξ_. For more information on this duality, including a proof of Eq. (28) and its graphical representation, see §III.4

and §III.6 in ref. 80. Consider now two discrete-time random walks on _G_, and , that start at the same vertex and are independent of {_B__x_}_x_∈_V_. If the common starting point is _x_ ∈ 

_V_, then we write to denote the expectation with respect to this starting point. If the starting point is chosen with respect to the uniform distribution, _π_, then this expectation is

denoted by . The random-walk probabilities, and , are understood in the same way. Since , for example, we will use these random walks to save notation when we compute the local frequencies

of strategy configurations. LEMMA 2. If _f_*0 := _f_10 + _f_00, then, for any configuration, _ξ_, we have _Proof_. For any configuration, _ξ_, and any _t_ > 0, by Theorem 3.1 in ref. 84.

See also Section 3 in that reference for discussions and related results of Eq. (32) in terms of coalescing random walks. Moreover, for any vertices _x_ and _y_ with _x_ ≠ _y_, we have which

is obtained by considering whether the first epoch time of the bivariate Markov chain (_B__x_, _B__y_) occurs before time _t_ or not. Notice that Eq. (33) is false if _x_ = _y_ since the

left-hand side vanishes but the integral term on the right-hand side is, in general, nonzero. This fact needs to be kept in mind when Eq. (33) is applied. Furthermore, using the duality of

Eq. (28), the voter-model integrals in question are We are now in a position to establish Eqs (29),(30),(31). By letting _t_ → ∞ in Eq. (32), we obtain Eq. (29) since vanishes at monomorphic

configurations. Since the graph has no self-loops, we have _X_0 ≠ _X_1 almost surely, thus, by Eq. (33) and the reversibility of the chain under , we have Integrating both sides of this

equation with respect to _t_ over (0, ∞) implies that which, by Eqs (29), (34), and (35), gives Eq. (30). The proof of the one remaining equation, Eq. (31), is similar except that we have to

take into account the fact that when applying Eq. (33). By reversibility, (_Y_1, _X_0, _X_1, _X_2) and (_X_3, _X_2, _X_1, _X_0) have the same distribution under . Therefore, by Eq. (33), it

follows that Integrating both sides of this equation with respect to _t_ over (0, ∞) yields from which we obtain The first and last equalities follow from reversibility, the third equality

from Eq. (40), and the fourth equality from the Markov property of at _n_ = 0, 2 and the fact that since the graph is regular. Eq. (31) then follows from Eqs (29), (30), (36) and (41). □ We

are now in a position to prove the first of our main results: THEOREM 3. In the donation game, for any configuration, _ξ_, we have the following expansion as _w_ → 0+: _Proof_. By Lemma 1,

it suffices to obtain the coefficient of _w_, i.e. the first order term, on the right-hand side of Eq. (22). Since the game under consideration is the donation game, a simple calculation

gives Therefore, Eq. (42) follows from the calculations of Lemma 2, which completes the proof. □ From Theorem 3, we see that, for small _w_ > 0, which gives the critical benefit-to-cost

ratio of Eq. (7). STRUCTURE COEFFICIENTS We now turn to a generalization of the critical benefit-to-cost ratio for arbitrary 2 × 2 games in which the payoff matrix is given by Eq. (12). Our

main result is the following: THEOREM 4. for all sufficiently small _w_ > 0 if and only if _Proof_. By the neutrality of the voter model, we have , thus By the first-order expansion of

Eq. (23), it follows that, for small _w_ > 0, By Eqs (22) and (23) and the neutrality of the voter model, we have and all that remains is to determine the coefficients of _a_ − _d_ and

_b_ − _c_ in Eq. (48). By considering Eq. (48) with the payoff values of the donation game rather than an arbitrary 2 × 2 game, we obtain Thus, using Theorem 3, we see that, when _b_ = −_c_,

and, when _b_ = _c_, from which we obtain Eq. (45). □ In other words, for all sufficiently small _w_ > 0 if and only if where _σ__ξ_ is the structure coefficient given by A simple

calculation shows that and, moreover, when the payoffs for the game are given by Eq. (13), this result reduces to Eq. (44). BD UPDATING Under BD updating, a player is first chosen to

reproduce with probability proportional to fitness (effective payoff). A neighbor of the reproducing player is then chosen uniformly-at-random for death, and the offspring of the reproducing

player fills this vacancy. The rate at which the player at vertex _x_ is replaced by an _i_-player is then The neutral version of this process (_w_ = 0) is a perturbation of the voter

model, and we can use techniques similar to those used for DB updating to establish our main results for BD updating. CRITICAL BENEFIT-TO-COST RATIOS Again, we first need a technical lemma:

LEMMA 5. For _i, j, l_ ∈ {0, 1}, _x_ ∈ _V_, and _ξ_ a configuration of cooperators and defectors, let and form the averages via Eq. (16). For any configuration, _ξ_, we have the following

first-order expansion as _w_ → 0+: _Proof_. The first-order expansion of Eq. (23) is valid under BD updating as well [see ref. 39, Theorem 3.8], except that the function of Eqs (24)–(25) is

defined in terms of the rates for BD updating rather than for DB updating. Writing whenever _ξ_(_y_) = _i_, we find that We then obtain Eq. (57) by applying this calculation to the

first-order expansion of Eq. (23). □ Our main result for BD updating is the following: THEOREM 6. In the donation game, for any configuration, _ξ_, we have the following expansion as _w_ → 

0+: _Proof_. For the donation game, the function of Eq. (58) simplifies to Therefore, by the calculations of Lemma 2, we see that which gives Eq. (59) and completes the proof. □ Since for

each mixed state, _ξ_, it follows that _ρ__ξ_,C(_w_) < _ρ__ξ_,C(0) for all sufficiently small _w_ > 0 whenever _ξ_ is not an absorbing state, so cooperation is always suppressed by

weak selection under BD updating. STRUCTURE COEFFICIENTS Although cooperation is never favored by weak selection under BD updating, we can still write down a condition for selection to favor

strategy _A_ in an arbitrary 2 × 2 game whose payoff matrix is given by Eq. (12): THEOREM 7. for all sufficiently small _w_ > 0 if and only if _Proof_. The same argument given in the

proof of Theorem 4 shows that Eq. (62) is equivalent to Solving for the coefficients of _a_ − _d_ and _b_ − _c_ as in the proof of Theorem 4 gives Eq. (62). □ Written differently, for all

sufficiently small _w_ > 0 if and only if where _σ__ξ_ is the structure coefficient given by STRATEGIC PLACEMENT OF COOPERATORS FOR DB UPDATING We turn now to the consequences of Theorem

3 for DB updating. PROPOSITION 8. Let _k_ ≥ 2 be fixed. In the limit of large population size, _N_ → ∞, the critical benefit-to-cost ratio converges uniformly to _k_ over all _k_-regular

graphs, _G_, of size _N_ and all configurations, _ξ_, on _G_. Proposition 8 follows immediately from the following technical result: LEMMA 9. For fixed _k_ ≥ 2 and for _N_ > 4_k_2 +1 such

that there exists a _k_-regular graph with _N_ vertices, where _G_ ranges over all _k_-regular graphs on _N_ vertices, and, for each _G, ξ_ ranges over all mixed configurations. _Proof_. By

the Cauchy-Schwarz inequality and the reversibility of the random walk, both and are bounded by . Therefore, for any such _G_ and any mixed _ξ_, it follows from Eq. (7) that which completes

the proof. □ PROPOSITION 10. For all configurations obtained by placing an arbitrary (but fixed) number of cooperators uniformly at random, the critical benefit-to cost ratio is given by

Eq. (2) in the main text. _Proof_. Fix a _k_-regular graph with _N_ vertices and, for 0 < _n_ < _N_, let U_n_ denote the uniform distribution on the set of configurations, _ξ_, with

exactly _n_ cooperators. Since U_n_ is independent of the graph geometry, whenever _x_ ≠ _y_. Therefore, by the definitions of _f__i_ and _f__ij_ in Eqs (14) and (15), It follows from Eq.

(7) in the main text that the critical benefit-to-cost ratio for U_n_ is which is independent of _n_ and coincides with Eq. (2). Furthermore, one can use Eqs (69) and (70) to see that the

coefficient of _w_ on the right-hand side of Eq. (42) under the random placement U_n_ is equal to which is consistent with Theorem 1 in ref. 39. □ REMARK 2 (Neutrality of random

configurations).On an arbitrary finite, connected social network, there is still an expansion in _w_ for fixation probabilities that generalizes Eq. (23) [see ref. 39, Theorem 3.8].

Moreover, for the donation game and a configuration given randomly by U_n_, this expansion takes the form where Γ1 and Γ2 are constants that are independent of _n, b_, and _c_. (See the

proof of Lemma 3.1 and the discussion of ‘Bernoulli transforms’ on p. 655–656 in ref. 39. For the linearity of the coefficient of _w_ in _b_ and _c_, see also ref. 34). By Eq. (73), the

benefit-to-cost ratio for any _n_-random configuration is independent of _n_, so random configurations with more cooperators are neither more nor less conducive to cooperation than those

with fewer. For a fixed graph, _G_, let _N_0 be the maximum number of vertices that can be chosen in such a way that no two of these vertices are within two steps of one another. We say that

a subset of vertices with this property is isolated. If the defectors in a configuration lie on isolated vertices, then we say that defectors are isolated. PROPOSITION 11. If _N_ > 2_k_,

then cooperation can be favored for a mixed configuration with _n_ cooperators whenever either 1 ≤ _n_ ≤_N_0 + 1 or 1 ≤ _N_ − _n_ ≤ _N_0 + 1. _Proof_. For any configuration, _ξ_, with _n_

cooperators, we have the inequalities In Eqs (74) and (75), equality is obtained by a configuration with _n_ isolated cooperators. Indeed, and depend on the number of cooperator-defector

paths and the number of cooperator-anything-defector paths in _ξ_, respectively, and each such path is defined by either an edge or two incident edges. On the other hand, at least one of

these inequalities is strict whenever _ξ_ does not have isolated cooperators: If two cooperators are adjacent to one another, then Eq. (74) is strict; if two cooperators are adjacent to the

same defector, then Eq. (75) is strict. In order to establish the proposition, we need to show that since, then, the critical benefit-to-cost ratio of Eq. (7) is finite. Moreover, since Eq.

(76) is invariant under conjugation, it suffices to consider configurations with _n_ cooperators, where . By Eqs (74)–(75), so it suffices to establish the inequality . Suppose, on the other

hand, that _N_ − _N_0 − 2_k_ < 0. By the definition of _N_0, we can then find a configuration with _N_ − 2_k_ + 1 isolated cooperators. Since each of these cooperators has _k_

neighboring defectors, and since none of these defectors have more than one cooperator as a neighbor, we have which contradicts the assumption that _N_ > 2_k_, as desired. □ REMARK 3. The

proof of Proposition 11 shows that whenever _N_ > 2_k_, in fact holds, where _G_ ranges over all _k_-regular graphs on _N_ vertices. This lower bound, max_G__N_0, is sharp, which can be

seen from the graph in Fig. 2(b) since this graph has size 9, is 4-regular, and satisfies _N_0 = 1. PROPOSITION 12. Suppose that _N_ > 2_k_. Let _ξ_ and _ξ_′ be configurations with _n_

and _n_ − 1 cooperators, respectively, such that defectors under both configurations are isolated. Then, _Proof_. Since the defectors in both _ξ_ and _ξ_′ are isolated, we have and it

follows at once that since _k_ ≥ 2, as desired. □ As a consequence of Proposition 12, we see that among the configurations with an isolated strategy (cooperators or defectors), the minimum

critical benefit-to-cost ratio is attained by any configuration with just a single cooperator. PROPOSITION 13. For a _k_-regular graph with _N_ > 2_k_, we have the following: * i if _N_0 

≥ 2, then, for any _n_ with 2 ≤ _n_ ≤ _N_0, there exists a configuration with _n_ cooperators whose critical benefit-to-cost ratio is smaller than that of a random configuration; * ii for

any configuration with exactly two cooperators, such that, furthermore, these two cooperators are neighbors, cooperation can be favored by weak selection. Moreover, the critical

benefit-to-cost ratio for this configuration is smaller than that of a random configuration. _Proof_. By Proposition 12, the critical benefit-to-cost ratio for any configuration with _n_ ≥ 2

isolated cooperators is greater than the critical benefit-to-cost ratio for any configuration with just a single cooperator. Recall now that this ratio for one cooperator is the same as the

ratio for _n_ randomly-placed cooperators39. By Eq. (43), the critical benefit-to-cost ratio for _ξ_ is of the form for some voter-model expectations, N_ξ_ and D_ξ_. Therefore, by a simple

averaging argument, we see that for each _n_ with 2 ≤ _n_ ≤ _N_0, there must exist a configuration with _n_ cooperators whose critical ratio is smaller than that of a random configuration,

Eq. (2), which completes the proof of part 1 of the proposition. Let _ξ_ be a configuration with two cooperators placed at adjacent vertices, _x_ and _y_. If _T_(_x, y_) is the number of

vertices adjacent to both _x_ and _y_, then straightforward calculations give It then follows from the definition of the critical benefit-to-cost ratio that which is smaller than the ratio

for random placement, Eq. (2), because _N_ > 2_k_, which gives part 2. □ EXAMPLES In Figs 4 and 5, we give examples of the relationship between the configuration and the critical

benefit-to-cost ratio on three small graphs. ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE: Chen, Y.-T. _et al_. Fixation Probabilities for Any Configuration of Two Strategies on Regular

Graphs. _Sci. Rep._ 6, 39181; doi: 10.1038/srep39181 (2016). PUBLISHER'S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. REFERENCES * Brosnan, S. F. & Bshary, R. Cooperation and deception: from evolution to mechanisms. Philos. Trans. R. Soc. London, Ser. B 365, 2593–2598 (2010). Article 

PubMed  PubMed Central  Google Scholar  * Nowak, M. A. Five rules for the evolution of cooperation. Science 314, 1560–1563 (2006b). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar

  * Zaggl, M. A. Eleven mechanisms for the evolution of cooperation. J. Inst. Econ. 10, 197–230 (2013). Google Scholar  * Nowak, M. A. Evolutionary Dynamics: Exploring the Equations of Life

(Belknap Press, 2006a). * Nowak, M. A., Sasaki, A., Taylor, C. & Fudenberg, D. Emergence of cooperation and evolutionary stability in finite populations. Nature 428, 646–650 (2004).

Article  ADS  CAS  PubMed  Google Scholar  * Brauchli, K., Killingback, T. & Doebeli, M. Evolution of cooperation in spatially structured populations. J. Theor. Biol. 200, 405–417

(1999). Article  CAS  PubMed  Google Scholar  * Durrett, R. Probability Models for DNA Sequence Evolution (Springer: New York, 2002). Book  MATH  Google Scholar  * Fu, F., Nowak, M. &

Hauert, C. Invasion and expansion of cooperators in lattice populations: prisoner’s dilemma vs. snowdrift games. J. Theor. Biol. 266, 358–366 (2010). Article  MathSciNet  PubMed  PubMed

Central  MATH  Google Scholar  * Helbing, D., Szolnoki, A., Perc, M. & Szabó, G. Punish, but not too hard: how costly punishment spreads in the spatial public goods game. New J. Phys.

12, 083005 (2010). Article  ADS  Google Scholar  * Hutson, V. & Vickers, G. T. Backward and forward traveling waves in evolutionary games. Methods Appl. Anal. 9, 159–176 (2002). Article

  MathSciNet  MATH  Google Scholar  * Hwang, S.-H., Katsoulakis, M. & Rey-Bellet, L. Deterministic equations for stochastic spatial evolutionary games. Theor. Econ. 8, 829–874 (2013).

Article  MathSciNet  MATH  Google Scholar  * Ifti, M., Killingback, T. & Doebeli, M. Effects of neighbourhood size and connectivity on the spatial Continuous Prisoner’s Dilemma. J.

Theor. Biol. 231, 97–106 (2004). Article  MathSciNet  PubMed  MATH  Google Scholar  * Jansen, V. A. A. & van Baalen, M. Altruism through beard chromodynamics. Nature 440, 663–666 (2006).

Article  ADS  CAS  PubMed  Google Scholar  * Kaveh, K., Komarova, N. L. & Kohandel, M. The duality of spatial death-birth and birth-death processes and limitations of the isothermal

theorem. R. Soc. Open Sci. 2, 140465 (2015). Article  ADS  MathSciNet  PubMed  PubMed Central  Google Scholar  * Killingback, T. & Doebeli, M. Spatial evolutionary game theory: hawks and

doves revisited. Proc. R. Soc. B 263, 1135–1144 (1996). Article  ADS  Google Scholar  * Killingback, T. & Doebeli, M. Self-organized criticality in spatial evolutionary game theory. J.

Theor. Biol. 191, 335–340 (1998). Article  CAS  PubMed  Google Scholar  * Komarova, N. L. Spatial stochastic models for cancer initiation and progression. Bull. Math. Biol. 68, 1573–1599

(2006). Article  MathSciNet  PubMed  MATH  Google Scholar  * Lindgren, K. & Nordahl, M. G. Evolutionary dynamics of spatial games. Physica D 75, 292–309 (1994). Article  ADS  MATH 

Google Scholar  * Nowak, M. A. & May, R. M. Evolutionary games and spatial chaos. Nature 359, 826–829 (1992). Article  ADS  Google Scholar  * Nowak, M. A., Tarnita, C. E. & Antal, T.

Evolutionary dynamics in structured populations. Philos. Trans. R. Soc. London, Ser. B 365, 19–30 (2009). Article  Google Scholar  * Perc, M. & Szolnoki, A. Social diversity and

promotion of cooperation in the spatial prisoner’s dilemma game. Phys. Rev. E 77 (2008). * Ranta, E., Lundberg, P. & Kaitala, V. Spatial games in Ecology of Populations 267–299

(Cambridge University Press, 2005). * Roca, C. P., Cuesta, J. A. & Sánchez, A. Evolutionary game theory: temporal and spatial effects beyond replicator dynamics. Phys. Life Rev. 6,

208–249 (2009). Article  ADS  PubMed  Google Scholar  * Schreiber, S. J. & Killingback, T. P. Spatial heterogeneity promotes coexistence of rock–paper–scissors metacommunities. Theor.

Pop. Biol. 86, 1–11 (2013). Article  MATH  Google Scholar  * Szabó, G., Antal, T., Szabó, P. & Droz, M. Spatial evolutionary prisoner’s dilemma game with three strategies and external

constraints. Phys. Rev. E 62, 1095–1103 (2000). Article  ADS  Google Scholar  * Szabó, G. & Hauert, C. Phase transitions and volunteering in spatial public goods games. Phys. Rev. Lett.

89 (2002). * Szolnoki, A. & Perc, M. Reward and cooperation in the spatial public goods game. EPL 92, 38003 (2010). Article  ADS  CAS  Google Scholar  * Van Cleve, J. & Lehmann, L.

Stochastic stability and the evolution of coordination in spatially structured populations. Theor. Pop. Biol. 89, 75–87 (2013). Article  MATH  Google Scholar  * Rand, D. G., Nowak, M. A.,

Fowler, J. H. & Christakis, N. A. Static network structure can stabilize human cooperation. Proc. Natl. Acad. Sci. USA 111, 17093–17098 (2014). Article  ADS  CAS  PubMed  PubMed Central

  Google Scholar  * Débarre, F., Hauert, C. & Doebeli, M. Social evolution in structured populations. Nat. Commun. 5 (2014). * Allen, B. & Nowak, M. A. Games on graphs. EMS Surv.

Math. Sci. 1, 113–151 (2014). Article  MathSciNet  MATH  Google Scholar  * Ohtsuki, H., Hauert, C., Lieberman, E. & Nowak, M. A. A simple rule for the evolution of cooperation on graphs

and social networks. Nature 441, 502–505 (2006). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Ohtsuki, H. & Nowak, M. A. The replicator equation on graphs. J. Theor.

Biol. 243, 86–97 (2006). Article  MathSciNet  PubMed  PubMed Central  MATH  Google Scholar  * Tarnita, C. E., Ohtsuki, H., Antal, T., Fu, F. & Nowak, M. A. Strategy selection in

structured populations. J. Theor. Biol. 259, 570–581 (2009b). Article  MathSciNet  PubMed  MATH  Google Scholar  * Sigmund, K. The Calculus of Selfishness (Princeton University Press, 2010).

* Maynard Smith, J. Evolution and the Theory of Games (Cambridge University Press, 1982). * Broom, M. & Rychtář, J. A general framework for analysing multiplayer games in networks using

territorial interactions as a case study. J. Theor. Biol. 302, 70–80 (2012). Article  MathSciNet  PubMed  MATH  Google Scholar  * Broom, M., Rychtář, J. & Stadler, B. T. Evolutionary

dynamics on graphs - the effect of graph structure and initial placement on mutant spread. J. Stat. Theory Pract. 5, 369–381 (2011). Article  MathSciNet  MATH  Google Scholar  * Chen, Y.-T.

Sharp benefit-to-cost rules for the evolution of cooperation on regular graphs. Ann. Appl. Probab. 23, 637–664 (2013). Article  MathSciNet  MATH  Google Scholar  * Lieberman, E., Hauert, C.

& Nowak, M. A. Evolutionary dynamics on graphs. Nature 433, 312–316 (2005). Article  ADS  CAS  PubMed  Google Scholar  * Maciejewski, W., Fu, F. & Hauert, C. Evolutionary game

dynamics in populations with heterogenous structures. PLoS Comp. Biol. 10, e1003567 (2014). Article  ADS  CAS  Google Scholar  * Santos, F. C., Santos, M. D. & Pacheco, J. M. Social

diversity promotes the emergence of cooperation in public goods games. Nature 454, 213–216 (2008). Article  ADS  CAS  PubMed  Google Scholar  * Shakarian, P., Roos, P. & Johnson, A. A

review of evolutionary graph theory with applications to game theory. Biosystems 107, 66–80 (2012) Article  PubMed  Google Scholar  * Szabó, G. & Fáth, G. Evolutionary games on graphs.

Phys. Rep. 446, 97–216 (2007). Article  ADS  MathSciNet  Google Scholar  * Szolnoki, A., Perc, M. & Szabó, G. Topology-independent impact of noise on cooperation in spatial public goods

games. Phys. Rev. E 80 (2009). * Taylor, P. D., Day, T. & Wild, G. Evolution of cooperation in a finite homogeneous graph. Nature 447, 469–472 (2007). Article  ADS  CAS  PubMed  Google

Scholar  * van Veelen, M., Garcia, J., Rand, D. G. & Nowak, M. A. Direct reciprocity in structured populations. Proc. Natl. Acad. Sci. USA 109, 9929–9934 (2012). Article  ADS  CAS 

PubMed  PubMed Central  MATH  Google Scholar  * Ohtsuki, H., Nowak, M. A. & Pacheco, J. M. Breaking the symmetry between interaction and replacement in evolutionary dynamics on graphs.

Phys. Rev. Lett. 98 (2007a). * Ohtsuki, H., Pacheco, J. M. & Nowak, M. A. Evolutionary graph theory: Breaking the symmetry between interaction and replacement. J. Theor. Biol. 246,

681–694 (2007b). Article  MathSciNet  PubMed  PubMed Central  MATH  Google Scholar  * Pacheco, J. M., Pinheiro, F. L. & Santos, F. C. Population structure induces a symmetry breaking

favoring the emergence of cooperation. PLoS Comp. Biol. 5, e1000596 (2009). Article  ADS  MathSciNet  CAS  Google Scholar  * Antal, T., Ohtsuki, H., Wakeley, J., Taylor, P. D. & Nowak,

M. A. Evolution of cooperation by phenotypic similarity. Proc. Natl. Acad. Sci. USA 106, 8597–8600 (2009). Article  ADS  CAS  PubMed  MATH  PubMed Central  Google Scholar  * Tarnita, C. E.,

Antal, T., Ohtsuki, H. & Nowak, M. A. Evolutionary dynamics in set structured populations. Proc. Natl. Acad. Sci. USA 106, 8601–8604 (2009a). Article  ADS  CAS  PubMed  PubMed Central 

Google Scholar  * Wardil, L. & Hauert, C. Origin and structure of dynamic cooperative networks. Sci. Rep. 4 (2014). * Wu, B. et al. Evolution of cooperation on stochastic dynamical

networks. PLoS ONE 5, e11187 (2010b). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Moran, P. A. P. Random processes in genetics. Math. Proc. Cambridge Philos. Soc. 54, 60–71

(1958). Article  ADS  MathSciNet  MATH  Google Scholar  * Akashi, H., Osada, N. & Ohta, T. Weak selection and protein evolution. Genetics 192, 15–31 (2012). Article  CAS  PubMed  PubMed

Central  Google Scholar  * Fu, F., Wang, L., Nowak, M. A. & Hauert, C. Evolutionary dynamics on graphs: efficient method for weak selection. Phys. Rev. E 79 (2009). * Mullon, C. &

Lehmann, L. The robustness of the weak selection approximation for the evolution of altruism against strong selection. J. Evol. Biol. 27, 2272–2282 (2014). Article  CAS  PubMed  Google

Scholar  * Wild, G. & Traulsen, A. The different limits of weak selection and the evolutionary dynamics of finite populations. J. Theor. Biol. 247, 382–390 (2007). Article  MathSciNet 

PubMed  MATH  Google Scholar  * Wu, B., Altrock, P. M., Wang, L. & Traulsen, A. Universality of weak selection. Phys. Rev. E 82 (2010a). * Wu, B., García, J., Hauert, C. & Traulsen,

A. Extrapolating weak selection in evolutionary games. PLoS Comp. Biol. 9, e1003381 (2013). Article  ADS  CAS  Google Scholar  * Fudenberg, D. & Imhof, L. A. Imitation processes with

small mutations. J. Econ. Theory 131, 251–262 (2006). Article  MathSciNet  MATH  Google Scholar  * Wu, B., Gokhale, C. S., Wang, L. & Traulsen, A. How small are small mutation rates? J.

Math. Biol. 64, 803–827 (2011). Article  MathSciNet  PubMed  MATH  Google Scholar  * Bromham, L. Why do species vary in their rate of molecular evolution? Biol. Lett. 5, 401–404 (2009).

Article  PubMed  PubMed Central  Google Scholar  * Loewe, L. & Hill, W. G. The population genetics of mutations: good, bad and indifferent. Philos. Trans. R. Soc. London, Ser. B 365,

1153–1167 (2010). Article  PubMed  PubMed Central  Google Scholar  * Lynch, M. Evolution of the mutation rate. Trends Genet. 26, 345–352 (2010). Article  CAS  PubMed  PubMed Central  Google

Scholar  * Otto, S. P. & Hastings, I. M. Mutation and selection within the individual in Mutation and Evolution 507–524 (Springer, 1998). * Hauert, C. & Imhof, L. Evolutionary games

in deme structured, finite populations. J. Theor. Biol. 299, 106–112 (2012). Article  MathSciNet  PubMed  MATH  Google Scholar  * Miękisz, J. Evolutionary game theory and population dynamics

in Lecture Notes in Mathematics 269–316 (Springer, 2008) (2008). * Ohtsuki, H. Evolutionary games in Wright’s island model: kin selection meets evolutionary game theory. Evolution 64,

3344–3353 (2010). Article  PubMed  Google Scholar  * Pichugin, Y., Gokhale, C. S., Garcia, J., Traulsen, A. & Rainey, P. B. Modes of migration and multilevel selection in evolutionary

multiplayer games. J. Theor. Biol. 387, 144–153 (2015). Article  MathSciNet  PubMed  MATH  Google Scholar  * Nagao, M., Sugimura, T. & Matsushima, T. Environmental mutagens and

carcinogens. Annu. Rev. Genet. 12, 117–159 (1978). Article  CAS  PubMed  Google Scholar  * Nunney, L. The real war on cancer: the evolutionary dynamics of cancer suppression. Evol. Appl. 6,

11–19 (2012). Article  PubMed  PubMed Central  Google Scholar  * McAvoy, A. & Hauert, C. Structural symmetry in evolutionary games. J. R. Soc. Interface 12, 20150420 (2015). Article 

PubMed  PubMed Central  Google Scholar  * Hindersin, L., Möller, M., Traulsen, A. & Bauer, B. Exact numerical calculation of fixation probability and time on graphs. Biosystems 150,

87–91 (2016). Article  PubMed  Google Scholar  * Ibsen-Jensen, R., Chatterjee, K. & Nowak, M. A. Computational complexity of ecological and evolutionary spatial dynamics. Proc. Natl.

Acad. Sci. USA 112, 15636–15641 (2015). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Voorhees, B. Birth-death fixation probabilities for structured populations. Proc. R. Soc.

A 469, 20120248 (2013). Article  ADS  MathSciNet  MATH  Google Scholar  * Grafen, A. An inclusive fitness analysis of altruism on a cyclical network. J. Evol. Biol. 20, 2278–2283 (2007).

Article  CAS  PubMed  Google Scholar  * Grafen, A. & Archetti, M. Natural selection of altruism in inelastic viscous homogeneous populations. J. Theor. Biol. 252, 694–710 (2008). Article

  MathSciNet  PubMed  MATH  Google Scholar  * Liggett, T. M. Interacting Particle Systems (Springer, 1985). * Rousset, F. A minimal derivation of convergence stability measures. J. Theor.

Biol. 221, 665–668 (2003). Article  PubMed  MATH  Google Scholar  * Lessard, S. & Ladret, V. The probability of fixation of a single mutant in an exchangeable selection model. J. Math.

Biol. 54, 721–744 (2007). Article  MathSciNet  PubMed  MATH  Google Scholar  * Ladret, V. & Lessard, S. Evolutionary game dynamics in a finite asymmetric two-deme population and

emergence of cooperation. J. Theor. Biol. 255, 137–151 (2008). Article  MathSciNet  PubMed  MATH  Google Scholar  * Chen, Y.-T., Choi, J. & Cox, J. T. On the convergence of densities of

finite voter models to the Wright–Fisher diffusion. Ann. Inst. Henri Poincaré Probab. Stat. 52, 286–322 (2016). Article  ADS  MathSciNet  MATH  Google Scholar  * Frucht, R. Graphs of degree

three with a given abstract group. Can. J. Math. 1, 365–378 (1949). Article  MathSciNet  MATH  Google Scholar  Download references ACKNOWLEDGEMENTS This research was supported by the Center

of Mathematical Sciences at Harvard University, the John Templeton Foundation, a grant from B. Wu and Eric Larson, the Natural Sciences and Engineering Research Council of Canada, and the

Office of Naval Research. Part of this research was done while Y.-T.C. visited NCTS Taipei. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Program for Evolutionary Dynamics, Harvard

University, Cambridge, 02138, MA, USA Yu-Ting Chen, Alex McAvoy & Martin A. Nowak * Center of Mathematical Sciences and Applications, Harvard University, Cambridge, 02138, MA, USA

Yu-Ting Chen * Department of Mathematics, University of Tennessee, Knoxville, 37996, TN, USA Yu-Ting Chen * Department of Mathematics, University of British Columbia, 1984 Mathematics Road,

Vancouver, V6T 1Z2, BC, Canada Alex McAvoy * Department of Mathematics, Harvard University, Cambridge, 02138, MA, USA Martin A. Nowak * Department of Organismic and Evolutionary Biology,

Harvard University, Cambridge, 02138, MA, USA Martin A. Nowak Authors * Yu-Ting Chen View author publications You can also search for this author inPubMed Google Scholar * Alex McAvoy View

author publications You can also search for this author inPubMed Google Scholar * Martin A. Nowak View author publications You can also search for this author inPubMed Google Scholar

CONTRIBUTIONS Y.-T.C., A.M. and M.A.N performed the research and wrote and reviewed the manuscript. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial

interests. RIGHTS AND PERMISSIONS This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included

in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain

permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS ARTICLE

CITE THIS ARTICLE Chen, YT., McAvoy, A. & Nowak, M. Fixation Probabilities for Any Configuration of Two Strategies on Regular Graphs. _Sci Rep_ 6, 39181 (2016).

https://doi.org/10.1038/srep39181 Download citation * Received: 16 August 2016 * Accepted: 18 November 2016 * Published: 22 December 2016 * DOI: https://doi.org/10.1038/srep39181 SHARE THIS

ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard

Provided by the Springer Nature SharedIt content-sharing initiative